地图作为信息的载体,是描述地球和研究复杂地理现象的最有效、最直观的工具,它以科学的符号系统、地图投影和综合方法表达复杂地理世界的空间结构和空间关系,是人类文明史上的伟大创想[1-3]。地球曲面和地图平面之间的矛盾构成了地图最基本的矛盾,解决这一矛盾的数学法则构成了地图的数学基础,这是地图最基本的特性之一,是地图科学性和精确性的重要体现。地图所采用的特殊数学法则便是地图投影。
地图投影学也称为数学制图学,是研究将地球椭球面(或球面)描写到地图平面上,建立地图数学基础的一门科学,它在地图制作和应用中起着“基础”和“骨架”作用,是地图编制前首要考虑的问题,同时它又是现代地图学的重要组成部分[4-7]。地图投影是地图的空间数学基础,是地图学的理论基础,是空间信息处理、传输和解译各个阶段必不可少的工具,其相关理论和方法在地图制图[8]、地理信息系统[9-10]、空间分析[11]、遥感制图[12]、大地测量[13]、航海导航[14]等领域中已经得到了广泛的应用。
地图投影的实质在于建立地球椭球面(或球面)与地图平面上的点之间的对应关系。地图投影计算是地图数学基础中的重要组成部分,并且是相当复杂的数学计算。地图投影需要处理涉及参考椭球的各类数学分析问题,从而不可避免地会遇到大量的椭球偏心率幂级数展开、隐函数高阶导数求取、复变函数运算等一系列复杂的符号推导过程。国内外许多著名的地图投影学者在地图投影正反解、地图投影变换、海图投影及变换方面进行了大量深入系统的研究,取得了一批显著的成果[15-36]。
值得注意的是,虽然前人对地图投影中的数学分析问题进行了大量的研究,并取得了丰富的研究成果,但由于历史条件和分析手段的限制,地图投影数学分析问题主要依靠人工推导完成,不仅级数展开式的次数不会很高,而且导出的表达式繁琐冗长,计算效率不高;有时为了计算上的方便采取近似处理,难免会导致一些小的偏差,影响了计算精度;有些算法则包含复杂的迭代计算,理论分析不甚方便;还有些算法表现为适用于特定参考椭球的数值形式,不便于推广应用。因此,地图投影数学分析问题解决得并非完美和理想。
计算机代数(computer algebra)在很多时候又被广义地理解为“符号计算”,成为与所谓“数值计算”相对的概念。计算机代数系统是计算机科学与数学分析和代数推导相结合的产物。计算机代数系统的优越性主要在于它能够进行大规模的代数运算,在一定程度上可以使科学研究和工程技术人员从枯燥烦琐的数学分析和代数推理中解脱出来,从而有效地提高工作效率,完成人工推导难以实现的运算过程,同时其程序化设计可以保证结果的准确性,目前流行的计算机代数系统有Mathematica、Maple、Mathcad等[37]。
近年来,海军工程大学地图投影研究团队和国内外地图投影研究学者,利用具有严格解析意义的计算机代数分析方法,借助计算机代数系统强大的数学分析能力,对地图投影领域中的一些典型数学分析过程进行了系统的研究,推导和建立了一系列理论上更为严密、形式上更为简单、精度上更为精确的地图投影新公式和新算法,实现了地图投影在一些具体数学分析问题上的突破和创新,丰富和完善了地图投影的理论体系。本文从椭球各纬度间正反解符号表达式、不同变形性质地图投影间的直接变换、高斯投影的复变函数表示、斜轴墨卡托投影数学分析、极区海图投影及变换等5个方面,对地图投影计算机代数分析的近期研究成果进行综述分析,以期为国内同行提供参考。
1 椭球各纬度间正反解符号表达式大地纬度、地心纬度、归化纬度、等距离纬度、等角纬度、等面积纬度是在测量和地图学中常见的6种纬度,实际计算中经常会遇到大地纬度和5种辅助纬度间的正反解问题[38]。
地心纬度、归化纬度与大地纬度之间存在明确的正切关系式,文献[39]利用拉格朗日共轭级数将其正反解展开式表示为正弦函数倍角项形式,但限于人工推导仅展至6倍。文献[40]借助计算机代数系统将倍角项扩展至10倍,并将展开式系数统一表示为椭球偏心率的幂级数形式,给出了我国常用大地坐标系下展开式的系数值,精度分析表明,归化纬度展开式的精度优于10-9″,地心纬度展开式的精度优于10-8″,均较传统公式提高3个数量级。文献[41]推导出了以归化纬度、地心纬度解算子午线弧长的展开公式,同时又根据拉格朗日反演定理,得到了由子午线弧长反解归化纬度、地心纬度的直接公式,正反解精度均高于传统基于大地纬度的展开式。
等距离纬度、等角纬度和等面积纬度都是大地纬度的函数,在等距离投影、等角投影和等面积投影表达式中经常用到它们的正解展开式,即将其展开为关于大地纬度的正弦函数倍角形式。这一过程涉及非常复杂的幂级数展开和复合函数高阶导数的求取,以往大都通过人工推导完成,推导过程复杂冗长,通常只能展至sin 8B(B为大地纬度),并且为推导方便采取的某些近似往往导致展开式系数的高阶项存在偏差。反解时由于大地纬度一般表现为这些纬度的隐函数或反函数形式,有的为非常复杂的超越函数,多采用基于正解公式的迭代法,这种方法不但计算效率低,而且最主要的是理论分析不甚方便;另一种方法是直接进行反解变换,即所谓的直接法。文献[22]经过复杂的Lagrange级数展开,文献[42]利用变系数线性插值方法,给出了以上3种纬度反解的直接展开式,但是由于历史条件的限制,其间许多推导过程都由人工完成,不仅展开式项数不高,而且展开式系数是原正解展开式系数的多项式形式,不便于记忆,计算也比较复杂,在实际应用中多以具体的数值形式给出,不便于推广应用。
借助计算机代数分析方法和计算机代数系统,文献[43]对等距离纬度、等角纬度和等面积纬度正解展开式进行了重新推导,发现并纠正了传统正解展开式系数高阶项中存在的偏差;文献[43—46]分别采用幂级数展开法、Hermite插值法、Lagrange级数法、符号迭代法推导出了形式一致、展开式系数完全相同的反解展开式,其中三角函数倍角项展至sin 8B(B为大地纬度),从而相互印证了4种方法的正确性,与传统反解展开式不同的是,反解系数不再是正解展开式系数的多项式形式或具体的数值形式,而是统一表示为椭球偏心率e的幂级数形式,对于不同的椭球,只需将椭球偏心率代入即可得到该椭球下的相关系数,便于推广使用。在此基础上,文献[40]系统推导出了三角函数倍角项展至sin 10B、系数展至e10的等距离纬度、等角纬度和等面积纬度正反解展开式,并给出了我国常用大地坐标系下展开式的系数值,精度分析表明,计算机代数系统下推导出的正反解展开式精度较传统人工导出的展开式最少提高2个数量级,最多提高4个数量级,具体情况如表 1所示。
| 正反解 | 传统人工导出展开式精度/(″) | 计算机代数系统导出展开式精度/(″) | 精度提高数量级 |
| 等距离纬度正解 | 10-5 | 10-7 | 2 |
| 等角纬度正解 | 10-4 | 10-8 | 4 |
| 等面积纬度正解 | 10-4 | 10-8 | 4 |
| 等距离纬度反解 | 10-4 | 10-8 | 4 |
| 等角纬度反解 | 10-4 | 10-8 | 4 |
| 等面积纬度反解 | 10-4 | 10-8 | 4 |
文献[47]对测量和地图学中6种常用纬度进行了系统比较,借助计算机代数系统推导出了常用纬度间的差异极值点及对应差异极值的符号表达式,并将其表示为关于偏心率e的幂级数形式;以CGCS2000椭球为例,对各纬度间的差异进行了数值分析和对比。结果表明,5种辅助纬度与大地纬度的差异极值点均在π/4右侧;地心纬度与大地纬度差异极值最大,归化纬度与大地纬度差异极值最小。
文献[48]利用等距离纬度、等角纬度和等面积纬度这3种纬度和大地纬度间的正反解展开式,导出了它们之间变换的直接展开式,并将式中系数统一表示为椭球偏心率e的幂级数形式并展至e10,解决了不同参考椭球下的变换问题,精度分析表明,直接展开式的计算精度优于10-8″,满足地图投影精密计算的需要。
2 不同变形性质地图投影间的直接变换地图投影根据投影性质可分为等距离投影、等角投影和等面积投影,根据投影后经纬线形状可分为圆柱投影、圆锥投影和方位投影。前人对这些投影间变换问题已进行了不少研究,特别是我国已故著名地图学家杨启和教授在地图投影变换领域取得了令国内外同行瞩目的成果,杨启和教授经过几十年的潜心研究,毕其一生之精力,集其研究之大成,于1989年出版了《地图投影变换原理与方法》这部巨著,使这个研究领域大大前进一步,该书于2000年被英国Taylor出版公司译为英文出版,是我国地图投影方面第一部在国外出版的学术著作,标志着我国地图投影变换研究在国际上的领先地位,对于推动地图学各分支学科的现代化水平和提高我国地图学在国际上的地位具有重要的意义。
值得注意的是,虽然前人对地图投影变换方法进行了大量的研究,并在一定程度上解决了许多问题,但还不够全面和充分,特别是对于地球椭球模型下不同变形性质间的投影变换,采用的是间接变换法,需要通过中间过渡的方法,反解出原地图投影点的椭球坐标,再代入新投影中求得该点在新投影下的直角坐标,而未能建立投影坐标间的直接关系式,由于椭球体下两种投影表达式较为复杂,而且变换中有时需要经过烦琐的迭代运算才能反解出大地纬度,使得计算过程变得相当复杂,计算效率不高。因此,需要研究地图投影直接变换问题,建立不同投影之间精确的对应关系,表达编图和制图过程的数学实质。地图投影间接变换和直接变换示意图如图 1所示。
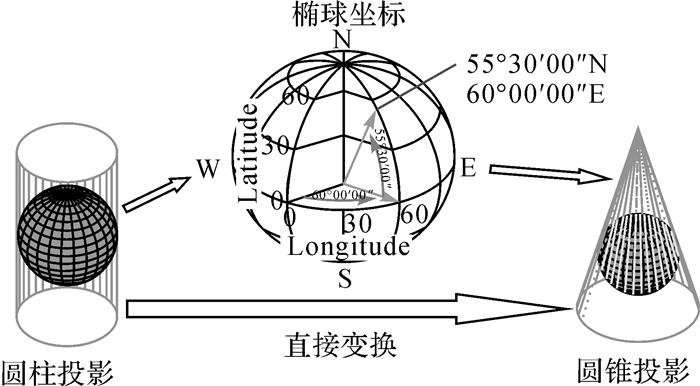
|
| 图 1 地图投影间接变换和直接变换示意图 Fig. 1 Sketch of indirect and direct transformations of map projection |
子午线弧长、等量纬度和等面积纬度函数是等距离投影、等角投影和等面积投影中的重要变量,分别是等距离纬度、等角纬度和等面积纬度的函数,它们之间的变换是实现不同变形性质地图投影间变换的基础,而这3种量之间的变换,传统上是通过解算大地纬度间接实现的,计算公式复杂冗长,不便于应用。
借助计算机代数分析方法和计算机代数系统,文献[49]推导出了子午线弧长正反解公式,并将系数统一表示为椭球偏心率的幂级数形式,克服了传统反解公式大多表示为具体数值形式的缺陷。文献[50—52]在等距离纬度、等角纬度和等面积纬度正反解展开式基础上,推导出了子午线弧长、等量纬度和等面积纬度函数之间变换的直接展开式,将展开式系数统一表示为椭球偏心率的幂级数形式,且展至e8。文献[40]进一步将展开式系数扩展至e10,并给出了我国常用大地坐标系下展开式的系数值,精度分析表明直接展开式的计算精度较传统间接变换公式最少提高2个数量级,最多提高6个数量级,可以满足地图投影精密计算需要。
在此基础上,文献[40,53—54]系统地建立了正轴圆柱投影之间、正轴圆锥投影之间及正轴圆柱投影和正轴圆锥投影间的直接变换模型,避免了过去“圆柱→椭球→圆锥”间接变换导致的误差,显著地提高了投影变换的计算精度和计算效率。与传统变换公式相比,这些直接变换模型形式更为简单,理论更为严密,便于测量和制图使用。
3 高斯投影的复变函数表示高斯投影被广泛用作地形图的数学基础,传统的高斯投影正(反)解公式表示为经差(横坐标)的实数型幂级数形式,虽然有容易理解和直观的优点,但表达式复杂冗长,而且对于正解中子午线弧长的计算,给出的是适用于特定椭球的数值公式,反解中底点纬度则需要迭代求出,较为烦琐[39];特别是实用中需要分带处理,经常划分为3°或6°带,如图 2所示。针对这一问题,文献[55—58]采用多种方法导出了适用范围更广的高斯投影算法,但由于没有摆脱实数表示的限制,仍然没有解决分带问题。
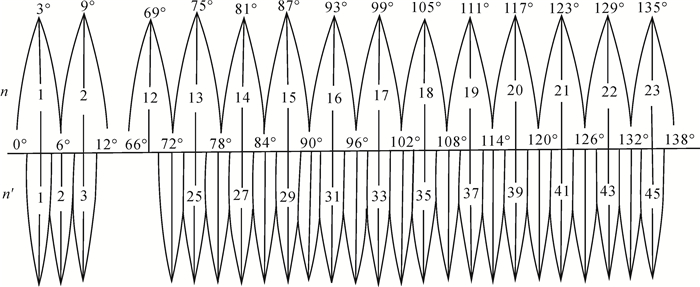
|
| 图 2 高斯投影分带示意图 Fig. 2 Sketch of zone dividing of Gauss projection |
鉴于高斯投影是一种等角投影,而复变函数作为一种强有力的数学方法,在等角投影中的优势是无可替代的,利用复变函数进行等角投影计算和公式推求具有简单、方便、准确的优点,近年来已有学者注意到这一问题并进行了研究。文献[59]采用椭球面在球面的局部描写,给出了复变函数表示的高斯投影近似式,计算精度较低,只能达到0.3 m。文献[60]讨论了横墨卡托投影的复变函数表示,但其给出的反解变换是在子午线弧长正解公式的基础上迭代得到的,计算过于烦琐。文献[61]基于一种有效的递推公式给出了任意带宽的高斯投影复变函数解法,但所给公式较为复杂,且递推过程耗时,计算效率较低。文献[62]给出了用复变函数表示的高斯投影正反解的Fortran程序并进行了计算。
借助计算机代数分析方法和计算机代数系统,文献[63—64]研究了椭球高斯投影的复变函数表示,将子午线弧长正反解公式拓展至复数域,导出了形式紧凑、结构简单的正反解公式,但在实际计算中需烦琐的迭代运算,影响了计算效率。文献[65]使用计算机代数系统研究了高斯投影复变换的数值计算方法,给出了复积分计算的积分级数分析法、椭圆积分函数法、直接积分法及利用系统函数求解变换方程。文献[66]并将等量纬度与子午线弧长变换的直接展开式拓展至复数域拓展至复数域,导出了复变函数表示的高斯投影正反解非迭代公式,不仅提高了计算精度,而且在一定程度上也简化了计算过程。文献[67]推导出了球面高斯投影复变函数表达式,根据复变函数及常用初等函数的定义,经过一系列数学分析过程,给出了球面高斯投影与横轴墨卡托投影等价性的严格证明。文献[68]在球面高斯投影复变函数表示的基础上,通过一系列数学变换,推导出了球面高斯投影正反解、经纬线投影方程、投影长度比及子午线收敛角公式的闭合式,与传统高斯投影幂级数公式相比,理论上更严密、形式上更紧凑。文献[69]在椭球高斯投影复变函数表示的基础上,通过借助双曲正弦和公式、双曲函数与三角函数间的函数关系,经过一系列恒等变换,将高斯投影复变函数坐标公式及对应的长度比、子午线收敛角公式等价变换为实数形式,具有“不分带”的优点,且表现形式更直观、清晰。文献[70]在高斯投影复变函数表示的基础上,给出了基于复数等角纬度、复数底点纬度的推导过程,得到了高斯投影正反解公式的实数解,其计算精度达0.1 mm,突破经典高斯投影带宽的限制,适应带宽可达60°。文献[71]借助计算机代数系统推导出了等角纬度关于子午线弧长的展开式,利用复变函数及双曲正切函数理论,得到了不同中央经线高斯投影间的变换公式,与传统高斯投影换带公式相比,具有更高的准确度及更宽的应用范围。文献[72—73]讨论了常用等角投影及其解析变换的复变函数表示,给出了高斯投影、墨卡托投影和等角圆锥投影正反解的复变函数表示模型,在此基础上系统地推导出了高斯投影、墨卡托投影和等角圆锥投影间解析变换的复变函数表达式。文献[74]导出了拉格朗日投影正反解的复变函数表达式,在此基础上系统地建立了该投影与高斯投影、墨卡托投影和等角圆锥投影间解析变换的复变函数表示模型。这些复数变换公式表现为含参考椭球第一偏心率的符号形式,可解决不同参考椭球下的变换问题,与传统的实数变换公式相比,其形式更为简单、理论更为严密。
4 斜轴墨卡托投影数学分析墨卡托投影是一类常用的等角投影,因投影面与地球椭球相对位置的不同,可将其分为正轴、横轴和斜轴墨卡托投影。正轴墨卡托投影适用于东西向赤道附近的测区,横墨卡托投影适于南北纵向沿经线的测区。显然,存在一些地理区域并不以赤道、经线、纬线为中线,而位于某一平面与地球或其他星体的交线附近,如图 3所示。针对这种情况的应用需求,人们展开了对斜轴墨卡托投影的研究。
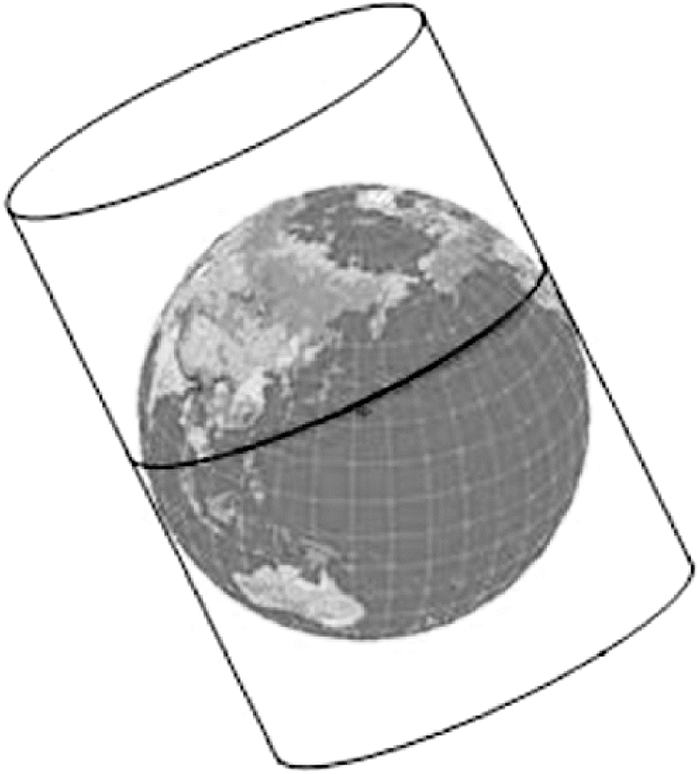
|
| 图 3 斜轴墨卡托投影示意图 Fig. 3 Sketch of oblique Mercator projection |
文献[75]对旋转椭球进行等角投影,得到椭球斜轴墨卡托投影,这种方法被用于美国阿拉斯加、马来亚半岛和婆罗洲、瑞士、意大利等国家或地区制图。文献[76]曾阐述了Hotine斜轴墨卡托投影是绘制地球资源卫星类型数据最合适的投影方式,曾用于热容量测绘卫星的投影成像。文献[77]基于正轴及横轴墨卡托投影的概念,在确保变换后的赤道投影前后长度不变的前提下,给出了椭球情况下斜轴墨卡托投影的算法。文献[36]引入复变函数对墨卡托投影体系进行了系统的研究,详细介绍了球面、椭球情况下的正轴、横轴、斜轴墨卡托投影方式。
随着国民经济的飞速发展,我国高速铁路建设、高等级公路建设、长距离的引水和输油管线建设等工程日益兴起。这些长大线状工程横跨东西南北,具有测区带状、路线长等显著特点,传统的横轴高斯投影只适用于南北条带区域的投影表示,应用于东西跨度较大的长大线状工程,将导致分带过于频繁、换带计算烦琐、信息要素表达零散等不足,而采用斜轴墨卡托投影可有效控制投影长度变形,避免分带计算。文献[78]介绍了斜圆柱投影的计算方法,使投影圆柱沿工程直伸中心线相切,从而克服了长度变形问题。文献[79]讨论了参考圆球的确定和定位,编制了计算软件,实现了从常用坐标系统向斜轴投影平面坐标的转换计算。文献[80—83]结合铁路线路的实测数据分析了斜墨卡托投影的应用效果,验证了方法的有效性。然而,上述文献为计算方便,往往将测区表面近似为球面,同时未考虑高差对于投影变形的影响,使得算法受距离限制,不适于长线型线路。因此,为更精确地表示测区,在长线型线路设计中需考虑地球扁率的影响,而这一问题往往涉及非常复杂冗长的数学分析,人工推导难度极大。
文献[84—86]提出将接近于长大线状工程的法截面进行旋转,得到法截面子午线椭球,借助计算机代数系统对法截面子午线椭球构建和变换涉及的复杂数学分析问题进行了深入研究,建立了法截面子午线椭球高斯投影、空间几何和工程应用理论体系,避免了高斯分带计算,减小了投影变形,在施工允许精度范围内将单个坐标系线路长度延伸至1000 km以上,甚至达到7000 km,有效提高了高斯投影在东西跨度较大区域的使用效率。文献[87]基于最小二乘、坐标系转换和椭球变换理论,借助计算机代数系统构建了斜轴变形椭球高斯投影方法,避免了因分带带来的误差,减小了投影综合变形,其数学模型更为简单,计算过程更为清晰。
5 极区海图投影及其变换随着全球气候变暖,极区商业价值及战略地位日渐凸显,对其进行资源调查及航线探索已成为近年来国际上争相关注的热点。海图对于极区航行具有不可或缺的支撑作用,而中低纬度采用的墨卡托投影由于长度变形过大而不宜在极区使用,选择合适的海图投影方式对编制极区航行所需航海图至关重要。
文献[88]提出横向和斜向导航技术,与之配合的投影方式应为兰伯特等角投影、极球面投影或横墨卡托投影,但没有对这些海图投影方式特性及使用方式进行进一步的详细分析与说明。文献[89]提出了利用陀螺作为跟踪仪的格网导航方法,建议在格网导航中使用斜向墨卡托投影。文献[90]提出了一种基于横墨卡托投影导航图的极区横向导航技术,将横向地理坐标系与横墨卡托投影结合以支持极区导航。1989年美军国防制图局(Defense Mapping Agency,DMA)推荐北纬84°至北极和南纬80°至南极间的图幅采用通用极球面投影(universal polar stereographic projection,UPS)。文献[91]对极球面投影上用直线直接代替大圆航线所造成的航向误差和位置误差进行了定性分析,对极区常用投影方式的导航应用研究更深入细致。文献[92]建议北极区域使用等距离方位投影和等角方位投影、近北极区域使用兰伯特圆锥投影和等距离圆锥投影。文献[93]认为在寻找出一种新的极地投影之前,墨卡托投影和日晷投影仍将作为编制北极航海图的首选投影。
以往对极区常用海图投影方式的投影特性及可用性分析,只给出了笼统的定性分析初步结论,对其变形特性、误差分布特性缺乏系统、深入、细致的理论推导和数值分析,特别是传统人工推导的极区海图投影算法存在以下有待解决的问题:基于球体模型导出,存在近似、精度不高的缺点;存在奇异问题或分带现象,表达式不统一;未能建立投影坐标直接变换的严密解析式,计算烦琐。
借助计算机代数分析方法和计算机代数系统,文献[94]分析了极球面投影的极区投影变形、经纬线形状及大圆航线与直线的逼近程度,结果表明极球面投影能够克服墨卡托投影不足,可满足极区海图投影要求。文献[95]针对现有研究中未充分考虑地球扁率对极区极球面投影误差影响的问题,研究了双重极球面投影下极区投影误差与各重基准纬度的关系。文献[96]研究了极球面投影上直线代替大圆航线量测距离的可行性,提出了一种基于等距圆的距离量测方法,解决了极球面投影海图上精确量测距离的问题。文献[97]建立了等距离正圆柱投影平面上等角航线方程并对其曲率进行了分析,提出了一种可满足给定精度要求的等角航线展绘算法。
鉴于陆图采用的高斯投影具有等角优势,在中央子午线附近变形较小,如极区海图采用高斯投影则便于陆海图的统一,但高斯投影传统实数公式仅在经差较小的条带内适用,传统复变函数表达式虽消除了分带的限制,但是由于等量纬度在极点存在奇异,使得复变函数表达式难以在极区应用。文献[98—99]推导出了极区球面高斯投影非奇异公式,满足了极区内连续投影的需求,基于该公式推导了极区经纬线投影方程,并结合日晷投影进行了长度变形及子午线偏移角分析,结果表明在极圈内高斯投影长度变形小于日晷投影。文献[100]在高斯投影复变函数的基础上,引入复变等角纬度的概念,避免等量纬度在极点的奇异性,并将极点作为高斯投影的坐标原点,建立了极区非奇异高斯投影复变函数表示形式,克服了传统高斯投影分带的缺陷,使得高斯投影在极区有一个统一完整的“一体化表示形式”,但在求得复数等角余纬度的过程中,使用了极点附近球近似的方法,一定程度上影响了正解推导过程的严密性。文献[101]建立了等角余纬度和等量纬度间的严密关系式,对其进行复数开拓,推导出了理论严密的极区不分带高斯投影正反解复数表达式,利用指数函数与三角函数间的关系式,进一步导出了极区高斯投影正反解实数表达式,在此基础上绘制了极区不分带高斯投影示意图,如图 4所示。

|
| 图 4 北极地区不分带高斯投影示意图 Fig. 4 Sketch of non-zonal Gauss projection in arctic regions |
文献[102]研究了极球面投影、横墨卡托投影和日晷投影的直接变换问题,系统地推导出了任意两种投影间的直接变换公式,可供极区海图投影变换和航海导航参数计算使用。文献[103]讨论了常用极区海图投影及其变换,给出了各类球面或椭球面投影及其变换公式,以及长度比或角度变形公式,主要包括等角投影、等面积投影、等距离投影和日晷投影,着重研究了等角投影及等角投影间的解析变换。
6 结论与展望借助现代计算机代数系统强大的数学分析功能和符号运算能力,将计算机代数分析方法应用于地图投影数学分析,不仅可以极大地提高地图投影数学分析过程的效率,而且可以推导出过去人工推导难以完成的公式和算法,实现地图投影学特定领域某些数学分析过程的创新。随着科学技术特别是空间科学和计算机科学技术的发展,地图投影的理论越来越科学化和体系化,地图投影的方法和种类越来越多样化,地图投影学已突破了传统的研究内容和研究方法,正在向进一步深化和多种专业知识的结合方向发展,新的研究和应用领域不断地开拓。笔者认为,地图投影计算机代数分析有待进一步开展的研究工作主要有以下几个方面:
(1) 空间地图投影计算机代数分析。空间地图投影[104-106]是近40年才出现的一个新的研究领域,是图像数学基础研究的前沿课题,是卫星遥感制图学发展必然产生的问题。空间地图投影涉及地球形状、地球自转、卫星轨道摄动等非常复杂的数学分析问题,传统人工推演均采用一定的近似分析方法和数值积分,借助计算机代数系统强大的符号运算能力,可以推导和建立理论上更为严密、形式上更为简单、精度上更为精确的空间地图投影新公式和新算法,揭示各类空间地图投影复杂数学模型和海量数据背后隐藏的规律,实现空间地图投影在一些具体数学分析问题上的突破和创新。
(2) 中小比例尺地图投影计算机代数设计与分析。中小比例尺地图投影在过去有过一些研究和分析,但由于受时代的局限,在分析深度、广度和精细程度上都显得比较粗浅,绝非完美。许多投影是人工拟合得出的数值形式,参数选取有一定的随机性,缺乏严格的数学基础。利用先进的计算机代数分析工具,可以全面对比各类中小比例尺地图投影特点,对以前缺乏数学基础的各类数值拟合投影方法尽可能给出符号化的通用数学准则和表达式,提高我国中小比例尺地图投影的理论研究和设计水平。
(3) 海图投影及航线绘算计算机代数分析。海图投影及航线绘算是海图制图和航线设计的理论基础,在海洋监测与调查、海洋划界和航海中有着广泛的应用。传统的海图投影及航线绘算公式和算法,大多表现为数值形式,普适性不高,符号形式的算法部分存在高阶项误差,同时在极区的应用和研究也很有限。利用计算机代数分析方法,借助计算机代数系统对其进行系统分析,可以将以往算法的数值形式改进为符号形式,建立更适合的新模型和新算法,完善海图投影及航线绘算的理论体系。
| [1] | 王家耀, 成毅. 论地图学的属性和地图的价值[J]. 测绘学报, 2015, 44(3): 237–241. WANG Jiayao, CHENG Yi. Discussions on the Attributes of Cartography and the Value of Map[J]. Acta Geodaetica et Cartographica Sinica, 2015, 44(3): 237–241. DOI:10.11947/j.AGCS.2015.20140406 |
| [2] | 王家耀, 何宗宜, 蒲英霞, 等. 地图学[M]. 北京: 测绘出版社, 2016. WANG Jiayao, HE Zongyi, PU Yingxia, et al. Cartography[M]. Beijing: Surveying and Mapping Press, 2016. |
| [3] | 李志林, 刘启亮, 高培超. 地图信息论:从狭义到广义的发展回顾[J]. 测绘学报, 2016, 45(7): 757–767. LI Zhilin, LIU Qiliang, GAO Peichao. Entropy-Based Cartographic Communication Models:Evolution from Special to General Cartographic Information Theory[J]. Acta Geodaetica et Cartographica Sinica, 2016, 45(7): 757–767. DOI:10.11947/j.AGCS.2016.20160235 |
| [4] | 吴忠性, 杨启和. 数学制图学原理[M]. 北京: 测绘出版社, 1989. WU Zhongxing, YANG Qihe. Principles of Mathematical Cartography[M]. Beijing: Surveying and Mapping Press, 1989. |
| [5] | 杨启和. 地图投影变换原理与方法[M]. 北京: 解放军出版社, 1989. YANG Qihe. Principles and Methods of Map Projection Transformation[M]. Beijing: PLA Press, 1989. |
| [6] | YANG Qihe, SNYDER J P, TOBLER W R. Map Projection Transformation:Principles and Applications[M]. London: Taylor & Francis, 2000. |
| [7] | 吕晓华, 李少梅. 地图投影原理与方法[M]. 北京: 测绘出版社, 2016. LÜ Xiaohua, LI Shaomei. Principles and Methods of Map Projection[M]. Beijing: Surveying and Mapping Press, 2016. |
| [8] | 何宗宜. 计算机地图制图[M]. 北京: 测绘出版社, 2008. HE Zongyi. Computer Aided Cartography[M]. Beijing: Surveying and Mapping Press, 2008. |
| [9] | 闾国年, 吴平生, 周晓波. 地理信息科学导论[M]. 北京: 中国科学技术出版社, 1999. LÜ Guonian, WU Pingsheng, ZHOU Xiaobo. Introduction to Geographical Information Science[M]. Beijing: China Science Technology Press, 1999. |
| [10] | 龚健雅. 地理信息系统基础[M]. 北京: 科学出版社, 2001. GONG Jianya. Foundation of Geographical Information System[M]. Beijing: Science Press, 2001. |
| [11] | 郭仁忠. 空间分析[M]. 2版. 北京: 高等教育出版社, 2001. GUO Renzhong. Spatial Analysis[M]. 2nd ed. Beijing: Higher Education Press, 2001. |
| [12] | 庞小平. 遥感制图与应用[M]. 北京: 测绘出版社, 2016. PANG Xiaoping. Remote Sensing Mapping and Its Application[M]. Beijing: Surveying and Mapping Press, 2016. |
| [13] | 孔祥元, 郭际明, 刘宗泉. 大地测量学基础[M]. 武汉: 武汉大学出版社, 2005. KONG Xiangyuan, GUO Jiming, LIU Zongquan. Foundation of Geodesy[M]. Wuhan: Wuhan University Press, 2005. |
| [14] | 边少锋, 纪兵, 李厚朴. 卫星导航系统概论[M]. 2版. 北京: 测绘出版社, 2016. BIAN Shaofeng, JI Bing, LI Houpu. Introduction to Satellite Navigation System[M]. 2nd ed. Beijing: Surveying and Mapping Press, 2016. |
| [15] | ADAMS O S. Latitude Developments Connected with Geodesy and Cartography with Tables, Including a Table for Lambert Equal-area Meridional Projection[M]. Washington D C:U.S. Government Printing Office, 1921. |
| [16] | THOMAS P D. Conformal Projections in Geodesy and Cartography[M]. Washington D C:U.S. Government Printing Office, 1952. |
| [17] | 方俊. 地图投影学-第二册[M]. 北京: 科学出版社, 1958. FANG Jun. Map Projection[M]. Beijing: Science Press, 1958. |
| [18] | 方炳炎. 地图投影学[M]. 北京: 地图出版社, 1978. FANG Bingyan. Map Projection[M]. Beijing: Map Press, 1978. |
| [19] | SNYDER J P. Map Projections:A Working Manual[M]. Washington D C:U.S. Government Printing Office, 1987. |
| [20] | 华棠. 海图数学基础[M]. 北京: 海潮出版社, 1985. HUA Tang. Mathematical Foundation of Chart[M]. Beijing: Haichao Press, 1985. |
| [21] | 丁佳波. 关于等角投影解析变换的补充[J]. 测绘学报, 1985, 11(1): 46–50. DING Jiabo. A Complement to the Analytical Transformation Between Conformal Projections[J]. Acta Geodaetica et Cartographica Sinica, 1985, 11(1): 46–50. |
| [22] | 孙群, 杨启和. 底点纬度解算以及等量纬度和面积函数反解问题的探讨[J]. 解放军测绘学院学报, 1985(2): 64–75. SUN Qun, YANG Qihe. The Research on the Computation of the Foot-Point Latitude and the Inverse Solution of Isometric Latitude and Area Function[J]. Journal of PLA of Surveying and Mapping, 1985(2): 64–75. |
| [23] | BOWRING B R. The Transverse Mercator Projection-A Solution by Complex Numbers[J]. Survey Review, 1990, 30(237): 325–342. DOI:10.1179/003962678791965183 |
| [24] | 胡毓矩, 龚剑文, 黄伟. 地图投影[M]. 北京: 测绘出版社, 1981. HU Yuju, GONG Jianwen, HUANG Wei. Map Projection[M]. Beijing: Surveying and Mapping Press, 1981. |
| [25] | CHENG Yang. The Conformal Space Projection[J]. Cartography and Geographic Information Systems, 1996, 23(1): 37–50. DOI:10.1559/152304096782512168 |
| [26] | GRAFAREND E W, SYFFUS R. The Solution of the Korn-Lichtenstein Equations of Conformal Mapping:the Direct Generation of Ellipsoidal Gauβ-Krüger Conformal Coordinates or the Transverse Mercator Projection[J]. Journal of Geodesy, 1998, 72(5): 282–293. DOI:10.1007/s001900050167 |
| [27] | GRAFAREND E W, YOU R J, SYFFUS R. Map Projection[M]. 2nd ed. Berlin: Springer-Verlag, 2014. |
| [28] | KESSLER F C. A Visual Basic Algorithm for the Winkel Tripel Projection[J]. Cartography and Geographic Information Science, 2000, 27(2): 177–183. DOI:10.1559/152304000783547939 |
| [29] | OZTAN O C, IPBUKER C, ULUGTEKIN N. A Numerical Approach to Pseudo-Projections on Example Franz Mayr Projection[J]. Journal of General Command of Mapping, 2001, 125: 37–50. |
| [30] | 吕晓华, 刘宏林. 地图投影数值变换方法综合评述[J]. 测绘学院学报, 2002, 19(2): 150–153. LÜ Xiaohua, LIU Honglin. A Comprehensive Appraisal of Numerical Transformation Method for Map Projection[J]. Journal of Institute of Surveying and Mapping, 2002, 19(2): 150–153. |
| [31] | 任留成. 空间投影理论及其在遥感技术中的应用[M]. 北京: 科学出版社, 2003. REN Liucheng. Theory of Space Map Projection with Its Applications in Remote Sensing[M]. Beijing: Science Press, 2003. |
| [32] | IPBUKER C, BILDIRICI I O. Computer Program for the Inverse Transformation of the Winkel Projection[J]. Journal of Surveying Engineering, 2005, 131(4): 125–129. DOI:10.1061/(ASCE)0733-9453(2005)131:4(125) |
| [33] | 孙达, 蒲英霞. 地图投影[M]. 南京: 南京大学出版社, 2005. SUN Da, PU Yingxia. Map Projection[M]. Nanjing: Nanjing University Press, 2005. |
| [34] | 钟业勋. 数理地图学-地图学及其数学原理[M]. 北京: 测绘出版社, 2007. ZHONG Yexun. Mathematical Cartography-Cartography and Its Mathematical Elements[M]. Beijing: Surveying and Mapping Press, 2007. |
| [35] | KARNEY C F F. Transverse Mercator with an Accuracy of A Few Nanometers[J]. Journal of Geodesy, 2011, 85(8): 475–485. DOI:10.1007/s00190-011-0445-3 |
| [36] | OSBORNE P. The Mercator Projection[M]. Edinburgh: Edinburgh University Press, 2013. |
| [37] | 边少锋, 许江宁. 计算机代数系统与大地测量数学分析[M]. 北京: 国防工业出版社, 2004. BIAN Shaofeng, XU Jiangning. Computer Algebra System and Mathematical Analysis in Geodesy[M]. Beijing: National Defense Industry Press, 2004. |
| [38] | 杨启和. 测量和地图学中应用的六种纬度及其变换关系式[J]. 测绘科技通讯, 1995, 18(3): 14–19. YANG Qihe. Six Kinds of Latitudes with Their Transformation Relations in Surveying and Mapping[J]. Science and Technology Newsletter, 1995, 18(3): 14–19. |
| [39] | 熊介. 椭球大地测量学[M]. 北京: 解放军出版社, 1988. XIONG Jie. Ellipsoidal Geodesy[M]. Beijing: PLA Press, 1988. |
| [40] | 李厚朴, 边少锋, 钟斌. 地理坐标系计算机代数精密分析理论[M]. 北京: 国防工业出版社, 2015. LI Houpu, BIAN Shaofeng, ZHONG Bin. Precise Analysis Theory of Geographic Coordinate System by Computer Algebra[M]. Beijing: National Defense Industry Press, 2015. |
| [41] | 过家春, 李厚朴, 庄云玲, 等. 依不同纬度变量的子午线弧长正反解公式的级数展开[J]. 测绘学报, 2016, 45(5): 560–565. GUO Jiachun, LI Houpu, ZHUANG Yunling, et al. Series Expansion for Direct and Inverse Solutions of Meridian in Terms of Different Latitude Variables[J]. Acta Geodaetica et Cartographica Sinica, 2016, 45(5): 560–565. DOI:10.11947/j.AGCS.2016.20140575 |
| [42] | 杨启和, 杨晓梅. 测量和地图学中应用的三种纬度函数及其反解变换的线性插值方法[J]. 测绘学报, 1997, 26(1): 92–94, 封3. YANG Qihe, YANG Xiaomei. Three Kinds of Latitudes in Surveying and Mapping and the Linear Interpolation Method for Inverse Solution[J]. Acta Geodaetica et Cartographica Sinica, 1997, 26(1): 92–94, 封3. |
| [43] | 边少锋, 纪兵. 等距离纬度等量纬度和等面积纬度展开式[J]. 测绘学报, 2007, 36(2): 218–223. BIAN Shaofeng, JI Bing. The Expansions of Rectifying Latitude, Conformal Latitude and Authalic Latitude[J]. Acta Geodaetica et Cartographica Sinica, 2007, 36(2): 218–223. DOI:10.3321/j.issn:1001-1595.2007.02.018 |
| [44] | 李厚朴, 边少锋. 辅助纬度反解公式的Hermite插值法新解[J]. 武汉大学学报(信息科学版), 2008, 33(6): 623–626. LI Houpu, BIAN Shaofeng. Derivation of Inverse Expansions for Auxiliary Latitudes by Hermite Interpolation Method[J]. Geomatics and Information Science of Wuhan University, 2008, 33(6): 623–626. |
| [45] | 王瑞, 李厚朴. 辅助纬度反解公式的Lagrange级数法推演[J]. 海洋测绘, 2008, 28(3): 18–23. WANG Rui, LI Houpu. The Derivation of the Inverse Expansions for Auxiliary Latitudes by Lagrange Series Method[J]. Hydrographic Surveying and Charting, 2008, 28(3): 18–23. |
| [46] | 李忠美, 边少锋, 孔海英. 符号迭代法解算椭球大地测量学反问题[J]. 海洋测绘, 2013, 33(1): 27–29, 33. LI Zhongmei, BIAN Shaofeng, KONG Haiying. Symbolic Iterative Method for Solving Inverse Problems in Ellipsoidal Geodesy[J]. Hydrographic Surveying and Charting, 2013, 33(1): 27–29, 33. |
| [47] | 李忠美, 李厚朴, 边少锋. 常用纬度差异极值符号表达式[J]. 测绘学报, 2014, 43(2): 214–220. LI Zhongmei, LI Houpu, BIAN Shaofeng. Symbolic Expressions of Difference Extrema Between Regular Latitudes[J]. Acta Geodaetica et Cartographica Sinica, 2014, 43(2): 214–220. DOI:10.13485/j.cnki.11-2089.2014.0031 |
| [48] | 李厚朴, 边少锋, 刘敏. 地图投影中三种纬度间变换直接展开式[J]. 武汉大学学报(信息科学版), 2013, 38(2): 217–220. LI Houpu, BIAN Shaofeng, LIU Min. Direct Expansions of Transformations Between Three Kinds of Latitudes Used in Map Projection[J]. Geomatics and Information Science of Wuhan University, 2013, 38(2): 217–220. |
| [49] | BIAN Saofeng, CHEN Yongbing. Solving An Inverse Problem of a Meridian Arc in Terms of Computer Algebra System[J]. Journal of Surveying Engineering, 2006, 132(1): 7–10. DOI:10.1061/(ASCE)0733-9453(2006)132:1(7) |
| [50] | 李厚朴, 刘敏, 孔海英, 等. 子午线弧长和等面积纬度函数变换的直接展开式[J]. 海洋测绘, 2011, 31(1): 17–19. LI Houpu, LIU Min, KONG Haiying, et al. The Direct Expansions for Transformations Between Meridian Arc and Authalic Latitude Function[J]. Hydrographic Surveying and Charting, 2011, 31(1): 17–19. |
| [51] | 李厚朴, 边少锋, 王克平. 等距离纬度和等量纬度变换的直接展开式[C]//第二十三届海洋测绘综合性学术研讨会. 呼伦贝尔: [s. n. ], 2013: 189-195. LI Houpu, BIAN Shaofeng, WANG Keping. The Direct Expansions for Transformations Rectifying and Isometric Latitudes[C]//Hydrographic Surveying and Charting Symposium of 24th General Meeting. Hulunbeier:[s.n.], 2013:149-153. |
| [52] | 李厚朴, 边少锋, 陈良友. 等面积纬度函数和等量纬度变换的直接解算公式[J]. 武汉大学学报(信息科学版), 2011, 36(7): 843–846. LI Houpu, BIAN Shaofeng, CHEN Liangyou. The Direct Calculating Formulae for Transformations between Authalic Latitude Function and Isometric Latitude[J]. Geomatics and Information Science of Wuhan University, 2011, 36(7): 843–846. |
| [53] | 李厚朴, 边少锋. 不同变形性质正轴圆柱投影和正轴圆锥投影间的直接变换[J]. 测绘学报, 2012, 41(4): 536–542. LI Houpu, BIAN Shaofeng. The Direct Transformations Between Normal Cylindrical and Conic Projections with Different Distortion Properties[J]. Acta Geodaetica et Cartographica Sinica, 2012, 41(4): 536–542. |
| [54] | BIAN Shaofeng, LI Houpu. Mathematical Analysis in Cartography By Means of Computer Algebra System[C]//Carlos Bateira. Cartography:A Tool for Spatial Analysis. Croatia:InTech, 2012. https://es.scribd.com/document/174630480/Cartography-A-Tool-for-Spatial-Analysis |
| [55] | ENGSAGER K E, PODER K. A Highly Accurate World Wide Algorithm for the Transverse Mercator Mapping (Almost)[C]//Proceedings of XXⅢ International Cartographic Conference (ICC2007). Moscow:[s.n.], 2007. https://link.springer.com/article/10.1007/s00190-011-0445-3 |
| [56] | BERMEJO-SOLERA M, OTERO J. Global Optimization of the Gauss Conformal Mappings of An Ellipsoid to A Sphere[J]. Journal of Geodesy, 2010, 84(8): 481–489. DOI:10.1007/s00190-010-0385-3 |
| [57] | KARNEY C F F. Transverse Mercator with an Accuracy of A Few Nanometers[J]. Journal of Geodesy, 2011, 85(8): 475–485. DOI:10.1007/s00190-011-0445-3 |
| [58] | KAWASE K. A General Formula for Calculating Meridian Arc Length and Its Application to Coordinate Conversion in the Gauss-Krüger Projection[J]. Bulletin of the Geospatial Information Authority of Japan, 2011, 59: 1–13. |
| [59] | 程阳. 复变函数与等角投影[J]. 测绘学报, 1985, 14(1): 51–60. CHENG Yang. Complex Function and Conformal Projection[J]. Acta Geodaetica et Cartographica Sinica, 1985, 14(1): 51–60. |
| [60] | BOWRING B R. The Transverse Mercator Projection—A Solution by Complex Numbers[J]. Survey Review, 1990, 30(237): 325–342. DOI:10.1179/003962678791965183 |
| [61] | KLOTZ J. Eine Analytische L?sung der Gauss-Krüger-Abbildung[J]. Zeitschrift für Versicherungswesen, 1993, 118(3): 106–116. |
| [62] | SCHUHR P. Transformationen Zwischen Ellipsoidischen Geographischen Konformen Gauss-Krüger-bzw. UTM-Koordinaten[J]. Forum, 1995(5): 259–264. |
| [63] | 边少锋, 柴洪洲, 金际航. 大地坐标系与大地基准[M]. 北京: 国防工业出版社, 2005. BIAN Shaofeng, CHAI Hongzhou, JIN Jihang. Geodetic Coordinate System and Datum[M]. Beijing: National Defence Industry Press, 2005. |
| [64] | 李厚朴, 边少锋. 高斯投影的复变函数表示[J]. 测绘学报, 2008, 37(1): 5–9. LI Houpu, BIAN Shaofeng. The Expressions of Gauss Projection By Complex Numbers[J]. Acta Geodaetica et Cartographica Ainica, 2008, 37(1): 5–9. DOI:10.3321/j.issn:1001-1595.2008.01.002 |
| [65] | 刘大海. 高斯投影复变换的数值计算方法[J]. 测绘科学技术学报, 2012, 29(1): 9–11. LIU Dahai. Gauss Projection Numerical Method for Complex Transformation[J]. Journal of Geomatics Science and Technology, 2012, 29(1): 9–11. |
| [66] | 李厚朴, 王瑞, 边少锋. 复变函数表示的高斯投影非迭代公式[J]. 海洋测绘, 2009, 29(6): 17–20. LI Houpu, WANG Rui, BIAN Shaofeng. The Non-Iterative Formulae of Gauss Projection By Complex Numbers[J]. Hydrographic Surveying and Charting, 2009, 29(6): 17–20. |
| [67] | 李忠美, 于金星, 李厚朴, 等. 高斯投影与横墨卡托投影等价性证明[J]. 海洋测绘, 2013, 33(3): 17–20. LI Zhongmei, YU Jinxing, LI Houpu, et al. The Verification of Equivalence Between Gauss and Transverse Mercator Projections[J]. Hydrographic Surveying and Charting, 2013, 33(3): 17–20. |
| [68] | 刘强, 边少锋, 李忠美. 球面高斯投影及其变形的闭合公式[J]. 海军工程大学学报, 2015, 27(1): 45–49, 58. LIU Qiang, BIAN Shaofeng, LI Zhongmei. Closed Formulae of Gauss Projection with Its Deformation on Sphere[J]. Journal of Naval University of Engineering, 2015, 27(1): 45–49, 58. |
| [69] | 边少锋, 刘强, 李忠美. 不分带的高斯投影实数公式[J]. 测绘通报, 2016(6): 6–9. BIAN Shaofeng, LIU Qiang, LI Zhongmei. Expressions of Non-Zonal Gauss Projection in Real Form[J]. Bulletin of Surveying and Mapping, 2016(6): 6–9. DOI:10.13474/j.cnki.11-2246.2016.0178 |
| [70] | 金立新, 许常文, 魏桂华. 高斯投影复变函数表示的实数解[J]. 海洋测绘, 2017, 37(2): 27–31. JIN Lixin, XU Changwen, WEI Guihua. Real Solution of Gauss Projection Based on Complex Function[J]. Hydrographic Surveying and Charting, 2017, 37(2): 27–31. |
| [71] | 刘强, 边少锋, 李忠美. 利用复变函数实现高斯换带的方法[J]. 海军工程大学学报, 2016, 28(1): 15–19. LIU Qiang, BIAN Shaofeng, LI Zhongmei. Transformation Between Gauss Projections with Different Central Meridians Based on Complex Function[J]. Journal of Naval University of Engineering, 2016, 28(1): 15–19. |
| [72] | 李厚朴, 边少锋, 李海波. 常用等角投影及其解析变换的复变函数表示[J]. 测绘科学技术学报, 2012, 29(2): 109–112, 117. LI Houpu, BIAN Shaofeng, LI Haibo. Expressions of Commonly Used Conformal Projections and Their Analytical Transformations by Complex Numbers[J]. Journal of Geomatics Science and Technology, 2012, 29(2): 109–112, 117. |
| [73] | 李厚朴, 边少锋. 高斯投影与墨卡托投影解析变换的复变函数表达式[J]. 武汉大学学报(信息科学版), 2009, 34(3): 279–273. LI Houpu, BIAN Shaofeng. Expressions for Analytical Transformation Between Gauss and Mercator Projections By Complex Numbers[J]. Geomatics and Information Science of Wuhan University, 2009, 34(3): 279–273. |
| [74] | 李胜全, 李厚朴, 边少锋. 拉格朗日投影与常用等角投影间解析变换的复变函数表示[J]. 武汉大学学报(信息科学版), 2012, 37(11): 1382–1385. LI Shengquan, LI Houpu, BIAN Shaofeng. Expressions of Analytical Transformations Between Lagrange and the Commonly Used Conformal Projections by Complex Numbers[J]. Geomatics and Information Science of Wuhan University, 2012, 37(11): 1382–1385. |
| [75] | HOTINE M. The Orthomorphic Projection of the Spheroid[J]. Empire Survey Review, 1946, 8(62): 300–311. DOI:10.1179/sre.1946.8.62.300 |
| [76] | SNYDER J P. Calculating Map Projections for the Ellipsoid[J]. The American Cartographer, 1979, 6(1): 67–76. DOI:10.1559/152304079784022727 |
| [77] | ENGELS J, GRAFAREND E. The Oblique Mercator Projection of the Ellipsoid of Revolution IEa2, b[J]. Journal of Geodesy, 1995, 70(1-2): 38–50. DOI:10.1007/BF00863417 |
| [78] | 李全海. 斜圆柱投影及其对GPS空间坐标的转换模型[J]. 同济大学学报, 2002, 30(1): 106–110. LI Quanhai. Model of Oblique Cylindrical Projection for Transforming GPS Space Coordinates to Plane Coordinates[J]. Journal of Tongji University, 2002, 30(1): 106–110. |
| [79] | 沙月进, 高洪兴, 胡伍生. 斜轴圆柱投影方法及其在交通工程中的应用研究[J]. 公路交通科技, 2004, 21(11): 20–22. SHA Yuejin, GAO Hongxing, HU Wusheng. Study on Oblique Cylindrical Projection Method and Its Application in Traffic Engineering[J]. Journal of Highway and Transportation Research and Development, 2004, 21(11): 20–22. DOI:10.3969/j.issn.1002-0268.2004.11.006 |
| [80] | 吕慧玲. 斜轴墨卡托投影方法在郑西客专中的应用研究[J]. 测绘信息与工程, 2009, 34(1): 26–28. Lü Huiling. Application of Oblique Mercator Projection Method to Zhengxi Special Passenger Transport Line[J]. Journal of Geomatics, 2009, 34(1): 26–28. |
| [81] | 陆鹏程, 林冬伟. 斜轴墨卡托投影模型及其应用分析[J]. 铁道勘察, 2010, 36(4): 26–29. LU Pengcheng, LIN Dongwei. Model for Oblique Mercator Projections as Well as Analysis on Its Application[J]. Railway Investigation and Surveying, 2010, 36(4): 26–29. |
| [82] | 刘家臣. 高速铁路精密工程控制测量精度研究[J]. 测绘与空间地理信息, 2011, 34(6): 215–218. LIU Jiachen. Research on Accuracy of Precise Engineering Control Survey for High-Speed Railway[J]. Geomatics & Spatial Information Technology, 2011, 34(6): 215–218. |
| [83] | 王文庆, 帅明明, 龚俊. 斜轴墨卡托投影在东西走向高速铁路中的应用[J]. 地理空间信息, 2013, 11(4): 152–153. WANG Wenqing, SHUAI Mingming, GONG Jun. Application of Oblique Mercator Projection in the East-West High-Speed Railway[J]. Geospatial Information, 2013, 11(4): 152–153. |
| [84] | 金立新, 付宏平. 法截面子午线椭球高斯投影理论[M]. 西安: 西安地图出版社, 2012. JIN Lixin, FU Hongping. Gaussian Projection Theory Based on Ellipsoid with Normal Section as the Central Meridian[M]. Xi'an: Xi'an Map Publishing House, 2012. |
| [85] | 金立新, 付宏平. 法截面子午线椭球空间几何理论[M]. 西安: 西安地图出版社, 2013. JIN Lixin, FU Hongping. Spatial Geometry Theory Based on Ellipsoid with Normal Section as the Central Meridian[M]. Xi'an: Xi'an Map Publishing House, 2013. |
| [86] | 金立新, 付宏平. 法截面子午线椭球工程应用研究[M]. 西安: 西安地图出版社, 2016. JIN Lixin, FU Hongping. Engineering Application Based on Ellipsoid with Normal Section as the Central Meridian[M]. Xi'an: Xi'an Map Publishing House, 2016. |
| [87] | 边少锋, 刘强, 李忠美, 等. 斜轴变形椭球高斯投影方法[J]. 测绘学报, 2015, 44(10): 1071–1077. BIAN Shaofeng, LIU Qiang, LI Zhongmei, et al. An Alteration of Gauss Projection Based on Oblique Deformed Ellipsoid[J]. Acta Geodaetica et Cartographica Sinica, 2015, 44(10): 1071–1077. DOI:10.11947/j.AGCS.2015.20140290 |
| [88] | FOX W A W. Transverse Navigation:An Alternative to the Grid System[J]. The Journal of Navigation, 1949, 2(1): 25–35. DOI:10.1017/S0373463300031519 |
| [89] | KENDALL E C. Gyro/Grid Navigation[J]. The Journal of Navigation, 1956, 9(4): 429–435. DOI:10.1017/S0373463300036699 |
| [90] | DYER G C. Polar Navigation-A New Transverse Mercator Technique[J]. The Journal of Navigation, 1971, 24(4): 484–495. DOI:10.1017/S0373463300022335 |
| [91] | NAUMANN J. Grid Navigation with Polar Stereographic Charts[J]. European Journal of Navigation, 2011, 9(1): 4–8. |
| [92] | SKOPELITI A, TSOULOS L. Choosing A Suitable Projection for Navigation in the Arctic[J]. Marine Geodesy, 2013, 36(2): 234–259. DOI:10.1080/01490419.2013.781087 |
| [93] | 李树军, 张哲, 李惠雯, 等. 编制北极地区航海图有关问题的探讨[J]. 海洋测绘, 2012, 32(1): 58–60. LI Shujun, ZHANG Zhe, LI Huiwen, et al. Research on Compilation of Nautical Charts of Arctic Regions[J]. Hydrographic Surveying and Charting, 2012, 32(1): 58–60. |
| [94] | 温朝江, 卞鸿巍, 王荣颖, 等. 极区极球面投影的可用性及误差分析[J]. 海军工程大学学报, 2014, 26(3): 42–47. WEN Chaojiang, BIAN Hongwei, WANG Rongying, et al. Availability and Error Analysis of Polar Stereographic Projection in Polar Navigation[J]. Journal of Naval University of Engineering, 2014, 26(3): 42–47. |
| [95] | 温朝江, 卞鸿巍, 陈秋, 等. 双重极球面投影的极区投影误差分析[J]. 海洋测绘, 2015, 35(1): 34–37. WEN Chaojiang, BIAN Hongwei, CHEN Qiu, et al. Error Analysis of Double Polar Stereographic Projection in Polar Regions[J]. Hydrographic Surveying and Charting, 2015, 35(1): 34–37. |
| [96] | 温朝江, 卞鸿巍, 边少锋, 等. 基于等距圆的极球面投影距离量测方法[J]. 武汉大学学报(信息科学版), 2015, 40(11): 1504–1508, 1512. WEN Chaojiang, BIAN Hongwei, BIAN Shaofeng, et al. A Distance Measuring Method on Polar Stereographic Charts Based on Equidistant Circles[J]. Geomatics and Information Science of Wuhan University, 2015, 40(11): 1504–1508, 1512. |
| [97] | 张志衡, 彭认灿, 董箭, 等. 极地海区等距离正圆柱投影平面上等角航线的展绘方法[J]. 测绘科学技术学报, 2015, 32(5): 535–538, 544. ZHANG Zhiheng, PENG Rencan, DONG Jian, et al. The Method for Describing Rhumb Line in Polar Sea on Equidistance Cylindrical Projection Plane[J]. Journal of Geomatics Science and Technology, 2015, 32(5): 535–538, 544. |
| [98] | 李忠美, 李厚朴, 边少锋. 极区横墨卡托投影非奇异公式及投影变形分析[C]//第二十四届海洋测绘综合性学术研讨会. 义乌: 中国测绘学会海洋测绘专业委员会, 2012: 189-195. LI Zhongmei, LI Houpu, BIAN Shaofeng. The Nonsingular Formulas and Deformation Analysis for Transverse Mercator Projection in Polar Regions[C]//Hydrographic Surveying and Charting Symposium of 24th General Meeting. Yiwu:CSGPC, 2012:189-195. |
| [99] | 张晓平, 边少锋, 李忠美. 极区高斯投影与日晷投影的比较[J]. 武汉大学学报(信息科学版), 2015, 40(5): 667–672. ZHANG Xiaoping, BIAN Shaofeng, LI Zhongmei. Comparisons Between Gauss and Gnomonic Projections in Polar Regions[J]. Geomatics and Information Science of Wuhan University, 2015, 40(5): 667–672. |
| [100] | 边少锋, 李忠美, 李厚朴. 极区非奇异高斯投影复变函数表示[J]. 测绘学报, 2014, 43(4): 348–352, 359. BIAN Shaofeng, LI Zhongmei, LI Houpu. The Non-Singular Formula of Gauss Projection in Polar Regions by Complex Numbers[J]. Acta Geodaetica et Cartographica Sinica, 2014, 43(4): 348–352, 359. DOI:10.13485/j.cnki.11-2089.2014.0052 |
| [101] | 李忠美, 边少锋, 金立新, 等. 极区不分带高斯投影的正反解表达式[J]. 测绘学报, 2017, 46(6): 780–788. LI Zhongmei, BIAN Shaofeng, JIN Lixin, et al. Forward and Inverse Expressions of Polar Gauss Projection without Zoning Limitations[J]. Acta Geodaetica et Cartographica Sinica, 2017, 46(6): 780–788. DOI:10.11947/j.AGCS.2017.20170009 |
| [102] | 李厚朴, 边少锋, 刘强, 等. 常用极区海图投影直接变换的闭合公式[J]. 海洋测绘, 2017, 37(2): 32–34, 38. LI Houpu, BIAN Shaofeng, LIU Qiang, et al. Closed Formulae of Direct Transformations Between Commonly Used Polar Chart Projections[J]. Hydrographic Surveying and Charting, 2017, 37(2): 32–34, 38. |
| [103] | 陈成. 极区海图投影及其变换研究[D]. 武汉: 海军工程大学, 2015. CHEN Cheng. The Research on Polar Chart Projection with Its Transformation[D]. Wuhan:Naval University of Engineering, 2015. http://www.docin.com/p-1505733922.html |
| [104] | COLVOCORESSES A P. Space Oblique Mercator[J]. Photogrammetric Engineering and Remote Sensing, 1974, 40(8): 921–926. |
| [105] | SNYDER J P. The Space Oblique Mercator Projection[J]. Photogrammetric Engineering and Remote Sensing, 1978, 44(5): 585–596. |
| [106] | REN Liucheng, CLARKE K C, ZHOU Chenghu, et al. Geometric Rectification of Satellite Imagery with Minimal Ground Control Using Space Oblique Mercator Projection Theory[J]. Cartography and Geographic Information Science, 2010, 37(4): 261–272. DOI:10.1559/152304010793454309 |



