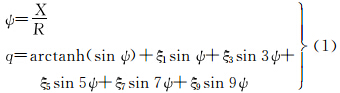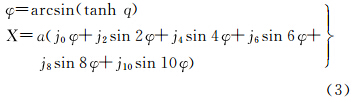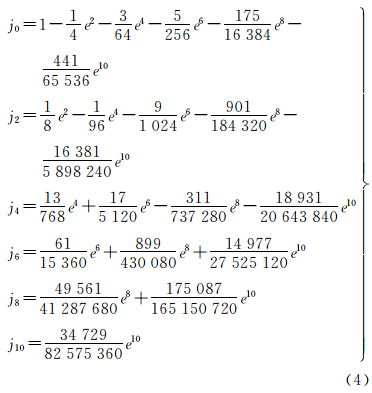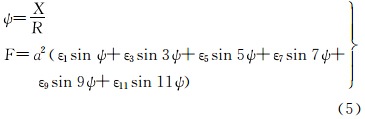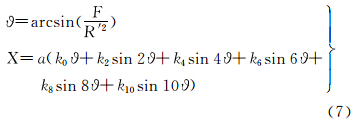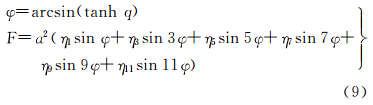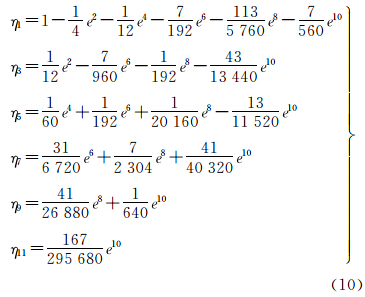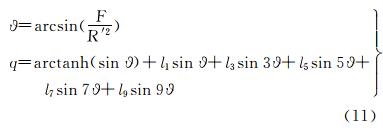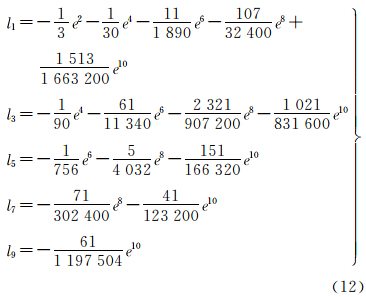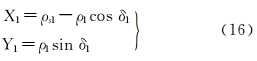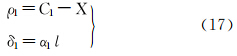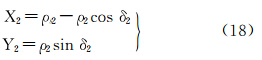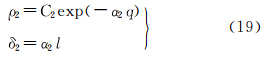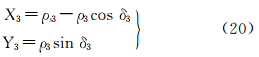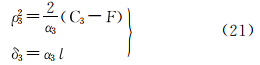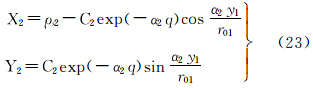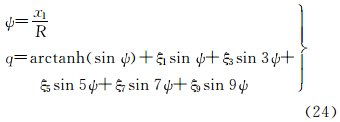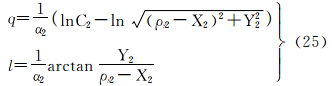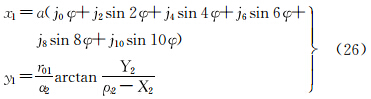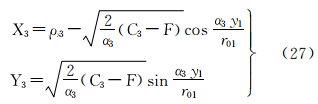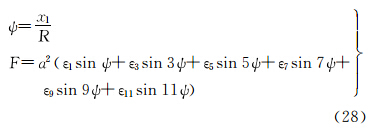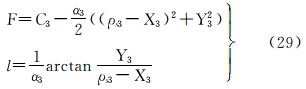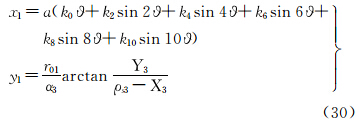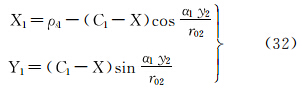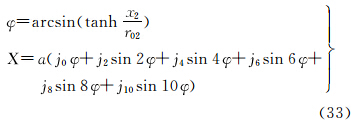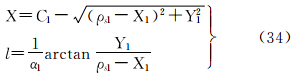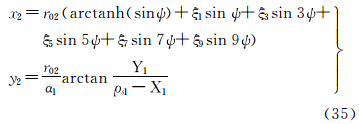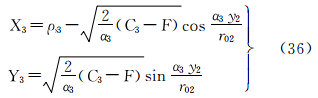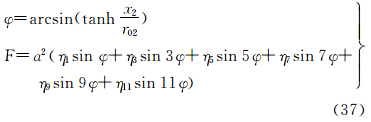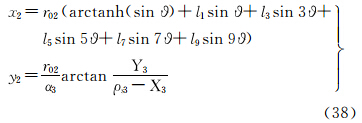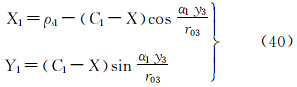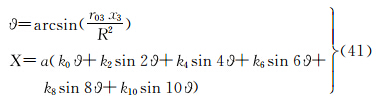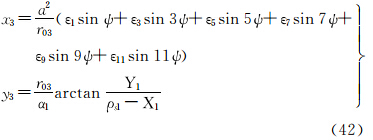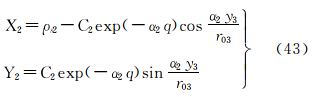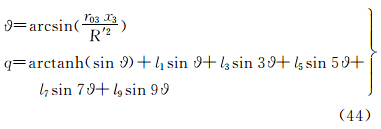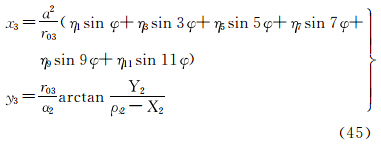2. 海岛(礁)测绘技术国家测绘地理信息局重点实验室，山东 青岛 266510
3. 中国科学院 测量与地球物理研究所，湖北 武汉430077
2. Key Laboratory of Surveying and Mapping Technology on Island and Reef, National Administration of Surveying， Mapping and Geoinformation, Qingdao 266510, China
3. Institute of Geodesy and Geophysics, Chinese Academy of Sciences, Wuhan 430077, China
1 引 言
正轴圆柱投影和正轴圆锥投影是在测量和地图制图中应用非常广泛的两类重要投影，航空图、海图、世界全图和区域地图等的绘制主要采用这两类投影方式[1, 2]，在实际生产中经常会遇到这两类投影间的变换问题。文献[3—6]对这一问题进行了深入研究，取得了卓有成效的成果，但对于椭球情形下不同变形性质投影间的变换，则是通过间接变换法实现的，计算思路可简单概括为“圆柱→椭球→圆锥”，由于需要反解出大地纬度，计算过程相当复杂，并且有的公式表现为具体的数值形式，仅能解决某一特定参考椭球下的变换问题，不便于推广使用。
子午线弧长、等量纬度和等面积纬度函数是不同变形性质正轴圆柱投影和正轴圆锥投影中的3类重要变量。这3类变量都是大地纬度的函数，它们和大地纬度间的正反算问题已得到国内外学者的深入研究并已有效解决[7, 8, 9, 10, 11, 12, 13, 14]，但对于它们之间的变换，传统上则是通过解算大地纬度间接实现的，不仅计算非常繁琐，而且不便于理论分析。笔者借助具有强大符号运算功能的计算机代数系统Mathematica[15]，对这一问题进行了新的研究，推导出它们之间变换的直接展开式[16, 17, 18]，为实现不同变形性质正轴圆柱投影和正轴圆锥投影间的直接变换提供了新的思路。本文利用文献[16]导出的子午线弧长、等量纬度和等面积纬度函数间变换的直接展开式，深入研究了不同变形性质正轴圆柱投影和正轴圆锥投影间的直接变换问题，建立了相应投影坐标间的直接变换模型。
2 子午线弧长、等量纬度和等面积纬度函数间变换的直接展开式[16] 2.1 子午线弧长和等量纬度间变换的直接展开式子午线弧长X变换至等量纬度q的直接展开式为
式中，R=a(1－e2)K0，a为参考椭球长半轴，e为参考椭球第一偏心率，系数为
等量纬度q变换至子午线弧长X的直接展开式为
式中,系数为
2.2 子午线弧长和等面积纬度函数间变换的直接展开式
子午线弧长X变换至等面积纬度函数F的直接展开式为
式中，系数为
等面积纬度函数F变换至子午线弧长X的直接展开式为
式中，R′2=a2(1－e2)A，系数为
2.3 等量纬度和等面积纬度函数间变换的直接展开式
等量纬度q变换至等面积纬度函数F的直接展开式为
式中,系数为
等面积纬度函数F变换至等量纬度q的直接展开式为
式中,系数为
3 不同变形性质正轴圆柱投影和正轴圆锥投影间的直接变换 3.1 不同变形性质的正轴圆柱投影和正轴圆锥投影 3.1.1 不同变形性质的正轴圆柱投影
等距离正轴圆柱投影的坐标公式为
等角正轴圆柱投影的坐标公式为
等面积正轴圆柱投影的坐标公式为
式(13)～式(15)中，l为经差；r0i(i=1,2,3)为基准纬度处的圆柱半径。
3.1.2 不同变形性质的正轴圆锥投影等距离正轴圆锥投影的坐标公式为
式中
等角正轴圆锥投影的坐标公式为
式中
式中，exp(-a2q)=e-a2q，e=2.718281828为自然对数的底。
等面积正轴圆锥投影的坐标公式为
式中
式(16)～式(21)中，ρsi、αi、Ci(i=1,2,3)为相应投影的投影常数，计算公式见文献[3]。
3.2 不同变形性质正轴圆柱投影和正轴圆锥投影间的直接变换模型 3.2.1 等距离正轴圆柱投影和等角正轴圆锥投影间的直接变换模型由式(13)可反解得X、l
将式(22)代入式(18)，顾及式(19)，可得等距离正轴圆柱投影直接变换至等角正轴圆锥投影的坐标关系式为
式中，q可根据式(1)表示为
由式(18)可反解得ρ2、δ2，将其代入式(19)可反解得q、l
将式(25)代入式(13)，并顾及式(3)，可得等角正轴圆锥投影直接变换至等距离正轴圆柱投影的坐标关系式为
式中,φ=arcsin(tanh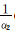
(lnC2－
ln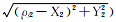
)。
将式(22)代入式(20)，并顾及式(21)，可得等距离正轴圆柱投影直接变换至等面积正轴圆锥投影的坐标关系式为
式中，F可根据式(5)表示为
由式(20)可反解得ρ3、δ3，将其代入式(21)可反解得F、l
将式(29)代入式(13)，并顾及式(7)，可得等面积正轴圆锥投影直接变换至等距离正轴圆柱投影的坐标关系式为
式中，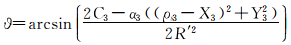
。
由式(14)可反解得q、l
将式(31)代入式(16)，并顾及式(17)，可得等角正轴圆柱投影直接变换至等距离正轴圆锥投影的坐标关系式为
式中，X可根据式(3)表示为
由式(16)可反解得ρ1、δ1，将其代入式(17)可反解得X、l
将式(34)代入式(14)，并顾及式(1)，可得等距离正轴圆锥投影直接变换至等角正轴圆柱投影的坐标关系式为
式中，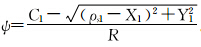
。
将式(31)代入式(20)，并顾及式(21)，可得等角正轴圆柱投影直接变换至等面积正轴圆锥投影的坐标关系式为
式中，F可根据式(9)表示为
将式(29)代入式(14)，并顾及式(11)，可得等面积正轴圆锥投影直接变换至等角正轴圆柱投影的坐标关系式为
式中，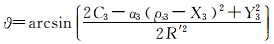
。
由式(15)可反解得
将式(39)代入式(16)，并顾及式(17)，可得等面积正轴圆柱投影直接变换至等距离正轴圆锥投影的坐标关系式为
式中，X可根据式(7)表示为
将式(34)代入式(15)，顾及式(5)，可得等距离正轴圆锥投影直接变换至等面积正轴圆柱投影的坐标关系式为
式中，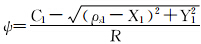
。
3.2.6 等面积正轴圆柱投影和等角正轴圆锥投影间的直接变换模型
将式(39)代入式(18)，并顾及式(19)，可得等面积正轴圆柱投影直接变换至等角正轴圆锥投影的坐标关系式为
式中，q可根据式(11)表示为
将式(25)代入式(18)，并顾及式(9)，可得等角正轴圆锥投影直接变换至等面积正轴圆柱投影的坐标关系式为
式中，φ=arcsin(tanh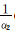(ln C2－
ln)。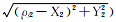
为验证本文建立的不同变形性质正轴圆柱投影和正轴圆锥投影间的直接变换模型的有效性与快捷性，同时为了与文献[3]给出的传统间接变换模型进行比较，以等角正轴圆锥投影变换至等面积正轴圆柱投影为例，选用CGCS2000椭球常数[19, 20]a=6378137m、1/f=298.257222101进行了计算分析，具体分析思路如下。
等角正轴圆锥投影的投影区域为18°N≤B≤54°N，双标准纬线分别取为B1=27°N，B2=45°N，经差变化范围为0°≤l≤30°，等面积正轴圆柱投影的基准纬度取为0°。取定大地纬度B和经差l，分别代入式(15)和式(18)可得等面积正轴圆柱投影坐标(x3,y3)和等角正轴圆锥投影坐标(X3,Y2)，将(X3,Y2)分别代入文献[3]给出的间接变换模型和本文建立的直接变换模型式(45)可得变换后的等面积正轴圆柱投影坐标，依次记为(x′3,y′3)和(x″3,y″3)，分别与(x3,y3)相减，可得间接变换模型的计算误差(Δx′3,Δy′3)和直接变换模型的计算误差(Δx″3,Δy″3)。
投影区域包含的点数可由大地纬度和经差方向的分辨率确定，取分辨率为1°×1°、0.5°×0.5°、0.1°×0.1° 3种情况，间接变换模型和直接变换模型的计算用时分别记为t1、t2，如表 1所示，分辨率为0.1°×0.1°时两种模型的计算误差统计情况如表 2所示。
| s | |||
| 分辨率 | 1°×1° | 0.5°×0.5° | 0.1°×0.1° |
| t1 | 4.391 | 11.313 | 275.391 |
| t2 | 0.469 | 1.813 | 45.359 |
| m | ||||
| 计算误差 | Δx′3 | Δy′3 | Δx″3 | Δy″3 |
| 最大值 | 7.1×10－4 | 9.3×10－10 | 1.4×10－8 | 9.3×10－10 |
| 最小值 | －6.3×10－4 | －2.3×10－9 | －2.8×10－8 | －2.8×10－9 |
由表 1可以看出，当分辨率为1°×1°(共37×31个点)时，间接变换模型用时为4.391s，直接变换模型用时仅为0.469s，约为间接变换模型用时的10.7%；当分辨率为0.1°×0.1°(共361×301个点)时，间接变换模型用时为275.391s，直接变换模型用时仅为45.359s，约为间接变换模型用时的16.5%。由表 2可以看出，传统间接变换模型的横坐标计算误差和直接变换模型的横坐标计算误差基本一致，均在10－9m量级；本文建立的直接变换模型的纵坐标计算精度相比于传统间接变换模型提高了4个数量级。
5 结 论本文研究了不同变形性质正轴圆柱投影和正轴圆锥投影间的变换问题，主要结论如下：
(1) 为避免传统间接变换“圆柱→椭球→圆锥”繁琐的计算过程，利用子午线弧长、等量纬度和等面积纬度函数间变换的直接展开式，建立了不同变形性质正轴圆柱投影和正轴圆锥投影间的直接变换模型，无需反解大地纬度即可实现投影变换。
(2) 本文建立的直接变换模型为含参考椭球第一偏心率的符形式，可解决两类投影在不同参考椭球下的变换问题，适合于计算机编程计算。
(3) 以等角正轴圆锥投影变换至等面积正轴圆柱投影为例，对本文建立的直接变换模型的有效性和快捷性进行了分析。结果表明，与传统间接变换模型相比，本文建立的直接变换模型提高了计算效率和计算精度。
| [1] | LI Guozao,YANG Qihe,HU Dingquan.Map Projections[M].Beijing:PLA Press,1993.(李国藻,杨启和,胡定荃.地图投影[M].北京:解放军出版社,1993.) |
| [2] | SUN Da,PU Yingxia.Map Projections[M].Nanjing:Nangjing University Press,2005.(孙达,蒲英霞.地图投影[M].南京:南京大学出版社,2005.) |
| [3] | YANG Qihe.The Theory and Method of Map Projection[M].Beijing:PLA Press,1989.(杨启和.地图投影变换原理与方法[M].北京:解放军出版社,1989.) |
| [4] | YANG Q H,SNYDER J P,TOBLER W R.Map Projection Transformation:Principles and Applications[M].London:Taylor&Francis,2000. |
| [5] | SNYDER J P.Map Projections-a Working Manual[M].Washington:U.S.Government Printing Office,1987. |
| [6] | YANG Xiaomei,YANG Qihe.A Reseach on the Transformation Models between Coordinates of Cylindrical and Conic Projections[J].Bulletin of Surveying and Mapping,1999(2):5-8.(杨晓梅,杨启和.圆锥投影和圆柱投影坐标变换模型研究[J].测绘通报,1999(2):5-8.) |
| [7] | ADAMS O S.Latitude Developments Connected with Geodesy and Cartography with Tables,Including a Table for Lambert Equal-area Meridional Projection[M].Washington DC:Government Printing Office,1921. |
| [8] | SUN Qun,YANG Qihe.The Research on the Computation of the Foot-point Latitude and the Inverse Solution of Isometric Latitude and Area Function[J].Journal of PLA Institute of Surveying and Mapping,1985(2):64-75.(孙群,杨启和.底点纬度解算以及等量纬度和面积函数反解问题的探讨[J].解放军测绘学院学报,1985(2):64-75.) |
| [9] | YANG Qihe,YANG Xiaomei.Three Kinds of Latitude Functions in Surveying and Mapping and Their Inverse Solution Using the Linear Interpolation Method[J].Acta Geodaetica et Cartographica Sinica,1997,26(1):92-93.(杨启和,杨晓梅.测量和地图学中应用的三种纬度函数及其反解变换的线性插值方法[J].测绘学报,1997,26(1):92-93.) |
| [10] | CRAIG R.Auxiliary Latitude Formulas:Finding the Coefficients Numerically and Symbolically[C]//Proceedings of Wolfram Technology Conference.America:Champaign,2006. |
| [11] | BIAN S F,CHEN Y B.Solving an Inverse Problem of a Meridian Arc in Terms of Computer Algebra System[J].Journal of Surveying Engineering,2006,132(1):7-10. |
| [12] | BIAN Shaofeng,JI Bing.The Expansions of Rectifying Latitude,Conformal Latitude and Authalic Latitude[J].Acta Geodaetica et Cartographica Sinica,2007,36(2):218-223.(边少锋,纪兵.等距离纬度等量纬度和等面积纬度展开式[J].测绘学报,2007,36(2):218-223.) |
| [13] | LI Houpu,BIAN Shaofeng.Derivation of Inverse Expansions for Auxiliary Latitudes by Hermite Interpolation Method[J].Geomatics and Information Science of Wuhan University,2008,33(6):623-626.(李厚朴,边少锋.辅助纬度反解公式的Hermite插值法新解[J].武汉大学学报:信息科学版,2008,33(6):623-626.) |
| [14] | WANG Rui,LI Houpu.The Derivation of the Inverse Expansions for Auxiliary Latitudes by Lagrange Series Method[J].Hydrographic Surveying and Charting,2008,28(3):18-23.(王瑞,李厚朴.辅助纬度反解公式的Lagrange级数法推演[J].海洋测绘,2008,28(3):18-23.) |
| [15] | BIAN Shaofeng,XU Jiangning.Computer Algebra System and Mathematical Analysis in Geodesy[M].Beijing:National Defense Industry Press,2004.(边少锋,许江宁.计算机代数系统与大地测量数学分析[M].北京:国防工业出版社,2004.) |
| [16] | LI Houpu.The Research of the Precise Computation Theory and Its Application Based on Computer Algebra System for Geodetic Coordinate System[D].Wuhan:Naval University of Engineering,2010.(李厚朴.基于计算机代数系统的大地坐标系精密计算理论及其应用研究[D].武汉:海军工程大学,2010.) |
| [17] | LI Houpu,LIU Min,KONG Haiying,et al.The Direct Expansions for Transformations between Meridian Arc and Authalic Latitude Function[J].Hydrographic Surveying and Charting,2011,31(1):17-19.(李厚朴,刘敏,孔海英,等.子午线弧长和等面积纬度函数变换的直接展开式[J].海洋测绘,2011,31(1):17-19.) |
| [18] | LI Houpu,BIAN Shaofeng,CHEN Liangyou.The Direct Calculating Formulae for Transformations between Authalic Latitude Function and Isometic Latitude[J].Geomatics and Information Science of Wuhan University,2011,36(7):843-846.(李厚朴,边少锋,陈良友.等面积纬度函数和等量纬度变换的直接解算公式[J].武汉大学学报:信息科学版,2011,36(7):843-846.) |
| [19] | CHEN Junyong.Chinese Modern Geodetic Datum-Chinese Geodetic Coordinate System 2000(CGCS2000) and Its Frame[J].Acta Geodaetica et Cartographica Sinica,2008,37(3):269-271.(陈俊勇.中国现代大地基准:中国大地坐标系统2000(CGCS2000)及其框架[J].测绘学报,2008,37(3):269-271.) |
| [20] | CHENG Pengfei,WEN Hanjiang,CHENG Yingyan,et al.Parameters of the CGCS2000 Ellipsoid and Comparisons with GRS80 and WGS84[J].Acta Geodaetica et Cartographica Sinica,2009,38(6):189-194.(程鹏飞,文汉江,成英燕,等.2000国家大地坐标系与GRS80和WGS84的比较[J].测绘学报,2009,38(6):189-194.) |