2. 甘肃铁道综合工程勘察院有限公司, 甘肃 兰州 730000;
3. 中铁第一勘察设计院集团有限公司, 陕西 西安 710043;
4. 海军驻天津地区航保军事代表室, 天津 300042
2. The General Engineering Survey Institute of Railways of Gansu co., LTD, Lanzhou 730000, China;
3. China Railway First Survey and Design Institute Group co., LTD, Xi'an 710043, China;
4. Military Delegate Office of Naval Navigation Guarantee in Tianjin, Tianjin 300042, China
近年来,极区日益成为国际争相关注的热点,选择合适的投影方式对于极区导航及极区科考具有重要意义[1-4]。高斯投影作为我国常用的一种等角投影方式,常用于大比例尺地形图的绘制。国内外学者对于高斯投影进行了广泛的研究,现有著作中关于高斯投影的研究成果包括高斯投影实数型幂级数展开式[5-8],高斯投影复变函数表达式[9-15],极区高斯投影表示等[16-17]。目前关于高斯投影的研究已经卓有成效。但是,各公式又受一定限制,如实数型公式常用于分带高斯投影,仅在经差较小的条带内适用;复变函数表达式中虽消除了分带的限制,但是由于等量纬度在极区的奇异现象,使得复变函数公式难以在极区应用;文献[16]中将地球视为球体,给出了球面极区高斯投影的闭合公式,虽实现了极区的统一表示,但不能满足极区高精度制图等工作;文献[17]给出了适用于极区的高斯投影复变函数公式,但在求得复数等角余纬度的过程中,使用了极点附近球近似的方法,一定程度上影响了正解推导过程的严密性。此外,文献[17]仅给出了极区高斯投影的正解公式,而相应反解公式、长度比及子午线收敛角公式并没有给出。鉴于此,为满足极区应用需求,完善高斯投影数学基础,本文拟通过严格的数学推导过程,给出理论上更严密的、可用于完整表示极区的高斯投影正解表达式、反解表达式,及对应的长度比和子午线收敛角公式。
1 非极区高斯投影表达式由文献[15]可知,高斯投影正解的非迭代复变函数表达式为
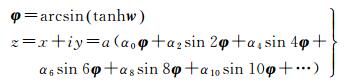 (1)
(1)
式中,a为地球长半轴,系数α0、α2、…、α10为地球椭球第一偏心率e的幂级数和,可由子午线弧长展开式确定,参见文献[15]。φ、w分别为复变函数开拓后的复数等角纬度和复数等量纬度
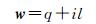 (2)
(2)
式中,q为等量纬度;l为大地经度。其中,等量纬度q为大地纬度B的表达式
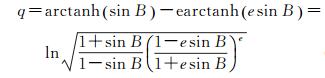 (3)
(3)
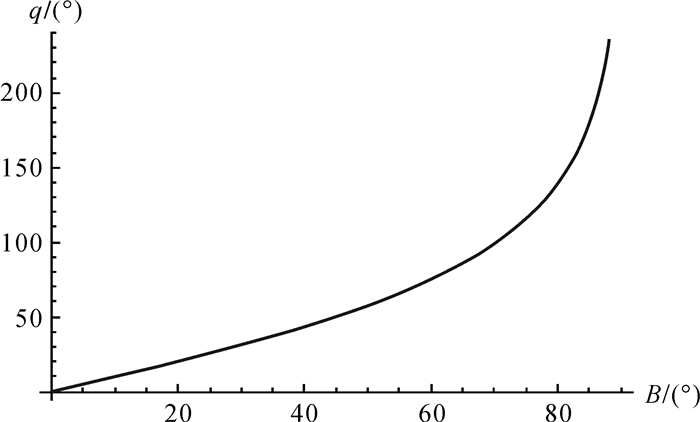
考虑到关系式arctanh(sin(-B))=-arctanh(sinB)和arctanh(esin(-B))=-arctanh(esinB),可得q(-B)=-q(B),即等量纬度q是大地纬度B的奇函数。当大地纬度B∈[0°, 90°]时,等量纬度q的变化曲线如图 1所示。
|
| 图 1 等量纬度q随大地纬度B的变化曲线 Fig. 1 Sketch of isometric latitude q with geodetic latitude B |
由图 1可以看出,在大地纬度B∈[0°, 90°]时,等量纬度q随着大地纬度B的增大而增大。当大地纬度B→90°时,等量纬度q趋向于无穷,考虑到函数的奇偶性,可知当点位于两极地区时,等量纬度q均出现奇异现象,进而使得式(2) 中的复数等量纬度w及式(1) 中的复数等角纬度φ奇异,以至于高斯投影公式(1) 难以在极区直接应用。
此外,由于式(1) 中tanhw=tanh(q+il),展开后包含tanh(il)=itan l,不适于经差l趋于±90°的情况,因此表达式(1) 一般用于区间D={(B, l):|l|<90°, |B|<90°}的绘图,如图 2所示。
|
| 图 2 非极区高斯投影示意图 Fig. 2 Sketch of Gauss projection in nonpolar region |
2 极区高斯投影正解表达式
为推导出可应用于极区的高斯投影公式,必须将式(1) 进行等价变换,由于该式是将子午线弧长公式进行复数开拓而得,因此可先将子午线弧长公式进行等价变形,根据文献[15]可知,子午线弧长X关于等角纬度φ的表达式为
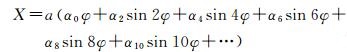 (4)
(4)
式中,系数α0、α2、…、α10同式(1)。根据文献[7]可知,等角纬度φ关于大地纬度B的表达式为
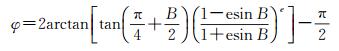 (5)
(5)
当点位于北半球时,大地纬度B、等角纬度φ为正;当位于南半球时,大地纬度B、等角纬度φ为负。
2.1 极区高斯投影正解复数公式当大地纬度B趋于90°时,等角纬度φ出现奇异。为消除奇异,可引入等角余纬度θ
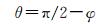 (6)
(6)
将式(6) 代入式(4),则子午线弧长X可以表示成关于等角余纬度θ的表达式
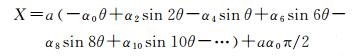 (7)
(7)
显然,式(7) 的奇异性取决于式中唯一的变量θ,为判断θ是否奇异,将式(5) 代入式(6),可得等角余纬度θ的表达式为
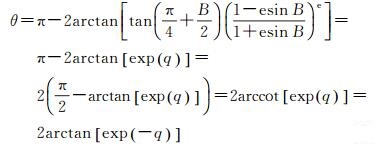 (8)
(8)
根据指数函数与对数函数互为反函数关系exp(lnx)≡x恒成立,可将q的表达式(3) 代入,可得
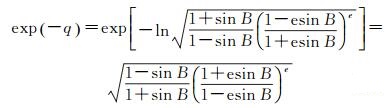 (9)
(9)
将式(9) 代入式(8),可知在大地纬度B=90°时,θ=0,即在北极点等角余纬度θ及式(7) 均不奇异。因此,可基于式(7),参考非极区高斯投影公式的推导过程,将子午线弧长X及等量纬度q向复数域开拓,进而得到极区高斯投影复变函数公式。
首先,根据复变函数的定义,用w=q+il代替式(8) 中的q,实现等角余纬度θ由实数域向复数域解析开拓,得到复数等角余纬度θ
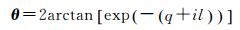 (10)
(10)
然后,以θ取代式(7) 中的θ,将式中的子午线弧长X变成高斯复数坐标z=x+iy(其中实部x为高斯纵坐标,虚部y为高斯横坐标),可得高斯投影表达式。为方便极区制图,再将表达式的零点由赤道移至北极点,即将纵坐标减去1/4子午线弧长(aα0π/2),而横坐标保持不变。在不引起混淆的情况下,平移后的纵、横坐标仍然使用(x, y)表示,略去推导,可得
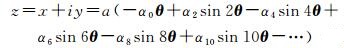 (11)
(11)
至此,可用于北极地区的高斯投影正解公式已推导完成,其正确性可由以下条件进行保证[18-19]:
(1) 当经差l为0°时,横坐标分量y=0,中央经线被表示成一条纵线;当纬度B为0°时,纵坐标分量x=-aα0π/2,赤道被表示成一条横线;与非迭代高斯投影复变函数式(1) 相比,该投影公式的坐标原点沿纵坐标发生平移,投影本质并未产生改变,中央经线及赤道为投影的对称轴。高斯投影第一个条件“中央经线和赤道为互相垂直的直线,而且为投影的对称轴”得以满足。
(2) 以上一系列变换均为复变函数的初等变换,且在主值范围内为单值解析函数,满足柯西―黎曼方程,变换过程中均保持等角性质。高斯投影第二个条件“投影无角度变形”得以满足。
(3) 当经差l为0°时,纵坐标分量x值减去赤道对应纵坐标值即为投影后的中央经线长度,它与自赤道起算至纬度B的子午线弧长相等,高斯投影第三个条件“中央经线投影后保持长度不变”得以满足。
2.2 极区高斯投影正解实数公式为了将复数等角余纬度θ表示成实部与虚部分开的形式,即θ=u+iv,利用关系式q=arctanh(sin φ)和exp(q+il)=exp(q)(cos l+isin l),根据复变函数与反正切函数的关系,可得
 (12)
(12)
经过变换,复数等角余纬度θ可被表示成实部与虚部分开的形式
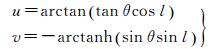 (13)
(13)
由式(13) 可以看出,当大地纬度B接近于90°时,θ→0,且经差l的取值范围可达到[-180°, 180°],即在北半球任一点上,复数等角余纬度θ均有一个确定的值,不存在奇异现象。
借助关系式sin(u+iv)=sin ucos iv+cos usin iv,sin iv=isinh v和cos iv=cosh v,将式(11) 的实部与虚部分开,可分别得高斯投影的纵、横坐标
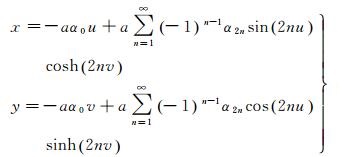 (14)
(14)
至此,可用于北极地区的高斯投影实数公式已推导完成。
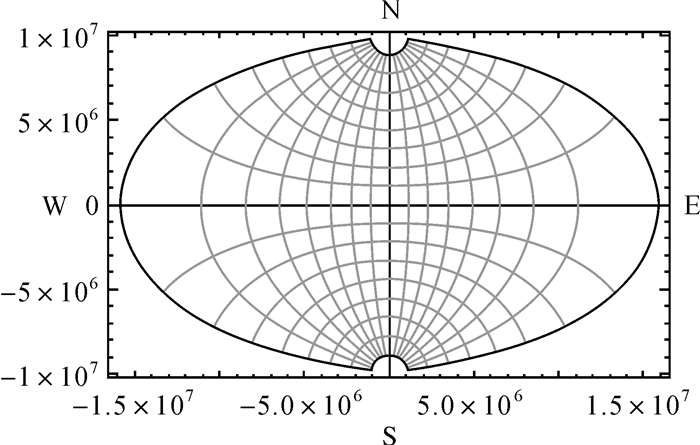
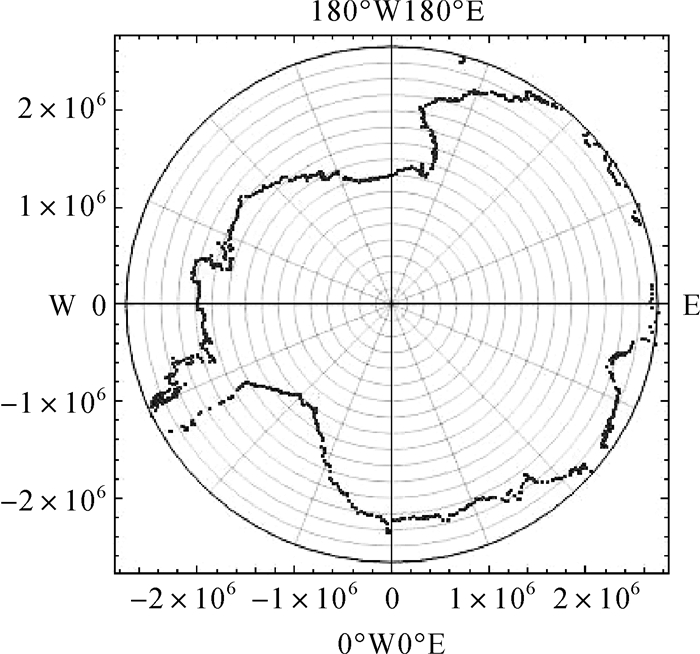
考虑到地球参考椭球的对称性,无需另外推算南极地区高斯投影公式。由于南半球与北半球相对于赤道面对称,可将地球椭球南极视为“新北极”,将南半球的点P(B, l)替换为P(-B, l)后,代入北极高斯投影公式中,即可获得与北极地图相同视角的南极地图,如图 3、图 4所示。

|
| 图 3 北极高斯投影示意图 Fig. 3 Sketch of Gauss projection in Arctic region |
|
| 图 4 南极高斯投影示意图 Fig. 4 Sketch of Gauss projection in Antarctic region |
由图 3、4可以看出,基于极区高斯投影公式,南、北极圈范围内被完整的展示。通过将高斯投影的坐标原点平移至极点,当经差|Δl|<90°时,高斯纵坐标为负,当经差|Δl|>90°,高斯纵坐标为正。经差Δl=0°, ±90°, ±180°的经线经投影后表示为直线,且这些直线为高斯坐标的对称轴。
3 极区高斯投影反解表达式为完善高斯投影数学体系,在推导出极区高斯投影正解表达式后,研究如何根据投影坐标反解其大地坐标具有重要意义。以下将给出详细的反解过程:
首先,可借助拉格朗日反解方法[20-21]或符号迭代法[22-23],推导出由北极地区高斯坐标x+iy反解复数等角余纬度θ的直接符号表达式。略去推导过程,有
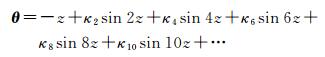 (15)
(15)
式中,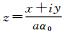
 (16)
(16)
然后,根据exp(-il)=cosl-isinl关系式,可将式(10) 等价变换为
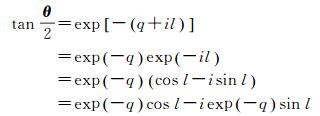 (17)
(17)
将式(17) 分解成实部与虚部分开的形式后,令
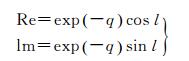 (18)
(18)
将式(18) 中的两式平方后相加,由exp(-q)>0,可以求得
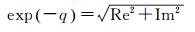 (19)
(19)
将式(19) 代入式(8),可得等角余纬度θ为
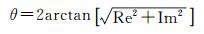 (20)
(20)
进而可得等角纬度φ=π/2-θ,代入等角纬度反解表达式,可求得大地纬度B为
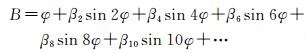 (21)
(21)
式中,系数β2、β4、…、β10可参见文献[15]。
当在极点处,高斯投影坐标为(0, 0),由上述过程可反解出纬度为B=π/2,此时该点不存在经差,可定义该点的经差为l=0。当B≠π/2时,根据式(18) 可将经差l分情况讨论
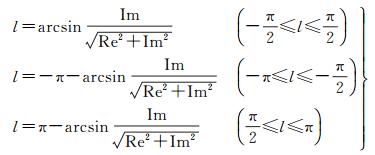 (22)
(22)
至此,无带宽限制的极区高斯投影反解表达式完成。同理,根据地球椭球的对称性,将根据以上公式求得的大地坐标P(B, l)改为P(-B, l),即可实现南极地区的高斯投影反解过程。
4 极区长度比和子午线收敛角公式在对高斯投影进行性质分析时,必然要推导出对应的长度比和子午线收敛角公式。借助复变函数来求解高斯投影问题时,尺度比和子午线收敛角就是解析函数在某点处的导数
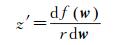 (23)
(23)
式中,r=NcosB,N为卯酉圈曲率半径。根据长度比和子午线收敛角的定义可知,长度比m为该导数的模,子午线收敛角γ为该导数幅角的反向,即
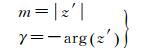 (24)
(24)
为求得式(23) 的具体表示形式,可将其等价变形为
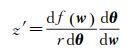 (25)
(25)
根据北极地区高斯投影正解公式,可得
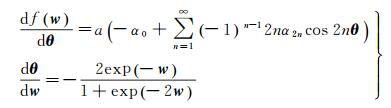 (26)
(26)
将式(26) 代入(25) 式,经化简可得
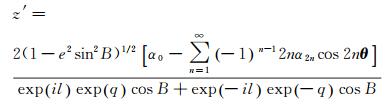 (27)
(27)
可以看出,式(27) 的分母中包含cosB,当在极点处B=90°时,分母为0。为消除式(27) 在北极点的奇异性,引入式(9),可得
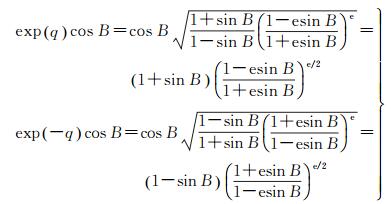 (28)
(28)
将式(28) 代入式(27),并化简可得
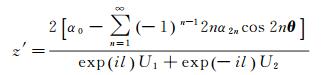 (29)
(29)
式中,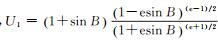
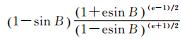
可以发现,当B=90°时,有θ=0,sinB=1,U1≠0,U2=0,式(29) 分母不为0。即,经一系列变换后,极区高斯投影长度比和子午线收敛角公式已不存在奇异现象,可以满足北极地区应用需求。
根据地球参考椭球的对称性,将南半球的点P(B, l)替换为P(-B, l),代入北极高斯投影正解表达式,获得与北极地图相同视角的南极地图后,则南极地区相应的长度比和子午线收敛角公式可采用同样的方法进行解算。
5 算例分析改进后的极区高斯投影公式与文献[15]中的公式仅在数值上相差1/4子午线弧长,实现了将投影中心平移到极点,并通过一系列数学变换,消去了文献[15]中公式在极点奇异的问题。由于在推导改进公式的过程中具有严谨的数学关系,故不需再与文献[15]中公式对比来验证改进后表达式的正确性。为验证本文推导公式的正确性及适用性,以下构建3个算例。
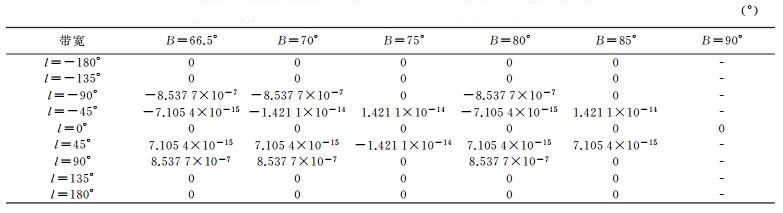
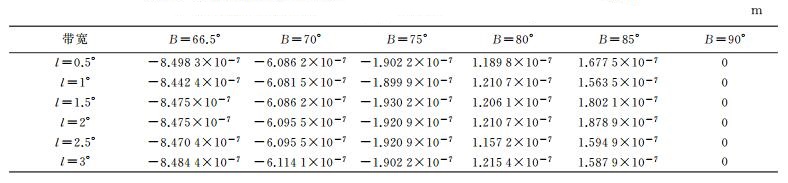
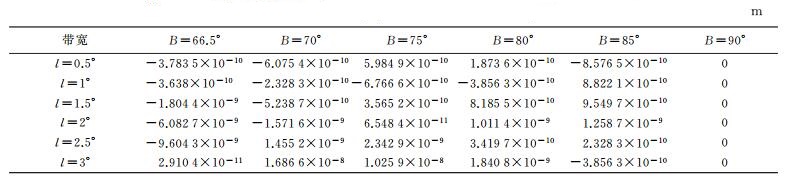
5.1 正解表达式的正确性验证为验证极区高斯投影正解公式的正确性,此处将展开至e10的本文公式与文献[8]中展开至经差的7次幂l7,并将原点平移至极点的高斯投影实数型幂级数展开式进行比较。以CGCS2000椭球(长半轴a=6 378 137 m,扁率f=1/298.257 222 101) 为例,在北极圈半个6°带宽P1={B∈[66.5°, 90°], l∈[0, 3°]}范围内,分别利用这两种公式计算高斯投影坐标,记Δx、Δy分别为这两种公式的纵、横坐标之差,具体数值分别列于表 1、表 2。
|
|
从表 1、2可以看出,与文献[8]中高斯投影实数型幂级数展开式计算的投影坐标相比,利用本文极区高斯投影正解公式计算的投影纵坐标差异量级在10-7 m,横坐标差异量级在10-8 m。在大地测量及制图作业中,这些差异可以忽略不计。该算例进一步在数值上证明极区高斯投影正解表达式的正确性。
5.2 反解表达式的正确性验证为验证极区高斯投影反解表达式的正确性,通过给定大地坐标的真值,先利用正解公式计算出严格的极区高斯投影坐标;再利用反解公式由高斯投影坐标推导出大地坐标的计算值;最后,将其与大地坐标真值进行比较,并将纬度、经差的差异值分别列于表 3、表 4。
从表 3、表 4可以看出,根据正解公式计算出极区高斯投影坐标后,再利用反解公式可解算出大地坐标的解算值,与大地坐标真值相比,其差异量级在10-7°,约为0.003″。在极点处,可利用本文反解公式计算出大地纬度值为B=90°,由于在该点处,经差失去意义,上文已定义该点经差为l=0°。该算例进一步在数值上证明极区高斯投影反解表达式的正确性。
5.3 长度比与子午线收敛角公式的适用性验证参照5.1节,在北极圈半个6°带宽范围内,与文献[8]中的实数型幂级数展开式进行比较,验证本文推导的长度比和子午线收敛角公式的正确性。为节省篇幅,此处不再赘述。
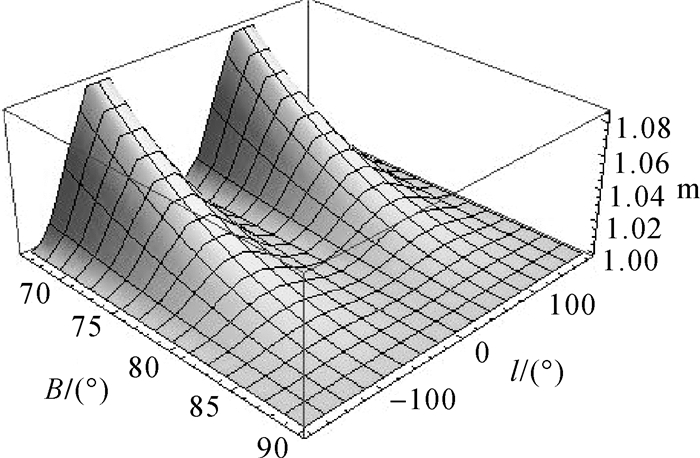
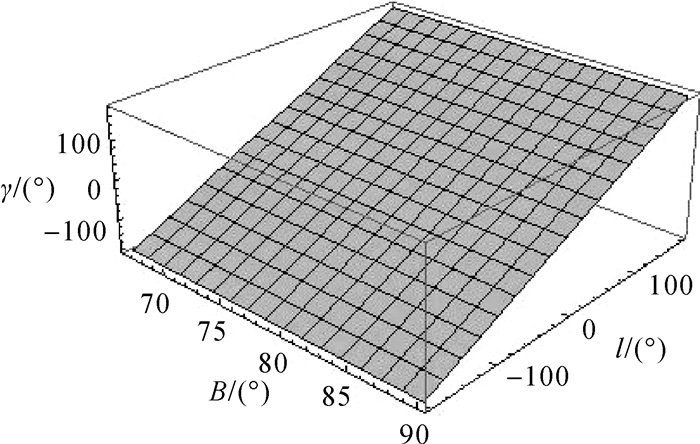
由于传统的高斯投影实数型公式被表示成经差的幂级数形式,而高斯投影平面被表示成分带的形式,以至于难以对极区进行一个完整的表示。由文中2、3节及算例5.2部分可以看出,极区高斯投影正、反解表达式可用于整个极区的表示。为说明本文推导出的长度比及子午线收敛角公式的适用性,可借助计算机代数系统[24-25]绘制出北极圈内P2={B∈[66.5°, 90°], l∈[-180°, 180°]}高斯投影长度比和子午线收敛角示意图,分别如图 5、图 6所示。
|
| 图 5 极区范围内高斯投影长度比 Fig. 5 Length deformation in polar region |
|
| 图 6 极区范围内高斯投影子午线收敛角 Fig. 6 Meridian convergence in polar region |
图 5、6中,投影长度比及子午线收敛角公式可以适用于整个极区。其中,投影长度比关于l=0°, ±90°, ±180°的经线对称;在l=0°, ±180°的经线上,投影长度比m=1。在l∈(0°, 180°)范围内,当纬度B一定时,即在同一纬线上,长度比先增大后减小,并在l=90°时出现最大值;在同一经线上,长度比随着纬度的增加而逐渐减小。图 6中,在l∈[-180°, 180°]范围内,子午线收敛角的值随着经差的增大而逐渐递增,并在l=0°的经线上,其值为0。
由于实数型幂级数形式的长度比和子午线收敛角公式通常用于分带的高斯投影,适用范围受到带宽的限制,而本文推导的长度比和子午线收敛角表达式可适用于整个极区范围,对于极区航海具有重要的参考价值。
6 结束语针对传统高斯投影公式在极区难以应用的问题,对高斯投影复变函数公式进行改进,推导出可应用于表示整个极区的高斯投影正、反解表达式,及对应的长度比和子午线收敛角公式,得出结论如下:
(1) 建立等角余纬度和等量纬度间的关系式,对其进行复数开拓,推导出理论严密的极区高斯投影正解表达式;借助符号迭代法,及指数函数与三角函数间的关系式,推导出可用于极区的高斯投影反解表达式。由于改进后的公式避免了极点奇异性,解决了传统高斯投影公式难以在极区应用的问题,对于完善高斯投影的数学体系具有重要意义。
(2) 在极区范围内,与实数型幂级数投影公式相比,利用本文正解公式计算的投影纵坐标差异量级为10-7 m,横坐标差异量级为10-8 m;与大地坐标真值相比,本文反解展开式计算的精度约为0.003″;这些差异在测量及制图学中可忽略不计,进一步从数值上验证了本文推导公式的正确性。
(3) 与实数型幂级数长度比及子午线收敛角公式相比,本文推导的极区高斯投影长度比和子午线收敛角公式消除了带宽的限制,可适用于整个极区范围,对于编制极区地图及极区航海导航具有重要参考价值。
| [1] | 李树军, 张哲, 李惠雯, 等. 编制北极地区航海图有关问题的探讨[J]. 海洋测绘, 2012, 32(1): 58–60. LI Shujun, ZHANG Zhe, LI Huiwen, et al. Research on Compilation of Nautical Charts of Arctic Regions[J]. Hydrographic Surveying and Charting, 2012, 32(1): 58–60. |
| [2] | 李振福, 李漪. 北极航线的世界航运网络格局影响分析[J]. 世界地理研究, 2014, 23(1): 1–9. LI Zhenfu, LI Yi. The Impact of the Arctic Route on the Global Shipping Network[J]. World Regional Studies, 2014, 23(1): 1–9. |
| [3] | 杨元喜, 徐君毅. 北斗在极区导航定位性能分析[J]. 武汉大学学报(信息科学版), 2016, 41(1): 15–20. YANG Yuanxi, XU Junyi. Navigation Performance of BeiDou in Polar Area[J]. Geomatics and Information Science of Wuhan University, 2016, 41(1): 15–20. |
| [4] | 刘文超, 卞鸿巍, 王荣颖, 等. 惯性导航系统极区导航参数解算方法[J]. 上海交通大学学报, 2014, 48(4): 538–543. LIU Wenchao, BIAN Hongwei, WANG Rongying, et al. A Calculating Method of Polar Navigation Parameters for Inertial Navigation System[J]. Journal of Shanghai Jiaotong University, 2014, 48(4): 538–543. |
| [5] | 王清华, 鄂栋臣, 陈春明, 等. 南极地区常用地图投影及其应用[J]. 极地研究, 2002, 14(3): 226–233. WANG Qinghua, E Dongchen, CHEN Chunming, et al. Popular Map Projections in Antarctica and Their Application[J]. Chinese Journal of Polar Research, 2002, 14(3): 226–233. |
| [6] | LAUF G B. Geodesy and Map Projections[M].Collingwood: TAFE Publications, 1983. |
| [7] | YANG Q H, SNYDER J P, TOBLER W R. Map Projection Transformation: Principles and Applications[M].London: Taylor & Francis, 2000. |
| [8] | 熊介. 椭球大地测量学[M].北京: 解放军出版社, 1988. XIONG Jie. Ellipsoidal Geodesy[M].Beijing: PLA Press, 1988. |
| [9] | BERMEJO-SOLERA M, OTERO J. Simple and Highly Accurate Formulas for the Computation of Transverse Mercator Coordinates from Longitude and Isometric Latitude[J]. Journal of Geodesy, 2009, 83(1): 1–12. DOI:10.1007/s00190-008-0224-y |
| [10] | KARNEY C F F. Transverse Mercator with an Accuracy of a Few Nanometers[J]. Journal of Geodesy, 2011, 85(8): 475–485. DOI:10.1007/s00190-011-0445-3 |
| [11] | SNYDER J P. Map Projections—a Working Manual[M].Washington D.C.: Government Printing Office, 1987. |
| [12] | 李厚朴, 边少锋. 高斯投影的复变函数表示[J]. 测绘学报, 2008, 37(1): 5–9. LI Houpu, BIAN Shaofeng. The Expressions of Gauss Projection by Complex Numbers[J]. Acta Geodaetica et Cartographica Sinica, 2008, 37(1): 5–9. DOI:10.3321/j.issn:1001-1595.2008.01.002 |
| [13] | 边少锋, 张传定. Gauss投影的复变函数表示[J]. 测绘学院学报, 2001, 18(3): 157–159. BIAN Shaofeng, ZHANG Chuanding. The Gauss Projection—a Solution by Complex Numbers[J]. Acta Geodaetica et Cartographica Sinica, 2001, 18(3): 157–159. |
| [14] | BOWRING B R. The Transverse Mercator Projection—a Solution by Complex Numbers[J]. Survey Review, 1990, 30(237): 325–342. DOI:10.1179/003962678791965183 |
| [15] | 李厚朴, 边少锋, 钟斌. 地理坐标系计算机代数精密分析理论[M].北京: 国防工业出版社, 2015. LI Houpu, BIAN Shaofeng, ZHONG Bin. Precise Analysis Theory of Geographic Coordinate System by Computer Algebra[M].Beijing: National Defense Industry Press, 2015. |
| [16] | 张晓平, 边少锋, 李忠美. 极区高斯投影与日晷投影的比较[J]. 武汉大学学报(信息科学版), 2015, 40(5): 667–672. ZHANG Xiaoping, BIAN Shaofeng, LI Zhongmei. Comparisons Between Gauss and Gnomonic Projections in Polar Regions[J]. Geomatics and Information Science of Wuhan University, 2015, 40(5): 667–672. |
| [17] | 边少锋, 李忠美, 李厚朴. 极区非奇异高斯投影复变函数表示[J]. 测绘学报, 2014, 43(4): 348–352. BIAN Shaofeng, LI Zhongmei, LI Houpu. The Non-singular Formula of Gauss Projection in Polar Regions by Complex Numbers[J]. Acta Geodaetica et Cartographica Sinica, 2014, 43(4): 348–352. DOI:10.13485/j.cnki.11-2089.2014.0052 |
| [18] | 孙达, 蒲英霞. 地图投影[M].南京: 南京大学出版社, 2005. SUN Da, PU Yingxia. Map Projections[M].Nanjing: Nanjing University Press, 2005. |
| [19] | 李国藻, 杨启和, 胡定荃. 地图投影[M].北京: 解放军出版社, 1993. LI Guozao, YANG Qihe, HU Dingquan. Map Projections[M].Beijing: PLA Press, 1993. |
| [20] | ADAMS O S. Latitude Developments Connected with Geodesy and Cartography with Tables, Including a Table for Lambert Equal-area Meridional Projection[M].Washington: Government Printing Office, 1921. |
| [21] | 过家春, 赵秀侠, 吴艳兰. 空间直角坐标与大地坐标转换的拉格朗日反演方法[J]. 测绘学报, 2014, 43(10): 998–1004. GUO Jiachun, ZHAO Xiulan, WU Yanlan. Transformation from Cartesian to Geodetic Coordinates Using Lagrange Inversion Theorem[J]. Acta Geodaetica et Cartographica Sinica, 2014, 43(10): 998–1004. DOI:10.13485/j.cnki.11-2089.2014.0152 |
| [22] | 李忠美, 边少锋, 孔海英. 符号迭代法解算椭球大地测量学反问题[J]. 海洋测绘, 2013, 33(1): 27–29, 33. LI Zhongmei, BIAN Shaofeng, KONG Haiying. Symbolic Iterative Method for Solving Inverse Problems in Ellipsoidal Geodesy[J]. Hydrographic Surveying and Charting, 2013, 33(1): 27–29, 33. |
| [23] | 陈成, 边少锋, 李厚朴. 一种解算椭球大地测量学反问题的方法及应用[J]. 海洋测绘, 2015, 35(6): 8–13. CHEN Cheng, BIAN Shaofeng, LI Houpu. A Method for Solving Inverse Problems in Ellipsoidal Geodesy and Its Application[J]. Hydrographic Surveying and Charting, 2015, 35(6): 8–13. |
| [24] | BIAN Shaofeng, LI Houpu. Mathematical Analysis in Cartography by Means of Computer Algebra System[C]//BATEIRA C. Cartography—A Tool for Spatial Analysis. Croatia: InTech, 2012. |
| [25] | BIAN Shaofeng, CHEN Yongbing. Solving An Inverse Problem of a Meridian Arc in terms of Computer Algebra System[J]. Journal of Surveying Engineering, 2006, 132(1): 7–10. DOI:10.1061/(ASCE)0733-9453(2006)132:1(7) |