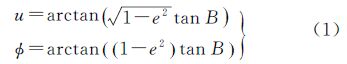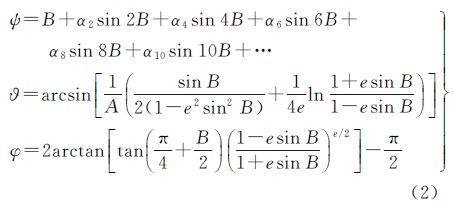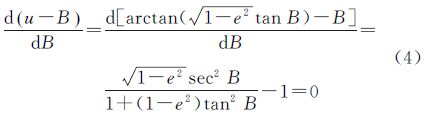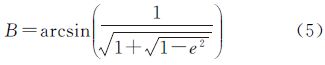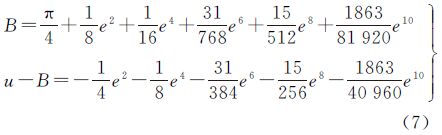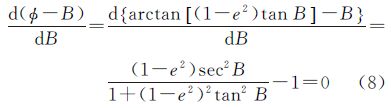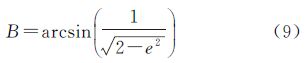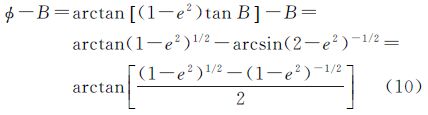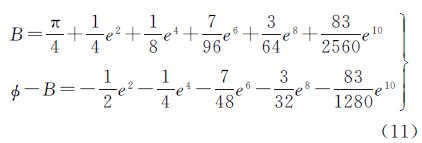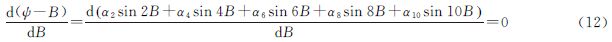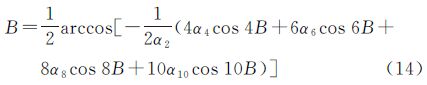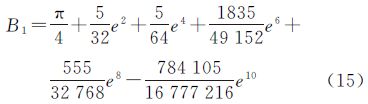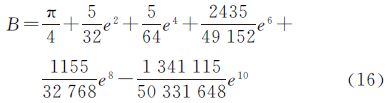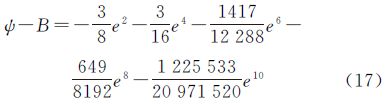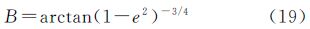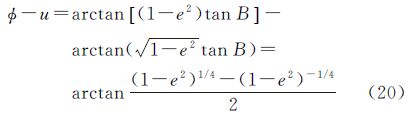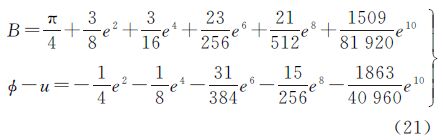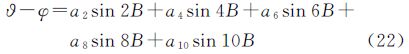2. 中国科学院 测量与地球物理研究所,湖北 武汉 430077
2. Institute of Geodesy and Geophysics,Chinese Academy of Sciences,Wuhan 430077,China
1 引 言
大地纬度是测量和地球科学计算中最常用的一种纬度,但是在测量和地图投影理论推导中,为满足某种投影性质,也常会用到其他5种辅助纬度(地心纬度、归化纬度、等距离纬度、等角纬度和等面积纬度)的概念[1, 2, 3, 4]。随着空间技术和计算机技术在大地测量及地图学中的应用和发展,研究大地纬度及其他5种辅助纬度间的关系以及它们之间的差异问题具有更加重要的实用价值。对于这一问题,国内外许多学者进行了深入研究,取得了显著成果。文献[4]推算出了大地纬度、地心纬度、归化纬度之间的关系以及它们的拉格朗日共轭级数展开式;文献[5, 6, 7, 8, 9, 10, 11]人工推导出了等角纬度、等面积纬度及等距离纬度展至sin8B展开式;文献[12, 13, 14, 15, 16]借助具有强大数学分析功能的计算机代数系统[17, 18, 19]推算出等面积纬度、等角纬度及等距离纬度的偏心率e的幂级数展开式,发现和纠正了人工推导的正解公式中某些项的偏差,推导出的系数具有更高的精确度。
从目前来看,前人对这一领域做了很多卓有成效的工作,但是却鲜有文献将这几种常用纬度进行系统比较。为丰富对这一问题的研究,使人们对这几种常用纬度形成较直观的认识,本文着重研究了常用纬度间的差异极值问题,推导出了常用纬度间差异极值点及对应差异极值的符号表达式,最后以CGCS2000参考椭球[20]为例,对常用纬度间的差异进行了数值分析和对比。
2 常用纬度定义根据文献[3]可知,归化纬度u、地心纬度Φ是大地测量学中常用纬度,记椭球偏心率为e,则它们关于大地纬度B的表达式为
又由文献[13]可知,等距离纬度ψ、等角纬度φ和等面积纬度θ是地图学中常用的3种纬度,它们与大地纬度B的关系式为
式中的系数如下
3 常用纬度间的差异极值符号表达式由于6种常用纬度相差微小,实际应用中经常会用到它们的差值表达式。为了解常用纬度间的差异情况,特别是差异极值点及其对应差异极值,可基于它们之间的差值表达式推导出常用纬度间的差异极值符号表达式。
3.1 辅助纬度与大地纬度差异极值符号表达式通过对辅助纬度与大地纬度的差值表达式进行求导,即可推算出辅助纬度与大地纬度差异极值点的解析表达式。以归化纬度为例
略去推导过程,可得归化纬度与大地纬度差异一阶导数为零的点
将式(5)代入归化纬度与大地纬度差值表达式的二阶导数进行检验,可知二阶导数不为零,即式(5)所示的大地纬度即为所求的差异极值点,将它代入归化纬度与大地纬度的差值表达式,即可推算出差异极值
为方便不同的辅助纬度与大地纬度差异极值间的比较,可进一步将式(5)、式(6)展开成偏心率e的幂级数形式
类似的,对地心纬度与大地纬度的差值表达式进行求导,如式(8)所示
略去推导过程,可得地心纬度与大地纬度差异一阶导数为零时对应的大地纬度
经检验,式(9)所示的大地纬度为极值点,将其代入地心纬度与大地纬度差值表达式,即可推算出地心纬度与大地纬度差异的极值
类似的,将式(9)、式(10)展开为关于偏心率e的幂级数形式
等距离纬度与大地纬度的关系式为关于偏心率e幂级数形式,可通过对它们的差值表达式求导,并利用迭代法推导出等距离纬度与大地纬度的差异极值点及对应的差异极值
即将cos2B项作为等式左边项,其他项移到等式右边,并对等式两端同时取反三角函数
由式(13)可以看出,由于地球椭球偏心率很小,在B∈[0,π/2]范围内,若要满足纬度差值表达式的导数为零,即等式左边首项近似为零,也就是差异极值点在B=π/4附近。
将初值B0=π/4代入式(14)进行迭代,经过1次迭代后的结果为
将B1代入式(14)继续进行第2次迭代,依此类推,可以发现第4次迭代结果与第3次迭代结果相比,它们扩展至e10的展开式中各项系数已不再发生变化,故迭代终止。略去推导过程,得差异极值点的符号表达式,如式(16)所示
将式(16)代入ψ-B表达式中,并对结果进行幂级数展开,可推导出等距离纬度与大地纬度差异的极值,如式(17)所示
由于等角纬度、等面积纬度与大地纬度的关系式形式复杂,求导后不便于解算,又由文献[13]知,它们扩展至sin10B的级数展开式也已具有相当高的精度,等角纬度和等面积纬度的正解展开式的精度均优于10-8″,故可采用与等距离纬度类似的方法,推导出它们与大地纬度的差异极值点及对应的差异极值符号表达式,最后结果列于表 1。
| 差值 | 差异极值点B | 对应差异极值 |
| μ-B | 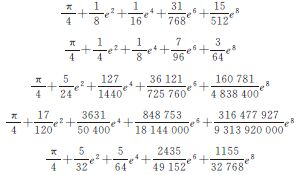 | 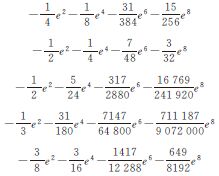 |
| Φ-B | ||
| φ-B | ||
| θ-B | ||
| ψ-B |
由表 1可以看出,各辅助纬度与大地纬度的差异极值点均在B=π/4右侧,且略有不同,各辅助纬度与大地纬度差异极值点按从小到大的顺序依次为:归化纬度、等面积纬度、等距离纬度、等角纬度和地心纬度。辅助纬度中与大地纬度差异极值的绝对值较大的是地心纬度以及等角纬度,且它们与大地纬度的差异极值十分接近;等距离纬度次之,而归化纬度与大地纬度的差异极值的绝对值最小。
3.2 辅助纬度之间差异极值符号表达式为系统地比较各常用纬度之间的差异,除对辅助纬度与大地纬度间的差异进行分析以外,需对辅助纬度之间的差异进行分析。以下分别对大地测量中常用的地心纬度与归化纬度间的差异,地图学中常用的等距离纬度、等角纬度以及等面积纬度之间的差异进行分析。与推导辅助纬度和大地纬度间差异极值点类似,通过对辅助纬度之间的差值表达式进行求导(以地心纬度与归化纬度间为例)
可得经检验,式(19)中所示大地纬度为地心纬度与归化纬度差异极值点,将它代入地心纬度与归化纬度的差值表达式,推算出两者的差异极值
为方便不同极值间的比较,将式(19)、式(20)展开为关于偏心率e的幂级数形式,可得差异极值点及对应极值的级数展开式
与地心纬度和归化纬度不同,地图投影理论中常用的3种纬度关于大地纬度的函数形式复杂,导致它们的差值表达式不便于求导,因此可借助计算机代数系统,将它们间的差值表达式进行级数展开,并按正弦函数的倍角形式将展开结果进行整理,略去推导过程,可得(以等面积纬度与等角纬度的差异极值点为例)
式中系数为对式(22)进行求导并采用迭代法,即可推算出等面积纬度与等角纬度之间的差异极值点。类似的,可推导出等角纬度、等面积纬度分别与等距离纬度间的差异极值点及对应极值,最后结果列于表 2。
| 差值 | 差异极值点 | 对应差异极值 |
| Φ-φ | 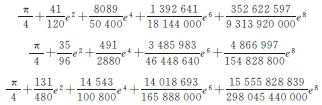 |  |
| ψ-φ | ||
| ψ-Φ |
由表 2可以看出,地图学中常用的3种纬度间的差异极值点均在B=π/4右侧,且存在微小差异。结合表 1可知,它们之间差异极值的绝对值均小于它们与大地纬度差异极值的绝对值,其中,等距离纬度与等面积纬度间差异极值的绝对值最小,而等面积纬度与等角纬度差异极值的绝对值最大。
4 算例分析由于地球椭球偏心率很小,且不同参考椭球的偏心率非常接近。为使人们对各纬度的差异在数值上有一个直观的认识,下面以CGCS2000参考椭球(e=0.081 819 191 042 8)为例,对6种常用纬度间的差异进行数值比较与分析。
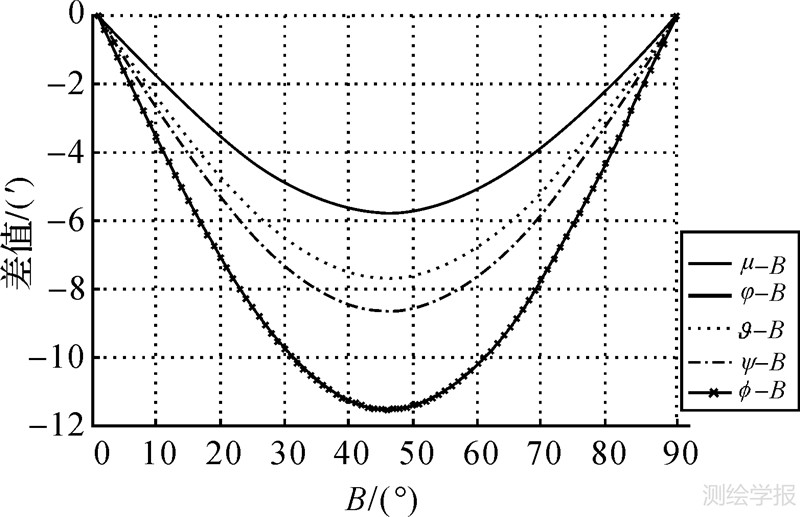
4.1 辅助纬度与大地纬度的差异极值为明确了解各辅助纬度与大地纬度的差异情况,可绘制出大地纬度B∈[0°,90°]范围内,各辅助纬度与大地纬度的差异曲线图,如图 1所示。表 3为大地纬度B∈[0°,90°]时,每隔15°对应的各辅助纬度与大地纬度间的差异。
|
| 图 1 辅助纬度与大地纬度的差异曲线图 Fig. 1 Chart of differences between auxiliary and geodetic latitudes |
| B | 0° | 15° | 30° | 45° | 60° | 75° | 90° |
| μ-B | 0 | -2′52.93″ | -4′59.71″ | -5′46.36″ | -5′00.21″ | -2′53.43″ | 0 |
| Φ-B | 0 | -5′45.36″ | -9′58.91″ | -11′32.72″ | -10′00.92″ | -5′47.37″ | 0 |
| φ-B | 0 | -5′45.33″ | -9′58.74″ | -11′32.34″ | -10′00.42″ | -5′47.01″ | 0 |
| θ-B | 0 | -3′50.55″ | -6′39.61″ | -7′41.87″ | -6′40.37″ | -3′51.32″ | 0 |
| ψ-B | 0 | -4′19.30″ | -7′29.47″ | -8′39.54″ | -7′30.41″ | -4′20.25″ | 0 |
由图 1及表 3可以看出,各辅助纬度与大地纬度差异的绝对值先变大后变小,且在大地纬度45°附近处,各辅助纬度与大地纬度的差异出现极值。
根据已推导出的各辅助纬度与大地纬度的差异极值点及对应的差异极值的符号表达式,可以计算出B∈[0°,90°]时,各辅助纬度与大地纬度间的差异极值,如表 4所示。
| 差值 | 差异极值点 | 对应差异极值 |
| μ-B | 45°02′53″ | -5′46.36″ |
| Φ-B | 45°05′46″ | -11′32.73″ |
| φ-B | 45°04′48″ | -11′32.34″ |
| θ-B. | 45°03′15″ | -7′41.87″ |
| ψ-B | 45°03′36″ | -8′39.55″ |
由图 1及表 4可以看出,辅助纬度与大地纬度的差异极值点均在B=45°右侧,在B=45°05′46″处,地心纬度与大地纬度的差异极值最大,差异绝对值最大达到11′32.73″。等距离纬度与大地纬度差异极值的绝对值次之,为8′39.55″,而归化纬度与大地纬度的差异最小,它们的差异绝对最大值为5′46.36″。等角纬度和地心纬度这两种纬度与大地纬度的差异十分接近,它们与大地纬度的差异曲线近乎重合。
4.2 辅助纬度间的差异极值为全面分析在CGCS2000参考椭球中常用纬度间的差异极值问题,可绘制出大地纬度B∈[0°,90°]时大地测量中常用的地心纬度与归化纬度间差异图,及地图学中常用等角纬度、等面积纬度及等距离纬度这3种纬度间的差异图,如图 2、图 3所示。

|
| 图 2 地心纬度与归化纬度差异图 Fig. 2 Chart of difference between geocentric and reduced latitudes |

|
| 图 3 等角纬度、等面积纬度、等距离纬度间的差异 Fig. 3 Chart of differences between conformal,equivalent and equidistant latitudes |
表 5为大地纬度B∈[0°,90°]时,每隔15°对应的辅助纬度间的差异。
| B | 0° | 15° | 30° | 45° | 60° | 75° | 90° |
| Φ-μ | 0 | -2′52″ | -4′59″ | -5′46″ | -5′01″ | -2′54″ | 0 |
| θ-φ | 0 | 1′55″ | 3′19″ | 3′50″ | 3′20″ | 1′56″ | 0 |
| ψ-φ | 0 | 1′26″ | 2′29″ | 2′53″ | 2′30″ | 1′27″ | 0 |
| ψ-θ | 0 | -29″ | -50″ | -58″ | -50″ | -29″ | 0 |
由图 2、图 3及表 5可以看出,在B∈[0°,90°]范围内,地心纬度与归化纬度间差异的绝对值和等角纬度、等面积纬度与等距离纬度间差异的绝对值都是先变大后变小,且这4种差异极值均出现在大地纬度45°附近。根据3.2中已推导出的极值符号表达式,可计算出辅助纬度间差异极值点及对应差异极值,如表 6所示。
| 差值 | 差异极值点 | 对应差异极值 |
| Φ-μ | 45°08′39″ | -5′46.36″ |
| θ-φ | 45°07′53″ | 3′50.47″ |
| ψ-φ | 45°12′16″ | 2′52.79″ |
| ψ-θ | 45°06′15″ | -57.68″ |
由图 2、图 3及表 6可以看出,地心纬度与归化纬度的差异极值点为B=45°08′39″,对应差异极值为-5′46.36″;地图学中常用的3种纬度间,等距离纬度与等角纬度间差异极值最大,为3′50.47″,而等距离纬度与等面积纬度间差异最小,它们差异的极值为-57.68″。
5 结 论本文对6种常用纬度间的差异进行了研究,推导出常用纬度间的差异极值点及对应极值的符号表达式,并以CGCS2000椭球为例,对它们进行了数值分析和对比,得出如下结论。
(1) 辅助纬度与大地纬度差异的绝对值随大地纬度的增大先变大后变小,且在B=π/4右侧,差异出现极值。其中,等角纬度与大地纬度差异极值的绝对值最大,极值符号表达式的首项为-e2/2;归化纬度与大地纬度差异极值绝对值最小,极值符号表达式的首项为-e2/4。
(2) 地图学中常用的3种纬度间,等面积纬度与等角纬度差异极值最大,极值符号表达式首项为e2/6;等距离纬度与等面积纬度差异极值最小,极值符号表达式首项为-e2/24。
(3) 将常用纬度间差异极值点及对应极值表示为符号形式,并统一展开为偏心率e的幂级数形式,该表达式易于比较分析,一定程度上丰富了测量及地图学数学分析理论。
| [1] | LV Zhiping, ZHANG Jianjun, QIAO Shubo. Basis of Geodesy[M].Beijing: Publishing House of Liberation Army, 2005. (吕志平, 张建军, 乔书波. 大地测量学基础[M]. 北京: 解放军出版社, 2005.) |
| [2] | HUA Tang. The Mathematical Basis of Chart [M]. Beijing: Haichao Press, 1985. (华棠. 海图数学基础[M].北京: 海潮出版社, 1985.) |
| [3] | WANG Rui, LI Houpu. Symbolic Expressions of the Track Calculation Methods Based on the Ellipsoidal Model[J]. Acta Geodaetica et Cartographica Sinica, 2010,39(2):151-155. (王瑞, 李厚朴.基于地球椭球模型的符号形式的航迹计算法[J].测绘学报, 2010,39(2):151-155.) |
| [4] | XIONG Jie. Ellipsoidal Geodesy[M]. Beijing: Publishing House of Liberation Army, 1988:18-23. (熊介.椭球大地测量学[M].北京: 解放军出版社, 1988:18-23.) |
| [5] | ADAMS O S. Latitude Developments Connected with Geodesy and Cartography with Tables, Including a Table for Lambert Equal-Area Meridional Projection[M]. Washington D C: Government Printing Office, 1921. |
| [6] | SNYDER J P. Map Projections: A Working Manual[M].Washington D C: Government Printing Office, 1987. |
| [7] | YANG Qihe. The Theory and Method of Map Projection [M]. Beijing: PLA Press, 1989. (杨启和.地图投影变换原理与方法[M]. 北京: 解放军出版社, 1989.) |
| [8] | YANG Q H, SNYDER J P, TOBLER W R. Map Projection Transformation: Principles and Application [M]. London: Taylor & Francis, 2000. |
| [9] | YANG Qihe, Yang Xiaomei. Three Kinds of Latitudes in Surveying and Mapping and the Liner Interpolation Method for Inverse Solution[J]. Acta Geodaetica et Cartographica Sinica, 1997, 26(1):92-95.(杨启和, 杨晓梅. 测量和地图学中应用的三种纬度函数及其反解变换的线性插值方法[J]. 测绘学报, 1997, 26(1): 92-95.) |
| [10] | WU Zhongxing, YANG Qihe. Principle of Mathematical Cartography[M]. Beijing: Surveying and Mapping Press, 1989. (吴忠性, 杨启和. 数学制图学原理[M].北京: 测绘出版社, 1989.) |
| [11] | SUN Qun, YANG Qihe. The Research on the Computation of the Foot-point Latitude and the Inverse Solution of Isometric Latitude and Area Function[J]. Journal of PLA of Surveying and Mapping, 1985(2): 64-75. (孙群, 杨启和. 底点纬度解算以及等量纬度和面积函数反解问题的探讨[J]. 解放军测绘学院学报, 1985(2): 64-75.) |
| [12] | BIAN Shaofeng, JI Bing. The Expansions of Rectifying Latitude, Conformal Latitude and Authalic Latitude[J]. Acta Geodaetica et Cartographica Sinica, 2007,36(2): 218-223. (边少锋, 纪兵. 等距离纬度等量纬度和等面积纬度展开式[J]. 测绘学报, 2007, 36(2): 218-223.) |
| [13] | BIAN S F, LI H P. Mathematical Analysis in Cartography by Means of Computer Algebra System[C]//Carlos Bateira. Cartography: A Tool for Spatial Analysis. Croatia: InTech, 2012. |
| [14] | LI Houpu. The Research on the Precise Calculation Theory of Geodetic Coordinate System and Its Application Based on Computer Algebra System[D]. Wuhan: Naval University of Engineering, 2010. (李厚朴. 基于计算机代数系统的大地坐标系精密计算理论及其应用研究[D]. 武汉: 海军工程大学, 2010.) |
| [15] | WANG Rui, LI Houpu.The Derivation of the Inverse Expansions for Auxiliary Latitudes by Lagrange Series Method[J].Hydrographic Surveying and Charting, 2008, 28(3): 18-23. (王瑞, 李厚朴.辅助纬度反解公式的Lagrange级数法推演[J]. 海洋测绘, 2008, 28(3): 18-23.) |
| [16] | LI Houpu, BIAN Shaofeng. Derivation of Inverse Expansions for Auxiliary Latitudes by Hermite Interpolation Method[J]. Geomatics and Information Science of Wuhan University, 2008, 33(6): 623-626. (李厚朴, 边少锋.辅助纬度反解公式的Hermite插值法新解[J].武汉大学学报:信息科学版, 2008, 33(6):623-626.) |
| [17] | BIAN Shaofeng, XU Jiangning. Computer Algebra System and Mathematical Analysis in Geodesy [M]. Beijing: National Defense Industry Press, 2004. (边少锋, 许江宁. 计算机代数系统与大地测量数学分析[M].北京: 国防工业出版社, 2004.) |
| [18] | BIAN S F, CHEN Y B. Solving and Inverse Problem of a Meridian Arc in Terms of Computer Algebra System[J]. Journal of Surveying Engineering, 2006, 132(2): 1-4. |
| [19] | BIAN Shaofeng, CHEN Liangyou, JI Bing. Application of Mathematica in Geodesy[J]. Geomatics Science and Engineering, 2004, 24(2): 25-28. (边少锋, 陈良友, 纪兵. Mathematica软件在大地测量中的应用[J].测绘科学与工程, 2004, 24(2): 25-28.) |
| [20] | CHEN Junyong. Chinese Modern Geodetic Datum:Chinese Geodetic Coordinate System 2000 (CGCS2000) and Its Frame[J]. Acta Geodaetica et Cartographica Sinica, 2008, 37(3): 269-271.(陈俊勇. 中国现代大地基准: 中国大地坐标系统2000 (CGCS2000)及其框架[J]. 测绘学报, 2008, 37(3): 269-271.) |