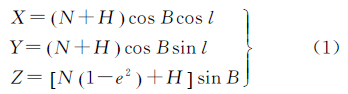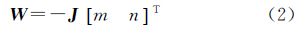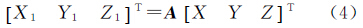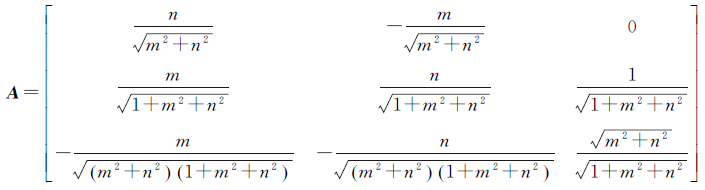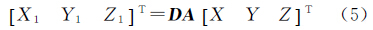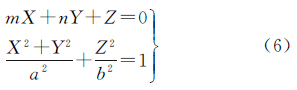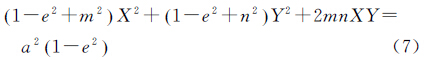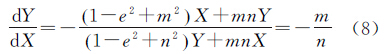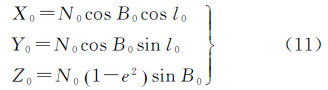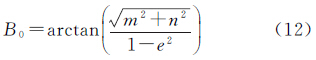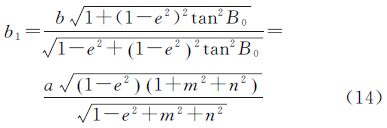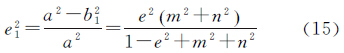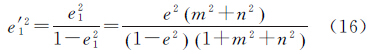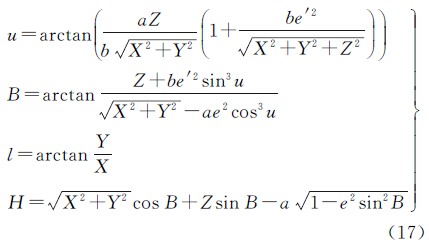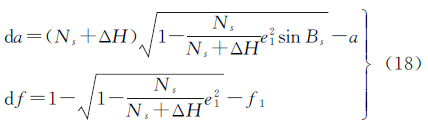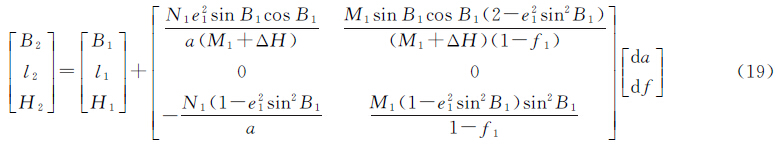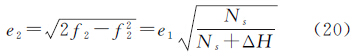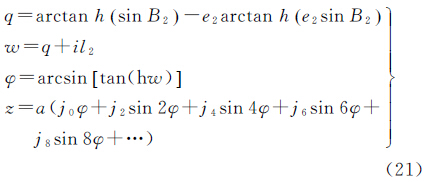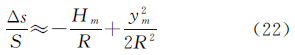2. 海军驻天津地区航保军事代表室,天津 300042
2. Military Delegate Office of Naval Navigation Guarantee, Tianjin 300042, China
1 引 言
目前,我国高速铁路建设进程不断加快,正进入提速扩容新阶段。在高速铁路线路控制测量中,投影长度变形很容易超限,这就需要采取相应措施减弱投影长度变形,使得变形控制在允许的范围之内。高斯投影[1, 2, 3, 4]作为我国常用的一种等角投影,常被用来绘制区域高精度地形图,来满足工程建设需求。在高斯投影中,控制投影长度变形就是控制高程归化改正和高斯投影变形的综合变形影响[5, 6, 7]。目前,国内外相关文献中多借助椭球膨胀法、椭球平移法及椭球变形法使得参考椭球面更接近测区表面,但是这些方法只解决了高程归化改正,却未有效解决高斯投影中横轴方向的变形[8, 9]。为减少东西跨度较大的线路因高斯分带带来的误差,目前国内有关斜轴投影的数学模型中,多将测区表面近似为球面进行处理,而不考虑高差对于投影变形的影响,无法真实地表示测区[10, 11, 12]。鉴于此,文献[13]中借助法截面子午线来建立斜轴椭球的方法,有效地减小了测区相对于斜轴椭球中央子午线的距离。然而,该方法需事先选择合适的基准点及线路方位角来确定斜轴椭球,使得运算过程及相关参数略显繁琐。考虑到空间三维坐标[14, 15, 16]在处理空间问题上的优越性及便利性,为解决东西跨度较大测区投影后变形超限的问题,本文基于最小二乘法、空间坐标系旋转及椭球变换等理论,提出一种新的方法来建立工程独立坐标系统对应椭球,进而实现测区斜轴高斯投影,文中称为“斜轴变形椭球高斯投影方法”,而相应的新椭球便命名为“斜轴变形椭球”。
2 斜轴变形椭球的构建斜轴变形椭球的基本思想是建立一个新椭球,该椭球相对于地球参考椭球E0(以下称“基础椭球”)进行了旋转、变形,使其中央子午线沿线路延伸方向,满足线路上各个控制点距高斯投影中央子午线距离很小,使横向坐标y值有效减小。同时,各点相对于新椭球面的大地高亦很小,能有效控制投影长度变形。在构建斜轴变形椭球的过程中,分别记E1为斜轴椭球,E2为斜轴变形椭球,具体步骤如图 1所示。
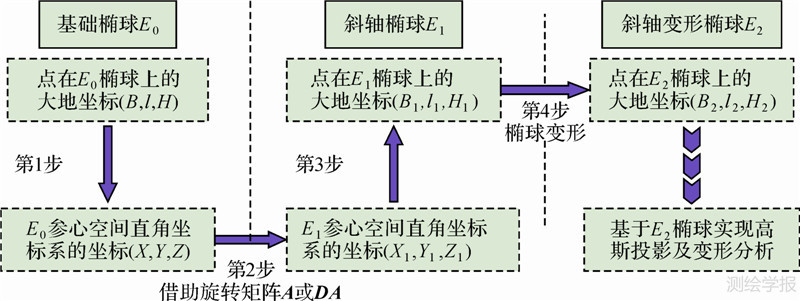 |
| 图 1 斜轴变形椭球的构建框架 Fig. 1 Frame of oblique deformed ellipsoid |
如图 2所示,在基础椭球E0中,以指向0°子午线与赤道交点C的方向为X轴,指向北极N的方向为Z轴,建立右手参心空间直角坐标系O—XYZ。
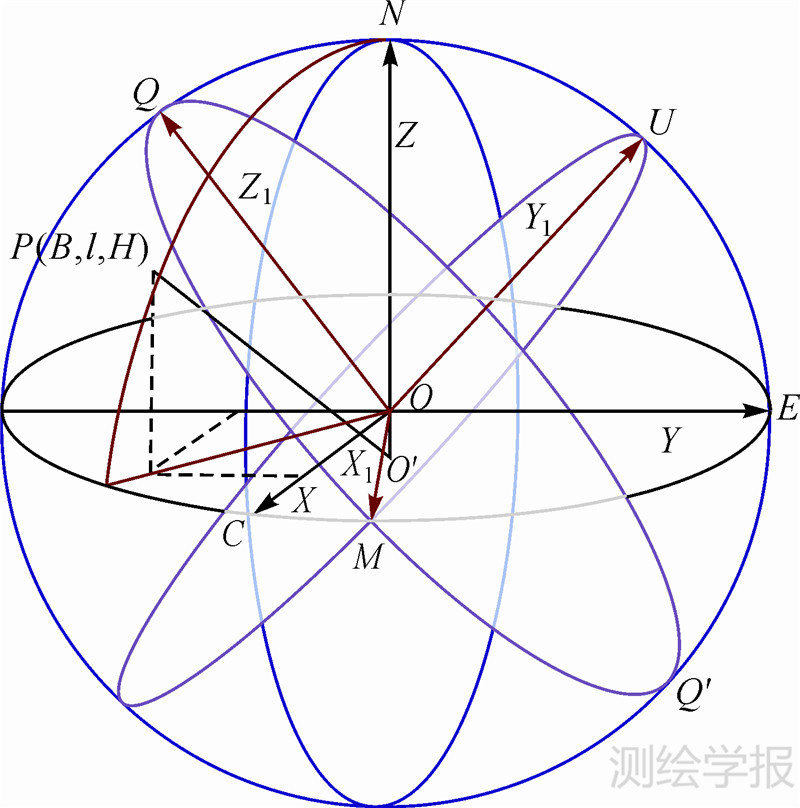 |
| 图 2 参心空间直角坐标系示意图 Fig.2 Sketch of space rectangular coordinate systems of ellipsoids2 |
则任意站点P的E0参心空间直角坐标P(X,Y,Z)可表示为
式中,(B,l,H)表示站点P相对于基础椭球E0的大地坐标;N为对应大地纬度B的卯酉圈曲率半径;e为E0椭球第一偏心率。已知线路在基础椭球E0上的分布靠近于某一截面椭圆,设截面椭圆QMQ′的法向量为α=[m n 1],则截面椭圆所在平面方程为mX+nY+Z=0。已知测区内点Pi(Bi,li,Hi)具有空间直角坐标Pi(Xi,Yi,Zi),则存在关系Zi=-mXi-nYi。以截面椭圆QMQ′作为斜轴椭球E1的中央子午线,为尽可能使更多的点位于该中央子午线附近,以满足高斯投影平面坐标中y坐标较小的要求,记W为点集Pi(Xi,Yi,Zi)的Z坐标列向量,J为对应的包含X、Y坐标矩阵,则有
借助最小二乘法,可解得系数为
在截面椭圆QMQ′中,点Q为极点,M为其与赤道的交点,OQ为短半轴,OM为长半轴。以短轴为旋转轴将截面椭圆进行旋转,可得斜轴椭球。以OQ为Z1轴,OM为X1轴,建立E1右手参心空间直角坐标系O—X1Y1Z1。在该坐标系中,各坐标轴的指向分别为OM、OU、OQ。将这3个向量进行单位化,可对斜轴椭球E1进行定位,得参心直角坐标系O—XYZ到O—X1Y1Z1的旋转矩阵为A。则有参心空间直角坐标系O—XYZ到O—X1Y1Z1的正向转换模型
式中以经过X1轴正方向与赤道交点的经线为斜轴椭球E1的0°子午线。值得注意的是,在将E0参心空间直角坐标系按照旋转矩阵A变换至E1参心空间直角坐标系后,X1轴的指向存在两种可能(指向测区或测区的反方向):当X1轴指向测区时,则可解得测点相对于斜轴椭球E1的经差很小,便于测量及制图工作。而当测区位于X1轴的反方向时,则经差的绝对值接近π,不便于高斯投影公式的应用。此时,需将该空间直角坐标系绕Z1轴旋转180°作为E1参心空间直角坐标系,令D=diag[-1-11],则有参心空间直角坐标系O—XYZ到O—X1Y1Z1的正向转换模型的第2种情况
2.2 斜轴椭球E1的参数
记极点Q在基础椭球E0上的大地纬度为B0,可通过以下步骤求得:
(1) 点Q在基础椭球E0的参心空间直角坐标系中的坐标。
因Q点位于截面大椭圆上,它同时满足地球椭球面方程及截面椭圆所在平面方程
将式(6)中的第1个方程代入第2个方程,消去Z并进一步化简,可得
因点Q是截面椭圆上纬度最高的点,则可转换为在一定约束条件下,求Z=-(mX+nY)最大值的问题。根据不变量判定二次曲线的类型,可知约束条件式(7)的图形是一个椭圆,则根据最优化理论,当椭圆上某点的斜率与直线的斜率相等时,目标函数Z取得最值,即
可解得满足最值条件下,X与Y的关系式为
将式(9)代入约束条件式(7),可解得该范围内满足Z值最大条件的X和Y,又考虑到点Q是截面椭圆的极点,即得到它在E0参心空间直角坐标系中的坐标Q(X0,Y0,Z0)为
(2) 参心空间直角坐标向大地坐标的转换。
由于点Q位于截面大椭圆上,是基础椭球E0表面上的一点,即它在基础椭球E0的大地坐标可表示为Q(B0,l0,0)。记Q(X0,Y0,Z0)是它在E0参心空间坐标系的空间直角坐标,则存在对应关系为
由于点Q满足B0∈[0,π/2],l0∈[-π,π]。当Z0=b时则意味着点Q位于北极点,此时椭球E1与基础椭球E0重合,B0=π/2。又考虑到地球上-π与π处的子午线重合,故认为B0∈(-π/2,π/2],l0∈(-π,π],并进一步表示成关于已知系数m、n的表达式,可得
而 式(13)中,在M=0的情形下:当n>0时,法向量在Y轴上的分量为正值,点Q位于Y轴的反方向,则l0=-π/2;当n≤0时,法向量在Y轴上的分量为非正值,点Q位于Y轴的非负方向,有l0=π/2。同理,在m>0的情形下:当n>0时,法向量在Y轴的分量为正值,此时点Q位于Y轴的反方向,有l0=arctan(n/m)-π;反之,当n≤0时,此时截面椭圆的法向量在Y轴上的分量为非正值,点Q位于Y轴的非负方向,有l0=arctan(n/m)+π。由于斜轴椭球E1的参数与极点Q在基础椭球E0上的大地纬度B0有关[17],最终这些参数可简化为关于m、n的表示式
短半轴
第一偏心率的平方 第二偏心率的平方 2.3 点在斜轴变形椭球E2上的大地坐标在解决空间直角坐标向大地坐标转换的问题中,文献[18]于1985年提出的改进算法是最佳的。对于任何位置上的点,按照该公式计算大地纬度,计算精度均高于10-7″,完全能够满足各部门的使用要求。该公式被表示为
式中,e′为椭球第二偏心率;u为中间变量。将点在E1参心空间直角坐标系中的坐标(X1,Y1,Z1)取代式中的(X,Y,Z),将斜轴椭球E1的短半轴b1取代式中的b,第二偏心率e′1代替式中的e′,即可推导出点在斜轴椭球E1上的大地坐标(B1,l1,H1)。考虑到当点在斜轴椭球E1上的大地高H1过大时,将该椭球直接进行高斯投影会导致投影综合变形较大,故在降低投影横坐标的同时,需尽可能地减小大地高,此时可借助椭球变换理论解决这一问题。由文献[9]可知,椭球变形法不会引起大地经度的变化,但对大地纬度和大地高均有影响,同时改变椭球的长半径、扁率,对应改变量与基准点所在位置及大地高变化量有关,即
式中,da、df及ΔH分别表示由斜轴椭球E1到斜轴变形椭球E2变换前后的长半径改变量、扁率改变量及基准点处的大地高改变量;f1是斜轴椭球E1的扁率;Bs表示基准点位于斜轴椭球E1上的纬度;Ns为基准点对应的卯酉圈曲率半径。记M1为斜轴椭球E1的子午圈曲率半径,根据椭球变形法的性质,可得点在斜轴变形椭球E2上的大地坐标为 3 斜轴变形椭球高斯投影方法 3.1 E2椭球大地坐标到高斯平面坐标换算记e2为斜轴变形椭球E2的第一偏心率,考虑到它与椭球扁率f2的关系,由式(18)可得
“斜轴变形椭球高斯投影方法”的定义为:以斜轴变形椭球E2为投影椭球,并以该椭球的中央子午线为基准进行与高斯投影一致的投影,属于等角横切椭圆柱投影。进行投影时,椭球的参数采用新椭球E2的几何参数,实现斜轴变形椭球E2上大地坐标到平面坐标的转换。其计算公式为
式中,q为点在斜轴变形椭球E2上的等量纬度;z=x+iy为对应的高斯投影平面复数坐标,其中x为纵坐标,y为横坐标;系数j0,j2,j4,…的设置参考文献[3]。特殊的,由于式(21)不适用于大地纬度B2→π/2的情况,当测区位于斜轴变形椭球E2的极区位置时,可借助极区高斯投影非奇异复变函数表示式进行计算[19]。值得强调的是,在“斜轴变形椭球高斯投影方法”过程中,式(17)中由空间直接坐标解算大地纬度B1的精度为10-7″时,则根据函数误差方法[20]进行计算可得:da的精度为10-14m,df的精度为10-21,进而求出B2的精度为10-7″,H2的精度为10-12m,l2不存在误差。最终,可得到高斯投影坐标的精度,其中纵坐标精度为10-5m,横坐标精度为10-6m。综上,经过一系列转换后所得到的高斯投影坐标可满足高精度的测量及制图需求。
3.2 高斯投影的长度变形分析在高斯投影中,长度变形主要由两部分构成:一是将测区表面归算至参考椭球面的高程归化长度变形,二是将参考椭球面投影至高斯平面上产生的投影长度变形。由文献[5]可知,高斯投影平面上的长度与地面长度之差,称之为长度综合变形
式中,等式右边第1项为高程归化长度变形;第2项为投影长度变形。Hm为测区边相对于参考椭球面的高程,ym为测区边横坐标的平均值,S为投影边长距离,R为测区边方向的参考椭球面法截弧的平均曲率半径。记R为测区平均曲率半径,可知在Hm超过150 m时,必须考虑高程对于长度变形的影响。由式(22)可以看出,当高斯投影平面坐标中横坐标ym=0时,则投影长度变形为0;测区越接近中央子午线,投影长度变形越小。当测区的平均高程Hm越小,高程归化长度变形越小。故为满足高精度制图需求,测区两边距离中央子午线的距离需尽可能缩短,同时测区表面需尽可能接近参考椭球面。
4 算例分析根据“××至××铁路控制测量成果报告”的内容,正线方案长约500 km,测区位于东经86°00′E—95°30′E,北纬36°00′N—42°00′N。线路海拔高程最大为3 163.6 m,最小为2 797.8 m。站点在基础椭球E0(CGCS2000[21])上的大地坐标参见表 1。为验证“斜轴变形椭球高斯投影方法”在减小投影综合变形方面的有效性,将其计算结果与“分带高斯投影方法”进行比较。
如果按照“分带高斯投影方法”,取中央子午线经度为93°,投影面海拔高程为H=2 830 m,测区最左端与中央子午线的距离为-241.5 km,测区最右端与中央子午线的距离为173.7 km,投影变形的最大值为676.299 mm/km,最小值为-15.833 mm/km。若要满足投影变形小于25 mm/km的要求,则需要将全线分为20个带。
如果按照“斜轴变形椭球高斯投影方法”,经计算,m=-0.635 205 028 071 340 8,n=-0.787 408 762 893 796 9。极点Q在E0椭球上的大地坐标为Q45°31′30.36″,51°06′24.48″,0。E1椭球的短半轴b1=6 367 293.563 969 489,第一偏心率e1=0.058 286 351 771 498。E0到E1参心空间直角坐标系的旋转矩阵为
选择基准点处的纬度Bs=56.5°,令ΔH=2 950 m对E1椭球进行变形,解得斜轴变形椭球E2的第一偏心率e2=0.058 272 893 136 337 34,并将采用“斜轴变形椭球高斯投影方法”计算的各站点长度变形列于表 1。经计算,测区最左端相对于斜轴变形椭球E2经差为-19′32.472″,它与中央子午线的距离为-19.3 km;测区最右端在E2椭球上的经差为10′37.944″,与中央子午线的距离为10 km。测区内大地高最大值为134.286 m,最小值为-135.042 m。可以看出,高程归化引起的长度变形最大绝对值为21.17 mm/km,高斯投影长度变形最大绝对值为9.19 mm/km,投影综合变形的最大值为22.2 mm/km,最小值为-20.5 mm/km,全线站点的综合长度变形均小于25 mm/km的规定值,达到满意效果。| 站点 编号 | 大地纬度B | 大地经度l | 大地高H/m | -Hm R | / | (mm km) |
ym2 2R2 | / | (mm km) |
Δs S | / | mm km |
| AHK1 | 36°22′34.635 3″ | 94°55′57.500 9″ | 2 833.33 | 21.17 | 1.07 | 22.24 | ||||||
| AHK2 | 36°22′02.237 3″ | 94°55′55.723 9″ | 2 836.65 | 20.26 | 0.8 | 21.06 | ||||||
| AHK3 | 36°21′26.575 5″ | 94°55′03.343 5″ | 2 855.6 | 16.59 | 0.41 | 17.00 | ||||||
| AHK4 | 36°21′20.613 2″ | 94°53′47.523 2″ | 2 855.6 | 16.11 | 0.22 | 16.34 | ||||||
| AHK5 | 36°21′14.637 5″ | 94°52′31.705 5″ | 2 855.6 | 15.64 | 0.09 | 15.73 | ||||||
| AHK6 | 36°22′01.955 3″ | 94°50′14.940 3″ | 2 871.3 | 13.00 | 0.06 | 13.05 | ||||||
| AHK7 | 36°36′45.902 1″ | 93°50′59.768 1″ | 2 808.13 | 14.39 | 7.81 | 22.20 | ||||||
| AHK8 | 37°00′34.241 9″ | 92°54′31.609 7″ | 2 933.15 | -5.95 | 9.19 | 3.23 | ||||||
| AHK9 | 38°02′55.851 6″ | 91°08′31.226 9″ | 2 921.22 | 9.06 | 2.46 | 11.52 | ||||||
| AHK10 | 38°21′21.217 4″ | 90°14′15.364 7″ | 3 097.39 | -21.05 | 0.5 | -20.56 | ||||||
本文通过建立斜轴变形椭球,提出“斜轴变形椭球高斯投影方法”,并结合实际工程线路进行分析,得出如下结论:
(1) 相对于“分带高斯投影方法”,建立“斜轴变形椭球”适用于东西跨度较大的测区,可有效避免因分带带来的误差,同时有效降低了高差带来的影响,减小了投影综合变形,该方法一定程度上丰富了高斯投影理论。
(2) 利用最小二乘法求得中央子午线所在平面,大大减小测区的高斯投影横坐标,使得测区位于斜轴椭球上的一个高斯投影条带内。当线路具有较大弯折时,为使得投影后横坐标值均能有效减小,可采用在弯折处将线路分段处理的方法。
(3) “斜轴变形椭球高斯投影方法”借助最小二乘法、坐标系旋转及椭球变换等理论,数学模型成熟、运算步骤清晰,可编制相关软件,以投入工程使用。
| [1] | XIONG Jie. Ellipsoidal Geodesy[M]. Beijing: Publishing Housing of PLA, 1988. (熊介. 椭球大地测量学[M]. 北京: 解放军出版社, 1988.) |
| [2] | YANG Qihe, SNYDER J P, TOBLER W R. Map Projection Transformation: Principles and Applications[M]. London: Taylor & Francis, 2000. |
| [3] | LI Houpu, BIAN Shaofeng. The Expression of Gauss Projection by Complex Numbers[J]. Acta Geodaetica et Cartographica Sinica, 2008, 37(1): 5-9. (李厚朴, 边少锋. 高斯投影的复变函数表示[J]. 测绘学报, 2008, 37(1): 5-9.) |
| [4] | SNYDER J P. Map Projections:A Working Manual[M]. Washington D C: Government Printing Office, 1987. |
| [5] | GONG Yusheng, ZHANG Liping, ZHAO Haiying. Implementation of Gauss Projection Method in High Altitude Area[J].Journal of Liaoning Technical University: Natural Science, 2014, 33(1): 51-55. (宫雨生, 张丽萍, 赵海莹. 高海拔地区高斯投影方法与实现[J]. 辽宁工程技术大学学报: 自然科学版, 2014, 33(1): 51-55.) |
| [6] | REN Xiaochun. Discussion on Horizontal Coordinate of Accurate Engineering Surveying for Ballastless Track of Passenger Dedicated Lines[J]. Railway Investigation and Surveying, 2008, 34(2): 1-4. (任晓春. 客运专线无碴轨道精密工程测量平面坐标系的探讨[J]. 铁道勘察, 2008, 34(2): 1-4.) |
| [7] | ZHAO Junsheng. LIU Yanchun, WANG Keping, et al. Discussion on the Distortion of Distance in Gauss Projection[J]. Hydrographic Surveying and Charting, 2007, 27(3): 9-11. (赵俊生, 刘雁春, 王克平, 等. 关于高斯投影长度变形的探讨[J]. 海洋测绘, 2007, 27(3): 9-11.) |
| [8] | YU Yajie, ZHAO Yingzhi, ZHANG Yuehua. The Establishment of Independent Coordinate System Based on the Ellipsoid Expansion Method[J]. Bulletin of Surveying and Mapping, 2011(12): 33-36. (于亚杰, 赵英志, 张月华. 基于椭球膨胀法实现独立坐标系统的建立[J]. 测绘通报, 2011(12): 33-36.) |
| [9] | KUANG Jinzhu, XIA Shenzhou. Establish Regional Coordinate System with Gauss-Kruger Projection Calculation through Ellipsoid Transformation[J]. Surveying and Mapping of Geology and Mineral Resources, 2011, 27(4): 11-14. (况金著, 夏神州. 通过椭球变换建立区域坐标系的高斯投影算法[J]. 地矿测绘, 2011, 27(4): 11-14.) |
| [10] | WANG Jiexian, WU Jicang, GAO Xiaobing. Oblique Mercator Projection and Its Applications on High Speed Railway Construction[J]. Geotechnical Investigation & Surveying, 2011, 39(8): 69-72. (王解先, 伍吉仓, 高小兵. 斜轴墨卡托投影及其在高铁建设工程中的应用[J]. 工程勘察, 2011, 39(8): 69-72.) |
| [11] | LV Huiling. Application of Oblique Mercator Projection Method to Zhengxi Special Passenger Transport Line[J]. Journal of Geomatics, 2009, 34(1): 26-28. (吕慧玲. 斜轴墨卡托投影方法在郑西客专中的应用研究[J]. 测绘信息与工程, 2009, 34(1): 26-28.) |
| [12] | LU Pengcheng, LIN Dongwei. Model for Oblique Mercator Projections as Well as Analysis on Its Applications[J]. Railway Investigation and Surveying, 2010, 36(4): 26-29. (陆鹏程, 林冬伟. 斜轴墨卡托投影模型及其应用分析[J]. 铁道勘察, 2010, 36(4): 26-29.) |
| [13] | JIN Lixin, FU Hongping. Gaussian Projection Theory Based on Ellipsoid with Normal Section as the Central Meridian[M]. Xi'an: Xi'an Map Publishing House, 2012. (金立新, 付宏平. 法截面子午线椭球高斯投影理论[M]. 西安: 西安地图出版社, 2012.) |
| [14] | ZENG Qixiong. Closed Formulae for Direct Solution of Geodetic Coordinates from Rectangular Space Coordinates[J]. Acta Geodaetica et Cartographica Sinica, 1981, 10(2): 83-95. (曾启雄. 空间直角坐标直接解算大地坐标的闭合公式[J]. 测绘学报, 1981, 10(2): 83-95.) |
| [15] | WANG Hongsheng. Transformation of Space Rectangular Coordinates[J]. Acta Geodaetica et Cartographica Sinica, 1982, 11(1): 38-45. (汪鸿生. 空间直角坐标的变换[J]. 测绘学报, 1982, 11(1): 38-45.) |
| [16] | SHEN Yunzhong, WEI Gang. Improvement of Three Dimensional Coordinate Transformation Model by Use of Interim Coordinate System[J]. Acta Geodaetica et Cartographica Sinica, 1998, 27(2): 161-165. (沈云中, 卫刚. 利用过渡坐标系改进3维坐标变换模型[J]. 测绘学报, 1998, 27(2): 161-165.) |
| [17] | BIAN Shaofeng, CHAI Hongzhou, JIN Jihang. Geodetic Coordinate System and Datum[M]. Beijing: National Defence Industry Press, 2005. (边少锋, 柴洪洲, 金际航. 大地坐标系与大地基准[M]. 北京: 国防工业出版社, 2005.) |
| [18] | BOWRING B R. The Accuracy of Geodetic Latitude and Height Equations[J]. Survey Review, 1985, 28(218): 202-206. |
| [19] | BIAN Shaofeng, LI Zhongmei, LI Houpu. The Non-singular Formula of Gauss Projection by Complex Numbers in Polar Regions[J]. Acta Geodaetica et Cartographica Sinica, 2014, 43(4): 348-352. (边少锋, 李忠美, 李厚朴. 极区非奇异高斯投影复变函数表示[J]. 测绘学报, 2014, 43(4): 348-352.) |
| [20] | FEI Yetai. Error Theories and Data Processing[M]. Beijing: China Machine Press, 2000. (费业泰. 误差理论与数据处理[M]. 北京: 机械工业出版社, 2000.) |
| [21] | CHEN Junyong.Chinese Modern Geodetic Datum:Chinese Geodetic Coordinate System 2000 (CGCS2000) and Its Frame[J]. Acta Geodaetica et Cartographica Sinica, 2008, 37(3): 269-271. (陈俊勇. 中国现代大地基准: 中国大地坐标系统2000 (CGCS2000) 及其框架[J]. 测绘学报, 2008, 37(3): 269-271.) |