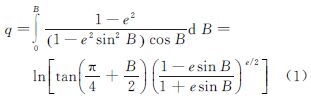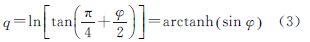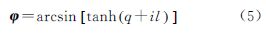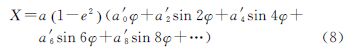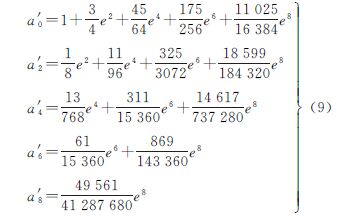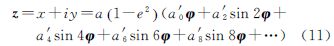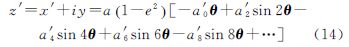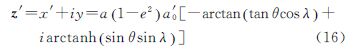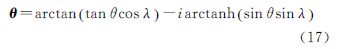1 引 言
近年来，随着极区的战略地位越来越受到国际关注，我国也日益重视极地考察工作，但与美俄等国相比，仍存在较大差距。为保障我国在极区事务中的国际地位及相关权益，须重视和加强极区的科学研究[1, 2, 3]。选择合适的投影方式对极区航海及科考图的绘制至关重要。极区通常采用日晷投影[4, 5]，该投影以极点为中心，且投影变形有对称的优点，但日晷投影仅与地球椭球相切于一点，随着极距增加投影变形也逐渐变大。而高斯投影与地球椭球相切于经圈，故在极区的长度变形必定小于日晷投影，且其在中央子午线上无投影变形。再考虑高斯投影具有保角优势，可正确反映极区的方位关系。可以说，极区高斯投影对于极区航海及科考图的绘制具有较重要的参考价值。然而传统高斯投影公式被表示成经差的幂级数形式，投影区域通常被划分为3°或6°带，使得极区难以形成完整的表达[6, 7]。针对这一问题，文献[8, 9, 10, 11]研究了高斯投影的复变函数表示，可使高斯投影避免分带现象，但因表达式中的等量纬度在极点存在奇异问题，不便于在极区应用。因此，既不受限于带宽又适用于极区的高斯投影公式仍待推导。又陆图通常采用高斯投影，海图在非极区使用墨卡托投影，在极区采用日晷投影，多种投影方式使得海图、陆图难以统一[12, 13, 14, 15]。鉴于此，本文推导出极区非奇异高斯投影复变函数表示式，该表达式使得极区无需分带且便于极区陆图与海图的统一应用，非常适于南极洲及北冰洋海域的一体化表示，可为极区科考及航海制图提供重要参考。
2 等角纬度的解析开拓欲研究高斯投影，离不开等量纬度，由文献[16]可知，等量纬度q与大地纬度B有如下数学关系
又由文献[7]可知，等角纬度φ与大地纬度B有如下关系 可得 式中，arctanh(·)表示反双曲正切函数。
考虑到复变函数在解决等角映射问题中具有不可替代的作用[17]，将上式拓展至复数域，以等量纬度q与经差l组成的复变量w=q+il代替q，则式(3)等号右端等角纬度φ开拓为复变等角纬度，记为φ，因此有
即 3 复变等角纬度表示的高斯投影正解
复变等角纬度表示的高斯投影正解可在子午线弧长展开的基础上经解析开拓得到。首先，写出用大地纬度表示的子午线弧长展开式为
式中，a、e分别为地球椭球长半轴和第一偏心率；系数a0、a2、…、a8可表示为椭球偏心率的幂级数，具体见文献[18]。
又大地纬度表示的等角纬度展开式为
式中，各系数b2、b4、b6、b8表达式具体可见文献[18]。
采用符号迭代法[19]推导出等角纬度反解展开式，并将展开式代入式(6)。最后，借助计算机代数系统Mathematica[20]对之进行级数展开和化简，则式(6)可变形为
式中 将解析开拓后的复变等角纬度φ代入式(8)，并将等式左端相应改写为高斯投影的复数坐标 式中，x、y分别为高斯投影纵横坐标。
则有
式(11)的正确性可进一步阐述如下：
(1) 因为由w所决定的φ及由φ所决定的z均为初等函数，且在其主值范围内是单值单叶解析函数，而解析函数必然满足保角映射条件，即高斯投影“正形”条件得以保证。
(2) l=0时，式(11)虚部消失，即横坐标y=0，纵坐标x即为子午线弧长公式。高斯投影条件“中央子午线投影后为直线”和“中央子午线投影后长度不变”得以保证。
因此，式(11)满足了高斯投影的全部条件。但与传统的高斯投影相比，避免了幂级数展开和分带现象。
4 极区非奇异高斯投影复变函数表示由于式(11)中的复变等角纬度φ是通过式(5)得到的，在极点时等量纬度趋近于无穷，会出现无法计算的奇点，但事实上这种只是数学定义上出现的可去奇点，将寻求另外的方法解决这一问题。
令
，式(11)可简化为
记复变等角余纬度为
将式(13)回代至式(11)并略去a(1－e2)a′0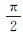
常数项，则将坐标原点从赤道平移至极点，即极点作为新坐标系原点(0,0)，经整理可得
即式(14)与式(11)相比，纵坐标平移而横坐标不变。对式(11)非主项作球近似，认为a′2=a′4=…=a′8=0，并将极点作为投影中心，则式(11)可变形为
又由于极点位于椭球旋转轴上，极点邻域近似可看作半径为a(1－e2)a′0的球体。略去推导，由文献[18]和文献[21]可得
式中，θ为实数等角余纬度，记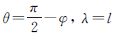
。
对比式(16)和式(15)可得
因此，复变等角余纬度表达式已知。
式(17)中θ表达式是根据建立极区球近似推算出的。通过引入复变等角余纬度的概念，式(14)在极区应用时无奇异性问题，也无需分带。因此，本文称之为“极区非奇异高斯投影一体化复变函数表示”。
5 算 例以CGCS2000参考椭球[22, 23](a=6378137m，α=1/298.257222101)为例，在极区范围内对以往高斯投影公式与本文推导出的极区非奇异公式进行比较并分析。(记x、x1、x2分别为本文推导的极区高斯投影复变函数、传统高斯投影幂级数、高斯投影复变函数纵坐标，y、y1、y2分别为这3个公式的横坐标。)
为验证本文公式的准确性和可靠性，首先与高斯投影传统幂级数形式作比较，分别计算出二者在一个高斯条带内的x、y方向上的差异，如图 1、图 2所示。
|
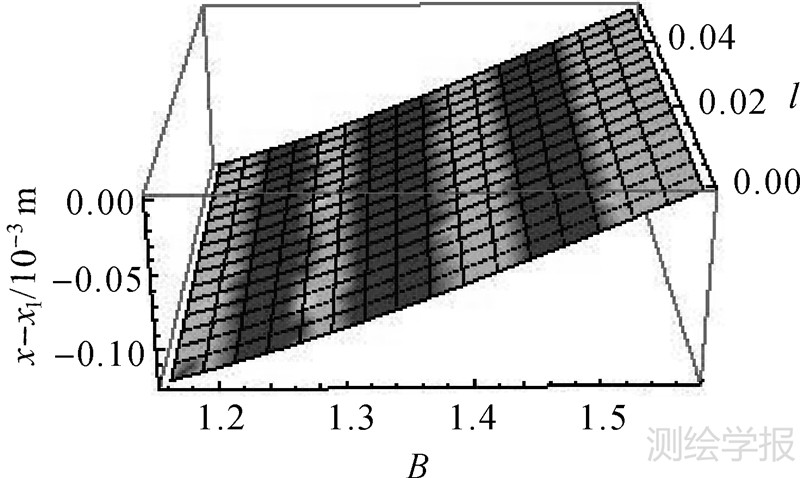
| 图 1 本文公式与高斯投影幂级数间纵坐标差异 Fig. 1 Differences of x coordinates between traditional power series and new expression of Gauss projection |
|
| 图 2 本文公式与高斯投影幂级数间横坐标差异 Fig. 2 Differences of y coordinates between traditional power series and new expression of Gauss projection |
从图 1、图 2可以看出，在B∈[66.55°,90°]范围内，本文推导出的“极区非奇异高斯投影一体化复变函数表示”与传统高斯投影幂级数公式在λ∈[0,3°]内的计算结果相比：地球椭球体上的点愈接近极点，两公式差异愈小；同一经差上，纵坐标值的差异随着纬度的增大而渐趋于0；同一纬线圈上，横坐标值差异随经差的增大而增大；在极区一个高斯条带内，两公式纵坐标差异在[－0.15×10－3m,0]范围内，横坐标差异在[0,5×10－6m]范围内。即本文推导出的“极区非奇异高斯投影一体化复变函数表示”在一个高斯投影条带内具有相当高的准确度。
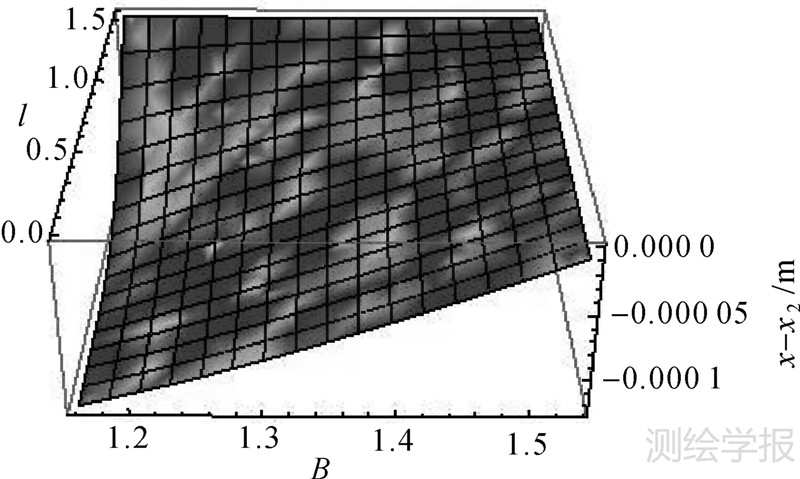
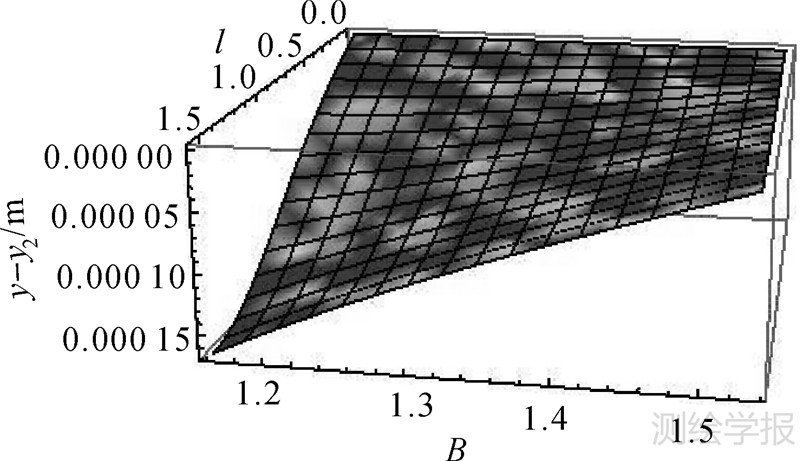
为确保本文公式在极区无限制带宽内的适用性，除验证该公式在一个高斯投影条带内的准确度之外，需与以往高斯投影复变函数表示式进行比较。由于以往高斯投影复变函数表示式在极点附近不适用，故以下对B∈[66.55°,88°]，λ∈[0,90°]范围内它与本文公式的纵、横坐标进行比较，如图 3、图 4所示。
|
| 图 3 本文公式与以往高斯投影复变函数表示式纵坐标差异 Fig. 3 Differences of x coordinates between traditional expression by complex numbers and new expression of Gauss projection |
|
| 图 4 本文公式与以往高斯投影复变函数表示式横坐标差异 Fig. 4 Differences of y coordinates between traditional expression by complex numbers and new expression of Gauss projection |
从图 3、图 4中可以看出，在该范围内本文公式与以往高斯投影复变函数表示间纵坐标绝对差异最大点位于在北极圈上，经差为0处，且该绝对差值小于0.00015m，即0.15mm。而横坐标绝对差异最大点位于北极圈上，经差为90°处，且该绝对差值小于0.0002m，即0.2mm。故得出结论：极区范围内，本文公式与以往高斯投影复变函数表示式在无限制带宽间的差异非常小，可满足极区测量及制图要求，且避免了以往公式在极区难以应用的问题。
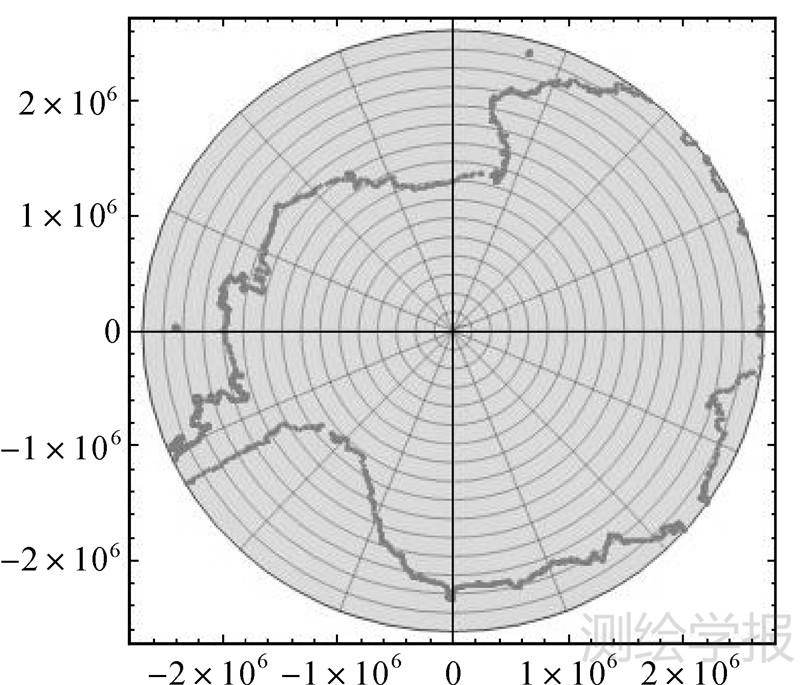
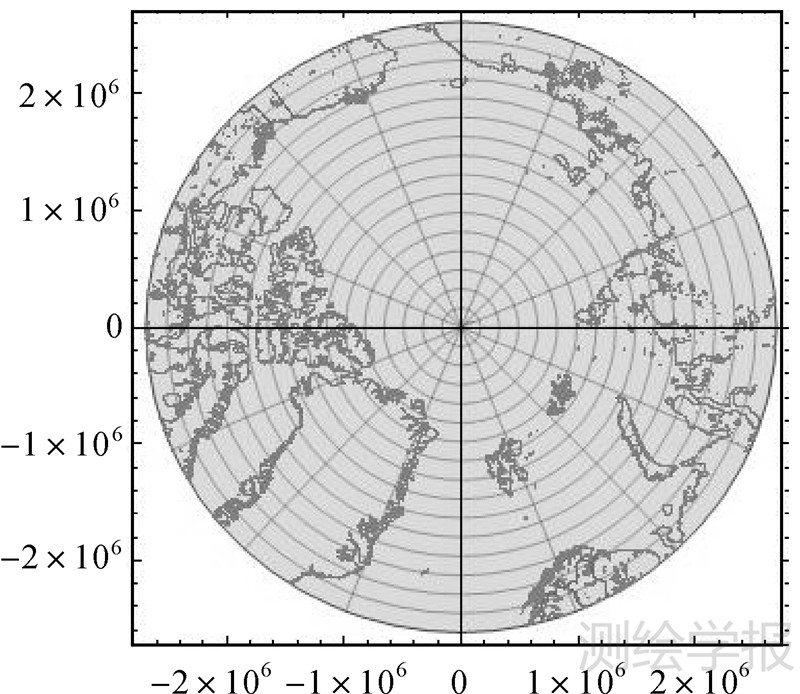
相对于传统高斯投影幂级数形式仅适用于高斯投影中绘制条带图，而以往高斯投影复变函数表示式在极区难以应用，本文推导出的极区非奇异高斯投影复变函数表示满足以极点作为投影中心，对极区进行连续投影作图，可实现极区海、陆图统一表示。又高斯投影具有保角优势，能更好地体现极区的方位关系，对于拟定航线、制定航行计划具有重要意义。基于本文推导出的极区非奇异公式，可分别绘制出南北极地区具有海岸线数据的高斯投影示意图，如图 5、图 6所示。
|
| 图 5 南极高斯投影示意图 Fig. 5 The sketch of Gauss projection in Antarctica region |
|
| 图 6 北极高斯投影示意图 Fig. 6 The sketch of Gauss projection in Arctic region |
本文通过引入复变等角纬度和复变等角余纬度的概念，讨论了高斯投影在极区的复变函数表示，得出如下结论：
(1) 本文推导出的公式克服了以往高斯投影复变函数表示在极区的奇异性，并避免传统高斯投影展成经差幂级数且需要分带的缺陷，形成了比较完美的“极区非奇异高斯投影一体化复变函数表示”。
(2) 与高斯投影传统幂级数形式及以往复变函数表示作比较，验证了“极区非奇异高斯投影复变函数表示”的高准确度与可靠性，解决了传统高斯投影在极区难以应用的问题。
(3) “极区非奇异高斯投影复变函数表示”在一定程度上丰富了现代地图投影数学理论基础，对极区航海及科考制图具有重要的参考价值。
| [1] | YE Jing. A Probe into the History, Current Situation and Prospect of Canadian Arctic Disputes[J]. Wuhan University Journal(Humanity Sciences), 2013, 66(2): 115-121. (叶静. 加拿大北极争端的历史、现状与前景[J]. 武汉大学学报:人文科学版, 2013, 66(2): 115-121.); |
| [2] | GEORGE W. National Security/Homeland Security Presidential Directive on Arctic Region Policy [EB/OL]. [2009-1-9]. http://www.cfr.org/publication/18215/national_security_ homelandsecurity_ presidential_directive_on_arctic_region_policy.html. |
| [3] | ZHU Ying, XUE Guifang. The Challenge of the Delimitation of the Continental Shelf to Antarctic Treaty System[J]. Journal of Ocean University of China(Social Sciences), 2012(1): 9-15. (朱英,薛桂芳.大陆架划界对南极条约体系的挑战[J].中国海洋大学学报:社会科学版, 2012(1): 9-15.); |
| [4] | HUA Tang. The Selection of Spherical Radius for Gnomonic Projection on Large and Medium Scale[J]. Acta Geodaetica et Cartographica ainica, 1984, 13(2): 141-151. (华棠. 大、中比例尺日晷投影图球半径的选择[J]. 测绘学报, 1984, 13(2): 141-151.); |
| [5] | DING Jiabo. Ellipsoidal Gnomonic Projection by Double Projection Method [J]. Journal of Wuhan Technical University of Surveying and Mapping, 2000, 25(2): 183-185. (丁佳波. 采用双重投影法的椭球面日晷投影[J].武汉测绘科技大学学报, 2000, 25(2): 183-185.); |
| [6] | LI Guozao, YANG Qihe, HU Dingquan. Map Projections [M]. Beijing: PLA Press, 1993:253-254.(李国藻, 杨启和, 胡定荃. 地图投影[M]. 北京: 解放军出版社, 1993: 253-254.) |
| [7] | YANG Qihe. The Theory and Method of Map Projection [M]. Beijing: PLA Press, 1989:8-13. (杨启和. 地图投影变换原理与方法[M]. 北京: 解放军出版社, 1989:8-13.) |
| [8] | BIAN Shaofeng, ZHANG Chuanding. The Gauss Projection-A Solution by Complex Numbers[J].Journal of Institute of Surveying and Mapping, 2001, 18(3): 157-159. (边少锋, 张传定.Gauss 投影的复变函数表示[J].测绘学院学报, 2001, 18(3): 157-159.); |
| [9] | LI Houpu, BIAN Shaofeng. The Expression of Gauss Projection by Complex Numbers[J]. Acta Geodaetica et Cartographica Ainica, 2008, 37(1): 5-9. (李厚朴, 边少锋. 高斯投影的复变函数表示[J]. 测绘学报, 2008, 37(1): 5-9.); |
| [10] | LI Houpu, BIAN Shaofeng. Expressions for Analytical Transformation between Gauss and Mercator Projections by Complex Numbers [J]. Geomatics and Information Science of Wuhan University, 2009, 34(3): 273-279. (李厚朴, 边少锋. 高斯投影与墨卡托投影解析变换的复变函数表达式[J]. 武汉大学学报:信息科学版, 2009, 34(3): 273-279.); |
| [11] | LI Houpu, WANG Rui, BIAN Shaofeng. The Non-iterative Formulae of Gauss Projection by Complex Numbers[J]. Hydrographic Surveying and Charting, 2009, 29(6):17-20.(李厚朴, 王瑞, 边少锋.复变函数表示的高斯投影非迭代公式[J]. 海洋测绘, 2009, 29(6):17-20.); |
| [12] | LI Shujun, ZHANG Zhe, LI Huiwen, et al. Research on Complication of Nautical Charts of Arctic Regions[J]. Hydrographic Surveying and Charting, 2012, 32(1): 58-60. (李树军, 张哲, 李惠雯, 等. 编制北极地区航海图有关问题的探讨[J]. 海洋测绘, 2012, 32(1): 58-60.); |
| [13] | CAO Yuchi, MOU Heng, JIANG Yu. Discussion on Arctic Passage [J]. World Shipping (Marine Technology), 2011, 34(10): 12-15. (曹玉墀, 牟珩, 姜玉. 北极航线探讨[J]. 世界海运(航海技术), 2011, 34(10): 12-15.); |
| [14] | WANG Qinghua, E Dongchen, CHEN Chunming, et al. Popular Map Projections in Antarctica and Their Application[J]. Chinese Journal of Polar Research, 2002, 14(3): 226-233. (王清华, 鄂栋臣, 陈春明, 等. 南极地区常用地图投影极其应用[J]. 极地研究, 2002, 14(3): 226-233.); |
| [15] | HUA Tang. Mathematical Basis for Chart [M]. Tianjin: Compass Department of the Admiralty, 1985. (华棠. 海图数学基础[M]. 天津: 海司航保部, 1985.) |
| [16] | BIAN Shaofeng, JI Bing. The Expressions of Rectify Latitude, Conformal Latitude and Authalic Latitude[J]. Acta Geodaetica et Cartographica Sinica, 2007, 36(2): 218-223. (边少锋, 纪兵. 等距离纬度等量纬度和等面积纬度展开式[J]. 测绘学报, 2007, 36(2): 218-223.); |
| [17] | CHENG Yang. Complex Function and Conformal Projection[J]. Acta Geodaetica et Cartographica Sinica, 2007, 36(2): 218-223. (程阳. 复变函数与等角投影[J]. 测绘学报, 2007, 36(2): 218-223.); |
| [18] | LI Houpu. The Research on the Precise Calculation Theory of Geodetic Coordinate System and Its Application Based on Computer Algebra System[D]. Wuhan: Naval University of Engineering, 2010: 35-38.(李厚朴. 基于计算机代数系统的大地坐标系精密计算理论及其应用研究[D]. 武汉: 海军工程大学, 2010:35-38.) |
| [19] | LI Zhongmei, BIAN Shaofeng, KONG Haiying. Symbolic Iterative Method for Solving Inverse Problems in Ellipsoidal Geodesy[J]. Hydrographic Surveying and Charting, 2013, 33(1): 27-29. (李忠美, 边少锋, 孔海英. 符号迭代法解算椭球大地测量学反问题[J]. 海洋测绘, 2013, 33(1): 27-29.); |
| [20] | BIAN Shaofeng, XU JiangNing. Computer Algebra System and Mathematical Analysis in Geodesy [M]. Beijing: National Defense Industry Press, 2004. (边少锋, 许江宁. 计算机代数系统与大地测量数学分析[M]. 北京: 国防工业出版社, 2004.) |
| [21] | LI Zhongmei, LI Houpu, BIAN Shaofeng. The Nonsingular Formulas and Deformation Analysis for Transverse Mercator Projection in Polar Regions[C]//Hydrographic Surveying and Charting Symposium of 24th General Meeting.Yiwu:CSGPC,2012.(李忠美, 李厚朴, 边少锋.极区横墨卡托投影非奇异公式及投影变形分析[C]//第二十四届海洋测绘综合性学术研讨会.义乌:中国测绘学会海洋测绘专业委员会,2012.) |
| [22] | CHENG Pengfei, WEN Hanjiang, CHENG Yingyan, et al. Parameters of the CGCS 2000 Ellipsoid and Comparisons with GRS80 and WGS84[J]. Acta Geodaetica et Cartographica Sinica, 2009, 38(3):189-194. (程鹏飞, 文汉江, 成英燕, 等. 2000国家大地坐标系椭球参数与GRS80和WGS84的比较[J]. 测绘学报, 2009,38(3):189-194.); |
| [23] | WANG Rui, LI Houpu. Symbolic Expression of Track Calculation Methods Based on the Ellipsoidal Model[J]. Acta Geodaetica et Cartographica Sinica, 2010, 39(2): 151-155. (王瑞, 李厚朴. 基于地球椭球模型的符号形式的航迹计算法[J]. 测绘学报, 2010, 39(2): 151-155.); |