栅格数据具有“属性明显,定位隐含”的固有特征[1],在编码时,根据是否对数据进行了压缩处理可分为直接栅格编码和压缩栅格编码。直接编码一般是对栅格单元编码直接记录,原理较为简单。然而,在实际操作中为提升编码效率,常通过压缩编码的方式,使用较小的数据量完成较大信息量的表达[2]。压缩编码可分为无损压缩编码与有损压缩编码:前者解压后可实现原始数据的完全恢复,但通常其压缩率较大,编码效率不高;后者通过牺牲部分数据精度降低压缩率,但其解压后无法实现原始数据的完全恢复。
当前,包括各种编码方法在内的栅格数据研究多集中于正四边形格网。然而,作为同样使用规则多边形进行空间镶嵌的正六边形格网,其在诸多方面较正四边形格网都具有优势。首先,在形态结构方面,正四边形格网中许多邻接单元以公共点的形式连接,这常导致面域不连续的情形。而正六边形格网中各邻接单元皆是共享边形式的连接,且邻接单元间中心距离都相同,这造就了其较强的各向同性,适用于空间运动、扩散等的模拟分析[3-4]。再者,在视觉显示方面,正六边形格网较正四边形格网有更高的单元紧凑度[5],其在表达精度上具有一定优势[6]。此外,人类对垂直和水平正交线特别敏感[7],正六边形格网结构能够有效避免正四边形格网中存在的此类正交线,减少视觉侵扰及注意力的分散[8-9]。鉴于上述优势,正六边形格网有着良好的应用潜力。比如,空间离散数据的集成显示及分析[10]。在全球离散格网构建的理论研究中,对正六边形格网有着广泛的关注[11-13],在实践应用领域,欧洲航天局2009年发射的SMOS卫星即使用六边形全球离散格网的形式对数据进行记录处理[14]。此外,正六边形格网在自然研究领域如地震数据分析[15]、飓风数据分析[16],社会研究领域如商店零售数据[17]、犯罪数据[18]等的研究分析中都发挥了重要作用。当以正六边形格网对栅格数据进行组织时,需对其编码等基础工作进行研究。此时栅格的形态、结构等较之于正四边形格网差异巨大,目前的编码方法难以直接套用,这也构成了本研究的基本动机。
当前对正六边形编码的相关研究多集中于全球离散格网领域[11, 19-20],以纯粹栅格数据为关注对象的研究较少,并且很少以数据压缩为主要研究目的。本文以正六边形栅格数据为研究对象,通过Gosper曲线工具的引入,有效顾及了正六边形格网形态结构及空间邻近性规则,建立了新型游程编码形式支持栅格数据的压缩编码。在依托Gosper曲线引导建立的编码框架下,对正六边形栅格数据的无损和有损压缩编码进行实现,完成数据的高效压缩,并对不同分辨率、不同精度损失等条件下的压缩编码进行分析比较。
1 编码工具 1.1 Gosper曲线优势Gosper曲线是一种空间填充曲线[21],不同迭代次数的Gosper曲线可以实现不同大小区域的覆盖。选择Gosper曲线作为正六边形栅格的编码工具源自其以下两个特性。首先,Gosper曲线具有良好的空间聚合性[22],这体现在曲线线性序列对平面欧氏距离的顾及上:曲线上次序相近的两节点,其欧氏距离一般也相近,反之亦然。良好的空间聚合性使Gosper曲线对地理学第一定律[23]有很好的顾及,适用于同样遵循此定律的空间数据的研究。Gosper曲线可以将空间上邻近的点通过一维的线性序列串联起来,获得二维空间数据的降维表达,便于数据的访问及操作。
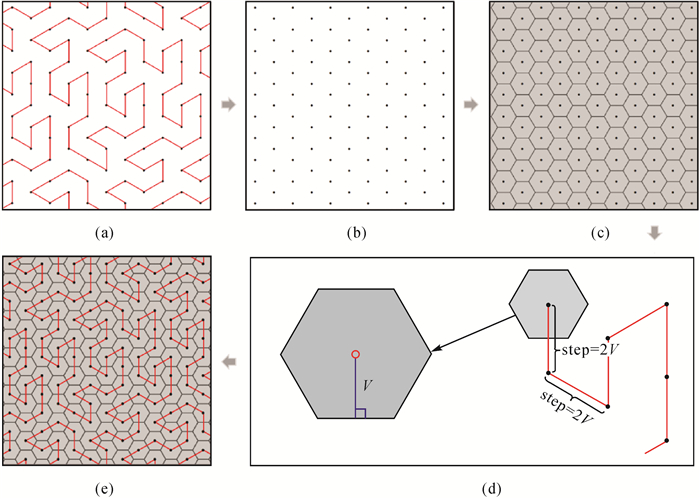
再者,就笔者研究关注的六边形栅格数据而言,Gosper曲线与其有着天然的亲密关联。一方面,如图 1(a)—(c)所示,将Gosper曲线节点作为发生元生成泰森多边形,将得到一系列无缝拼接、形状面积完全相同的正六边形集合,这在相关研究中已有应用[24]。另一方面,如图 1(d)—(e)所示,发现在任意正六边形格网上,通过调整Gosper曲线参数,可以使曲线上每个节点与各正六边形中心点重合,从而建立曲线节点与正六边形的一一对应关系,实现Gosper曲线对正六边形单元的索引。
|
| 图 1 Gosper曲线与正六边形格网的关系 Fig. 1 Relationship between Gosper curve and hexagonal grid |
1.2 Gosper曲线构造
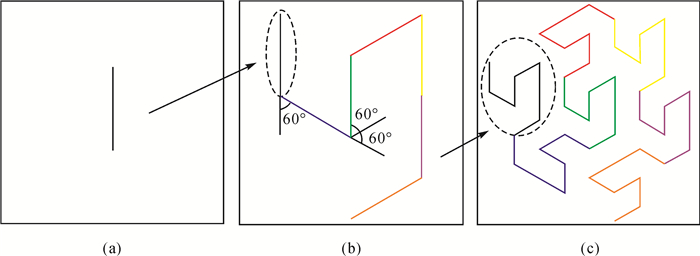
本文中Gosper曲线通过L系统[25]生成,其本质为基于规则对初始编码不断替代产生构图编码。Gosper曲线的初始L系统编码为“A”,替代规则为将编码中“A”替换为“A-B—B+A++AA+B-”,将“B”替换为“+A-BB—B-A++A+B”。其中A和B表示对应步长的直线段绘制,“+”代表顺时针旋转60°,“-”代表逆时针旋转60°。结合上述含义,对构图编码进行绘制,即可实现图 2所示的Gosper曲线迭代生长,得到最终曲线结果。在正六边形格网中,各单元中心点与其六邻域单元中心点连线长度皆相同,且相邻连线所形成的夹角皆为60°。所以,选择格网中正六边形中心点作为绘制起始点,将相邻六边形中心点连线长度作为绘制步长,以60°为单位旋转角度,即可使绘制的曲线节点与各正六边形中心点重合。
|
| 图 2 构建Gosper曲线 Fig. 2 Construction of Gosper curve |
如图 1(d),对于边心距为V的正六边形所构造的格网,选定正六边形中心点为起始点并将Gosper曲线生成步长设定为2V,即可使曲线节点与六边形中心点重合,从而建立曲线与正六边形格网的对应关系,此对应关系即是正六边形栅格单元H与Gosper曲线节点编码G的双向关联关系,f(H)=G:对于格网中任意单元h(h∈H),通过f(h)=g可以确定其Gosper编码值g;反之,对于Gosper曲线的每个节点编码g∈G,使用逆映射函数f-1(g)=h,可获取节点对应的正六边形单元h。在进行正六边形栅格操作时,映射函数f及其逆映射函数f-1可分别作用于编码与解码过程。
2 编码方法在进行栅格数据编码时,根据编码对象可分为面向要素边界链的编码(如弗里曼编码[26])和面向要素面域的编码(如游程编码[27])。本文采用后一种,其存在两种数据组织方式:一是以各要素面域为编码对象,每个要素面域拥有一个编码集合;二是将图幅范围内所有要素面域作为一个面域集合进行整体编码[28]。第1种对象性较强,便于各要素区域编码结果的统计分析,所以本文采用该方式。
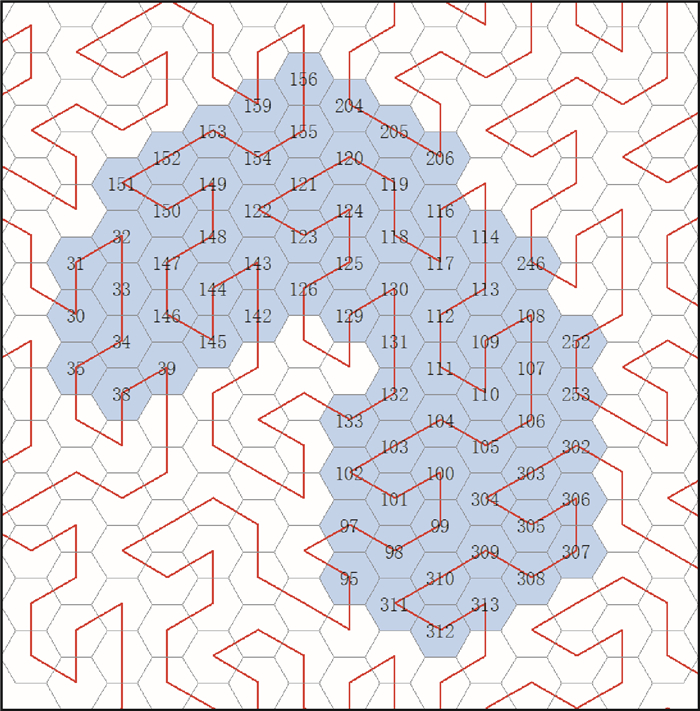
2.1 Gosper直接编码基于Gosper曲线的编码属于填充曲线编码[13],直接编码时,首先将Gosper曲线覆盖栅格区域,在曲线的线性引导下,通过映射函数f(h)=g,可以确定目标区域中每个栅格单元的Gosper编码值。对于目标区域,通过(g1, g2, …, gn)表示其编码结构,其中gn(n=1, 2, 3, …)为各单元的Gosper编码值。对于图 3中目标区域,其直接编码可通过表 1进行记录。
|
| 图 3 使用Gosper曲线对目标区域编码 Fig. 3 Using Gosper curve to encode target region |
| Gosper 直接编码 |
(30, 31, 32, 33, 34, 35, 38, 39, 95, 97, 98, 99, 100, 101, 102, 103, 104, 105, 106, 107, 108, 109, 110, 111, 112, 113, 114, 115, 116, 117, 118, 119, 120, 121, 122, 123, 124, 125, 126, 129, 130, 131, 132, 133, 142, 143, 144, 145, 146, 147, 148, 149, 150, 151, 152, 153, 154, 155, 156, 159, 204, 205, 206, 246, 252, 253, 302, 303, 304, 305, 306, 307, 308, 309, 310, 311, 312, 313) |
直接编码存在一定的数据冗余,特别是追求数据的高精度显示时,较高的分辨率势必会造成数据量的增加,同时,当邻域单元普遍有着相同的属性值,会造成大量的数据冗余问题。在空间数据与大数据紧密结合的今天[29],针对栅格数据量大、冗余等问题,有必要对数据压缩编码方法进行研究。
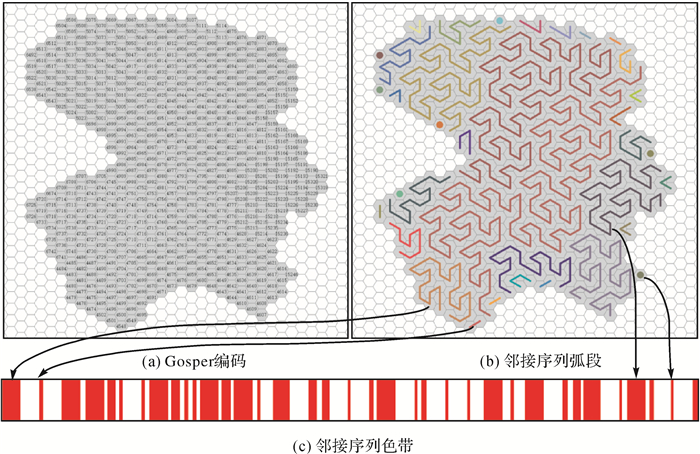
2.2 Gosper无损压缩编码如图 4(a)所示,对于完成Gosper直接编码的目标区域,将其中编码值相互邻近的编码集合定义为邻接序列,图 4(b)中覆盖在目标区域上被其切割破碎的各色弧段即为这些邻接序列的有形展现。由于邻接序列使用连续的数值编码记录同一要素信息,造成数据表达上的冗余, 所以,本文采用游程编码的形式,通过二元组(g,l)对邻接序列进行压缩表示,其中g为邻接序列起始单元的编码值,l为邻接序列的长度也即游程长度。如表 2所示,通过游程编码表达原始数据,实现对目标区域的Gosper无损压缩编码。
|
| 图 4 目标区域Gosper无损压缩 Fig. 4 Gosper lossless compression for target region |
| 序号 | 编码 |
| 1 | 4474, 29 |
| 2 | 4548, 2 |
| 3 | 4607, 38 |
| 4 | 4648, 24 |
| 5 | 4673, 4 |
| 6 | 4679, 2 |
| ⋮ | ⋮ |
| Gosper 无损压缩编码 |
(4474, 29, 4548, 2, 4607, 38, 4648, 24, 4673, 4, 4679, 2, 4691, 2, 4695, 166, 4862, 5, 4870, 2, 4875, 2, 4878, 113, 4992, 5, 4998, 58, 5059, 1, 5067, 9, 5104, 4, 5111, 4, 6492, 1, 6504, 3, 6508, 15, 6538, 1, 6541, 3, 6674, 1, 6696, 1, 6705, 16, 6725, 2, 6733, 10, 15150, 3, 15156, 4, 15161, 9, 15186, 1, 15190, 41, 15234, 3, 15246, 1, 15319, 3) |
解压缩时,利用游程编码中起始单元编码及对应游程长度即可确定编码集合,结合逆映射函数f1(g)=h完成编码集合到正六边形集合的转换,从而实现数据的无损解压复原。为便于进一步观察一维线性序列特征,将各邻接序列按顺序及长度比例映射到直线色带上。如图 4(c)所示,色带中各红色片段即代表目标区域自身邻接序列,白色片段为连接它们的非自身邻接序列。为了在有限空间内显示,长度小于或等于10的邻接序列按比例确定其片段长度,长度大于10的邻接序列使用较长的定长片段表示。依此对一维线性序列的数据特征分析发现,大量较短白色片段的存在阻碍了各红色片段的联通,导致目标区域需编码邻接序列的数量较大。同时,色带中存在大量较短红色片段,它们对应的短邻接序列,与长邻接序列占据同样的编码表达量。以上都在一定程度上影响了编码表达效率,也为有损的编码压缩提供了着力点。
2.3 Gosper有损压缩编码本文借助Gosper曲线良好的空间聚合性,对长度较短的邻接序列,通过改变邻接序列对应正六边形集合的归属进行邻近融合。由于Gosper曲线的二维邻接关系对一维邻接关系的良好顾及,所以相互邻接的各编码,其对应的正六边形也依然保持邻接关系。这就保证了融合操作在要素区域的周边邻域进行,避免多部件多边形的产生。
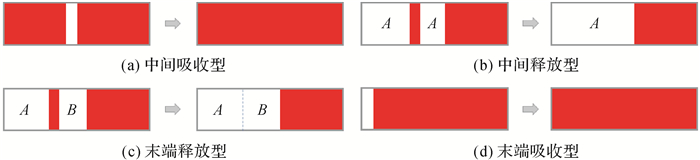
邻接序列融合是产生精度损失的根源,而融合长度直接影响精度损失的大小。将融合长度阈值定义为t,所有长度小于t的邻接序列都将被判定为短邻接序列进行融合处理。从执行操作的目标区域角度,按作用效果可将融合分为两种形式:吸收型融合和释放型融合。前者通过将非自身邻接序列划归到自身区域,实现短邻接序列的接收和重新整合;后者则通过变更自身邻接序列的归属,剔除短邻接序列。按照融合发生的相对位置又可分为中间型融合和末端型融合:中间型融合作用于彼此相邻的3条邻接序列,其中位于两端的邻接序列有相同的要素归属,通过更改中间邻接序列的归属联通两端邻接序列,将3条邻接序列融合为一条;末端型融合针对两条相邻的邻接序列,通过改变其中一条的归属,将它们融合为一条邻接序列。上述几种融合形式在目标区域组合会产生4种类型的融合:中间吸收型融合、中间释放型融合、末端吸收型融合、末端释放型融合。其中,目标区域执行中间吸收型融合与末端释放型融合,剩余两种融合属于其他区域执行上述两种融合时对目标区域造成的影响。执行融合操作时,首先对所有要素区域进行中间型融合,再进行末端型融合。
借助邻接序列色带的简单形式,对发生在目标区域的4种融合类型进行说明。首先进行中间吸收型融合,如图 5(a)所示,目标区域的两条邻接序列被非自身短邻接序列阻隔而无法联通,通过融合将非自身邻接序列吸收,新形成的邻接序列继续参与后续融合,直至目标区域中不存在满足中间吸收融合条件的邻接序列。如图 5(b)所示,当目标区域中的短邻接序列阻断的两条非自身邻接序列属于同一要素区域A时,A执行中间吸收型融合吸纳了短邻接序列,对于目标区域则完成了一次中间释放型融合。当数据中所有要素区域都完成中间融合后,对于依然存在的短邻接序列进行末端融合。如图 5(c)所示,目标区域中的短邻接序列阻断的两条邻接序列分属于A、B两个不同的要素,将短邻接序列划分给长度较短的B要素邻接序列,完成末端释放型融合。当目标区域作为末端型融合的邻接序列接收方,如图 5(d)所示,即完成了一次末端吸收型融合。以上,目标区域通过吸收和释放两个融合过程,完成短邻接序列的有效剔除。
|
| 图 5 邻接序列4种融合类型的色带表示 Fig. 5 Color band representation of four fusion types of adjacency sequences |
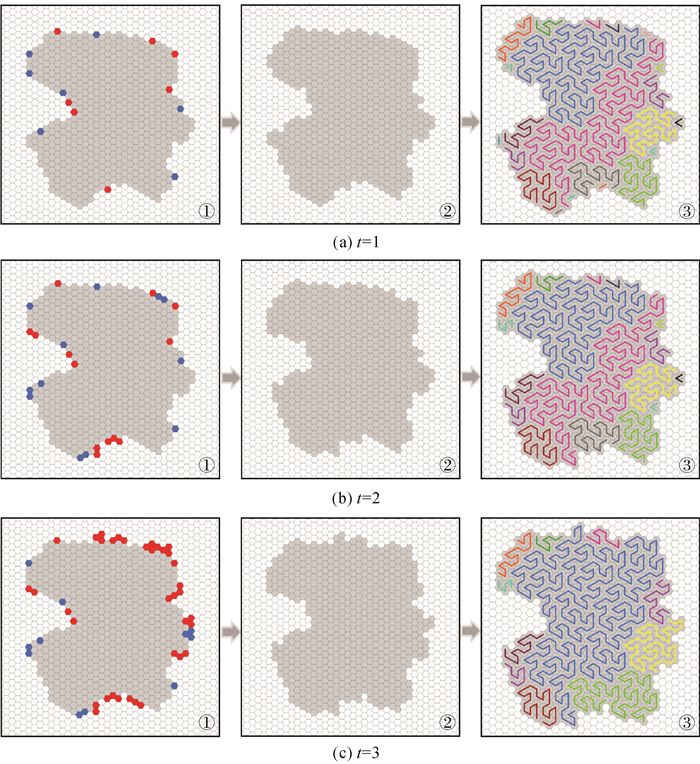
t值的不同会对融合结果中的邻接序列数目产生影响,对图 4中的目标区域分别进行t=1、t=2、t=3等不同阈值约束下的融合操作,通过图 6中的色带可以发现:随着t值的增大,红色片段不断减少,即邻接序列数目不断减少。图 7展示了对应的平面区域融合情形,(a)、(b)、(c)中的①蓝色和红色区域表示语义发生变化的单元,蓝色区域是被目标区域剔除的单元,红色区域为被吸纳的单元。对(a)、(b)、(c)中②新形成区域的邻接序列进行游程编码,即可完成Gosper有损压缩编码。观察(a)、(b)、(c)中③同样可知,随着t值的不断增大,邻接序列对应的各弧段数目随之减小。另一方面,t值也左右着数据精度,较大的t值会导致较大的精度损失,包括几何精度损失及语义精度损失。构建以下公式进行融合效果及精度方面的评价,融合率式(1)用以衡量融合效果
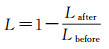 (1)
(1)

|
| 图 6 不同融合阈值约束下的目标区域邻接序列色带 Fig. 6 Color bands of adjacent sequences produced by different fusion thresholds |
|
| 图 7 平面空间中不同融合阈值约束下的结果 Fig. 7 Fusion results in different fusion thresholds inplane space |
式中,分子Lafter为融合后邻接序列总数;分母Lbefore为融合前邻接序列总数;融合率大表明能通过融合操作很好的完成表达量的精简。
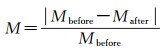 (2)
(2)
式中,Mbefore和Mafter分别为融合前后要素区域的面积,使用面积变化率衡量几何精度损失。式(3)通过语义变化率衡量融合过程中的语义精度损失,分子部分为要素区域发生语义变化的单元总数目
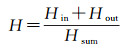 (3)
(3)
式中,Hin为被吸收的单元数目;Hout为被释放的单元数目;分母Hsum为融合前要素区域单元的总数。
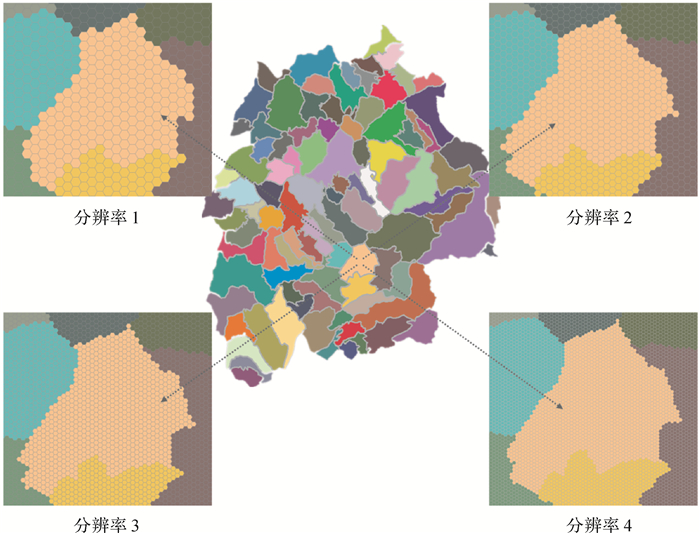
3 试验如图 8所示,试验数据共包含97块图斑,选择4种分辨率下的正六边形栅格数据进行压缩编码试验。各分辨率下栅格单元的边心距分别为100、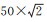
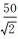
|
| 图 8 多分辨率栅格数据 Fig. 8 Multi-resolution raster data |
3.1 Gosper无损压缩试验
在各分辨率下进行Gosper无损压缩编码试验,以Gosper直接编码中的编码表达量为基准,将经过Gosper无损压缩后的编码表达量与之求商计算压缩率,各分辨率数据整体压缩率结果如表 3所示。随着分辨率的提高,压缩率不断减小,从最低分辨率下24.95%的压缩率,逐渐降至10%以下。
| 分辨率 | 压缩率/(%) |
| 分辨率1 | 24.95 |
| 分辨率2 | 18.09 |
| 分辨率3 | 12.97 |
| 分辨率4 | 9.25 |
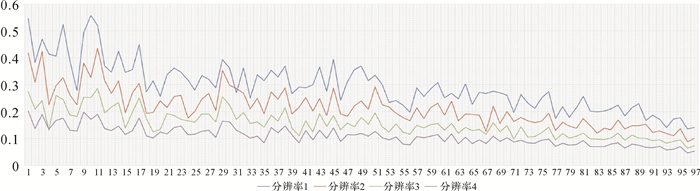
进一步分析各分辨率下要素个体的压缩率。选择图斑面积这一要素属性,将各要素按面积进行降序排列后,观察其压缩率变化。如图 9所示,横轴为按面积排列的各要素,从左向右其面积依次递增,纵轴为压缩率。在每个分辨率下将各要素压缩率进行连线形成折线图,各分辨率折线的堆叠顺序也体现了上述压缩率随分辨率的变化规律。并且,随着要素面积的增大,各要素压缩率大致上呈递减趋势,在以上4个分辨率中都存在此规律。
|
| 图 9 要素个体Gosper无损压缩率 Fig. 9 Compression ratios of Gosper lossless compression for single objects |
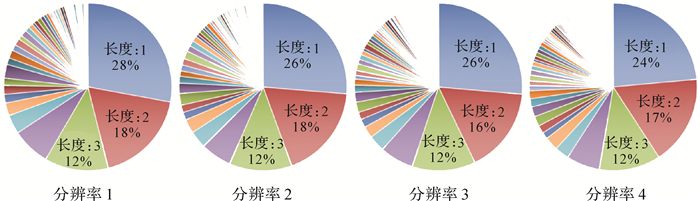
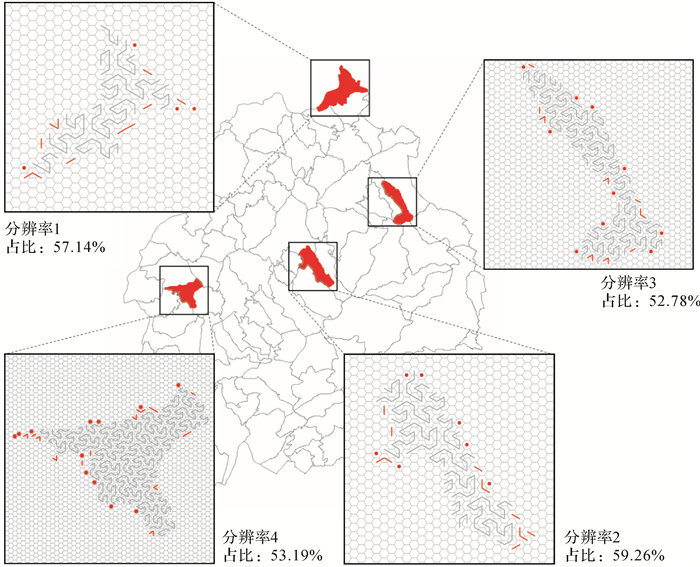
通过统计压缩后的各邻接序列长度,分析编码效率。如图 10所示,各分辨率下都存在大量长度较短的邻接序列,如长度在1~3之间的邻接序列占据了大部分的比重。通过观察图 11中抽取的各分辨率下部分要素区域邻接序列对应弧段,可进一步印证上述结论,各要素区域边缘都有大量红色短弧段的存在。而实际上,如表 4所示,长度在1~3之间的短邻接序列所描述的栅格单元在单元总数目中只占很少的比重。一方面,数据中存在大量的短邻接序列;另一方面,短邻接序列表达的往往为少量的细节信息。即用较大份额的表达量描述了较小比例的对象,这就降低了编码效率。
|
| 图 10 各分辨率邻接序列长度统计饼图 Fig. 10 Pie charts of the length of adjacency sequences in each resolution |
|
| 图 11 各分辨率下要素区域弧段抽样 Fig. 11 Regional segments samples in each resolution |
| 分辨率 | 短邻接序列栅格单元数/个 | 短邻接序列栅格单元占比/(%) |
| 分辨率1 | 2253 | 12.63 |
| 分辨率2 | 3191 | 8.94 |
| 分辨率3 | 4448 | 6.23 |
| 分辨率4 | 6238 | 4.33 |
3.2 Gosper有损压缩试验
为进一步较少表达量,提升编码效率,在4个分辨率下,分别设定t=1、t=2、t=3融合阈值进行Gosper有损压缩编码试验,表 5显示了各分辨率不同融合阈值约束下的压缩结果及精度损失情况。易知在各分辨率下,随着对精度要求的不断降低,融合率不断上升。但是随着分辨率的变大,融合率有不断下降的趋势,这是因为高分辨率下又出现了更多更长的弧段,既定阈值内涉及的弧段比例受到了压缩。通过该试验可知,使用Gosper有损压缩甚至可以完成对大部分弧段的融合,有效实现表达量的精简。对各分辨率下不同t值导致的整体精度损失进行分析。其中面积变化率及语义损失率都是对要素个体计算后求取均值的结果。在融合过程中,随着t值的增大,面积变化率与语义损失率均在增加。但是,分辨率的变大不断降低精度损失的比例,以t=3时为例,面积变化率从分辨率1时的5.82%不断下降至分辨率4时的2.21%,语义损失率从17.49%不断下降至6.19%。综上,有损压缩可以通过较低的面积变化率及语义损失率换取较高的融合率,尤其在高分辨率下,达到等量级融合率所需代价更小。
| 分辨率 | 融合前邻接序列数 | 融合阈值 | 融合后邻接序列数 | 融合率/(%) | 面积变化率/(%) | 语义损失率/(%) |
| 分辨率1 | 2226 | t=1 | 1303 | 41.46 | 1.80 | 6.47 |
| t=2 | 890 | 60.02 | 3.85 | 12.84 | ||
| t=3 | 719 | 67.70 | 5.82 | 17.49 | ||
| 分辨率2 | 3228 | t=1 | 1891 | 41.42 | 1.06 | 4.71 |
| t=2 | 1327 | 58.89 | 2.05 | 9.20 | ||
| t=3 | 1090 | 66.23 | 3.46 | 12.77 | ||
| 分辨率3 | 4630 | t=1 | 2692 | 41.86 | 0.71 | 3.33 |
| t=2 | 1954 | 57.80 | 1.43 | 6.24 | ||
| t=3 | 1577 | 65.94 | 2.36 | 8.93 | ||
| 分辨率4 | 6664 | t=1 | 4051 | 39.21 | 0.39 | 2.19 |
| t=2 | 2843 | 57.34 | 1.07 | 4.50 | ||
| t=3 | 2378 | 64.32 | 2.21 | 6.19 |
3.3 对比试验
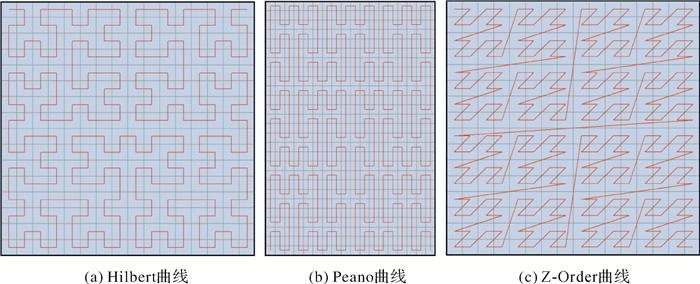
为进行对比,对其他类型的空间填充曲线进行考察,发现它们对应的空间镶嵌基本构造单元皆不是正六边形单元。如图 12所示,常见的Hilbert曲线、Peano曲线、Z-Order曲线等填充曲线对应的空间镶嵌皆为正四边形格网。这些曲线固有的形态结构,使它们难以像Gosper曲线一样,在正六边形格网中直接应用,这也进一步体现了Gosper曲线在正六边形格网中的应用优势。
|
| 图 12 其他填充曲线 Fig. 12 Other filling curves |
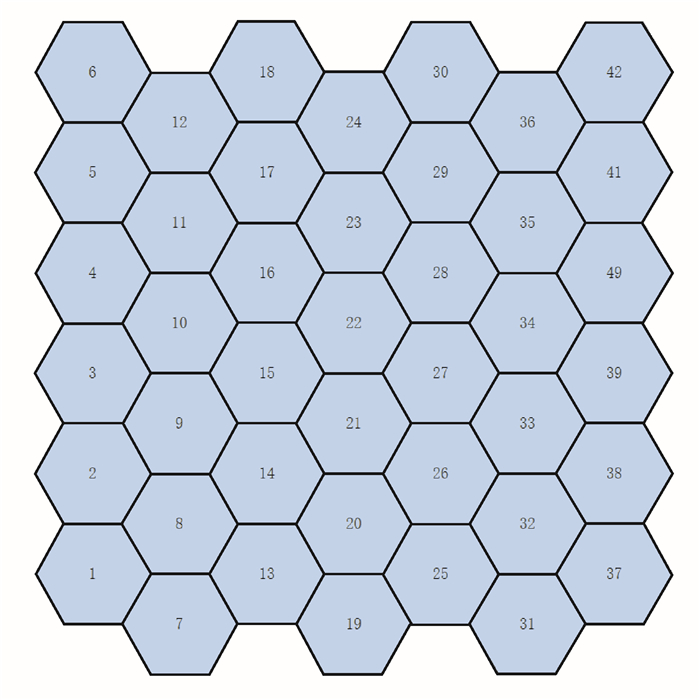
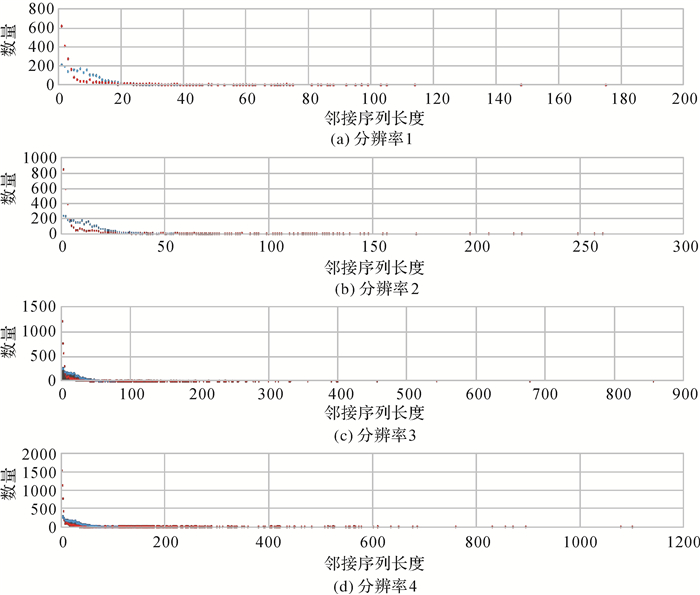
所以,本文选择简单的行编码方式,基于同一份数据开展对比试验。如图 13所示,行编码是对格网中单元按其对齐方向依次进行编码。以相同的方法统计其直接编码、游程编码数据量后,得到行编码的无损压缩试验结果如表 6所示。通过对比可知,虽然Gosper编码的无损压缩结果在多个分辨率下拥有压缩率上的优势,但这种优势并不明显,即二者在压缩率上并无质的差距。然而,通过图 14统计两种方式中各长度的邻接序列数量可以明显发现,在各分辨率下,Gosper编码的邻接序列在两个长度极端都有数量上的优势。一方面,其存在较多长邻接序列,能将大量邻接编码串联起来,具有较高的编码效率;另一方面,大量的短邻接序列为邻接序列融合提供了丰富的素材,可以通过上文介绍的融合方法对它们进行有效剔除,进一步提高编码效率,降低压缩率。而行编码方式中邻接序列长度分布较为聚集,不仅缺少编码效率较高的长邻接序列,而且短邻接序列数目也相对少,造成邻接序列融合缺少着力点。同时,行编码方式具有直线扫描的单向性,不具备类似Gosper曲线迂回的走向特征,难以通过中间编码将要素区域中的邻接序列串联,邻接序列融合的可操作性差。综上,与行编码方式相比,Gosper编码方式自身形态优势使其可以获得更高的编码效率。
|
| 图 13 行编码 Fig. 13 Row coding illustration |
| (%) | |
| 分辨率 | 行编码压缩率 |
| 分辨率1 | 24.91 |
| 分辨率2 | 18.14 |
| 分辨率3 | 13.12 |
| 分辨率4 | 9.4 |
|
| 图 14 邻接序列长度统计散点图(蓝色:行编码;红色:Gosper编码) Fig. 14 Scatter plot of the adjacency sequence length (Blue: Row coding, Red: Gosper coding) |
4 结论
本文研究正六边形栅格数据的压缩编码,通过引入Gosper曲线工具建立编码框架,构建新型游程编码,完成了栅格数据的高效压缩。经试验验证,Gosper无损压缩编码能有效实现正六边形栅格数据的压缩。在此基础上,结合不同的精度、压缩率需求,Gosper有损压缩编码能进行不同程度的数据量精简。其利用Gosper曲线曲折迂回的形态,通过自定义阈值约束下的邻接序列融合,进一步减小数据表达量,较之于普通的行编码方式,在压缩率上可操作空间更大。当处理精度要求较高的数据时,例如需存档的原始数据,可以使用无损压缩的方式记录,通过解压实现数据的无损复原,减少数据存储量的同时避免数据精度损失。在允许一定精度损失的应用中,有损压缩能以较小的精度损失摒除细节信息,进一步减少数据存储量,便于数据的传输交换。在网络环境下减少用户下载时间,以较低的成本达到近似的认知效果。特别的,其通过不同的融合阈值控制进行不同程度的压缩可以视为一种数据综合,能应用于地理要素渐进式传输等业务。通过多分辨率栅格数据的实验,表明此压缩编码在高分辨率数据压缩中表现良好,随分辨率的升高,其压缩率不断下降。此外,还量化评价了不同程度的表达量精简所造成的几何精度、语义精度等方面的损失,概括其一般规律。与此同时,也存在不足之处,例如,如何根据不同的分辨率及精度需求选择合适的融合阈值等问题,这也是后续研究的重点问题。
| [1] |
邬伦, 刘瑜.
地理信息系统:原理、方法和应用[M]. 北京: 科学出版社, 2001.
WU Lun, LIU Yu. Geographic information system:theories, methods and applications[M]. Beijing: Science Press, 2001. |
| [2] |
张宏, 温永宁, 刘爱利, 等.
地理信息系统算法基础[M]. 北京: 科学出版社, 2006.
ZHANG Hong, WEN Yongning, LIU Aili, et al. Foundation of geographic information system algorithm[M]. Beijing: Science Press, 2006. |
| [3] | HOFMANN P, TIEDE D. Image segmentation based on hexagonal sampling grids[J]. South-Eastern European Journal of Earth Observation and Geomatics, 2014, 3: 173–177. |
| [4] | BIRCH C P D, OOM S P, BEECHAM J A. Rectangular and hexagonal grids used for observation, experiment and simulation in ecology[J]. Ecological Modelling, 2007, 206(3-4): 347–359. DOI:10.1016/j.ecolmodel.2007.03.041 |
| [5] | CARR D B, OLSEN A R, WHITE D. Hexagon mosaic maps for display of univariate and bivariate geographical data[J]. Cartography and Geographic Information Systems, 1992, 19(4): 228–236. DOI:10.1559/152304092783721231 |
| [6] | SCOTT D W. A note on choice of bivariate histogram bin shape[J]. Journal of Official Statistics, 1988, 4(1): 47–51. |
| [7] | COPPOLA D M, PURVES H R, MCCOY A N, et al. The distribution of oriented contours in the real world[J]. Proceedings of the National Academy of Sciences of the United States of America, 1998, 95(7): 4002–4006. DOI:10.1073/pnas.95.7.4002 |
| [8] | CARR D B. Looking at large data sets using binned data plots[R]. Richland, WA (USA): Pacific Northwest Laboratory, 1990. |
| [9] | CARR D B, LITTLEFIELD R J, NICHOLSON W L, et al. Scatterplot matrix techniques for large N[J]. Journal of the American Statistical Association, 1987, 82(398): 424–436. |
| [10] | BATTERSBY S E, STREBE D, FINN M P. Shapes on a plane:evaluating the impact of projection distortion on spatial binning[J]. Cartography and Geographic Information Science, 2017, 44(5): 410–421. DOI:10.1080/15230406.2016.1180263 |
| [11] |
童晓冲, 贲进, 张永生.
全球多分辨率六边形网格剖分及地址编码规则[J]. 测绘学报, 2007, 36(4): 428–435.
TONG Xiaochong, BEN Jin, ZHANG Yongsheng. The subdivision of global multi-resolution hexagonal grid and the rules of address coding[J]. Acta Geodaetica et Cartographica Sinica, 2007, 36(4): 428–435. DOI:10.3321/j.issn:1001-1595.2007.04.012 |
| [12] |
贲进.地球空间信息离散网格数据模型的理论与算法研究[D].郑州: 信息工程大学, 2005. BEN Jin. A study of the theory and algorithms of discrete global grid data model for geospatial information management[D]. Zhengzhou: Information Engineering University, 2005. |
| [13] |
赵学胜, 贲进, 孙文彬, 等.
地球剖分格网研究进展综述[J]. 测绘学报, 2016, 45(S1): 1–14.
ZHAO Xuesheng, BEN Jin, SUN Wenbin, et al. Overview of the research progress in the earth tessellation grid[J]. Acta Geodaetica et Cartographica Sinica, 2016, 45(S1): 1–14. DOI:10.11947/j.AGCS.2016.F001 |
| [14] | SUESS M, MATOS P, GUTIERREZ A, et al. Processing of SMOS level 1C data onto a discrete global grid[C]//Proceedings of 2004 IEEE International Geoscience and Remote Sensing Symposium. Anchorage, AK, USA: IEEE, 2004, 3: 1914-1917. |
| [15] | DHARMAWAN R D, SUHARYADI, FARDA N M. Geovisualization using hexagonal tessellation for spatiotemporal earthquake data analysis in indonesia[C]//Proceedings of International Conference on Soft Computing in Data Science. Singapore: Springer, 2017: 177-187. |
| [16] | SHELTON T, POORTHUIS A, GRAHAM M, et al. Mapping the data shadows of hurricane sandy:uncovering the sociospatial dimensions of 'big data'[J]. Geoforum, 2014, 52: 167–179. DOI:10.1016/j.geoforum.2014.01.006 |
| [17] | POLISCIUC E, MAÇÃS C, ASSUNÇÃO F, et al. Hexagonal gridded maps and information layers: a novel approach for the exploration and analysis of retail data[C]//Proceedings of SIGGRAPH ASIA 2016 Symposium on Visualization. Macau, China: ACM, 2016: Article No. 6. |
| [18] | ROTH R E, ROSS K S, MACEACHREN A M. User-centered design for interactive maps:a case study in crime analysis[J]. ISPRS International Journal of Geo-Information, 2015, 4(1): 262–301. DOI:10.3390/ijgi4010262 |
| [19] |
白建军.
基于正八面体的四孔六边形球面格网编码及索引[J]. 遥感学报, 2011, 15(6): 1125–1137.
BAI Jianjun. Location coding and indexing aperture 4 hexagonal discrete global grid based on octahedron[J]. Journal of Remote Sensing, 2011, 15(6): 1125–1137. |
| [20] |
王蕊, 贲进, 杜灵瑀, 等.
平面四孔六边形格网系统编码运算[J]. 测绘学报, 2018, 47(7): 1018–1025.
WANG Rui, BEN Jin, DU Lingyu, et al. Encoding and operation for the planar aperture 4 hexagon grid system[J]. Acta Geodaetica et Cartographica Sinica, 2018, 47(7): 1018–1025. DOI:10.11947/j.AGCS.2018.20170374 |
| [21] | MANDELBROT B B, AIZENMAN M. Fractals:form, chance, and dimension[J]. Physics Today, 1979, 32(5): 65. DOI:10.1063/1.2995555 |
| [22] | HAVERKORT H, VAN WALDERVEEN F. Locality and bounding-box quality of two-dimensional space-filling curves[J]. Computational Geometry, 2010, 43(2): 131–147. DOI:10.1016/j.comgeo.2009.06.002 |
| [23] | TOBLER W R. A computer movie simulating urban growth in the detroit region[J]. Economic Geography, 1970, 46: 234–240. DOI:10.2307/143141 |
| [24] |
信睿, 艾廷华, 何亚坤.
Gosper地图的非空间层次数据隐喻表达与分析[J]. 测绘学报, 2017, 46(12): 2006–2015.
XIN Rui, AI Tinghua, HE Yakun. Visualisation and analysis of non-spatial hierarchical data of gosper map[J]. Acta Geodaetica et Cartographica Sinica, 2017, 46(12): 2006–2015. DOI:10.11947/j.AGCS.2017.20160596 |
| [25] | LINDENMAYER A. Mathematical models for cellular interactions in development[J]. Journal of Theoretical Biology, 1968, 18(3): 280–299. DOI:10.1016/0022-5193(68)90079-9 |
| [26] | FREEMAN H. On the encoding of arbitrary geometric configurations[J]. IRE Transactions on Electronic Computers, 1961, EC-10(2): 260–268. DOI:10.1109/TEC.1961.5219197 |
| [27] |
吴华意, 龚健雅, 李德仁.
无边界游程编码及其矢栅直接相互转换算法[J]. 测绘学报, 1998, 27(1): 63–68.
WU Huayi, GONG Jianya, LI Deren. Non-boundary run-length encoding system for raster and its relevant algorithms[J]. Acta Geodaetica et Cartographica Sinica, 1998, 27(1): 63–68. DOI:10.3321/j.issn:1001-1595.1998.01.010 |
| [28] |
王结臣, 芮一康, 刘杰.
GIS中面的游程编码表达、实现与应用[J]. 测绘科学, 2008, 33(4): 26–28.
WANG Jiechen, RUI Yikang, LIU Jie. Run-length encoding system about area:representation, implement and applications in GIS[J]. Science of Surveying and Mapping, 2008, 33(4): 26–28. DOI:10.3771/j.issn.1009-2307.2008.04.008 |
| [29] |
王家耀.
时空大数据时代的地图学[J]. 测绘学报, 2017, 46(10): 1226–1237.
WANG Jiayao. Cartography in the age of spatio-temporal big data[J]. Acta Geodaetica et Cartographica Sinica, 2017, 46(10): 1226–1237. DOI:10.11947/j.AGCS.2017.20170308 |



