2. 61287部队, 四川 成都 610000
2. Troops 61287, Chengdu 610000, China
全球离散格网系统(discrete global grid system,DGGS)是一种以整个地球为研究对象、以地理空间位置数字化表达为主要特征的新型数据模型。它将地表剖分为均匀统一的层次格网单元结构,并给每个单元赋予全局唯一的地址编码代替传统地理坐标参与运算和操作[1]。与传统空间数据模型相比,其优势体现在:面向全球,能够提供全球一致的空间基准;天然多尺度,有助于处理多源、异构地理空间数据;纯编码运算,有助于提高数据处理效率。
与三角形、四边形相比,六边形具有拓扑关系一致、采样效率高等特点,有助于提高空间分析算法精度[2-3]和可视化表达效果[4-5],其主要缺陷是不具备自相似性,无法直接建立多分辨率格网单元层次关系。文献[6]提出一种多维数据结构,二维特例可通过“广义平衡三进制”(generalized balanced ternary,GBT)运算实现不同层次六边形单元的编码索引[7]。文献[8]改进GBT的不足,提出HIP(hexagonal image processing)结构,并将其应用于影像处理。文献[9-11]区分奇(偶)层建立了平面三孔六边形格网系统的单元编码索引并将其扩展到球面,在此基础上,文献[12]实现了傅里叶变换算法。但这类方案对奇(偶)层单元分别处理,增加了编码运算复杂度,索引效率不高。文献[3, 13-15]采用“单元隶属图形”建立六边形格网的编码索引,主要不足是破坏了六边形单元的完整性。文献[16-17]借助格网单元中心与顶点建立了平面四孔六边形格网系统的“四元平衡结构”(hexagonal quad balanced structure,HQBS)并将其扩展到球面,主要缺陷是概念模型复杂,且会在编码运算中会出现“正则化”失败需要回退重算的情况,严重影响索引效率[18]。
综上所述,单元编码索引是六边形全球离散格网系统研究的核心问题之一,平面格网系统层次关系描述及编码方案设计则是该问题的突破口。现有成果仍然存在不足,亟须改进完善。本文根据平面四孔六边形格网结构特点,设计“六边形格点四叉树”(hexagon lattice quad tree,HLQT)层次编码结构,定义编码运算等效代替格网单元的几何操作,归纳编码运算规律并实现了对应的算法。借助编码运算,设计并实现二维直角坐标与单元编码的相互转换算法,通过对比试验验证本文方案的正确性与优越性。
1 编码方案设计为了便于讨论,本文将平面离散格网系统的单元中心定义为“格点”,作为单元的等效替代对象,四孔六边形剖分产生的格点以及剖分规律如图 1所示:第n(n≥1)层格点是由第n-1层格点与n-1层单元各边中点组合而成,第n-1层单元边长是第n层单元边长的2倍,单元方向不随层次变化。
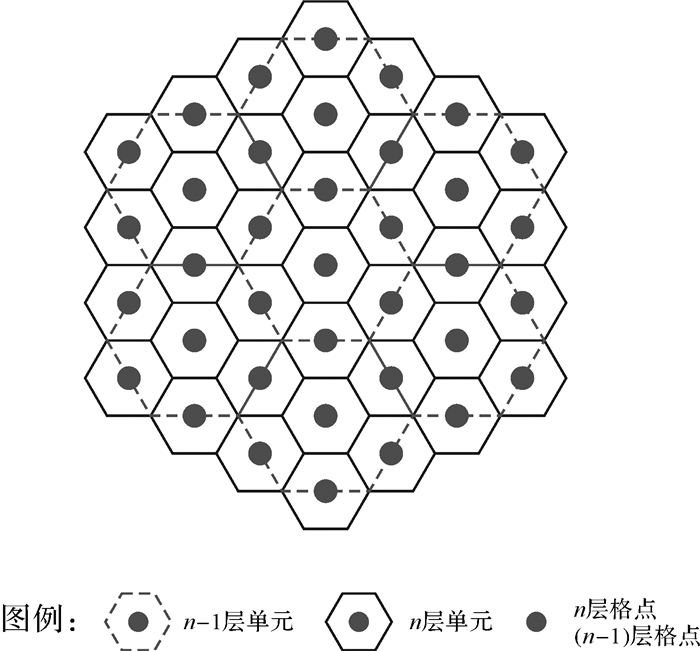
|
| 图 1 四孔六边形格网系统格点与剖分规律示意图 Fig. 1 Diagram of lattice points and subdivision rules for the aperture 4 hexagonal grid |
格点位置通常采用笛卡尔坐标描述[10, 14, 17, 19-20],这种方法虽然直观形象、便于理解,但因采用了二维独立变量(如x、y),表达形式不简洁且不易与编码建立联系。故本文采用复数表示格点位置[21-22],建立平面四孔六边形格点系统的唯一性描述方案[23]。
在复数平面上,令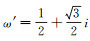
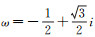
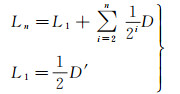 (1)
(1)
Ln(n≥1)表示第n层格点集合。式(1)中“∑”并不是集合之间的并(∪),而是集合之间相加,即从参与计算的n个集合中任选一个元素,一共n个元素求和。图 2所示为L1与L2层次关系示意图。L1为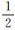
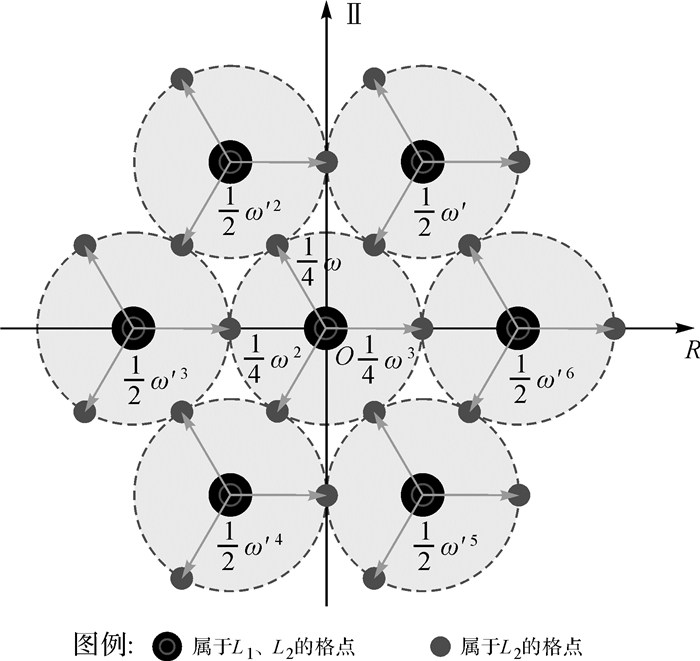
|
| 图 2 L1与L2格点层次关系示意 Fig. 2 Diagram of hierarchical relationship between L1 and L2 |
以上描述方案具有唯一性,生成的子单元互不重叠,每个子单元具有唯一的父单元。Ln是典型的四叉树层次结构,即随着剖分层次的深入,L1中的每个格点都分别生长为一颗独立的四叉树,这为格网编码提供了理论依据。
以上方案还表明:四孔六边形格点系统与实数域上的二进制、八进制、十进制等定位计数系统的本质完全相同,是复数域上一种特定形式的“数”[24]。该定位计数系统的进制为2,数字位集合为D′和D。对于x∈Ln,其具体形式为
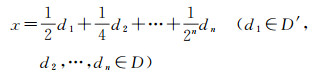 (2)
(2)
或与十进制数类似,省略幂指数的底,式(2)可记为
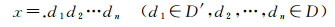 (3)
(3)
式(3)中的小数点表示格点随剖分层次向内部生长,越来越密集。用不同大小和颜色的点表示L1~L5中的元素,它们在复平面上的分布如图 3所示。
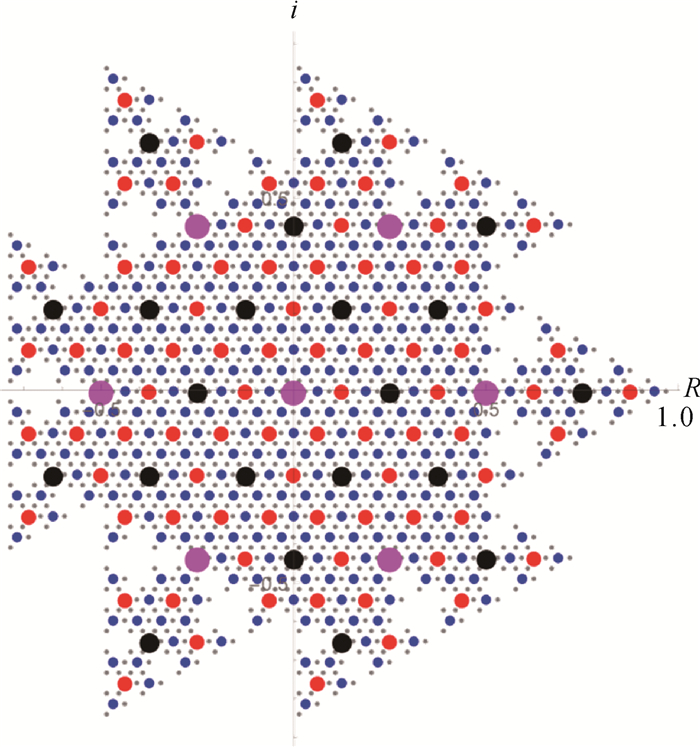
|
| 图 3 L1~L5在复平面上的分布 Fig. 3 Distribution of L1~L5 in the complex plane |
为了便于计算机处理,需要对格网系统中的每个单元指定一个地址码,这一过程称为“编码”。编码方案必须满足完整性、唯一性与层次性[19]。
根据式(3),取di幂指数,称为码元,即d1=ω′e→e(1≤e≤6),di=ωe→e(1≤e≤3, 2≤i≤n),则数字位集合D′替换为码元集合E′={0, 1, 2, 3, 4, 5, 6},数字位集合D替换为码元集合E={0, 1, 2, 3}。得到x∈Ln的唯一编码标识e1e2…en(e1∈E′, ei∈E, 2≤i≤n)。显然,该编码方案还满足完整性和层次性的要求。
L3的完整编码如图 4所示,不同格点层次隶属和关联用不同大小的圆和三角形表示。将这一格点层次结构命名为“六边形格点四叉树”(hexagon lattice quad tree,HLQT)。
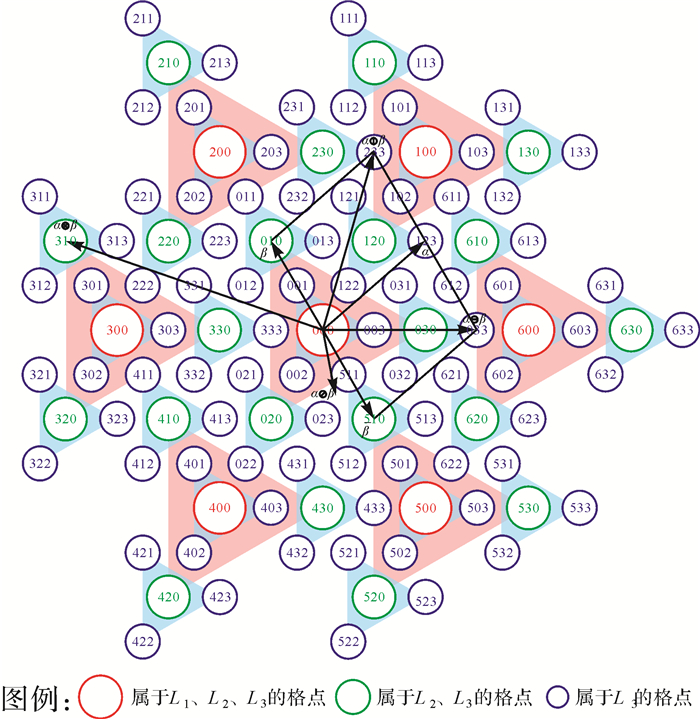
|
| 图 4 L3编码及运算示意图 Fig. 4 Representation of codes in the 3rd level and examples of code arithmetic |
2 编码运算规律
HLQT编码记录了某一格点与原点(编码全部为0的格点)的距离和方位,是复数平面上“定位计数系统”的等效表示。因此格点对应复数之间的各类运算可从二维复数平面空间降维到一维编码空间中实现,且编码相较于浮点数更适合计算机处理,可有效提高计算效率。
2.1 定义在复数平面上,任意两复数的加、减法满足平行四边形法则。在HLQT编码集合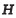
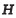
令α=α1α2…αn,β=b1b2…bn,编码加法计算方式与十进制加法类似,从右侧末位码元(即an或bn)开始,向左侧首位码元(即a1或b1)逐位计算,可表示为
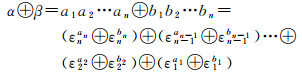 (4)
(4)
其中
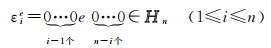 (5)
(5)
i-1与n-i表示码元0的个数。当i=1时,e∈{0, 1, 2, 3, 4, 5, 6};当i>1时,e∈{0, 1, 2, 3}。εiai⊕εibi计算结果的后n-i位都为码元0,这与十进制加法相同,计算至第i位时,其右侧n-i位均计算完毕,不参与运算。因此,式(5)在计算时可记作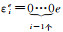
对于首位编码码元(i=1),其运算规律以表 1加法表的形式给出,表中左列与首行为对应相加码元。由于相加结果会超出原始7个码元集合,因此增加{10, 20, 30, 40, 50, 60, 100, 200, 300, 400, 500, 600}12个首层格点编码,其复数平面位置可其相加码元的向量加法运算得出。
| ⊕ | 0 | 1 | 2 | 3 | 4 | 5 | 6 |
| 0 | 0 | 1 | 2 | 3 | 4 | 5 | 6 |
| 1 | 1 | 100 | 20 | 2 | 0 | 6 | 10 |
| 2 | 2 | 20 | 200 | 30 | 3 | 0 | 1 |
| 3 | 3 | 2 | 30 | 300 | 40 | 4 | 0 |
| 4 | 4 | 0 | 3 | 40 | 400 | 50 | 5 |
| 5 | 5 | 6 | 0 | 4 | 50 | 500 | 60 |
| 6 | 6 | 10 | 1 | 0 | 5 | 60 | 600 |
对于非首位码元相加(i>1),除了得到当前位的计算结果码元,还会在左侧首位至第i-1位产生进位码元,具体规律如下
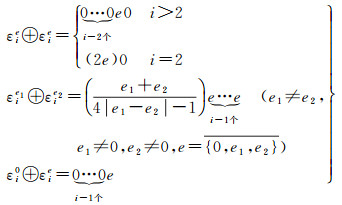 (6)
(6)
每一位进位码元再根据式(6)或表 1相加,直至得到当前位最终计算结果码元。在计算过程中,层次i(1≤i<n)对应加法位上进位码元个数为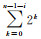
(1) 0⊕e=e,0作为进位码元无累加意义,1, 2, 3作为进位码元有累加意义。
(2) 当e1, e2∈{1, 2, 3},计算
因此在计算过程中,不计算0并优先计算相同码元后,每层剩余需相加的码元不会超过3个,剩余最多情况时,所需相加的码元集合为{1, 2, 3}。
(3) 不必开辟大量内存存放码元,只需统计各码元出现次数,提高计算效率。
此外,在计算过程中,还需要对首位编码溢出的情况加以控制:
(1) 先将相加为0的编码消除,这样剩余编码个数不超过3个。
(2) 因为没有建立码元{10, 20, 30, 40, 50, 60}的加法表,为了避免其进行加法运算,对剩余编码,先进行间隔相加,如1⊕3=2;然后,将相同编码相加,如1⊕1=100。
图 5(a)为编码加法运算示例2322⊕1033=100,201,其中黑色、灰色不带下划线和带下划线码元分别表示原始相加码元、计算结果码元和进位码元。图 5(b)是根据上述运算规律所设计的算法流程。
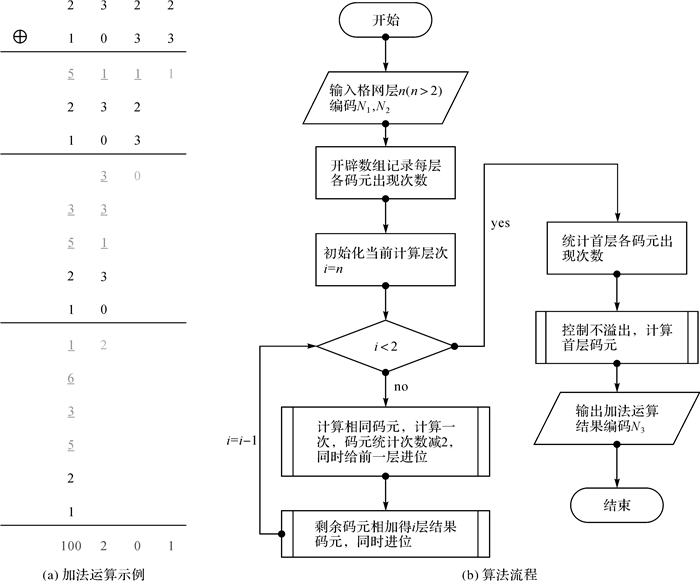
|
| 图 5 编码加法运算示例与算法流程 Fig. 5 Example and flow chart for add operation |
3 坐标与编码转换
采用一维格网编码代替传统二、三维笛卡尔坐标参与运算是全球离散格网系统具有较高数据处理效率的重要原因。尽管在格网系统中,单元操作可完全通过编码实现,但目前大部分空间数据仍采用地理坐标或投影坐标给出。为了保证现有数据进、出格网系统,必须建立笛卡尔实数坐标与单元编码码元序列之间的对应关系。
坐标到编码的转换本质是根据编码规则,记录逼近坐标点所经过各层次单元的编码,逼近路径的不同导致转换效率差异。本文借助编码运算实现的转换,以矢量相加的“平行四边形法则”为依据,避开了层次路径的迭代,具有直观、高效的特点。
3.1 二维直角坐标转换为编码给定二维直角坐标已知的点p(x, y),利用平行四边形法则,将点p投影到两条特定的坐标轴上,得到两条轴上对应的分量编码α1和α2,再通过编码加法运算,计算出点p所属单元编码α。
图 6为二维直角坐标到编码的转换示意图,格网层次为2,编码前3位为首层编码,最后一位为第二层编码。引入三轴坐标系O-IJK作为投影坐标轴,原点与O-XY一致,J轴与Y轴一致,I、J、K轴之间正向夹角120°,按顺时针方向排列,将360°平面分成6个象限。
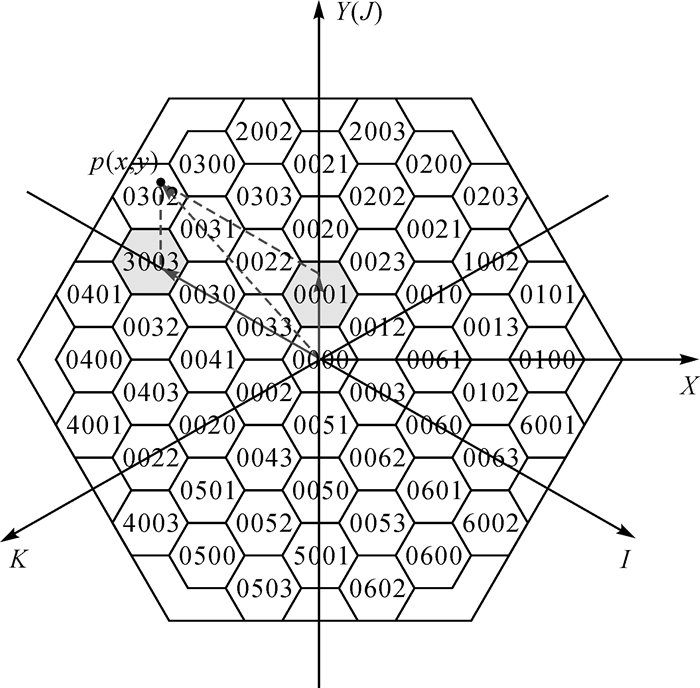
|
| 图 6 平面坐标与编码转换示意 Fig. 6 Transformation between geographic coordinates and codes |
投影坐标轴的选择可由点p和原点O连线与X轴的夹角θ的正切值来判断。I、J、K轴是过一列连续排列格点的直线,位于其上格点编码α的后n-1位编码N{n-1},与所在坐标轴和其编号k有如下关系
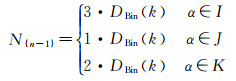 (7)
(7)
式中,DBin(k)代表编号k的二进制数序列,编号k为单元在轴上的位置,可由投影长度计算得到。αi的首位编码N0虽不符合二进制规律,但其与k之间的关系也很容易归纳。最后,根据编码加法运算规律,可得
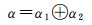 (8)
(8)
格点本质上就是复平面上一种特殊形式的数,编码是其另一种有效的表达方式,因此编码与格点的复数平面坐标可以相互转化。将编码按复进制展开,计算其在复数平面上的实部坐标x和虚部坐标y,得到格点的二维直角坐标(x, y)。
假设格网层次为n,某单元编码α=e1e2…en,根据码元与数字位间的关系有
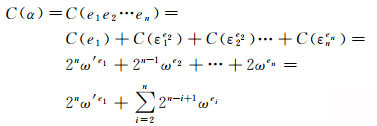 (9)
(9)
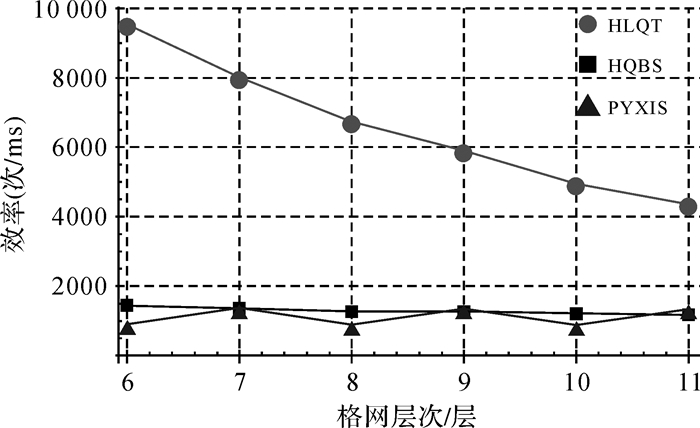
为了验证以上算法的效率,笔者采用Visual C++ 2012开发工具分别实现了HLQT、PYXIS[11]和HQBS[16-17]的编码加法,以及HLQT和HQBS的二维直角坐标与编码相互转换算法。由于HLQT与HQBS方案编码总数会随着层次升高急剧增加,因此在加法算法中这两种方案随机选取固定个数编码,两两相加。全部程序编译为Release版本,并在一台兼容机(软件配置:Windows 7 x64旗舰版+SP1;硬件配置:Intel Core i5-6500 CPU@3.20GHZ,8G RAM,KingSton 120GB SSD)上进行测试。统计各算法6—11层的运算效率,加法运算与转换算法效率分别为单位时间内作加法运算的次数和完成转换的坐标或编码个数,取10次测试的平均值,结果见表 2、表 3、图 7、图 8所示。
| 层次 | 算法 | |||||||
| PYXIS | HQBS | HLQT | ||||||
| 单元个数 | 运算效率/(次/ms) | 单元个数 | 运算效率/(次/ms) | 单元个数 | 运算效率/(次/ms) | |||
| 6 | 1261 | 893 | 4096 | 1442 | 5000 | 9540 | ||
| 7 | 4039 | 1363 | 3000 | 1354 | 5000 | 8011 | ||
| 8 | 11605 | 885 | 3000 | 1265 | 5000 | 6734 | ||
| 9 | 35839 | 1351 | 3000 | 1260 | 5000 | 5892 | ||
| 10 | 105469 | 874 | 3000 | 1212 | 5000 | 4946 | ||
| 11 | 320503 | 1340 | 3000 | 1177 | 5000 | 4355 | ||
|
| 图 7 编码加法运算效率对比 Fig. 7 Efficiency comparison of code addition |
|
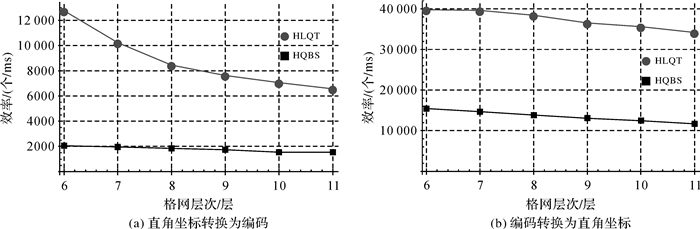
| 图 8 二维直角坐标与编码转换算法效率对比 Fig. 8 Efficiency comparison of transform algorithms |
| 层次 | 算法 | ||||||||||
| HQBS | HLQT | ||||||||||
| (x, y)→α | α→(x, y) | (x, y)→α | α→(x, y) | ||||||||
| 坐标个数 | 运算效率/(个/ms) | 编码个数 | 运算效率/(个/ms) | 坐标个数 | 运算效率/(个/ms) | 编码个数 | 运算效率/(个/ms) | ||||
| 6 | 288000 | 2043 | 4096 | 15457 | 222021 | 12755 | 4096 | 39783 | |||
| 7 | 334800 | 1958 | 16384 | 14651 | 222021 | 10224 | 16384 | 39613 | |||
| 8 | 214289 | 1840 | 65536 | 13823 | 222021 | 8449 | 65536 | 38448 | |||
| 9 | 305000 | 1729 | 262144 | 13051 | 222021 | 7631 | 262144 | 36550 | |||
| 10 | 565929 | 1534 | 1048576 | 12451 | 222021 | 7058 | 1048576 | 35623 | |||
| 11 | 675000 | 1548 | 4194304 | 11683 | 222021 | 6565 | 4194304 | 34164 | |||
文献[17]验证了HQBS编码运算效率要优于PYXIS,这与图 7的结果基本一致。因此本文在转换算法中,只对比HQBS与HLQT的效率。
试验结果表明:
(1) HLQT编码加法的平均运算效率约为PYXIS算法的6倍、HQBS算法的5倍。这是因为PYXIS奇(偶)分层编码,导致加法查找表比较复杂,而HLQT无须区分奇(偶)层,查找表规模较小(首位为7×7,其余位为4×4);HQBS单元中心与顶点混合编码,导致运算规则复杂且易出现编码“正则化”失败需要退回重算的情况,而HLQT只对格点编码,运算规律更直接,因而效率较高。
(2) HLQT的二维直角坐标向编码转换的平均运算效率大约是HQBS的5倍。这主要得益于HLQT的高率编码运算,且转换算法中位于I、J、K 3轴上参与加法运算的HLQT编码在码元结构上具有二进制数特征,采用效率极高的二进制运算直接得到计算结果。
(3) HLQT的编码向二维直角坐标转换的平均运算效率是HQBS的3倍。因为HQBS算法涉及较多浮点数运算,而HLQT将浮点数运算处理为等效的整数运算,提高了运算效率。因码元个数随层次升高线性增加,二者效率均呈线性化下降趋势。
5 总结与展望本文根据平面四孔六边形格网系统结构特点,采用复进制数描述单元层次关系并设计了HLQT层次编码结构。该结构只对格点编码,码元具有明确几何意义,编码方案和编码运算具有严密的理论基础,克服了PYXIS奇(偶)分层编码、HQBS单元中心与顶点混合编码的不足,概念模型简单,编码运算和编码转换效率较高。为了建立四孔六边形全球离散格网的编码运算体系,下一步还需研究HLQT在球面上的扩展方案。
| [1] | GOODCHILD M F, YANG Shiren. A Hierarchical Spatial Data Structure for Global Geographic Information Systems[J]. CVGIP:Graphical Models and Images Processing, 1992, 54(1): 31–44. DOI:10.1016/1049-9652(92)90032-S |
| [2] | SAHR K, WHITE D, KIMERLING A J. Geodesic Discrete Global Grid Systems[J]. Cartography and Geographic Information Science, 2003, 30(2): 121–134. DOI:10.1559/152304003100011090 |
| [3] |
贲进, 童晓冲, 周成虎, 等.
正八面体的六边形离散格网系统生成算法[J]. 地球信息科学学报, 2015, 17(7): 789–797.
BEN Jin, TONG Xiaochong, ZHOU Chenghu, et al. Construction Algorithm of Octahedron Based on Hexagon Grid Systems[J]. Journal of Geo-Information Science, 2015, 17(7): 789–797. |
| [4] | SAHR K. Hexagonal Discrete Global Grid Systems for Geospatial Computing[J]. Archives of Photogrammetry, Cartography and Remote Sensing, 2011, 22(2): 363–376. |
| [5] | BIRCH C P D, OOM S P, BEECHAM J A. Rectangular and Hexagonal Grids Used for Observation, Experiment and Simulation in Ecology[J]. Ecological Modelling, 2007, 206(3-4): 347–359. DOI:10.1016/j.ecolmodel.2007.03.041 |
| [6] | LUCAS D. A Multiplication in N-Space[J]. Proceedings of the American Mathematical Society, 1979, 74(1): 1–8. |
| [7] | GIBSON L, LUCAS D. Spatial Data Processing Using Generalized Balanced Ternary[C]//Proceedings of IEEE Conference on Pattern Recognition and Image Processing. Las Vegas, Nevada: IEEE, 1982: 566-571. |
| [8] | MIDDLETON L, SIVASWAMY J. Hexagonal Image Processing:A Practical Approach[M]. London: Springer, 2005. |
| [9] | SAHR K M. Discrete Global Grid Systems: A New Class of Geospatial Data Structures[D]. Ashland: University of Oregon, 2005: 71-102. http://dl.acm.org/citation.cfm?id=1124006 |
| [10] | SAHR K. Location Coding on Icosahedral Aperture 3 Hexagon Discrete Global Grids[J]. Computers, Environment and Urban Systems, 2008, 32(3): 174–187. DOI:10.1016/j.compenvurbsys.2007.11.005 |
| [11] | PETERSON P. Close-packed, Uniformly Adjacent Multiresolutional, Overlapping Spatial Data Ordering: US, 8400451[P]. 2013-03-19. |
| [12] | VINCE A, ZHENG X. Arithmetic and Fourier Transform for the PYXIS Multi-resolution Digital Earth Model[J]. International Journal of Digital Earth, 2009, 2(1): 59–79. DOI:10.1080/17538940802657694 |
| [13] |
贲进. 地球空间信息离散网格数据模型的理论与算法研究[D]. 郑州: 信息工程大学, 2005. BEN Jin. A Study of the Theory and Algorithm of Discrete Global Grid Data Model for Geospatial Information Management[D]. Zhengzhou: Information Engineering University, 2005. http://cdmd.cnki.com.cn/article/cdmd-90008-2007051587.htm |
| [14] |
贲进, 童晓冲, 汪磊, 等.
利用球面离散格网组织空间数据的关键技术[J]. 测绘科学技术学报, 2010, 27(5): 382–386.
BEN Jin, TONG Xiaochong, WANG Lei, et al. Key Technologies of Geospatial Data Management Based on Discrete Global Grid System[J]. Journal of Geomatics Science and Technology, 2010, 27(5): 382–386. |
| [15] |
贲进, 童晓冲, 元朝鹏.
孔径为4的全球六边形格网系统索引方法[J]. 测绘学报, 2011, 40(6): 785–789.
BEN Jin, TONG Xiaochong, YUAN Chaopeng. Indexing Schema of the Aperture 4 Hexagonal Discrete Global Grid System[J]. Acta Geodaetica et Cartographica Sinica, 2011, 40(6): 785–789. |
| [16] |
童晓冲. 空间信息剖分组织的全球离散格网理论与方法[D]. 郑州: 信息工程大学, 2010. TONG Xiaochong. The Principle and Methods of Discrete Global Grid Systems for Geospatial Information Subdivision Organization[D]. Zhengzhou: Information Engineering University, 2010. http://kns.cnki.net/KCMS/detail/detail.aspx?filename=chxb201104026&dbname=CJFD&dbcode=CJFQ |
| [17] | TONG Xiaochong, BEN Jin, WANG Ying, et al. Efficient Encoding and Spatial Operation Scheme for Aperture 4 Hexagonal Discrete Global Grid System[J]. International Journal of Geographical Information Science, 2013, 27(5): 898–921. DOI:10.1080/13658816.2012.725474 |
| [18] |
贲进. 六边形格网系统的复进制数模型[R]. 第八届全国地图学与地理信息系统学术大会论文集, 南京: [s. n. ], 2016. BEN Jin. The Model of Complex Number with a Radix System for the Hexagonal Grid System[C]. Proceedings of the 8th National Conference on Cartography and Geography Information System, Nanjing: [s. n. ], 2016. |
| [19] |
张永生, 贲进, 童晓冲.
地球空间信息球面离散网格——理论、算法及应用[M]. 北京: 科学出版社, 2007.
ZHANG Yongsheng, BEN Jin, TONG Xiaochong. Discrete Global Grids for Geospatial Information:Principles, Methods and It's Applications[M]. Beijing: Science Press, 2007. |
| [20] |
白建军.
基于正八面体的四孔六边形球面格网编码及索引[J]. 遥感学报, 2011, 15(6): 1125–1137.
BAI Jianjun. Location Coding and Indexing Aperture 4 Hexagonal Discrete Global Grid Based on Octahedron[J]. Journal of Remote Sensing, 2011, 15(6): 1125–1137. |
| [21] | VINCE A. Indexing the Aperture 3 Hexagonal Discrete Global Grid[J]. Journal of Visual Communication & Image Representation, 2006, 17(6): 1227–1236. |
| [22] | VINCE A. Indexing A Discrete Global Grid[C]//Special Topics in Computing and ICT Research, Advances in Systems Modelling and ICT Applications, Volume Ⅱ. Kampala: Fountain Publishers, 2006: 3-17. |
| [23] | BEN Jin, LI Yalu, ZHOU Chenghu, et al. Algebraic Encoding Scheme for Aperture 3 Hexagonal Discrete Global Grid System[J]. Science China Earth Sciences, 2018, 61(2): 215–227. DOI:10.1007/s11430-017-9111-y |
| [24] | KNUTH D E. The Art of Computer Programming, Volume 2:Seminumerical Algorithms[M]. London: Addison-Wesley, 1969. |
| [25] | GARRETT B, SAUNDERM L. A Survey of Modern Algebra[M]. 5th ed. Beijing: Posts & Telecom Press, 1977. |



