大数据时代,如何从海量数据中挖掘有效信息以发现深层规律成为各领域学者关注和研究的热点问题。数据的抽象性与巨量性一道,阻碍着人类对其认知理解,需要相关技术方法满足直观、概览的需求。可视化为此提供了可靠的解决方案,但选择何种可视化方式促进认知是亟待解决的问题。大数据中存在大量以文本的方式描述事物构成、性质、类型等本体特征的非空间数据,层次数据即是其中一类。过去,通常使用多叉树、TreeMap[1]等可视化方式表达层次数据。然而,多叉树中上下方位及边连接所提供的视觉线索难以直观反映包含关系,同时要素属性很难在多叉树中得到合理表达[2],其较低的空间利用率也是不容忽视的问题[3]。TreeMap克服了上述缺陷,但其进行空间剖分时视觉感生硬,缺乏美感及艺术性。文献[4]总结了层次数据可视化的相关因素,基本概括了层次数据的各种表达形式,但笔者认为其主要存在以下不足:①未对视觉变量进行有效利用;②忽略了空间位置的重要意义;③表达过于抽象,未能充分调动人的认知天赋,往往专业人士才能理解。
人类的生活离不开与空间的交互,在此过程中不断培养视觉熟悉与空间思维,空间形象思维促进了人对事物的认知理解。从纸质地图到电子导航地图,再到虚拟现实技术,皆在借助人类空间思维高效地完成信息的传递任务。随着信息公开化的日益深入,大量无定位特征的纯语义数据不断涌现,许多专家学者希望借助人类的空间思维,使用空间语言表达此类抽象数据,以降低认知负荷,空间化思想应运而生。空间化是针对不具备空间属性的数据,完成从高维抽象空间至低维可视空间的系统转换,利用人类潜在经验,以空间事物的形式促进数据的表达与挖掘[5-6]。文献[7]阐述了空间化的框架并介绍其应用,在语义数据挖掘方面,文献[8]较早借助空间化思想表达文本数据。地图是展示空间信息的常用工具,其亦可作为非空间数据的表达载体,即隐喻地图,隐喻地图是通过构造虚拟地图空间,以地图要素展示语义信息的可视化表达手段[9]。作为空间化的一种形式,隐喻地图通过将陌生领域的抽象非定位数据表达为大众熟悉的地图对象,从而建立源目标(地图对象)与对象目标(表达对象)间的映射联系,达到以熟悉、可感的形式展示陌生、抽象内容之目的。例如,Aureka软件[10]以地形图形式对专利信息进行梳理表达,即“专利地图”,引发广泛关注,是隐喻地图领域的经典作品。
隐喻地图对层次数据可视化存在的问题给出了相应解决方案:传统地图学为可视化表达提供了经典原理与方法,如Bertin视觉参量理论[11];通过对地理学第一定律的实现,将属性上相近的要素布设为地图上临近的对象,赋予空间位置重要含义;千百年来在制图识图过程中的经验证明,地图符合人类认知习惯,甚至学龄前儿童也能进行地图阅读[12]。文献[13]研究得出空间相关信息占信息总量的57%,而非传统认为的80%,非空间信息领域的扩张并不代表空间思维及方法作用域的缩减,地图在解决传统空间问题的同时,亦可作用于非空间问题的分析。
当前隐喻地图的成果较少,文献[14]选取会议摘要数据,使用自组织映射技术(SOM)进行主题聚类生成地图;还有研究将表达关系数据的关联图转换为地图的形式表达[15-16];文献[17]利用六边形随机扩散实现地图区域的填充。其中,文献[15]和文献[16]的方法仅能作用于网络数据,对层次数据并不适用,文献[14]中的方法需对数据进行聚类,并不适合本身即有明显结构特征的层次数据,文献[17]中地图模块间缝隙过大,可视化效果较差。文献[18]提出了Gosper地图,其利用Gosper空间填充曲线作为引导,通过反空间索引的方式将节点布设在正六边形地图单位上,基于层次结构自下而上对子区域合并构造地图。Gosper地图很好地顾及了层次数据节点相邻关系,空间上的无缝拼接也带来良好的可视效果,可以作为研究层次数据的理想框架。但当前研究多侧重于其生成技术等方面的介绍,对其具体的应用研究不足,很少涉及地图表达、分析等方面的工作。
本文借助人类空间形象思维认知优势及对地图的熟悉,利用地图隐喻思想对抽象层次数据进行类地图表达。基于Gosper地图进行丰富扩充,结合经典地图学方法设计地图,以典型自然地貌隐喻数据特征,在生成地图上对多尺度技术及焦点上下文思想进行综合应用,通过地图可视化方式窥探抽象数据特征、挖掘潜在规律。与以往将新可视化技术、方法引入地图的研究不同,本研究力图扩展地图应用外沿,将地图学的经典方法应用于非空间数据的表达分析,以地图的视角研究问题。
1 基于Gosper曲线的层次数据隐喻地图表达与分析如图 1中结构所示,本节阐述Gosper地图的生成原理及特点,介绍地图隐喻的表达方法,结合对多尺度分析、变形地图等的论述,为综合运用上述理论方法进行层次数据分析的试验提供理论基础。

|
| 图 1 理论结构图 Fig. 1 Theoretical structure diagram |
1.1 Gosper地图生成原理
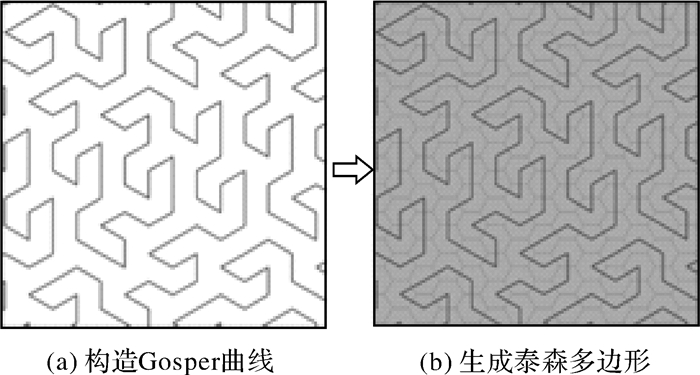
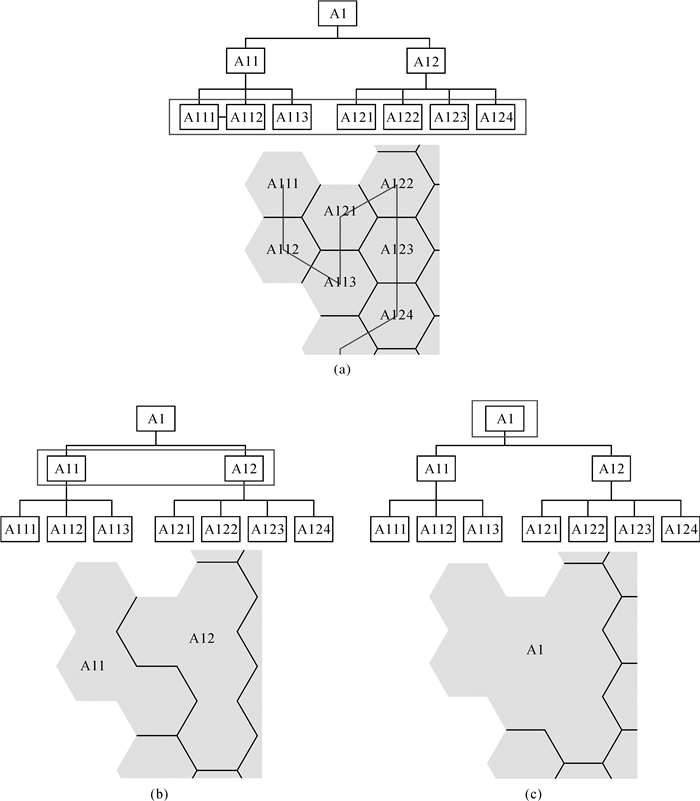
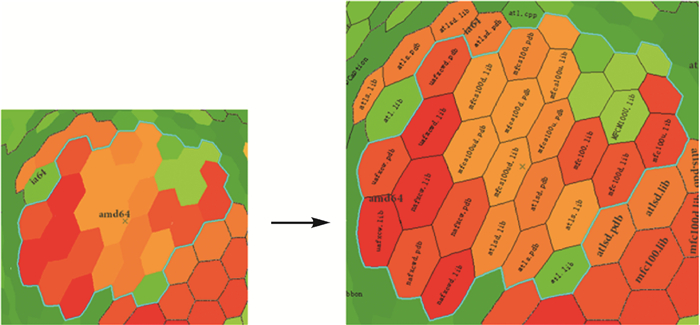
生成Gosper地图首先需按分形规则构建Gosper曲线(图 2(a)),利用曲线节点作为发生元构造泰森多边形,形成蜂窝状底图(图 2(b))。依照Gosper曲线引导顺序,将层次数据叶子节点排布在曲线节点对应的正六边形上。再根据父子节点包含关系,对下层子节点区域融合得到父节点区域(如图 3),自下而上重复此过程,生成体现层次数据嵌套包含关系的多边形集合。
|
| 图 2 地图底图生成 Fig. 2 Generate the base map |
|
| 图 3 Gosper地图生成原理 Fig. 3 The producing principle of Gosper map |
Gosper地图使用正六边形作为构造地图的基本单元,具有无缝拼接、结构稳定、易于扩展等优点。与栅格图像常用的正四边形单元相比,正六边形在邻域扩展时区域连续性更强,其相邻区域皆是以共享边为基础的强连接,而正四边形相邻区域中存在以共享点为基础的弱连接关系。在Gosper曲线的引导下,数据与地图间建立起严格映射,层次数据节点的相邻关系能得到很好的顾及,层次包含关系也便于通过面域嵌套迅速实现。较之于类似的Hilbert曲线引导下的规则格网剖分[19](如图 4),Gosper地图中六边形集合构建的区域避免了过于规整的几何形态,提升了地图美感,同时其边缘形态与真实地图边界有极高的相似度,增加了其地图相似性。

|
| 图 4 皮亚诺曲线网格剖分结果 Fig. 4 The split result of Peano curve |
1.2 地图隐喻表达
隐喻表达中常用具象化、空间化的方法促进对抽象事物的理解[20],如“恩重如山”、“情深似海”此类表达方式,皆是借助人对自然景观的熟悉印象描摹抽象事物特征。隐喻地图以地图为载体表达抽象数据,可以借用熟悉的地图属性特征反映数据特点,亦可通过构造地形地貌图的方式辅助数据表达。使用要素面积表达数值大小是抽象数据具象化中常用的手段,较之于抽象数值对比,对面积大小的判定更为直观。区域面积是地图的重要属性,Gosper地图由正六边形叶子节点自下而上融合构建,故其节点区域面积的大小反映了包含叶子节点数目的多寡,可以此实现通过有形的区域面积隐喻抽象的节点数目,也为利用面积的横向对比分析叶子节点的数量分布提供了便利。通过构建Gosper地图,各数据项都在地图空间上拥有了对应的位置。对于需要分析表达的目标属性,将属性值转换为相应位置的地形数据(如高程值),制作虚拟地形,并借鉴经典地图用色,生成地貌晕渲图。建立自然地貌与抽象数据间的联系,通过地貌特点隐喻数据特征,如使用较高的地势表达较大的数值,通过水深隐喻层次数据的纵深等,利用此类直观可感的空间场景调动用户形象思维,提升其兴趣,加深对数据的理解。
1.3 多尺度分析研究问题的出发尺度决定了研究结果的精度,为满足不同精度需求,需在不同尺度上分析问题。地图中对尺度的研究十分重视,在早期介绍空间化的文章中也强调了尺度的应用[6]。文献[21]研究尺度的隐喻作用,结果表明人可以将空间分辨率的改变同层次的变化相联系。在多尺度技术方面,LOD技术可视作多粒度、多层次的切片集合,通过不同的尺度控制,可以对不同切片进行可视化展示[22]。本文将LOD技术引入隐喻地图的研究分析,建立地图切片、LOD级别、地图比例尺间对应关系。结合不同表达分析需求,控制展示反映不同层次语义信息的地图切片,以便在不同尺度上对数据展开分析挖掘工作。
首先,将空间上重合的各地图面域进行分离,按层次为其赋予LOD等级。如图 5所示,对于层次树上游节点所对应的区域,为其设定较小的LOD等级,随着层次的深入,展示细节信息的子节点区域对应较高的LOD等级。以上建立了基于LOD等级的多层次场景集合,LOD级别的递增对应着面域剖分的逐层深入,细节信息也进一步得到展现。同一比例尺下,细节信息的增加有时会导致图上符号密度过大的问题,影响观察效果,需要通过变换比例尺进行调节。比例尺范围与不同级别LOD场景的一般对应关系为:小比例尺范围下显示LOD级别较低的地图场景,大比例尺下则对应高级别的LOD地图场景。在较小的比例尺下,地图视野范围较广,低级别的LOD地图表达较为概略,适合进行面向数据整体的宏观性分析,但缺少对数据细节方面的展示。随着分析的深入,叠加LOD级别较高的地图场景以展示更多细节信息,为锁定分析目标,将图面切换至较大比例尺下对细节内容进行精确显示。较之于上一地图场景,此时的地图视野范围收缩,但表达的信息更为详实,适合进行微观的个体研究。

|
| 图 5 Gosper地图LOD级别划分 Fig. 5 LOD level of Gosper map |
隐喻地图与LOD技术的结合,将往常用于地图空间分析的方法过程应用至抽象数据的分析,丰富地图视角的同时,有效顾及了层次数据的结构特征,便于对其进行全方位剖析,粗犷尺度用以研究数据宏观规律如整体分布、变化趋势,精细尺度则利于理解微观差异。尺度变化提供了由粗至细研究问题的动态视角,顺应层次数据自上而下展开的结构。通过地图概览发现宏观分布规律,转换尺度锁定特征目标,继而在微观尺度下对目标进行精细分析。
1.4 变形地图在可视化中为顾及主题表达、特征发现,有些重点内容需突出显示,而另一些内容则需弱化,焦点+上下文(focus+context)技术[23]是常用的表达手段。焦点+上下文在凸显局部细节的同时顾及整体上下文信息,使受众在对局部特征研究的同时,又不失对整体的把握,便于特征的快速发现及分析。本研究通过Cartogram(即变形地图)实现焦点+上下文表达,对隐喻地图作变形处理,在保持各区域相对位置关系和拓扑结构的基础上,将对象属性信息映射为其面积大小[24]。
变形地图主要有间断型、连续型、球形等多种形式,选择时顾及的因素包括拓扑邻接性的保持、对原始形状的保持、面积对属性的反映等几点[25]。Gosper地图的生成依靠子节点区域自下而上的融合,需要变形后的区域依然保持无缝的拓扑邻接,同时,还应在视觉上保证其地图特征,只有连续型变形地图能满足上述需求。本研究采用基于扩散算法[26]的开源软件ScapeToad对原始几何数据进行处理,实现连续型变形地图的构建。层次数据中各叶子节点对应的底层区域是构造Gosper地图的基本单元,对其进行提取后,选择变形所依据的属性值并设定变形参数进行变形操作,使变形后各要素的面积能反映其属性值的相对大小。变形结果不仅依赖原始数据的形态,还与夸张系数的设置密切相关,实际操作中,为获得理想变形结果,应结合不同的变形需求设定相应的夸张系数。变形后的各几何单元依然遵从原本的邻接关系,并且保持无缝拼接的状态,借助层次数据的归属包含关系,通过面域融合由子节点区域形成父节点区域,自下而上地完成其他节点区域的变形。变形后的结果弱化或夸大了某些要素的几何形态,为受众提供宏观上的比对而非面积的精细比较,因为受众有时并不在意各要素间的细微差异,而是探寻与众不同的特征要素,或获取其分布概览。
在隐喻地图上实现Cartogram技术,使地图要素表达抽象对象的同时,可以对其属性信息进行有效彰显突出。通过地图载体表达统计数据,将地图与统计图两者优点相结合,使用有形可感的面积反映抽象数值属性,达到以形象思考代替抽象思考的目的。同时,各要素相对位置关系得到有效顾及,便于开展特征定位及挖掘等结合上下文的相关分析。
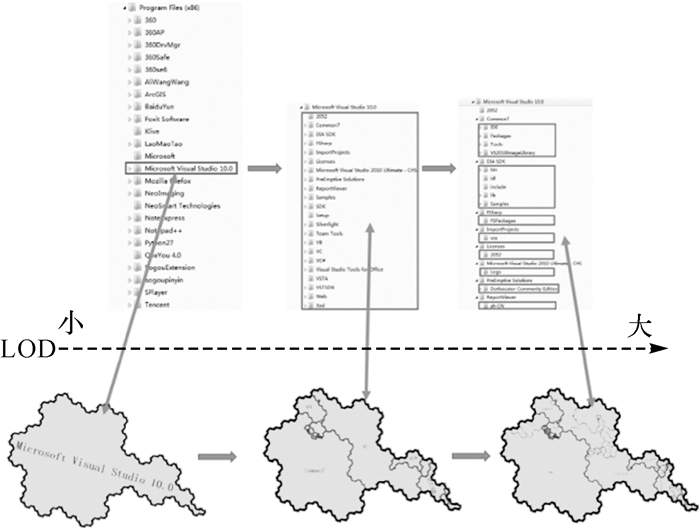
2 应用案例计算机文件系统属于典型的层次结构数据,本节综合运用上述理论对其进行表达、分析,试验数据为Microsoft Visual Studio 10.0文件夹,共计22 621个文件夹和文件。首先通过遍历建立文件的层次树结构,由2.1中的方法将层次树转换为层次地图(图 6),基于层次地图,进行文件数量分布、大文件群落定位、文件纵深分析等试验。

|
| 图 6 层次地图 Fig. 6 Level map |
2.1 文件数量分布
作为文件系统的最小组成单元,文件与地图上的正六边形构建单元相对应,节点区域面积反映了对应文件夹包含的文件数量。LOD级别的递增对应地图上边界分割的不断细化,代表各级文件逐层展开(图 7),通过运用LOD技术,可以在不同层次的文件夹中开展文件数量分布的研究。
|
| 图 7 文件树与层次地图的层次对应关系 Fig. 7 The corresponding relation of document tree and level map |
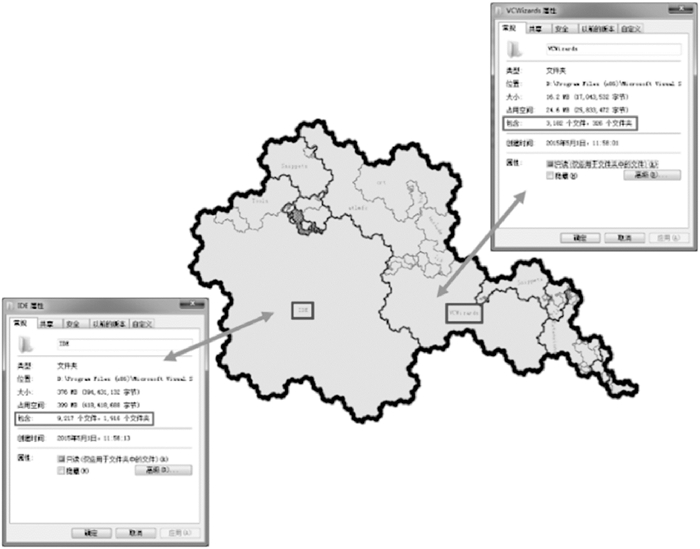
如对图 8中IDE区域与VCWizards区域进行面积比对,易知前者所对应的节点明显拥有更多叶子节点,即VCWizards文件夹内拥有更多的文件。相比Windows操作系统中右键查询属性的方式,目视判读更为简单直观。较之于单个文件作抽象数字间的对比,面积的横向对比提供了一种形象可感的方式,使受众能以全局视角观察文件数量的分布,实现系统中难以操作的同层次文件跨节点比对。
|
| 图 8 地图疆域表达与系统文件属性查询对比 Fig. 8 The contrast of territory metaphor and file attribute query |
叠加不同级别的LOD地图场景,在各尺度下进行节点面积横向比对。发现较小LOD级别地图中的区域面积分布极度不均衡,这意味着各浅层文件夹中文件数量的失衡,具体表现为,文件数量分布大体遵从帕累托法则,少数几个文件夹占据大量的文件数量份额,如图 8中IDE区域占据了图上近一半的面积,与其他区域呈现鲜明对比。随着地图LOD级别的增加,图上疆域不断被细分,此种现象逐渐减弱,直至地图完全被分割为正六边形集合。
2.2 大文件群落定位在系统中以文件属性查询的方式难以对大文件的分布情况进行宏观把握。通过地貌晕渲图可以概览大文件的全局分布,夸张的变形地图则使具体大文件得以凸显,将变形地图与LOD技术结合,能从多个尺度对大文件或大文件群落进行定位分析,完成大文件的全局概览到具体发现的动态过程。
基于文件大小制作地貌晕渲图,如图 9所示,仿照地貌图特点,大文件区域呈现红色高地势,小文件区域则用绿色低平地形表达。叠加第2级LOD地图的边界,发现高地势地形大部分集中于VC区域,Common7区域边缘也有部分中高地势分布。VC区域显著的高地势地形又可分为上下两部分,上面部分呈现聚集分布,下面部分则为离散分布。

|
| 图 9 虚拟地貌晕渲图 Fig. 9 Virtual topographic map |
如图 10所示,结合2.4节理论,根据文件所占系统空间对其几何形态进行夸张处理,由于各文件间大小差异巨大,直接选择文件大小作为夸张系数,要素间的面积呈现巨大差异,Microsoft Visual Studio 10.0文件夹中几个超大型文件得以在图中被直观反映出来。
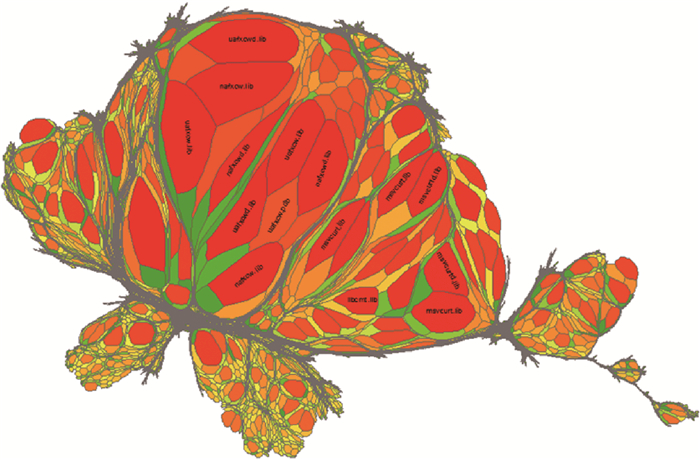
|
| 图 10 变形地图 Fig. 10 Deformation map |
但上述方法过渡挤压了上下文要素,模糊层次隶属关系,在需要结合上下文环境或层次关系进行的分析中并不适用。此处取文件大小的Log值作为夸张系数,得到结果如图 11(b)。几何形态因子的加入,与颜色一道显著提高了文件大小的辨识度,强化了区分效果。如图 11所示,较之于(a)和(b)、(c)更能对大文件群落进行有效的凸显,以下基于变形后的文件地图进行多尺度定位分析。
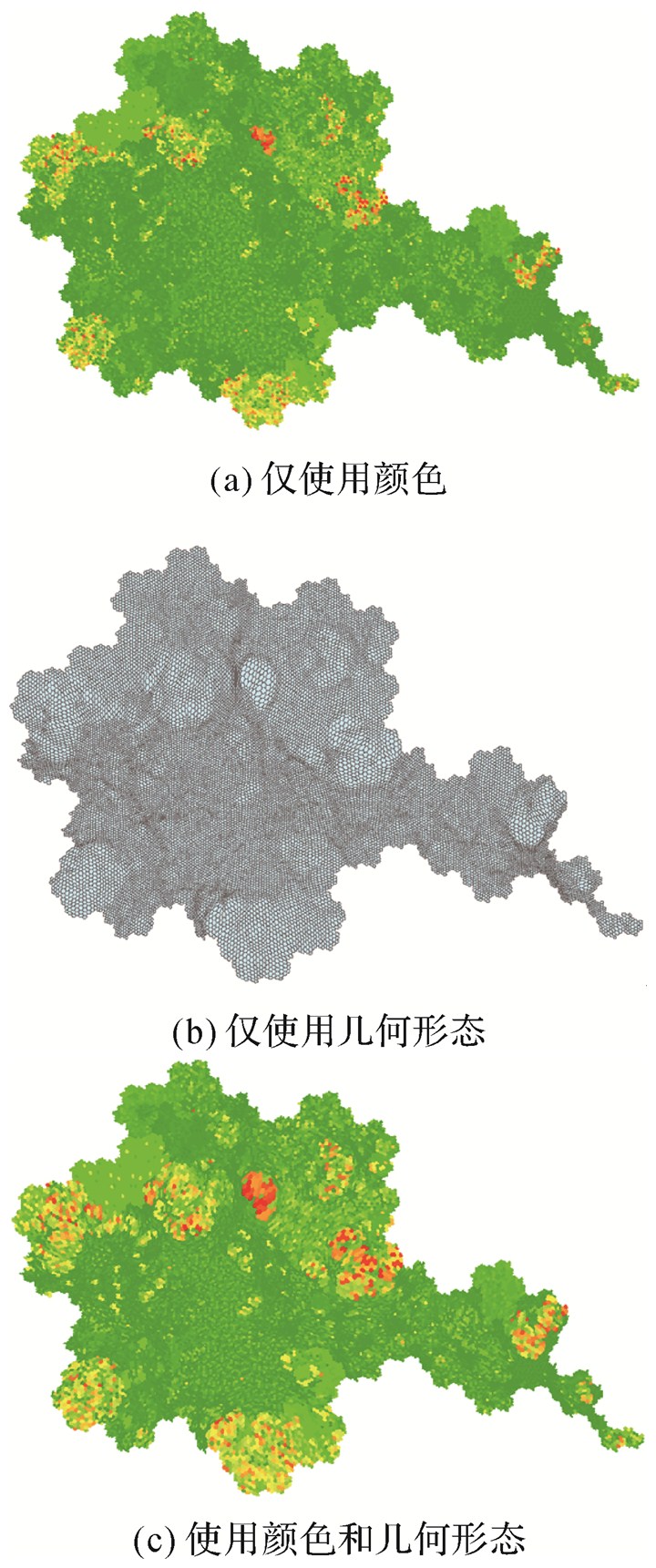
|
| 图 11 对比颜色与几何形态凸显文件大小时的效果 Fig. 11 Contrast the highlights result of color and geometry |
对第2层级的文件地图进行整体分析(图 12(a)),易知大文件群落主要分布在Microsoft Visual Studio 10.0的VC文件夹中,Common7中较大的几个文件群落也被凸显出来,与之前使用地貌晕渲图所得的宏观结论一致。将目标锁定于VC中的大文件群落,变化尺度到达下一层级文件夹,地图被更细化的边界分割(图 12(b)),大文件群被划分为上下两部分,分别位于VC文件夹下的atlmfc和lib文件夹中,在lib中明显偏红的色调意味着其包含了众多大型文件,其内部呈星斑离散分布的态势也印证了地貌晕渲图中得到的宏观结论。
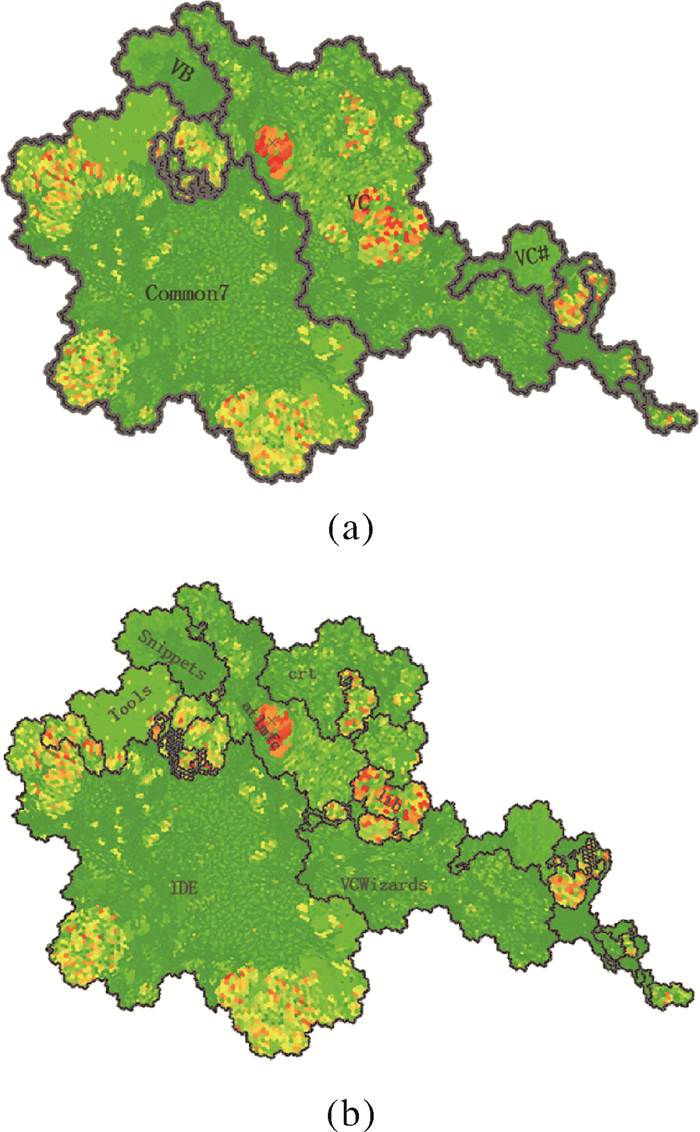
|
| 图 12 第2层级与第3层级地图 Fig. 12 Level two map and level three map |
进一步变化尺度,通过地图放大将视角聚焦在两个大文件群(图 13),上方的大文件群被完全包含在lib文件夹中,其内部大文件高度聚集的状态也与地貌晕渲图中所得结论一致。而下方的大文件群落则被几个文件夹共同分割,还有一部分已到达此分支的底层,成为代表文件的六边形单位。

|
| 图 13 第4层级地图(概览及放大后细节) Fig. 13 Level four map (the overview and the details after zooming in) |
尺度持续变化,地图不断被分割的更为精细,如图 14所示,当目标区域最终呈现为单个文件区域集合时,即可得到大文件精确的位置及名称信息,与图 10中得到凸显的大文件一致。地图为大文件的定位搜索提供了概览直观的图形化描述,LOD与Cartogram技术的结合,使各层级文件特征得到有效凸显,便于在多个尺度上定位大文件群落,促进了大文件的归属关系判别及精确发现。
|
| 图 14 由第5层级变换至第6层级地图 Fig. 14 Transformation from level five to level six map |
2.3 文件纵深分析
文件对应节点在层次树中的深度即为文件的纵深,可简单理解为从最外层文件夹到达目标文件所需点击次数。如图 15所示,基于文件的纵深属性制作虚拟水深图,以水深隐喻文件的纵深,借鉴海洋地图样式,低地势的深蓝色区域对应文件节点纵深大,而高地势、泛白区域对应的文件节点纵深小。在较低尺度的地图上,通过虚拟水深图可以概览目标文件夹中各文件的纵深分布。从图上可知纵深较大的文件集中分布于Common7文件夹中,而VC文件夹则包含了大部分浅纵深文件,说明从整体上,Common7文件夹比VC文件夹有更复杂的层次嵌套。

|
| 图 15 虚拟水深图 Fig. 15 Virtual submarine map |
不同的层次树其结构往往呈现巨大差异,同一层次树各分支的结构也不尽相同,有些分支纵深差异很大,有些则比较均衡。对于体量巨大的文件层次树结构的分析,通过对水深图颜色、地势的整体观察,往往更为直观。如在图 15中分布在Common7和VC中的两片大面积的浅蓝色区域,表征着其内部文件节点深度分布十分均匀,文件间纵深差异不大。从区域整体深度分布看,Common7区域整体纵深分布较均匀,无大范围的深度倾斜,局部深度分布有差异,类似图 16(a)中层次树描述的状态。VC区域局部深度分布十分均匀,但上下两部分整体深度差异明显,即整体深度呈不对称分布,可反映图 16(b)中层次树的状态。
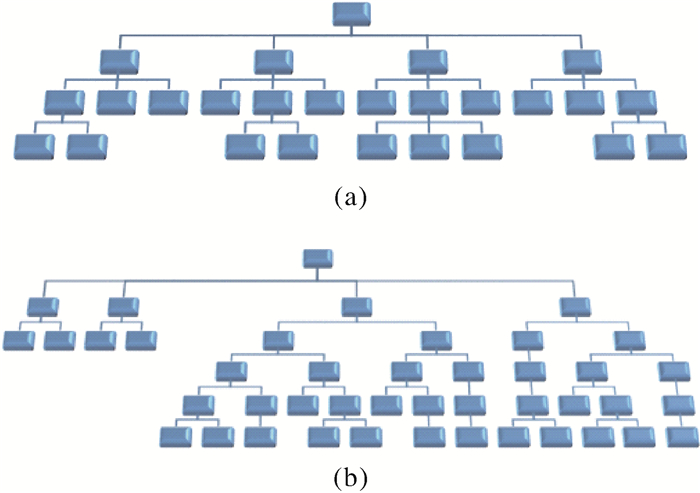
|
| 图 16 层次树 Fig. 16 Hierarchical tree |
变化LOD级别,从多个尺度观察文件夹纵深分布情况,发现层次越浅的文件夹,其内部深度呈不均匀分布的可能性越大,随着层次的深入文件夹内的深度分布愈发均匀。如图 17,在第4层级的LOD地图中,红线标注的Deployment、src、AppWiz等文件夹,其内部深度基本呈均匀分布。
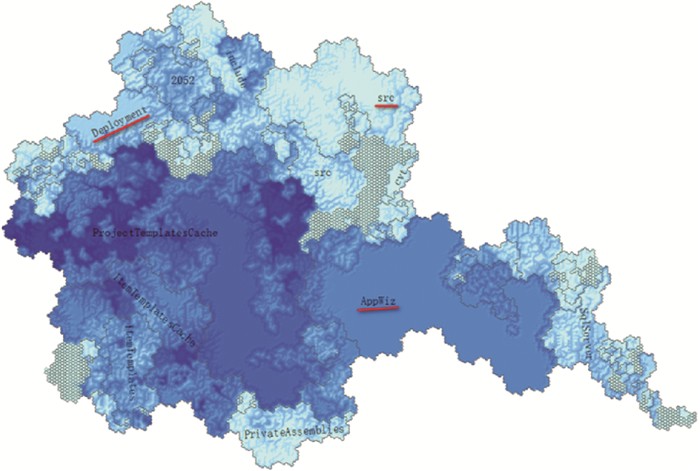
|
| 图 17 第四层级水深图 Fig. 17 Level four submarine map |
2.4 与现有方法对比
较之于TreeMap、多叉树等当前表达层次数据常用的方式,本文借助地图表达抽象层次数据。地图面域相互嵌套包含的特点用以反映层次归属关系更为直观,作为常用的空间数据表达载体,地图具有认知上的便利性,其不规则的几何形态、多样的色彩表现形式,带来艺术美感的同时,也丰富了数据表达形式。与同样使用Gosper地图的研究相比,文献[18]主要关注地图生成技术,简单展示数据层次结构,而本文则侧重地图表达分析,如通过引入地貌隐喻促进数据的理解,并结合多尺度分析及变形地图等方法进一步辅助数据的分析挖掘工作。通过探索更多的隐喻地图表达形式,并引入相关地图分析方法,尝试将地图作为一种抽象数据分析工具而非单纯的数据展示平台。
3 结论本文借助隐喻地图的思想,对层次数据进行可视化表达及分析研究。主要创新在于:①将Gosper地图引入文件夹数据分析,实现非空间数据的空间化分析;②以地图空间思维研究非空间数据,通过地貌图、水深图等具有隐喻色彩的地图形式将抽象问题具象化,降低受众的认知负荷;③综合运用LOD、Cartogram技术,并将二者有效结合用于探究特征区域,发现隐藏规律。
本研究欲借助人类对空间事物的熟悉,以直观可感的地图语言降低受众对非空间抽象数据的认知难度,从而增加潜在受众数目。地图一直是人类认识、理解地理空间的常用工具,地图学为空间事物的认知、空间问题的分析提供了一系列有效的理论方法,本研究采用地图隐喻,为表达分析抽象数据开辟了崭新视角,使地图领域的技术方法焕发新生命力。今后还将探究更多的地图可视化形式,挖掘地图表达、分析非空间数据的潜力。
| [1] | JOHNSON B, SHNEIDERMAN B.Tree-maps:A Space-filling Approach to the Visualization of Hierarchical Information Structures[C]//Proceedings of 1991 IEEE Conference on Visualization.San Diego, CA:IEEE, 1991:284-291. http://dl.acm.org/citation.cfm?id=949654 |
| [2] | YANG Muye, BIUK-AGHAI R P.Enhanced Hexagon-Tiling Algorithm for Map-Like Information Visualisation[C]//Proceedings of the 8th International Symposium on Visual Information Communication and Interaction.Tokyo, AA, Japan:ACM, 2015:137-142. https://www.semanticscholar.org/paper/Enhanced-Hexagon-Tiling-Algorithm-for-Map-Like-Yang-Biuk-Aghai/3f6b14a2f3f530ec340be37fa278ead9413f338e |
| [3] | BRULS M, HUIZING K, VAN WIJK J J.Squarified Treemaps[M]//DE LEEUW W C, VAN LIERE R.Data Visualization 2000.Vienna:Springer, 2000:33-42. |
| [4] | SCHULZ H J, HADLAK S, SCHUMANN H. The Design Space of Implicit Hierarchy Visualization:A Survey[J]. IEEE Transactions on Visualization and Computer Graphics, 2011, 17(4): 393–411. DOI:10.1109/TVCG.2010.79 |
| [5] | SKUPIN A, FABRIKANT S I.Spatialization[M]//WILSON JOHN P, FOTHERINGHAM A S.The Handbook of Geographic Information Science.Massachusetts:Blackwell Publishing Ltd, 2007. |
| [6] | SKUPIN A, BUTTENFIELD B P.Spatial Metaphors for Visualizing Information Spaces[C]//Proceedings of ACSM/ASPRS Annual Convention and Exhibition.Seattle, WA:ACSM, 1997:116-125. https://core.ac.uk/display/24612689 |
| [7] | FABRIKANT S I, SKUPIN A.Cognitively Plausible Information Visualization[C]//DYKES J, MACEACHREN A M, KRAAK M J.Exploring Geovisualization.Amsterdam:Elsevier, 2005. https://www.sciencedirect.com/science/article/pii/B978008044531150453X |
| [8] | WISE J A, THOMAS J J, PENNOCK K, et al.Visualizing the Non-visual:Spatial Analysis and Interaction with Information from Text Documents[C]//Proceedings of 1995 Information Visualization.Atlanta, GA:IEEE, 1995:51-58. |
| [9] |
艾廷华.
大数据驱动下的地图学发展[J]. 测绘地理信息, 2016, 41(2): 1–7.
AI Tinghua. Development of Cartography Driven by Big Data[J]. Journal of Geomatics, 2016, 41(2): 1–7. |
| [10] | MircoPatent, Aureka.http://www.micropatent.com/(2017-5-15) |
| [11] | BERTIN J.Semiology of Graphics:Diagrams, Networks, Maps[M].BERG W J, Trans.Madison:University of Wisconsin Press, 1983. |
| [12] | BLADES M, BLAUT J M, DARVIZEH Z, et al. A Cross-Cultural Study of Young Children's Mapping Abilities[J]. Transactions of the Institute of British Geographers, 1998, 23(2): 269–277. DOI:10.1111/tran.1998.23.issue-2 |
| [13] | HAHMANN S, BURGHARDT D. How Much Information Is Geospatially Referenced? Networks and Cognition[J]. International Journal of Geographical Information Science, 2013, 27(6): 1171–1189. DOI:10.1080/13658816.2012.743664 |
| [14] | SKUPIN A. The World of Geography:Visualizing a Knowledge Domain with Cartographic Means[J]. Proceedings of the National Academy of Sciences of the United States of America, 2004, 101(S1): 5274–5278. |
| [15] | MASHIMA D, KOBOUROV S, HU Yifan. Visualizing Dynamic Data with Maps[J]. IEEE Transactions on Visualization and Computer Graphics, 2012, 18(9): 1424–1437. DOI:10.1109/TVCG.2011.288 |
| [16] | GRONEMANN M, JVNGER M.Drawing Clustered Graphs as Topographic Maps[C]//Proceedings of the 20th International Symposium.Berlin Heidelberg:Springer, 2012:426-438. |
| [17] | BIUK-AGHAI R P, PANG C I, SI Y W. Visualizing Large-scale Human Collaboration in Wikipedia[J]. Future Generation Computer Systems, 2014, 31: 120–133. DOI:10.1016/j.future.2013.04.001 |
| [18] | AUBER D, HUET C, LAMBERT A, et al. Gospermap:Using a Gosper Curve for Laying Out Hierarchical Data[J]. IEEE Transactions on Visualization and Computer Graphics, 2013, 19(11): 1820–1832. DOI:10.1109/TVCG.2013.91 |
| [19] |
陈宁涛, 王能超, 陈莹.
Hilbert曲线的快速生成算法设计与实现[J]. 小型微型计算机系统, 2005, 26(10): 1754–1757.
CHEN Ningtao, WANG Nengchao, CHEN Ying. Fast Generation Algorithm Design and Realization of Hilbert Curve[J]. Mini-micro Systems, 2005, 26(10): 1754–1757. DOI:10.3969/j.issn.1000-1220.2005.10.016 |
| [20] | LAKOFF G, JOHNSON M. Metaphors We Live By:With A New Afterword[M]. Chicago: University of Chicago Press, 2008. |
| [21] | FABRIKANT S I.Evaluating the Usability of the Scale Metaphor for Querying Semantic Spaces[C]//Foundations of Geographic Information Science International Conference on Spatial Information Theory.Berlin Heidelberg:Springer, 2001:156-172. |
| [22] |
艾廷华, 周梦杰, 陈亚婕.
专题地图属性信息的LOD表达与TreeMap可视化[J]. 测绘学报, 2013, 42(3): 453–460.
AI Tinghua, ZHOU Mengjie, CHEN Yajie. The LOD Representation and TreeMap Visualization of Attribute Information in Thematic Mapping[J]. Acta Geodaetica et Cartographica Sinica, 2013, 42(3): 453–460. |
| [23] | FURNAS G W.Generalized Fisheye Views[C]//Proceedings of the SIGCHI Conference on Human Factors in Computing Systems.Boston, Massachusetts:ACM, 1986:16-23. |
| [24] | DENT B D. Communication Aspects of Value-by-Area Cartograms[J]. The American Cartographer, 1975, 2(2): 154–168. DOI:10.1559/152304075784313278 |
| [25] | KEIM D A, PANSE C, NORTH S C. Medial-Axis-Based Cartograms[J]. IEEE Computer Graphics and Applications, 2005, 25(3): 60–68. DOI:10.1109/MCG.2005.64 |
| [26] | GASTNER M T, NEWMAN M E J. Diffusion-Based Method for Producing Density-Equalizing Maps[J]. Proceedings of the National Academy of Sciences of the United States of America, 2004, 101(20): 7499–7504. DOI:10.1073/pnas.0400280101 |



