2. 信息工程大学地理空间信息学院, 河南 郑州 450052
2. College of Surveying and Mapping, Information Engineering University, Zhengzhou 450052, China
地球剖分格网 (earth tessellation grid,ETG) 是基于 (椭) 球体的一种可以无限细分,但又不改变形状的地球拟合格网,当细分到一定程度时,可以达到模拟地球的目的。其规则的层次剖分结构,使不同空间分辨率的格网之间具有严格的变换关系,为分布不均匀、尺度不等的地理现象数据融合提供了统一的表达模式。而现代矩阵理论和场论则为统一描述和表达复杂、多样的地理现象提供了可靠的理论基础[1]。因此,地球格网的离散性、层次性和全球连续性特征,既符合计算机对数据离散化处理的要求,又摒弃了地图投影的束缚,有望从根本上解决传统平面模型在全球时空数据管理与多尺度操作上的数据断裂、几何变形和拓扑不一致性等问题[2-4]。进入21世纪以来,随着空间大数据的飞速发展和全球经济一体化的不断深入,许多应用领域如全球环境变化监测、灾害应急预警、资源可持续开发、大型工程设计、国防安全乃至战争等,越来越频繁地使用大范围 (甚至全球) 多分辨率、多类型的海量数据进行综合分析,以获得更高质量的决策结果。因此,在现代对地观测技术和全球应用的双重驱动下,地球剖分格网系统的功能也从早期的空间数据索引、地图定位框架与地理现象表达,开始向多源空间数据融合、公共地理服务及大数据分析与挖掘等新功能进行全方位地拓展[1, 5],已成为目前国际GIS学术界一个新的研究热点。
近期,国际学术界和相关应用部门从不同的侧面对ETG进行了深入研究。2000年3月和2004年8月,由美国地理信息与分析中心组织,在California分别召开了第一、二届“International Conference on Discrete Global Grids”学术讨论会,专门进行了全球离散格网理论方法的探讨与成果交流;2014年开放地理信息联盟 (OGC) 成立了全球离散格网 (global discrete grid) 标准化工作组,以促进其在跨领域 (或学科) 互操作的进展[6];近年来,我国中科院地理所、中国矿业大学、信息工程大学、武汉大学、北京大学、南京师范大学等多家高校院所涌现了相应的研究团队,对地球格网系统模型、算法及应用进行了较为深入的探讨,推动我国在该领域的研究进展和应用示范。另外,在地理、测绘、GIS、计算机、数据库管理及其他相关专业领域的主要国际学术期刊和会议上,有关地球剖分格网的研究论文和报告也明显增多。为了方便对近期研究成果的梳理,本文拟从剖分建模、编码计算、质量评价及应用模式4个方面,对地球剖分格网的近期研究成果进行综述分析。
1 地球格网的剖分建模方法在地球剖分格网系统中,剖分方法是格网编码、索引计算及操作应用的基础,研究成果也最为丰富。早期的地球格网剖分方法主要有:经纬度格网、正多面体格网及自适应格网。经纬度格网是应用最早的、最常规的科学查询和空间剖分方法之一。一般情况下,传统地图的分带分幅都是以经纬度格网框架为基础进行的,而大多数地图投影都采用经纬度坐标作为球面上点位的参数,来建立与笛卡尔坐标系相对应的投影方程式。所以,现存的许多数据集、处理算法和系统软件都是以经纬度格网为基础。球面正多面体格网是把球体的内接正多面体 (正四面体、正六面体、正八面体、正十二面体、正二十面体) 的边投影到球面上作为大圆弧段,形成球面三角形 (或四边形、五边形、六边形) 的边覆盖整个球面,作为全球剖分的基础,然后对球面多边形进行递归细分,形成全球连续的、近似均匀的球面层次格网结构。自适应球面格网剖分是以球面上实体要素为基础,并按实体的某种特征剖分球面单元,如球面Voronoi生长点的分布是根据不同应用标准组合的,如数据密度分布、系统操作类型和最大最小单元限制等,格网单元是根据实体数据的密度大小进行自适应调整的,即自适应格网或不规则格网。文献[7]对上述3种剖分方法进行了总结,并对不同剖分格网的优缺点及适应性进行了详细的对比分析。
近年来,随着智慧地球、大数据、云计算等技术在地球空间信息领域的不断推进,海量的卫星影像数据、高效的存取索引技术及其不同领域分析的应用需求不断增长,地球剖分格网体系研究也呈现新的特点。近期格网剖分建模研究成果主要集中在四边形剖分、等积剖分、立体剖分3种类型。
1.1 球面四边形格网剖分球面四边形 (包括球面菱形、球面长方形和球面正方形) 与平面正方形栅格比较相似,其格网单元非常适合常规的显示设备、现存数据结构及常用的笛卡尔坐标系,特别是纹理图像的存储及矩阵像素高效处理[8]。所以,球面四边形在许多领域被用作表达球面空间数据的基础,如地形渲染、环境制图、游戏设计、表面建模及地球表达等[9]。
在球面四边形剖分格网中,为了有效地处理高纬地区 (或极点) 格网单元的面积和形状变形,一些学者和应用部门采用变间隔的四边形经纬网剖分方案。例如文献[10]提出了一种划分方法更细、格网单元面积相差更小的格网划分方法;文献[11]提出一个面积完全相等的变间隔经纬四边形剖分方法。这些方法虽然保证了绝大多数格网的面积相等,易于完成基于离散点的表面建模和统计计算,但其格网单元的邻近关系变得更加复杂,不利于空间索引和查询[12];文献[13]提出一种新的变间隔经纬四边形剖分方法——退化四叉树格网剖分,其经纬格网单元几何变形稳定收敛、结构简单,邻近关系有规律、便于邻近索引,其在不同领域的应用模式还需要进一步的探讨;文献[14]提出一个基于极点的四元四边形格网 (quaternary quadrangle mesh) 结构,其在极点区域剖分成半六边形,其他区域剖分成球面四边形,这样全球格网形成一个统一的四边形层次剖分结构,以满足全球 (特别是极点区域) 空间数据高效索引、可视化及分析。另外,文献[15]应用Arc Macro Language (AML) 设计一种快速而稳定的经纬度四边形格网面积计算工具,该算法建立在椭球面与球面的等积投影基础上,并自动计算不同层次的格网面积,方便处理不同空间尺度、多领域 (土地利用评价、自然灾害评估和植被建模等) 的数据。
其他类型的球面四边形剖分模型,例如:文献[8]把Fuller1946年提出基于截半立方体 (cuboctahedron-based) 的制图投影方法扩张到球面四边形 (且对边相等),通过一个线性转换,该球面四边形可投影成4个边具有同样固定尺度值 (same constant scale) 的平行四边形,并分析了不同层次菱形格网的特点及变形;文献[9]为了保持全球数据在不同分辨率转换之间的连续及流畅性,提出一个基于内接正方体的数字地球框架,其中全球四边形格网是按二叉树剖分而成的,不同尺度之间提供更多的分辨率数据以保持转换的平滑性。
1.2 等积格网剖分为了有效地进行空间统计分析,等积格网剖分成为许多地统计领域研究的热点。其中多数应用等积投影的剖分方法,如早期常用的Snyder等积投影,文献[16]对Snyder等积双向投影进行了优化、评价及分析,认为其中一些投影方法可能存在一些问题。例如,可能在某些特殊点产生奇异性,或需用迭代方法寻找他的相互关系,而迭代将会降低处理的效率。近期,针对不同内接正多面体与球面的等积投影变换主要有:文献[17]提出了正二十面体到球面的三角形等积投影;文献[18]提出了正六面体到球面四边形等积投影,即通过正方形地图中心与椭球中心,应用等积双射 (bijection) 投影,可以把一个地球北半球的均匀细化格网等积投影到正方形平面地图上。同理也可以反投影到椭球面上,构建椭球面 (或旋转体面) 等积均匀的格网体系;文献[19]又提出了正八面体到球面的三角形等积双向投影,在此基础上文献[20]应用最大边的限制约束,对三角形顶点进行了优化配置。另外,也有部分学者直接在球面上进行等积剖分,如文献[21]提出一种递归带状球面等面积 (recursive zonal equal area) 格网剖分算法,即达到了球面格网面积相等,且格网直径最小;文献[22]设计开发了HEALPix (hierarchical equal area iso-latitude pixelization) 系统,广泛应用于局部影像处理、多分辨率应用及快速球面谐波变换等方面。
其他成果还有文献[23]提出了一个“slice-and-dice”方法,包括两部分:等面积剖分 (slice) 和等面积定位 (dice),该方法应用2个等积投影——平行小圆弧投影和面向顶点的大弧投影。平行小圆弧投影使多面体的边保持固定比例和不间断,并消除了对多面体面中心的任何变形。而面向顶点的大弧投影也保持了多面体的边不间断,更重要的是仅产生微小的尖点;文献[24]基于平行平面投影 (Parallel plane projection) 的方法构建了等积格网系统,该系统格网在保持等积的同时,角度及长度变形随纬度增加而增加。但这种直接的剖分将产生少量的破碎格网需要特殊处理;文献[25]构建从在多层次等积三角形基础上,探讨了全球气象特征的动态跟踪方法,特别是跨越高纬度 (或南北极) 地区;文献[26]依据球面四边形面积计算公式和几何形状均匀性控制条件,制定了球面 (或半球面) 等积剖分的一般约束准则,构建等面积的格网系统。在剖分时,将半球面拆分一个中心圆形和多若干个圆环,保证圆环的面积为中心圆形面积的整数倍,根据格网几何变形限定条件将圆环再细分为多干个等面积的格网,已应用于Monte Carlo方法的分层抽样分析。但是该格网系统的本质是依据格网几何限定条件通过条件圆环之间的纬度差来实现等面积格网的生成,与Seong格网类似,格网之间邻近关系复杂。
1.3 立体网格剖分为了更好地表达和模拟大范围地球表面及其上下空间的形态及变化,例如地壳板块运动、大气环流、海洋环流、近地空间环境等。国内外学者把地球剖分格网系统从球面扩展到球体,衍生出“地球立体空间格网系统”[27-29]。近期成果主要有:球体经纬网格、球体立方体网格、球体退化八叉树网格、地球圈层立体网格、球体阴阳网格、球体棱柱网格等。
球体经纬网格是按一定间距采用经线、纬线及球面对球体三维空间进行格网剖分,具有经纬一致性及正交性等优点,广泛应用于三维地质建模、全球大气模拟、地球物理流体实验室、地震波反演模型等领域。然而,与球面经纬格网类似,球体经纬格网沿两极及球心方向逐渐收缩,造成格网粒度悬殊,导致数据冗余及增加计算开销[30]。球体立方体网格是将正六面体的6个平面投影至球面,对6个球面四边形分别采用连接中点的方式不断递归剖分,然后将该球面格网按比例缩放至各半径位置,形成三维格网。该类型格网形状较为简单,均由球面六面体构成,除初始六面体的角点处之外,其他格网均为正交[31],但由于格网的边长不是经纬弧线,丧失了地理一致性,特别是在径向上均未做过特殊处理,导致格网沿球心方向不断收敛。虽然有学者在不同半径位置处采用了不同球面层次的格网[32],能有效避免格网沿球心方向的格网收敛问题,但由于在边界处使用了非球面的缝合方式,使得格网在边界处不正交,同时也使得其几何形状较为复杂。
文献[33]提出了球体退化八叉树网格 (spheroid degenerated-octree grid,SDOG),是球面退化四叉树网格的三维扩展,具有地理一致性、正交性、粒度近似性、非重叠性及多层次性特征。SDOG及其扩展已被用于全球岩石圈板块及其温度场的三维建模与可视化、全球大气温度的三维建模与可视化、全球电离层的三维建模与可视化、全球DEM及影像的可视化等方面[34]。SDOG实现了对纯几何球体的三维格网剖分,但未明确赋几何球体以实际含义,导致实际应用中存在不同的纯几何球体与实际物理空间的映射问题。SDOG仅能提供三个维度的粒度同步变化的多分辨格网,却无法提供不同维度的粒度异步变化的多分辨率格网。
此外,文献[28]提出的地球圈层立体网格——即混合式网格划分和圈层结构结合的立体空间网格,其在同心球面上保持与传统球面网格的剖分一致性,充分考虑了地球立体空间上实体和现象的圈层分布特征,且能在不改变原有网格结构基础上进行空间上的拓展;文献[29]提出GeoSOT网格,并将其拓展到三维立体空间,GeoSOT网格采用Z曲线进行编码,实现部分空间计算;文献[35]借鉴阴阳耦合的东方哲学思想,设计了一种粒度近似的三维格网—Yin-Yang格网。文献[30]将光线追踪体可视化与球体阴阳网格结合,实现对地球热对流的可视化仿真;文献[36]将球面三角网沿径向方向自然延伸,构建了一种球面粒度局部近似的球体三棱柱格网用于地幔对流试验。文献[37—38]采用了类似的方法,将球面三角网向内延伸,但在径向上采用了不连续面 (如Moho和Gutenberg) 的划分方式,主要用于地震波速度场的三维建模及地震波的传输时间计算。该两类格网虽不存在格网重叠问题,但却丧失了地理一致及正交等特性,同时Ballard基于不连续面径向划分使得格网的使用具有排他性,难以被其他应用所采用。
2 地球格网的编码计算格网单元的编码运算是地球剖分格网系统的核心,它支撑着整个系统空间数据的快速索引及应用分析的高效计算。目前学术界针对不同格网系统的特点,结合实际应用需求设计了多种编码运算方案。这些成果按照编码原理大致划分为层次编码运算、填充曲线编码运算和整数坐标编码运算3类[39]。
2.1 层次编码运算层次编码采用平面、球 (参考椭球) 面上递归剖分产生的层次结构标识单元。若在低层次 (低分辨率) 单元集合C上进行层次剖分,得到高层次 (高分辨率) 单元集合F,则对于单元f∈F有唯一的单元c∈C与之对应,即f是c的子单元。
给定初始层次单元的码元,后续层次的单元用后缀 (前缀) 码元表示,从而完成编码过程。若单元c的编码记为α,其子单元fi的编码为αi,i是添加到α后面的后缀整数码元。i的取值范围由该编码方案的“基底”b决定,因此有i∈[0, b-1]。基底一般还与编码运算,如邻近操作、编码转换、频率域处理等相关[40-42]。
叠合 (congruent) 剖分产生的父、子单元边界完全重合[41],层次关系简单明确,最适合采用层次编码建立标识。例如,在GoogleMap、WorldWind数据组织中应用的四孔矩形格网,采用“四叉树”层次编码方案[43]。其他叠合剖分格网系统也可采用类似的编码方案,如四元三角网 (quaternary triangular mesh,QTM)[2]、SCENZ-Grid[44]、椭球四叉树[45]等。
非叠合 (incongruent) 六边形剖分产生的父、子单元边界不完全重合[41],层次关系比较复杂,在一定条件下才能采用层次编码建立标识。三孔六边形格网系统编码方案PYXIS[42]将子单元被划分为“中心子单元”和“顶点子单元”两类,中心子单元的中心与其父单元的中心重合,而顶点子单元则有3个不同的父单元。类似的方案还有二十面体的改进平衡三进制 (icosahedral modified generalized balanced ternary)[46]、中心位置索引 (central place indexing)[47]。四孔六边形格网系统编码方案HQBS (hexagonal quaternary balanced structure)[48]将同一层次上的单元中心与顶点组合构建四叉树结构并编码,通过特定规则剔除顶点编码,剩下的即为单元编码,若当前单元的编码串为α,则αi(0≤i≤3) 不一定是其子单元的编码,需要进一步判断。尽管HQBS无需考虑单元类型,且四叉树编码也减少了码元数量,但其数学模型过于复杂,不易理解。
层次编码的每一位码元都记录了到达当前单元经过的父单元,因此编码方案本质上描述了格网系统不同层次单元之间隶属关系的“树”状结构。定义码元之间的运算,通过其运算规则可在树状层次结构上计算出与给定编码串单元在空间上相互关联的邻近、父子单元。一般而言,层次编码运算均需通过查找表实现。叠合剖分格网系统层次关系明确,对应的查找表比较简单,因而编码运算效率较高。特别是四叉树层次编码运算可直接转化为二进制操作,无需查找表辅助,执行效率极高,在诸多领域应用广泛[49]。非叠合剖分格网系统层次关系不明确,对应的查找表比较复杂,因而编码运算效率会受到影响。PYXIS针对自身的“七叉树”编码运算设计了规模较大的查找表,因码元运算无法直接转化为二进制操作且在运算过程中需要检查编码唯一性,导致运算效率无法达到四叉树编码的水平[48]。HQBS虽然在六边形格网系统上成功建立了四叉树编码结构,但是由于在运算过程中需要判断是否为有效格点并检查编码唯一性 (正则化)[50],导致运算效率不高。
总之,层次编码运算较好地顾及了单元层次隶属关系表达需求,在执行层次相关操作 (如查找上层父单元、下层子单元) 时效率极高。相比之下,利用层次编码运算进行邻域处理的效率较低,尤其对于非叠合剖分格网,邻近单元搜索必须借助查找表实现,对效率的影响较大。另外,层次编码方案仅考虑了单元空间上的分布特点,没有关注单元数据存储和快速访问的需求,因此在数据随机访问量较大的情况下,效率不具优势。
2.2 填充曲线编码运算填充曲线编码是根据空间填充曲线设计的编码方案,而空间填充曲线是一种能够通过递归覆盖指定区域的一维曲线[51]。对于t∈T(T⊂R),空间填充曲线f(t) 建立了T到Q⊂R2的映射。根据能够访问Q中每个单元的填充曲线,通过T中连续排列单元的阶段,可以定义Q中单元的编码。Q中单元的一维编码α在T中均有定义 (即T中增加单位步长,α增长)。借助映射函数f(f(α)∈Q),可计算出编码α在Q唯一对应的单元。给定从T到Q的映射,其逆映射f-1(从Q中单元到T的唯一编码) 也可确定。
根据函数f的性质,可以设计出不同的空间填充曲线,如Hilbert曲线、Peano曲线、Sierpinski曲线和Morton (Z) 曲线等。这些曲线一般在最小定义域上都有自己的基本填充图形,对更大区域的填充是这些基本图形的重复变换。一般情况下,若基本图形覆盖n个单元,采用n孔剖分可获得下一层的填充区域。通过这种方式,填充曲线与格网层次递归剖分建立关联。
由于填充曲线中并未直接包含格网层次的任何信息,需要选择基底是的数建立编码标识。对于n孔剖分,通常选择n或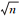
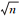
填充曲线具有空间聚合特性,即二维空间中位置相邻或相近的单元映射到填充曲线上仍然保持原来的邻近关系。因此,借助基于填充曲线的编码运算可有效提高格网数据的磁盘访问效率。例如:在正二十面体和正八面体上采用Morton码对四孔菱形格网编码[52-53];应用Sierpinski空间填充曲线索引三角形单元[54];利用L空间填充曲线球面三角区域四叉树[55],并给出了面片结点的生成、访问及寻址算法等。近期,文献[34]提出了耦合退化Z(CDZ) 填充曲线,并将其应用于球体退化八叉树格网的编码;文献[29]提出了Z填充曲线的一维四位码元、二维两位码元编码方案,并设计了编码代数算法。而在地形绘制中,空间填充曲线可提供三角条带和顶点的一维排序,适合用于GPU和外存算法。
总体而言,填充曲线编码较好地顾及了单元邻近关系表达的需求,在执行邻域操作时效率较高。如果单元数据能在物理上按照填充曲线存储,可大大提高数据访问效率。在某些特殊情况下,填充曲线编码与层次编码等效。
2.3 整数坐标编码运算整数坐标编码是最简单直接的单元编码方案,基本思想是在格网空间中定义m个坐标轴A1、…、Am。单元的m维整数坐标 (i1, i2, …, im) 即是编码,其中ij是沿着Aj坐标轴前进的步长数。对于单元递归剖分,添加下标r表示分辨率[56]。对于绝大多数格网系统,m通常取2或3。例如,文献[12, 56]均采用二维整数坐标编码,文献[57-59]采用三维编码描述单元重心并建立索引,取得了较好的试验结果。为了将二维编码扩展到多面体上,可将多面体展开到平面并在每个面上分别定义自己的局部坐标系统。为了区别每个面上的单元,可在索引上添加面的标识。这样,索引[f, (a, b)r]表示面f上层次为r的单元 (a, b)。
总体而言,整数坐标编码运算的优势体现在单元邻域处理非常高效,层次关系计算的复杂度与格网自身结构有关。与层次编码类似,整数坐标编码也仅考虑了单元空间上的分布特点,没有顾及单元数据存储和快速访问的需求。
3 格网质量评价与变形分析全球离散格网模型属于场模型,其格网单元大小决定了格网对地表要素所表示的精度,而这种精度决定了从地理要素中获取信息的细微程度。在二维GIS常用的平面栅格模型中,其格网单元是完全均匀统一的正方形格网,同一层次的单元具有表达地理要素的相同尺度及其空间位置的相同精度,其误差的传播也是线性的、可控的。但是 (椭) 球面是流形空间,在数学上与欧氏空间是不同胚的,直接在 (椭) 球面上无法递归剖分出像平面栅格那样完全相同的格网单元[60]。这种球面格网单元的非均匀性、变形分布的不规则性以及变形随层次变化的复杂性,大大增加了全球离散格网模型在空间数据表达、分析与决策的不确定性。目前,球面格网质量评价的研究成果相对较少,大致可分为如下3类。
3.1 格网评价准则早期的参考准则是由Goodchild于1992年提出,被称为“Goodchild准则”[61];其后经过学者们的不断补充和修改,Kimerling等[60]把它归纳整合为14条,即格网完全覆盖球面且不重叠、格网面积相同、格网拓扑结构相同、格网几何形状相同、格网是紧致的、格网边在投影中是直线、任何两个邻近格网的边是连接这两个格网中心的大弧平分线、组成格网系统的不同分辨率的格网形成了一个高度规则的层次结构、一个格网有且只有一个参考点、参考点到邻近格网是等距的、参考点和格网具有规则性且对应一套有效的编码系统、格网系统与传统的地理坐标对应关系 (或转换关系) 简单、格网系统的格网具有任意分辨率、格网参考点是其对应格网的中心。Clark[62]分别从普适性 (universality)、权威性 (authority)、简洁性 (succinctness)、确定性 (definitive)、完备性 (exhaustive)、层次性 (hierarchy)、唯一性 (uniqueness)、直观性 (intuitive)、易操作性 (tractable)、精确性 (accurate) 等10个方面对上述准则进行了定性评价分析,并指出这些标准更关注格网单元的几何特征而非拓扑特征。
通用的“Goodchild准则”作为研究全球格网划分所遵循的一般准则,是对全球离散格网系统的理想描述。但是,任何一个全球离散格网系统在数学上不可能同时满足上述全部指标,实际上,某些标准是相互矛盾的,部分标准可能在某些方面是重复的[60]。在实际应用中,不同的应用条件对标准的要求也不一样,有些应用对某些标准要求高,而对其他标准要求较低。所以,一个比较优秀的格网系统应该是根据具体的应用条件选择一个合理的平衡。
3.2 格网评价指标基于“Goodchild准则”构造部分可以量化的格网评价指标,进而通过分析各指标值来寻找格网模型的几何变形特征。例如,文献[63]在应用全球离散格网进行大气建模过程中,构造了“Cell Wall Midpoint Ratio”指标;文献[64]利用密实度评价指标 (单元周长与面积的比值) 分析不同格网剖分方法的变形特征;文献[60]基于单元面积、密实度和格网中心点距3个指标对球面格网的几何变形特征进行了分析;文献[65]基于“参考点到邻近格网是等距的”及“任何两个邻近格网的边是连接两个格网中心的大圆弧平分线”这两条标准,构造了“Coefficient of Variation (CV)”和“Cell Wall Midpoint Ratio”两个指标,并应用这些指标对比分析了几种剖分模型的变形特征;张斌等[66]构造了一个球面三角形格网“模糊相似度”评价指标;另外,明涛等[67]通过计算每个格网结点到邻近节点的距离、结点与两邻近节点间连线的夹角,作为格网节点空间分布均匀性的评价标准;Zhou等[14]从能量的角度出发,通过计算球面格网总的电势能来评价格网节点分布的均匀性。
总体看来,目前基于“Goodchild准则”构造的格网评价因子指标,反映的是单一层次格网单元的面积、方向及形状变形特征,缺乏不同层次格网变形的关联关系。而由于球面格网的非均质性,其变形特征随剖分层次的不同而发生空间“聚合”或“散射”变化。这样缺乏尺度特性的评价指标很难进行多层次格网变形的综合评估和可靠性分析。
3.3 单元变形的层次传播多尺度空间数据的融合及综合分析是全球离散格网系统的基础特征,不同尺度的空间数据是通过不同层次格网的单元表达的。所以,格网单元变形的尺度变化趋势是指随着剖分层次的增加,格网单元几何变形的空间分布状态、总体变化趋势及收敛特征性。自20世纪90年代以来,部分国外学者就对格网单元在不同初始多面体、不同剖分方法、不同投影方式,产生的几何变形特征及层次变化状态进行了对比分析[60, 62, 64, 68-69]。如White等[68]对比分析了5种正多面体产生的球面格网单元,在不同剖分层次的几何变形;并进一步以二十面体、八面体为基础,选择了4孔径、9孔径两种剖分方法[64],分析了球面三角形格网单元面积和形状在5种不同投影方法 (即Gnomonic投影、Fuller’s Dymaxion投影、Snyder等积多面体投影、球面直接剖分和递归多面体投影) 在不同层次的变形分布及变化趋势;Kimerling等[60]应用统计中的变形阈值、平均值及标准差对比分析了球面格网单元几何变形的层次特征,认为等积性和层次嵌套性是实际应用中处理海量多尺度空间数据首先考虑的因素,并推荐ISEA (icosahedral snyder equal area) 是目前计算和操作最有效率的选择之一。
近期,部分学者探讨了格网单元几何变形随剖分层次的增加而呈现的收敛特征,如赵学胜等[70]详细分析了基于八面体的QTM格网,随剖分层次的增加,三角形单元长度与面积变形分别收敛于1.73和1.86。在文献[71]中又提出了一种基于“纬线环”的QTM三角格网剖分模型,使单元的面积变形收敛于1.38;白建军等[72]进一步扩展到椭球面,其QTM三角格网的边长与面积变形则分别收敛于1.74和1.88;贲进等[73]分析了球面六边形的长度变形收敛于1.3,并给出了格网变形在不同层次的空间分布状态。几何变形的收敛性为格网单元的变形分析及计算提供了阈值基础,并使格网变形的误差传播与控制成为可能。
其他还有,球面格网单元几何稳定性分析[67]、球面格网印迹 (grid imprinting) 分析[74]、矢量线在格网绘制中的误差控制[75]等等。但是,目前的研究还很少涉及球面格网变形在不同位置、不同层次上的传播模式及有效控制方法。
4 地球格网的应用模式随着地球剖分格网研究成果的不断丰富,其在不同领域的应用也逐渐开展起来。下面分别从政府组织机构、商业软件系统、具体行业领域等3个方面,给出一些具有代表性的应用范例。
4.1 政府组织及机构应用美国联邦地理数据委员会认为需要有一个全国性的格网系统来打破行政界线和区域操作权限的约束,避免不同坐标系统之间转换的困难和地图制图的混乱。同时,为了配合本土反恐任务和支持美国军方的全球信息网格计划,2001年将UTM参考系的格网方案重新确定为国家标准,称为“美国国家格网”(United States National Grid, USNG),并设计了一套美国国家的空间位置描述编码[1]。美国灾难事故调查与救援委员会地理位置标识规定:在陆地灾难事故查找救援响应、陆地/航空协同、陆地查找救援坐标响应等业务应用中优先采用USNG剖分格网标识位置,在其他业务应用中也建议将剖分格网标识作为经纬度坐标的补充手段[76]。此外,美国国家地理空间情报局提出了世界地理参考系统Georef及全球区域参考系统GARS。Georef是一个基于经纬度坐标的地球表面位置描述系统,通过对地球进行5次划分,分别构建了15°×15°,1°×1°,1′×1′,0.1′×0.1′,0.01′×0.01′五级格网[1],主要用于飞行导航,特别是空军各作战单元之间的位置报告;而GARS作为Georef等格网系统的补充,是为美军发展一套适合于空地坐标表达的标准全球地理位置编码系统,满足美国国国防部提出作战系统与指挥机构协同运作的需要。
此外,澳大利亚和新西兰政府在Landcare Research计划中,设计了一套SCENZ-Grid[77],该格网的初始划分方法与GeoFusion相似,并被用于国土空间分析与科学数据的采集;在产品与工程领域,2009年欧洲空间局在生命行星计划 (Living Planet Program) 中发射了SMOS卫星,该卫星采用六边形全球离散格网系统的方式记录与处理全球空间数据[78]。此外,我国天地图采用的也是等经纬度格网进行分层和分块剖分。
4.2 商业系统及数据集应用在目前国内外常用的相关系统平台中,美国NASA发布的开源软件系统World Wind是采用等经纬度全球剖分的典型系统;而Google Earth采用的是变经纬度全球格网,经差固定,纬度方向则是在UTM投影基础上再做等间隔划分,两极地区特殊处理;GeoFusion[79]则按内接正六面体,将全球划分为6个区域,其中4个处于南北纬45°之间,采用矩形格网覆盖。两个处于高纬地区,采用三角形格网覆盖,并集成在ArcGIS系列产品ArcGlobe中;加拿大PYXIS公司的Peterson设计了全球六边形离散格网的PYXIS索引结构[80],在此基础上,还研究出了一套新型的全球空间数据组织、融合与显示方法,并融合了IPV6等网络新技术[81]。围绕PYXIS的核心技术与方法,有学者构建了一整套二维的六边形坐标系统和基于菱形层次结构的六边形格网系统[82-83],能够满足数字地球框架的有效应用,并在此基础上研究了多分辨率的球面格网曲线[84]。
同时,很多全球数据集的组织也采用经纬度剖分格网,如美国USGS提供的GTOPO 30数据集和GMTED2010数据集 (http://lta.cr.usgs.gov/);NASA提供的JGP95E5′、SRTM、ASTER-GDEM数据集等 (https://earthdata.nasa.gov/)。也有一些全球数据集采用变经纬度格网,如美国国家影像与制图局NIMA (http://www.niama.mil/) 提供的数字高程数据采用了纬度间隔固定 (3弧秒),而经度间隔从赤道到两极逐渐增大的方案等。
4.3 不同行业领域的应用近年来,地球剖分格网在许多领域的应用不断扩展。代表性的有国际卫星云气侯项目 (International Satellite Cloud Climatology Project) 设计的ISCCP GRID (http://isccp.giss.nasa.gov/docs/mapgridinfo.html)、在全球海洋和冰川模拟中常用的POP GRID和ORCA GRID (http://www.ncl.ucar.edu/Applications/),它们利用非均匀的矩形单元覆盖整个海洋,只是在两极处的处理有所区别。由于多面体剖分具有全球单元几何形态均匀的特点,特别是不存在高纬地区单元变形严重的问题,因此在空间数据索引、全球可视化、资源监测以及气象、海洋等领域全球性应用中,表现出较明显的优势。典型的应用包括:空间数据索引[3, 40, 45, 54, 57]、傅里叶变换[42]、制图综合[2]、全球土地监测[78, 85]、全球元胞自动机模拟[86-87]、全球洋流分析[88-90]、全球气候模型[91-92]、海洋路径规划[93]、全球可视化系统Crusta[94]、全球数据访问编码GeoJSON-LD[95]等。
立体剖分格网的应用领域主要是地球内部地质构造、地震场模拟及空域规划分析等。如地壳内部对流[31]、动态环境建模[96]、全球板块构造和地幔流动[97]、全球地震波三维速度场建模[32, 98]、高阶有限体元的磁流体力学MHD研究[99]、地壳板块可视化[100]、地月球空间环境建模[101]以及空间碎片碰撞预警模拟[102]。
5 问题讨论及进一步研究工作大数据时代的到来为地球剖分格网系统提供了机遇,并有可能发展成为空间大数据管理与分析的框架平台之一。国内外相关研究虽然已经取得了一些进展,但总体而言,相关成果还是分散的,且试验性居多。从本质上讲,现有的地理剖分格网系统还局限在“数据结构”的层次上,仅适合于数据管理、编码索引等,其应用也主要集中在气象分析、海洋模拟或环境监测等定位精度不高的领域。还远远没有达到作为“数据模型”框架的层面上,无法满足大范围、高精度的数据表达应用与空间大数据综合分析的需求。主要存在的关键问题及进一步的研究工作如下。
5.1 完备的理论基础从上面的分析可以看出,现有的地球剖分格网系统成果大都是从试验、归纳或统计中得出的,缺乏系统完备的理论基础支持。在传统的笛卡尔空间,欧氏几何为空间向量数据提供理论基础,而数学形态学、现代矩阵理论和场论为空间栅格数据的表达和分析提供了理论支持。但是球面是流形空间,与欧氏空间是不同胚的,球面没有全局光滑的参数化过程,总是存在映射误差。而传统处理方法是把地球的近似 (椭) 球面格网铺展成平面格网 (如正方形格网),扭曲了 (椭) 球面上各向异性的度量为各向同性的欧氏空间,适合表达和处理地球表面局部区域数据和低精度计算,在进行大区域乃至全球多尺度地形建模和空间分析时,将导致全球数据的重叠、断裂、几何变形及拓扑关系的不一致性,使得大区域 (或全球) 内的度量计算和空间分析是不精确的,甚至是没有意义的。从现有成果看,大部分球面离散格网中都存在几何上的特殊单元 (奇异单元) 或几何变形,这对全球空间数据的管理与可视化表达可能影响不大。但是奇异单元会引起产生不同位置的拓扑奇异结构,将会为全球空间数据的准确性分析埋下隐患。能否从表达球面流形的黎曼几何、共形几何等,找到表达地球剖分格网几何与拓扑关系的完备理论体系?将成为打破地球剖分格网进展瓶颈的首要工作。
5.2 高效的编码计算高效、简便的单元编码运算及索引是全球离散格网系统的核心问题。目前学术界对格网编码数学模型、编码方法、编码运算等理论问题仍缺乏深入、透彻的探究。建立格网编码数学模型的根本目的是揭示编码的数学本质,这对编码方案的设计和索引算法的优化具有非常重要的引领作用。Vince等学者采用“格点”(lattice),即两个线性无关向量的整数组合,表示单元中心。目前这类编码模型只适用于特定格网系统,是否能推广到全部格网系统有待研究。编码本质上是坐标的等效降维表达,其结构和性质直接影响格网系统应用的效能。目前各种编码方案都没有找出码元设计和分布的理论依据,只是通过观察归纳出编码的特点及性质,无法给出严格证明。这在理论上是不完备的,极有可能给实际应用埋下隐患,且改进完善困难。目前的研究表明,在平面格网系统上,单元编码集合对加、减、乘法均封闭。这表明编码运算法则很可能独立于具体的编码方案而存在,对其规律的抽象和证明,可为编码运算相关算法的设计和优化提供最直接的支持。
5.3 可靠的精度保障全球离散格网模型属于场模型,其格网单元大小决定了格网对地表要素所表示的精度,而这种精度决定了我们从地理要素中获取信息的细微程度。在二维GIS常用的平面栅格模型中,其格网单元是完全均匀统一的正方形格网,同一层次的单元具有表达地理要素的相同尺度及其空间位置的相同精度,其误差的传播也是线性的、可控的。但是 (椭) 球面是流形空间,在数学上与欧氏空间是不同胚的,直接在 (椭) 球面上无法递归剖分出像平面栅格那样完全相同的格网单元。这种球面格网单元的非均匀性、变形分布的不规则性以及变形随层次变化的复杂性,大大增加了全球离散格网模型在空间数据表达、分析与决策的不确定性。目前国内外学者探讨了不同球面格网几何变形的空间分布状态、总体变化趋势及收敛特征性,而很少涉及球面格网变形在不同位置、不同层次上的传播模式及控制方法。这样在具体应用中,就缺乏相应明确的可靠性量化指标,来保证空间数据在全球离散格网模型下的表达分析精度及其质量等级,极大地限制其实际应用的范围与深度。因此,为了适应当前空间大数据的飞速发展和不断增强的综合应用需求 (如灾害应急决策、大型工程设计、国防安全、地理国情普查与监测等),急需研究和构建一种 (椭) 球面格网变形的质量评估体系与误差控制模型,以保障全球离散格网模型在多领域应用的可靠性和可信度。
| [1] | 周成虎, 欧阳, 马廷. 地理格网模型研究进展[J]. 地理科学进展, 2009, 28(5): 657–662. ZHOU Chenghu, OU Yang, MA Ting. Progresses of Geographical Grid Systems Researches[J]. Progress in Geography, 2009, 28(5): 657–662. |
| [2] | DUTTON G H. A Hierarchical Coordinate System for Geoprocessing and Cartography[M]. Berlin Heidelberg: Springer-Verlag, 1999: 230. |
| [3] | KOLAR J. Representation of the Geographic Terrain Surface Using Global Indexing[C]//Proceeding of 12th International Conference on Geoinformatics. Sweden:University of Gävle, 2004:321-328. |
| [4] | 胡鹏, 刘沛兰, 胡海, 等. 地球信息的度量空间和Global GIS[J]. 武汉大学学报 (信息科学版), 2005, 30(4): 317–321. HU Peng, LIU Peilan, HU Hai, et al. Metric Space of Earth Information and Global GIS[J]. Geomatics and Information Science of Wuhan University, 2005, 30(4): 317–321. |
| [5] | VAN OOSTEROM P, STOTER J. 5D Data Modelling:Full Integration of 2D/3D Space, Time and Scale Dimensions[C]//Proceedings of the 6th International Conference, GIScience 2010. Berlin Heidelberg:Springer-Verlag, 2010:310-324. |
| [6] | PRUSS M. The Promise of Discrete Global Grid Systems[J]. GeoConnexion International Magazine, 2014, 7-8: 16–17. |
| [7] | 赵学胜, 王磊, 王洪彬, 等. 全球离散格网的建模方法及基本问题[J]. 地理与地理信息科学, 2012, 28(1): 29–34. ZHAO Xuesheng, WANG Lei, WANG Hongbin, et al. Modeling Methods and Basic Problems of Discrete Global Grids[J]. Geography and Geo-Information Science, 2012, 28(1): 29–34. |
| [8] | CRIDER J E. A Geodesic Map Projection for Quadrilaterals[J]. Cartography and Geographic Information Science, 2009, 36(2): 131–147. DOI:10.1559/152304009788188781 |
| [9] | AMIRI A M, BHOJANI F, SAMAVATI F.One-to-Two Digital Earth[C]//Proceedings of the 9th International Symposium, ISVC 2013.Berlin Heidelberg:Springer-Verlag, 2013:681-692. |
| [10] | BJØRKE J T, NILSEN S. Examination of a Constant-area Quadrilateral Grid in Representation of Global Digital Elevation Models[J]. International Journal of Geographical Information Science, 2004, 18(7): 653–664. DOI:10.1080/13658810410001705334 |
| [11] | SEONG J C. Implementation of An Equal-Area Gridding Method for Global-Scale Image Archiving[J]. Photogrammetric Engineering & Remote Sensing, 2005, 71(5): 623–627. |
| [12] | SAHR K. Location Coding on Icosahedral Aperture 3 Hexagon Discrete Global Grids[J]. Computers, Environment and Urban Systems, 2008, 32(3): 174–187. DOI:10.1016/j.compenvurbsys.2007.11.005 |
| [13] | 赵学胜, 崔马军, 李昂, 等. 球面退化四叉树格网单元的邻近搜索算法[J]. 武汉大学学报 (信息科学版), 2009, 34(4): 479–482. ZHAO Xuesheng, CUI Majun, LI Ang, et al. An Adjacent Searching Algorithm of Degenerate Quadtree Grid on Spherical Facet[J]. Geomatics and Information Science of Wuhan University, 2009, 34(4): 479–482. |
| [14] | ZHOU Mengyun, CHEN Jing, GONGJianya. A Pole-Oriented Discrete Global Grid System:Quaternary Quadrangle Mesh[J]. Computers & Geosciences, 2013, 61: 133–143. |
| [15] | SANTINI M, TARAMELLI A, SORICHETTA A. ASPHAA:A GIS-Based Algorithm to Calculate Cell Area on a Latitude-Longitude (Geographic) Regular Grid[J]. Transactions in GIS, 2010, 14(3): 351–377. DOI:10.1111/j.1467-9671.2010.01200.x |
| [16] | HARRISON E, MAHDAVI-AMIRI A, SAMAVATI F.Analysis of Inverse Snyder Optimizations[M]//GAVRILOVA M L, TAN C J K. Transactions on Computational Science XVI.Berlin Heidelberg:Springer-Verlag, 2012:134-148. |
| [17] | TEANBY N A. An Icosahedron-Based Method for Even Binning of Globally Distributed Remote Sensing Data[J]. Computers & Geosciences, 2006, 32(9): 1442–1450. |
| [18] | ROŞCA D, PLONKA G. Uniform Spherical Grids via Equal Area Projection from the Cube to the Sphere[J]. Journal of Computational and Applied Mathematics, 2011, 236(6): 1033–1041. DOI:10.1016/j.cam.2011.07.009 |
| [19] | ROŞCA D, PLONKA G. An Area Preserving Projection from the Regular Octahedron to the Sphere[J]. Results in Mathematics, 2012, 62(3-4): 429–444. DOI:10.1007/s00025-012-0286-2 |
| [20] | HOLHOŞ A, ROŞCA D. An Octahedral Equal Area Partition of the Sphere and Near Optimal Configurations of Points[J]. Computers & Mathematics with Applications, 2014, 67(5): 1092–1107. |
| [21] | LEOPARDI P. A Partition of the Unit Sphere into Regions of Equal Area and Small Diameter[J]. Electronic Transactions on Numerical Analysis, 2006, 25: 309–327. |
| [22] | GÓRSKI K M, HIVON E, BANDAY A J, et al. HEALPix:A Framework for High-Resolution Discretization and Fast Analysis of Data Distributed on the Sphere[J]. The Astrophysical Journal, 2005, 622(2): 759–771. DOI:10.1086/apj.2005.622.issue-2 |
| [23] | VAN LEEUWEN D, STREBE D. A "Slice-and-Dice" Approach to Area Equivalence in Polyhedral Map Projections[J]. Cartography and Geographic Information Science, 2006, 33(4): 269–286. DOI:10.1559/152304006779500687 |
| [24] | MA Ting, ZHOU Chenghu, XIE Yichun, et al. A Discrete Square Global Grid System Based on the Parallels Plane Projection[J]. International Journal of Geographical Information Science, 2009, 23(10): 1297–1313. DOI:10.1080/13658810802344150 |
| [25] | MASSEY N. Feature Tracking on the Hierarchical Equal Area Triangular Mesh[J]. Computers & Geosciences, 2012, 44: 42–51. |
| [26] | BECKERS B, BECKERS P. A General Rule for Disk and Hemisphere Partition into Equal-Area Cells[J]. Computational Geometry, 2012, 45(7): 275–283. DOI:10.1016/j.comgeo.2012.01.011 |
| [27] | 吴立新, 余接情. 地球系统空间格网及其应用模式[J]. 地理与地理信息科学, 2012, 28(1): 7–13. WU Lixin, YU Jieqing. Earth System Spatial Grid and Its Application Modes[J]. Geography and Geo-Information Science, 2012, 28(1): 7–13. |
| [28] | 曹雪峰. 地球圈层空间网格理论与算法研究[D]. 郑州: 解放军信息工程大学, 2012. CAO Xuefeng.Research on Earth Sphere Shell Space Grid Theory and Algorithms[D]. Zhengzhou:The PLA Information Engineering University, 2012. |
| [29] | 程承旗, 任伏虎, 濮国梁, 等. 空间信息剖分组织导论[M]. 北京: 科学出版社, 2012. CHENG Chengqi, REN Fuhu, PU Guoliang, et al. Introduction to Spatial Information Partition and Organization[M]. Beijing: Science Press, 2012. |
| [30] | OHNO N, KAGEYAMA A. Visualization of Spherical Data by Yin-Yang Grid[J]. Computer Physics Communications, 2009, 180(9): 1534–1538. DOI:10.1016/j.cpc.2009.04.008 |
| [31] | STEMMER K, HARDER H, HANSEN U. A New Method to Simulate Convection with Strongly Temperature-and Pressure-Dependent Viscosity in a Spherical Shell:Applications to the Earth's Mantle[J]. Physics of the Earth and Planetary Interiors, 2006, 157(3-4): 223–249. DOI:10.1016/j.pepi.2006.04.007 |
| [32] | KOMATITSCH D, RITSEMA J, TROMP J. The Spectral-Element Method, Beowulf Computing, and Global Seismology[J]. Science, 2002, 298(5599): 1737–1742. DOI:10.1126/science.1076024 |
| [33] | WU Lixin, YU Jieqing. A New Digital Earth Reference Model:Spheroid-Based 3D Grid for Earth System (3DGES)[C]//Proceedings of the SPIE 7840, 6th International Symposium on Digital Earth:Models, Algorithms, and Virtual Reality. Beijing:SPIE, 2009:784003. |
| [34] | 余接情, 吴立新, 訾国杰, 等. 基于SDOG的岩石圈多尺度三维建模与可视化方法[J]. 中国科学:地球科学, 2012, 55(6): 1012–1020. YU Jieqing, WU Lixin, ZI Guojie, et al. SDOG-based Multi-Scale 3D Modeling and Visualization on Global Lithosphere[J]. Science China Earth Sciences, 2012, 55(6): 1012–1020. DOI:10.1007/s11430-012-4387-2 |
| [35] | KAGEYAMA A, SATO T. The "Yin-Yang Grid":An Overset Grid in Spherical Geometry[J]. Geochemistry, Geophysics, Geosystems, 2004, 5(9): Q09005. |
| [36] | BAUMGARDNER J R. Three-Dimensional Treatment of Convective Flow in the Earth's Mantle[J]. Journal of Statistical Physics, 1985, 39(5): 501–511. |
| [37] | BALLARD S, HIPP J R, YOUNG C J. Efficient and Accurate Calculation of Ray Theory Seismic Travel Time Through Variable Resolution 3D Earth Models[J]. Seismological Research Letters, 2009, 80(6): 989–999. DOI:10.1785/gssrl.80.6.989 |
| [38] | BALLARD S, YOUNG C, HIPP J, et al.A global 3D P-velocity Model of the Earth's Crust and Mantle for Improved Event Location[C]//European Geosciences Union General Assembly, 2-7 May, 2010.Vienna, Austria:EGU, 2010. |
| [39] | AMIRI A M, SAMAVATI F, PETERSON P. Categorization and Conversions for Indexing Methods of Discrete Global Grid Systems[J]. ISPRS International Journal of Geo-Information, 2015, 4(1): 320–336. DOI:10.3390/ijgi4010320 |
| [40] | GOODCHILD M F, YANG Shiren. A Hierarchical Spatial Data Structure for Global Geographic Information Systems[J]. CVGIP:Graphical Models and Image Processing, 1992, 54(1): 31–44. DOI:10.1016/1049-9652(92)90032-S |
| [41] | SAHR K, WHITE D, KIMERLING A J. Geodesic Discrete Global Grid Systems[J]. Cartography and Geographic Information Science, 2003, 30(2): 121–134. DOI:10.1559/152304003100011090 |
| [42] | VINCE A, ZHENG X. Arithmetic and Fourier Transform for the PYXIS Multi-resolution Digital Earth Model[J]. International Journal of Digital Earth, 2009, 2(1): 59–79. DOI:10.1080/17538940802657694 |
| [43] | 吕雪锋, 程承旗, 龚健雅, 等. 海量遥感数据存储管理技术综述[J]. 中国科学:技术科学, 2011, 54(12): 3220–3232. LÜ Xuefeng, CHENG Chengqi, GONG Jianya, et al. Review of Data Storage and Management Technologies for Massive Remote Sensing Data[J]. Science China Technological Sciences, 2011, 54(12): 3220–3232. DOI:10.1007/s11431-011-4549-z |
| [44] | GIBB R G. The rHEALPix Discrete Global Grid System[C]//Proceedings of the 9th Symposium of the International Society for Digital Earth (ISDE). Halifax:IOP, 2016, 34:012012. |
| [45] | OTTOSON P, HAUSKA H. Ellipsoidal Quadtrees for Indexing of Global Geographical Data[J]. International Journal of Geographical Information Science, 2002, 16(3): 213–226. DOI:10.1080/13658810110095075 |
| [46] | SAHR K M. Discrete Global Grid Systems:A New Class of Geospatial Data Structures[D].Eugene, OR:University of Oregon, 2005. |
| [47] | SAHR K. Central Place Indexing Systems:US, US9311350[P]. 2016-12-04. |
| [48] | TONG Xiaochong, BEN Jin, WANG Ying, et al. Efficient Encoding and Spatial Operation Scheme for Aperture 4 Hexagonal Discrete Global Grid System[J]. International Journal of Geographical Information Science, 2013, 27(5): 898–921. DOI:10.1080/13658816.2012.725474 |
| [49] | BOSCHETTI L, ROY D P, JUSTICE C O. Using NASA's World Wind Virtual Globe for Interactive Internet Visualization of the Global MODIS Burned Area Product[J]. International Journal of Remote Sensing, 2008, 29(11): 3067–3072. DOI:10.1080/01431160701733023 |
| [50] | 童晓冲, 贲进. 空间信息剖分组织的全球离散格网理论与方法[M]. 北京: 测绘出版社, 2016. TONG Xiaochong, BEN Jin. The Discrete Global Grid Theory and Method of Spatial Information Partition Organization[M]. Beijing: Surveying and Mapping Press, 2016. |
| [51] | MOON B, JAGADISH H V, FALOUTSOS C, et al. Analysis of the Clustering Properties of the Hilbert Space-Filling Curve[J]. IEEE Transactions on Knowledge and Data Engineering, 2001, 13(1): 124–141. DOI:10.1109/69.908985 |
| [52] | WHITE D. Global Grids from Recursive Diamond Subdivisions of the Surface of An Octahedron or Icosahedron[J]. Environmental Monitoring and Assessment, 2000, 64(1): 93–103. DOI:10.1023/A:1006407023786 |
| [53] | 白建军, 赵学胜, 陈军. 基于线性四叉树的全球离散格网索引[J]. 武汉大学学报 (信息科学版), 2005, 30(9): 805–808. BAI Jianjun, ZHAO Xuesheng, CHEN Jun. Indexing of Discrete Global Grids Using Linear Quadtree[J]. Geomatics and Information Science of Wuhan University, 2005, 30(9): 805–808. |
| [54] | BARTHOLDI JJ, GOLDSMAN P. Continuous Indexing of Hierarchical Subdivisions of the Globe[J]. International Journal of Geographical Information Science, 2001, 15(6): 489–522. DOI:10.1080/13658810110043603 |
| [55] | 袁文, 程承旗, 马蔼乃, 等. 球面三角区域四叉树L空间填充曲线[J]. 中国科学E辑工程科学材料科学, 2004, 47(3): 265–280. YUAN Wen, CHENG Chengqi, MA Ainai, et al. LCurve for Spherical Triangle Region Quadtrees[J]. Science in China SeriesE Engineering & Materials Science, 2004, 47(3): 265–280. |
| [56] | MAHDAVI-AMIRIA, HARRISONE, SAMAVATIF. Hexagonal Connectivity Maps for Digital Earth[J]. International Journal of Digital Earth, 2015, 8(9): 750–769. DOI:10.1080/17538947.2014.927597 |
| [57] | VINCE A. Indexing the Aperture 3 Hexagonal Discrete Global Grid[J]. Journal of Visual Communication and Image Representation, 2006, 17(6): 1227–1236. DOI:10.1016/j.jvcir.2006.04.003 |
| [58] | BEN Jin, TONG Xiaochong, CHEN Rongguo. A Spatial Indexing Method for the Hexagon Discrete Global Grid System[C]//Proceedings of the 18thInternational Conference onGeoinformatics.Beijing:IEEE, 2010:1-5. |
| [59] | 白建军. 基于正八面体的四孔六边形球面格网编码及索引[J]. 遥感学报, 2011, 15(6): 1125–1137. BAI Jianjun. Location Coding and Indexing Aperture 4 Hexagonal Discrete Global Grid Based on Octahedron[J]. Journal of Remote Sensing, 2011, 15(6): 1125–1137. |
| [60] | KIMERLING J A, SAHR K, WHITE D, et al. Comparing Geometrical Properties of Global Grids[J]. Cartography and Geographic Information Science, 1999, 26(4): 271–288. DOI:10.1559/152304099782294186 |
| [61] | GOODCHILD M E. Criteria for Evaluation of Global Grid Models for Environmental Monitoring and Analysis[R]. NCGIA Technical Report 94-7, 1994. |
| [62] | CLARKE K C.Criteria and Measures for the Comparison of Global Geocoding Systems[M]//GOODCHILD M F, KIMERLING A J.Discrete Global Grids:A Web Book. Santa Barbara:University of California Press, 2002. |
| [63] | HEIKES R, RANDALL D A. Numerical Integration of the Shallow-Water Equations on A Twisted Icosahedral Grid. Part Ⅱ. A Detailed Description of the Grid and An Analysis of Numerical Accuracy[J]. Monthly Weather Review, 1995, 123(6): 1881–1887. DOI:10.1175/1520-0493(1995)123<1881:NIOTSW>2.0.CO;2 |
| [64] | WHITE D, KIMERLING A J, SAHR K, et al. Comparing Area and Shape Distortion on Polyhedral-Based Recursive Partitions of the Sphere[J]. International Journal of Geographic Information Science, 1998, 12(8): 805–827. DOI:10.1080/136588198241518 |
| [65] | GREGORY M J, KIMERLING A J, WHITE D, et al. A Comparison of Intercell Metrics on Discrete Global Grid Systems[J]. Computers, Environment and Urban Systems, 2008, 32(3): 188–203. DOI:10.1016/j.compenvurbsys.2007.11.003 |
| [66] | 张斌, 苑争一, 赵学胜, 等. 一种基于模糊相似度的球面格网几何变形评价指标[J]. 地理与地理信息科学, 2015, 31(5): 20–24, 29. ZHANG Bin, YUAN Zhengyi, ZHAO Xuesheng, et al. An Geometry Deformation Evaluation Index of the Spherical Discrete Grid Based on the Fuzzy Similarity[J]. Geography and Geo-Information Science, 2015, 31(5): 20–24, 29. |
| [67] | 明涛, 庄大方, 袁文, 等. 几种离散格网模型的几何稳定性分析[J]. 地球信息科学, 2007, 9(4): 40–43, 99. MING Tao, ZHUANG Dafang, YUAN Wen, et al. Comparison of Geometrical Stability of Several Discrete Grid Systems[J]. Geo-Information Science, 2007, 9(4): 40–43, 99. |
| [68] | WHITE D, KIMERLING A, OVERTON W. Cartographic and Geometric Components of a Global Sampling Design for Environmental Monitoring[J]. Cartography and Geographic Information Systems, 1992, 19(1): 5–22. DOI:10.1559/152304092783786636 |
| [69] | KIMERLING J A, OVERTON S W, WHITE D. Statistical Comparison of Map Projection Distortions within Irregular Areas[J]. Cartography and Geographic Information Science, 1995, 22(3): 205–221. DOI:10.1559/152304095782540348 |
| [70] | 赵学胜, 孙文彬, 陈军. 基于QTM的全球离散格网变形分布及收敛分析[J]. 中国矿业大学学报, 2005, 34(4): 438–442. ZHAO Xuesheng, SUN Wenbin, CHEN Jun. Distortion Distribution and Convergent Analysis of the Global Discrete Grid Based on QTM[J]. Journal of China University of Mining & Technology, 2005, 34(4): 438–442. |
| [71] | 赵学胜, 苑争一, 赵龙飞, 等. 一种改进的近似等面积QTM剖分模型[J]. 测绘学报, 2016, 45(1): 112–118. ZHAO Xuesheng, YUAN Zhengyi, ZHAO Longfei, et al. An Improved QTM Subdivision Model with Approximate Equal-Area[J]. ActaGeodaetica et CartographicaSinica, 2016, 45(1): 112–118. DOI:10.11947/j.AGCS.2016.20140598 |
| [72] | 白建军, 孙文彬, 赵学胜. 基于QTM的WGS-84椭球面层次剖分及其特点分析[J]. 测绘学报, 2011, 40(2): 243–248. BAI Jianjun, SUN Wenbin, ZHAO Xuesheng. Character Analysis and Hierarchical Partition of WGS-84 Ellipsoidal Facet Based on QTM[J]. Acta Geodaetica et Cartographica Sinica, 2011, 40(2): 243–248. |
| [73] | 贲进, 童晓冲, 张永生, 等. 球面等积六边形离散网格的生成算法及变形分析[J]. 地理与地理信息科学, 2006, 22(1): 7–11. BEN Jin, TONG Xiaochong, ZHANG Yongsheng, et al. A Generation Algorithm of Spherical Equal-Area Hexagonal Discrete Gird and Analysis of Its Deformation[J]. Geography and Geo-Information Science, 2006, 22(1): 7–11. |
| [74] | PEIXOTO P S, BARROS S R M. Analysis of Grid Imprinting on Geodesic Spherical Icosahedral Grids[J]. Journal of Computational Physics, 2013, 237(1): 61–78. |
| [75] | 于文率, 童晓冲, 贲进, 等. 全球六边形离散格网的矢量线数据绘制精度控制[J]. 地球信息科学学报, 2015, 17(7): 804–809. YU Wenshuai, TONG Xiaochong, BEN Jin, et al. The Accuracy Control in the Process of Vector Line Data Drawing in the Hexagon Discrete Global Grid System[J]. Journal of Geo-Information Science, 2015, 17(7): 804–809. |
| [76] | 陆楠. 导航定位网格编码研究[D]. 北京: 北京大学, 2013. LU Nan.Research on Grid Encoding Navigation and Positioning[D].Beijing:Peking University, 2013. |
| [77] | PURSE M, OLIVER S, LEWIS A, et al. Specification of a Global Nested Grid System for Use by Australia and New Zealand[C]//Proceedings of the 7th eResearch Australasia Conference.Brisbane:[s.n.], 2013. |
| [78] | SUESS M, MATOS P, GUTIE? RREZ A, et al. Processing of SMOS Level 1C Data onto a Discrete Global Grid[C]//Proceedings of IEEE International Geoscience and Remote Sensing Symposium.Anchorage, AK:IEEE, 2004, 3:1914-1917. |
| [79] | GeoFusion[EB/OL].[2010-03-11].http://www.geofusion.com/. |
| [80] | PETERSON P. Closed-Packed Uniformly Adjacent, Multi-Resolutional Overlapping Spatial Data Ordering:US, US 8400451 B2[P]. 2011-09-13. |
| [81] | PYXIS.The WorldViewTM Difference:A Digital Earth[EB/OL]. http://www.pyxisinnovation.com/Products/Studio. |
| [82] | MAHDAVI-AMIRI A, HARRISON E, SAMAVATI F. Hexagonal Connectivity Maps for Digital Earth[J]. International Journal of Digital Earth, 2014, 8(9): 1–20. |
| [83] | MAHDAVI-AMIRI A, HARRISON E, SAMAVATI F. Hierarchical Grid Conversion[J]. Computer-Aided Design, 2016, 79: 12–26. DOI:10.1016/j.cad.2016.04.005 |
| [84] | ALDERSON T, MAHDAVI-AMIRI A, SAMAVATI F. Multiresolution on Spherical Curves[J]. Graphical Models, 2016, 86: 13–24. DOI:10.1016/j.gmod.2016.05.002 |
| [85] | WAGNER W. Implementation Plan for A Soil Moisture Product for NWP[R]. ASCAT Soil Moisture Report Series No.5. Vienna:Institute of Photogrammetry and Remote Sensing, Vienna University of Technology, 2005. |
| [86] | KIESTER A R, SAHR K. Planar and Spherical Hierarchical, Multi-Resolution Cellular Automata[J]. Computers, Environment and Urban Systems, 2008, 32(3): 204–213. DOI:10.1016/j.compenvurbsys.2008.03.001 |
| [87] | VENTRELLA J. Glider Dynamics on the Sphere:Exploring Cellular Automata on Geodesic Grids[J]. Journal of Cellular Automata, 2011, 6(2-3): 245–256. |
| [88] | KIDD R A, TROMMLER M, WAGNER W. The Development of a Processing Environment for Time-Series Analysis of SeawindsScatterometer Data[C]//Proceedings of 2003 IEEE International Geoscience and Remote Sensing Symposium.Toulouse:IEEE, 2003, 6:4110-4112. |
| [89] | CHEN Chunguang, XIAO Feng. Shallow Water Model on Cubed-Sphere by Multi-Moment Finite Volume Method[J]. Journal of Computational Physics, 2008, 227(10): 5019–5044. DOI:10.1016/j.jcp.2008.01.033 |
| [90] | LI S, XIAO Feng. A Global Shallow Water Model Using High Order Multi-Moment Constrained Finite Volume Method and Icosahedral Grid[J]. Journal of Computational Physics, 2010, 229(5): 1774–1796. DOI:10.1016/j.jcp.2009.11.008 |
| [91] | RINGLER T D, HEIKES R P, RANDALL D A. Modeling the Atmospheric General Circulation Using A Spherical Geodesic Grid:A New Class of Dynamical Cores[J]. Monthly Weather Review, 2000, 128(7): 2471–2490. DOI:10.1175/1520-0493(2000)128<2471:MTAGCU>2.0.CO;2 |
| [92] | RANDALL D A, RINGLER T D, HEIKESR P, et al. Climate Modeling with Spherical Geodesic Grids[J]. Computing in Science & Engineering, 2002, 4(5): 32–41. |
| [93] | TSATCHA D, SAUXÉ, CLARAMUNT C. A Bidirectional Path-Finding Algorithm and Data Structure for Maritime Routing[J]. International Journal of Geographical Information Science, 2014, 28(7): 1355–1377. DOI:10.1080/13658816.2014.887087 |
| [94] | BERNARDIN T, COWGILL E, KREYLOS O, et al. Crusta:A New Virtual Globe for Real-Time Visualization of Sub-Meter Digital Topography at Planetary Scales[J]. Computers & Geosciences, 2011, 37(1): 75–85. |
| [95] | ADAMS B. Wāhi, A Discrete Global Grid Gazetteer Built Using Linked Open Data[J/OL].International Journal of Digital Earth, 2016, doi:10.1080/17538947.2016.1229819.(inpress) |
| [96] | KARSSENBERG D, DE JONG K. Dynamic Environmental Modelling in GIS:1. Modelling in Three Spatial Dimensions[J]. International Journal of Geographical Information Science, 2005, 19(5): 559–579. DOI:10.1080/13658810500032362 |
| [97] | STADLER G, GURNIS M, BURSTEDDE C, et al. The Dynamics of Plate Tectonics and Mantle Flow:From Local to Global Scales[J]. Science, 2010, 329(5995): 1033–1038. DOI:10.1126/science.1191223 |
| [98] | SANFORD B, JAMES R, YOUNG C. Efficient and Accurate Calculation of Ray Theory Seismic Travel Time through Variable Resolution 3D Earth Models[J]. Seismological Research Letters, 2009, 80(6): 990–1000. |
| [99] | IVAN L, SUSANTO A, DE STERCK H, et al. High-Order Central ENO Finite-Volume Scheme for MHD on Three-Dimensional Cubed-Sphere Grids[C]//Proceedings of the 7th International Conference on Computational Fluid Dynamics (ICCFD7).Big Island, Hawaii:ICCFD, 2012. |
| [100] | YU Jieqing, WU Lixin, LI Zhifeng, et al. An SDOG-based Intrinsic Method for Three-Dimensional Modelling of Large-Scale Spatial Objects[J]. Annals of GIS, 2012, 18(4): 267–278. DOI:10.1080/19475683.2012.727865 |
| [101] | 张宗佩, 万刚, 曹雪峰, 等. 地月圈层空间立体网格技术及其编码转换方法[J]. 测绘通报, 2015(6): 20–23, 27. ZHANG Zongpei, WAN Gang, CAO Xuefeng, et al. Earth-Lunar Shell Space Solid Grid Technology and Coding-Conversion[J]. Bulletin of Surveying and Mapping, 2015(6): 20–23, 27. DOI:10.13474/j.cnki.11-2246.2015.0169 |
| [102] | 陈磊, 白显宗, 梁彦刚. 空间目标轨道数据应用——碰撞预警与态势分析[M]. 北京: 国防工业出版社, 2015. CHEN Lei, BAI Xianzong, LIANG Yangang. Orbital Data Applicationsfor Space Object:ConjunctionAssessment and Situation analysis[M]. Beijing: National Defence Industry Press, 2015. |


