2. 航天工程大学, 北京 101416;
3. 地理信息工程国家重点实验室, 陕西 西安 710054;
4. 城市空间信息工程北京市重点实验室, 北京 100000
2. Space Engineering University, Beijing 101416, China;
3. State Key Laboratory of Geo-information Engineering, Xi'an 710054, China;
4. Beijing Key Laboratory of Urban Spatial Information Engineering, Beijing 100000, China
运动恢复结构方法(structure from motion,SFM)是一种计算机视觉三维重建技术,可由影像恢复出运动相机的位置、姿态以及所摄场景的三维结构,且对参与重建的影像没有约束要求,通用性较强[1-2]。运动恢复结构方法实现的策略大体上可分为增量式和全局式。增量式运动恢复结构方法(ISFM)是从2张或者3张影像的重建开始,增量式的添加新的影像后再进行重建,直到完成所有影像的重建。全局式SFM采用平移矩阵和旋转矩阵分别一次性全局求解的方法,因其省去了不断重建的步骤,一定程度上解决了增量式SFM效率低下的问题[3]。但当影像姿态、尺度或者畸变较大时,全局式SFM会出现解算不稳定的问题,甚至导致解算失败,而增量式SFM的解算结果则更加稳健。对于全局式SFM,当重建的影像很多时,一般采用分组重建的方法,其本质上也是一种增量式SFM的思想。对于无序影像的三维重建,增量式SFM是一种更受欢迎的策略方法。
文献[4]采用基于特征的骨骼提取策略对影像进行分组重建,有效提高了重建的效率,采用光束法平差来降低分组重建带来的精度损失。文献[5]以距离的重叠为度量将各个组聚集形成一个树,重建时遵循从树的叶子到根的顺序。该方法将整体重建问题分解为较小的实例,然后分别解决和组合,具有较低的计算复杂度。文献[6]在初始重建数据集选择、关系图构建以及新影像添加策略等方面均采用3幅影像为基本单元,一定程度上提高了增量式SFM重建的稳健性,但导致重建的效率降低。文献[7]对SFM重建时匹配点误差剔除的RANSAC方法进行了阈值参数自适应估计,提高了误差剔除的效果。文献[8]通过构建初始的粗略模型对剩余的影像进行全注册,然后采用并行处理的方法提高SFM重建的效率。文献[9]提出了一种顾及影像拓扑关联关系的运动恢复结构算法,利用无人机自身的飞行数据构建影像拓扑关联关系,缩小了特征匹配时的影像搜索范围,与传统SFM算法相比,重建精度相当,但提高了重建效率。文献[10]面对大重叠度的无人机图像处理挑战,提出利用无人机飞行数据构建了一个拓扑连接网,并将该拓扑连接网嵌入到SFM过程,显著提高了计算效率。目前开源的SFM软件很多,其中VisualSFM[11]、OPENMVG(https://github.com/openMVG/openMVG)、MVE[12]以及COLMAP[13]等是目前重建效果比较好的开源SFM软件。
当前增量式SFM虽然在重建的速度、精度和稳健性等方面已取得了大幅进步,但是面对无人机影像、近景影像和互联网影像等不同类型的数据重建需求时,上述这些问题依然是增量式SFM需要继续妥善解决的关键性技术问题。本文主要瞄准稳健性和精度两个方面,在充分借鉴现有研究成果的基础上,设计了一种稳健性增强和精度提升的增量式运动恢复结构方法,稳健性增强和精度提升主要体现在误匹配点剔除、下一张影像添加策略和平差时减弱误差点影响等方面。
1 方法原理如图 1所示,本文增量式SFM开始于影像的特征提取,然后进行特征点匹配和误差剔除,并利用影像匹配结果构建的影像关系图。由于正确的影像关系图是进行增量式SFM计算的基础,本文的增量式SFM将采用基础矩阵和单应矩阵对影像关系图进行几何验证[8]。本文增量式SFM的重建过程是以2张影像的初始化为基础,再循环进行新影像注册、前方交会、外点滤波和局部光束法平差等步骤。每当新影像注册量达到设定的阈值或者所有影像全部注册完毕后都会进行一次全局光束法平差,以提高增量式SFM重建的几何质量。
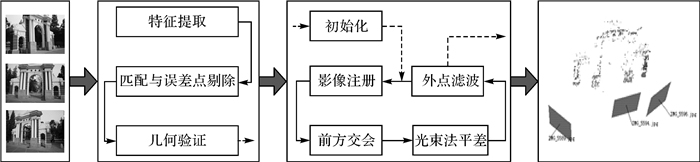
|
| 图 1 本文增量式SFM主要流程 Fig. 1 The main flow of the proposed ISFM |
目前主流SFM软件在面对无人机影像数据、近景影像数据以及利用互联网搜索引擎下载的大尺度影像等各种类型的影像数据时,常出现精度过低或重建失败等现象[1, 13-14]。这主要是因为对影像匹配阶段产生的噪声没有进行很好的处理以及影像增量重建的顺序不够优化。针对这些问题,本文增量式SFM计算流程主要采用顾及特征响应值的参数自适应RANSAC方法和稳健的平差优化方法对噪声进行处理,以及采用更加科学的下一张影像添加策略优化影像重建的顺序,进而提高系统重建的稳健性和重建的精度。
1.1 顾及特征响应值的参数自适应RANSAC方法利用不变特征(如:SIFT、SUFT、ASIFT和KAZE等)[15-16]算子进行特征提取和匹配后,难免会出现一些误匹配点,虽然可以采用RANSAC算法进行误差剔除[17],但其效率和误差点剔除的效果都差强人意,实际应用中存在两个方面的问题。第一,采用经典RANSAC算法剔除匹配误差点时对所有影像均使用一个全局固定值的方法,这导致一些特殊困难地区的影像往往会出现得到的同名特征点数量不足或者误差点剔除不理想的问题。第二,采用经典RANSAC算法进行单应矩阵或者基础矩阵计算时,一般将每个特征点被选中的概率设置为同一个值,这显然是不合理的,实际上每个特征点的定位精度与成为正确特征点的概率是不相同的。针对这个两个问题,本文提出一种顾及特征响应值的参数自适应RANSAC方法。
RANSAC算法依赖于一个关键的T阈值。该T值通常取的是一个人为设定的经验值,但在SFM增量重建时无论该T值设定多少,都不能提供适合所有输入影像的最佳精度。如果T阈值设置的太小,内点数量就会很少,导致同名特征点数量不足;反之,则会吸收大量的外点,导致参数估计精度不高。如何自适应设置内外点的阈值成为误匹配剔除的关键。本文增量式SFM采用虚警值最小化作为评价准则的自适应参数RANSAC误匹配剔除方法[7]。式(1)是该方法的核心计算公式
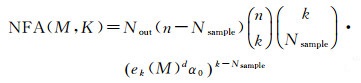 (1)
(1)
式中,M表示待求解的模型参数;k表示假设正确样本的数量;n表示样本总数;Nsample为RANSAC随机采样的数量;Nout为利用Nsample个采样点计算出来的模型的个数;ek(M)为根据参数M计算出的误差中第k小值;α0为随机误差是1个像素的概率;d为误差的维度。自适应参数的RANSAC误匹配剔除方法解决了人为设定全局T阈值导致的个别图像不适应问题,进而提高了误匹配点剔除的效果。本文在上述自适应参数RANSAC误匹配剔除方法的基础上,对其中每次迭代选取样本点的策略作了进一步优化。以SIFT特征点为例,图像中提取出来的每个SIFT特征点对应的DOG响应值是不相同,拥有较大DOG响应值的SIFT特征点一般具有较高的定位精度和较高的可靠性[16, 18],因此应该具有较大的概率成为样本点。基于上述思想,本文构建了顾及特征响应值的样本点选取方法,采用两步概率函数抽取的思路实现。具体如下:
(1) 设影像特征响应值的取值范围为(rmin, rmax),将该取值范围平均划分为k(i=1, 2, …, k)个区间,区间按照特征响应值的大小进行排列,即编号大的区间对应的特征响应值也大。
(2) 统计每个特征响应值区间特征点的数量numi(i=1, 2, …, k)。
(3) 当抽样时,第i个区间被选到的概率函数公式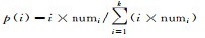
(4) 第i个区间内的特征点被抽到的概率函数公式为pi(x)=1/numi。
1.2 下一张影像评分添加策略在重建过程中,需要不断地向增量式SFM系统中添加新的影像(下一张影像)来继续后面的增量式重建。下一张影像的添加对后续的重建过程影响很大,主要包括影像位姿估计的精度和前方交会的质量。一幅不合适的下一张影像加入系统中,甚至会导致影像注册的失败或者无法进行后续的重建,因此研究一种稳健的下一张影像添加策略尤为重要。当前普遍的下一张影像添加策略为从剩余影像集中选择可视物方点数量(注:可视物方点数量指已经识别出的物方点在当前影像上成像的数量)最多的影像作为下一张影像,通常基于可视物方点并采用PnP算法[19]恢复新影像的位姿信息。然而,新影像位姿信息恢复的精度不仅与可视物方点的数量有关系,也与可视物方点在像方的分布有关系[20-21]。为兼顾可视物方点的数量与分布对影像注册精度的影响,本文设置了下一张影像的添加评分加策略,具体如下:
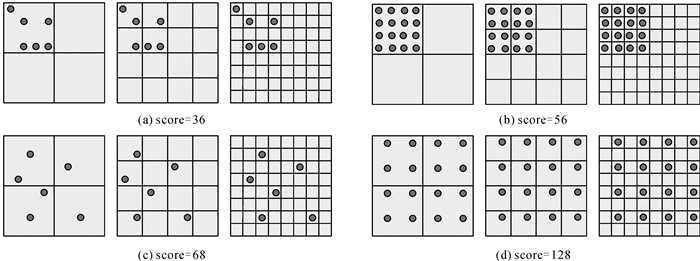
这种评分方法使得拥有更多可视物方点和更好点位分布的影像获得高的分数,反之则获得低的分数。本文将待评分影像划分成L级金字塔格网,下一级格网Li的尺寸为上一级格网Li+1尺寸的1/2,每个格网cell(Li, indexj)的状态只有“空”和“满”两种状态。当可视物方点落到格网中时,即cell(Li, indexj)的状态由“空”变成“满”时,影像对应的分数score增加一定的分数。需要注意每个格网只对score的分数增加贡献一次。基于以上原理,影像的评分函数如式(2)所示
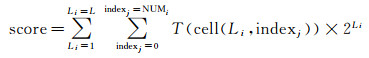 (2)
(2)
式中,NUMi为Li级格网中格网的数量;T(cell(Li, indexj))为选择函数,当cell(Li, indexj)的状态为“空”时T(cell(Li, indexj))=0,反之当cell(Li, indexj)的状态为“满”时T(cell(Li, indexj))=1。图 2为本文方法依据式(2)计算的示例。
|
| 图 2 本文影像评分算例(L=3) Fig. 2 An example of image score calculation(L=3) |
为加快下一张影像的寻找效率,本文首先对所有未注册的影像中可视物方点数量是否大于人工设定的最小阈值NVmin进行判断,得到影像数量为m的集合Ψ,然后对Ψ中的所有影像采用式(2)计算分数值,最后对Ψ中所有影像的分数值scorek(k=1, 2, …, m)进行排序,分数值最高的scorek对应的影像就是下一步增量SFM需要添加的新影像。
1.3 稳健平差优化为减弱增量重建累计误差的影响,在每次影像注册和前方交会后一般需要进行一次光束法平差优化。考虑到增量式SFM系统重建时影像之间局部关联性特点,增量式SFM并不需要每一步增量重建都进行全局光束法平差,仅需要对与新增影像最相关的若干影像进行局部光束法平差即可。只有当增量重建达到一定比例后,增量式SFM系统才会进行一次全局光束法平差。增量式SFM系统的平差优化部分不仅要考虑平差的计算效率问题,更重要的是要考虑平差的稳健性问题,即对含有噪声的数据如何进行合理的优化处理。
增量式SFM系统处理的影像数据表现为尺度变化大和噪声目标干扰多的特点,因此难免将大量的噪声点引入平差优化部分。本文考虑到在影像匹配处理时,轨迹越长的同名点具有越高的可靠性,其稳定性也越好,因此在平差时可以给予其更高的权重。本文采用了一种能够顾及特征点轨迹长度的稳健代价权函数[21],以提高区域网平差的稳健性,具体表达式如式(3)
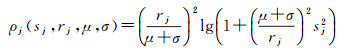 (3)
(3)
式中,sj表示第j个物方点的像方反投影误差;rj表示其轨迹长度;μ和σ表示已重建部分特征点轨迹长度的均值和方差。对于每一个独立的残差,除以均值和方差的和归一化了,得到的结果作为稳健代价函数的权重。较高的特征点轨迹长度,代表可靠性更高,相应的观测值被赋予更高的权重,因此光束法平差的代价函数可以表示为式(4)
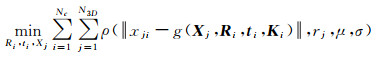 (4)
(4)
本文试验影像数据包括无人机影像数据、近景影像数据和互联网影像数据,下面分别对这些数据进行详细介绍:
(1) 无人机影像数据。在河南登封地区,采用天宝固定翼无人机搭载SONY_α5100相机拍摄获取了563张影像,航高150 m,影像地面分辨0.04 m,影像大小(像素)为6000×4000。该组数据对应的地面高差范围在150 m左右,地面覆盖非常丰富包括庄稼、草地、湖泊、居民地以及交通设施等,如图 3(a)所示。

|
| 图 3 本文图像数据集截图 Fig. 3 Image data set screenshot |
(2) 近景影像数据。近景影像数据为清华大学清华门数据,采用Canon EOS 5D相机拍摄,共68张影像,影像大小为4368×2912,影像采用环绕式拍摄方式,如图 3(b)所示。
(3) 互联网影像数据。利用百度搜索引擎下载了两组大尺度影像数据集,其中国家体育场(鸟巢)的影像数据338张,影像大小从1024×768到4928×3264,如图 3(c)所示;天安门影像数据302张,影像大小从1200×857到8000×6000,如图 3(d)所示。
试验环境:基于本文方法开发了WINDOWS环境下的增量重建系统SurpassMap,本文下述所有试验均在该系统下完成,系统硬件平台为英特尔酷睿i7、主频2.6 GHz 8核,内存32 GB,显卡为4 GB英伟达QuadroK2200。
2.2 试验结果与分析图 4为利用本文方法对登封无人机影像、清华门影像、鸟巢互联网影像和天安门互联网影像实现的三维重建均取得成功。考虑到这些数据的重建难度,从整体上证明了本文方法的正确性和稳健性。为证明本文方法的3个创新贡献点的效果,本文进一步设计了3个试验,其中试验1对应本文的顾及特征响应值的参数自适应RANSAC方法,试验2对应本文的下一张影像高精度添加策略,试验3对应本文的稳健平差优化和与其他部分SFM开源软件的横向对比。3个试验具体情况如下:

|
| 图 4 本文方法三维重建结果 Fig. 4 Three-dimension reconstruction results |
试验1:从本文数据集中选取5组具有代表性的影像进行试验,包括湖泊、人工建筑、草地、近景雕塑和互联网大尺度变化影像等。试验中首先利用SIFT算法对所选数据集影像进行特征提取与匹配,然后采用一般的RANSAC方法(设定经验阈值1.0)和本文的顾忌特征响应值的参数自适应RANSAC方法分别求解基础矩阵,最后统计内点数量、求解基础矩的中误差以及内外点阈值等信息,其中的内外点阈值是指根据内外点残差分布反推如果采用RANSAC方法应该设置的内外点阈值大小(表 1)。
| 试验数据 | 初始匹配点数 | RANSAC | 本文参数自适应方法 | 内外点阈值/pixel | ||
| 内点数量 | 中误差/pixel | 内点数量 | 中误差/pixel | |||
| 湖泊 | 3764 | 3274 | 0.30 | 3546 | 0.26 | 1.13 |
| 人工建筑 | 2215 | 1592 | 0.28 | 1525 | 0.16 | 0.91 |
| 草地 | 560 | 420 | 0.43 | 445 | 0.38 | 1.62 |
| 近景雕塑 | 210 | 128 | 0.73 | 152 | 0.45 | 1.99 |
| 大尺度影像 | 380 | 230 | 0.65 | 278 | 0.57 | 1.74 |
对表 1的基础矩阵统计结果进行分析可得出如下结论:
(1) 利用本文的顾及特征响应值的参数自适应RANSAC方法计算基础矩阵的中误差明显小于普通的RANSAC方法。这主要是因为本文方法自主估计了科学合理的阈值,以及采用了顾及特征响应值的选取样本点策略对不同定位精度的特征点给予不同的选样概率,因此可最大限度地保留正确的匹配点。从内点数量上来看,本文方法的内点数量在大多数情况下也要多于普通的RANSAC方法。
(2) 从内外点的阈值来看,不同影像的内外点阈值浮动范围较大,从0.91个像元到1.99个像元。如果采用RANSAC方法,即使凭借经验也难以设置合理的阈值进行外点的剔除,这也表明了本文方法的必要性。
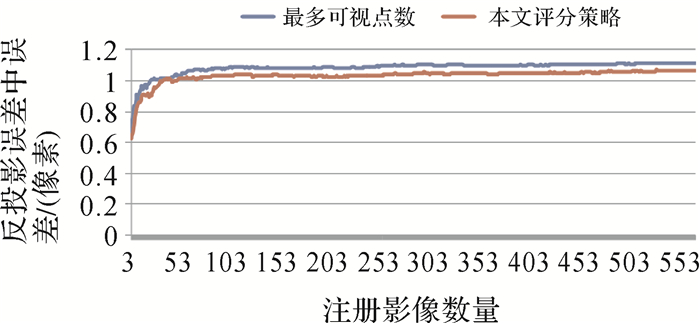
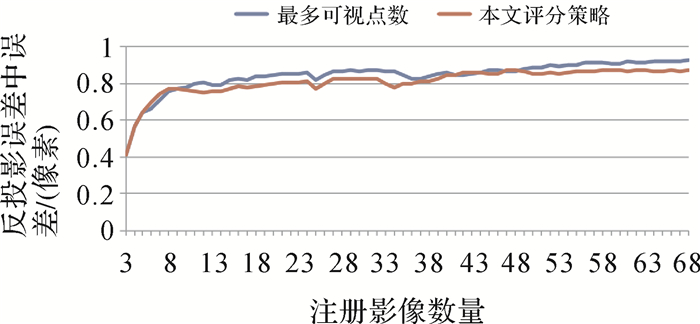
试验2:为验证本文基于评分方法的下一张影像添加策略方法(简称本文评分策略)与传统的基于最多可视物方点数下一张影像添加方法(简称最多可视点数)的效果,采用两种方法构建的增量式SFM流程分别对登封无人机数据和清华门数据进行重建试验。初始影像对为同名点数量最多的影像对,每添加一张新影像后顺序进行注册、前方交会和局部光束法平差优化等步骤,同时记录反投影中误差(像素)。基于上述试验数据结果,得到如图 5和图 6所示的反投影中误差随注册影像数量的变化曲线。从图中可以发现在相同影像注册数量时,本文评分策略方法比最多可视点数方法的重建精度更高,这证明本文基于评分方法构建下一张影像添加的策略方法是正确的和有效的。
|
| 图 5 下一张影像添加策略重建精度对比(登封无人机影像) Fig. 5 The next image adds policy reconstruction accuracy comparison (Dengfeng UAV images) |
|
| 图 6 下一张影像添加策略重建精度对比(清华门影像) Fig. 6 The next image adds policy reconstruction accuracy comparison (Tsinghua gate images) |
试验3:试验时,首先采用本文增量SFM结合常规光束法平差[22](BA+SurpassMap)、本文增量SFM结合稳健区域网平差(RBA+SurpassMap)、开源软件VisualSFM和开源软件COLMAP对本文4组试验数据分别进行处理,然后对成功注册的影像数量(表 2中简称:数量)和重投影均方根误差[23](表 2中简称:误差)进行统计分析。
| 试验数据 | VisualSFM | COLMAP | BA+SurpassMap | RBA+SurpassMap | |||||||
| 数量 | 误差/pixel | 数量 | 误差/pixel | 数量 | 误差/pixel | 数量 | 误差/pixel | ||||
| 登封 | 563 | 1.51 | 563 | 0.58 | 563 | 0.57 | 563 | 0.57 | |||
| 清华门 | 68 | 1.68 | 68 | 0.67 | 68 | 0.65 | 68 | 0.63 | |||
| 鸟巢 | 93 | 3.37 | 143 | 2.97 | 159 | 2.87 | 172 | 2.82 | |||
| 天安门 | 115 | 2.69 | 122 | 1.97 | 129 | 1.94 | 131 | 1.91 | |||
对表 2的重建计算结果进行分析可得出如下结论:
(1) 对比RBA+SurpassMap和BA+Surpass Map的重投影均方根误差可以发现,当平差数据中噪声比较小时,常规光束法平差的精度与本文稳健区域网平差的精度相当,如登封无人机数据处理结果所示。当平差数据中噪声比较大时,采用稳健代价函数对于噪声具有一定的稳健性,可显著提高平差重建的精度,如鸟巢数据和天安门数据的处理结果所示。
(2) 在SFM增量重建过程,影像成功注册的数量与特征点提取与匹配方法、初始化像对的选择、影像添加策略以及平差优化方法等因素均有关系。在本次试验中,表 2中的4种重建方法均采用SIFT特征提取与匹配方法,以及为排除干扰,4种重建方法的初始化像对的选择策略均采用同名点数量最多的方法。如表 2所示,由于登封无人机数据和清华门数据的数据质量很好,采用4种方法均可实现百分百注册。而对于搜索引擎下载的鸟巢影像数据和天安门影像数据,由于这种影像数据集内影像之间在重叠度、位姿、尺度和色调等方面存在的巨大差异,对影像注册提出了很大的挑战。对比VisualSFM和COLMAP、BA+SurpassMap方法,由于采用顾及特征响应值的参数自适应RANSAC方法可更好的剔除复杂影像数据集匹配产生的误匹配点,以及采用下一张影像评分添加策略优化影像注册顺序,影像成功注册数量明显提高了。对比BA+SurpassMap方法、RBA+SurpassMap由于采用了本文的稳健平差优化方法,也在一定程度上提高了影像注册的成功率。
(3) 在特征提取匹配后,尽管本文采用了顾及特征响应值的参数自适应RANSAC方法对误匹配点进行了有效剔除,但仍会残留一些误匹配点。特别是对利用搜索引擎下载的鸟巢影像数据和天安门影像数据进行处理时,由于这种影像数据集的复杂性导致在进入平差阶段时仍有相当一部分误匹配点,故在平差阶段对这种含有数据噪声(误匹配点)的数据进行处理时采用本文稳健平差优化方法可以有效提高重建的精度。
(4) 采用本文完整技术方案的RBA+SurpassMap与VisualSFM和COLMAP进行对比可以发现,本文方法在影像注册的成功率和重建的精度方面均有所提高,这进一步证明了本文技术方法的正确性与有效性。
3 总结本文对增量式运动恢复结构中存在的问题进行了梳理,进而有针对性地构建了一种稳健性增强和精度提升的增量式运动恢复结构方法。选取无人机低空影像、近景影像和利用搜索引擎下载的互联网影像等数据进行了试验测试,结果证明本文方法中提出的顾及特征响应值的参数自适应RANSAC方法、下一张影像高精度添加策略和稳健平差优化可显著增强重建的稳健性和提升重建的精度。未来不仅将采用更多类型的影像数据对本文方法进行广泛的测试,而且也将采用视觉词袋技术和并行计算技术来提高本文方法重建的效率。
| [1] | SZELISKI R. Structure from motion[J]. Near Eastern Archaeology, 2017, 77(3): 187–191. |
| [2] | DIETRICH J T. Riverscape mapping with helicopter-based structure-from-motion photogrammetry[J]. Geomorphology, 2016, 252(1): 144–157. |
| [3] |
李劲澎, 姜挺, 肖达, 等.
基于关系图的无人机影像三维重建[J]. 光学精密工程, 2016, 24(6): 1501–1509.
LI Jinpeng, JIANG Ting, XIAO Da, et al. On diagram-based three-dimensional reconstruction of UAV image[J]. Optics and Precision Engineering, 2016, 24(6): 1501–1509. |
| [4] | SNAVELY N, SEITZ S M, SZELISKI R. Skeletal graphs for efficient structure from motion[C]//Proceedings of 2008 IEEE Conference on Computer Vision and Pattern Recognition. Anchorage, AK: IEEE, 2008: 1-8. |
| [5] | FARENZENA M, FUSIELLO A, GHERARDI R. Structure-and-motion pipeline on a hierarchical cluster tree[C]//Proceedings of the 12th IEEE International Conference on Computer Vision Workshops, ICCV Workshops. Kyoto, Japan: IEEE, 2009: 1489-1496. |
| [6] | KLOPSCHITZ M, IRSCHARA A, REITMAYR G, et al. Robust incremental structure from motion[C]//Proceedings of the 3rd International Symposium on 3D Data Processing, Visualization and Transmission. Toronto: [s.n.], 2010: 1-8. |
| [7] | MOULON P, MONASSE P, MARLET R. Adaptive structure from motion with a contrario model estimation[C]//Proceedings of the 11th Asian Conference on Computer Vision. Berlin: Springer, 2012: 257-270. |
| [8] | SHAH R, DESHPANDE A, NARAYANAN P J. Multistage SFM: revisiting incremental structure from motion[C]//Proceedings of the 2nd International Conference on 3D Vision. Tokyo, Japan: IEEE, 2014: 417-424. |
| [9] |
许志华, 吴立新, 刘军, 等.
顾及影像拓扑的SfM算法改进及其在灾场三维重建中的应用[J]. 武汉大学学报(信息科学版), 2015, 40(5): 599–606.
XU Zhihua, WU Lixin, LIU Jun, et al. Modification of SfM algorithm referring to image topology and its application in 3-dimension reconstruction of disaster area[J]. Geomatics and Information Science of Wuhan University, 2015, 40(5): 599–606. |
| [10] | XU Zhihua, WU Lixin, GERKE M, et al. Skeletal camera network embedded structure-from-motion for 3D scene reconstruction from UAV images[J]. ISPRS Journal of Photogrammetry and Remote Sensing, 2016, 121(1): 113–127. |
| [11] | WU Changchang. Visual SfM: a visual structure from motion system[CP/OL].[2017-05-05]. http://ccwu.me/vsfm/. |
| [12] | FUHRMANN S, LANGGUTH F, GOESELE M. MVE: a multi-view reconstruction environment[C]//Proceedings of the Eurographics Workshop on Graphics and Cultural Heritage. Darmstadt, Germany: ACM, 2014: 11-18. |
| [13] | SCHONBERGER J L, FRAHM J M. Structure-from-motion revisited[C]//Proceedings of 2016 IEEE Conference on Computer Vision and Pattern Recognition. Las Vegas, NV: IEEE, 2016: 4104-4113. |
| [14] | FRAHM J M, FITE-GEORGEL P, GALLUP D, et al. Building rome on a cloudless day[C]//Proceedings of the 11th European Conference on Computer Vision. Heraklion, Crete, Greece: Springer-Verlag, 2010: 368-381. |
| [15] |
闫利, 费亮, 叶志云, 等.
大范围倾斜多视影像连接点自动提取的区域网平差法[J]. 测绘学报, 2016, 45(3): 310–317, 338.
YAN Li, FEI Liang, YE Zhiyun, et al. Automatic tie-points extraction for triangulation of large-scale oblique multi-view images[J]. Acta Geodaetica et Cartographica Sinica, 2016, 45(3): 310–317, 338. |
| [16] |
于英, 张永生, 薛武, 等.
影像连接点均衡化高精度自动提取[J]. 测绘学报, 2017, 46(1): 90–97.
YU Ying, ZHANG Yongsheng, XUE Wu, et al. Automatic tie points extraction with uniform distribution and high precision[J]. Acta Geodaetica et Cartographica Sinica, 2017, 46(1): 90–97. DOI:10.11947/j.AGCS.2017.20160320 |
| [17] | CHEN Yisong, CHAN A B, LIN Zhouchen, et al. Efficient tree-structured SfM by RANSAC generalized procrustes analysis[J]. Computer Vision and Image Understanding, 2017, 157(2): 179–189. |
| [18] | WU Changchang. SiftGPU: A GPU implementation of scale invariant feature transform (SIFT)[EB/OL]. (2012-02-07). https://blog.csdn.net/archielau/article/details/7907387. |
| [19] | LEPETIT V, MORENO-NOGUER F, FUA P. EPnP:An accurate O(n) solution to the pnp problem[J]. International Journal of Computer Vision, 2009, 81(2): 155–166. DOI:10.1007/s11263-008-0152-6 |
| [20] |
于英.无人机动态摄影测量若干关键技术研究[D].郑州: 信息工程大学, 2014. YU Ying. Research on key technologies of UAV dynamic photogrammetry[D]. Zhengzhou: Information Engineering University, 2014. |
| [21] |
薛武.无人机影像定位优化技术研究[D].郑州: 信息工程大学, 2017. XUE Wu. Research on optimization technology of UAV images positioning[D]. Zhengzhou: Information Engineering University, 2017. |
| [22] |
薛武, 张永生, 赵玲, 等.
增量式SFM与POS辅助光束法平差精度比较[J]. 测绘学报, 2017, 46(2): 198–207.
XUE Wu, ZHANG Yongsheng, ZHAO Ling, et al. Compareison of the accuracy of incremental SFM with POS-aided bundle adjustment[J]. Acta Geodaetica et Cartographica Sinica, 2017, 46(2): 198–207. DOI:10.11947/j.AGCS.2017.20160274 |
| [23] |
李德仁, 袁修孝.
误差处理与可靠性理论[M]. 2版. 武汉: 武汉大学出版社, 2013.
LI Deren, YUAN Xiuxiao. Error processing and reliability theory[M]. 2nd ed. Wuhan: Wuhan University Press, 2013. |


