2. 地理信息工程国家重点实验室, 陕西 西安 710054
2. State Key Laboratory of Geo-information Engineering, Xi'an 710054, China
空中三角测量是影响摄影测量成果精度的主要因素。空中三角测量主要包括连接点提取和光束法平差两个环节[1-2]。由于不同影像之间存在尺度、色差和摄影角度等差别,这些差别使得影像连接点自动提取效果常常难以令人满意[3]。
近年来,计算机视觉领域中影像不变特征提取与匹配技术的日益成熟推动了影像连接点提取技术的进步[4-5]。影像不变特征提取与匹配技术的一般过程为:首先采用不变特征检测器进行特征提取,然后通过计算生成特征描述向量完成特征匹配。比较典型的不变特征检测器有:具有仿射不变性的Harris-Affine算法、具有尺度不变性的SIFT算法、SURF算法、KAZE算法以及具有视角不变性的ASIFT算法。常用的特征描述符有SIFT描述符、DAISY描述符、二值描述符等[6-9]。在众多影像局部特征描述符中,SIFT描述符应用最广,它对尺度、旋转、亮度以及一定大小的视角变化都具有不变性,因此本文选用SIFT不变特征提取算法进行连接点自动化提取的研究。虽然SIFT算法计算复杂度高,但其计算速度可通过GPU进行并行加速[10]。
采用不变特征进行影像空三连接点提取是目前连接点提取的主流技术方法。文献[11]采用SIFT算法进行异源高分辨率光学卫星遥感影像匹配,并通过RANSAC算法和多项式拟合迭代法等多种策略剔除了误匹配点。文献[12]利用POS信息对倾斜影像纠正消除因大倾角引起的仿射变形,通过SIFT匹配和特征追踪自动获取多视连接点。尽管目前基于不变特征进行影像空三连接点提取技术取得了一些成果,但仍存在不少问题。本文从连接点提取的正确率、分布合理性以及定位精度等方面考虑,主要解决以下3个问题。
(1) 随着航空传感器成像分辨率的不断提高,使得单幅影像上出现重复纹理的概率大幅增加。此外,沙漠、海岛和雪地等特殊地区影像存在大量的弱纹理区域。影像中的重复纹理和弱纹理将严重降低SIFT匹配的正确率。
(2) 采用SIFT算法使得单幅影像上的连接点数量常常达到几千甚至上万的数量级。根据边界效应理论,当连接点的数量达到一定数量后,随着连接点数量的继续飙升并不会提高光束法平差的精度,反而成为计算的负担。简单采用多视重叠度准则对点位进行筛选剔除的方法[13],极容易导致连接点分布不均进而影响光束法平差精度。
(3) SIFT算法本身主要是强调不变特征的识别性能而非定位精度。虽然SIFT算法在特征提取阶段通过插值技术提供了亚像素的坐标位置,但由于特征点提取与匹配的相对独立性,这使得匹配的同名点对不能实现位置上的精确对应[4-5]。
以上述3个问题为导向,基于SIFT特征构建了一种均衡化高精度影像连接点自动提取方法,选取中国嵩山遥感定标场有人机影像数据和西北沙漠地区无人机影像数据对本方法的效果进行了试验分析,试验结果证明了本方法的正确性和有效性。
1 方法原理 1.1 方法流程本文连接点提取方法适用于有人机或无人机面阵影像数据。此外,本文影像之间的关系(大于设定的重叠度阈值)已经通过辅助数据(飞控数据、POS数据等)计算重叠度[12, 14]得到或者通过低分辨率影像数据增量重建得到[15]。
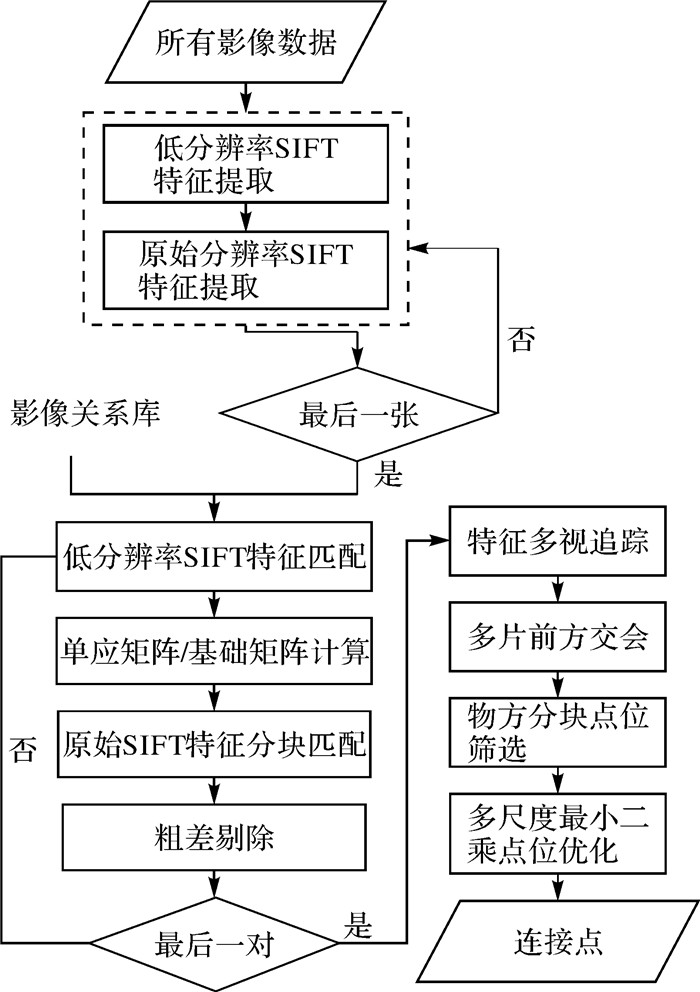
如图 1所示,本文方法流程包括4个阶段:①在对影像提取完SIFT特征后,为避免重复纹理的干扰,首先用低分辨率影像计算单应矩阵和基础矩阵,然后进行单应矩阵和基础矩阵双重约束下的分块匹配,最后根据子块匹配结果计算精确的单应阵和基础矩阵以实现对本块匹配结果的粗差剔除;②采用并查集数据结构实现SIFT特征的多视追踪,然后通过多片前方交会得到物方点坐标;③在物方空间构建均匀格网,计算每个物方点平均反投影误差和多视重叠度的加权值,设定阈值并依据冒泡排序方法对点位进行筛选,保证连接点分布相对的均匀;④采用最小二乘匹配对筛选得到的SIFT连接点坐标位置进行精化。
|
| 图 1 连接点提取流程 Fig. 1 Flowchart of tie points extraction |
1.2 SIFT特征分块提取与匹配
对每张影像都进行两次SIFT特征提取,第1次SIFT特征提取是在低分辨率影像上进行。第2次SIFT特征提取是在原始分辨率影像上进行,具体方法是:将原始分辨率影像划分成若干影像块,在特征提取时根据每个影像块的信息熵设置不同的提取参数(DOG阈值、边缘阈值、检测金字塔层级等),这使得提取到的特征点分布相对均匀[4]。
从影像关系库中任取出一对立体影像,采用比值法对两张影像的低分辨率SIFT特征进行匹配,再通过RANSAC方法计算两张影像之间的单应矩阵H。设原始分辨率立体影像上有同名像点对(x, y)和(x′, y′),根据单应矩阵的定义得到如式(1)所示的对应关系
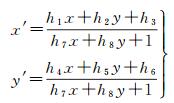 (1)
(1)
式中, hi(i=1,2, …,8)是单应矩阵H的8个元素。
将右影像的4个角点坐标代入式(1)中计算出4个透视变换坐标,以这4个透视变换坐标为顶点的四边形与左影像的交集即为左影像上这两幅影像的重叠区域。同理,可求得右影像上这两幅影像的重叠区域。将左影像重叠区域划分成多个子块,同样依据式(1)将每一个子块的4个角点坐标投影到右影像上,由于透视变换的原因,右影像上相应的4个角点构成的四边形通常是一个不规则的四边形,选取该不规则四边形的外接矩形作为左影像子块在右影像上的对应区域。
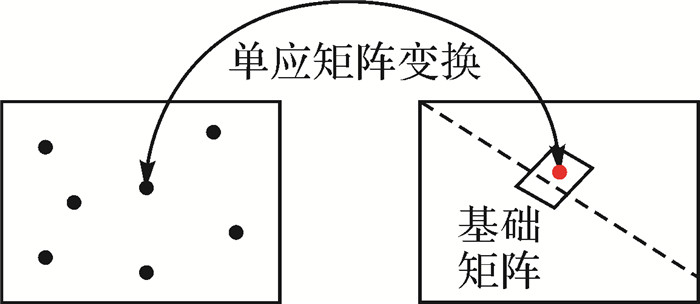
以影像子块为单位对原始分辨率SIFT特征进行单应阵和基础矩阵约束下的比值法匹配,再用子块匹配结果计算两影像对应子块之间精确的单应矩阵和基础矩阵,并利用这两个矩阵对匹配结果进行粗差剔除,其原理如图 2所示。SIFT分块匹配通过搜索空间的压缩使得因重复纹理导致的奇异匹配点干扰大幅减少,故可一定程度上提高匹配的成功率。
|
| 图 2 双矩阵约束与误差剔除原理 Fig. 2 Principle of double matrix constraint and error elimination |
1.3 特征多视追踪
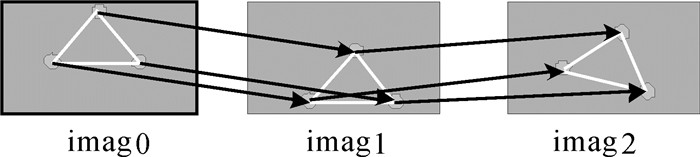
SIFT特征分块提取与匹配实现了两张影像特征点之间的对应,而摄影测量空三光束法平差需要多视连接点方能取得较好的平差精度。如图 3所示,通过将每一组两两匹配的结果进行查找和追踪,即可实现特征的多视追踪。
|
| 图 3 多视追踪 Fig. 3 Multi-view tracks |
本文采用并查集数据结构[16-17]高效地实现了特征的多视追踪,具体过程如下。
(1) 创建并查集节点,节点数量等于所有影像的原始分辨率SIFT特征数量之和。
(2) 若像点a和像点b是同名像点,则对节点a和节点b执行并查集中的查找操作(Find)来判断两个节点的根节点是否相同。如果两个节点的根节点相同则跳过,否则通过执行并查集中的合并操作(Join)将节点a的根节点修改为节点b。
(3) 将匹配链表上所有的同名像点进行步骤(2)处理,然后取出具有相同根节点的节点即实现了SIFT特征的多视追踪。
1.4 基于物方分块的点位筛选采用多片前方交会方法[18-19]对特征多视追踪结果进行计算生成物方点坐标,并利用共线条件方程反算得到每个物方点的反投影误差ϕi以及所有物方点的平均投影误差ϕ。
(1) 统计物方点在平面上的分布范围Xmin、Xmax、Ymin和Ymax,在平面上划分平行于X轴和Y轴的二维格网,格网的尺寸一般设为单张影像地面覆盖范围的1/9或者1/12。设格网单元X方向和Y方向的尺寸分别为X_size和Y_size,则X和Y方向的格网数量X_num和Y_num为
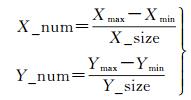 (2)
(2)
(2) 循环计算每个物方点所在的格网编号,并统计每个格网中物方点的数量,若格网中物方点的数量大于指定的阈值κ,则转到步骤(3)。
(3) 依据式(3)计算格网中每一个物方点的Valuei值,该值是点位反投影误差和多视重叠度值Oi的加权计算值
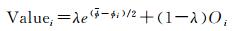 (3)
(3)
采用冒泡法对格网中点的Valuei进行从大到小排序,取前κ个作为该格网有效物方点。
1.5 最小二乘匹配坐标位置精化在物方点位筛选结束后,SIFT特征点的坐标精度可由最小二乘匹配进行优化提高[20]。SIFT特征点的信息由位置(p)、尺度(σ)和方向(θ)组成。设物方点P在影像I1、I2、…、In上成像的像点为m1(pm1, σm1, θm1)、m2(pm2, σm2, θm2)、…、mn(pmn, σmn, θmn),计算物方点P与I1、I2、…、In摄站中心之间的距离D1、D2、…、Dn。若D1是所有距离中的最小值,则选m1(pm1, σm1, θm1)为最小二乘匹配的基准点,然后让m1分别与其他的同名像点进行最小二乘匹配。下面以同名像点对m1和m2为例进行最小二乘匹配说明。
设σm1>=σm2,s=(σm1/σm2),θ=(θm1-θm2)。以m1和m2为中心的两个相关窗口分别为W1和W2,大小为(2w+1)×(2w+1)。记m2窗口邻域坐标为p=[x y]T,Η·p表示对坐标p依据矩阵Η进行透视变换,则窗口W1和W2可表示为[21]
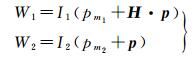 (4)
(4)
式中,Η中含义如下
 (5)
(5)
式中,sx、sy分别为x、y方向的缩放因子,δ为窗口W1和W2之间的相对旋转角度。由于m1和m2为同名像点,则有式(6)成立
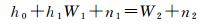 (6)
(6)
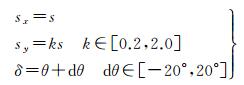 (7)
(7)
式中,h0、h1为窗口之间线性灰度畸变参数,n1、n2为与坐标有关的影像随机噪声。对式(6)进行线性化得到误差方程式,通过最小二乘平差求解得到像点坐标精确值。在进行最小二乘平差求解之前先利用SIFT特征信息按式(7)对仿射相关参数sx、sy和δ的初始值进行设置[22],并以NCC最大为准则搜索确定k和dθ的最佳值[4-5]。
2 试验与分析 2.1 试验数据与评价方法第1组试验数据是在中国嵩山遥感定标场用“运5”飞机搭载飞思IXA180面阵CCD相机和Applanix POS AV510设备获得了航空影像和位姿数据。该组影像数据对应区域的地物信息丰富且重复纹理较多,非常适合验证本方法的匹配效果和点位筛选效果。此外,中国嵩山遥感定标场航空几何定标场占地64 km2,分级布设了214个亚厘米级精度的永久性地面标志,可为本文连接点提取方法提供物方几何精度验证条件[23]。第2组试验数据是用固定翼无人机在西北沙漠地区搭载Canon EOS 5DS获取的沙漠无人机影像,沙漠无人机影像由于纹理贫乏使得连接点的自动提取异常困难。表 1对两组试验数据的影像大小、地面分辨率(GSD)、重叠度等与本文试验相关的具体参数信息进行了详细的介绍。依据本文方法,基于Win7 64位系统、VC++2010、GDAL1.8 64位和CUDA5.5开发了影像三维建模软IMAGE SURPASS的空三处理模块,本文如下的试验均采用该软件模块完成。试验中的计算机配置为:英特尔酷睿i7、主频3.2 GHz 8核,内存32 GB,显卡为4 GB英伟达QuadroK2200。
| 测试数据 | 影像大小 /像素 |
像元大小 /um |
焦距 /mm |
GS D /cm |
旁向重叠 度/% |
航向重叠 度/% |
影像数量 |
| 嵩山影像 | 10 328×7760 | 5.2 | 55 | 10 | 63 | 73 | 787 |
| 沙漠影像 | 8688×5792 | 4.2 | 35 | 15 | 52 | 74 | 1209 |
采用如下3种指标方法对本文连接点提取效果进行评价。
(1) 通过目视检查的方法,查看连接点提取的正确性与分布情况。
(2) 对提取出的连接点进行空三光束法平差,通过反投影误差分析连接点提取的精度。反投影误差的计算见式(8)
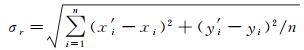 (8)
(8)
式中,(xi, yi)为原始像点观测值;(x′i, y′i)为平差后物方点反投影到原始影像的像点坐标;n为像点个数。
(3) 设定一定数量的检查点,在少量控制点参与下,对连接点进行光束法平差,通过比较检查点的平差坐标与外业坐标来分析连接点提取的效果[20]。检查点精度分析计算见式(9)
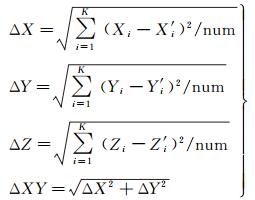 (9)
(9)
式中, (Xi, Yi, Zi)为平差坐标;(X′i, Y′i, Z′i)为外业坐标;num为检查点的个数;ΔX、ΔY和ΔZ分别为3个坐标方向的精度,ΔZ同时也表示高程方向的精度;ΔXY为平面精度。
2.2 连接点提取效果采用本文连接点提取方法(IMAGE SURPASS的空三处理模块)对787张嵩山影像和1209张沙漠影像分别进行了处理,成功提取出连接点的个数分别为1 253 100和330 359,数据处理时间分别为9.67 h和10.54 h。本文方法的数据处理时间包括特征提取、特征匹配、多视追踪、点位筛选和点位优化等5个部分,其中特征提取和特征匹配已采用了GPU并行加速,其余3个部分暂未采用任何加速措施。部分图像的提取效果如图 4和图 5所示,图 4和图 5中的小圆点用于标识连接点,红色箭头连线为人工加上去用于标识个别同名像点。从目视上看可得出如下几点结论。

|
| 图 4 嵩山影像连接点(Image i (i=1, 2, 3, 4)为同一地物不同摄站的影像) Fig. 4 Tie points of Songshan image(Image i (i=1, 2, 3, 4) are from different stations for the same object) |

|
| 图 5 沙漠影像连接点(Image i (i=1, 2, 3, 4)为同一地物不同摄站的影像) Fig. 5 Tie points of desert image(Image i (i=1, 2, 3, 4) are from different stations for the same object) |
(1) 对嵩山影像和沙漠影像各随机抽取了50个连接点进行同名像点目视检查,检查结果表明50个连接点均为正确的连接点(同名像点定位精度优于1像素)。连接点目视检查全部正确是本文方法中的多种技术共同作用的结果,具体为:首先,采用影像分块变参数的提取策略,在纹理信息丰富的影像子块特征提取时本文方法自动提高特征检测的门槛阈值,这样得到的特征点具有比较高的识别度,不容易出现匹配错误;其次,在影像匹配阶段采用具有压缩搜索空间特点的分块匹配和带约束的比值法匹配策略,这有利于提高匹配的正确率;最后,本文连接点提取方法在像方采用单应阵和基础矩阵进行了粗差剔除,然后在物方又通过顾及反投影误差和多视重叠度的点位筛选技术也在一定程度上剔除了部分粗差连接点。
(2) 沙漠影像数据纹理匮乏且重复,但本文方法依然提取了足够量的连接点,这是因为本文方法采用分块不变特征提取与匹配技术,每个影像块根据各自信息熵采用不同的特征提取参数。当对纹理信息匮乏的影像子块进行特征提取时,本文方法自动降低特征检测的门槛阈值,这可增加检测到的特征点数量。本文的影像分块不变特征提取与匹配技术对影像纹理的变化具有较强适应能力,不仅实现了特征点提取数量的自适应,而且也提高了匹配的正确率。
2.3 定位精度分析对嵩山影像和沙漠影像分别进行光束法平差[24],通过反投影误差σr在和检查点实际精度ΔXY与ΔZ等指标进行精度分析[25],平差结果如表 2所示,表中本文方法指采用了本文整体连接点提取方法,表中本文方法变形A指采用本文方法但不使用基于物方分块的点位筛选技术,表中本文方法变形B指采用本文方法但不使用最小二乘匹配坐标位置精化技术。在嵩山影像数据处理中,控制点个数为2表示对角布设控制,控制点个数为4表示4个角布设控制,控制点个数为5表示4个角和1个中心点布设控制。
| 数 据 |
平差方法 | 控制点 个数 |
检查点 个数 |
连接点 个数 |
平均反投影 误差/像素 |
实际精度/m | |
| 平面 | 高程 | ||||||
| 嵩 山 数 据 |
本文方法 | 2 | 18 | 1 253 100 | 0.36 | 0.114 | 0.162 |
| 4 | 16 | 1 253 100 | 0.36 | 0.103 | 0.142 | ||
| 5 | 15 | 1 253 100 | 0.36 | 0.097 | 0.135 | ||
| 本文方法变形A | 2 | 18 | 1 878 326 | 0.45 | 0.145 | 0.182 | |
| 4 | 16 | 1 878 326 | 0.45 | 0.108 | 0.147 | ||
| 5 | 15 | 1 878 326 | 0.45 | 0.116 | 0.153 | ||
| 本文方法变形B | 2 | 18 | 1 253 100 | 0.48 | 0.158 | 0.187 | |
| 4 | 16 | 1 253 100 | 0.48 | 0.114 | 0.161 | ||
| 5 | 15 | 1 253 100 | 0.48 | 0.126 | 0.167 | ||
| 嵩山 数据 |
本文方法 | - | - | 330 359 | 0.52 | - | - |
| 本文方法变形A | - | - | 351 468 | 0.56 | - | - | |
| 本文方法变形B | - | - | 330 359 | 0.72 | - | - | |
分析表 2可得出如下结论。
(1) 本文连接点提取方法取得了比较满意的效果,嵩山数据平差后计算的平均反投影误差为0.36像素,沙漠数据平差后计算的平均反投影误差为0.52像素。此外,控制点的引入不影响光束法像方平差的平均反投影误差精度,这是因为平均反投影误差反映的是内符合精度。对于嵩山影像数据,当控制点的数量上升为4个时物方检查点的精度已经比较高,分别是平面精度约为1个GSD,高程精度约为1.5个GSD。当控制点的数量增加到5个时,对精度提升不大,这说明4个控制点的控制方案已经有效消除了坐标系之间的绝对误差,所以实际测量时可考虑只在测区的4个角各布设1个控制点,进而减少外业布设控制点的工作量。注:嵩山影像数据覆盖范围内有部分控制点风化损坏、难以辨识,另有部分点被植物等覆盖,经人工甄别,共有18个点可以正常使用。
(2) 对于嵩山影像数据和沙漠影像数据,采用基于物方分块的点位筛选技术时,物方格网大小分别设置为(258 m×258 m)和(326 m×290 m),单个格网内点数量阈值κ分别设置为150和100,则提取到的连接点数量比例分别减少了33%和6%,但像方精度反而分别提高了0.09像素和0.04像素。这是因为物方分块的点位筛选技术不仅可以提升平差的几何强度,还能剔除了一些粗差点,故提高了平差的精度。对于沙漠数据采用基于物方分块的点位筛选技术对于精度提高的效果不甚明显,其原因是沙漠数据纹理匮乏导致提取出来的连接点数量不够多,所以使得物方分块点位筛选技术的作用力不足。
(3) 对于嵩山影像数据和沙漠影像数据,采用SIFT特征点采用最小二乘匹配技术像方精度分别提高了0.12像素和0.18像素。这是因为本文采用SIFT点位信息初始化最小二乘匹配的参数,对提高最小二乘匹配精度非常有效。本文结果同时表明SIFT特征的定位结果虽为亚像素级,但依然还有较大提高空间。
3 结论本文对影像连接点自动提取技术中存在的问题进行了梳理,进而有针对性地构建了一种均衡化高精度的影像连接点提取方法,选取嵩山影像数据和沙漠影像数据进行了试验测试,结果证明本文方法在重复纹理、弱纹理处理、连接点筛选和连接点高精度定位等方面具有优势。未来将对连接点数量、分布情况以及定位精度等因素与光束法平差精度之间更深层次的内在关系进行研究,使得连接点提取更加有的放矢,同时也将采用更多类型的影像数据对方法进行广泛的测试。
| [1] | 于英.无人机动态摄影测量若干关键技术研究[D].郑州:信息工程大学, 2014. YU Ying. Research on Key Technologies of UAV Dynamic Photogrammetry[D]. Zhengzhou:Information Engineering University, 2014. |
| [2] | 薛武.无人机视频地理信息定标与直播处理技术[D].郑州:信息工程大学, 2014. XUE Wu. The Calibration of UAV Video Geo-information and Live Processing Technology[D]. Zhengzhou:Information Engineering University, 2014. |
| [3] | SCHINDLER K, HARTMANN W, HAVLENA M. Recent Developments in Large-scale Tie-point Search[C]//Proceedings of the 55th Photogrammetric Week. Stuttgart:ETH, 2015:7-11. |
| [4] | 杨化超, 张书毕, 张秋昭. 基于SIFT的宽基线立体影像最小二乘匹配方法[J]. 测绘学报, 2010, 39(2): 187–194. YANG Huachao, ZHANG Shubi, ZHANG Qiuzhao. Least Squares Matching Methods for Wide Base-line Stereo Images Based on SIFT Features[J]. Acta Geodaetica et Cartographica Sinica, 2010, 39(2): 187–194. |
| [5] | 杨化超, 张磊, 姚国标, 等. 局部单应约束的高精度图像自动配准方法[J]. 测绘学报, 2012, 41(3): 401–408. YANG Huachao, Zhang Lei, YAO Guobiao, et al. An Automated Image Registration Method with High Accuracy Based on Local Homography Constrain[J]. Acta Geodaetica et Cartographica Sinica, 2012, 41(3): 401–408. |
| [6] | BAY H, TUYTELAARS T, VAN GOOL L. Surf:Speeded up Robust Features[C]//Proceedings of the 9th European Conference on Computer Vision. Berlin Heidelberg:Springer, 2006:404-417. |
| [7] | YU Guoshen, MOREL J M. Asift:An Algorithm for Fully Affine Invariant Comparison[J]. Image Processing On Line, 2011(1): 2105–2132. |
| [8] | ALCANTARILLA P F, BARTOLI A, DAVISON A J. KAZE Features[C]//Proceedings of the 12th European Conference on Computer Vision. Berlin Heidelberg:Springer, 2012:214-227. |
| [9] | 罗楠, 孙权森, 陈强, 等. 结合SURF特征点与DAISY描述符的图像匹配算法[J]. 计算机科学, 2014, 41(11): 286–290, 300. LUO Nan, SUN Quansen, CHEN Qiang, et al. Image Matching Algorithm Combining SURF Feature Point and DAISY Descriptor[J]. Computer Science, 2014, 41(11): 286–290, 300. |
| [10] | WU Changchang. SiftGPU:A GPU Implementation of Scale Invariant Feature Transform (SIFT)[EB/OL]. (2011-06-30).[2015-12-13]. http://cs.unc.edu/~ccwu/siftgpu. |
| [11] | 戴激光, 宋伟东, 贾永红, 等. 一种新的异源高分辨率光学卫星遥感影像自动匹配算法[J]. 测绘学报, 2013, 42(1): 80–86. DAI Jiguang, SONG Weidong, JIA Yonghong, et al. A New Automatically Matching Algorithm for Multi-source High Resolution Optical Satellite Images[J]. Acta Geodaetica et Cartographica Sinica, 2013, 42(1): 80–86. |
| [12] | 闫利, 费亮, 叶志云, 等. 大范围倾斜多视影像连接点自动提取的区域网平差法[J]. 测绘学报, 2016, 45(3): 310–317, 338. YAN Li, FEI Liang, YE Zhiyun, et al. Automatic Tie-points Extraction for Triangulation of Large-scale Oblique Multi-view Images[J]. Acta Geodaetica et Cartographica Sinica, 2016, 45(3): 310–317, 338. DOI:10.11947/j.AGCS.2016.20140673 |
| [13] | BARAZZETTI L, REMONDINO F, SCAIONI M. Extraction of Accurate Tie Points for Automated Pose Estimation of Close-range Blocks[C]//ISPRS Technical Commission Ⅲ Symposium on Photogrammetric Computer Vision and Image Analysis. Saint-Mandé, France:ISPRS, 2010. |
| [14] | 肖雄武, 郭丙轩, 李德仁, 等. 一种具有仿射不变性的倾斜影像快速匹配方法[J]. 测绘学报, 2015, 44(4): 414–421. XIAO Xiongwu, GUO Bingxuan, LI Deren, et al. A Quick and Affine Invariance Matching Method for Oblique Images[J]. Acta Geodaetica et Cartographica Sinica, 2015, 44(4): 414–421. DOI:10.11947/j.AGCS.2015.20140048 |
| [15] | 许志华, 吴立新, 刘军, 等. 顾及影像拓扑的SfM算法改进及其在灾场三维重建中的应用[J]. 武汉大学学报(信息科学版), 2015, 40(5): 599–606. XU Zhihua, WU Lixin, LIU Jun, et al. Modification of SfM Algorithm Referring to Image Topology and Its Application in 3-Dimension Reconstruction of Disaster Area[J]. Geomatics and Information Science of Wuhan University, 2015, 40(5): 599–606. |
| [16] | CHEN Tianze, CHEN Limin. A Union Matching Method for SAR Images Based on SIFT and Edge Strength[J]. IEEE Journal of Selected Topics in Applied Earth Observations and Remote Sensing, 2014, 7(12): 4897–4906. DOI:10.1109/JSTARS.2014.2341173 |
| [17] | ALSTRUP S, THORUP M, GRTZ I L, et al. Union-find with Constant Time Deletions[J]. ACM Transactions on Algorithms (TALG), 2014, 11(1): 6. |
| [18] | EISENBEIβ H. UAV Photogrammetry[D]. Zürich:ETH, 2009. |
| [19] | 崔红霞, 林宗坚, 杨洪, 等. 无人飞艇低空数码影像多视摄影测量[J]. 光电工程, 2008, 35(7): 73–78. CUI Hongxia, LIN Zongjian, YANG Hong, et al. Multiview Photogrammetry Using Low Altitude Digital Images from Unmanned Airship[J]. Opto-Electronic Engineering, 2008, 35(7): 73–78. |
| [20] | 纪松.多视匹配策略与优化方法研究[D].郑州:信息工程大学, 2012. JI Song. Study on the Strategy and Improvement Method of Multi-view Matching Technology[D]. Zhengzhou:Information Engineering University, 2012. |
| [21] | 姚国标, 邓喀中, 张力, 等. 融合互补仿射不变特征的倾斜立体影像高精度自动配准方法[J]. 测绘学报, 2013, 42(6): 869–876. YAO Guobiao, DENG Kazhong, ZHANG Li, et al. An Automated Registration Method with High Accuracy for Oblique Stereo Images Based on Complementary Affine Invariant Features[J]. Acta Geodaetica et Cartographica Sinica, 2013, 42(6): 869–876. |
| [22] | HUO Chunlei, PAN Chunhong, HUO Leigang, et al. Multilevel SIFT Matching for Large-size VHR Image Registration[J]. IEEE Geoscience and Remote Sensing Letters, 2012, 9(2): 171–175. DOI:10.1109/LGRS.2011.2163491 |
| [23] | 张永生. 高分辨率遥感测绘嵩山实验场的设计与实现--兼论航空航天遥感定位精度与可靠性的基地化验证方法[J]. 测绘科学技术学报, 2012, 29(2): 79–82. ZHANG Yongsheng. Design and Implementation of Songshan Test Field for High Resolution Remote Sensing and Mapping[J]. Journal of Geomatics Science and Technology, 2012, 29(2): 79–82. |
| [24] | 袁修孝. POS辅助光束法区域网平差[J]. 测绘学报, 2008, 37(3): 342–348. YUAN Xiuxiao. POS-supported Bundle Block Adjustment[J]. Acta Geodaetica et Cartographica Sinica, 2008, 37(3): 342–348. |
| [25] | 汪韬阳, 张过, 李德仁, 等. 资源三号测绘卫星影像平面和立体区域网平差比较[J]. 测绘学报, 2014, 43(4): 389–395. WANG Taoyang, ZHANG Guo, LI Deren, et al. Comparison between Plane and Stereo Block Adjustment for ZY-3 Satellite Images[J]. Acta Geodaetica et Cartographica Sinica, 2014, 43(4): 389–395. DOI:10.13485/j.cnki.11-2089.2014.0058 |


