2. 地理信息工程国家重点实验室, 陕西 西安 710054;
3. 矿山空间信息技术国家测绘地理信息局重点实验室, 河南 焦作 454003;
4. 91039部队, 北京 102400
2. State Key Laboratory of Geo-information Engineering, Xi'an 710054, China;
3. Key Laboratory of Mine Spatial Information Technologies of National Administration of Surveying, Mapping and Geo-information, Jiaozuo 454003, China;
4. 91039 Troops, Beijing 102400, China
随着航空航天技术、传感器技术、计算机技术的发展,航空摄影测量已经进入了全数字化时代。特别是定位测姿系统(position and orientation system,POS)的引入,大大提高了航空摄影测量的精度和效率[1-3]。但是,由于平台、载荷造价高昂,航空摄影测量的门槛依然很高,仍旧是一项专业性很强的工作,制约了其进一步发展。无人机技术的快速发展与应用,为航空摄影提供了新的平台,无人机摄影测量逐渐成为国内外学者研究的热点[4-11]。无人机的兴起与应用虽然大大降低了航空摄影的门槛,但是现有的数据后处理手段却表现出了一定的不适用。主要是因为目前广泛应用的光束法区域网平差对于数据获取有着严格的要求:相机要事先经过几何定标,获取影像的同时得到影像的POS数据,地面要有一定数量分布合理的控制点。但是目前广泛使用的中小型固定翼无人机却难以满足上述条件,所以常规的光束法区域网平差无法处理无人机数据。
具体来讲,受限于无人机的稳定性,获取影像的姿态通常变化较大、重叠不规整,再考虑成本与风险等因素,无人机通常不搭载测量级的POS设备,仅有导航设备获取的相机曝光点的概略位置姿态信息,所以采用传统的数字摄影测量的理论方法处理无人机数据时常常会出现连接点提取失败、平差精度低甚至失败等问题[7-11]。
近年来在计算机视觉领域兴起的运动恢复结构(structure from motion,SFM)方法能够利用一定数量的具有重叠的影像恢复出相机的位置、姿态和场景的三维结构,该算法对影像采集的要求低,且不依赖于特定的假设条件、自动化程度高、通用性好,有很好的应用前景[12-17]。但是目前国内外学者关于SFM的研究尚停留在在如何提高处理的效率、自动化程度、算法的鲁棒性等方面,对于算法的精度能否满足地图测绘的要求尚无定论,与摄影测量光束法平差精度的对比研究相对较少。因此针对SFM的精度开展研究,重点与传统的POS辅助光束法平差进行了比较分析。
依托中国嵩山遥感定标场的高精度地面控制网,分别利用无人机航摄数据和有人机航摄数据验证无POS数据下SFM的精度能否满足地形图规范要求,并与POS辅助光束法区域网平差的精度进行了比较。在分析研究试验结果的基础上,给出了航摄数据后处理的若干建议。
1 SFM介绍 1.1 基本原理SFM是计算机视觉中多视图三维重建的核心技术,structure代表“3D point cloud of the scene”,motion代表“camera location and orientation”,SFM的直观解释即“get the point cloud from moving cameras”,核心思想为通过特征匹配获取多视图影像之间的同名点,然后最小化特征点的重投影误差以求解射影矩阵、相机内参数和特征点世界坐标的最大似然估计[18-19]。
具体来讲,在计算机视觉中,物方点j坐标为Xj,在影像i上的坐标为xij,二者满足以下关系
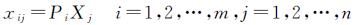 (1)
(1)
式中,P=K[R|t];K为相机的内参数矩阵;R为相机的旋转矩阵;t为相机的平移矩阵。SFM就是通过多视影像自动匹配获取特征点的轨迹信息即xij,然后计算相邻影像之间相对的的旋转R和平移T,在物方点影像重投影误差最小的约束下(式(2))求解P和Xj的最大似然估计
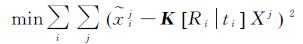 (2)
(2)
如果没有引入地面控制点作为绝对约束,解算出的结果为自定义坐标系下的坐标,还需要通过空间相似变换转换到地理坐标系下。该问题本质上为非线性最小二乘优化问题,通常采用Levenberg-Marquart方法来迭代答解。
Levenberg-Marquart方法本质上是一种启发式的阻尼高斯牛顿法(式(3))
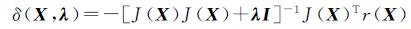 (3)
(3)
在计算机视觉中广泛使用。通过启发式方法在每一步动态调整λ,算法在高斯牛顿法和梯度下降法之间灵活地切换,这样既能保证算法的收敛,又具有较快的收敛速度[20-21]。
如果误差减少,则令λ←0.1λ,如果误差增大,则令λ←10λ;当
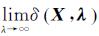
按照初始位置、姿态的计算方式,SFM可以分为增量式SFM(incremental SFM,ISFM)、全局SFM(global SFM,GSFM)。增量式SFM在特征匹配的基础上精心选择初始像对得到两幅影像的初始化模型,然后迭代式增加一幅或者多幅影像,对新增加的公共特征点进行三角化,并重新平差解算模型坐标和相机参数,直到所有影像添加完毕[7, 22]。全局SFM则不依赖于迭代优化重建框架,只需一次性优化即可完成整个三维重建过程,即利用约束条件一次性求解影像的旋转R和平移T[7]。但由于数据缺失和外点的存在,大多数情况下全局SFM不存在闭合解,且对错误的特征点匹配非常敏感,甚至一个错误点就会导致失败[23-25]。而在实际应用中外点几乎是难以避免的,因此全局SFM具有一定的局限性。本文主要研究增量式SFM,下面对其进行重点介绍。
1.2 增量式SFM主要步骤目前,增量式SFM在三维重建中取得了比较成功的应用,其主要步骤如下。
1.2.1 特征点检测利用特征点检测算法在影像上提取特征点,然后利用特征描述符号对特征进行描述,以用于后续的匹配。通常要求特征的描述信息具有旋转、缩放、平移不变性,以应对可能出现的影像视角、光照变化对匹配造成的干扰,增强匹配的稳健性。特征检测算法以SIFT及其改进算法最具有代表性[26]。
1.2.2 特征匹配及轨迹生成特征匹配即将不同影像上提取的特征进行匹配,以寻找物方点在不同影像上的对应像点。值得注意的是,增量式SFM最初应用于近景摄影重建时,由于影像的数量较少、分辨率较低,大多数算法通常采用穷尽的搜索方法来进行匹配,即所有影像两两分别匹配[26-29]。当影像数量较多、分辨率较高时,这种方法会带来巨大的时间开销。文献[7, 14]在处理无人机遥感数据时,利用自驾仪记录下的影像位置姿态数据有效降低了匹配的计算量,提高了处理的速度。匹配结束后,利用RANSAC算法对误匹配进行剔除,得到可靠的匹配点。
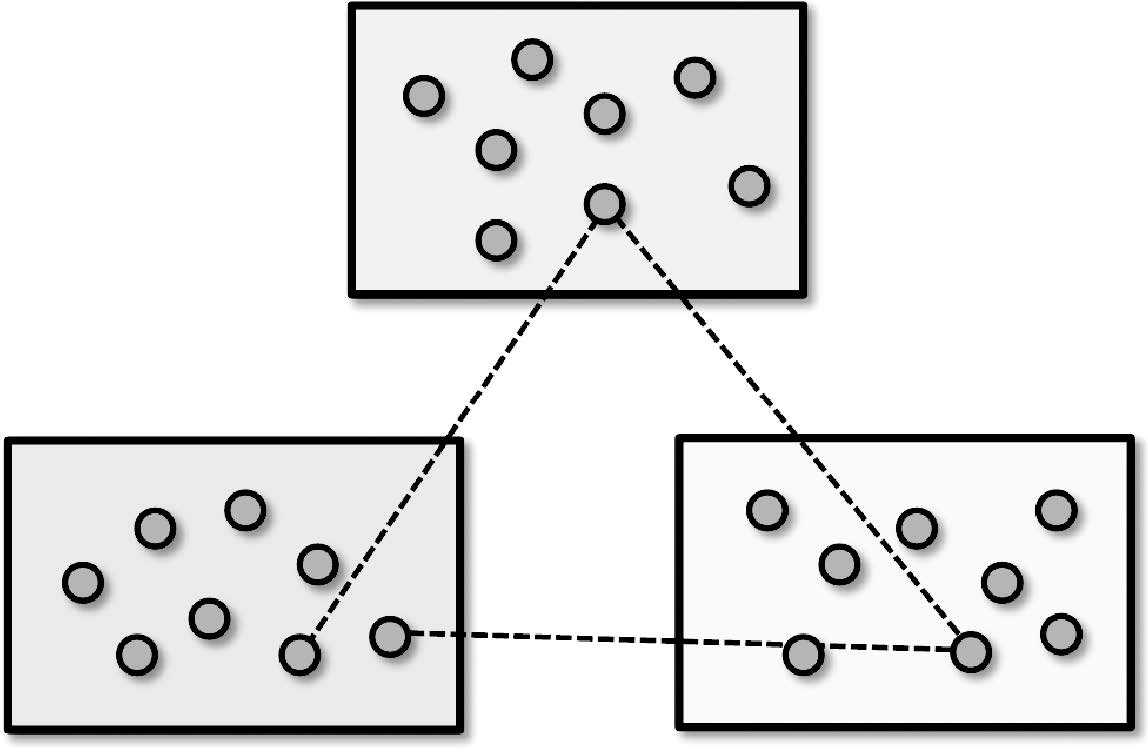
影像两两匹配结束后,可以利用所有相关影像间的匹配关系来提取多视匹配点,即得到特征点的“轨迹”,如图 1。如果将影像集中所有影像的所有特征点都视为一个单体,任意一对匹配点对应的单体构成连通关系,具有联通性的单体构成的集合即为一个多视匹配点,则多视匹配点的提取问题可以转化为动态连通性问题[30]。
通过特征匹配不仅得到影像之间的同名特征,也获取了影像之间的空间相对关系,这对于后面的迭代求解具有重要意义。
|
| 图 1 特征点轨迹 Fig. 1 Track of feature points |
1.2.3 迭代求解
影像位置姿态的求解过程是迭代式增加的,主要过程如下。
(1) 选择同名点最多的像对作为初始像对,根据同名点信息计算影像之间的旋转R和平移T,然后同名光线交会(三角化)得到物方空间初始模型。
(2) 利用影像的辅助数据(EXIF、自驾仪数据等),特征匹配结果选择新的影像添加到现有模型中,根据初始模型物方坐标和特征匹配结果计算新添加影像的旋转R和平移T,同名光线交会得到新的模型点,利用所有的模型点重新优化所有影像的位置和姿态。
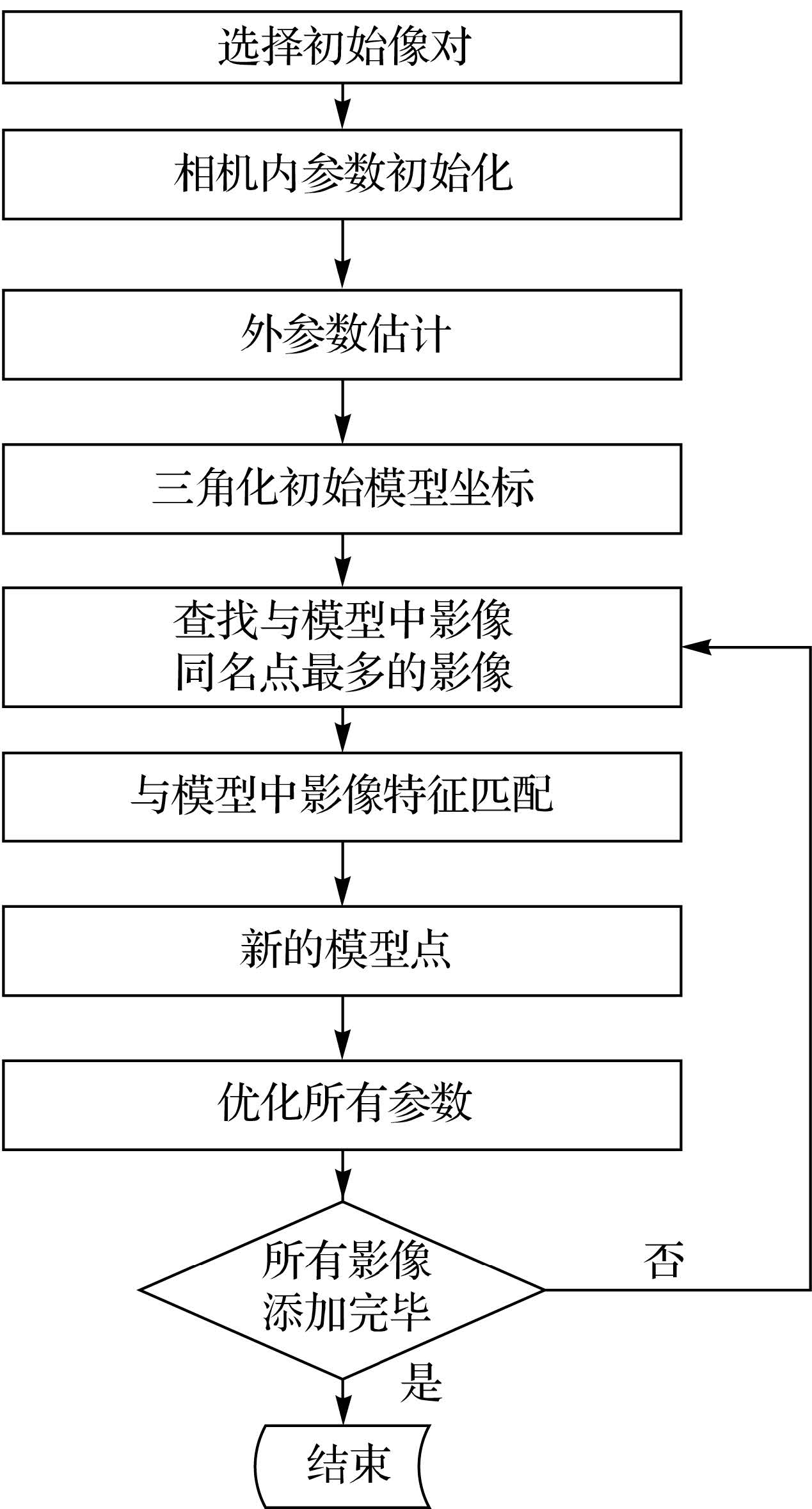
(3) 通过不断增加新的影像并迭代优化模型点坐标和相机内外参数,直到所有影像添加完毕,所有影像再统一进行平差优化,得到所有影像内外参数和模型点优化后的三维坐标,算法的流程如图 2所示。
|
| 图 2 SFM流程 Fig. 2 Workflow of SFM |
1.3 增量式SFM与POS辅助光束法平差的区别
在摄影测量中空中三角测量按照平差单元可以分为航带法、独立模型法和光束法。其中,光束法区域网平差是以光线作为平差单元,理论最为严密[31],特别是随着POS在航空摄影中的使用,POS辅助区域网平差技术取得了较快的发展。多位学者围绕POS辅助光束法平差开展了一系列的研究,主要包括摄影测量与非摄影测量观测值的联合平差、可靠性研究、系统误差的补偿、粗差的检测与定位等[2-3, 32-35, 38],研究成果大大提升了摄影测量的作业效率和精度。
综合比较增量式SFM与光束法区域网平差,二者的相同之处主要有:
(1) 都需要通过一定数量、分布合理的连接点(特征点)将离散的影像“连接”起来,连接点(特征点)的提取与匹配是必不可少的环节。
(2) 基本的成像模型是相同的,在计算机视觉中称为“针孔成像模型”,在摄影测量中称为“共线条件方程”,二者的本质是相同的。
(3) 在平差解算的过程中都考虑到了相机镜头畸变的影响,即可以同时求解相机的内方位元素(内参数)和畸变参数,计算机视觉中称之为“自标定”,摄影测量中称为“自检校”。
然而,增量式SFM与POS辅助光束法区域网平差在以下方面存在明显的区别:
(1) 增量式SFM对于数据输入的要求较低,即便只有影像、没有任何其他辅助信息的情况下,仍然可以在射影空间实现场景的三维重建。
(2) 由于特征提取和匹配、平差解算的过程均不需要人工干预,所以增量式SFM自动化程度较高。
(3) 增量式SFM中特征提取与匹配的过程不依赖于POS数据,对于纹理匮乏、重复区域仍然具有很强的适应性,这在处理无人机数据中体现得尤为明显。
(4) POS辅助光束法平差中,对于POS数据的依赖主要体现在两个方面,一是在特征点的提取匹配过程中,利用POS数据预测同名点的位置;二是在平差解算中,将POS数据作为影像外方位元素的初始值,使得非线性最小二乘估计快速收敛到全局最优解。而增量式SFM通过逐一增加新的影像并不断更新的方式逐渐得到未知数的近似值,而后统一再进行LM估计,这也是二者最本质的区别。
2 增量式SFM与POS辅助光束法平差精度对比试验为了进行增量式SFM与光束法区域网平差的对比试验,在中国嵩山遥感定标场进行了航摄飞行。分别利用有人航测飞机“运5”和无人直升飞机搭载飞思面阵CCD相机和Applanix POS设备获得航空影像和POS数据,并分别用增量式SFM和光束法区域网平差两种方法进行了处理。
需要说明的是,为了增加对比试验的可信性和说服力,两组数据的影像均带有高精度的POS数据以便于对比分析,但是增量式SFM计算过程中并未利用影像的POS数据。在精度评价时采用完全相同数量和分布的地面控制点和检查点。
2.1 嵩山遥感定标场简介嵩山遥感定标场是由信息工程大学、武汉大学、中国资源卫星应用中心等单位共同建设的国家级航空航天遥感定标场。定标场布设有地面埋石点、雷达角反射器、辐射靶标、分辨率靶标、气象观测设施等,可对航空航天可见光、多光谱、合成孔径雷达等多种类型的传感器进行几何定标、分辨率定标、辐射定标,目前已成功应用在ADS40、DMC、UCD、“资源三号”、“天绘一号”等传感器的定标中。其中,航空几何定标场占地约64 km2,分级布设了214个永久性高精度控制点,用于各种机载相机或传感器的定标,如图 3所示[36]。所采用的试验数据就是在航空几何定标场航摄数据,测区地形以丘陵为主。

|
| 图 3 嵩山航空几何定标场 Fig. 3 Songshan geometry calibration field |
2.2 无人直升机航摄数据对比试验
2015年10月,信息工程大学利用无人直升机在嵩山航空几何定标场进行了飞行试验,航摄基本情况如表 1所示。
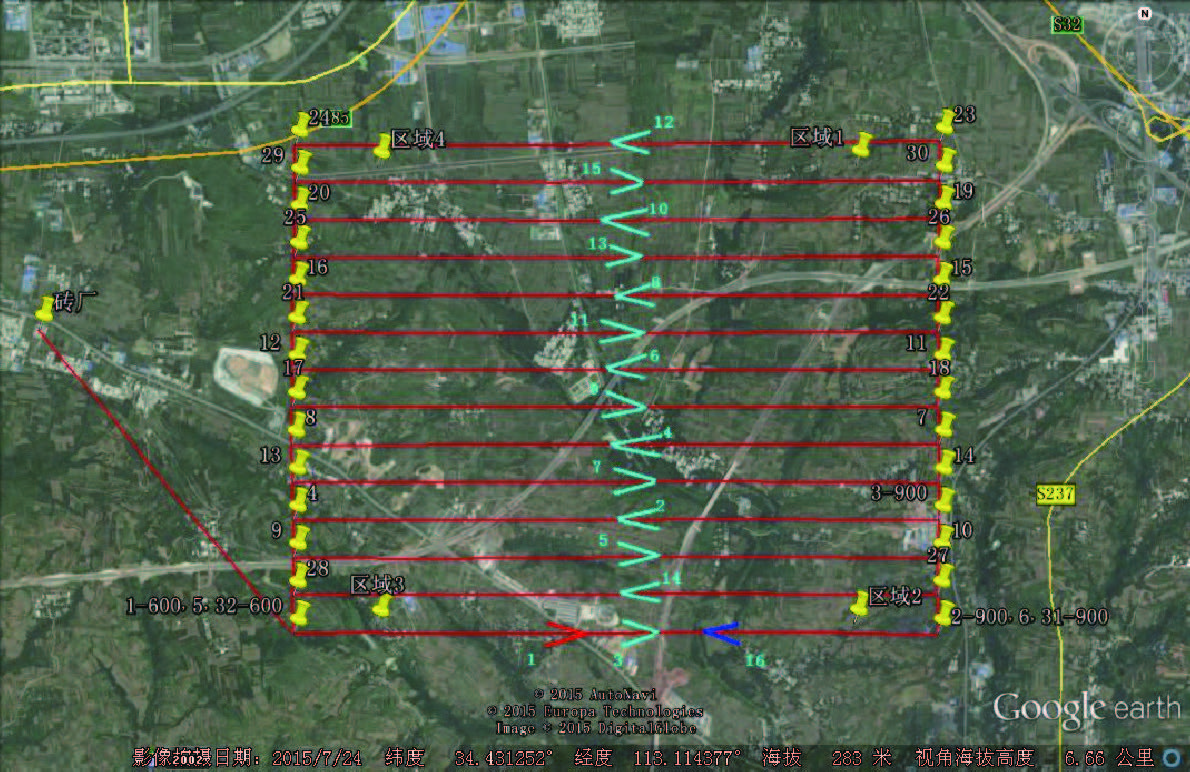
飞行区域的面积约25 km2,东西方向共飞行16条航线,航线分布示意图如图 4所示,选取了9个地面控制点和12个检查点,分布情况如图 5所示(Δ表示平高控制点,о代表检查点)。
| 飞行平台 | 无人直升机 |
| 相机 | Phase One AMC180 |
| 影像大小 | 10 328×7760 |
| POS设备 | Applanix AV310 |
| 航摄时间 | 2015年10月 |
| 相对航高 | 500 m |
| 地面分辨率 | 5 cm |
|
| 图 4 航线分布示意 Fig. 4 Sketch map of flight route |

|
| 图 5 地面控制点及检查点分布 Fig. 5 Distribution of GCP/CP |
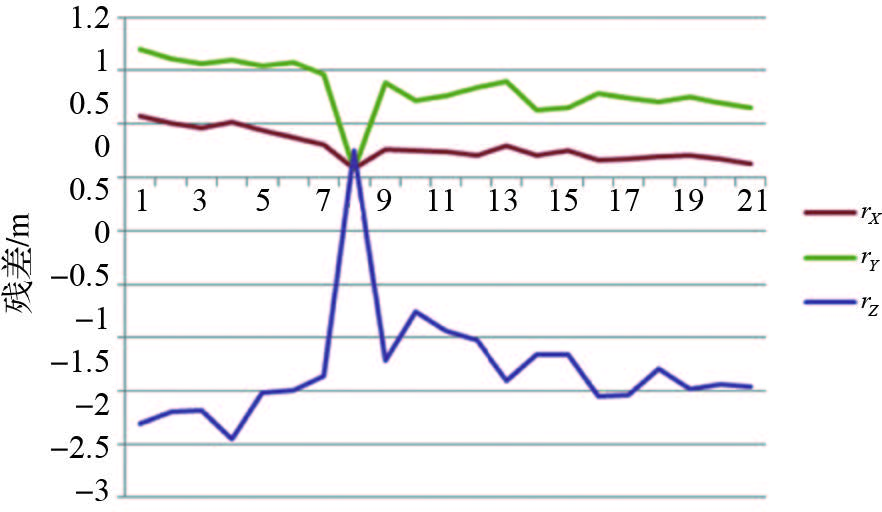
首先利用机载POS数据进行了直接地理定位试验,将21个地面点作为检查点,检查点残差中误差如表 2所示,各检查点的残差分布如图 6。
|
| 图 6 检查点物方残差 Fig. 6 Residual error of check points in object space |
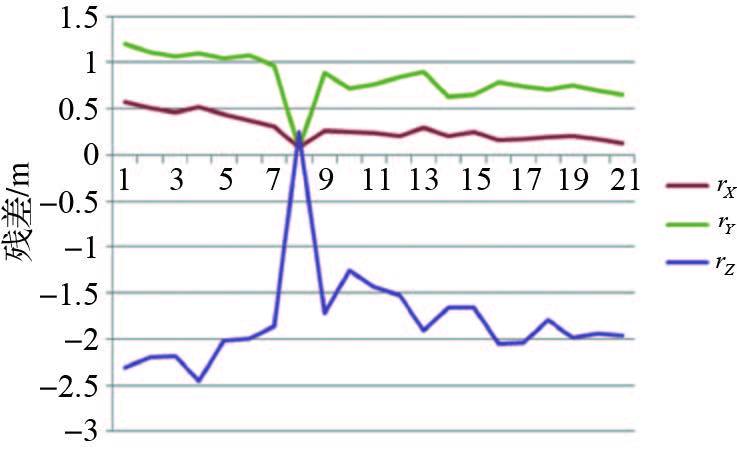
从表 2和图 6可以看出,无地面控制点的情况下,直接地理定位精度较差,检查点残差具有一定的系统性。分析可能的原因主要有相机镜头畸变、POS安装的系统误差等。在地面控制点不参与平差的情况下,通过提取影像连接点,进行了自由网光束法平差,对精度进行了统计,检查点中误差如表 3所示,残差如图 7所示。
|
| 图 7 检查点物方残差 Fig. 7 Residual error of check points in object space |
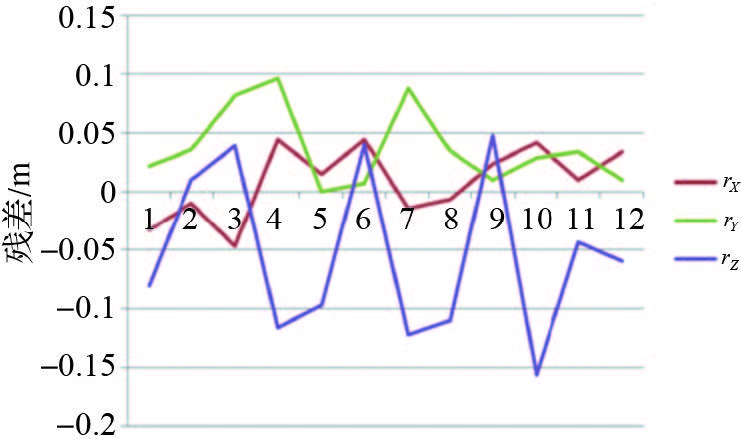
从自由网平差的结果来看,检查点的中误差明显减小,主要的原因是通过光束法平差抵消了部分偶然误差的影响。然后,利用图 5中的9个地面控制点,在POS数据辅助下进行了自检校光束法区域网平差,相机附加参数模型采用Brown模型,平差的结果如表 4,各检查点的残差如图 8。
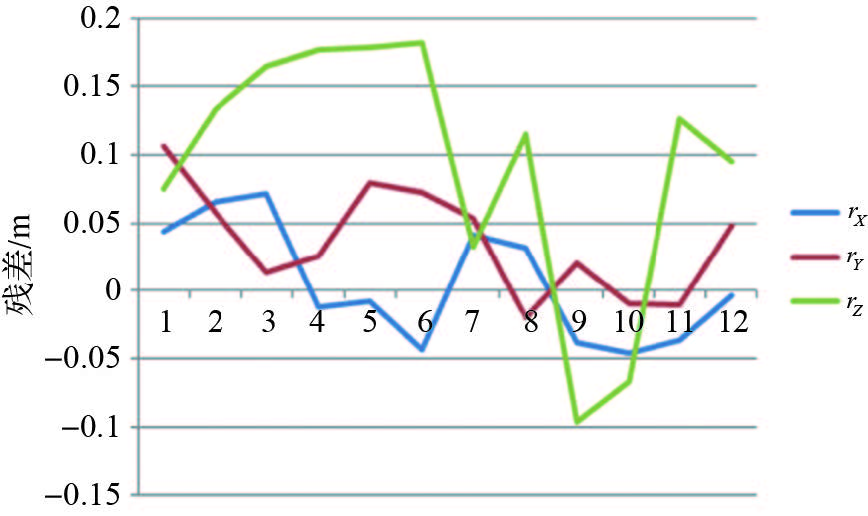
最后,采用增量式SFM方法,通过特征提取与匹配、迭代求解,采用9个控制点进行平差解算,同时对相机进行了自标定。检查点的中误差如表 5所示,残差分布如图 9所示。
|
| 图 8 检查点物方残差 Fig. 8 Residual error of check points in object space |
|
| 图 9 检查点物方残差 Fig. 9 Residual error of check points in object space |
从上述结果可以看出:增量式SFM的精度远优于POS AV310直接地理定位和自由网光束法平差的精度;与POS辅助光束法平差的精度相比:平面精度均为1个GSD左右,高程精度稍逊色一些,光束法平差约为1.7个GSD,增量式SFM约为2.5个GSD。试验的结果是令人欣喜的,在不借助任何POS信息的情况下,取得如此的精度实属不易。既然都需要利用少量的地面控制点,增量式SFM不依赖于POS数据的优势则意义重大,因为测量级的POS设备价格昂贵,而且体积、重量较大,对无人机平台要求很高,常用的中小型无人机不能满足其要求。而采用增量式SFM方法可以摆脱对于POS的依赖,降低了对遥感平台的要求,减少了作业的成本。
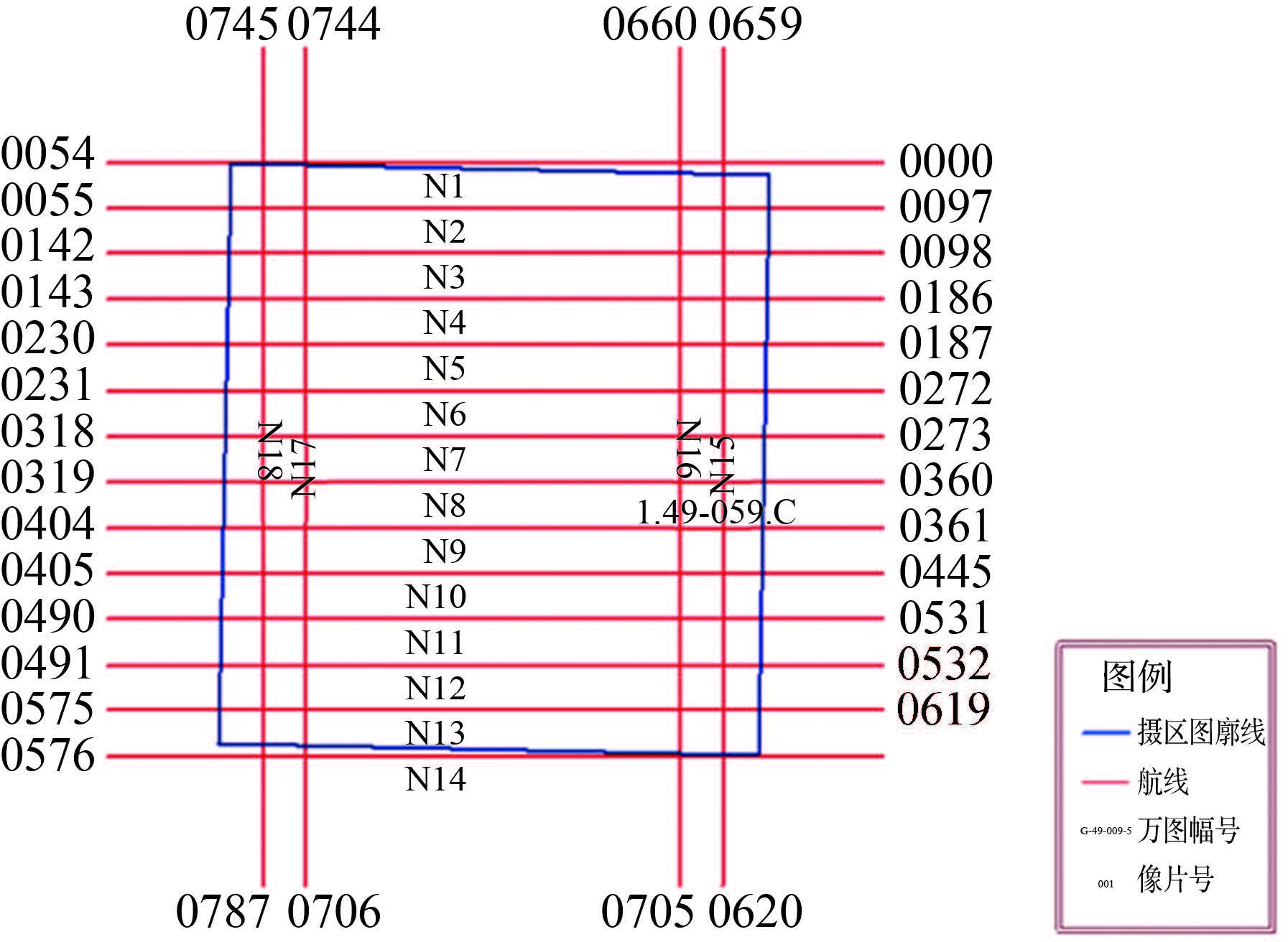
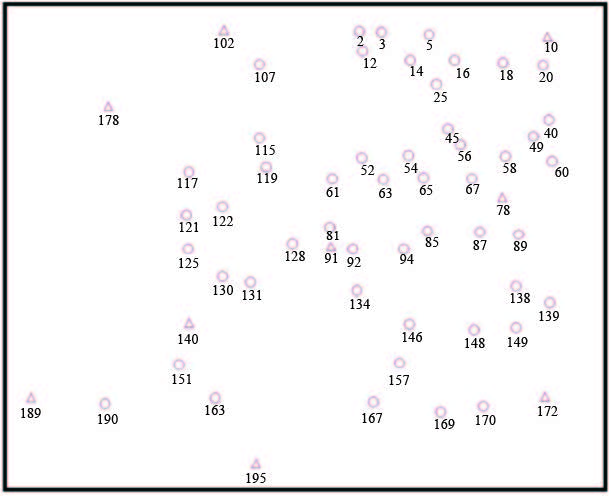
2.3 有人驾驶飞机航摄数据对比试验为了更全面地对两种方法进行对比试验,采用有人驾驶航测飞机(运5)航摄数据对两种方法进行测试。采用的影像为2013年在嵩山遥感定标场飞行获得,飞行区域的面积约64 km2,东西方向共飞行14条航线,南北方向飞行了4条构架航线,航摄基本情况如表 6所示,航线分布示意如图 10所示。选取了9个地面控制点和50个检查点,分布情况如图 11所示(Δ表示平高控制点,о代表检查点)。
| 飞行平台 | 运5 |
| 相机 | Phase One AMC180 |
| 影像大小 | 10 328×7760 |
| POS设备 | Applanix AV510 |
| 航摄时间 | 2013年5月 |
| 相对航高 | 1000 m |
| 地面分辨率 | 10 cm |
|
| 图 10 航线分布示意图 Fig. 10 Sketch map of flight route |
|
| 图 11 地面控制点及检查点分布 Fig. 11 Distribution of GCP/CP |
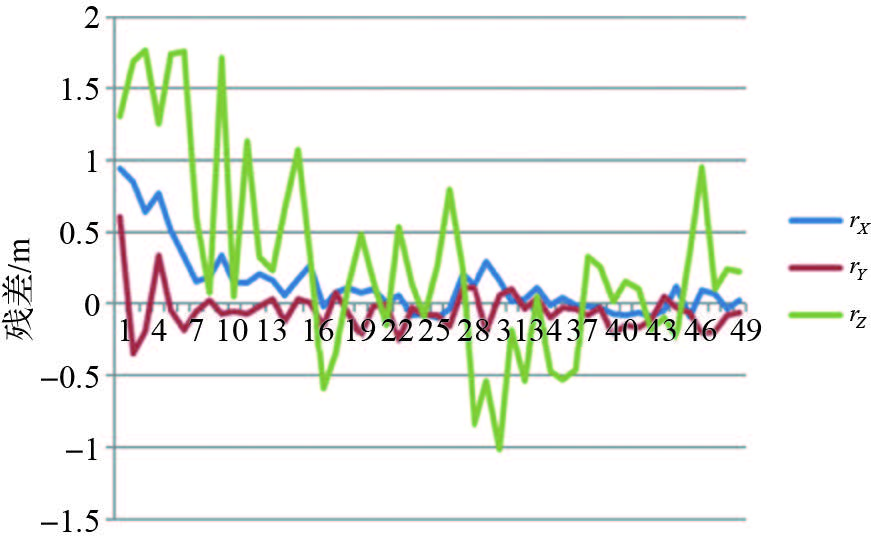
与无人机数据处理的流程类似,首先利用POS数据进行直接地理定位,50个检查点的中误差如表 7所示,残差如图 12所示。
|
| 图 12 检查点物方残差 Fig. 12 Residual error of check points in object space |
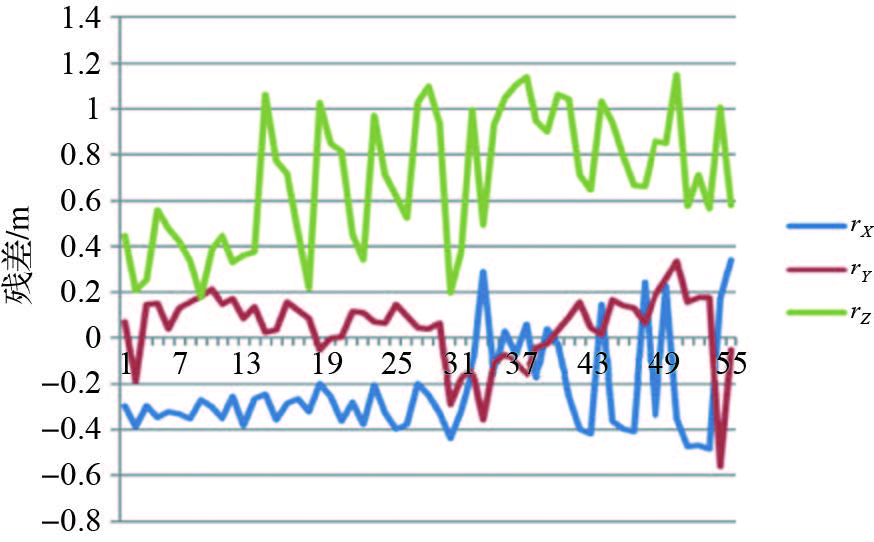
利用POS数据,恢复出影像航摄时的相对位置关系,提取影像连接点,进行自由网平差,测区内50个检查点物方残差中误差如表 8所示,残差如图 13所示。
|
| 图 13 检查点物方残差 Fig. 13 Residual error of check points in object space |
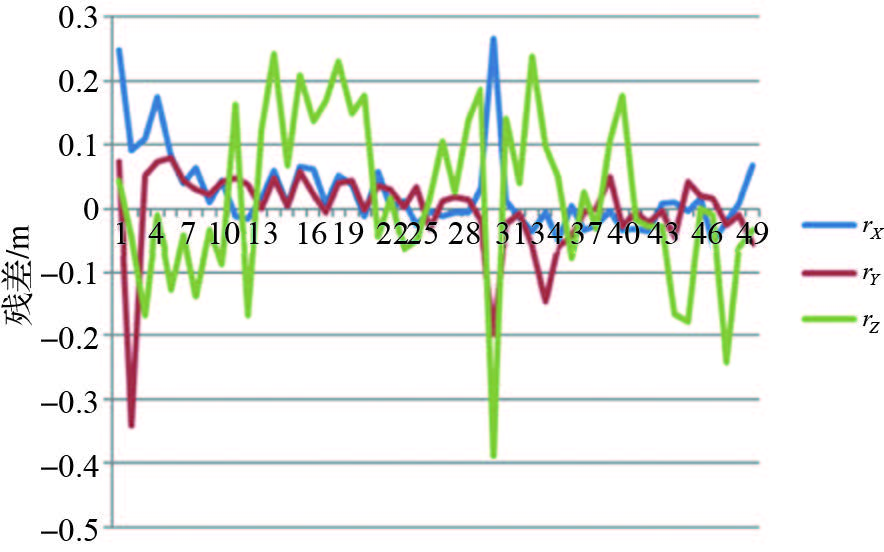
同样,在POS数据辅助下进行了自检校光束法区域网平差,附加参数模型为Brown模型,平差的结果如表 9,各检查点的残差如图 14所示。
|
| 图 14 检查点物方残差 Fig. 14 Residual error of check points in object space |
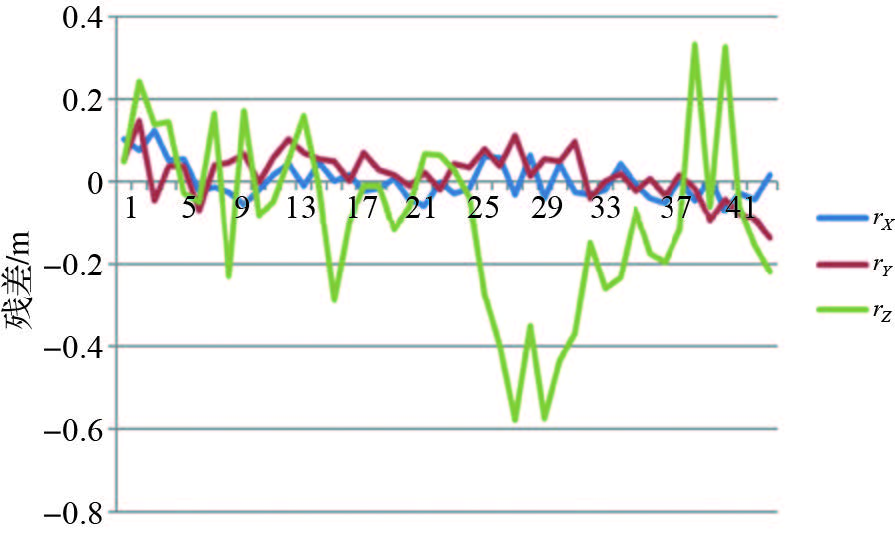
最后,采用增量式SFM方法,通过特征提取与匹配、迭代求解,仅利用影像本身恢复出了所有影像的位置和姿态,同时对相机进行了自标定。检查点的中误差如表 10所示,残差如图 15所示。
|
| 图 15 检查点物方残差 Fig. 15 Residual error of check points in object space |
对比分析增量式SFM与摄影测量方法的处理结果可以发现,自检校光束法平差的整体精度最高,增量式SFM的平面精度与之相当,高程精度略差。也就是说采用相同数量和分布的地面控制点的情况下,增量式SFM能够取得与POS辅助自检校光束法平差相当的精度。这具有十分重要的意义:当没有POS数据时,利用增量式SFM仍然可以取得比较理想的精度。
2.4 总 结在对增量式SFM与摄影测量光束法平差进行理论分析与比较的基础上,采用嵩山定标场数据进行了对比试验,结果表明增量式SFM可以取得与光束法平差相当的精度。参考《数字航空摄影测量空中三角测量规范》关于1∶500、1∶1000地形图制图的要求(表 11)[37],将试验结果重新进行了对比,“是”表示能够满足成图要求,“否”表示不能满足成图要求,如表 12所示。
| m | |||||
| 成图比例尺 | 平面位置中误差 | 高程中误差 | |||
| 平地 | 丘陵地 | 平地 | 丘陵地 | ||
| 1∶500 | 0.175 | 0.175 | 0.175 | 0.28 | |
| 1∶1000 | 0.35 | 0.35 | 0.28 | 0.35 | |
| 成图比例尺 | 直接地理定位 | 自由网平差 | 自检校平差 | ISFM |
| 1∶500 | 否 | 否 | 是 | 是 |
| 1∶1000 | 否 | 否 | 是 | 是 |
由表 12可以看出,在搭载了高精度的POS设备时,直接地理定位仍然难以满足成图规范要求,必须引入少量地面控制点通过自检校光束法平差提高空三的精度以满足规范。而如果采用增量式SFM,即便没有POS数据的辅助,利用与自检校光束法平差相同数量和分布的地面控制点仍然可以满足成图规范的要求。这在实际生产作业中就具有明显的优势,不依赖于POS数据则可以大大降低硬件购置的成本、减轻传感器系统的重量,使得数据获取系统更廉价、更轻便。
3 结 论本文针对摄影测量中的POS辅助光束法平差和计算机视觉中的增量式SFM进行了对比研究,主要对其精度进行了对比分析。利用无人直升机和有人驾驶飞机航摄数据分别进行了试验,结果表明增量式SFM的精度与POS辅助光束法平差基本相当,均可以满足1∶500、1∶1000成图的要求。
针对两种方法的特点,对航空摄影测量数据后处理提出几点建议:在应急条件下,可以利用机载POS数据进行直接地理定位或者自由网空中三角测量,提供快速地理空间信息服务;在执行常规作业任务时,则无需使用价格昂贵的POS设备,在少量地面控制点的辅助下,采用增量式SFM方法仍然能够满足大比例尺成图的精度要求,同时降低作业成本。
| [1] | 张永生, 邹晓亮, 刘军, 等. 航空遥感数字传感器信息处理系统[M]. 北京: 星球地图出版社, 2007. ZHANG Yongsheng, ZOU Xiaoliang, LIU Jun, et al. The Aerial Digital Sensor Information Processing System[M]. Beijing: Planet Map Press, 2007. |
| [2] | 刘军. GPS/IMU辅助机载线阵CCD影像定位技术研究[D]. 郑州:信息工程大学, 2007. LIU Jun. Research on GPS/IMU Aided Airborne Linear Array CCD Image Positioning Technology[D]. Zhengzhou:Information Engineering University, 2007. |
| [3] | 王冬红. 机载数字传感器几何标定的模型与算法研究[D]. 郑州:信息工程大学, 2011. WANG Donghong. A Study on the Mathematic Model and Algorithm of the Geometric Calibration of Airborne Digital Sensor[D]. Zhengzhou:Information Engineering University, 2011. http://cdmd.cnki.com.cn/Article/CDMD-90008-1012325172.htm |
| [4] | 张永生. 现场直播式地理空间信息服务的构思与体系[J]. 测绘学报, 2011, 40(1): 1–4. ZHANG Yongsheng. The Conception and Architecture of Live-service for Geospatial Information[J]. Acta Geodaetica et Cartographica Sinica, 2011, 40(1): 1–4. |
| [5] | 于英. 无人机动态摄影测量若干关键技术研究[D]. 郑州:信息工程大学, 2014. YU Ying.Research on Key Technologies of UAV Dynamic Photogrammetry[D]. Zhengzhou:Information Engineering University, 2014. |
| [6] | 薛武. 无人机视频地理信息定标与直播处理方法[D]. 郑州:信息工程大学, 2014. XUE Wu. The Calibration of UAV Video Geo-Information and Live Processing Technology[D]. Zhengzhou:Information Engineering University, 2014. |
| [7] | 郭复胜. 无人机图像的三维重建方法研究[D]. 北京:中国科学院大学, 2013. GUO Fusheng. 3D Reconstruciotn from UAV Images[D]. Beijing:University of Chinese Academy of Sciences, 2013. http://d.wanfangdata.com.cn/Thesis/Y2286626 |
| [8] | REMONDINO F, BARAZZETTI L, NEX F, et al. UAV Photogrammetry for Mapping and 3d Modeling-current Status and Future Perspectives[J]. International Archives of the Photogrammetry, Remote Sensing and Spatial Information Sciences, 2011, XXXVIII-1(C22): 25–31. |
| [9] | NEX F, REMONDINO F. UAV for 3D Mapping Applications:A Review[J]. Applied Geomatics, 2014, 6(1): 1–15. DOI:10.1007/s12518-013-0120-x |
| [10] | REHAK M, SKALOUD J. Fixed-wing Micro Aerial Vehicle for Accurate Corridor Mapping[J]. ISPRS Annals of the Photogrammetry, Remote Sensing and Spatial Information Sciences, 2015, II-1/W1: 23–31. DOI:10.5194/isprsannals-II-1-W1-23-2015 |
| [11] | EISENBEIβ H.UAV Photogrammetry[D]. Zurich, Switzerland:ETH, 2009. |
| [12] | BARAZZETTI L, REMONDINO F, SCAIONI M. Combined Use of Photogrammetric and Computer Vision Techniques for Fully Automated and Accurate 3D Modeling of Terrestrial Objects[C]//Proceedings of the SPIE 7447, Videometrics, Range Imaging, and Applications X. San Diego, CA:SPIE, 2009:74470M-74470M-12. |
| [13] | HELLER J, HAVLENA M, JANCOSEK M, et al. 3D Reconstruction from Photographs by CMP SFM Web Service[C]//Proceedings of the 201514th IAPR International Conference on Machine Vision Applications. Tokyo:IEEE, 2015:30-34. |
| [14] | 许志华, 吴立新, 刘军, 等. 顾及影像拓扑的SfM算法改进及其在灾场三维重建中的应用[J]. 武汉大学学报(信息科学版), 2015, 40(5): 599–606. XU Zhihua, WU Lixin, LIU Jun, et al. Modification of SFM Algorithm Referring to Image Topology and Its Application in 3-dimension Reconstruction of Disaster Area[J]. Geomatics and Information Science of Wuhan University, 2015, 40(5): 599–606. |
| [15] | WU Changchang, AGARWAL S, CURLESS B, et al. Multicore Bundle Adjustment[C]//Proceedings of the 2011 IEEE Conference on Computer Vision and Pattern Recognition. Providence, RI:IEEE, 2011:3057-3064. |
| [16] | BARAZZETTI L, REMONDINO F, SCAIONI M, et al. Fully Automatic UAV Image-based Sensor Orientation[C]//Proceedings of the 2010 Canadian Geomatics Conference and Symposium of Commission I. 2010. |
| [17] | 沈永林, 刘军, 吴立新, 等. 基于无人机影像和飞控数据的灾场重建方法研究[J]. 地理与地理信息科学, 2011, 27(6): 13–17. SHEN Yonglin, LIU Jun, WU Lixin, et al. Reconstruction of Disaster Scene from UAV Images and Flight-control Data[J]. Geography and Geo-Information Science, 2011, 27(6): 13–17. |
| [18] | HARTLEY R, ZISSERMAN A. 计算机视觉中的多视图几何[M]. 韦穗, 杨尚骏, 章权兵, 等, 译. 合肥:安徽大学出版社, 2002. HARTLEY R, ZISSERMAN A. Multiple View Geometry in Computer Vision[M]. WEI Sui, YANG Shangjun, ZHANG Quanbing, et al, trans. Hefei:Anhui University Press, 2002. |
| [19] | 斯蒂格, 尤里奇, 威德曼. 机器视觉算法与应用[M]. 杨少荣, 吴迪靖, 段德山, 译. 北京:清华大学出版社, 2008. STEGER C, ULRICH M, WIEDEMANN C. Machine Vision Algorithms and Applications[M]. YANG Shaorong, WU Dijing, DUAN Deshan, trans. Beijing:Tsinghua University Press, 2008. |
| [20] | TRIGGS B, MCLAUCHLAN P F,HARTLEY R I,et al. Bundle Adjustment:A Modern Synthesis[M]//TRIGGS B, ZISSERMAN A, SZELISKI R. Vision Algorithms:Theory and Practice. Berlin:Springer, 2000:298-372. |
| [21] | MADSEN K, NIELSEN H B, TINGLEFF O. Methods for Non-linear Least Squares Problems[M]. 2nd ed. Lyngby:Informatics and Mathematical Modelling, Technical University of Denmark, 2004. http://www.oalib.com/references/7919388 |
| [22] | SNAVELY N, SEITZ S M, SZELISKI R. Photo Tourism:Exploring Photo Collections in 3D[J]. ACM Transactions on Graphics (TOG), 2006, 25(3): 835–846. DOI:10.1145/1141911 |
| [23] | STURM P, TRIGGS B. A Factorization Based Algorithm for Multi-Image Projective Structure and Motion[M]//BUXTON B, CIPOLLA R. Computer Vision-ECCV'96. Berlin Heidelberg:Springer, 1996:709-720. |
| [24] | TOMASI C, KANADE T. Shape and Motion from Image Streams under Orthography:A Factorization Method[J]. International Journal of Computer Vision, 1992, 9(2): 137–154. DOI:10.1007/BF00129684 |
| [25] | KAHL F, HARTLEY R. Multiple-view Geometry Under the L∞-norm[J]. IEEE Transactions on Pattern Analysis and Machine Intelligence, 2008, 30(9): 1603–1617. DOI:10.1109/TPAMI.2007.70824 |
| [26] | LOWE D G.Object Recognition from Local Scale-invariant Features[C]//Proceedings of the Seventh IEEE International Conference on Computer Vision. Kerkyra:IEEE, 1999, 2:1150-1157. |
| [27] | JAVERNICK L, BRASINGTON J, CARUSO B. Modeling the Topography of Shallow Braided Rivers Using Structure-from-motion Photogrammetry[J]. Geomorphology, 2014, 213: 166–182. DOI:10.1016/j.geomorph.2014.01.006 |
| [28] | |
| [29] | SNAVELY N. Bundler:Structure from Motion (SFM) for Unordered Image Collections[EB/OL].[2013-07-12]. phototour.cs.washington.edu/bundler/. |
| [30] | 卢俊. 基于无序多视影像的三维重建关键技术研究[D]. 郑州:信息工程大学, 2015. LU Jun. Study on 3D Reconstruction Key Technology of Unordered Multi-view Images[D]. Zhengzhou:Information Engineering University, 2015. http://cdmd.cnki.com.cn/Article/CDMD-90005-1016058447.htm |
| [31] | 江延川. 解析摄影测量学[M]. 郑州: 郑州测绘学院, 1991. JIANG Yanchuan. Analytical Photogrammetry[M]. Zhengzhou: Zhengzhou Institute of Surveying and Mapping, 1991. |
| [32] | GALLER B A, FISHER M J. An Improved Equivalence Algorithm[J]. Communications of the ACM, 1964, 7(5): 301–303. DOI:10.1145/364099.364331 |
| [33] | 袁修孝. POS辅助光束法区域网平差[J]. 测绘学报, 2008, 37(3): 342–348. YUAN Xiuxiao. POS-supported Bundle Block Adjustment[J]. Acta Geodaetica et Cartographica Sinica, 2008, 37(3): 342–348. |
| [34] | 许妙忠, 刘丽, 涂辛茹. 基于ORIMA的ADS40几何精度评估[J]. 测绘科学技术学报, 2010, 27(5): 341–344. XU Miaozhong, LIU Li, TU Xinru. Geometric Accuracy Assessment of ADS40 Imagery Using ORIMA[J]. Journal of Geomatics Science and Technology, 2010, 27(5): 341–344. |
| [35] | 李德仁, 袁修孝. 误差处理与可靠性理论[M]. 2版. 武汉: 武汉大学出版社, 2012: 55-56. LI Deren, YUAN Xiuxiao. Error Processing and Reliability Theory[M]. 2nd ed.. Wuhan: Wuhan University Press, 2012: 55-56. |
| [36] | 张永生. 高分辨率遥感测绘嵩山实验场的设计与实现——兼论航空航天遥感定位精度与可靠性的基地化验证方法[J]. 测绘科学技术学报, 2012, 29(2): 79–82. ZHANG Yongsheng. Design and Implementation of Songshan Test Field for High Resolution Remote Sensing and Mapping[J]. Journal of Geomatics Science and Technology, 2012, 29(2): 79–82. |
| [37] | 中华人民共和国国家质量监督检验检疫总局, 中国国家标准化管理委员会. GB/T 23236-2009数字航空摄影测量空中三角测量规范[S]. 北京:中国标准出版社, 2009:2. General Administration of Quality Supervision, Inspection and Quarantine of the People's Republic of China. GB/T 23236-2009 Specifications for Aerotriangulation of Digital Aerophotogrammetry[S]. Beijing:China Standard Press, 2009:2. http://www.doc88.com/p-192105654401.html |
| [38] | 王涛. 线阵CCD传感器实验场几何定标的理论与方法研究[D]. 郑州:信息工程大学, 2012. WANG Tao. Study on Theories and Methods of Linear CCD Sensor Geometric Calibration Based on Field[D].Zhengzhou:Information Engineering University, 2012. |


