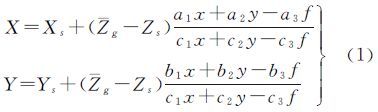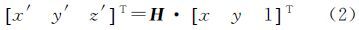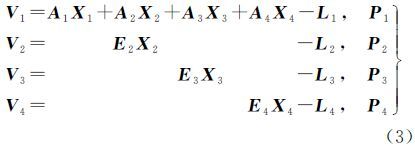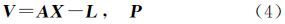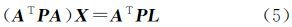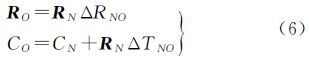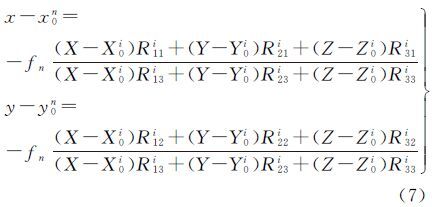随着机载倾斜多相机系统的发展,倾斜影像已经成为地图、城市三维重建等应用的主要数据源,其中涉及的公司包括Blomoblique、IGI、Leica、Midas、Pictometry、Vexcel/Microsoft、VisionMap等。通过在同一飞行平台上搭载多台传感器,倾斜摄影技术可以同时从多个角度采集影像,克服了正射影像只能从垂直角度拍摄的局限,可以获得近地高分辨率的建筑物立面信息,使得目前高昂的三维建模成本大大降低,但是倾斜摄影数据后处理目前仍然是国内外研究的一个热点和难点问题。常见的倾斜多相机系统普遍采用Maltese-cross相机配置[1]如图 1所示,即1个下视相机和4(或6)个斜视相机组合方式(下文中的倾斜影像指下视与斜视影像的总和),斜视相机倾斜角一般在45°左右,根据相机设计的不同,同测站的下视与斜视相机可能有重叠或无重叠。

|
| 图 1 Maltese-cross 1+4倾斜多相机系统示意图 Fig. 1 The maltese-cross multi-camera configuration diagram |
倾斜影像空三作为倾斜影像数据产品生产的关键步骤之一[2, 3, 4, 5],主要涉及连接点提取和光束法区域网平差两个环节。由于区域网平差的相关理论和算法都已经比较成熟,因此倾斜影像空三的难点在于多视影像间的连接点自动提取。大部分传统的摄影测量商业软件在进行连接点提取时都使用标准的影像匹配技术,如归一化相关系数匹配(NCC)和最小二乘匹配(LSM),但这些方法仅适用于影像尺度一致的垂直摄影情形[1, 6]。由于倾斜影像具备多角度、大倾角的特点,传统匹配方法无法解决立体匹配中的遮挡、几何变形、几何断裂、影像大幅旋转等瓶颈问题,同时斜轴透视的场景深度变化带来基高比剧烈变化,都使得倾斜影像间的转点变得更加困难。部分近景摄影测量匹配技术能够处理仿射变形影像匹配(如ASIFT、MSER等)[7, 8, 9, 10, 11, 12],但算法效率较低,无法适用于高分辨率倾斜影像匹配问题。另一方面,由于倾斜多视影像数量庞大,且影像间的重叠关系复杂,如何快速地确定序列影像间的公共连接点也是一个问题。文献[13]提出了一种快速、简单的无序影像间的特征追踪算法,有效地将立体像对间的对应关系扩展到多视影像,使用并查集算法来解决对应关系的融合问题,与其他算法相比具有更低的复杂度并可以获取更多的连接点。
国内对于倾斜影像空三的研究尚处于起步阶段,国外对该问题研究已经取得了一定成果。文献[1, 14]提出了一种影像串联算法,通过GNSS/IMU给定的外方位初值约束相关影像间的特征提取,在相对定向过程中引导影像的串联,由于使用Apero软件进行区域网平差,文中算法连接点提取采用的是一种增量式重建思路,并未充分利用POS的先验信息,增加了算法的处理时间,且采用无控制点区域网平差,没有利用检查点对结果进行精度评定;文献[15]提出在区域网平差过程中添加场景约束信息(如水平、垂直、直角条件),可以有效减少地面控制点的数目同时提高平差和相机自检校的可靠性,但文中算法需要人工提取场景中的约束信息,不利于倾斜影像全自动空三的实现。文献[16, 17]指出充分利用POS的先验信息能够有效提高连接点的匹配成功率和效率,但文中算法主要针对传统垂直摄影航带间的转点问题,无法直接用于倾斜多视影像间的连接点自动提取。
本文提出了一种自动连接点提取算法:首先利用POS信息进行影像匹配像对预测,并对倾斜影像纠正消除因大倾角引起的仿射变形,通过SIFT匹配和特征追踪自动获取匹配连接点;给出了倾斜多视影像空三的两种平差模型;最后利用3种典型的倾斜相机数据进行了空三试验。
1 自动连接点提取SIFT算法[18, 19, 20]以其尺度、旋转不变性并能克服一定程度仿射变形和光照变化在影像匹配领域得到广泛应用。同方向倾斜立体像对由于拍摄角度一致,仿射变形小,因此SIFT算法能够成功匹配,但无法适用于不同方向倾斜像对间的匹配问题。ASIFT算法具有完全的仿射不变性,通过在经度和纬度方向进行视角变化采样,模拟各个仿射变化下的影像,进而利用SIFT算法进行特征提取和匹配,但由于使用穷举匹配策略,在实际应用中受到很大限制。目前的倾斜摄影系统(Pictometry、UltraCam、SWDC-5等)都配备了GPS/IMU设备,在获取影像数据的同时能够得到高精度的POS数据。借鉴ASIFT仿射不变特征算法思想,首先利用POS信息进行斜视影像纠正,消除因大倾角与旋转角引起的影像几何变形;接着利用文献[20]中的SIFT算法对纠正后影像进行特征提取并归算至原始影像,进而利用SIFT描述符完成特征匹配;最后,利用文献[13]中的特征追踪算法实现倾斜多视影像间连接点对应关系的快速确定。
1.1 斜视影像纠正给定影像的外方位元素初值和设计航高,根据共线条件方程能够得到影像在地面上的投影四边形“轨迹”
式中,Xs、Ys、Zs为外方位线元素初值;a1、a2、…、c3为旋转矩阵元素;f为焦距;Zg为由所有影像的外方位线元素均值与设计航高计算得到的平均高程面;(x,y)为像主点为原点的像平面坐标;(X,Y)为像点投影到平均高程面上的地面坐标。给定影像4个角点像素坐标及其对应的地面坐标后,可求解原始影像与纠正后影像间的单应变换矩阵H 式中,(x,y)、(x′,y′)分别表示原始影像像点和纠正后影像对应点的坐标。利用数字微分纠正即可获取纠正后的影像,斜视影像纠正效果如图 2所示。从纠正结果可以看出,影像间由于大倾角和大旋转角引起的变形已经基本消除,只剩下由于地形起伏引起的像点位移。由于倾斜多视影像间公共的连接点一般都位于平坦地区,建筑物上的连接点较少(少数点位于建筑物顶部),而这些区域在经过上述斜视纠正后基本消除了仿射变形影响,因此能够利用SIFT算法匹配到公共特征点。

|
| 图 2 斜视影像纠正结果 Fig. 2 The Rectification result of oblique image |
由于大范围倾斜影像空三处理涉及的影像数目庞大,且倾斜影像间重叠关系复杂,倾斜影像的匹配策略对算法效率影响显著,本文首先根据初始POS数据及倾斜相机配置信息确定满足条件的候选匹配像对,主要依据如下:
(1) 重叠率:根据POS信息计算每张影像在地面的投影多边形轨迹,依据轨迹间的重叠率来判断,剔除小于指定阈值THRoverlap(默认取0.30)的匹配像对;两多边形的重叠率计算公式为
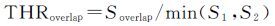
(2) 相机配置:对于同测站下视与斜视有重叠度的倾斜相机系统,不考虑重叠率大小,保留下视与斜视匹配像对。
获取满足条件的候选匹配像对后,首先利用SIFT特征进行初始匹配,由于倾斜影像分辨率较高,在特征提取时对纠正后的斜视影像进行分块(如1600×1600)特征提取,并利用式(2)将特征点坐标归算至原始影像;接着基于核线约束和单应约束采用随机一致性估计算法(RANSAC)[21]对匹配特征进行粗差剔除。
1.3 特征追踪特征追踪是指在序列影像中跟踪同一物方点的位置。利用图论的思想,将每个影像上的特征点作为独立节点,同名像点对应关系作为边,由此序列影像间的多视对应关系搜索可以转换为整个图中有几条连通分支的问题,利用并查集数据结构可以有效处理。
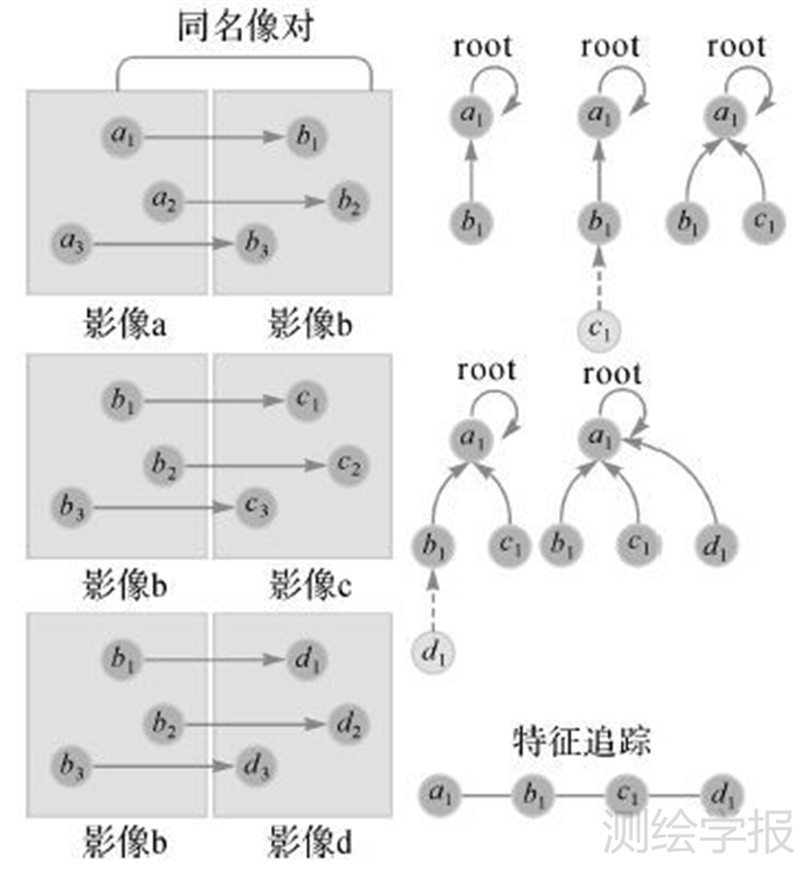
下面以一个有效特征追踪a1-b1-c1-d1为例来阐述特征追踪原理,如图 3所示。
|
| 图 3 并查集算法实现特征追踪原理 Fig. 3 The feature tracking theory using union-find algorithm |
(1) 遍历所有影像上的特征点,在图中创建对应的节点,即a1、a2、a3、…、d3。
(2) 遍历所有的同名像点匹配列表,首先执行影像a-b同名像对时,连接a1和b1节点,取a1作为根节点;添加影像b-c同名像对,连接c1和b1节点,执行并查集算法的Find操作,判断两者的根节点是否属于同一节点。如果不是,则执行并查集算法中的Join操作,将c1节点的根节点修改为b1节点的根节点;否则,直接跳过;类似地继续添加影像b-d同名像对,连接d1和b1节点,判断二者的根节点是否相同,如果不是,修改d1节点的根节点为b1节点的根节点。
(3) 执行完毕,即可得到一个有效的特征追踪a1-b1-c1-d1。
经过上述过程,可以获取初始的特征追踪结果。设定每张影像上有效的连接点数目阈值THRNtrPerImg(默认取20)及每个连接点的重叠度阈值THRNipPerTr(默认取3),剔除不满足上述阈值的影像及连接点。当POS初始精度较差时,可以通过提高重叠度阈值来剔除误匹配点,获取一个较高精度外定向结果后,再降低阈值获取更多的连接点数目。
1.4 多片前方交会多片前方交会有两方面的作用:一方面为区域网平差提供一个良好的物方点初值;另一方面,由于倾斜影像空三物方连接点对应的可见影像数目远高于传统垂直摄影情形,最高可达几十度重叠,因此可以利用观测值的一致性检验来进一步剔除残留的粗差点。
由文献[14]可知,当倾斜影像空三的连接点中含有大量的粗差点时,平差的收敛性会受到极大影响,甚至无法收敛。多片前方交会过程中的粗差剔除分为两个阶段:
1.4.1 前方交会计算所有像点的平均反投影误差σ′0及每个连接点对应像点的最大反投影误差err(i),设定阈值THRreproj=3σ′0,剔除最大反投影误差不满足err(i)≤THRreproj的连接点。
1.4.2 高程滤波经过上述步骤获取的连接点依然存在少量噪声点,需要利用高程滤波加以剔除。计算所有连接点的平均高程Haverage及高程的方差σH,考虑到倾斜摄影的研究对象为陆地表面且连接点高程分布相对集中,一般将大于3倍中误差以上的连接点视为粗差点,剔除高程不满足Hi-Haverage≤3σH的连接点。
2 区域网平差 2.1 最小二乘平差与传统摄影测量区域网平差相比,倾斜影像空三在数学模型上基本一致,主要不同点在于像点观测值数目远远多于传统垂直摄影情形,本文采用带附加参数的自检校区域网平差[22],将自检校参数、控制点坐标及外方位元素视为带权观测值,平差的基本误差方程为
式中,X1为外方位元素和加密点坐标的改正数向量;L1为像点观测值向量;P1为像点观测值的权;X2为控制点坐标的改正数向量;P2为控制点坐标观测值的权;X3为外方位元素改正数向量;P3为外方位元素观测值的权;X4为自检校参数向量;P4为自检校参数观测值的权;A1、A2、A3、A4为对应误差方程式的系数矩阵;E2、E3、E4为单位阵。式(3)可简化为法方程为
2.2 倾斜影像区域网平差模型在倾斜多视影像区域网平差中,可以采用以下两种模型:
2.2.1 附加约束参数模型假设整个倾斜成像系统满足刚性不变条件,考虑同一测站下视与斜视相机间的约束关系,采用6个偏心参数来描述两者之间的变换。同一测站下视和斜视相机的外方位线元素分别记为CN、CO,旋转矩阵记为RN、RO,斜视相机相对于下视相机的相对定向元素记为ΔTNO、ΔRNO,则有
2.2.2 独立模型同一测站下视与斜视影像间的外方位元素相互独立,基于共线条件方程整体求解所有影像的内外方位元素
式中,x0n、y0n、fn为第n个相机的主点和焦距;X0i、Y0i、Z0i为第i张影像的外方位线元素;R11i、R12i、…、R33i为第i张影像的旋转矩阵元素;x、y为像点观测值的像平面坐标;X、Y、Z为对应物方点坐标。在附加参数模型中,整个航飞过程中同测站下视与斜视相机间的偏心参数保持不变,以1+4型相机配置为例:假设有N个测站,则外方位元素未知参数的个数为6N+6×5个,而采用独立模型的外方位元素未知参数的个数为6N×5个。当测站数目庞大时,采用附加参数模型可以有效减少影像外方位元素未知参数数目,但同时由于忽略了倾斜相机间的非刚性变形和相机曝光的不同步性,会引入一定的系统误差。在POS精度较差时,可先对下视影像进行空三并利用偏心参数获取斜视相机优化的外方位元素初值。独立模型虽然增加了未知参数的数目,平差解算的系统内存占用更高,但是由于采用最严格的数学模型,可以获得最高的精度,本文采用独立模型进行区域网平差解算。
3 试验与分析 3.1 试验数据试验选取典型的3种倾斜相机数据:组装轻量级倾斜相机、SWDC-5相机、UltraCam相机数据进行了试验,数据的相关描述见表 1。其中,第1组数据含有地面控制点,用于进行倾斜空三与传统空三对比试验及其倾斜空三的实际精度评定,如果单独采用下视影像,与传统空三没有区别;第2、3组数据无地面控制点,用于测试本文算法对国内外流行的倾斜摄影系统和大数据量的适应性。基于Win7 64位系统采用VC++2010、CUDA 6.0开发了倾斜影像自动空三软件Mogas-AT,硬件平台为Dell Precision工作站,处理器为英特尔酷睿i7-4910MQ、主频2.90 GHz,内存16 GB,显卡为4 GB英伟达Quadro K3100M。
| 组别 | 测试 | 影像大小/像素 | 像元大小/um | 焦距/mm | GSD/cm | 相机配置 | 影像数目 | 航高/m | 下视重叠度/(%) | 含控制点 | |||||
| 数据 | 下视 | 斜视 | 下视 | 斜视 | 下视 | 斜视 | 下视 | 斜视 | 航向 | 旁向 | |||||
| 1 | 组装轻量型 | 5616×3744 | 5616×3744 | 6.3 | 6.3 | 35 | 35 | 4 | 1+4 | 181×1 | 181×5 | 220 | 70 | 30 | √ |
| 2 | UltraCam | 11 674×7514 | 6870×4520 | 6.0 | 5.2 | 51 | 80 | 4.7 | 1+6 | 286×1 | 286×6 | 400 | 83 | 80 | × |
| 3 | SWDC-5 | 8206×6078 | 8200×5960 | 6.0 | 6.0 | 82.1 | 99.8 | 5.8 | 1+4 | 385×1 | 3854 | 800 | 70 | 30 | × |
试验组装倾斜成像系统采用1+4相机配置方式,相机型号为Cannon EOS 5D,同一测站下视相机与斜视相机有重叠,测区范围为2.2 km×1.4 km,共飞行5条航带,测区中均匀分布有14个控制点,其中下视与倾斜影像(包括下视)的重叠关系及控制点分布如图 4所示。

|
| 图 4 组1试验测区影像重叠关系及控制点分布图 Fig. 4 Images overlap relationship and control points distribution |
分别对仅用下视影像和倾斜影像采用独立模型进行不同控制点数目的区域网平差试验,其中控制点数目为0代表无控制点区域网平差。连接点提取耗时包括特征提取、特征匹配、特征追踪3部分耗时,利用像点的平均反投影误差σr与检查点的实际精度两项指标进行精度评定,其结果如表 2、图 5、图 6所示。
| 控制方案 | 影像数据 | GSD/cm | 检查点数 | 连接点提取耗时/min | 平差耗时/min | 像点数目 | 连接点数 | 平均反投影误差/pixel | 实际精度/m | |
| 平面 | 高程 | |||||||||
| 0控制点 | 下视 | 4.0 | 14 | 5.48/0.12/0.02 | 0.183 | 78 162 | 25 440 | 0.463 | 0.159 8 | 1.983 1 |
| 倾斜 | 39.38/9.13/0.55 | 2.18 | 681 155 | 153 379 | 0.786 | 0.110 2 | 1.040 9 | |||
| 1中心点 | 下视 | 4.0 | 13 | 5.48/0.12/0.02 | 0.22 | 78 162 | 25 440 | 0.463 | 0.247 7 | 0.214 1 |
| 倾斜 | 39.38/9.13/0.55 | 2.33 | 681 155 | 153 379 | 0.786 | 0.089 7 | 0.099 6 | |||
| 2对角点 | 下视 | 4.0 | 12 | 5.48/0.12/0.02 | 0.20 | 78 162 | 25 440 | 0.463 | 0.1451 | 0.277 9 |
| 倾斜 | 39.38/9.13/0.56 | 2.37 | 681 155 | 153 379 | 0.786 | 0.075 5 | 0.114 5 | |||
| 3角点 | 下视 | 4.0 | 11 | 5.48/0.12/0.02 | 0.20 | 78 162 | 25 440 | 0.463 | 0.158 0 | 0.286 8 |
| 倾斜 | 39.38/9.13/0.53 | 1.93 | 681 155 | 153 379 | 0.786 | 0.031 2 | 0.090 5 | |||
| 4角点 | 下视 | 4.0 | 10 | 5.48/0.12/0.02 | 0.20 | 78 162 | 25 440 | 0.463 | 0.111 0 | 0.258 4 |
| 倾斜 | 39.38/9.13/0.55 | 1.93 | 681 155 | 153 379 | 0.786 | 0.030 8 | 0.080 3 | |||
|
注:1.像点的平均反投影误差计算公式${\sigma _r} = \sqrt {[{{(x' - x)}^2} + {{(y' - y)}^2}]/n} $,式中(x,y)为原始像点观测值;(x′,y′)为利用平差后物方点反投影到原始影像的像点坐标。
2.实际精度是由n个检查点的计算坐标与其野外测量坐标的较差Δi(i=X,Y,Z)计算的平差中误差,即${\mu _i} = \sqrt {\sum {\Delta _i^2/n} } ;{\mu _{平面}} = \sqrt {\mu _X^2 + \mu _Y^2} $。 | ||||||||||
|
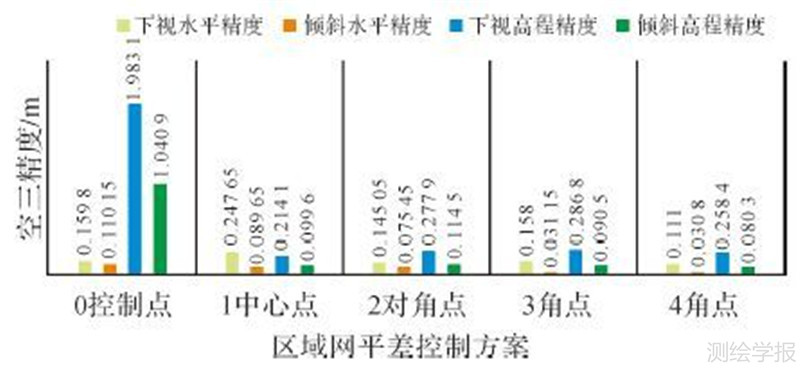
| 图 5 下视与倾斜影像空三精度对比 Fig. 5 The triangulation precision comparison between nadir and oblique images |
|
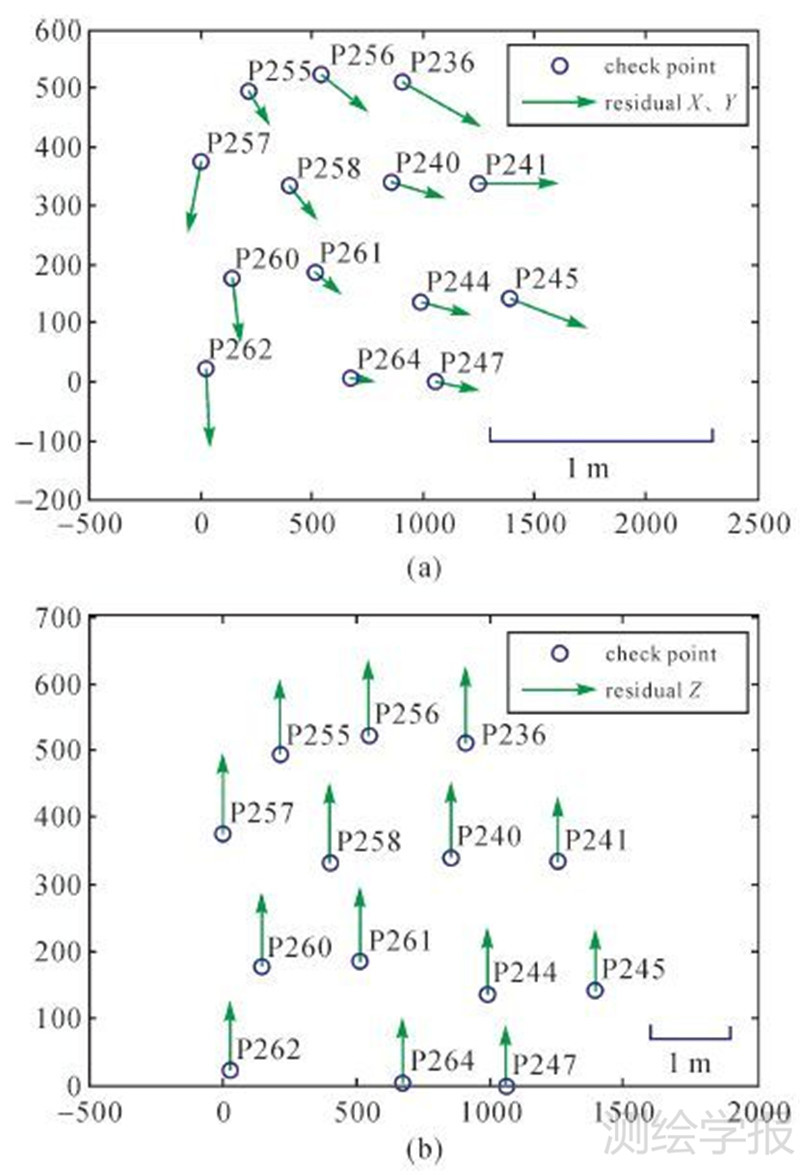
| 图 6 无控制点平差的残差分布图 Fig. 6 The triangulation residuals without ground control points |
由上述结果得到以下结论:
(1) 倾斜影像空三精度优于传统下视影像空三精度。在各种控制方案下,倾斜影像空三的水平和垂直精度都要高于下视影像空三,且精度提高约为2~3倍。分析可知,这是因为在倾斜影像空三过程中引入了斜视影像上的像点观测值,增加了多余观测值数目,提高了匹配的可靠性:一方面,可以解决诸如相似纹理、遮挡等困难区域匹配的多义性和误匹配问题;另一方面,较大的匹配冗余有利于匹配粗差的自动定位和剔除。由表 2中结果可以看出,倾斜影像空三的连接点数目约为下视影像空三连接点数目的6倍,像点观测值数目约为9倍。倾斜影像空三可以达到水平方向0.75 GSD,高程方向2.0 GSD。
| 倾斜影像数据类型 | 连接点提取耗时/min | 平差耗时/min | 像点数目 | 连接点数目 | 平均反投影误差/像素 |
| UltraCam | 30.95/22.75/1.02 | 2.85 | 601 698 | 155 299 | 0.555 |
| SWDC-5 | 68.07/33.63/2.23 | 7.43 | 1 348 733 | 338 609 | 1.344 |
(2) 无控制点情况下,将POS获取的外方位元素作为带权观测值参与平差不能有效提高区域网平差的精度。图 6是无控制点区域网平差残差分布图,可以看出检查点定位结果存在明显的系统误差,说明POS数据含有一定的系统误差。当含有一个中心点时,倾斜空三的精度能够得到显著提高。因此,在倾斜影像空三处理时,要发挥POS精度的潜力依然需要少量的外业控制点。
(3) 控制点数目对倾斜影像空三的精度影响与传统下视影像空三相一致。当使用3个角点的控制方案时,区域网平差的精度已经达到一个较好的水平,再增加控制点数目对精度的提高十分有限。因此,在实际的倾斜影像外业控制点布设时,一般只需3个角点。倾斜影像空三的高程精度低于平面精度,当采用1个中心点时,倾斜影像空三的高程精度与平面精度相当,增加控制点数目时,水平精度仍可得到进一步的提高,高程精度提升不明显。
(4) 控制点的引入不影响区域网平差的像点平均反投影误差精度,这是因为平均反投影误差反映的是像点残差的内符合精度,控制点的引入不会影响平差收敛程度,只是相当于对连接点物方坐标进行绝对定向,将其纳入到控制点所在的坐标系统下。
下视影像空三与倾斜影像空三试验结果如图 7和图 8所示。

|
| 图 7 下视影像与倾斜影像空三结果视图 Fig. 7 The triangulation result view of nadir and oblique image |
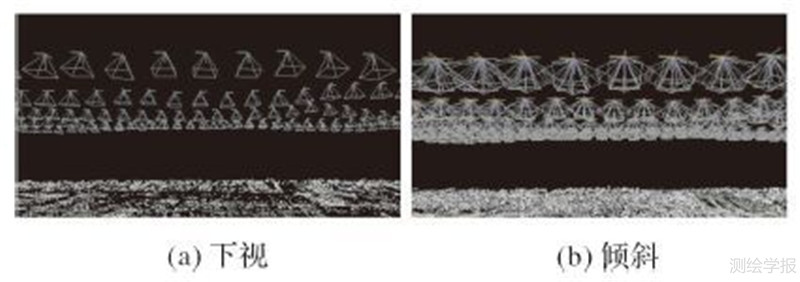
|
| 图 8 下视影像与斜视影像空三外方位元素放大图 Fig. 8 The enlarged view of EO after bundle adjustment |
为了验证本文算法对各类倾斜摄影系统和大数据量的支持,分别对UltraCam和SWDC-5倾斜影像数据进行了试验,由于上述两个试验数据均无地面控制点,仅以像点的平均反投影误差进行精度评定。为了减少连接点提取耗时,下述试验中SIFT特征提取初始层级取2(即对原始影像进行2次降采样),结果如图 9和图 10所示。

|
| 图 9 微软UltraCam倾斜影像数据空三处理结果 Fig. 9 The triangulation results of microsoft UltraCam oblique images |

|
| 图 10 SWDC-5倾斜影像空三处理结果 Fig. 10 The triangulation results of SWDC-5 oblique images |
上述试验结果表明:
(1) 本文算法对当前国内外常见的倾斜摄影系统UltraCam、SWDC-5等能够很好地支持,由于算法均采用CUDA GPU进行并行加速,处理效率远高于传统空三软件,主要处理耗时集中在特征提取和匹配阶段。无控制点情况下,SWDC-5倾斜数据空三的像点平均反投影误差在1.34像素,UltraCam倾斜数据的像点平均反投影误差可以达到0.56像素。
(2) 本文算法能够适应大范围倾斜影像数据处理,试验的两个数据集影像数目都在2000张以上,一次性处理影像数目的上限与算法无关,主要由系统存储容量决定。所有空三处理过程均为全自动,因此,能够有效提高作业效率,节约测图成本。
4 结论和展望本文对倾斜多视影像的自动连接点提取和空三进行了研究,试验选取了3款国内外流行的倾斜摄影系统,结果表明:本文的方法能够适应各种倾斜摄影系统,所有空三过程均为全自动处理,可适用于大范围倾斜影像空三处理,能有效提高作业效率;相同条件下倾斜影像空三的整体精度优于传统垂直摄影空三,实际精度可以达到水平方向0.75 GSD,高程方向2.0 GSD。后续将进一步研究倾斜影像空三适合的加权模型,以及如何进一步提高连接点提取的效率。
| [1] | RUPNIK E, NEX F, REMONDINO F. Oblique Multi-camera Systems-orientation and Dense Matching Issues[C]//International Archives of the Photogrammetry, Remote Sensing and Spatial Information Sciences, Volume XL-3/W1, EuroCOW 2014, the European Calibration and Orientation Workshop. Castelldefels:ISPRS,2014:107-114. |
| [2] | FDIETER D, RDIETER M. Oblique Image Data Processing:Potential, Experiences and Recommendations[EB/OL].(2013-06-08)[2014-01-30]. http://www.ifp.uni-stuttgart.de/publications/phowo13/090Fritsch.pdf |
| [3] | KARBØ N, SCHROTH R. Oblique Aerial Photography:A Status Review[EB/OL].(2009-10-03)[2014-01-30]. http://www.ifp.uni-stuttgart.de/publications/phowo09/140Karbo.pdf |
| [4] | WANG Yandong, SCHULTZ S, GIUFFRIDA F. Pictometry's Proprietary Airborne Digital Imaging System and Its Application in 3D City Modelling[C]//International Archives of Photogrammetry, Remote Sensing and Spatial Information Sciences:XXXVⅡ(B1). Beijing:ISPRS,2008:1065-1069. |
| [5] | GRUBER M, PONTICELLI M, WIECHERT A. UltraCam, A Brand for Continuous Devlopments[EB/OL].(2011-11-25)[2014-01-30]. http://www.ifp.uni-stuttgart.de/publications/phowo11/110Gruber.pdf |
| [6] | SHRAGAI Z, EVEN-PAZ A, KLEIN I. Automatic Tie-point Extraction Using Advanced Approaches[C]//Proceedings of the ASPRS 2011 Annual Conference.Milwaukee,Wisconsin:[s.n.],2011. |
| [7] | CODREANU V, DONG Feng, LIU Baoquan, et al. Gpu-Asift:A Fast Fully Affine-invariant Feature Extraction Algorithm[C]//Proceedings of 2013 International Conference on High Performance Computing and Simulation. Helsinki:IEEE, 2013:474-481. |
| [8] | MOREL J M, YU Guoshen. Asift:A New Framework for Fully Affine Invariant Image Comparison[J]. SIAM Journal on Imaging Sciences, 2009, 2(2):438-469. |
| [9] | YU Guoshen, MOREL J M. A Fully Affine Invariant Image Comparison Method[C]//Proceedings of IEEE International Conference on Acoustics, Speech and Signal Processing.Taipei:IEEE, 2009:1597-1600. |
| [10] | MIKOLAJCZYK K, SCHMID C. Scale & Affine Invariant Interest Point Detectors[J]. International Journal of Computer Vision, 2004, 60(1):63-86. |
| [11] | MIKOLAJCZYK K,TUYTELAARS T,SCHMID C,et al. A Comparison of Affine Region Detectors[J]. International Journal of Computer Vision, 2005, 65(1-2):43-72. |
| [12] | YANG Huachao,ZHANG Shubi,WANG Yongbo.Robust and Precise Registration of Oblique Images Based on Scale-invariant Feature Transformation Algorithm[J]. IEEE Geoscience and Remote Sensing Letters,2012, 9(4):783-787. |
| [13] | MOULON P, MONASSE P. Unordered Feature Tracking Made Fast and Easy[C]//Proceedings of the 9th European Conference on Visual Media Production. London:CVMP,2012. |
| [14] | RUPNIK E, NEX F, REMONDINO F. Automatic Orientation of Large Blocks of Oblique Images[C]//International Archives of the Photogrammetry, Remote Sensing and Spatial Information Sciences, Volume XL-1/W1, ISPRS Hannover Workshop 2013.Hannover:ISPRS,2013:299-304. |
| [15] | GERKE M, NYARUHUMA A. Incorporating Scene Constraints into the Triangulation of Airborne Oblique Images[C]//ISPRS Conference:High-resolution Earth Imaging for Geospatial Information:ISPRS XXXVⅢ 1-4-7/WS. Hannover:ISPRS, 2009:4-7. |
| [16] | 袁修孝. POS辅助光束法区域网平差[J]. 测绘学报, 2008, 37(3):342-348. YUAN Xiuxiao. POS-supported Bundle Block Adjustment[J]. Acta Geodaetica et Cartographica Sinica, 2008, 37(3):342-348. |
| [17] | 袁修孝, 明洋. POS辅助航带间航摄影像的自动转点[J]. 测绘学报, 2010, 39(2):156-161. YUAN Xiuxiao, MING Yang. POS-supported Matching Method for Aerial Images between Neighboring Strips[J]. Acta Geodaetica et Cartographica Sinica, 2010, 39(2):156-161. |
| [18] | LOWE D G. Distinctive Image Features from Scale-Invariant Keypoints[J]. International Journal of Computer Vision, 2004, 60(2):91-110. |
| [19] | SUN Yanbiao, ZHAO Liang, HUANG Shoudong, et al. L2-SIFT:SIFT Feature Extraction and Matching for Large Images in Large-scale Aerial Photogrammetry[J]. ISPRS Journal of Photogrammetry and Remote Sensing, 2014, 91:1-16. |
| [20] | WU Changchang. Siftgpu:A Gpu Implementation of Scale Invariant Feature Transform(SIFT)[EB/OL].(2009-10-03)[2014-01-30]. http://www.cs.unc.edu/-ccwu/siftgpu/ |
| [21] | FISCHLER M A, BOLLES R C. Random Sample Consensus:A Paradigm for Model Fitting with Applications to Image Analysis and Automated Cartography[J]. Communications of the ACM, 1981, 24(6):381-395. |
| [22] | 李德仁, 袁修孝. 误差处理与可靠性理论[M]. 武汉:武汉大学出版社, 2002. LI Deren, YUAN Xiuxiao. Error Processing and Reliability Theory[M]. Wuhan:Wuhan University Press, 2002. |