2. 黑龙江省水利科学研究院, 黑龙江 哈尔滨 150080;
3. 福建省交通建设工程试验检测有限公司, 福建 福州 350000
2. Heilongjiang Provincial Hydraulic Research Institute, Harbin 150080, China;
3. Fujian Traffic Construction Engineering Test & Inspection Co., Ltd, Fuzhou 350000, China
河冰的输移是河冰工程中研究的重要内容。解冻期,流凌多以碎冰块为主,且冰块较厚。随水流运动的流凌有时会由于河道形态以及流速的变化形成冰塞或冰坝。这些现象或束窄断面或堵塞河道,进而产生水位雍高的现象,发生决堤、漫滩等自然灾害。同时流凌体积大、速度快,会与护岸和整治建筑物发生碰撞,产生破坏性现象。尤其在我国北方地区,流凌现象常见且明显。黑龙江作为我国十分重要的一条界河,在解冻时期经常会有大量的河冰输移现象。黑龙江的护岸受到流冰的正面撞击与侧面磨损所造成的破坏会涉及国土损失问题,长此以往产生后果的严重性不言而喻。因此,加强对护岸工程的再一次防护对于北方河流而言,意义重大。目前,关于河冰的数值模拟研究:姜坤[1]基于冰水二相流分析了弯道设置取水口后水流的变化和浮冰运动的特点。宋小艳[2]对潜冰底面的压力分布进行了三维数值模拟研究,得到了考虑潜冰宽度影响的潜冰底面文丘里效应压强和前缘效应压强的计算公式,并在此基础上提出了潜冰底面水压力的估算公式。李辉辉等[3-4]基于离散元方法对碎冰运动及其对群桩的冲击进行数值模拟,并分析了冰块尺寸、冰厚和冰速对桩结构所受冰荷载的影响。
护岸工程按形式可分为坡式护岸、坝式护岸、墙式护岸以及其他形式护岸[5]。目前,对于丁坝与流凌运动关系的研究几乎没有。本文针对坝式护岸研究丁坝的布置形式对于流凌演进的影响,具体基于90°弯道河流,丁坝的不同布置形式对于流凌运动的影响进行了数值模拟,总结出相关规律,同时与模型试验结果对比证明数值模拟可以很好的模拟流凌运动,可作为相关研究的重要手段之一。
1 理论与数值方法 1.1 控制方程与湍流模型一般认为,无论湍流运动多么复杂,非稳态的连续方程和Navier-Stokes方程对于湍流的瞬时运动仍然是适用的[6]。为了考虑脉动的影响,使用笛卡尔坐标系,引入张量中的指标符号,时均形式的连续方程与Reynolds时均Navier-Stokes方程表示为
| $ \begin{array}{l} \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\frac{{\partial \rho }}{{\partial {\rm{t}}}} + \frac{\partial }{{\partial {x_i}}}\left( {\rho {u_i}} \right) = 0\\ \;\frac{{\partial \rho }}{{\partial t}}\left( {\rho {u_i}} \right) + \frac{\partial }{{\partial {x_i}}}\left( {\rho {u_i}{u_j}} \right) =-\frac{{\partial p}}{{\partial {x_i}}} + \frac{\partial }{{\partial {x_j}}}\left( {\mu \frac{{\partial {u_i}}}{{\partial {x_i}}}-\rho \overline {{u_i}'{u_j}'} } \right) + {S_i} \end{array} $ |
在RNGk-ε模型中,通过大尺度运动与修正后的粘度项来体现小尺度的影响,而这些小尺度会从控制方程中去除。所得到的k方程和ε方程,与标准k-ε模型非常相似:
| $ \begin{array}{l} \;\;\;\;\;\;\frac{{\partial \left( {\rho k} \right)}}{{\partial t}} + \frac{{\partial \left( {\rho k{u_i}} \right)}}{{\partial {x_i}}} = \frac{\partial }{{\partial {x_j}}}\left[{{\alpha _k}{\mu _{{\rm{eff}}}}\frac{{\partial k}}{{\partial {x_j}}}} \right] + {G_k} + \rho \varepsilon \\ \frac{{\partial \left( {\rho \varepsilon } \right)}}{{\partial t}} + \frac{{\partial \left( {\rho \varepsilon {u_i}} \right)}}{{\partial {x_i}}} = \frac{\partial }{{\partial {x_j}}}\left[{{\alpha _\varepsilon }{\mu _{{\rm{eff}}}}\frac{{\partial \varepsilon }}{{\partial {x_j}}}} \right] + \frac{{C_{1\varepsilon }^*}}{k}{G_k} -{C_{2\varepsilon }}\rho \frac{{{\varepsilon ^2}}}{k} \end{array} $ |
RNGk-ε模型可以更好地处理高应变率及流线弯曲程度较大的流动。而对近壁区内的流动,本文采用壁面函数法,最终与RNGk-ε模型联合求解。
1.2 利用VOF模型的欧拉多相流VOF模型假定存在于控制体积中的所有不混溶的流体之间共享速度、压力和温度场。描述体积分数运输的守恒方程为
| $ \frac{d}{{{\rm{d}}t}}\int_V {{\alpha _i}{\rm{d}}V} + \int_S {{\alpha _i}\left( {v-{v_g}} \right) \cdot {\rm{d}}a = \int_V {\left( {{s_{{\alpha _i}}}-\frac{{{\alpha _i}}}{{{\rho _i}}}\frac{{D{\rho _i}}}{{Dt}}} \right){\rm{d}}V} } $ |
离散元法是一种用于模拟大量离散颗粒之间相互作用的数值方法。离散元模型是拉格朗日建模方法的一种扩展。因此,离散元模型中固体颗粒与流体间相互作用的方式与拉格朗日相作用方式一致。真实的冰块被建模为离散单元,材料模型用于表示单组分固体,同时定义恒定密度方程,以此来表示冰颗粒的性质。同时,动量守恒方程控制材料颗粒的流动。材料颗粒受到重力、水流拖曳力、自定义体力等。因此,水流的作用便可施加于冰颗粒上。但是本文并不考虑流动过程中冰颗粒相变的问题,忽略热传递。离散元模型粒子的动量平衡源自材料粒子的动量平衡,而离散元建模引入了额外的力代表颗粒间相互作用以及颗粒与边界的相互作用:
Fb=Fg+Fu+Fc
式中:
Fc=Σ相邻粒子F接触+Σ相邻边界F接触
运动的DEM粒子方程还包括角动量守恒方程
| $ \frac{d}{{{d_t}}}{L_p} = \frac{d}{{{d_t}}}\left( {{{\rm{I}}_p}{\omega _p}} \right) = \sum {_{相邻粒子}} {T_{接触}} + \sum {_{相邻边界}} + {T_{接触}} $ |
其中接触扭矩计算公式为
| $ {T_c} = {r_c} \times {F_c}-{\mu _r}|{r_c}||{F_c}|\frac{{{\omega _p}}}{{|{\omega _p}|}} $ |
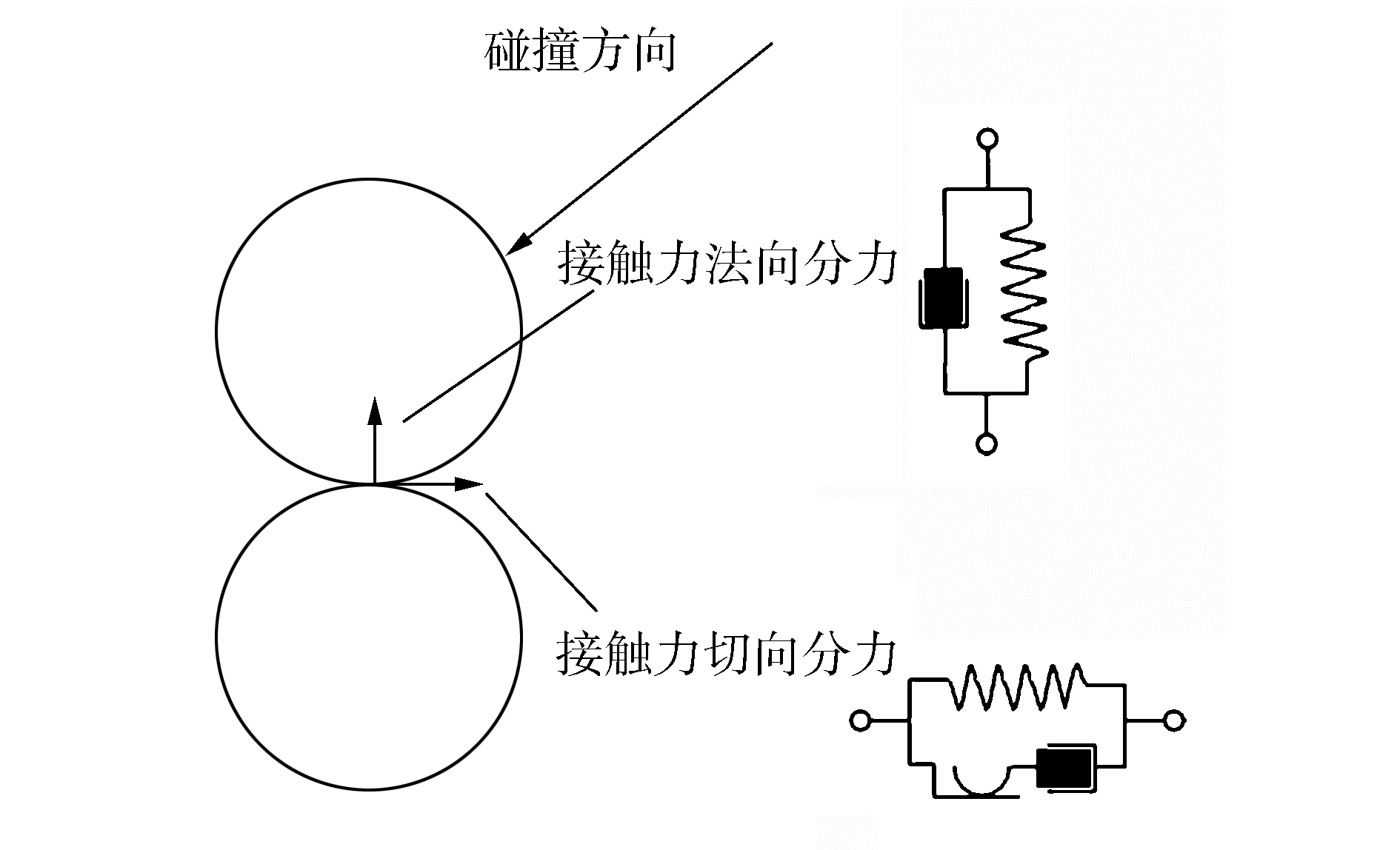
颗粒间的碰撞力采用弹簧缓冲器模型的变形体模拟。弹簧产生推挤颗粒的排斥力,缓冲器代表粘性阻尼,二者结合可以模拟非完全弹性的碰撞类型。接触点处的力被建模为一对弹簧缓冲振荡器。一对平行的线性弹簧缓冲器模型表示法向力,另一对与滑块串联的平行的线性弹簧缓冲器代表相对于接触平面法线矢量的切向方向力。其中,弹簧都是弹性部分的响应,而缓冲器则模拟碰撞过程中的能量消耗。如图 1所示。
|
Download:
|
| 图 1 离散元颗粒接触模型 | |
本文选取的碰撞模型是基于Hertz-Mindlin接触理论的非线性弹簧阻尼器接触模型的变体。两个球体A和B之间的力由以下一组方程描述:
F接触=Fn+Ft
其中:
法向力:
Fn=-Kndn-Nnvn
法向弹簧刚度:
| $ {K_n} = \frac{4}{3}{{\rm{E}}_{eq}}\sqrt {{d_n}{R_{eq}}} $ |
法向阻尼:
| $ {N_n} = \sqrt {\left( {5{K_n}{M_{eq}}} \right)} {N_{n\;\;{\rm{damp}}}} $ |
同理,
切向力:
| $ {F_t} =-{K_t}{d_t}-{N_t}{v_t} $ |
切向弹簧刚度:
| $ {K_t} = 8{G_{eq}}\sqrt {{d_t}{R_{eq}}} $ |
切向阻尼:
| $ {N_t} = \sqrt {\left( {5{K_t}{M_{eq}}} \right)} {N_{t\;\;{\rm{damp}}}} $ |
对于离散元颗粒与边界壁面的碰撞,理论方程与离散元颗粒之间的碰撞相同。但是,边界壁面的半径和质量都考虑为无穷大,因此,其等效半径与等效质量则与离散元颗粒相同。
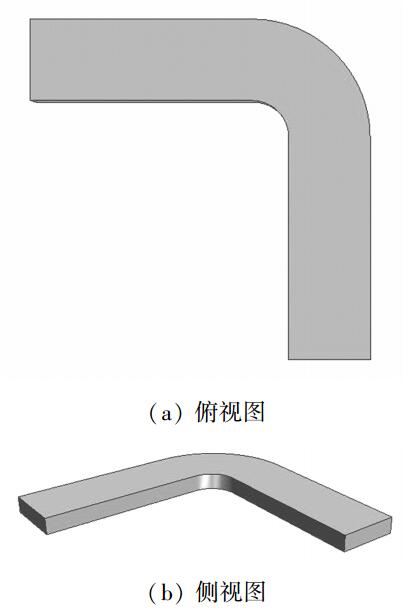
2 数值模拟模型建立 2.1 计算区域本文选取与实验模型相一致的流域尺寸,水槽宽度为1.1 m,入口和出口的直线段均为3 m。弯道內弧半径为0.5 m,外弧半径为1.6 m。水槽深度为0.3 m。如图 2所示。
|
Download:
|
| 图 2 计算区域示意 | |
根据丁坝的有无、数量与布置情况分为5种计算工况,见表 1。本文计算区域中布置的丁坝均为长40 cm,宽5 cm的正挑非淹没丁坝。
|
|
表 1 计算工况 |
本文对计算区域采用六面体结构化网格,水槽整体X和Y方向的网格尺寸大小为0.05 m,Z方向加密处理,网格大小为0.01 m。同时,对于布置丁坝的工况,对丁坝附近进行加密处理。
以工况1为例,网格设置如图 3。

|
Download:
|
| 图 3 工况1网格划分 | |
本文计算的流体域采用欧拉两相流,液体为水,气体为空气。运用VOF方法捕捉自由液面。通过VOF模型设置水深0.18 m。入口设置为速度入口,本文全部工况的水流速度为0.2 m/s。出口设置为压力出口,顶面为速度入口,水槽底面、侧面与丁坝均为混凝土壁面,糙率为0.021。
2.4 离散元模型设置 2.4.1 离散元尺寸与材料冰采用离散元模型模拟,颗粒为球形颗粒,本文模拟相同粒径大小的冰,取冰颗粒直径为0.04 m。冰的材料参数见表 2。
|
|
表 2 冰的材料参数 |
本文模拟了冰与冰、冰与壁面之间的碰撞,较好地反映真实情况。冰与冰、冰与壁面之间的接触采用Hertz Mindlin接触模型,不考虑冰颗粒破损的情况,模型原理与依据见1.4节相关公式,参数选取同时参考文献4,相关参数见表 3。
|
|
表 3 Hertz Mindlin接触模型相关参数 |
离散元在水槽宽度上均匀分布,颗粒流率为20个/s。计算时长总计60 s,前20 s投放冰颗粒。
3 数值模拟结果分析投放的冰颗粒在水槽宽度上均匀分布,因此可以清晰地看见不同位置的冰颗粒运动情况。本文分析不同工况下,冰颗粒运动的整体情况以及冰颗粒与护岸的相互作用位置,总结相关规律,进而对90°弯道水流的丁坝布置提出指导性建议。
3.1 工况1冰颗粒与护岸作用情况分析根据对流凌运动现象的观察可以看出,冰颗粒对凹岸碰撞与冲刷磨损严重,且碰撞与冲刷磨损范围大。从弯道首部至下游直道段都会受到上游来冰撞击,且冰颗粒与护岸发生碰撞后,会沿护岸向下游继续运动,产生冲刷磨损。而上游继续向护岸运动的流凌会与护岸附近的冰发生碰撞,以此会加剧原本在护岸周围的冰对护岸的磨损破坏作用。
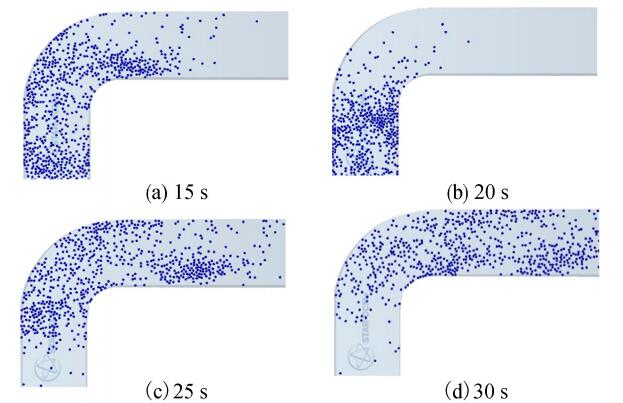
由于弯道水槽的流场特性,凸岸一侧的流速大,因此,根据图 4可以看出,靠近凸岸运动的流凌运动速度快,会较早运动至下游,一部分流凌会与下游顺直段发生碰撞。而弯道部分多由靠近凹岸一侧约水槽宽度一半的流凌先发生碰撞破坏,继而发生连续的冲刷磨损破坏。
|
Download:
|
| 图 4 工况1不同时刻流凌运动俯视图 | |
由于在直道尾部加置一个约为水槽宽度三分之一的正挑丁坝,束窄断面,使得凸岸弯道处流速更大,最大流速会达到0.5 m/s。靠近凸岸一侧的流凌会跟主流线运动,运动轨迹较工况1更加偏靠凹岸,因此,此种布置形式也减少了流凌密集度大时凸岸一侧流凌对凸岸护岸的冲刷磨损。
对于此种工况,在流场中会形成两个主要的回流区。第1个回流区出现在丁坝后部,从弯道与入口直道段呈30°的位置开始到弯道尾部结束,是一个逆时针的回流区。第2个回流区出现在凸岸一侧,从弯道尾部开始,在下游直道段,长度约为1.6 m,为顺时针回流区。
根据图 5可以看出,当流凌运动到回流区时,会跟随回流区水流出现从下游运动到上游的现象。观察流凌运动情况,可以发现直接碰撞到凹岸弯道处的流凌几乎没有。20 s之后第1个回流区内出现流凌。尽管凹岸弯道会由此受到冲刷磨损,但是相较于工况1,流凌数量大幅度减小,因此可以看出此处布置丁坝可以十分有效的防治凹岸弯道受到上游流凌的碰撞,并且减少带来的冲刷磨损。

|
Download:
|
| 图 5 工况2不同时刻流凌运动俯视图 | |
此工况为基于工况2单一丁坝布置形式出现的现象,进行的丁坝优化布置调整。由于在上游直道与弯道衔接处布置单一丁坝,较为突兀的束窄了水槽断面,使得流场中主流线流速过大。同时,本工况对回流区较长的现象也可进一步改善,以更大程度地减小冲刷磨损。
本工况在弯道首部30°的位置加置一个同样尺寸的正挑丁坝。该工况1与工况2的主流线大致走向一致,但是主流线最大流速稍有减小,约为0.42 m/s。减小的主流线流速使得上游流凌可以更为缓和的流向下游,一定程度上减小了碰撞与冲刷磨损。
本工况出现3个明显的回流区。第1个出现在两丁坝中间,回流区内流速极小,可视作静水区域。第2个出现在弯道丁坝后,从弯道丁坝至弯道尾部,形成一个逆时针的回流区。第3个仍是出现在凸岸一侧,从弯道尾部开始,在下游直道段,长度约为1.38 m,为顺时针回流区,长度较工况2短。不同时刻流凌运动如图 6。

|
Download:
|
| 图 6 工况3不同时刻流凌运动俯视图 | |
本工况将弯道处的丁坝向下游方向移动,布置在与弯道首部呈60°的位置。主流线方向仍为从凸岸弯道向凹岸直道。由于两丁坝间距明显加大,束窄段的长度变长,突变速度不再明显,弯道处流场过渡较为平缓。相比之前双丁坝工况布置形式,主流线靠近下游直线段最大速度明显减小,最大速度约为0.38 m/s,上游流凌速度明显减小。
本工况流场出现3处明显回流区。第一处位于两丁坝之间,第二处从弯道丁坝后开始至弯道尾部,回流区范围较小。第三处位于凸岸一侧,从弯道尾部开始,在下游直道段,长度约为1.3 m,为顺时针回流区,较之前双丁坝的情况都有明显的减小。
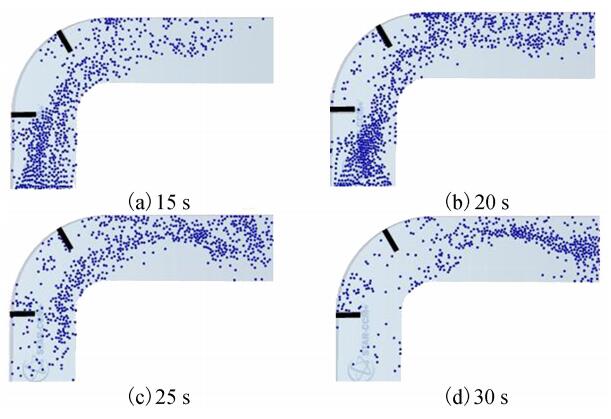
根据图 7可以看出,可以发现一小部分上游运动下来的流凌会与弯道丁坝发生碰撞,速度逐渐减小至0,停留在弯道丁坝前,随后慢慢进入回流区,继续向上游运动。这时,弯道丁坝就起到了拦截部分上游运动速度较快冰凌,防止其直接撞击护岸结构的作用。将冰凌对护岸结构的直接碰撞力转化为冰凌对丁坝的撞击力,很大程度上起到了护岸建筑物的保护作用。
|
Download:
|
| 图 7 工况4不同时刻流凌运动俯视图 | |
本工况在弯道首部、尾部与上、下游直道连接处各布置一个同尺寸的正挑丁坝。相比较其他双丁坝布置形式,主流线在下游没有更加明显的偏向凹岸,靠近两侧护岸的水流速度仅为0.1 m/s。
流场中出现的3个主要回流区,最明显的回流区位于两丁坝之间,范围较大。其他两个回流区,相比较其他双丁坝布置形式,有明显的变化。尽管这两个回流区位置仍在丁坝后部和凸岸直线段处,但是影响范围极小,回流区宽度仅为0.25 m左右,范围缩小50%左右。
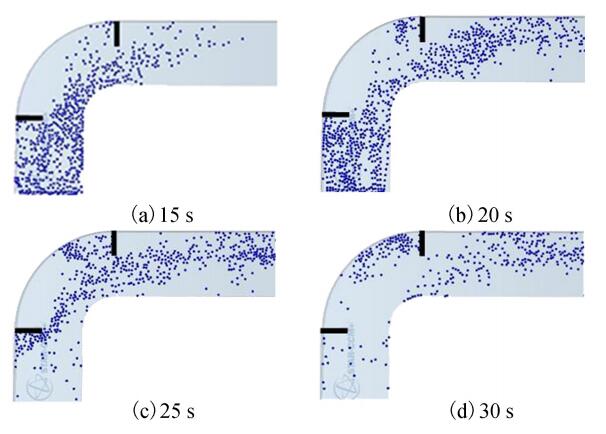
根据图 8可以看出,约90%的上游流凌沿主流线向下游运动,不会停滞在丁坝之间。只有余下的少部分流凌会直接碰撞护岸或丁坝,停滞在下游丁坝前,逐渐进入回流区。而这一部分流凌还会与上游运动的流凌发生碰撞,从而减小上游流凌直接与护岸和丁坝碰撞的速度,减弱由此带来的破坏性影响。
|
Download:
|
| 图 8 工况5不同时刻流凌运动俯视图 | |
同一模型的物理模型试验在黑龙江省水利科学研究院水利创新大厅进行。弯道处试验图如图 9。

|
Download:
|
| 图 9 弯道处实验 | |
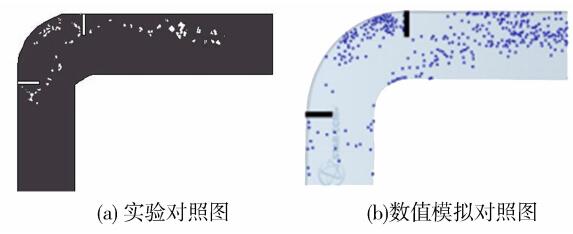
试验中,弯道两侧与底面均由砖墙浇砌,水泥抹面,表面平整。丁坝采用不透水的复合板,在浇砌弯道水槽两侧时,预先在砖墙内埋置木方,以方便丁坝在不同位置处的安置。丁坝采用90°固角和螺丝固定于弯道水槽两侧的木方上,并将橡皮泥加固于丁坝与两侧边界的衔接处。同时,实验采用北京尚水公司开发的流场实时测量系统和冰排流场测量与分析系统对各工况流场与流凌运动进行监测。观察现象,将数值模拟与模型试验的同种工况结果进行对比,以工况5为例对比同一时刻实验与数值模拟结果运动图像,如图 10~12。

|
Download:
|
| 图 10 工况5在15 s时流凌运动俯视图 | |

|
Download:
|
| 图 11 工况5在25 s时流凌运动俯视图 | |
|
Download:
|
| 图 12 工况5在30 s时流凌运动俯视图 | |
如图 10~12,发现流凌运动轨迹大致相同,对于丁坝的布置对流凌运动的影响规律相同,因此研究表明基于Star-CCM+软件平台的此种数值模拟方法可以较好地模拟流凌在水流中的运动,在今后的工程实际应用中,可广泛应用以达到提升工程价值,降低工程造价的作用。
5 结论通过对90°弯道水流中不同丁坝布置形式下流凌的运动情况进行数值模拟,发现并概括出如下规律:
1) 对于90°弯道水流,如果不采用丁坝等护岸建筑物,上游流凌会对凹岸弯道造成严重的碰撞破坏与冲刷磨损,因此考虑在凹岸弯道附近布置丁坝,加强对护岸结构的保护。
2) 对于90°弯道水流,单丁坝布置形式可以有效地减少上游流凌对弯道护岸结构的碰撞破坏,但对于冲刷磨损的现象有待改善。
3) 对于90°弯道水流,采用双丁坝布置形式,结合弯道双丁坝水流特性,观察现象,分析不同位置的丁坝布置形式对于上游流凌运动情况的影响。针对每一种工况,全面详细地分析了流凌与护岸作用的方式,对弯道河流布置丁坝护岸建筑物有指导意义。
4) 将数值模拟结果与实验结果比对,现象基本一致,因此,本文数值模拟方法可作为分析流凌运动,设计水工建筑物的有效方法之一。
5) 为了更全面的分析,流凌的不同尺寸,分布密度,水流速度,丁坝的挑角可作为今后研究的方向。
| [1] |
姜坤. 冰期弯道河冰运动特性数值模拟研究[D]. 合肥: 合肥工业大学, 2014. http://cdmd.cnki.com.cn/Article/CDMD-10359-1015568839.htm
( 0) 0)
|
| [2] |
宋小艳, 赵新, 刘博静. 渠道潜冰底面水压力分布特性的数值模拟研究[J]. 水资源与水工程学报, 2014, 25(1): 117-121. ( 0) 0)
|
| [3] |
李辉辉, 张宝森, 翟必垚, 等. 基于离散元方法的竖直群桩冰荷载分析[J]. 南水北调与水利科技, 2017, 15(1): 126-131. ( 0) 0)
|
| [4] |
刘炳慧, 管效仲, 鞠文昌. 松花江航道整治建筑物防冻防冰措施研究[J]. 水道港口, 2009, 30(3): 187-190. ( 0) 0)
|
| [5] |
沈洪道. 河冰研究[M]. 霍世青, 李世明, 饶素秋, 等, 译. 郑州: 黄河水利出版社, 2010.
( 0) 0)
|
| [6] |
王福军. 计算流体动力学分析[M]. 北京: 清华大学出版社, 2004.
( 0) 0)
|
| [7] |
美国陆军工程兵团. 河冰管控工程设计手册[M]. 汪易森, 杨开林, 张滨, 等, 译. 北京: 中国水利水电出版社, 2013.
( 0) 0)
|
| [8] |
王军, 陈胖胖, 隋觉义. 稳封期天然河道冰塞堆积的数值模拟[J]. 水利学报, 2011, 42(9): 1117-1121. ( 0) 0)
|
| [9] |
金占军. 冰水两相流输水浮冰受力特性研究[D]. 北京: 中国水利水电科学研究院, 2016. http://cdmd.cnki.com.cn/Article/CDMD-82301-1016282103.htm
( 0) 0)
|
| [10] |
MORSE B, RICHARD M. A field study of suspended frazil ice particles[J]. Cold regions science and technology, 2009, 55(1): 86-102. DOI:10.1016/j.coldregions.2008.03.004 ( 0) 0)
|
| [11] |
SHEN H T, SU Junshan, LIU Lianwu. SPH simulation of river ice dynamic[J]. Journal of computational physics, 2000, 165(2): 752-770. DOI:10.1006/jcph.2000.6639 ( 0) 0)
|
| [12] |
狄少丞, 季顺迎, 薛彦卓. 船舶在平整冰区行进过程的离散元分析[J]. 海洋工程, 2017, 35(3): 59-69. ( 0) 0)
|
| [13] |
薛彦卓, 倪宝玉. 极地船舶与浮体结构物力学问题研究综述[J]. 哈尔滨工程大学学报, 2016, 37(1): 36-40. ( 0) 0)
|
 2018, Vol. 45
2018, Vol. 45


