2. 哈尔滨工程大学 计算机科学与技术学院, 黑龙江 哈尔滨 150001
2. College of Computer Science and Technology, Harbin Engineering University, Harbin 150001, China
结构物限强度的计算目前主要有4种方法,即直接计算法、理想结构单元法、逐步破坏法和非线性有限元法[1]。直接计算法多用于评估单甲板梁的极限强度,但需要大量实验数据验证,对不同船型需进行单独分析,且其所得结果不精确,不适用于工程计算[2]。理想结构单元法在1974年首先提出[3],其优点是复杂计算简单化,精简节点自由度,但某些因素被忽略, 导致结果精度较低。逐步破坏法比较简单,计算较快,但其只能求解有关弯曲的极限强度,无法分析整船或者结构物的破坏和响应[4]。本文依据船级社规范,首先利用典型箱型梁验证非线性有限元法的有效性,然后通过非线性有限元方法分别进行双体船、三体船、半潜式海洋平台在不同危险工况下的极限强度计算,总结出一套行之有效的极限强度计算方法,为以后的多浮体的海洋结构物极限强度校核提供参考。
1 经典箱型梁极限强度的分析与验证 1.1 箱型梁极限强度数值方法计算很多研究人员专门设计箱型梁结构,对其进行极限强度的分析,其实验数据已经相当成熟,并且被引用多次用来证明某种去求解极限强度方法的准确性[5-8]。现在,在前人箱型梁模型的基础上,使用非线性有限元的方法计算典型箱型的梁极限强度,与先前的计算结果进行分析比较,以更好地开展研究工作。
1.1.1 一种典型箱型梁的引入本文采用S. Saad-Eldeen教授课题组设计的一种典型箱型梁结构[8]:箱型梁长为1 400 mm,宽为800 mm,高为600 mm。箱型梁的上方板壳结构有5根相聚150 mm的纵向加强筋。在箱型梁的左侧和右侧板壳结构上各有2根纵向的不对称分布的加强筋。在箱型梁的下方板壳结构上,只有中间1条加强筋是纵向的。加强筋的材料均为扁钢。在箱型梁的周围采用扁钢沿着环向进行加固,并且扁钢之间的距离为400 mm。具体箱型梁结构如图 1、2所示。

|
Download:
|
| 图 1 箱型梁剖面视图 | |

|
Download:
|
| 图 2 箱型梁俯视图 | |
箱型梁的具体板厚和加强筋尺寸见表 1。
|
|
表 1 测温数据对比 |
此箱型梁设计的是中垂状态,材料均为低碳钢,材料的基本属性具体为:
1) 弹性模量E——206 000 N/mm2
2) 密度ρ——7.85×10-9 t/mm3
3) 泊松比v——0.3
4) 屈服强度σ——235 MPa
1.1.2 讨论失稳情况在此箱型梁处于中垂状态时,箱型梁的甲板结构受压,可能发生屈曲;底板结构受拉,可能发生屈服。而甲板结构受压情况复杂,可能发生板材失稳也有可能发生骨材失稳,甚至不发生失稳;而底板结构受拉情况简单,只可能发生屈服破坏或者没有破坏。想要计算箱型梁在中垂状态下的极限强度,只需计算出甲板板、甲板纵骨最小值与材料屈服极限值相比较,并且取其3个值的最小值,当作箱型梁的屈服极限值,并用其与箱型梁的剖面模数相乘即可得到甲板的极限强度,得到的值和底板的屈服强度与其剖面模数的乘积作比较,取其小者,即为整个箱型梁所能承受的最大弯矩。
下面将进行以下3种情况的讨论:
1) 甲板失稳
由箱型梁模型可知,甲板的板材被分成150 mm×400 mm大小的板格,由于长宽比很大,故可视为纵式骨架板。由结构物强度知识可以得到[6],纵式骨架板的欧拉应力计算公式为
| $ {\sigma _E} = \frac{{4{{\rm{ \mathsf{ π} }}^2}D}}{{{b^2}t}} $ |
式中:
| $ D = \frac{{E{t^2}}}{{12\left( {1-{\nu ^2}} \right)}} $ |
由上文可知,箱型梁的弹性模量E取206 000 N/mm2,泊松比ν取0.3,所以得
| $ {\sigma _E} = 80{\left( {\frac{{100t}}{b}} \right)^2} $ | (1) |
如果求出欧拉应力σE的数值比箱型梁材料的屈服强度σ大,则要进行板的减缩修正。甲板板在失稳前,板中压应力沿板宽度均匀分布;失稳后,板仍能继续工作,但是板中压应力重新分布,出现刚性区和柔性区,二者应力不同。甲板板失稳后,一个板格宽度b之内,刚性区面积A刚和柔性区A柔各占一半,板的减缩系数φ可通过式(2)求解:
| $ \varphi = \frac{{{\sigma _E}}}{{{\sigma _1}}} $ | (2) |
式中σ1是采用一般梁的弯曲理论计算船体得到的船体总纵弯曲应力:
| $ {\sigma _1} = \frac{M}{I}Z $ | (3) |
失稳后的板形式上仍可视作刚性构件,只要将板的柔性面积乘以减缩系数φ即可。
换言之,该板的不工作面积即被减缩掉的面积ΔA为
ΔA=A柔(1-φ)
箱型梁剖面模数WS的公式为
| $ {W_S} = \frac{I}{Z} $ | (4) |
如图 3所示,假设中和轴的初始位置在底板底部,即图中Y轴所在的位置,计算箱型梁对Y轴的面积矩为3.88×107 mm3,又因为箱型梁的剖面面积为1.20×104 mm2,用面积矩除以剖面面积得到数值为3.22×102 mm,即箱型梁剖面中性轴相对于基准轴Y轴的位置为在Y轴上方3.22×102 mm处。

|
Download:
|
| 图 3 箱型梁初始中和轴位置 | |
经过进一步计算可以得到箱型梁的相对于中和轴的惯性矩I=7.71×108 mm4。
由式(1)可得,箱型梁的欧拉应力σE为594 MPa,比箱型梁材料的屈服强度σ=235 MPa还要大,所以此箱型梁甲板板在材料达到屈服极限之前不会发生失稳。
2) 甲板骨材失稳
在杆件的稳定性检查中,甲板纵桁化为弹性基础梁,甲板纵骨可按单跨压杆计算。计算公式为
| $ {\sigma _E} = \frac{{{{\rm{ \mathsf{ π} }}^2}Ei}}{{{l^2}A}} $ | (5) |
本文计算纵骨及带板面积A采取欧美的计算方法,即
| $ A = f + {b_e}t $ | (6) |
如图 4所示,其中带板be取值为

|
Download:
|
| 图 4 带板宽度示意 | |
| $ {b_e} = \min \left( {b, l/6} \right) $ | (7) |
如果纵骨的欧拉应力超过材料的屈服极限,则应进行非弹性修正。对于短、中长杆而言,其修正后的临界应力σcr拟合公式为
| $ {\sigma _{cr}} = {\sigma _s}-\frac{{{\sigma _s}^2}}{{4{\sigma _E}}} $ |
对于细长杆而言,其修正后的临界压力σcr为
| $ {\sigma _{cr}} = {\sigma _E} = \frac{{{{\rm{ \mathsf{ π} }}^2}E}}{{{\lambda ^2}}} $ | (8) |
其中柔度λ计算公式为
| $ \lambda = \frac{l}{{\sqrt {i/A} }} $ |
对于文中的箱型梁模型而言,杆件的跨度l为400 mm,宽度b为150 mm,所以由式(7)得带板宽度be取值为66.7 mm。
由式(6)得A=3.82×102 mm2,又因为纵骨截面对其中性轴惯性矩I=5.66×103 mm4,由式(5)可得骨材得欧拉应力σE=1.91×102 MPa,比材料的极限强度小,所以在箱型梁材料达到极限强度之前,骨材会发生屈曲破坏。
由于文中的骨材可视为细长杆,由式(8)得其临界应力σcr=1.91×102MPa,所以骨材会在箱型梁材料达到屈服极限之前发生失稳。
3) 底板失稳
在考虑甲板板以及甲板骨材的时候,由于中垂情况下其为受压构件,所以有可能会发生屈服,但是底部构件在中垂状态下,只承受拉力,所以只可能发生屈服,不会失稳。板材屈服的极限强度为235 MPa,所以底板屈服即是底板受拉应力超过235 MPa。
1.1.3 箱型梁极限弯矩的确定根据以上3种情况的讨论,可以发现,在箱型梁处于中垂状态时,其极限强度需要分为底板极限强度和甲板极限强度2部分,并且取其最小值。
又因为在底部时的剖面模数与甲板的剖面模数不同,由式(4)可得,甲板的剖面模数为2.77×106 mm3,底板的剖面模数为3.21×106 mm3。所以,对于甲板而言,其骨材为易损构件,并且其临界应力σcr=191 MPa,由式(3)可得,其甲板的极限弯矩为530 k·Nm,底板的极限弯矩为754 k·Nm。故本文箱型梁在中垂弯曲时,通过数值计算其所能承受的最大弯矩为530 k·Nm。
由于本文采用的S. Saad-Eldeen教授课题组设计箱型梁的极限弯矩经验值568.94 MPa,通过数值计算所得结果与经验值有6.7%的误差。由于数值计算没有考虑板与板之间的相互联系以及其他非线性变化,故与经验值误差在10%以内就能达到所要求的精度。
1.1.4 达到极限弯矩时转角的确定下面,将通过数值计算的方法求解使箱型梁达到极限弯矩时在两端所需加载的转角,为下文利用有限元软件求解箱型梁极限强度做准备。
在求解箱型梁的转角时,可以把箱型梁看作一根实心简支梁,只考虑其弹性模量E和剖面惯性矩I,其他例如板的屈曲、非线性等忽略不计。
根据结构力学理论,图 5表示简支梁的受力。

|
Download:
|
| 图 5 简支梁弯矩转角模型 | |
简支梁的转角计算公式为
| $ {\theta _{01}} = \frac{{{M_1}l}}{{3EI}} + \frac{{{M_2}l}}{{6EI}} $ | (9) |
由上文的数据,将弹性模量E=2.06×105 N/mm2、I=2.03×109 mm4、l=1 400 mm,M1=M2=530 k·Nm带入式(9)可得转角θ01大小为0.003 rad,而在实际用有限元软件计算的过程中,因为考虑到材料之间的连接以及材料的非线性,所以其加载的角度上限一般在θ01的1~2倍。这就是在后文用有限元计算弯矩时加载转角的计算依据。
1.2 箱型梁极限强度非线性有限元方法验证本文基于以上数据建立模型。建模采用PATRAN软件,计算求解使用ABAQUS软件。在PATRAN软件中,以mm为基本单位建立箱型梁。模型按照中国船级社有限元建模规范,x轴方向指向船体的纵向,向船首方向为正;y轴方向指向船体的横向,向左舷为正;z轴方向为船体的垂向,向上为正。由于模型为箱型梁,没有实船的复杂性,故将模型原点设置在船横剖面与纵剖面中心处。
建模划分网格类型选择Quad单元,网格大小为12.5 mm,宽度方向、高度方向和长度方向的单元数分别为64、48、112,建立的有限元模型如图 6所示。

|
Download:
|
| 图 6 箱型梁有限元网格划分模型 | |
模型建造完成之后,利用ABAQUS有限元软件计算其极限强度。在ABAQUS软件中,按照S. Saad-Eldeen教授课题组所采用的低碳钢材料对模型软件附上基本属性。
在ABAQUS软件中,本文采用动态分析模式,利用MPC约束形式加载转角或者位移,输出弯矩位移曲线。在经典箱型梁模型极限强度分析中,只考虑总纵弯曲的极限强度,在两端端面中点建立2个参考点,将2个端面节点以MPC约束形式固结到2个参考点上,然后将2个参考点绕y轴施加反向、同等大小的0.004 rad转角,使箱型梁达到中垂状态。在此状态下输出弯矩位移曲线,此时弯矩即为中垂弯矩。具体如图 7所示。

|
Download:
|
| 图 7 箱型梁有限元计算模型 | |
进行计算之后可得弯矩转角曲线,如图 8所示。

|
Download:
|
| 图 8 箱型梁转角弯矩曲线 | |
经过计算,得到此箱形梁的在加载0.002 46 rad时,达到弯矩最大值5.603×108 N·mm,此时,箱型梁达到中垂状态时的最大极限弯矩,如果继续施加转角,箱型梁材料发生屈服,整个箱型梁结构发生破坏,不能再维持其基本形态,箱型梁整体弯矩开始下降。在S. Saad-Eldeen教授所做的有关此箱型梁的实验中,得到箱型梁的中垂状态时的极限弯矩经验值为5.689 ×108 N·mm,本文计算结果与之相比较可得误差很小,为1.5%,说明用ABAQUS有限元软件计算箱型梁极限强度具有很高的精确度,计算结果真实可信,计算方法行之有效。
2 多浮体海洋结构物极限强度计算基于上述箱型梁极限强度非线性有限元计算方法,下面分别就双体船、三体船以及半潜式海洋平台求解其极限强度。
2.1 建立模型同种类型的每艘船或者每个海洋平台的结构都不可能完全相同,有的甚至差别很大,本文不能够一一建立模型。为了方便简洁地介绍每种船型或者海洋平台的极限强度计算方法,本文将用不同形状箱型梁组合成船体或者海洋平台的基本结构,用于分析每种海洋结构物的危险工况以及用ABAQUS有限元软件分析计算时转角的加载方式。
由于本文是使用简单箱型梁来组合成船体和海洋平台结构,所以具体结构的细节并不能很好地展现出来,并且上层建筑结构均舍去,仅仅能够模拟出海洋结构物主要结构,用于论文的分析与验证。另外,在研究有限元软件计算结构极限强度时发现,结构简单的箱型梁划分3种不同大小的网格时,其最终计算结果均非常接近,与经验值的误差很小。

|
Download:
|
| 图 9 箱型梁3种大小的网格划分时弯矩转角曲线对比 | |
本文将每个模型的有限元网格划分偏大,以便更快速更高效地提取有效信息,得出有效的计算方法。
模型建立时使用材料所附属性均为:
弹性模量E——206 000 N/mm2
密度ρ——7.85×10-9 t/mm3
泊松比v——0.3
屈服强度σ——235 MPa
板材厚度t——1 mm
极限强度的主要决定因素为结构的剖面模数以及材料属性。在保证剖面模数以及材料特性相同的情况下,可以利用组合箱型梁搭建基本模型,使其具备多浮体结构物的基本特征。基于该计算思路,分别对双体船、三体船、半潜式海洋平台3类典型多浮体结构物建立有限元模型如图 10。

|
Download:
|
| 图 10 3种典型多浮体海洋结构物箱型梁组合模型 | |
根据工程实践和规范要求,分别选取双体船、三体船和半潜式海洋平台的危险工况如表 2所示[9-14]。
|
|
表 2 几种典型多浮体结构物工况选取 |
双体船由2个片体通过连接桥连接而成。在上文的研究中,双体船的危险工况可分为4种:总纵弯曲、总横弯曲、横向扭转、纵向扭转。其中,总纵弯曲分为中垂和中拱2个状态。分别对不同工况下双体船施加的转角上限如表 3所示。
|
|
表 3 不同工况下双体船施加转角上限 |
在ABAQUS软件中,本文采用动态分析模式,利用MPC约束形式加载转角或者位移,输出弯矩位移曲线。几种不同工况下的计算结果如图 11所示。

|
Download:
|
| 图 11 双体船不同工况转角弯矩曲线 | |
计算可得,双体船结构典型工况下极限强度如表 4所示。
|
|
表 4 双体船结构典型工况下极限弯矩及对应转角 |
三体船由主船体和2个片体共用1个甲板连接而成。其中3个船体均为细长体,三体船的片体由于结构较弱,长度有限,不参与整体的总纵强度,片体只是起着保证船的横向稳性的作用。同双体船,三体船的主要危险工况有4种:总纵弯曲、总横弯曲、横向扭转、纵向扭转。其中,总纵弯曲分为中垂和中拱2个状态。
分别对不同工况下三体船施加的转角上限如表 5所示。
|
|
表 5 不同工况下三体船施加转角上限 |
几种不同工况下计算结果如图 12所示。
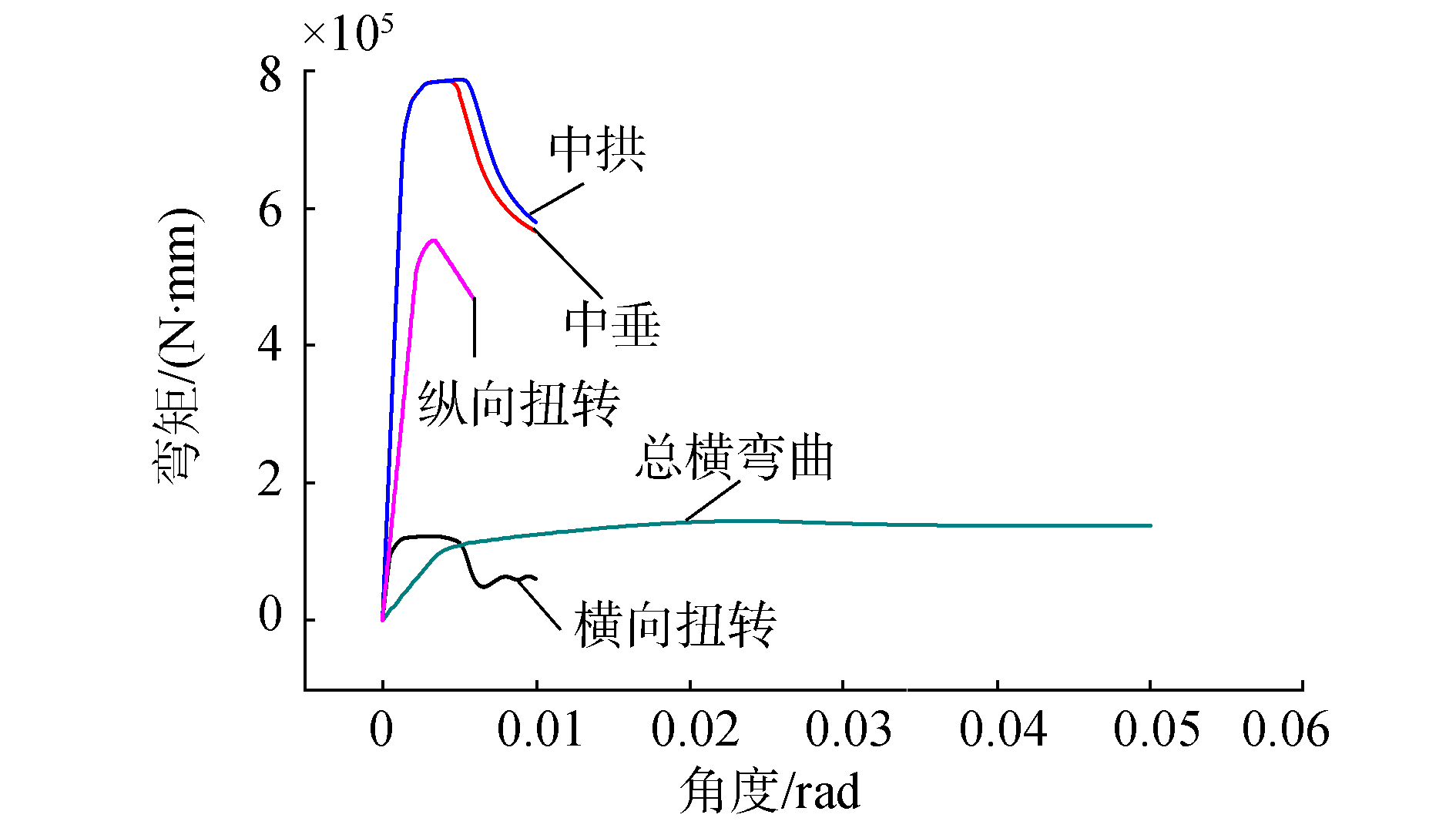
|
Download:
|
| 图 12 三体船不同工况转角弯矩曲线 | |
计算可得,双体船结构典型工况下极限强度如表 6所示。
|
|
表 6 三体船结构典型工况下极限弯矩及对应转角 |
本文研究的半潜式海洋平台经过前文的论证分析,共有3种危险工况:总纵弯曲、总横弯曲、横向扭转。其中,总纵弯曲包括中拱和中垂2种状态。下面将进行每种危险工况下的极限强度的求解。
分别对不同工况下半潜式海洋平台施加的转角上限如表 7所示。
|
|
表 7 不同工况下半潜式海洋平台施加转角上限 |
几种不同工况下计算结果如图 13所示。

|
Download:
|
| 图 13 三体船不同工况转角弯矩曲线 | |
计算可得,半潜式海洋平台结构典型工况下极限强度如表 8所示。
|
|
表 8 半潜式海洋平台工况下极限弯矩及对应转角 |
本文利用ABAQUS有限元软件,通过验证经典箱型梁的极限强度来确定有限元法的有效性以及精度,然后根据双体船、三体船以及半潜式海洋平台三种典型多浮体海洋结构物的结构特点建立其相对应的组合箱型梁模型,并且根据相应规范确定其危险工况。之后,本文针对每一工况进行相应的极限强度分析并给出其相应的分析方法。通过以上所述研究,本文得到以下结论:
1) 本文采用数值计算的方法计算经典箱型梁极限强度的计算,得到的数值在误差允许范围之内。利用数值计算方法可以确定箱型梁在达到极限强度时梁的转角大小,为有限元方法计算结构物强度提供一个确定加载转角上限的依据。
2) 利用有限元方法对结构进行极限强度分析,与数值方法相比,有限元方法结果准确可靠并且精确度很高,因为有限元软件考虑了结构之间的相互作用以及材料的非线性特性,这是数值方法难以做到的。
3) 分别对双体船、三体船、半潜式海洋平台3种典型的多浮体海洋结构物进行了极限强度计算,得到了典型工况下的极限弯矩及对应转角。
本文还可以在以下方面进行改进与后续研究:
1) 本文只是将船舶与海洋结构物用箱型梁简单地模拟出来,与实际结构模型差别较大,故在计算船舶与海洋结构物极限强度时,本文仅仅只是提供一个参考,具体有关结构的实际加载方式还需结合实际情况分析。
2) 本文选择的均为船级社规范里有关弯矩或者扭矩的危险工况,而对于剪切力这样的工况,本文因其较为复杂没有进行具体的说明,故工况条件与计算方法还有待改进与完善。
3) 本文进行极限强度计算时,划分网格较大,有可能会带来一些偏差,因此在以后研究中应该细化网格进一步分析。
| [1] |
RECKLING K A. Behavior of box girder under bending and shear[C]//Proceeding of the International Ship & Offshore Structures Congress (ISSC). Pairs, 1979: 46-49.
( 0) 0)
|
| [2] |
甄春博, 王天霖, 于鹏垚. 基于直接计算的三体船结构疲劳强度影响因素分析[J]. 中国舰船研究, 2017, 12(3): 86-90. ( 0) 0)
|
| [3] |
UEDA Y, SHERIF R. An ultimate transverse strength analysis of ship structures[J]. Journal of the society of naval architects of Japan, 1974, 1974(136): 309-324. DOI:10.2534/jjasnaoe1968.1974.136_309 ( 0) 0)
|
| [4] |
李恒, 郎元荣. 船舶与海洋工程结构极限强度分析[J]. 科技资讯, 2015, 13(7): 68. ( 0) 0)
|
| [5] |
GARBATOV Y, SAAD-ELDEEN S, SOARES C G. Hull girder ultimate strength assessment based on experimental results and the dimensional theory[J]. Engineering structures, 2015, 100: 742-750. DOI:10.1016/j.engstruct.2015.06.003 ( 0) 0)
|
| [6] |
FAULKNER D. A review of effective plating to be used in the analysis of stiffened plating in bending and compression[J]. Journal of ship research, 1975, 19(1): 1-17. ( 0) 0)
|
| [7] |
KIM D K, PEDERSEN P T, PAIK J K, et al. Safety guidelines of ultimate hull girder strength for grounded container ships[J]. Safety science, 2013, 59: 46-54. DOI:10.1016/j.ssci.2013.04.006 ( 0) 0)
|
| [8] |
SAAD-ELDEEN S, GARBATOV Y, SOARES C G. Experimental assessment of the ultimate strength of a box girder subjected to severe corrosion[J]. Marine structures, 2011, 24(4): 338-357. DOI:10.1016/j.marstruc.2011.05.002 ( 0) 0)
|
| [9] |
康杰豪, 贺远松, 谭开忍, 等. 轮印载荷下多跨梁最危险工况分析与优化[J]. 中国舰船研究, 2016, 11(6): 56-64. ( 0) 0)
|
| [10] |
陈攀. 双体客船波浪载荷及强度计算分析[J]. 船舶工程, 2015, 37(11): 1-5, 13. ( 0) 0)
|
| [11] |
李雨辰, 唐昌德. 筒形三体铝合金艇有限元强度分析[J]. 南通航运职业技术学院学报, 2016, 15(1): 39-43. ( 0) 0)
|
| [12] |
耿彦超, 胡嘉骏, 王辉. 三体船波浪外载荷设计规范参数研究[C]//中国造船工程学会船舶力学学术委员会. 2015年船舶水动力学学术会议论文集. 哈尔滨: 中国造船工程学会船舶力学学术委员会, 2015: 5. http://cpfd.cnki.com.cn/Article/CPFDTOTAL-ZGZC201507001060.htm
( 0) 0)
|
| [13] |
彭丹丹, 傅杰, 刘昆. 深海半潜式钻井平台上部船体极限承载力分析[J]. 船舶, 2015(6): 40-44. ( 0) 0)
|
| [14] |
吴连强, 王磊, 陈行, 等. 半潜式海洋平台的建造与质量管理研究[J]. 才智, 2013(9): 334. ( 0) 0)
|
 2018, Vol. 45
2018, Vol. 45


