欠驱动系统的控制问题一直是近年来研究的热点和难点,一般来说,大多数海面上航行的船舶都属于欠驱动系统。这类系统都具有强非线性、高耦合、模型参数不确定性的特点[1],为控制器的设计带来很多困难。
船舶的曲线航迹跟踪控制在船舶控制理论中具有重要的实际意义。很多路径规矩与避障的研究中,最终都面临曲线航迹的控制问题[2]。目前已知的曲线航迹跟踪控制的理论中,主要有输出反馈控制法、状态反馈控制法、输出重定义方法以及级联方法等[3-5],这类控制器一般对被控模型的参数有较高的要求,这导致在很多的实际应用如模型参数不确定或参数扰动较大的情况下,控制器设计困难。Fossen[6]提出了一种自适应积分视线航迹跟踪控制器,DO等[7]提出了一种全局鲁棒自适应航迹跟踪控制器,也有很多学者提出使用滑模控制器实现船舶曲线航迹跟踪[8-10],但在很多方法中期望航迹的设定都是时间t的函数,即要求船舶在某一时刻达到某一具体位置,这在许多情况中是不必要的,可能没有对船舶到达某一位置的时间做限制。
在以上问题的考虑中,本文提出一种基于航向控制的滑模控制律的设计方法,实现对已知曲线航迹的跟踪控制。且曲线航迹的定义与时间无关。由于所用船舶模型并未提供实现直接侧移的装置,所以为典型的欠驱动控制系统。
1 航迹 1.1 航迹方程本文中的期望航迹定义为一固定的、可用二维数学模型完全描述的平面曲线。要求曲线充分光滑,其一阶导数可求。可用式(1)表示:
| $ {{y}_{d}}=f\left( {{x}_{d}} \right) $ | (1) |
基于一般性、简洁性、概括性的思想,本文仿真过程中使用以下3种期望航迹。并分别对其进行控制器的设计,以及仿真验证。
其一为一条固定直线,可描述为
| $ {{y}_{d}}=k{{x}_{d}}+d $ |
式中:(xd, yd)为期望航迹,k为直线斜率,d为截距。
其二为一圆心、半径已知的圆形曲线,可在实际仿真中被描述为
| $ {{\left( {{x}_{d}}-{{x}_{0}} \right)}^{2}}+{{\left( {{y}_{d}}-{{y}_{0}} \right)}^{2}}=R^2 $ |
式中:(x0, y0)为圆形航迹的圆心,R为圆形的半径。
其三可描述为一条正弦曲线
| $ {{y}_{d}}=A\sin \left( w{{x}_{d}}+m \right)+D $ |
式中:A为曲线幅值,w为相位角。
1.2 期望航向角求取在控制过程中,假使船舶位置为其质心所在坐标(x, y)。并且规定在每一个位置(x, y),在期望航迹线上都能找到唯一确定点(xr, yr),其与船舶当前位置(x, y)的直线距离最短(这里不考虑在期望航迹中与船舶当前距离最短的点同时存在几个的情况),并规定船舶沿期望航迹线向右行驶,如图 1。

|
Download:
|
| 图 1 期望航迹与船相关变量示意 | |
在(xr, yr)点上作光滑期望轨迹线的切线,与X轴夹角φd即当前期望航向角(如图 1)。经由几何运算可得
| $ {{\varphi }_{d}}=\arctan \left( \frac{{{y}_{r}}-y}{{{x}_{r}}-x} \right)-\rm{ }\!\!\pi\!\!\rm{ }/2 $ | (2) |
另外,当航迹为圆时,式(2)可简化为
| $ {{\varphi }_{d}}=\arctan \left( \frac{y-{{y}_{0}}}{x-{{x}_{0}}} \right)-\rm{ }\!\!\pi\!\!\rm{ }/2 $ | (3) |
此时(x0, y0)为固定点,即可直接求φd对时间t的导数。
当航迹为直线时,可直接指定φd=k。
1.3 遍历法求取期望航迹中(xr, yr)点在期望航迹中与船当前位置(x, y)距离最短的点(xr, yr)可使用局部遍历法求取。所谓局部遍历法描述如下:
1) 在期望航迹中指定一起始点(xi, yi)作为起点,计算出与船当前位置(x, y)的对应距离Di。
2) 根据期望航迹在(xi, yi)处的导数求出下一个邻接点的增量(Δxi, Δyi),具体求法如式(4),以此计算下一个邻接点距(x, y)的距离Di+1。下一个邻接点可表示为
| $ \left( {{x}_{i+1}},{{y}_{i+1}} \right)=\left( {{x}_{i}}+\Delta {{x}_{i}},f\left( {{x}_{i}}+\Delta {{x}_{i}} \right) \right) $ |
3) 若Di+1≤Di,继续步骤2),并将i=i+1。若Di+1>Di,则记录(xi+1, yi+1)作为(xr, yr)。
假设期望航迹在(xi, yi)处的导数为
| $ \left\{ \begin{array}{l} \frac{{\Delta {y_i}}}{{\Delta {x_i}}} = \kappa \\ \Delta {l^2} = \Delta x_i^2 + \Delta y_i^2 \end{array} \right. $ |
整理可得
| $ \left\{ \begin{array}{l} \Delta {x_i} = \pm \frac{{\Delta l}}{{\sqrt {1 + {\kappa ^2}} }}\\ \Delta {y_i} = \kappa \Delta {x_i} \end{array} \right. $ | (4) |
若(xr, yr)处期望航向满足φd∈(-π/2, π/2),Δxi取正;φd∈[-π, -π/2]∪(π/2, π],则Δxi取负。另外,易知当
本文采用的三自由度船舶运动模型[11],即
| $ \left\{ \begin{array}{l} \dot x = u\cos \varphi - v\sin \varphi \\ \dot y = u\sin \varphi + v\cos \varphi \\ \dot \varphi = r \end{array} \right. $ |
式中(x, y, φ)分别为船在世界坐标系三自由度的横向位置、纵向位置和艏摇角,(u, v, r)分别为船在随动坐标系三自由度的纵向速度、横向速度、艏摇角速度。假设U为船舶在航行过程中u、v的矢量和,即
| $ \left\{ \begin{array}{l} \dot x = U\cos \varphi \\ \dot y = U\sin \varphi \\ \dot \varphi = r \end{array} \right. $ |
关于船舶的航向采用自动舵控制,为了简化,将自动舵控制器设计为一阶线性野本方程[9]
| $ T\ddot \varphi + \dot \varphi = K\delta $ |
式中:K、T分别为船舶的回转性指数和操纵性指数,δ为控制舵输入角。
考虑航向控制过程中非线性的影响,在以上一阶野本方程中加入非线性项,得到一阶非线性野本方程
| $ T\ddot \varphi + \dot \varphi + \alpha {{\dot \varphi }^3} = K\delta $ |
式中α为非线性模型系数。整理以上公式,得到需要的被控数学模型的最终描述
| $ \left\{ \begin{array}{l} \dot x = U\cos \varphi \\ \dot y = U\sin \varphi \\ \dot \varphi = r\\ \dot r = - \frac{r}{T} - \frac{{\alpha {r^3}}}{T} + \frac{{K\delta }}{T} \end{array} \right. $ | (4) |
很多航向控制以及直线航迹控制的控制器设计中,由于不考虑纵向位移的变化,通常将模型第1项省略以简化。本文在设计航迹控制器的时候,期望航向角依赖船舶的横向以及纵向位置,所以模型的第1项不可省略。
2.2 设计S面控制器一般性地,光滑曲线可以分解为无数条长度趋近于0的微小线段,即可以把曲线看做无限条微小线段连成的折线。取常规模糊控制器规则表的主对角线数值连成的折线,可以用一个Sigmid曲线函数来拟合[8],形式为
| $ y = \frac{{2.0}}{{1.0 + \exp \left( { - kx} \right)}} - 1.0 $ |
使用Sigmid曲线函数设计的控制器被称作S面控制器:
| $ u = \frac{{2.0}}{{1.0 + \exp \left( { - {k_1}e - {k_2}\dot e} \right)}} - 1.0 $ |
式中:u为被控对象的控制输入,k1、k2为控制器参数,e、

|
Download:
|
| 图 2 不同k值下Sigmid型曲线函数 | |
图 2中,控制器参数k值变化,致使Sigmid曲线变化。k值越大,同样输入情况下,控制器输出越大,即控制度增强。k值不变的sigmid曲线中,控制器输入量的绝对值越小,其控制输出越小。在控制理论中,S面控制可看做是简易的模糊控制器,具有模糊控制的思想,由于其设计方便,控制效果明显,这里选择做偏差距离de的控制器。
在船舶航迹跟踪控制的过程中,船舶所在的每一点位置坐标都可以在期望航迹中获得2.3节中所述的(xr, yr),并得到与船当前位置(x, y)的直线距离, 记做de(具体参照图 1),这里称之为与期望航迹的偏航误差。易知,0≤|de| < M,M为船舶距期望航迹的距离上界。
| $ {d_e} = \sqrt {{{\left( {x - {x_r}} \right)}^2} + {{\left( {y - {y_r}} \right)}^2}} $ |
鉴于船舶欠驱动的特征,不能直接使用控制量实现对de的跟踪控制。这里设计一个在船舶跟踪期望航迹的过程中期望航向角的补偿角φofs作为偏航误差的控制量,
| $ \left\{ \begin{array}{l} {u_m} = \frac{{2.0}}{{1.0 + \exp \left( { - k{d_e}} \right)}} - 1.0\\ {\varphi _{ofs}} = {k_p}{u_m} \end{array} \right. $ |
式中:um为S面控制器根据偏航误差得到的控制参数,um∈(-1, 1),kp可看做是实际航行中船舶的最大转向舵角,k为控制器参数。
2.3 设计航向滑模控制器滑模控制法是一种“变结构”的非连续控制方法[12],其非线性表现为控制的不连续性,该控制特性可以迫使系统沿着规定的状态轨迹作小幅度的上下振动,同时对外界干扰及参数不确定具有良好的自适应性能,最终到达期望状态,即所谓的“滑动模态”运动。一般选择滑模面为
| $ \mathit{\boldsymbol{S}} = \dot e + \lambda e,\left( {\lambda > 0} \right) $ |
选取lyapunov法作为滑模面存在条件,即定义一个正定的lyapunov函数
| $ V\left( {x,t} \right) = \frac{1}{2}{\mathit{\boldsymbol{S}}^{\rm{T}}}\mathit{\boldsymbol{S}} \ge 0 $ |
式中:x为状态变量,t为系统时间。设计控制器使
一般参考控制律可被设计为
| $ u = \hat u - k\left( {x,\dot x} \right){\mathop{\rm sgn}} \left( \mathit{\boldsymbol{S}} \right) $ |
式中:
为了消除滑模控制中的“抖振”现象[13],采用
| $ u = \hat u - k\left( {x,\dot x} \right){\rm{sat}}\left( {\mathit{\boldsymbol{S}}/\mathit{\Phi }} \right) $ |
式中Φ为边界层厚度。
| $ {\rm{sat}}\left( {\mathit{\boldsymbol{S}}/\mathit{\Phi }} \right) = \left\{ \begin{array}{l} \mathit{\boldsymbol{S}}/\mathit{\Phi },\left| {\mathit{\boldsymbol{S}}/\mathit{\Phi }} \right| \le 1\\ {\mathop{\rm sgn}} \left( {\mathit{\boldsymbol{S}}/\mathit{\Phi }} \right),\left| {\mathit{\boldsymbol{S}}/\mathit{\Phi }} \right| > 1 \end{array} \right. $ |
设计滑模面之前,首先定义航向跟踪误差
| $ {\varphi _e} = \varphi - {\varphi _d} - {\varphi _{{\rm{ofs}}}} $ |
式中φofs为3.2节中与偏航误差de相关的期望航向角的补偿角。这里令
| $ {{\dot \varphi }_e} = \dot \varphi - {{\dot \varphi }_d} = r - {{\dot \varphi }_d} $ |
| $ {{\ddot \varphi }_e} = \ddot \varphi - {{\ddot \varphi }_d} = \dot r - {{\ddot \varphi }_d} $ |
航迹为一直线时,φd为常值,明显
航迹为圆形时,由式(2)可以直接求得对φd的1阶、2阶导数:
| $ {{\dot \varphi }_d} = \frac{{x\dot y - {x_0}\dot y - x\dot y + x{{\dot y}_0}}}{{{y^2} + y_0^2 + {x^2} + x_0^2 - 2y{y_0} - 2x{x_0}}} $ |
| $ \begin{array}{*{20}{c}} {{{\ddot \varphi }_d} = \left[ {\left( {x\ddot y - \ddot xy - {x_0}\ddot y + {y_0}\ddot x} \right)\left( {{y^2} + y_0^2 + {x^2} + x_0^2 - } \right.} \right.}\\ {\left. {2x{x_0} - 2y{y_0}} \right) - \left( {x\dot y - {x_0}\dot y - \dot xy + {y_0}\dot x} \right)}\\ {\left. {\left( {2x\dot x + 2y\dot y - 2{x_0}\dot x - 2{y_0}\dot y} \right)} \right]/}\\ {\left( {^{y2} + {y^2}_0 + {x^2} + {x^2}_0 - 2x{x_0} - 2y{y_0}} \right)2} \end{array} $ |
考虑到控制律中,需要使用式(4)的第4项,同时必须保证航向补偿角的有效性,故滑模面设计为
| $ \mathit{\boldsymbol{S}} = {{\dot \varphi }_e} + \lambda \int_0^t {{\varphi _e}\left( \tau \right){\rm{d}}\tau } $ | (5) |
对滑模面求导,得到
| $ \mathit{\boldsymbol{\dot S}} = {{\ddot \varphi }_e} + \lambda {\varphi _e} = \dot r - {{\ddot \varphi }_d} + \lambda \left( {\varphi - {\varphi _d} - {\varphi _{ofs}}} \right) $ |
由前面介绍控制律的设计规律,加上消除抖振的过程,滑模控制律可以设计为
| $ \delta = \hat \delta - {k_1}{\rm{sat}}\left( {\mathit{\boldsymbol{S}}/\mathit{\Phi }} \right) $ |
为使系统渐进稳定,定义Iyapunov函数为
| $ V = \frac{1}{2}T{\mathit{\boldsymbol{S}}^2} $ |
式中T为船舶的操纵性指数。求Iyapunov函数的导数[14],可得
| $ \begin{array}{*{20}{c}} {\dot V = T\mathit{\boldsymbol{S\dot S}} = }\\ {\mathit{\boldsymbol{S}}T\left( {\dot r - {{\ddot \varphi }_d} + \lambda \varphi - \lambda {\varphi _d} - \lambda {\varphi _{ofs}}} \right) = }\\ {\mathit{\boldsymbol{S}}\left( { - r - \alpha {r^3} + K\delta - T{{\ddot \varphi }_d} + } \right.}\\ {\left. {\lambda T\varphi - \lambda T{\varphi _d} - \lambda T{\varphi _{ofs}}} \right)} \end{array} $ |
令
| $ \begin{array}{*{20}{c}} {K\delta = r + \alpha {r^3} + T{{\ddot \varphi }_d} - \lambda T\varphi + }\\ {\lambda T{\varphi _d} + \lambda T{\varphi _{ofs}} - {k_1}{\rm{sat}}\left( {\mathit{\boldsymbol{S}}/\mathit{\Phi }} \right)} \end{array} $ | (6) |
则可得
| $ \begin{array}{*{20}{c}} {\dot V = - {k_1}{\rm{sat}}\left( {\mathit{\boldsymbol{S}}/\mathit{\Phi }} \right)\mathit{\boldsymbol{S}} = }\\ {\left\{ \begin{array}{l} - {k_1}{\mathit{\boldsymbol{S}}^2}/\mathit{\Phi ,}\left| {\mathit{\boldsymbol{S}}/\mathit{\Phi }} \right| \le 1\\ - {k_1}\left| \mathit{\boldsymbol{S}} \right|,\left| {\mathit{\boldsymbol{S}}/\mathit{\Phi }} \right| > 1 \end{array} \right.} \end{array} $ | (7) |
由式(7)可知,
由式(6)可得
| $ \begin{array}{*{20}{c}} {\delta = \left( {r + \alpha {r^3} + T{{\ddot \varphi }_d} - \lambda T\varphi + \lambda T{\varphi _d} + } \right.}\\ {\left. {\lambda T{\varphi _{ofs}} - {k_1}{\rm{sat}}\left( {\mathit{\boldsymbol{S}}/\mathit{\Phi }} \right)} \right)/K} \end{array} $ |
仿真实验中,采用某实船参数作为参考:其中航速U=7.7 m/s,回转性指数K=-0.478,操纵性指数T=216,非线性化参数α=30。
跟踪直线期望航迹的仿真试验控制器参数:k=10,λ=0.01,kp=10/57.3,k1=0.5,Φ=0.01。期望航迹设定为:yd=xd,xd∈(0, ∞)。仿真结果如图 3~8所示。

|
Download:
|
| 图 3 直线航迹下船横向位置变化 | |
|
Download:
|
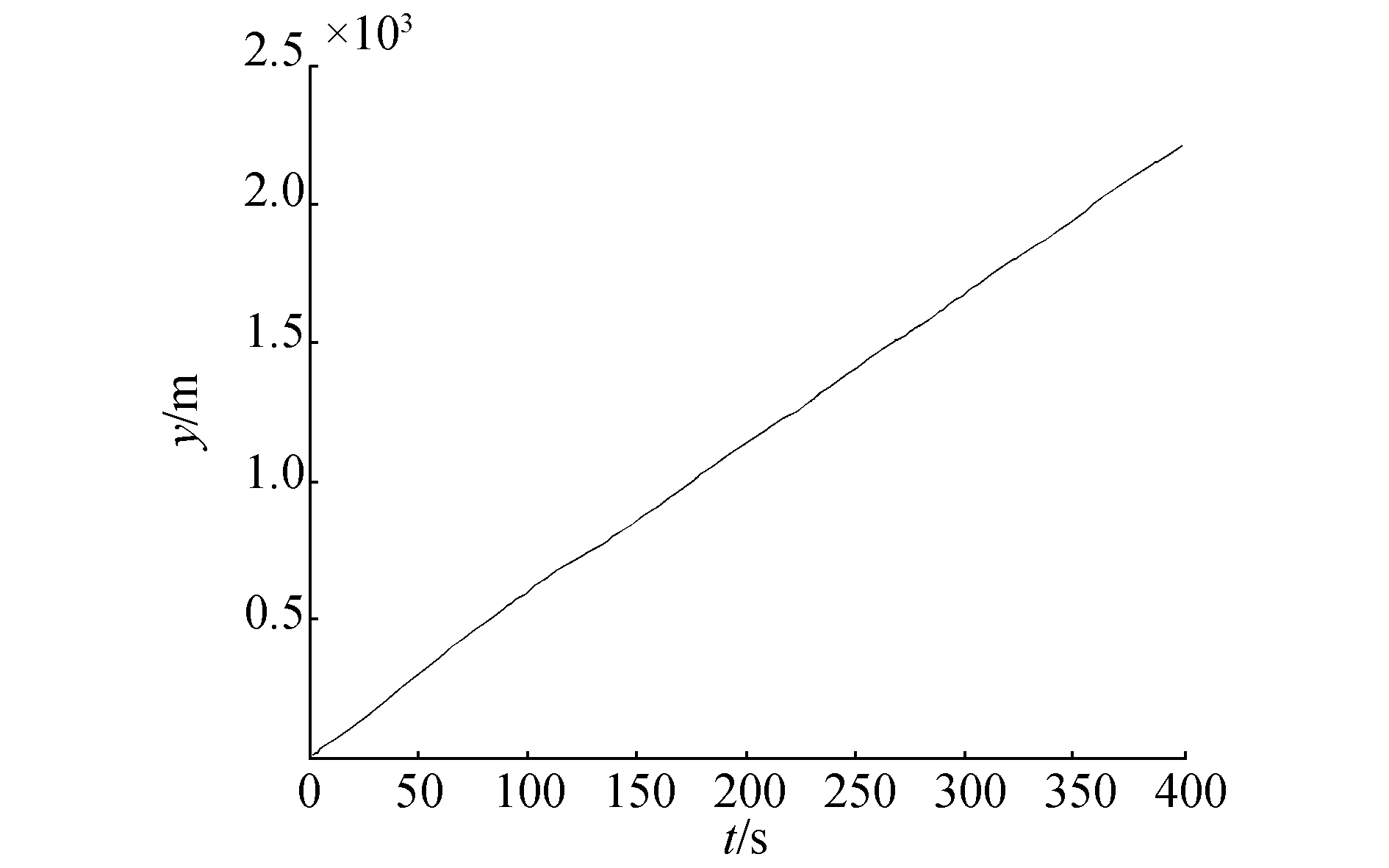
| 图 4 直线航迹下船纵向位置变化 | |
|
Download:
|
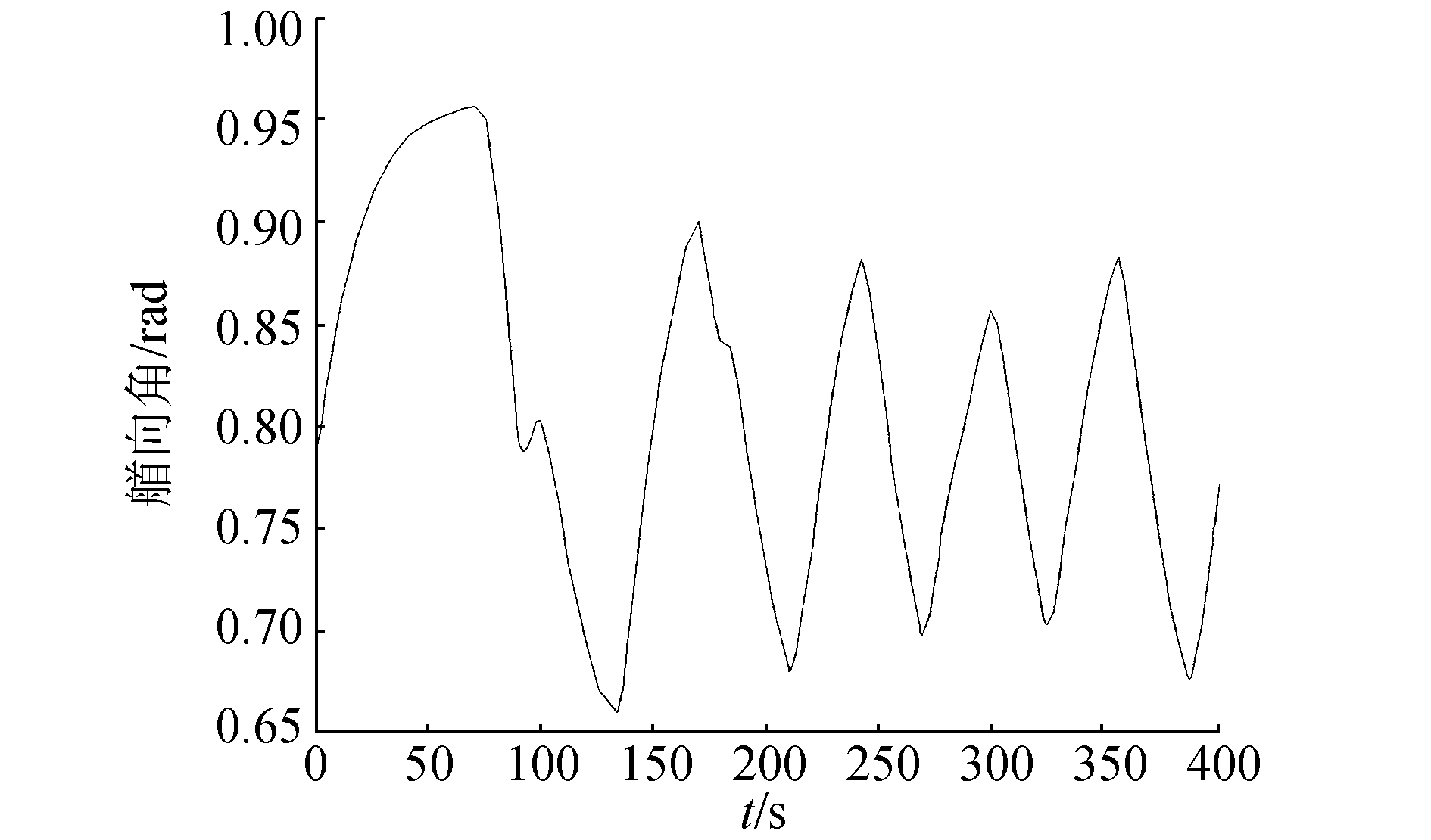
| 图 5 直线航迹下船艏向角变化 | |
|
Download:
|
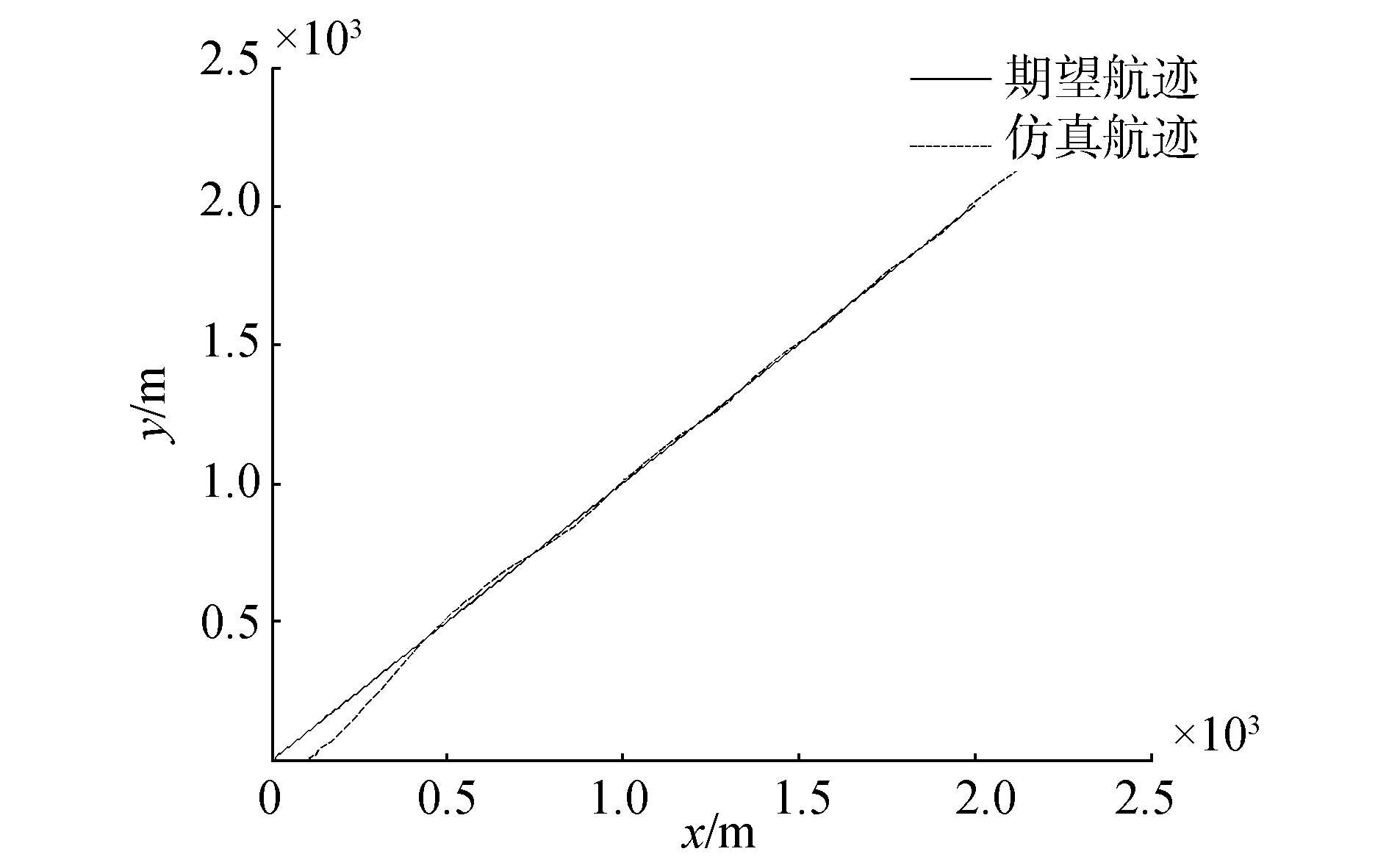
| 图 6 直线航迹下期望航迹与仿真航迹的比较 | |
|
Download:
|
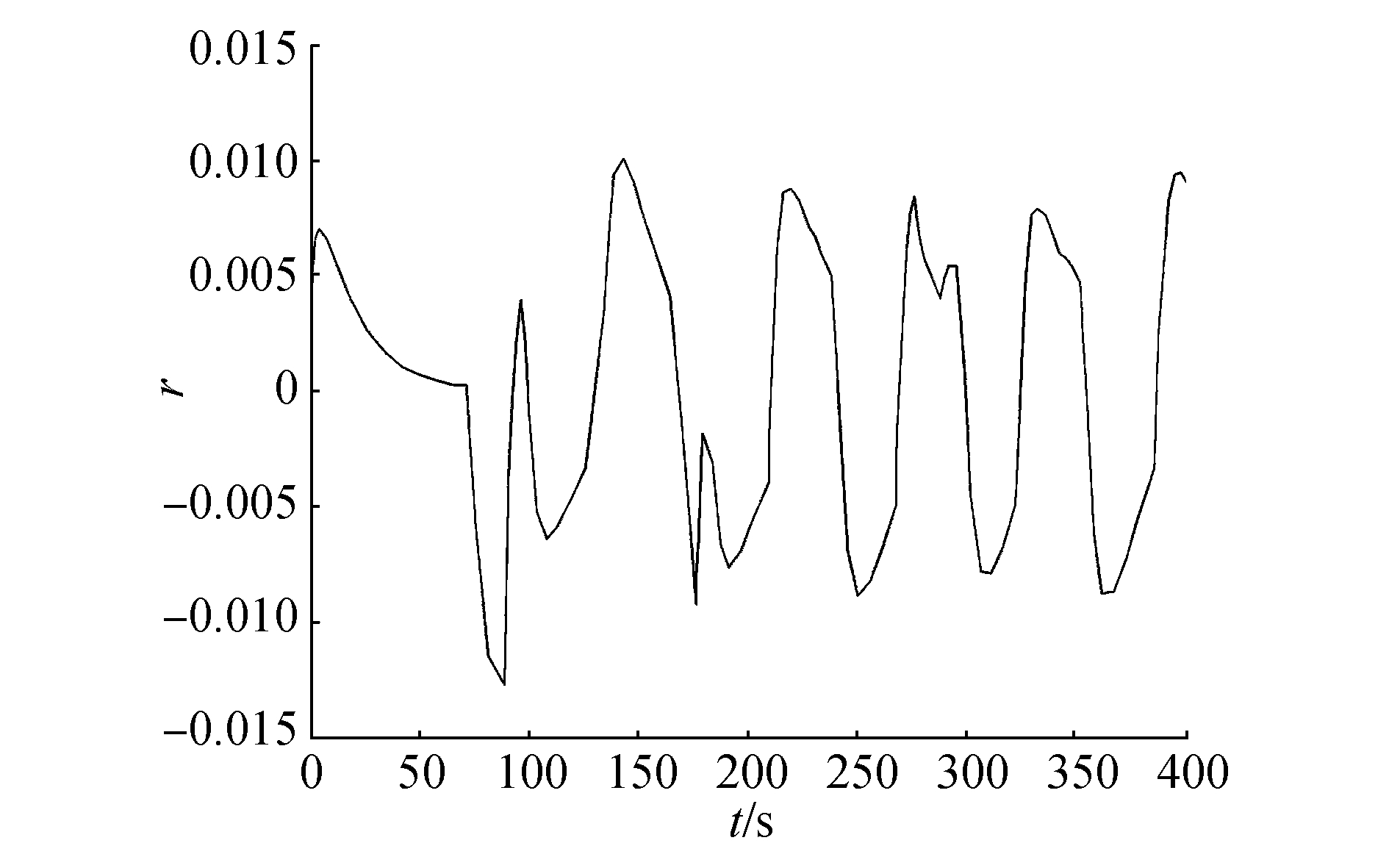
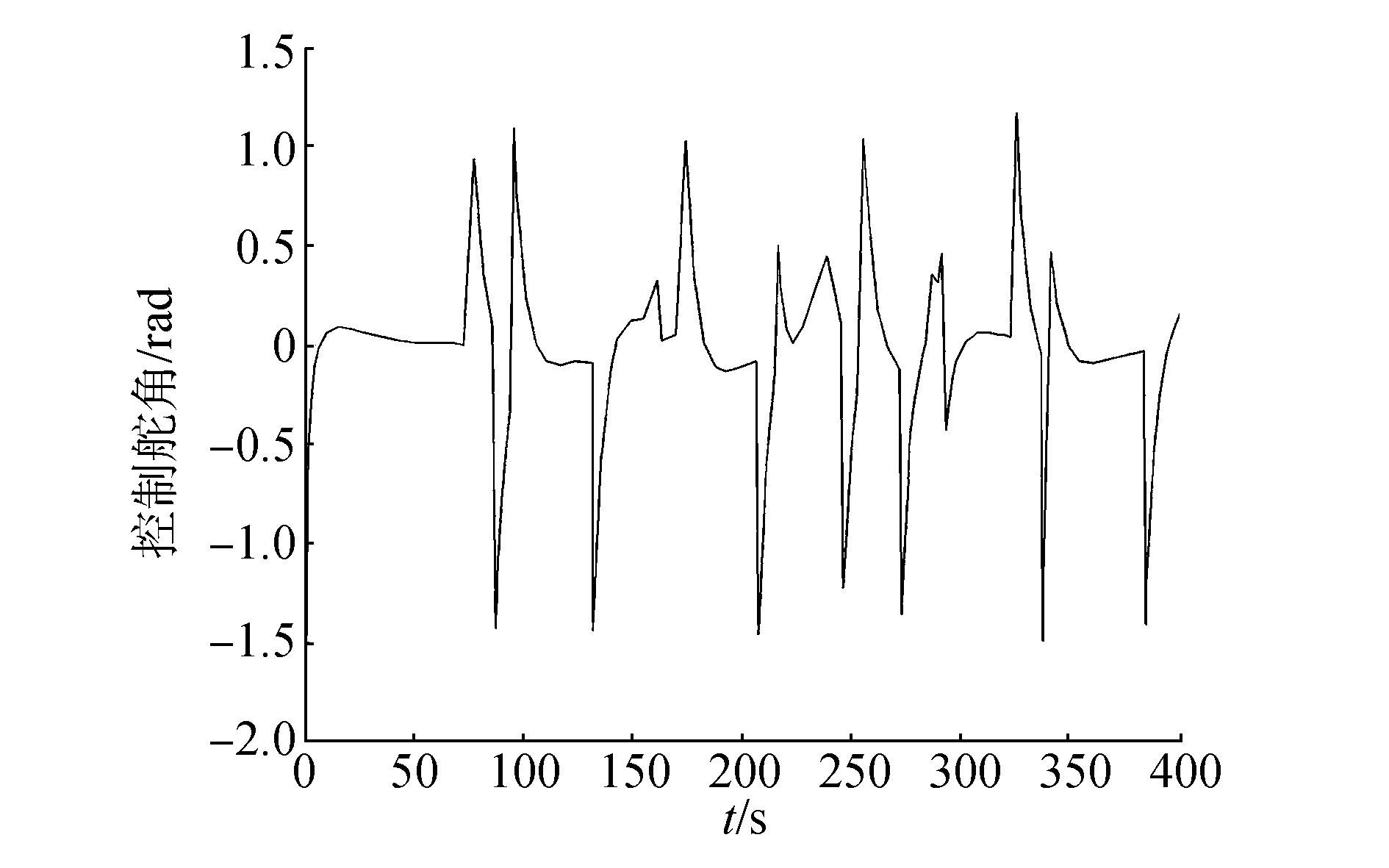
| 图 7 直线航迹下艏向角变化率变化曲线 | |
|
Download:
|
| 图 8 直线航迹跟踪中控制舵角变化曲线 | |
跟踪圆形期望航迹的仿真试验控制器参数为:k=10,λ=0.001,kp=10/57.3,k1=0.1,Φ=0.008。期望航迹设定为x0=0, y0=0, R=1 000。
|
Download:
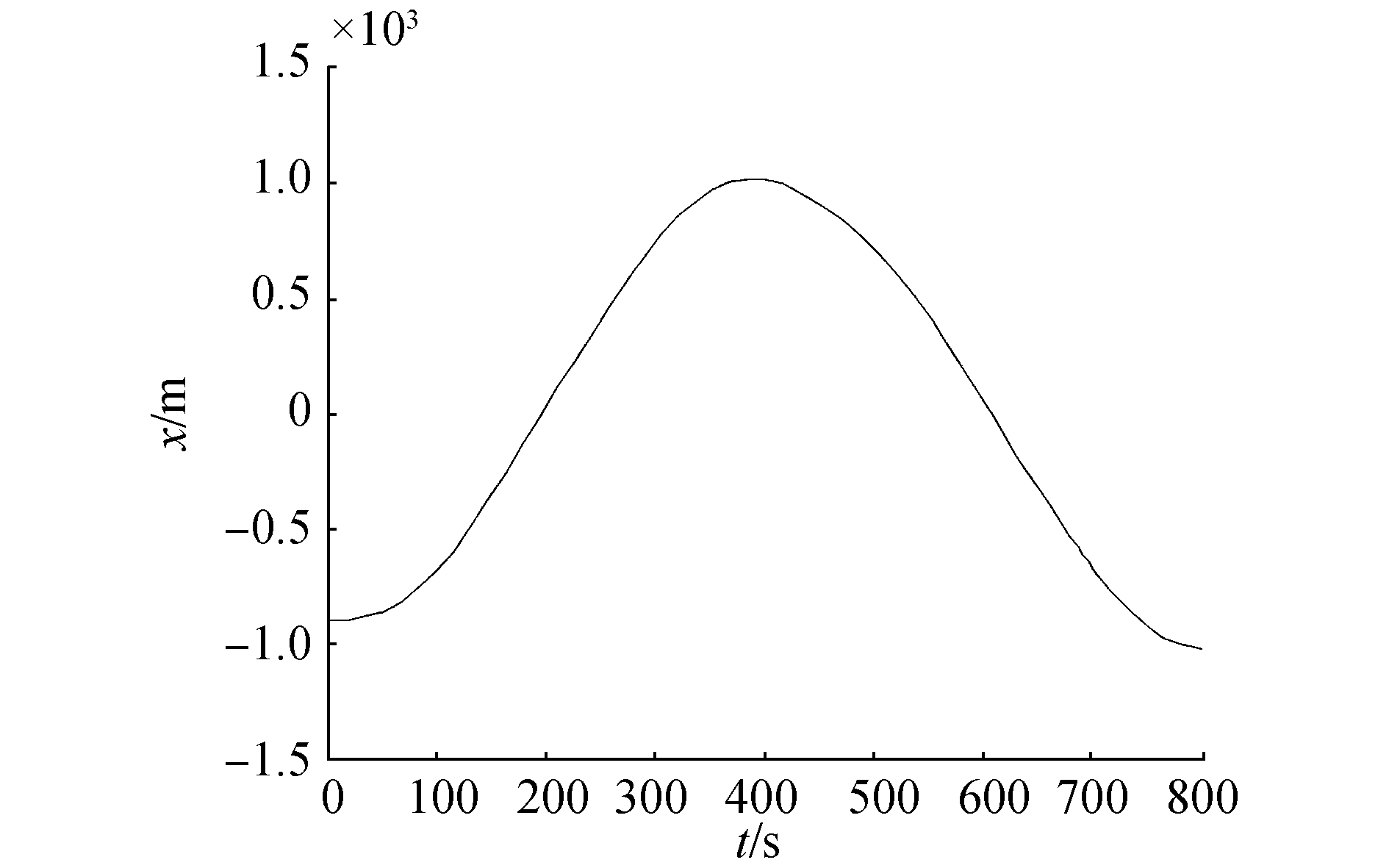
|
| 图 9 圆形航迹仿真横向位置变化 | |
|
Download:
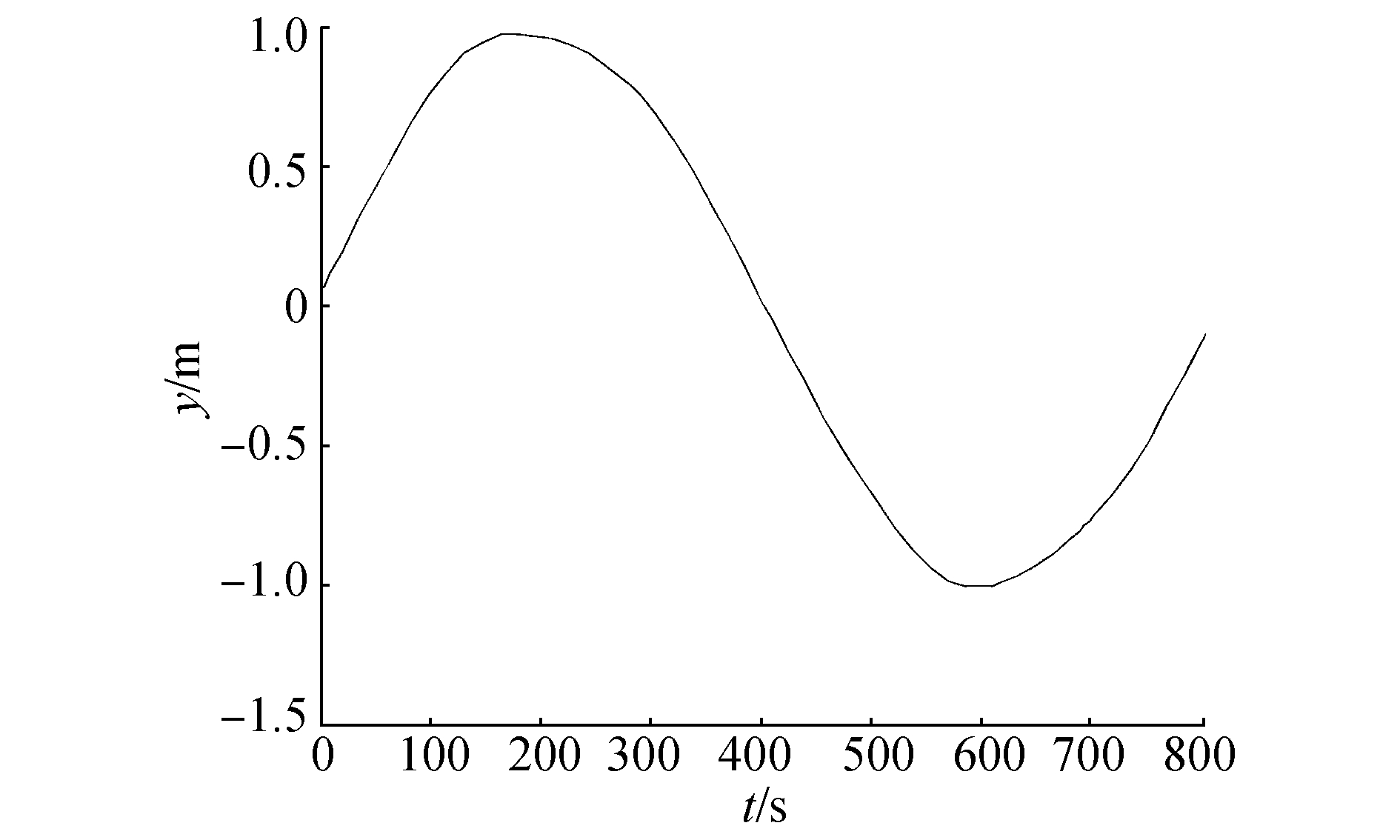
|
| 图 10 圆形航迹仿真纵向位置变化 | |

|
Download:
|
| 图 11 圆形航迹仿真中期望航迹与仿真航迹比较 | |
|
Download:
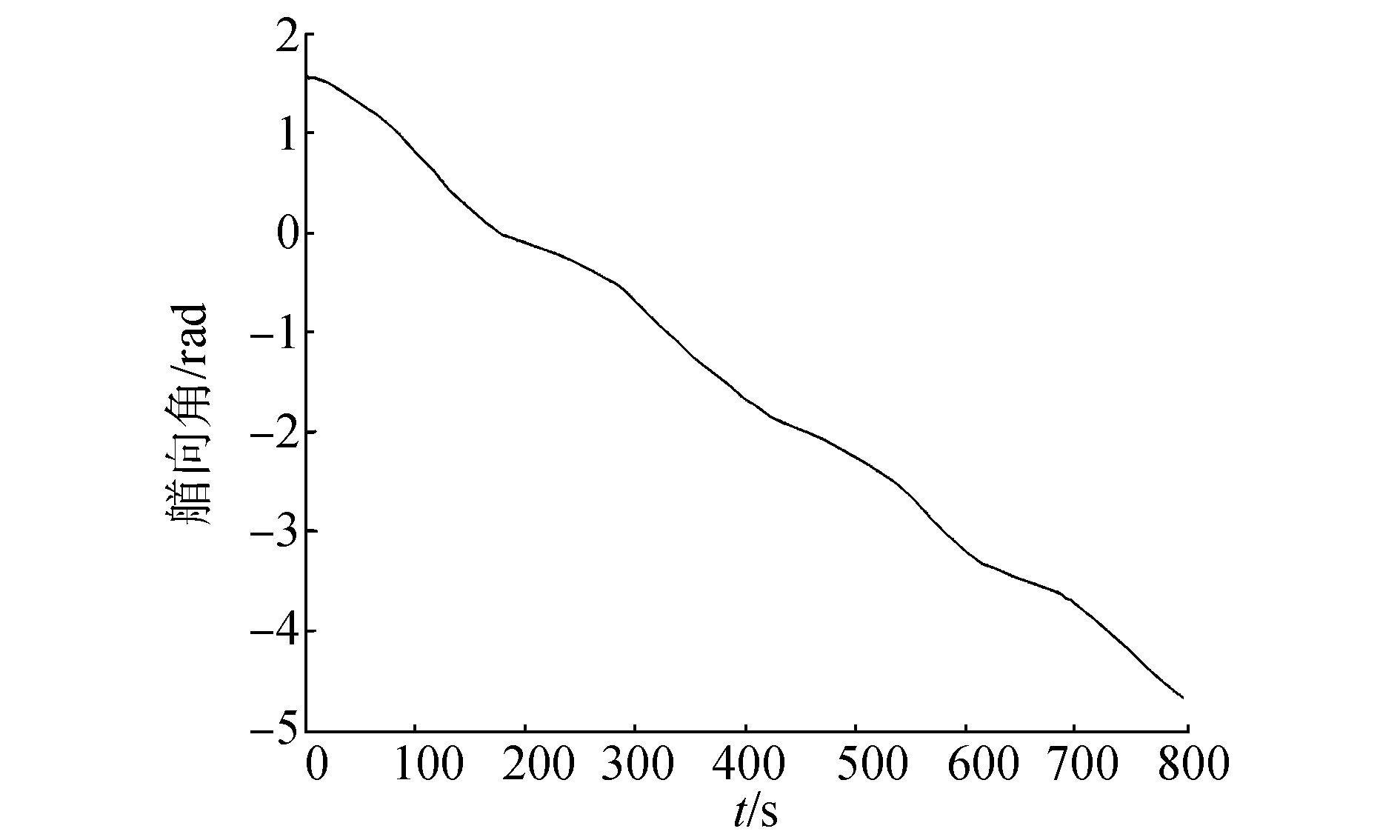
|
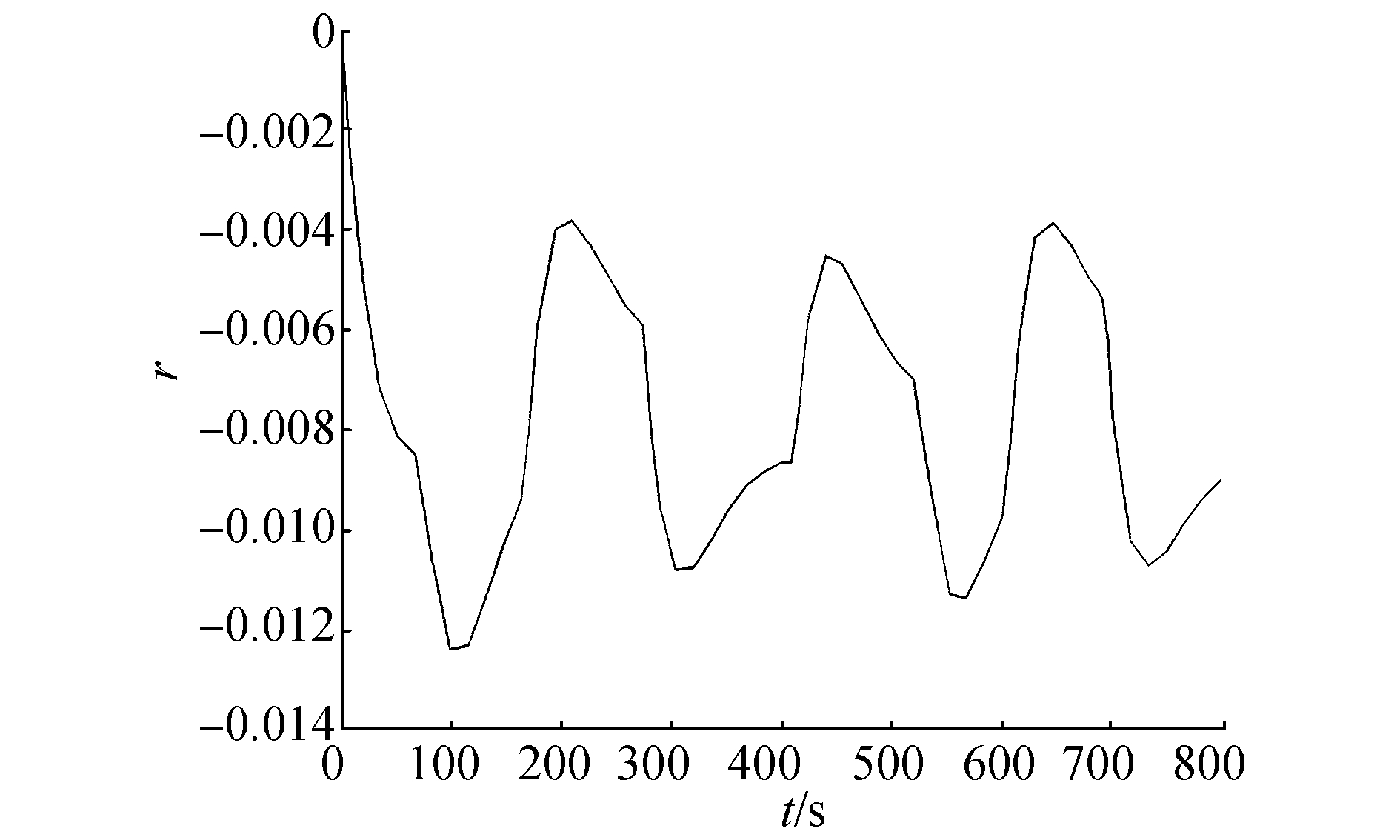
| 图 12 圆形航迹仿真中艏向角变化 | |
|
Download:
|
| 图 13 圆形航迹仿真艏向角变化率变化 | |

|
Download:
|
| 图 14 圆形航迹仿真中控制舵角变化 | |
跟踪正弦曲线期望航迹的仿真试验控制器参数为:k=10,λ=0.004,kp=10/57.3,k1=1,Φ=0.01。
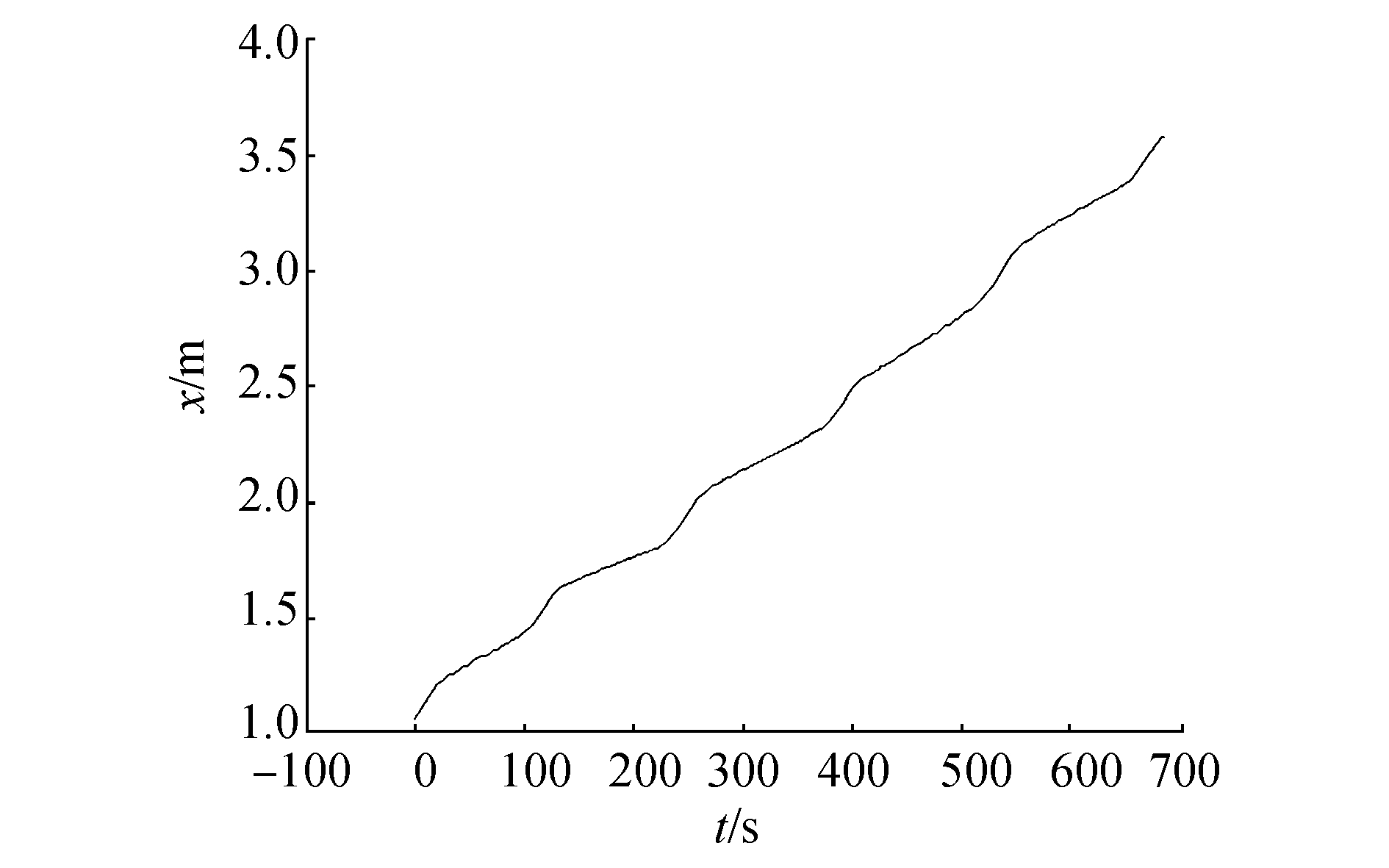
期望航迹设定为A=500,ω=π/500,m=0,D=0。仿真实验结果如图 15~20所示。
|
Download:
|
| 图 15 正弦曲线航迹仿真横向位置变化 | |

|
Download:
|
| 图 16 正弦曲线仿真纵向位置变化 | |
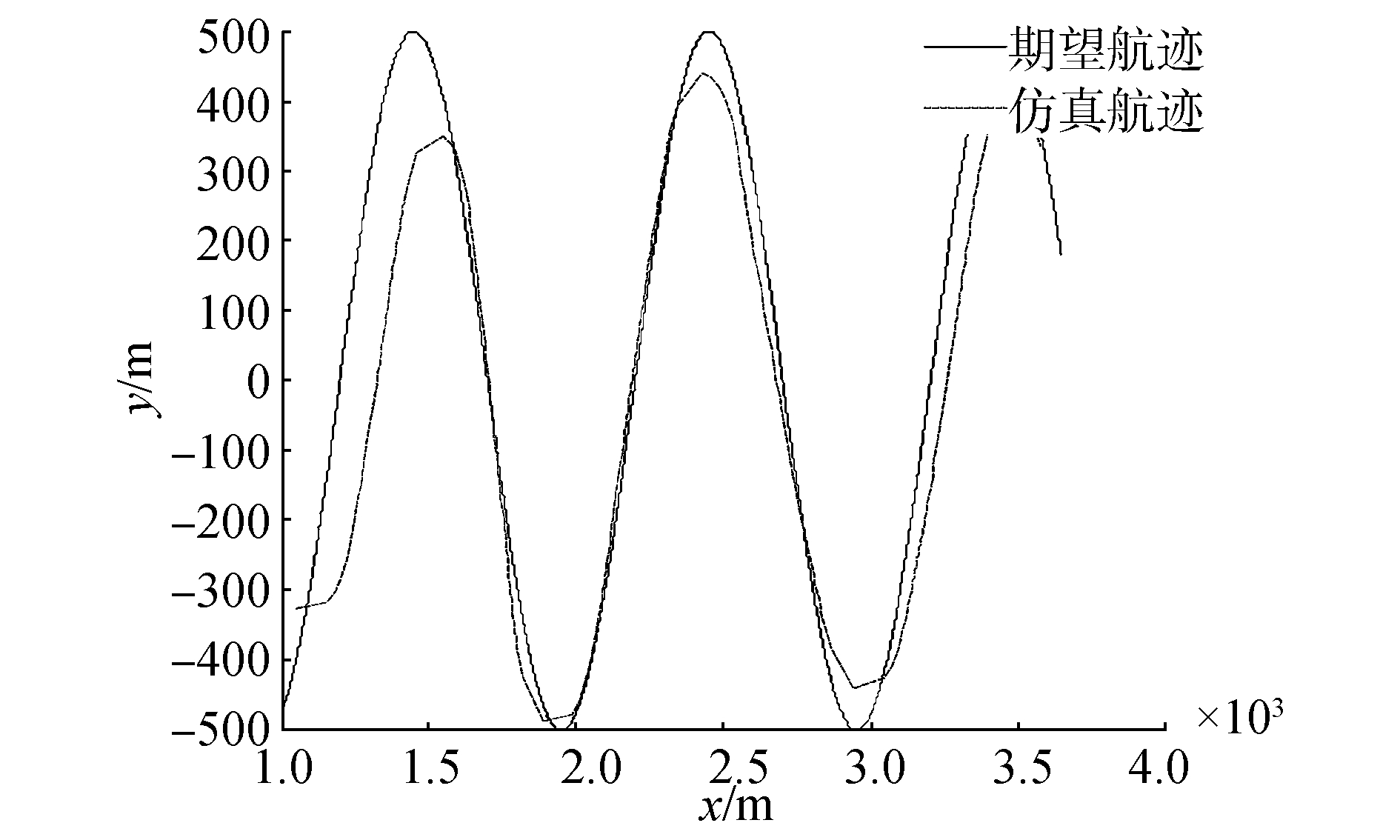
|
Download:
|
| 图 17 正弦曲线仿真期望航迹和仿真航迹比较 | |
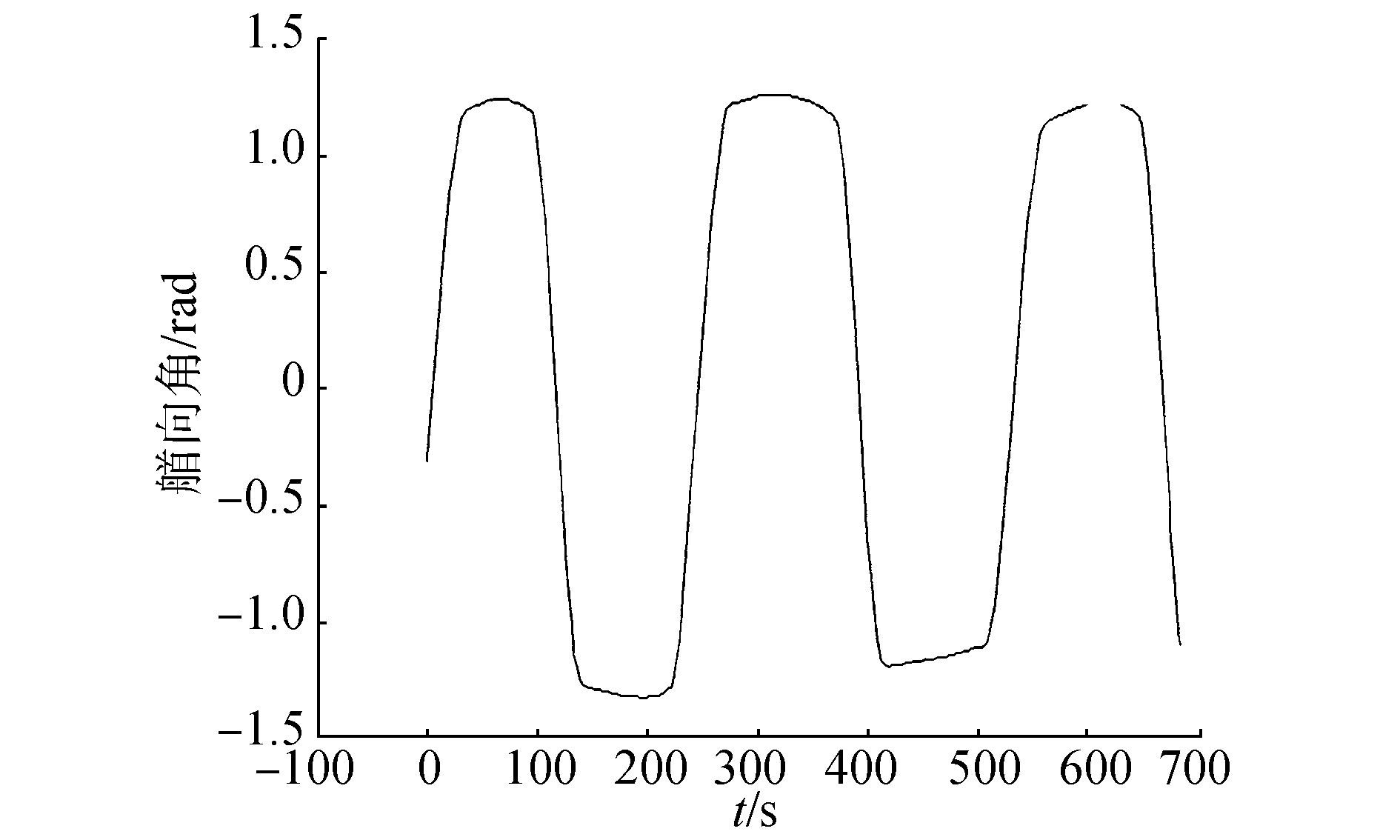
|
Download:
|
| 图 18 正弦曲线仿真艏相角变化 | |

|
Download:
|
| 图 19 正弦航迹仿真艏向角变化率变化 | |

|
Download:
|
| 图 20 正弦航迹仿真控制舵角变化 | |
本文讨论了船舶在野本非线性模型下,基于航向跟踪的曲线航迹跟踪滑模控制律的设计方法。并利用S面的模糊控制思想设计控制器实现了消除船舶与期望航迹的偏航误差的目的。仿真结果说明滑模控制器可以有效地跟踪期望航向,并在期望航向不断变化的曲线航迹跟踪控制过程中,实现其航迹跟踪目的,保证了系统的稳定。
| [1] |
郝华. 欠驱动水面船舶镇定控制的研究[D]. 大连: 大连海事大学, 2016. http://www.wanfangdata.com.cn/details/detail.do?_type=degree&id=Y2999070
( 0) 0)
|
| [2] |
曾薄文, 朱齐丹, 于瑞亭. 欠驱动水面船舶的曲线航迹跟踪控制[J]. 哈尔滨工程大学学报, 2011, 32(10): 1317-1322. DOI:10.3969/j.issn.1006-7043.2011.10.010 ( 0) 0)
|
| [3] |
杨树仁. 船舶航迹控制算法的研究与仿真[D]. 长春: 吉林大学, 2014. http://cdmd.cnki.com.cn/Article/CDMD-10183-1014295430.htm
( 0) 0)
|
| [4] |
JIANG Zhongping. Global tracking control of underactuated ships by Lyapunov's direct method[J]. Automatica, 2002, 38(2): 301-309. DOI:10.1016/S0005-1098(01)00199-6 ( 0) 0)
|
| [5] |
程金. 水面船舶的非线性控制研究[D]. 北京: 中国科学院自动化研究所, 2007: 1-95. http://cdmd.cnki.com.cn/Article/CDMD-80146-2008114593.htm
( 0) 0)
|
| [6] |
FOSSEN T I, LEKKAS A M. Direct and indirect adaptive integral line-of-sight path-following controllers for marine craft exposed to ocean currents[J]. International journal of adaptive control and signal processing, 2017, 31(4): 445-463. DOI:10.1002/acs.v31.4 ( 0) 0)
|
| [7] |
DO K D. Global robust adaptive path-tracking control of underactuated ships under stochastic disturbances[J]. Ocean engineering, 2016, 111: 267-278. DOI:10.1016/j.oceaneng.2015.10.038 ( 0) 0)
|
| [8] |
DO D, PAN Jie. Robust and adaptive path following for underactuated autonomous underwater vehicles[C]//Proceedings of the American Control Conference. Denver, CO, USA: IEEE, 2003: 1994-1999. http://www.sciencedirect.com/science/article/pii/S0029801804000940
( 0) 0)
|
| [9] |
LEFEBER E, PETTERSEN K Y, NIJMEIJER H. Tracking control of an underactuated ship[J]. IEEE transactions on control systems technology, 2003, 11(1): 52-61. DOI:10.1109/TCST.2002.806465 ( 0) 0)
|
| [10] |
ASHRAFIUON H, MUSKE K R, MCNINCH L C, et al. Sliding-mode tracking control of surface vessels[J]. IEEE transactions on industrial electronics, 2008, 55(11): 4004-4012. DOI:10.1109/TIE.2008.2005933 ( 0) 0)
|
| [11] |
王建国, 吴恭兴, 万磊, 等. 广义S面的水下机器人控制器设计[J]. 电机与控制学报, 2009, 13(S1): 144-148. ( 0) 0)
|
| [12] |
FAHIMI F. Sliding-mode formation control for underactuated surface vessels[J]. IEEE transactions on robotics, 2007, 23(3): 617-622. DOI:10.1109/TRO.2007.898961 ( 0) 0)
|
| [13] |
秦梓荷, 林壮, 李平, 等. 基于LOS导航的欠驱动船舶滑模控制[J]. 中南大学学报:自然科学版, 2016, 47(10): 3605-3611. ( 0) 0)
|
| [14] |
王耀禄. 欠驱动船舶轨迹跟踪滑模非线性控制研究[D]. 大连: 大连海事大学, 2015. http://www.wanfangdata.com.cn/details/detail.do?_type=degree&id=Y2903516
( 0) 0)
|
 2018, Vol. 45
2018, Vol. 45


