2. 苏州大学 苏州纳米科技协同创新中心, 江苏 苏州 215123;
3. 哈尔滨工程大学 机电工程学院, 黑龙江 哈尔滨 150001;
4. 苏州大学附属第一医院, 江苏 苏州 215000
2. Collaborative Innovation Center of Suzhou Nano Science and Technology, Soochow University, Suzhou 215123, China;
3. College of Mechanical and Electrical Engineering, Harbin Engineering University, Harbin 150001, China;
4. The First Affiliated Hospital of Soochow University, Suzhou 215000, China
原发性肝癌是常见的消化系统恶性肿瘤之一,其中约85%为肝细胞癌。目前,肝癌已成为全球第二大癌症相关死亡原因,每年新增肝癌患者30万~100万例[1-2]。肝癌的治疗复杂,部分肝脏切除手术是避免患者死亡和肝癌转移最好的方法,但手术过程中医生无法直观地观察到肝脏内部的组织结构。应用增强现实(augment reality,AR)技术能够将虚拟肝脏模型叠加到真实图像或视频中,为医生提供更多手术信息[3]。通过图像配准可以将肝脏虚拟模型与真实肝脏的位置重叠,叠加的虚拟模型能够清晰地显示肝脏的内部结构,为医生提供直观的指导。为了保证增强现实指导的准确性,叠加的虚拟模型必须与真实场景的肝脏保持一致,虚拟模型需要实时进行相应的切割和变形。
肝脏模型的切割既要满足一定的准确性, 又要满足一定的实时性。实时性、稳定性和真实性是衡量切割效果的关键因素[4],直接决定了切割的效果。实时性与切割的刷新率有关,为了达到流畅的切割效果,通常要求刷新率不低于25 Hz。这就需要算法满足一定的时间复杂度和空间复杂度要求[5-7]。
用于增强现实的虚拟模型需要由患者CT图像或MRI图像重建得到,目前三维重建的方法主要有2大类:体绘制、面绘制。体绘制效果更好,能更好地反映患者体内真实情况,但体绘制模型计算量巨大,很难满足实际使用的需求。面绘制模型计算量小,便于操作,是目前主流的三维重建方法[8]。
针对面绘制的模型,切割方法又主要有面模型切割法和体模型切割法。面模型切割法由顶点连接成大量三角形构成模型的表面网格。切割过程中主要通过对三角形单元进行操作,改变模型网格的拓扑结构。体模型切割法需要将网格模型进行多面体划分,使模型内部以多面体单元填充,切割过程中主要对多面体单元进行操作,常用的多面体有四面体、六面体和超六面体[9]。目前大多数学者集中于四面体切割法的研究,根据不同的剖分策略可将四面体切割的方法分为去除法和体元剖分法[10]。去除法是由Bronielsen等[11]提出的,去除法的基本思想是通过碰撞检测找到与手术器械发生碰撞的四面体单元,将其从模型中删除。但其真实感差,切口边缘会产生严重的锯齿。体元剖分法真实感强,切口细腻,但其计算量巨大,随着切割的进行,单元体数量急剧增加,很难满足实时性要求[12]。另外Mor[13]提出了一种累进切割法,其基本思想是在手术刀完全掠过某四面体单元之前提前将其分裂。存在计算量大的问题。Nienhuys[14]和Serby等[15]提出了一种移动顶点的方法,在切割过程中搜索切割路径附近的顶点,将其移动到切割线上。但这种移动模型顶点容易产生退化单元。
目前针对面模型切割的研究较少,各种方法分别存在计算量大和网格质量差的问题,且大多数方法只对表面切割进行了研究,没有对切割面进行研究。本文针对上述问题对面模型切割的顶点移动法进行了研究和优化,并按照Delaunay三角剖分准则对局部三角面片进行重构,最后对切割面的构造进行了研究。
1 切割算法如图 1所示,本文算法的核心思路为:
|
Download:
|
| 图 1 移动顶点算法思路 Fig. 1 Block diagram of moving vertex algorithm | |
1) 进行碰撞检测,获得切割点具体位置;
2) 搜索最近顶点,将搜索到的最近点移动到切割点的位置;
3) 优化局部面片,检测最近点附近的退化三角形并进行优化;
4) 分裂网格,将切割线两侧的顶点分别向不同的方向移动一定的距离以形成切口;
5) 构造切割面,连接相应顶点形成切割面。
以上所有计算在一帧中完成,称为一个计算帧,即每一个计算帧从检测到切割操作开始,切割面构造完结束。
1.1 碰撞检测碰撞检测用于决定何时发生切割并得到切割位置,是后续一切操作的基础。如图 2所示,常用的碰撞检测方法为包围盒法,其中包围盒又分为包围球、轴对齐包围盒(AABB包围盒)、方向包围盒(OBB包围盒)和离散方向凸包围盒(k-Dops包围盒)[16-17]。包围盒算法简单,计算量小,但无论哪种包围盒都无法完全贴合模型。为了能够精确地检测切割位置,本文针对面模型切割提出了一种新的碰撞检测方法。

|
Download:
|
| 图 2 包围盒算法对比示意 Fig. 2 Comparison of bounding box algorithms | |
在模型切割仿真中,切割工具的简化形式有3种:1)将切割工具视为与网格表面的一系列碰撞点;2)使用简单的平面或直线表示切割工具; 3)渲染出完整的切割工具,但在切割计算时使用其中轴线进行计算[18]。本文使用第3种方法(如图 3),在手术刀刀刃上固定2个点Se和St,使用2点之间的连线进行切割计算。

|
Download:
|
| 图 3 本文所采用手术刀具示意 Fig. 3 Schematic diagram of surgical knife used in this article | |
在切割过程中从点Se向点St投射一条光线,如果光线被肝脏模型遮挡无法到达St即发生切割。检测到切割后查找遮挡光线的三角面片,记为切割三角形ΔT1T2T3。该三角面片所在平面可以由三点式平面方程得到:
| $ \left| \begin{array}{l} \;x - {x_{T1}}\;\;\;\;\;y - {y_{T1}}\;\;\;\;\;\;z - {z_{T1}}\\ {x_{T2}} - {x_{T1}}\;{y_{T2}} - {y_{T1}}\;\;{z_{T2}} - {z_{T1}}\\ {x_{T3}} - {x_{T1}}\;{y_{T3}} - {y_{T1}}\;\;{z_{T3}} - {z_{T1}} \end{array} \right| = 0 $ | (1) |
过点Se和点St的直线由两点式直线方程等到:
| $ \frac{{x - {x_{st}}}}{{{x_{se}} - {x_{st}}}} = \frac{{y - {y_{st}}}}{{{y_{se}} - {y_{st}}}} = \frac{{z - {z_{st}}}}{{{z_{se}} - {z_{st}}}} $ | (2) |
由式(1)、(2)即可得到切割点的精确位置Ci(xi, yi, zi)。
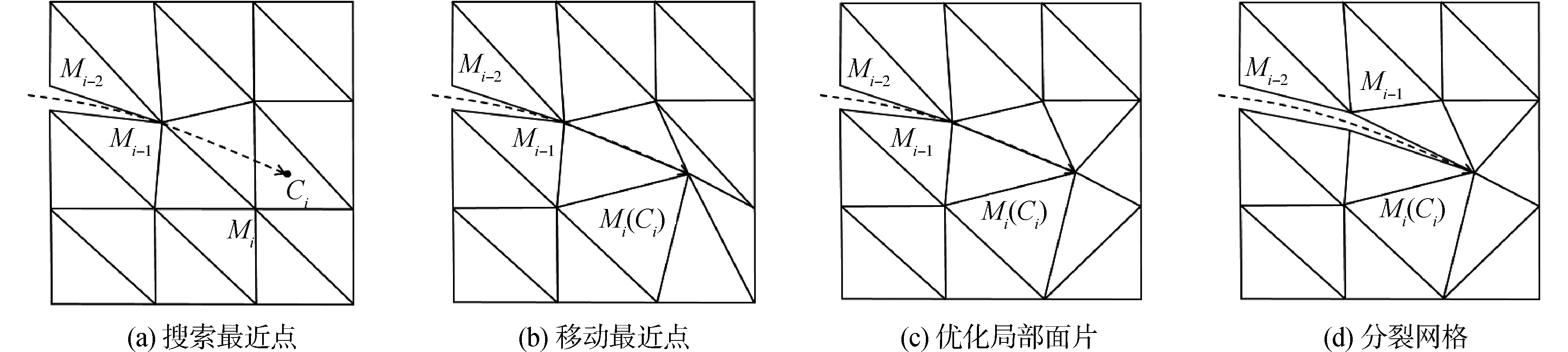
1.2 搜索最近点在本文方法中准确地获取到最近点是算法的关键,其结果决定了切割能否成功以及切割的最终效果。本文使用与传统模型切割不同的计算频率,本文方法中手术刀每移动一定距离,进行一次碰撞检测和切割计算,该方法不仅具有更好的延迟反馈,还能通过设置不同的步长来调整计算频率,在精度和效率之间取得平衡。
通过计算ΔT1T2T3的顶点与切割点Ci距离的方式搜索最近点,但最近点并不总是取计算得出距离最近的点,在切割过程中应该避免图 4所示的特殊情况。

|
Download:
|
| 图 4 特殊的最近点 Fig. 4 Special closest point | |
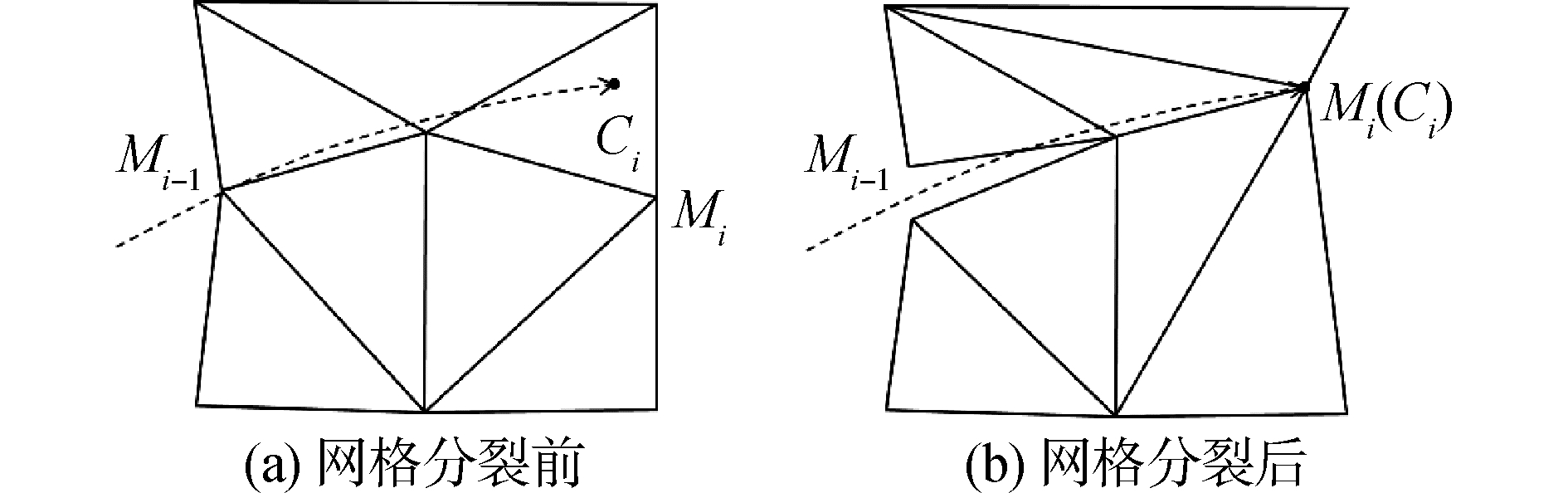
在图 4中,当相临2次计算得到的最近点Mi-1和Mi为一个四边形的2个相对顶点时,Mi-1和Mi没有直接连接,无法形成切割线,三角面片不能正常分裂。故每次计算得到临时最近点Mi后,需要对其和上一个最近点Mi-1进行判断,判断条件为:点Mi-1属于当前切割三角形ΔT1T2T3或点Mi属于上一个切割三角形ΔT1T2T3。满足该条件说明点Mi和点Mi-1属于同一个三角形,2个点由三角形的一条边相连,能够正常形成切割线。若不满足判断条件,取距离次之的点做为临时最近点再进行判断,如果如图 5所示点Mi-1和Mi仍然不能直接连接, 则取第3个点做为临时最近点。如果仍然不满足条件,表示步长设置过大,2次切割检测跨过了若干三角形,导致点Mi和点Mi-1所属的2个三角形没有公共边或公共点,此时应适当减小检测步长。
|
Download:
|
| 图 5 特殊的次最近点 Fig. 5 Special second closest point | |
狭长或小面积的退化三角形会影响后续的切割计算,还会导致模型显示质量下降。切割使用的原始模型遵循Delaunay三角剖分原则,不包含退化三角形。本文的移动顶点法每次只移动一个顶点,故不会出现小面积三角形,但并不能避免出现狭长三角形。因为本文的方法每次只移动一个最近点Mi,狭长三角形也只会出现在包含点Mi的三角形中。为了消除狭长三角形,只需要对包含点Mi的三角形进行检测优化即可。
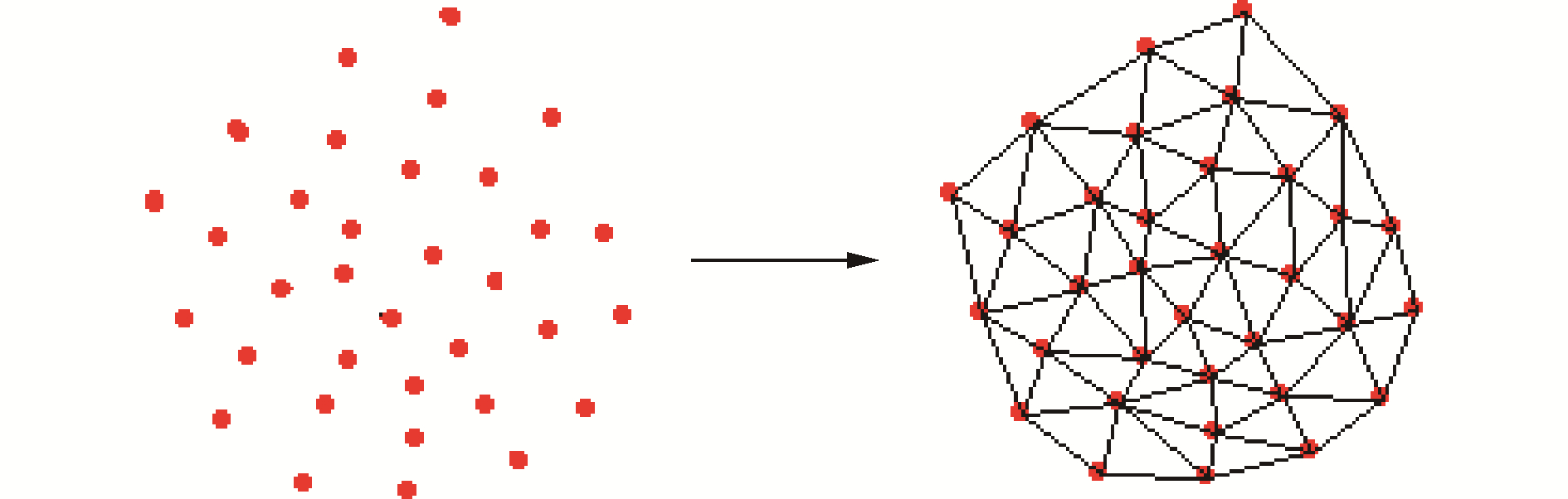
Delaunay三角剖分是一种由给定点集V形成优质表面网格的算法。Delaunay三角剖分包含2个重要准则,一个是空圆特性:在Delaunay三角网中任一三角形的外接圆中不存在V中的其他顶点;另一个是最大化最小角特性:在给定点集V可能形成的三角剖分中,Delaunay三角剖分所形成的三角形的最小角最大[19]。
|
Download:
|
| 图 6 Delaunay三角剖分 Fig. 6 Delaunay triangulation | |
在本文方法中,模型顶点点集V并不是固定不变的,随着切割的进行,总会有部分顶点坐标发生变化,不能直接使用Delaunay三角剖分。但在4个顶点构成的2个相临三角形中,如果2个三角形的外接圆范围内均不包含第4个顶点,则这4个顶点满足空圆特性,否则总是可以连接四边形的另一个对角线使其满足空圆特性。且满足空圆特性连接方式的最小角大于不满足空圆特性连接方式的最小角。即满足空圆特性的连接方式也满足最大化最小角特性。

|
Download:
|
| 图 7 交换对角线 Fig. 7 Exchange diagonal | |
本文方法对每个包含最近点Mi的三角形和其相临三角形组成的点集进行空圆特性判断,将不满足空圆特性的点集按照上述方式重新连接。保证每次移动最近点后三角面片中没有退化三角形。
1.4 构造切割面在网格模型的切割研究中更多的研究集中于模型表面的切割。不同于先生成完整的切割线再计算切口的方法,渐进式切割的计算是随着切割动作逐渐进行的,切割面的构造必须也是逐渐进行的。对于本文的方法即在每次顶点移动后对切割面进行计算。另外由于在渐进式切割中不能确定当前计算帧切割是否结束,所以在构造切割面时每一个计算帧都要按照切割结束来生成闭合的切割面。图 8以切割线左侧部分为例说明切割面的构造方法。

|
Download:
|
| 图 8 切割面的构造过程 Fig. 8 Cutting surface construction process | |
为了使切割真实性更好,通过在每一个计算帧中记录手术刀尖端Sti的坐标的方式得到切割深度。然后依次连接点Mi、Sti-1、Mi-1和点Mi-1、Sti-1、Sti-2构成ΔMiSti-1Mi-1和ΔMi-1Sti-1Sti-2即可形成完整的切割面。
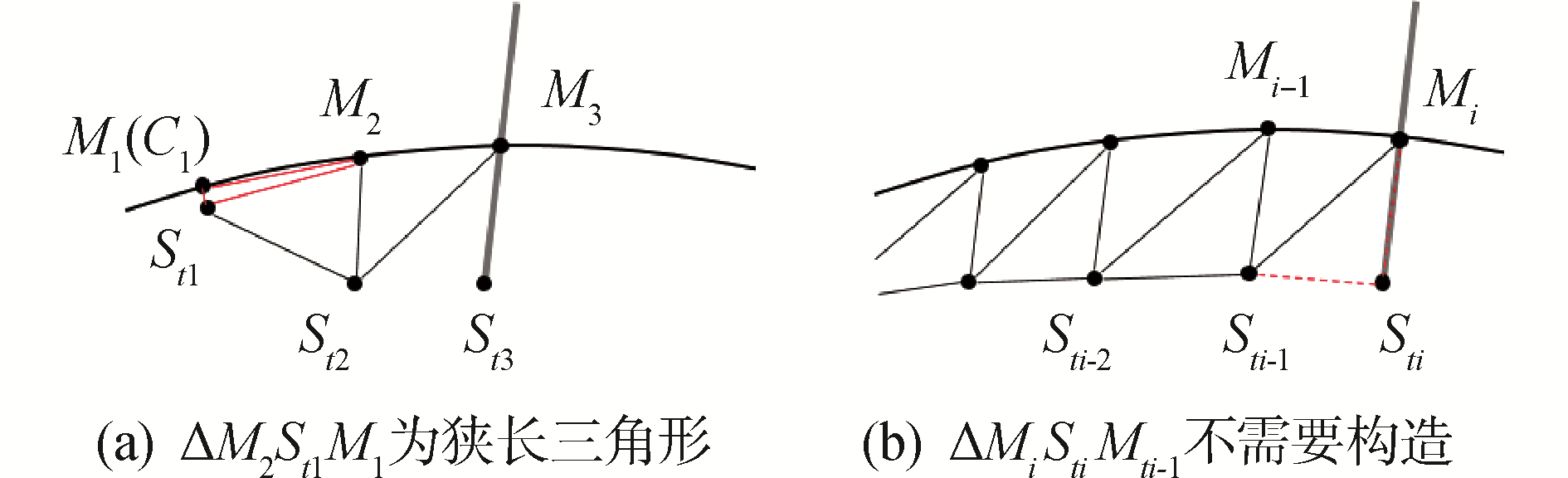
由于每次碰撞检测为一个计算帧,因此手术刀接触模型的瞬间即为第一个计算帧,此时表面最近M1与手术刀尖端点St1距离很近,可认为点M1与点St1完全重合,ΔM2St1M1为狭长的退化三角形,故只保留点M1,删除点St1和ΔM2St1M1。另外,在每一个计算帧中,切割线左右部分共用点Mi、点Sti和点Sti-1,即共用ΔMiStiSti-1,所以不需要构造ΔMiStiSti-1。但在下一个切割循环中点Mi变为Mi-1并在三角面片的分裂过程中被复制一份连接切割线右侧三角形,左右部分不再共用ΔMiStiSti-1,所以该三角形需要在下一个计算帧中构造(如图 9)。
|
Download:
|
| 图 9 切割面上的特殊三角形 Fig. 9 Special triangle on the cutting surface | |
使用上述针对面模型切割的移动顶点法对肝脏模型进行切割实验。实验硬件环境为:Intel Core i3- 8100(主频3.6 GHz),8 G内存,NVIDIA Geforce GTX1050Ti显卡,在Unity 2018.2和Visual Studio 2015中使用C#语言进行编程实现。使用的肝脏模型是经患者CT扫描分割后三维重建得到,由8 706个顶点和15 872个三角形单元组成。
图 10展示了针对面模型切割的移动顶点法的切割效果,图 10(a)为直接将移动顶点法应用于面模型切割的效果。在点M1移动后,出现退化三角形概率较大,虽然随着切割的进行,随后的顶点移动有可能使退化三角形正常化重新变成正常三角形,但不能保证每一个退化三角形都能正常化。图 10(b)为使用本文提出的方法优化的结果。在原移动顶点法出现退化三角形的位置经过交换对角线的操作后成功消除了退化三角形,每次顶点移动后都进行检测优化可以确保每一个退化三角形都能正常化。图 10(c)为本文方法构造出的切割面。本文致力于肝脏面模型切割的拓扑结构变化研究,不涉及生物力学和变形,肝脏切口大小通过一个参数控制。为了更好的显示切割面,图 10(c)将切口大小参数进行了适当的放大。当切口较小时切口边缘顶点移动距离小不会出现退化三角形,如图 10(c)切口增大时切口边缘将出现退化三角形。在实际操作中不能预测切口大小,故需要对切口边缘的三角形进行优化,使用与最近点相关三角形优化相同的方法对切口边缘三角形优化结果如图 10(d)。

|
Download:
|
| 图 10 模型切割效果 Fig. 10 Model cutting effect | |
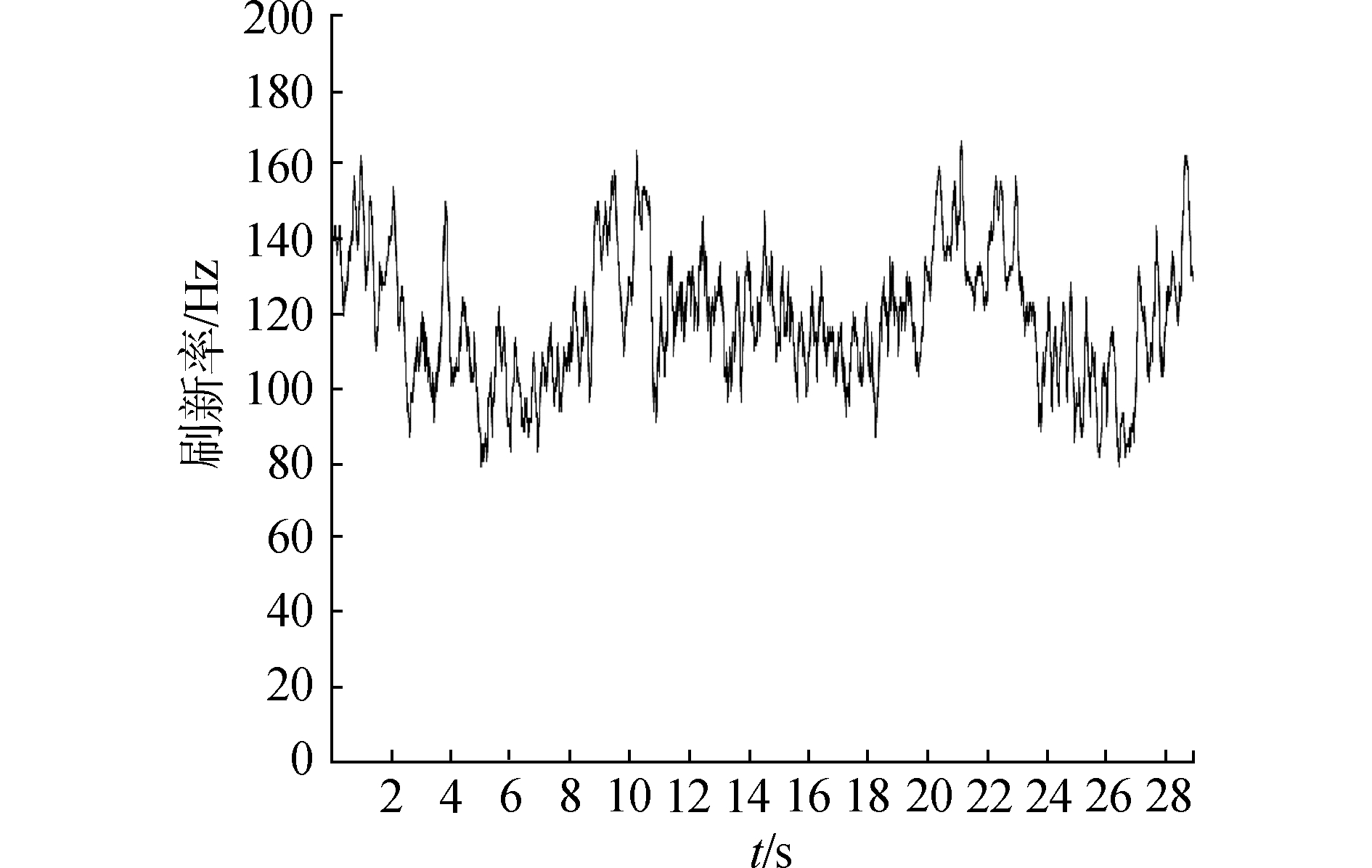
另外本文对切割过程中出现切割路径交叉和多次切割的情况进行了实验,如图 11,并记录了实验过程的刷新率。实验显示本文的方法具有良好的稳定性。切割过程中,图像的平均刷新率达到了119 Hz(如图 12),为模拟组织变形的计算留出了足够的空间。

|
Download:
|
| 图 11 多路径、交叉切割示意 Fig. 11 Schematic diagram of multi-path, cross cutting | |
|
Download:
|
| 图 12 交叉切割实验刷新率 Fig. 12 Cross cutting experiment refresh rate | |
1) 本文提出光线投射算法进行精确的切割检根据Delaunay三角剖分准则对顶点移动后的局部面片进行了优化和重构以消除原移动顶点法可能出现的退化的畸形三角形。
2) 本文还提出了一种针对面模型切割的切割面构造方法,能够在渐进切割过程中逐步生成完整闭合的切割面,切面真实度大大提高。
3) 本文提出的方法很好地解决表面切割模型的实时性问题并具有良好的稳定性,且实时刷新率能够稳定在119±2 Hz,具有很好的实时性。
| [1] |
徐细明. 肝癌的免疫治疗进展[J]. 中国临床新医学, 2019, 12(4): 347-353. XUN Ximing. Progress in immunotherapy of hepatocellular carcinoma[J]. Chinese journal of new clinical medicine, 2019, 12(4): 347-353. DOI:10.3969/j.issn.1674-3806.2019.04.01 (  0) 0)
|
| [2] |
季兴祖, 周敏华, 刘忠达, 等. 吴玉生教授辨治肝癌经验介绍[J]. 浙江中西医结合杂志, 2019, 29(1): 2-5. JI Xingzu, ZHOU Minhua, LIU Zhongda, et al. Professor Wu Yusheng's experience in treating hepatic carcinoma[J]. Zhejiang journal of integrated traditional Chinese and western medicine, 2019, 29(1): 2-5. DOI:10.3969/j.issn.1005-4561.2019.01.002 (  0) 0)
|
| [3] |
王壮雄, 李林容, 王芳元, 等. 虚拟和增强现实技术在肝脏外科中的应用[J]. 实用医学杂志, 2018, 34(7): 1210-1212. WANG Zhuangxiong, LI Linrong, WANG Fangyuan, et al. Application of virtual and augmented reality technology in liver surgery[J]. The journal of practical medicine, 2018, 34(7): 1210-1212. DOI:10.3969/j.issn.1006-5725.2018.07.040 (  0) 0)
|
| [4] |
张小瑞, 王澎湃, 孙伟, 等. 虚拟手术中软组织切割模型研究进展[J]. 计算机应用研究, 2017, 34(9): 2561-2569. ZHANG Xiaorui, WANG Pengpai, SUN Wei, et al. Research progress on soft tissue cutting model in virtual surgery[J]. Application research of computers, 2017, 34(9): 2561-2569. DOI:10.3969/j.issn.1001-3695.2017.09.001 (  0) 0)
|
| [5] |
NEALEN A, MÜLLER M, KEISER R, et al. Physically based deformable models in computer graphics[J]. Computer graphics forum, 2006, 25(4): 809-836. DOI:10.1111/j.1467-8659.2006.01000.x (  0) 0)
|
| [6] |
徐少平, 李春泉, 江顺亮, 等. 基于无网格的软组织切割模型的研究进展[J]. 中国生物医学工程学报, 2012, 31(1): 123-128. XU Shaoping, LI Chunquan, JIANG Shunliang, et al. Cutting simulation model for soft tissue surgery based on meshless method[J]. Chinese journal of biomedical engineering, 2012, 31(1): 123-128. DOI:10.3969/j.issn.0258-8021.2012.01.019 (  0) 0)
|
| [7] |
鲍义东. 粘弹性软组织建模和切割及虚拟仿真实验研究[D]. 哈尔滨: 哈尔滨工业大学, 2016. BAO Yidong. Research on viscoelasticity soft tissue modeling and cutting and virtual simulation experiment[D]. Harbin: Harbin Institute of Technology, 2016. (  0) 0)
|
| [8] |
李龙威. 基于面绘制的心脏三维数据可视化方法研究[J]. 黑龙江八一农垦大学学报, 2017, 29(4): 105-108. LI Longwei. Visualization method research of 3D cardiac data based on the surface rendering[J]. Journal of Heilongjiang August First Land Reclamation University, 2017, 29(4): 105-108. DOI:10.3969/j.issn.1002-2090.2017.04.024 (  0) 0)
|
| [9] |
郭忠峰, 邵岩. 基于质点-弹簧的肝脏虚拟手术力反馈研究[J]. 现代制造技术与装备, 2018(2): 70-72. GUO Zhongfeng, SHAO Yan. Force feedback study on liver virtual surgery based on particle-spring[J]. Modern manufacturing technology and equipment, 2018(2): 70-72. DOI:10.3969/j.issn.1673-5587.2018.02.034 (  0) 0)
|
| [10] |
程强强. 虚拟手术仿真系统中软组织切割模型研究[D]. 南昌: 南昌大学, 2018. CHENG Qiangqiang. Study on cutting model of soft tissue in virtual surgical simulation system[D]. Nanchang: Nanchang University, 2018. (  0) 0)
|
| [11] |
BRO-NIELSEN M. Finite element modeling in surgery simulation[J]. Proceedings of the IEEE, 1998, 86(3): 490-503. (  0) 0)
|
| [12] |
廖志芳, 黄晓宇, 郁松, 等. 虚拟手术中的软组织切割方法综述[J]. 软件导刊, 2010, 9(8): 14-16. LIAO Zhifang, HUANG Xiaoyu, YU Song, et al. Cutting of soft tissue in virtual surgery system[J]. Software guide, 2010, 9(8): 14-16. (  0) 0)
|
| [13] |
MOR A B, GHATTAS O, JARAMAZ B, et al. Progressive cutting with minimal new element creation of soft tissue models for interactive surgical simulation[D]. Pittsburgh: Carnegie Mellon University, 2001.
(  0) 0)
|
| [14] |
NIENHUYS H W, VAN DER STAPPEN A F. A surgery simulation supporting cuts and finite element deformation[C]//Proceedings of the 4th International Conference. Utrecht, Netherlands: Springer, 2001: 145-152.
(  0) 0)
|
| [15] |
SERBY D, HARDERS M, SZÉKELY G. A new approach to cutting into finite element models[C]//Proceedings of the 4th International Conference. Utrecht, Netherlands: Springer, 2001: 425-433.
(  0) 0)
|
| [16] |
于瑞云, 赵金龙, 余龙, 等. 结合轴对齐包围盒和空间划分的碰撞检测算法[J]. 中国图象图形学报, 2018, 23(12): 1925-1937. YU Ruiyun, ZHAO Jinlong, YU Long, et al. Collision detection algorithm based on AABB bounding box and space division[J]. Journal of image and graphics, 2018, 23(12): 1925-1937. DOI:10.11834/jig.180050 (  0) 0)
|
| [17] |
胡春安, 谢伟超, 王振东. 依赖包围盒紧密率及多层建模结构的混合碰撞检测算法[J]. 科学技术与工程, 2018, 18(16): 74-80. HU Chunan, XIE Weichao, WANG Zhendong. Hybrid collision detection algorithm relying on the tightness ratio of bounding volume and multi-layer modeling structure[J]. Science technology and engineering, 2018, 18(16): 74-80. DOI:10.3969/j.issn.1671-1815.2018.16.012 (  0) 0)
|
| [18] |
BRUYNS C D, SENGER S, MENON A, et al. A survey of interactive mesh-cutting techniques and a new method for implementing generalized interactive mesh cutting using virtual tools[J]. The journal of visualization and computer animation, 2002, 13(1): 21-42. DOI:10.1002/vis.275 (  0) 0)
|
| [19] |
高莉. 改进的Delaunay三角剖分算法研究[D]. 兰州: 兰州大学, 2015. GAO Li. An improved Delaunay triangulation algorithm[D]. Lanzhou: Lanzhou University, 2015. (  0) 0)
|
 2021, Vol. 42
2021, Vol. 42


