2. 中国水产科学研究院渔业机械仪器研究所, 上海 200092;
3. 中国水产科学研究院 农业部远洋渔船与装备重点实验室, 上海 200092
2. Fishery Machinery and Instrument Research Institute, Chinese Academy of Fishery Sciences, Shanghai 200092, China;
3. Chinese Academy of Fishery Sciences, Key Laboratory of Ocean Fishing Vessel and Equipment, Ministry of Agriculture, Shanghai 200092, China
在大型中水层拖网渔船工作过程中,因海浪波动、船体拐弯倾斜引起左右曳纲长短不一致,使得拖网网型变差导致大量鱼群从网中逃逸,影响捕鱼效率,通常采用被动补偿系统进行海浪位移补偿,钢丝绳应自动放长保证一定涨紧力。国内外研究集中在位移升沉补偿方面,但对升降补偿装置带来的钢丝绳张力、压强的研究较少,仅有的研究包括数值分析和方针研究,有矛盾之处,难以取得有价值的研究[1]。本研究通过建立数学模型并对其仿真分析,重点设计实验过程,研究钢丝绳涨紧力、蓄能器压强的变化规律,为设计选型、驱动控制提供可靠依据, 从而达到更好的补偿效果。
1 波浪被动补偿装置及数学模型被动补偿也被称为恒张力补偿,当摇摆台上升时,缸筒会随着摇摆台一起上升,补偿油缸所连接的活塞杆在惯性作用下停留在平衡位置,无杆腔内的油液被压入蓄能器中并储存能量;当摇摆台下降时,缸筒随着平台一起下降,活塞杆有保持停留在平衡位置的趋势,无杆腔从蓄能器中吸入油液,蓄能器中的气体膨胀并释放能量。通过蓄能器蓄能与释放能量的过程来减缓钢丝绳受力变化,保证钢丝绳始终处于恒定值范围内,图 1为被动补偿系统的液压原理图[2]。

|
图 1 被动补偿系统的液压原理图 Fig.1 Hydraulic principle diagram of passive compensation system |
气体多变过程分为定压过程、定温过程、绝热过程、定容过程。波浪位移补偿装置蓄能器内的容积、温度、压强是变量值,与外界没有热量交换,符合绝热过程的条件,满足关系式PVn=常数。
设(P1, V1)为蓄能器在某一状态时的气体压强和体积,(P2, V2)为另一状态时的气体压强和气体的体积,则蓄能器内的气体绝热状态方程为
| $ {{P}_{2}}V_{2}^{n}={{P}_{1}}V_{1}^{n} $ | (1) |
| $ \rm{ln}{{\mathit{P}}_{1}}+\mathit{n}\rm{ln}{{\mathit{V}}_{1}}=\rm{ln}{{\mathit{P}}_{2}}+\mathit{n}\rm{ln}{{\mathit{V}}_{2}} $ | (2) |
| $ n=~\frac{\rm{ln}{{\mathit{P}}_{2}}-\rm{ln}{{\mathit{P}}_{1}}}{\rm{ln}{{\mathit{V}}_{1}}-\rm{ln}{{\mathit{V}}_{2}}}=\frac{\rm{ln}\frac{{{\mathit{P}}_{2}}}{{{\mathit{P}}_{1}}}}{{\rm{ln}}\frac{{{V}_{0}}+A\left( {{h}_{1}}-200 \right)}{{{V}_{0}}+A\left( {{h}_{2}}-200 \right)~}} $ | (3) |
式中:A为蓄能器的截面积, V0是初始时刻的体积,h1、h2分别是某时刻的气体体积。
气体状态方程的n值受外界影响较大[3],通过实验测试该波浪补偿装置中蓄能器内的压强和缸筒位移的10组数值,将第i组和第i+1组的数值代入式(3)可得到i组的n值计算结果,如表 1所示。
| 表 1 蓄能器采样值 Tab.1 Accumulator′s sample values |
气体绝热状态方程的n值如图 2所示。n值具有时变性,在1.2~1.6内变化,取10组数据的平均值计算结果为n=1.38。

|
图 2 气体状态方程n值计算结果 Fig.2 Gas state equation′s n value |
以关键的油缸活塞杆为研究对象,当缸筒向下移动时,缸筒位移增大,油缸内无杆腔的体积增大,油压减小,蓄能器内的油液通过安全球阀进入油缸,气体体积增大。活塞杆受两边钢丝绳的涨紧力作用,活塞杆的下端面受油液的压强,以及油液的粘性阻尼力,活塞杆的受力简化模型如图 3所示[4-5]。

|
图 3 活塞杆简化受力模型 Fig.3 Piston rod′s simplified mechanical model |
活塞杆的动力学方程为[6]
| $ m{{{\ddot{x}}}_{1}}+c{{{\dot{x}}}_{1}}+k{{x}_{1}}=2F-{{P}_{2}}A $ | (4) |
式中:x1为油缸位移(绞纲机不转),
| $ \begin{align} & {{V}_{2}}={{V}_{1}}+\Delta V={{V}_{1}}+{{x}_{1}}A={{V}_{1}}+\frac{1}{2}xA \\ & \ \ \ \ \ \ {{P}_{2}}={{P}_{1}}{{\left( ~\frac{{{V}_{1}}}{{{V}_{1}}+0.5A} \right)}^{1.38}} \\ \end{align} $ | (5) |
P1为蓄能器平衡位置时的压强,将式(5)代入式(4)整理得到钢丝绳涨紧力与位移的关系式为
| $ F=\frac{m}{4}\ddot{x}+\frac{c}{4}\dot{x}+\frac{{{P}_{1}}A}{2}{{\left( \frac{{{V}_{1}}}{{{V}_{1}}+0.5A} \right)}^{1.38}} $ | (6) |
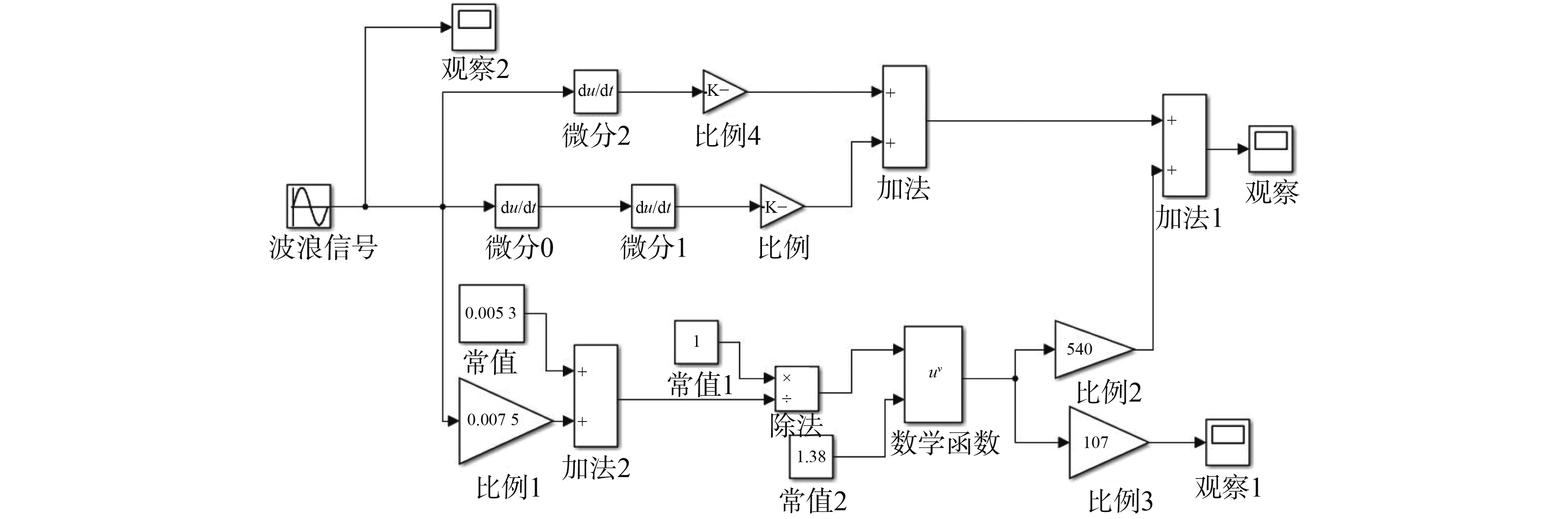
以式(5)为依据利用Matlab/Simulink提供的仿真模块建立被动补偿系统涨紧力与位移之间的仿真模型如图 4所示。仿真模型中Sine Wave3模块用于表征起升重物的钢丝绳长度其振幅为h,周期T,设定波浪引起的钢丝绳长度变化为正弦波,输入其他已知参数,在Matlab/Simulink中进行系统的仿真。
|
图 4 Simulink仿真模型 Fig.4 Simulation model used in Simulink |
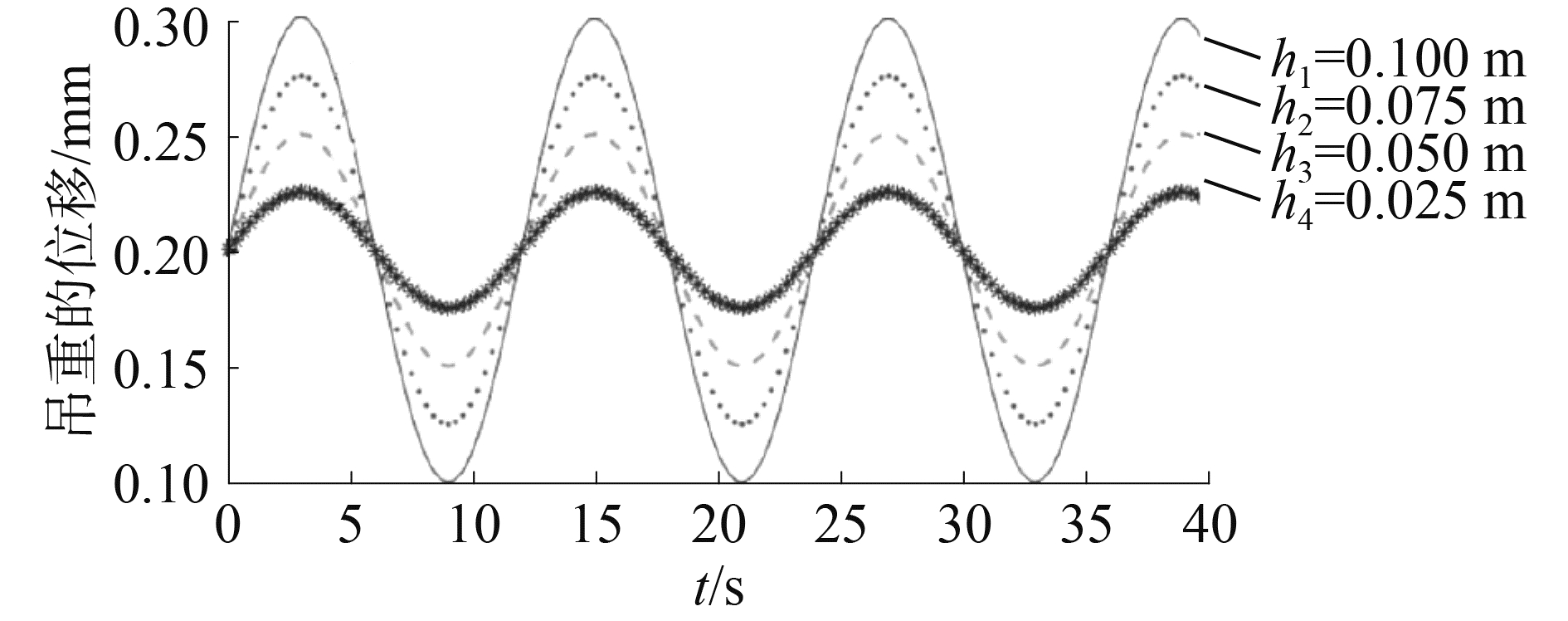
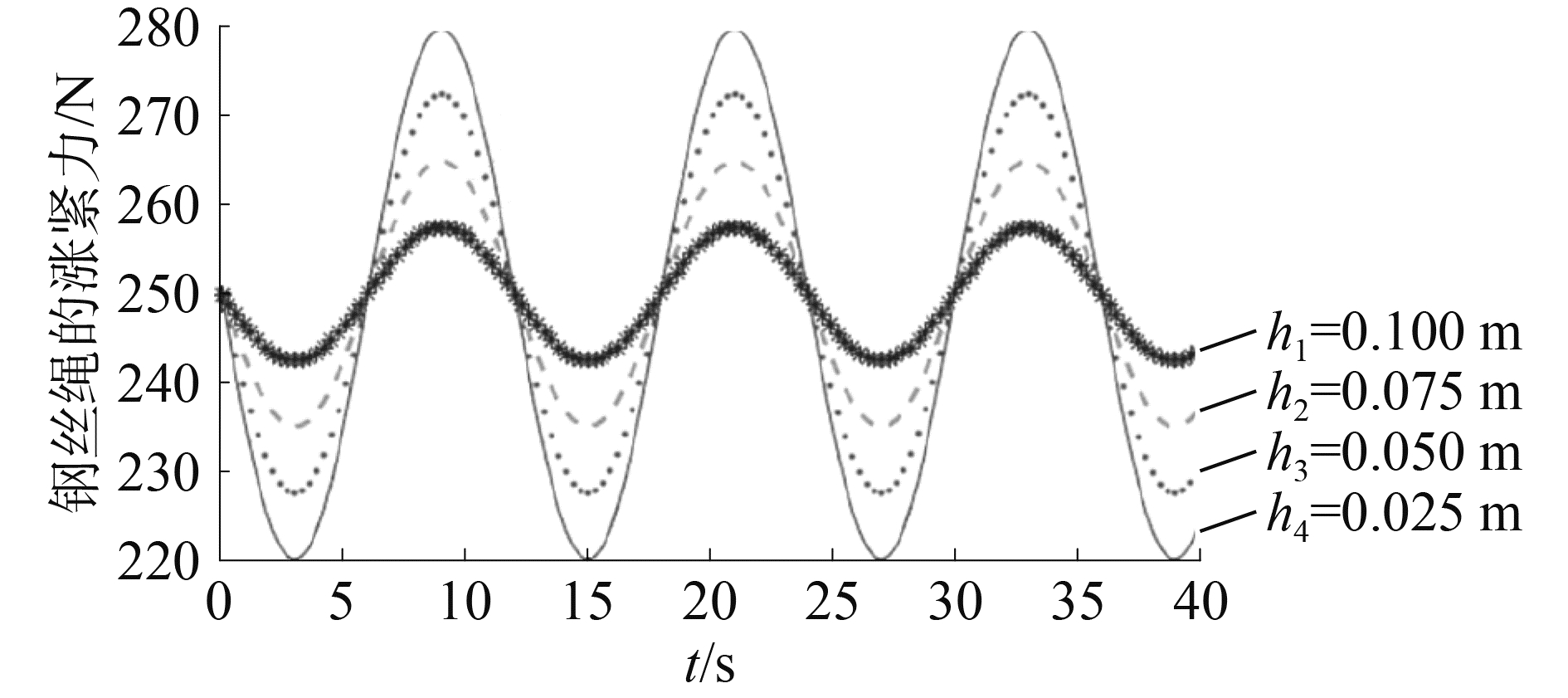
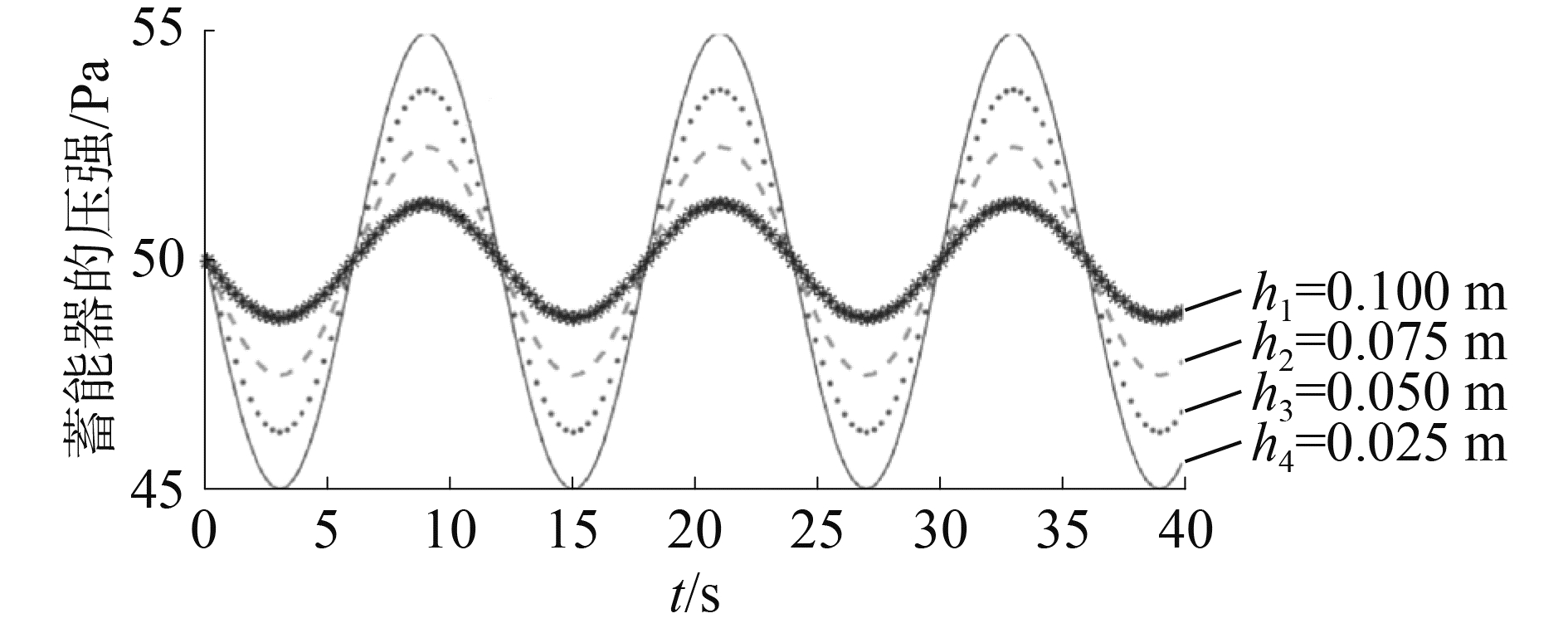
设定活塞杆的质量m、阻尼系数c、平衡位置的压强P1、面积A不变,设置吊重的正弦波振幅h分别为0.025、0.05、0.075、0.1 m,设置频率为π/2,不同位移下的涨紧力和压强的变化如图 5~7所示。钢丝绳的涨紧力、蓄能器的压强成周期性变化,周期与吊重位移变化的周期一样;随着吊重位移的增大,钢丝绳的涨紧力和蓄能器的压强减小;当摇摆台的位移有100 mm的高度变化时,钢丝绳的涨紧力稳定在220~280 N的变化范围内,蓄能器的压强稳定在45~55 Pa的范围内,蓄能器内的气体压强变化幅度远小于钢丝绳的压强变化。
|
图 5 吊重的位移波动 Fig.5 Hoist′s displacement fluctuation |
|
图 6 不同位移下钢丝绳的涨紧力变化 Fig.6 Wire rope′s pulling force change with different displacements |
|
图 7 不同位移下钢丝绳的涨紧力、蓄能器内压强变化 Fig.7 Accumulator′s pressure change with different displacements |
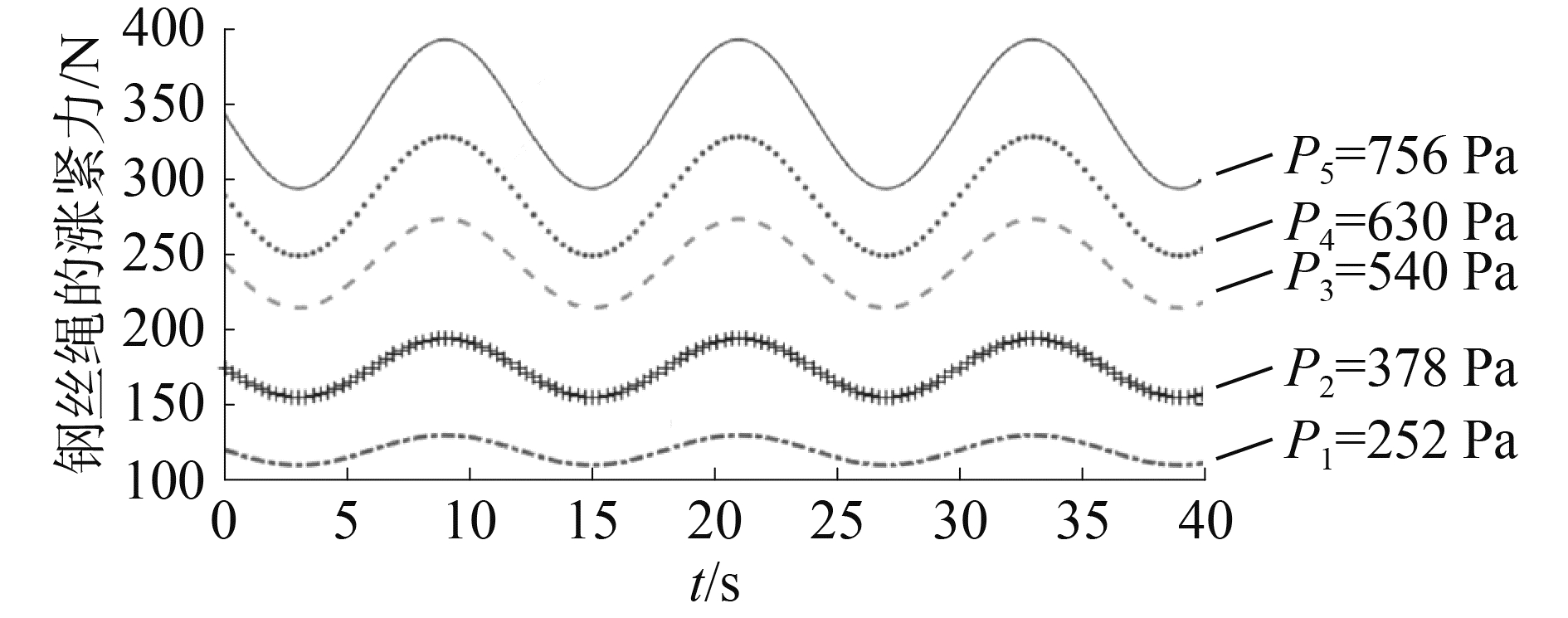
设定活塞杆的质量m、阻尼系数c、位移h、面积A不变,分别设置蓄能器的平衡位置压强为252、378、540、630、756 Pa,不同初始压强下的涨紧力和压强变化如图 8、9所示。仿真结果显示平衡位置的压强越大,钢丝绳的涨紧力和蓄能器的压强越大,且相应涨紧力与压强的变化振幅大,为保证涨紧力与压强的稳定,应保证蓄能器的平衡位置时的压强小于一定的值。
|
图 8 不同压强下钢丝绳的涨紧力变化 Fig.8 Wire rope′s pulling force change with different pressures |
|
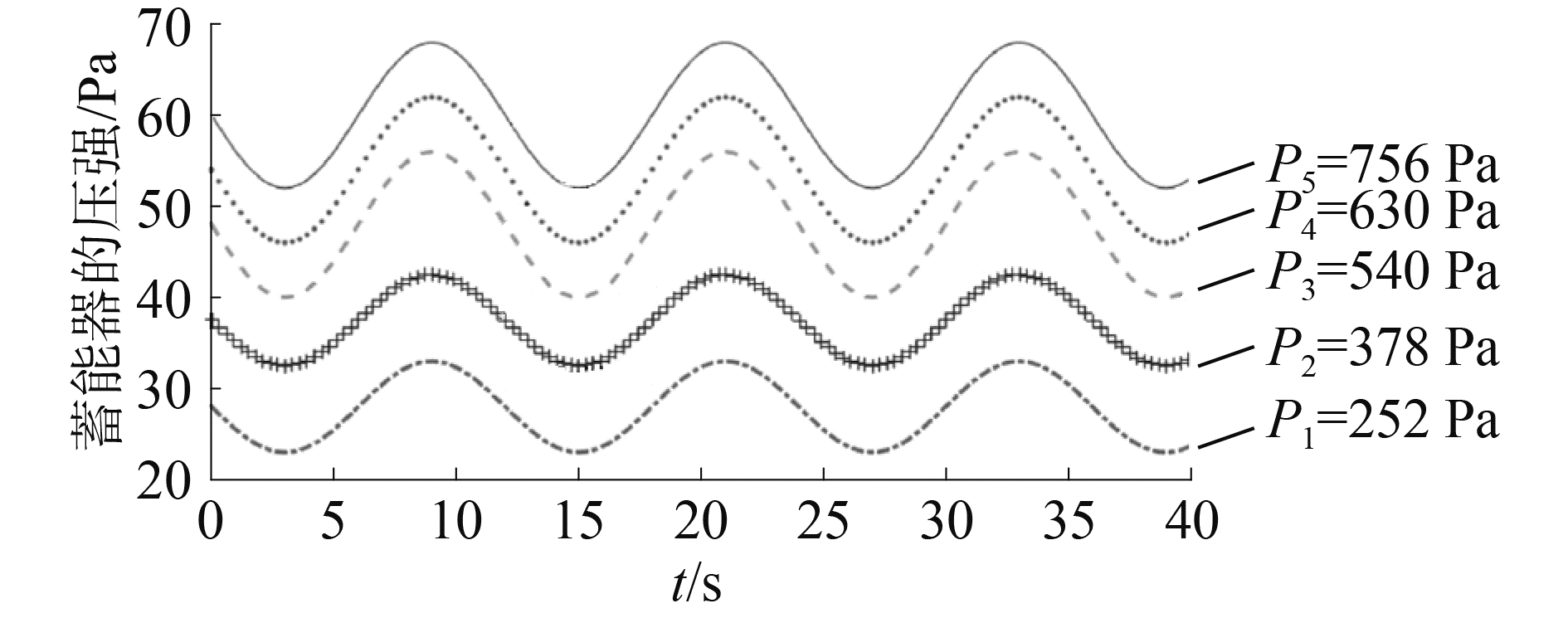
图 9 不同压强下蓄能器的压强变化 Fig.9 Accumulator′s pressure change with different pressures |
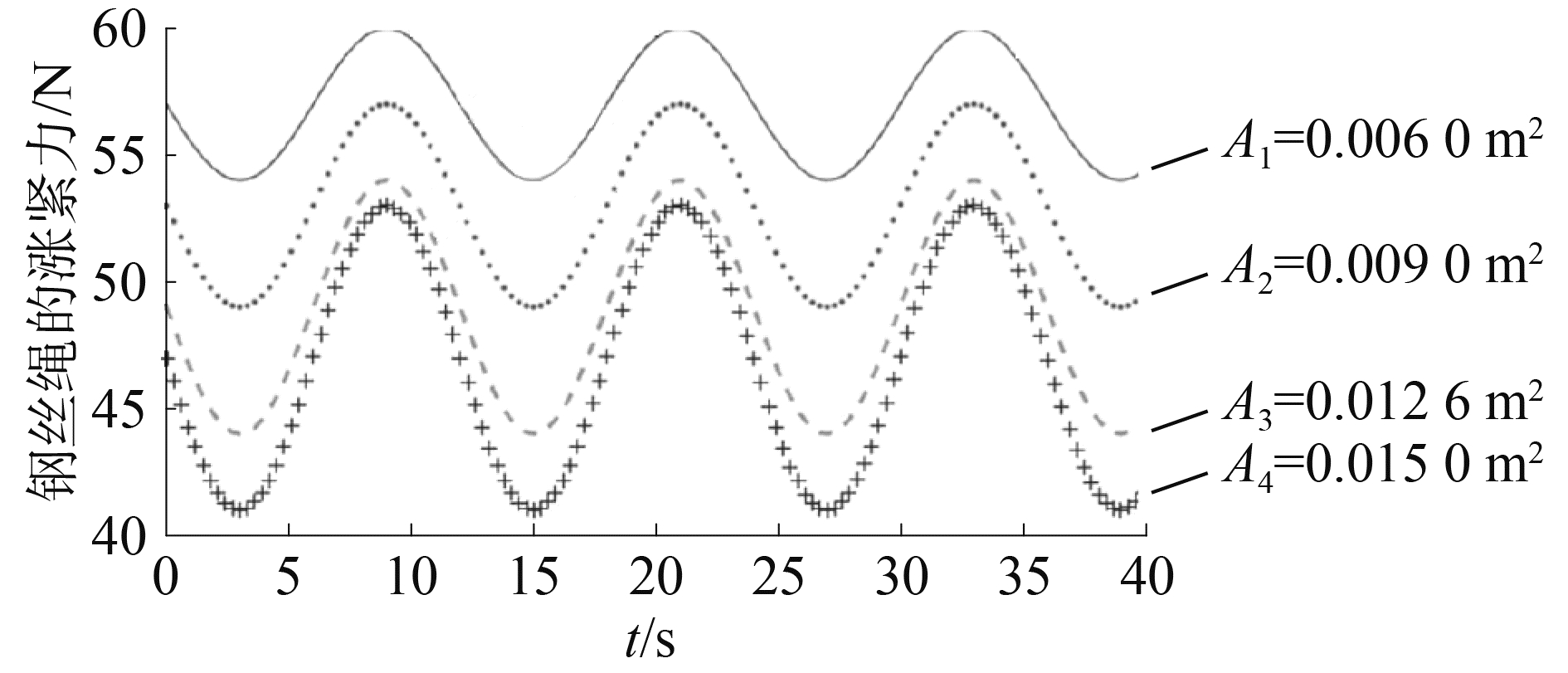
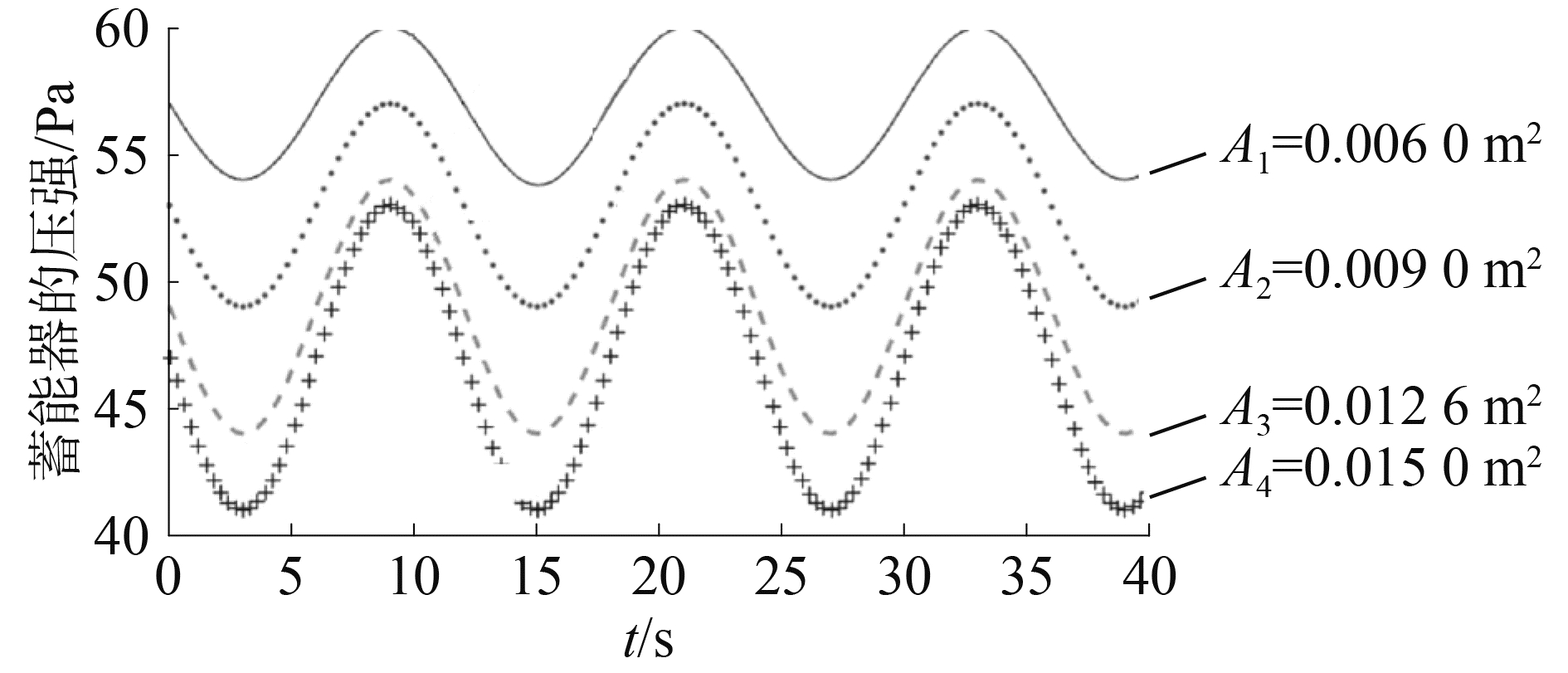
设定活塞杆的质量m、阻尼系数c、吊重绳位移h、蓄能器平衡位置时的压强P1不变,分别设置蓄能器的截面积0.006、0.009、0.0126、0.015 m2,不同面积下的涨紧力和压强如图 10、11所示。仿真结果显示随着面积的增大,钢丝绳的涨紧力、蓄能器的压强减小;但相应涨紧力与压强的变化幅度增大。
|
图 10 不同面积下钢丝绳的涨紧力变化 Fig.10 Wire rope′s pulling force change with different areas |
|
图 11 不同面积下蓄能器的压强变化 Fig.11 Accumulator′s pressure change with different areas |
试验地点选在某室内施工现场,将波浪被动补偿系统固定在波浪模拟摇摆台上,该模拟平台能够产生前后、左右、上下的正弦振动趋势,波浪模拟实验平台如图 12所示。还可以实时检测钢丝绳的涨紧力值、蓄能器的压强值。

|
图 12 波浪模拟实验平台 Fig.12 Wave simulation experiment platform |
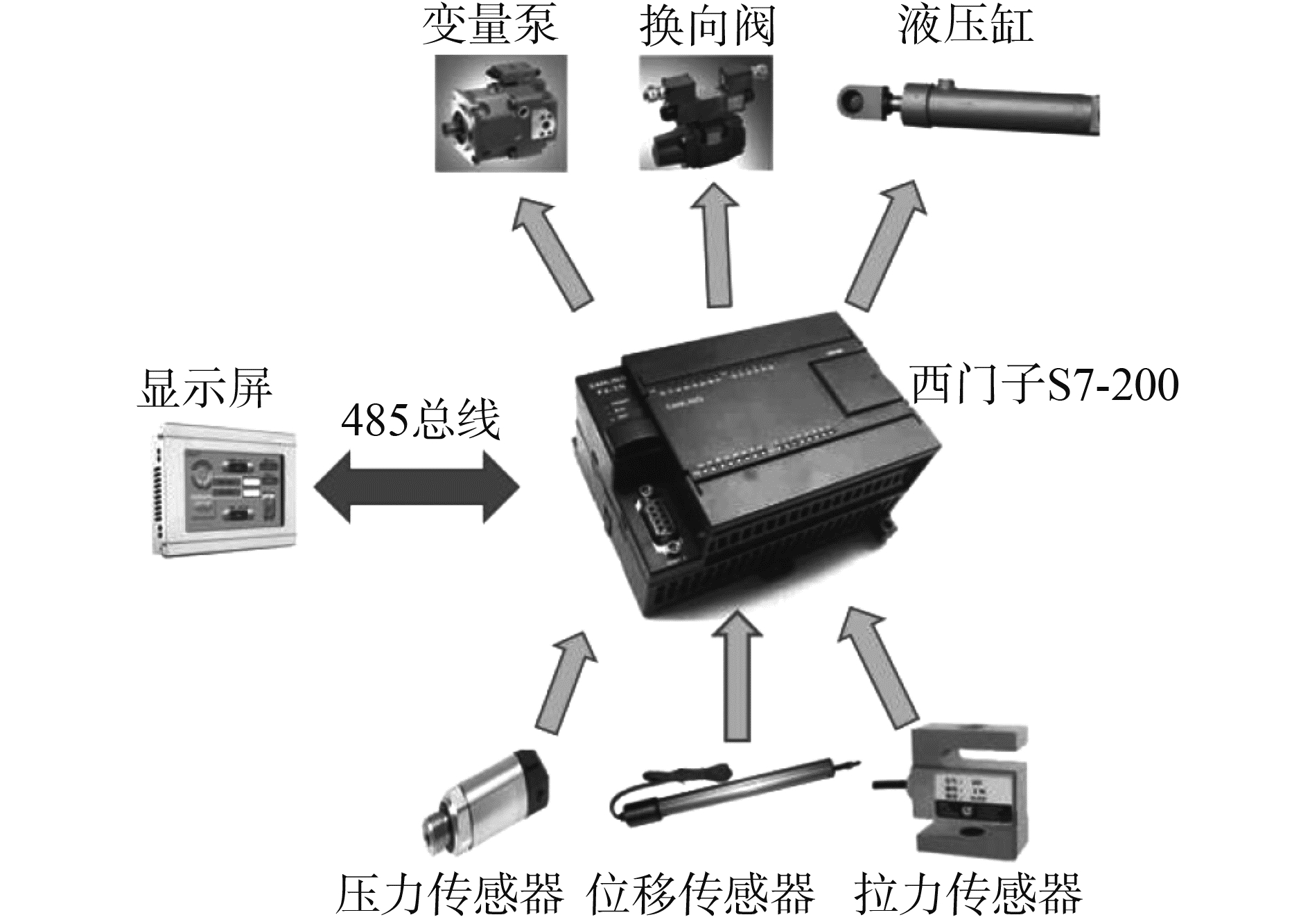
本系统选用的传感器为Huba Control公司的511类型压强、涨紧力传感器、位移传感器,传感器的测压范围为0~500 Pa,输出为电流输出,范围为0~20 mA。该传感器能够抗冲击、抗震动。除此之外还有变量泵、换向阀、震源液压缸。该系统选用西门子S7~1200可编程控制器,系统控制器通过输入输出接口与传感器、液压元件相连进行实时数据采集,控制器通过485总线与上位机显示屏进行实时通信。图 13是控制系统的硬件连接示意图。
|
图 13 控制系统的硬件连接 Fig.13 Control system′s hardware connection |
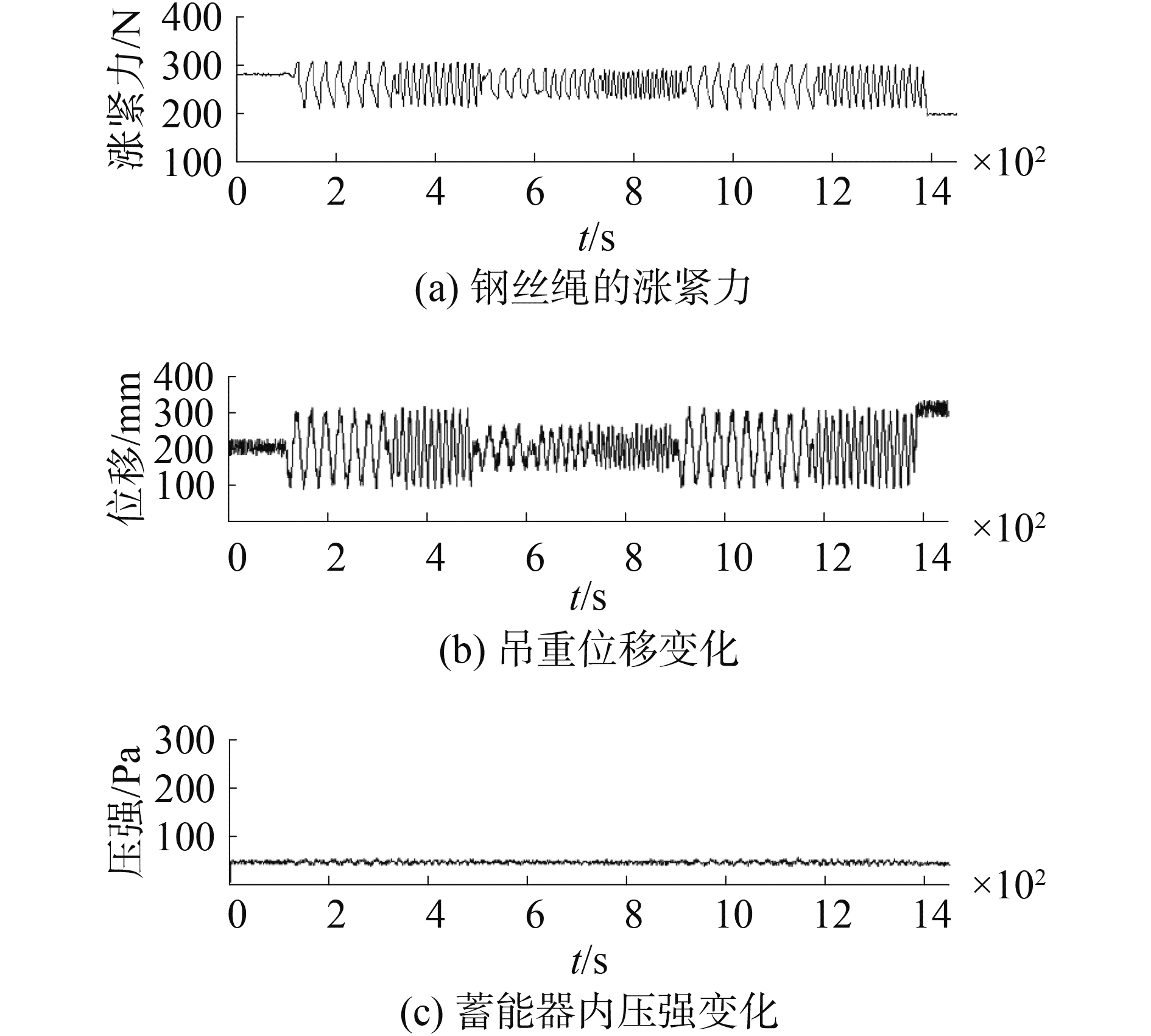
被动补偿装置活塞杆的质量m为25.31 kg、蓄能器平衡位置的体积V为5.3 L、蓄能器的截面积A为0.012 6 m2、蓄能器的充气压强为50 Pa。实验过程中分T1、T2、T3、T4、T5五个时间段,通过压强传感器、涨紧力传感器、位移传感器记录实验数据。采集的实验数据时间以分钟显示,每分钟采集到60个数据等,以1 s时间作为递增值,计算每个数据的具体采集时间。曲线拟合如图 14所示。
|
图 14 整个阶段的传感器检测值 Fig.14 Sensors′ feedback value in the whole stage |
根据采样定理,采样频率要大于信号最高频率的2倍,才能无失真地保留信号的完整信息。实验中位移信号的最大角速度π/3,所以信号的最短周期6 s。根据采样定理,在摇摆台的每一周时间内至少采集两次数值才能波形不失真,因此每分钟采集的点数应满足:x≥2n=20(次),而实验数据的采集频率为每分钟60次,因此实验数据完全满足采样定理,无波形失真现象。
2.3 数据分析实验过程分为5个阶段,通过控制摇摆台振幅、变化频率、基准值,研究不同状况下钢丝绳和蓄能器的受力特性[7-25]。
1) 阶段1(T1):0~100 s。
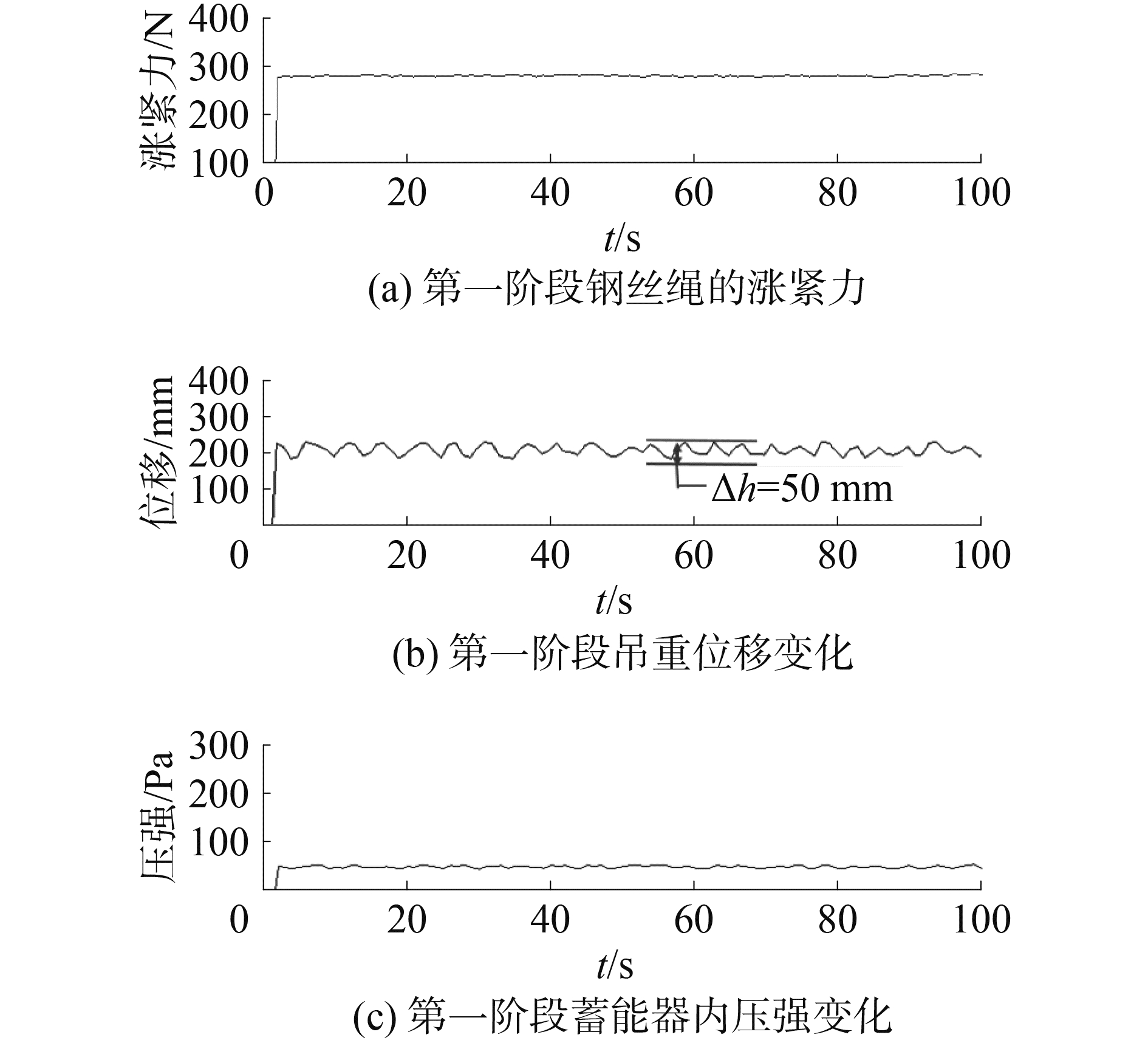
在该阶段内通过控制摇摆台得到的吊重油缸位移变化范围在50 mm内,钢丝绳的涨紧力稳定在270 N,钢丝绳涨紧力的波动很小;蓄能器内压强稳定在49 Pa附近的小范围内波动。根据仿真图 6、7所示的波形,位移波动越大,压强和涨紧力波动越大,由图 15实验数据,得到结论:当油缸位移变化范围小于50 mm时,压强和涨紧力将稳定在某一数值。
|
图 15 第一个阶段的传感器检测值 Fig.15 Sensors′ feedback value in the first stage |
2) 阶段2(T2):100~500 s。
在该阶段内控制油缸位移变化范围在200 mm内,在100~350 s的时间内位移先以t1=60 s的时间为周期进行周期变化,在350~500 s的时间内以t2=20 s的时间为周期进行周期变化;数据显示钢丝绳涨紧力变化幅度80 N,在260 N上下波动;蓄能器压强的变化幅度为10 Pa,在45 Pa上下波动。钢丝绳的涨紧力和蓄能器的压强跟随油缸位移的周期变化而呈现周期变化,相应的变化周期与油缸位移变化周期相一致;当油缸位移增大时,钢丝绳的涨紧力和蓄能器的压强减小;当油缸位移减小时,钢丝绳的涨紧力和蓄能器的压强增大;当位移处于波峰状态时,压强和涨力处于波谷,当位移处于波谷状态时,压强和张力处于波峰状态;位移与涨力、压强的变化趋势相反。这与仿真结果相一致。
3) 阶段3(T3):时间500~900 s。
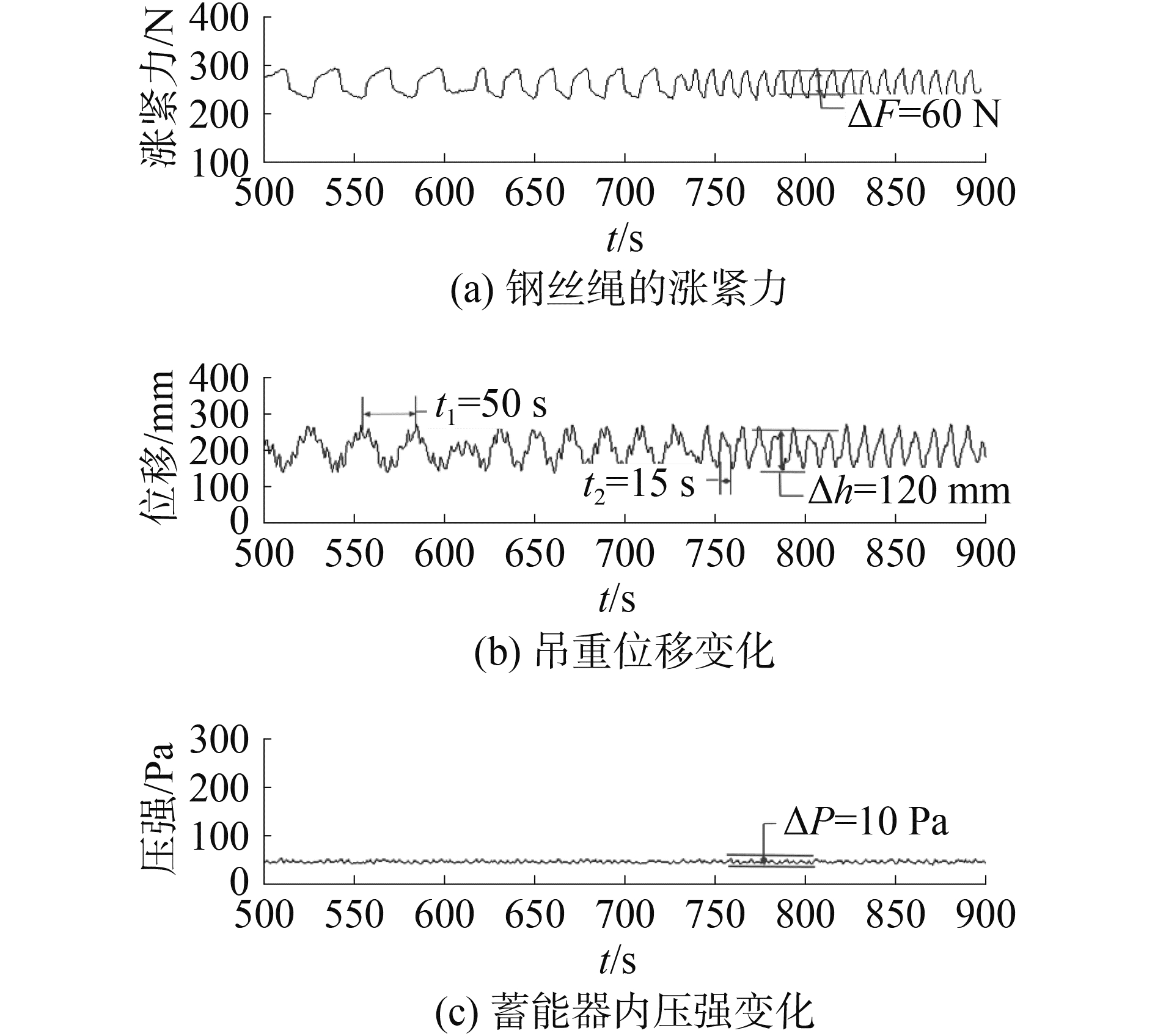
在该阶段内减小油缸位移的变化幅度,稳定在120 mm内,在500~750 s的时间内位移先以t1=50 s的时间为周期进行周期变化,在750~900 s的时间内以t2=15 s的时间为周期进行周期变化。钢丝绳涨紧力变化幅度在60 N范围内,维持在260 N上下波动;蓄能器的压强变化幅度在10 Pa的范围内,维持在45 Pa上下波动。
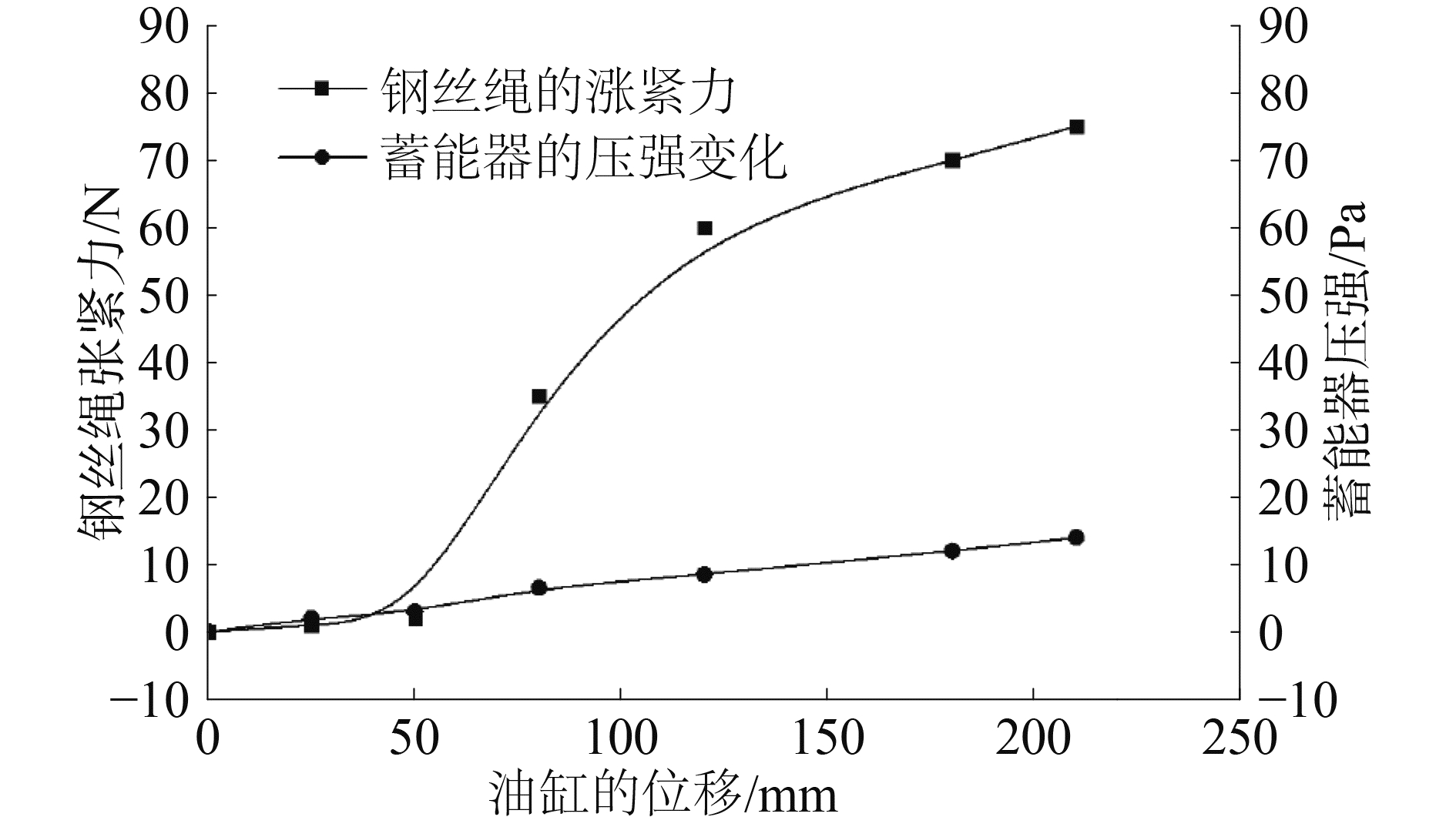
综合图 15~17,以油缸位移为横坐标、以压强和涨紧力的变化范围为纵坐标,绘制如图 18所示的变化趋势。随着油缸位移的增大,钢丝绳的涨紧力和蓄能器的压强变化幅度增大,且涨力的变化幅度大于压强的变化幅度。为保持涨力和压强的稳定应保持油缸的位移变化幅度小于50 mm。

|
图 16 第2个阶段的传感器检测值 Fig.16 Sensors′ feedback value in the second stage |
|
图 17 第3个阶段的传感器检测值 Fig.17 Sensors′ feedback value in the third stage |
|
图 18 传感器检测值幅度的变化趋势 Fig.18 The trend of sensors′ feedback value amplitude |
4) 阶段4(T4):时间900~1 400 s。
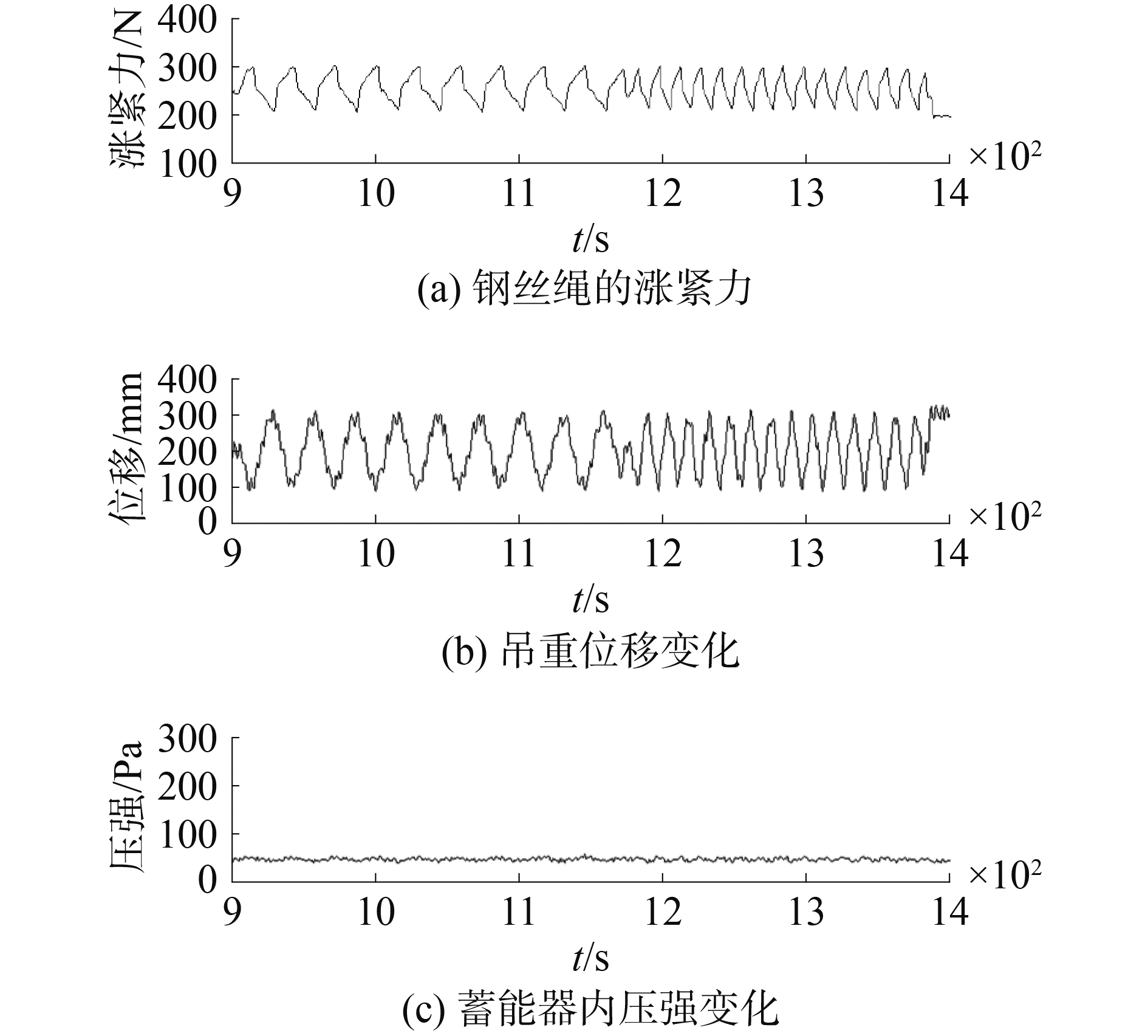
在该阶段内控制油缸位移的变化幅度在200 mm内,在900 s~1 170 s的时间内位移先以t1=30 s的时间为周期进行周期变化,在1 170~1 400 s的时间内以t2=15 s的时间为周期进行周期变化,如图 19所示范区。
|
图 19 第4个阶段的传感器检测值 Fig.19 Sensors′ feedback value in the fourth stage |
第4阶段内1 000 s~1 100 s内的数据如图 20所示。在钢丝绳涨紧力的一个变化周期T=30 s内,t1=4 s、t2=11 s、t3=3 s、t4=12 s,计算相应的涨紧力变化速度v1=12.5 N/s、v2=3.64 N/s、v3=13.3 N/s、v4=4.17 N/s。在t1阶段油缸位移减小,缸筒向上移动,由于活塞杆的惯性滞留,油压瞬间激增,对钢丝绳冲击力瞬间增大;t2阶段,吊重、活塞杆向上运动,惯性影响因素减小;t3阶段油缸位移增大,缸筒向下移动活,由于吊重、活塞杆的惯性滞留,钢丝绳涨紧力在自身吊重的重力作用下瞬间增大;t4阶段,吊重、活塞杆向下运动,惯性影响因素减小,处于失重状态,钢丝绳涨紧力递减速度减缓。

|
图 20 第4阶段内的传感器检测值 Fig.20 Sensors′ feedback value in part time |
5) 阶段5(T5):时间1 400~1 500 s
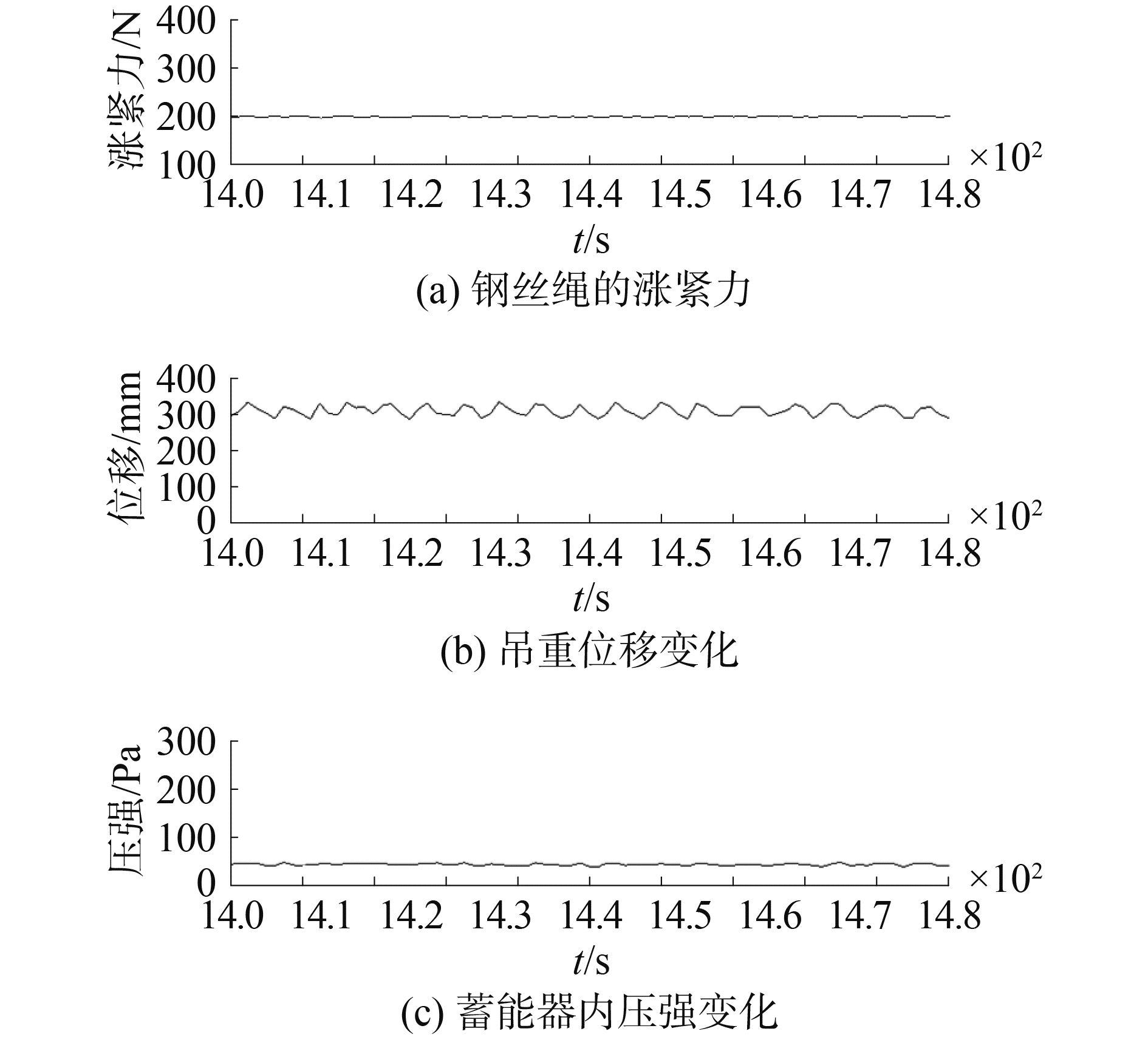
在该阶段内控制吊重位移的变化幅度在50 mm内,钢丝绳的涨力稳定在305 N,钢丝绳涨力的波动很小;蓄能器内压强稳定在48 Pa附近的小范围内波动。对比前4个阶段,在油缸位移变动幅度相同时,位移振动基值越大,钢丝绳的涨紧力和蓄能器的压强越小,如图 21所示。
|
图 21 第五个阶段内的传感器检测值 Fig.21 Sensors′ feedback value in the fifth stage |
1) 钢丝绳的涨紧力和蓄能器的压强跟随油缸位移的周期变化而呈现周期变化,油缸位移与钢丝绳涨紧力、蓄能器压强的变化趋势相反。
2) 随着油缸位移的增大,钢丝绳的涨紧力变化幅度和蓄能器的压强变化幅度增大,且涨紧力的变化幅度大于压强的变化幅度。为保持涨紧力和压强的稳定应保持摇摆台的位移变化幅度小于50 mm。
3) 在钢丝绳张力的一个周期内分为4个阶段,受惯性力作用,各阶段的涨紧力变化速率不一样。
4) 通过仿真分析得到,钢丝绳的涨紧力、蓄能器的压强与蓄能器平衡位置时的充气压强和面积有关。蓄能器平衡位置时的充气压强越大,涨紧力与压强越大;蓄能器的面积越大,张力与压强越小。
| [1] |
任克忍, 沈大春, 王定亚, 等. 海洋钻井升沉补偿系统技术分析[J]. 石油机械, 2009, 37(9): 125-128. REN Keren, SHEN Dachun, WANG Dingya, et al. Analysis of ocean drilling heave compensation system[J]. China petroleum machinery, 2009, 37(9): 125-128. (  0) 0)
|
| [2] |
李万莉. 工程机械液压系统设计[M]. 上海: 同济大学出版社, 2011. LI Wanli. Design of hydraulic system of construction machinery[M]. Shanghai: TongJi University Press, 2011. (  0) 0)
|
| [3] |
张迎春, 宁艳平, 陆元三. 大容量活塞式蓄能器的使用[J]. 液压与气动, 2013(1): 86-88. ZHANG Yingchun, NING Yanping, LU Yuansan. Application of large capacity piston accumulator[J]. Chinese hydraulics&pneumatics, 2013(1): 86-88. (  0) 0)
|
| [4] |
郑相周, 罗友高. 基于并列机构的大洋采矿补偿平台构型设计分析[J]. 中国机械工程, 2014, 14(18): 1565-1567. ZHENG Xiangzhou, LUO Yougao. Design analysis of ocean mining compensation based on parallel mechanism[J]. China mechanical engineering, 2014, 14(18): 1565-1567. (  0) 0)
|
| [5] |
徐小军, 何平, 徐循, 等. 基于DSP的主动式波浪补偿起重机控制系统设计[J]. 国防科技大学学报, 2008, 30(1): 110-114. XU Xiaojun, HE Ping, XU Xun, et al. Design of control system for an active heave compensation crane with DSP[J]. Journal of National University of Defense Technology, 2008, 30(1): 110-114. (  0) 0)
|
| [6] |
张彦廷, 刘振东, 姜浩, 等. 浮式钻井平台升沉补偿系统主动力研究[J]. 石油矿场机械, 2010, 39(4): 1-4. ZHANG Yanting, LIU Zhendong, JIANG Hao, et al. Study on active force of compensation system for floating drilling platform[J]. Oil field equipment, 2010, 39(4): 1-4. (  0) 0)
|
| [7] |
刘贺, 李彬, 胡晓东. 波浪补偿起艇绞车的研究[J]. 上海造船, 2008(2): 30-31. LIU He, LI Bin, HU Xiaodong. The study of heave compensation boat-lifting winch[J]. Shanghai shipbuilding, 2008(2): 30-31. (  0) 0)
|
| [8] |
TAKAGAWA S.A new concept design of heave compensation system for longer life of cables[D].Tokyo:The University of Tokyo, 2015.
(  0) 0)
|
| [9] |
LIU Jianxia, HOU Zhongxi, CHEN Xiaoqing, et al. Experimental and numerical study on the aero-heating characteristics of blunted waverider[J]. Applied thermal engineering, 2013, 51(1): 301-314. (  0) 0)
|
| [10] |
CUI Kai, LI Guangli, XIAO Yao. Aerodynamic performance study of high pressure capturing wing configuration[J]. AIAA applied aerodynamics conference, 2015, 6(33): 22-26. (  0) 0)
|
| [11] |
LOBBIA M, SUZUKI K. Multidisciplinary design optimization of hypersonic transport configurations using waveriders[J]. AIAA applied aerodynamics conference, 2014, 6(19): 16-20. (  0) 0)
|
 2017, Vol. 38
2017, Vol. 38


