2. 西北工业大学 航海学院, 陕西 西安 710072
2. School of Marine Science and Technology, Northwestern Polytechnical University, Xi'an 710072, China
舰船浸入海水中时,由于存在不同金属结构件的电化学反应,海水中会产生腐蚀电流,同时,为了防止船体的腐蚀,各种人为外加的保护系统也会向海水中输出电流[1-3]。当舰船在航行过程中,由于螺旋桨转动引起轴系接触电阻发生周期性变化,使得海水中腐蚀、防腐蚀电流也随之发生周期性脉动,从而在海水中激发出极低频的交变电磁场,称为轴频电磁场[4-5]。轴频电磁场具有明显的线谱和谐波特征,易于接收和处理,构成了水雷的近场威胁,是水下目标探测系统和自导系统较为理想的目标信号源[6]。
在研究舰船极低频电磁场产生机理及推导其表达式的过程中,首先需要建立准确的场源数学模型[7]。早期建模方法以边界元方法为主,Iwata提出采用边界元方法建模分析舰船的腐蚀相关电场[8],通过该模型能够更加合理的设计防腐保护系统;Adey采用边界元模型预测并研究腐蚀相关的电场和磁场[9];Keddie在边界元建模方法基础上提出了快速多极方法[10],该方法大大减少了计算量。但是,边界元建模需要编制大型边界元软件,且只能计算结构参数、工作状态已知的合作目标,且在计算全空间的电场和磁场分布时还存在较大困难。偶极子建模则由于它可对任意目标进行电磁特征的分析和预测,且模型相对简洁,因此在实际应用中更加具有吸引力。近些年,国内外在该方向的研究主要采用偶极子源法。熊露等直接采用电偶极子模型进行建模[11],但是,文献中并没有给出电流距如何确定;Wimmer等采用按一定规则排列的离散电偶极子进行等效[12],再利用实测场数据,通过反演来获得未知模型参数,该思路的实现需要依靠矛盾方程组的求解,在一定程度上增加了难度;陈聪等在电偶极子模型的基础上提出了电流线模型[13],指出场源不仅包含保护系统中心点到螺旋桨距离的等效电流线,还包括海水中分布的空间电流,在求解时需要对未知的空间分布电荷进行求解。
腐蚀相关的电流由于海水这一良导体的存在,与螺旋桨、转动轴、船壳等形成闭合回路。借鉴极低频发信台的原理,本文提出以该环路为线索,对舰船进行电流环建模,这种新的建模方法考虑了海水的良导电性,同时对空间分布电流产生电磁场的物理过程给出解释,从物理意义角度进行建模,因此更加符合实际中的轴频电磁场场源。同时,在提高模型精度的前提下减少了计算量和实测数据量,因此更适合用于舰船腐蚀相关极低频电磁场的研究。
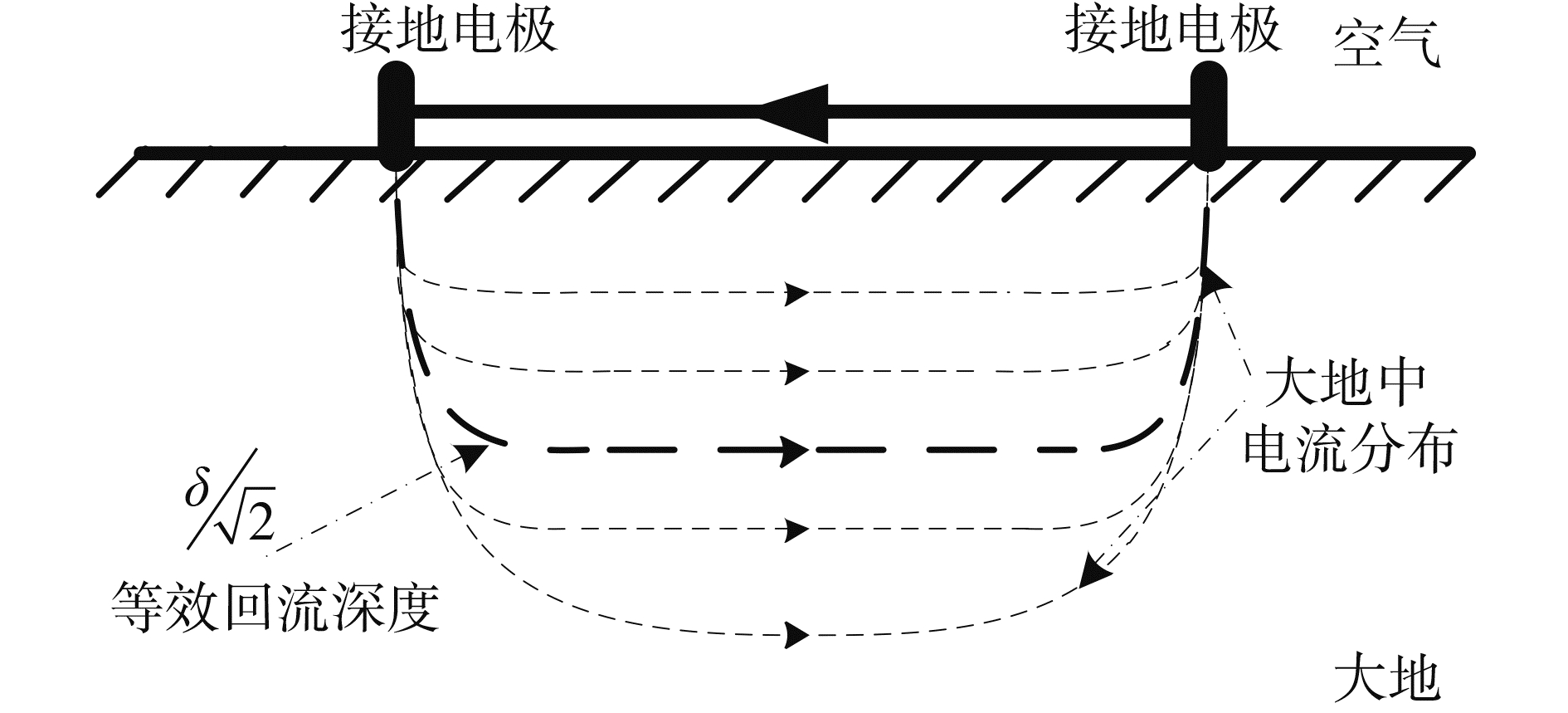
1 轴频电磁场的电流环模型文献[14]介绍了极低频发信台模型,在高电阻率地区距离为L的大地处架设接地天线,由间距数十公里的接地电极、电缆与穿透地下的电流形成一个电流环,极低频发信台的架设原理如图 1所示,其中δ为回流深度。这样架设天线的原因是极低频频段电磁波在空气中波长达到103~104 km,若采用辐射效率高的1/4波长天线在技术上是不可行的,而直接在空气中相距数十公里的两点架设水平天线,等效为水平电偶极子模型,其电偶极矩为IL,其中I为电缆中电流值,L为两个接地电极间距。该天线由于远小于该频段电磁波的波长,辐射出的电磁场场强又很弱,在海洋深处的潜艇接收不到信号。若将水平天线两端接地,通过大地的导电性将接地水平天线与穿透地下的电流构成电流环,以该电流环向外辐射电磁场,从而提高辐射功率,使海洋深处的潜艇能够接收发信台的指示信息。
|
图 1 极低频发信台原理示意图 Fig.1 Schematic diagram of electremely low frequency transmitting station |
电流环向外辐射电磁波,不仅仅只由直接在空气中架设水平天线部分,还包括在大地中形成的闭合回路部分。也就是说,若将接地的水平天线等效为电偶极子模型,其实际电偶极矩IΔL的距离ΔL不等于两个电极间的距离L。
对于海水中的轴频电磁场场源,由于导电媒质海水的存在,也将腐蚀相关的电流构成了电流环,因此本文采用电流环模型对场源进行建模。要建立电流环模型,首先要了解电流在海水中的分布情况。
1.1 海水中电流分布海水的电导率与海水中的离子种类、各种离子的浓度、温度和压力等因素有关,而压力对电导率的影响又较小,因此,本文将海水看作均匀的导电媒质。众所周知,均匀导电媒质中的电流是按指数规律随距离而衰减的[15],即
| $ i = {i_0}{{\rm{e}}^{ - {\rm{j}}kz}} $ | (1) |
式中:i0是海面的电流密度, k为海水中电磁波的波数,即
| $ k = \sqrt {\left( {{\omega ^2}\varepsilon - {\rm{j}}\omega \sigma } \right){\mu _0}} \approx \sqrt {\omega \sigma {\mu _0}} {{\rm{e}}^{ - {\rm{j}}\frac{{\rm{ \mathsf{ π} }}}{4}}} $ | (2) |
式中:ω为信号的角频率,σ为海水的电导率,μ0为磁导率。假设海水为半无限大媒质,地面深度定义为0 m,无穷远处的距离为∞,则对式(1)从0到∞进行积分,得
| $ \int_0^\infty {i{\rm{d}}z} = - {\rm{j}}\frac{{{i_0}}}{k} \approx \frac{{{i_0}\delta }}{{\sqrt 2 }}{{\rm{e}}^{ - {\rm{j}}\frac{{\rm{ \mathsf{ π} }}}{4}}} $ | (3) |
其中
| $ \delta = \frac{1}{{\sqrt {{\rm{ \mathsf{ π} }}f\sigma {\mu _0}} }} $ | (4) |
称为海水的趋肤深度,趋肤深度是用来表征趋肤效应的重要参量,定义为当电磁波从表面进入导电媒质一段距离而使得其幅度衰减到原来(表面)幅度的1/e时的这段距离。如果将通有交变电流信号的两个电极置于刚刚淹没入水面处,那么,均匀导电媒质中分布的电流等效于集中在
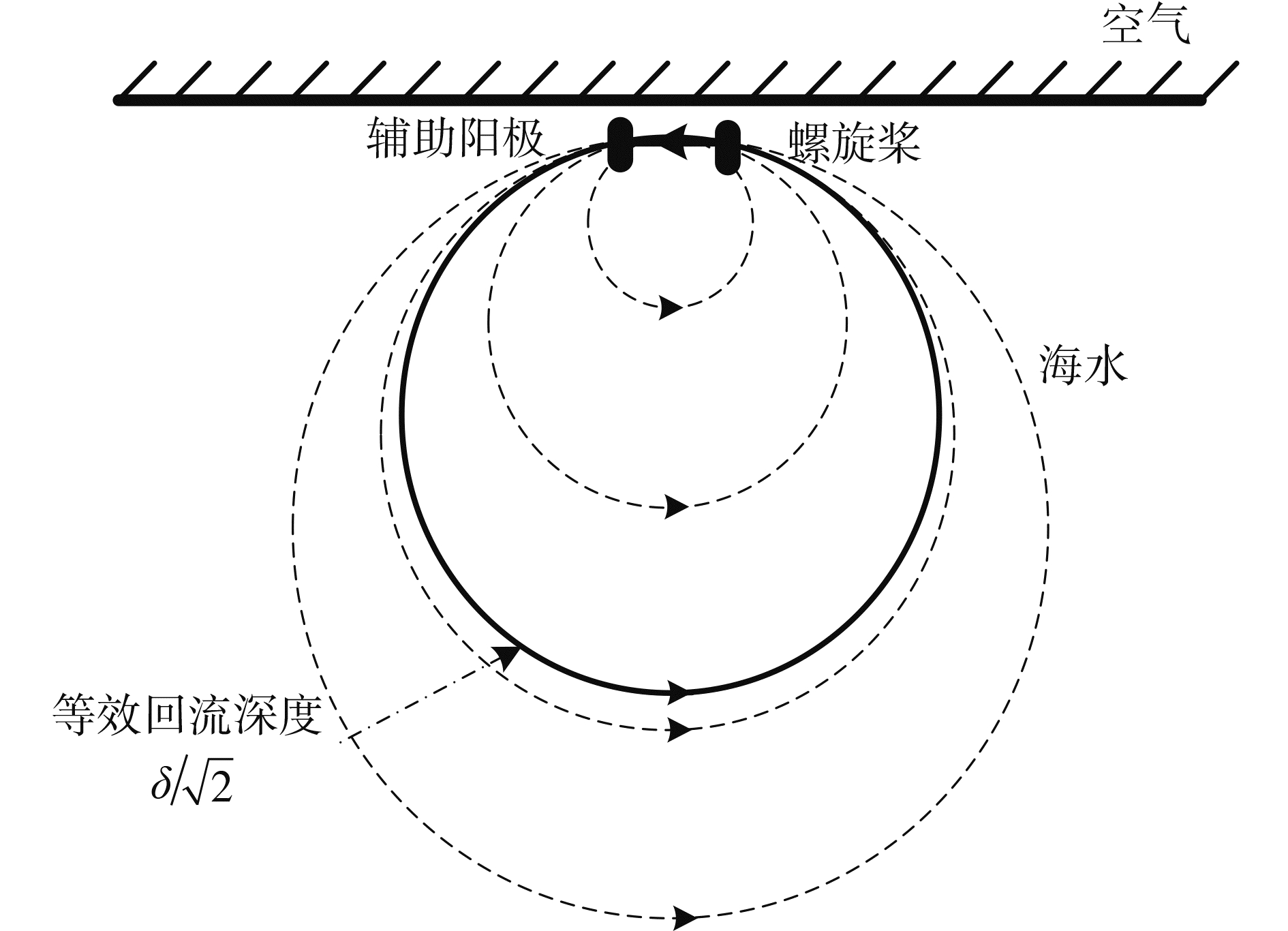
对于舰船的腐蚀相关轴频电磁场,依据文献[13]中提出的电流线思路,可以将该电流线等效为连接电缆,两端等效为接入导电媒质的2个电极,海水的良导电性使2个电极和等效连接电缆构成闭合回路,该闭合回路和极低频发信台原理一致,因而舰艇腐蚀相关电磁场场源也可等效为电流环模型,如图 2所示。
|
图 2 轴频电磁场场源电流环模型示意图 Fig.2 Schematic diagram of current loop model from shaft-rate electromagnetic field |
通过式(4)可以计算,当信号频率为3 Hz时,其等效回流深度为
分析可知,电流环模型的环电流的大小I为在螺旋桨汇聚流入转动轴的电流,环面积S为弦(保护系统中心到螺旋桨的距离)与曲线(等效回流)组成的闭合曲面的面积。本文假设电流环模型的电流矩为IS。
文献[16]采用波动方程方法推导了三层媒质模型中电偶极子模型的电磁场的传播表达式为
| $ \left\{ \begin{array}{l} {E_z} = \int_{ - \infty }^\infty {A_1^{{\rm{hed}}}{{\rm{e}}^{{\rm{j}}{u_1}z}}{\rm{H}}_1^{\left( 1 \right)}\left( {\lambda \rho } \right)\cos \varphi {\rm{d}}\lambda } \\ {H_z} = \int_{ - \infty }^\infty {C_1^{{\rm{hed}}}{{\rm{e}}^{{\rm{j}}{u_1}z}}{\rm{H}}_1^{\left( 1 \right)}\left( {\lambda \rho } \right)\sin \varphi {\rm{d}}\lambda } \end{array} \right. $ | (5) |
式中:C1hed、A1hed代表海水中水平电偶极子产生的电磁波的波幅度,Ez、Hz分别为z方向的电场强度、磁场强度,H1(1)(λρ)为0阶Hankel函数,ρ为水平传播距离。
三层媒质模型中电流环模型(电流环可以等效为磁偶极子)的电磁场传播表达式为
| $ \left\{ \begin{array}{l} {E_z} = \int_{ - \infty }^\infty {A_1^{{\rm{hmd}}}{{\rm{e}}^{{\rm{j}}{u_1}z}}{\rm{H}}_1^{\left( 1 \right)}\left( {\lambda \rho } \right)\sin \varphi {\rm{d}}\lambda } \\ {H_z} = \int_{ - \infty }^\infty {C_1^{{\rm{hmd}}}{{\rm{e}}^{{\rm{j}}{u_1}z}}{\rm{H}}_1^{\left( 1 \right)}\left( {\lambda \rho } \right)\cos \varphi {\rm{d}}\lambda } \end{array} \right. $ | (6) |
式中:A1hmd、C1hmd表示海水中水平磁偶极子产生的电磁波的波幅度。
文献[15]用矢量位方法推导了两层媒质模型中电偶极子模型的电磁场的传播表达式为
| $ \left\{ \begin{array}{l} {E_\rho } = - {\rm{j}}\frac{{\omega \mu I{\rm{d}}l}}{{4{\rm{ \mathsf{ π} }}k_1^2}}\int_0^\infty {\left( {{{\rm{e}}^{ - {\rm{j}}{\gamma _1}\left| {z - d} \right|}} - P{{\rm{e}}^{ - {\rm{j}}{\gamma _1}\left( {z + d} \right)}}} \right)} \cdot \\ \;\;\;\;\;\;\;\;{J_1}\left( {\lambda \rho } \right){\lambda ^2}{\rm{d}}\lambda \\ {H_\varphi } = - {\rm{j}}\frac{{I{\rm{d}}l}}{{4{\rm{ \mathsf{ π} }}}}\int_0^\infty {\left( {\frac{{{{\rm{e}}^{ - {\rm{j}}{\gamma _1}\left| {z - d} \right|}}}}{{{\gamma _1}}} - P{{\rm{e}}^{ - {\rm{j}}{\gamma _1}\left( {z + d} \right)}}} \right)} \cdot \\ \;\;\;\;\;\;\;\;{J_1}\left( {\lambda \rho } \right){\lambda ^2}{\rm{d}}\lambda \end{array} \right. $ | (7) |
两层媒质模型中电流环模型的电磁场的传播表达式为
| $ \left\{ \begin{array}{l} {E_\varphi } = \frac{{{\rm{j}}\omega \mu IS}}{{4{\rm{ \mathsf{ π} }}}}\int_0^\infty {\left[ {{{\rm{e}}^{ - {\rm{j}}{\gamma _1}\left| {z - d} \right|}} - Q{{\rm{e}}^{ - {\rm{j}}{\gamma _1}\left( {z + d} \right)}}} \right]{\lambda ^2}{J_1}\left( {\lambda \rho } \right){\rm{d}}\lambda } \\ {H_\rho } = \frac{{IS}}{{4{\rm{ \mathsf{ π} }}}}\int_0^\infty {\left[ {\frac{{{{\rm{e}}^{ - {\rm{j}}{\gamma _1}\left| {z - d} \right|}}}}{{{\gamma _1}}} - Q{{\rm{e}}^{ - {\rm{j}}{\gamma _1}\left( {z + d} \right)}}} \right]{\lambda ^2}{J_1}\left( {\lambda \rho } \right){\rm{d}}\lambda } \end{array} \right. $ | (8) |
还有一些学者通过波动方程[18]、傅里叶变换[16]和矢量位方法[15]分别推导了水平/垂直电偶极子和水平/垂直磁偶极子在分层媒质中电磁波的传播表达式,通过对式(5)~(8)传播表达式及文献中的对比分析,发现采用电偶极子模型分析其在介质中辐射电磁场时,电场ED和磁场HD的表达式都可变换成如下形式[15]
| $ {E_D} = \frac{{\omega {\mu _0}IL}}{{4{\rm{ \mathsf{ π} }}}}\int_0^\infty {{f_1}\left( t \right){g_1}\left( {t,\lambda } \right){\rm{d}}t} $ | (9) |
| $ {H_D} = {\rm{j}}\frac{{IL}}{{4{\rm{ \mathsf{ π} }}}}\int_0^\infty {{f_2}\left( t \right){g_2}\left( {t,\lambda } \right){\rm{d}}t} $ | (10) |
式中:L为等效电流距(在后面的验证试验中为电极对间距)。采用电流环模型分析其在介质中辐射电磁场时,电场EL和磁场HL的表达式同样可变换成与上面相同的形式[17]
| $ {E_L} = \frac{{{\rm{j}}\omega {\mu _0}IS}}{{4{\rm{ \mathsf{ π} }}}}\int_0^\infty {{f_3}\left( t \right){g_3}\left( {t,\lambda } \right){\rm{d}}t} $ | (11) |
| $ {H_L} = \frac{{IS}}{{4{\rm{ \mathsf{ π} }}}}\int_0^\infty {{f_4}\left( t \right){g_4}\left( {t,\lambda } \right){\rm{d}}t} $ | (12) |
式中:S为电流环面积。式(9)~(12)中,fn(t)为慢变函数,当λ很大时,gn(t, λ)振荡非常快。
为了简便分析模型中变量对场强的影响,且两个模型求出的结果更具有对比性,对式(9)~(12)分别做如下归一化处理
| $ {X^ * } = \frac{X}{{{X_{\max }}}} $ | (13) |
即
| $ E_D^ * = \frac{{IL}}{{{{\left( {IL} \right)}_{\max }}}} $ | (14) |
| $ H_D^ * = \frac{{IL}}{{{{\left( {IL} \right)}_{\max }}}} $ | (15) |
| $ E_L^ * = \frac{{IS}}{{{{\left( {IS} \right)}_{\max }}}} $ | (16) |
| $ H_L^ * = \frac{{IS}}{{{{\left( {IS} \right)}_{\max }}}} $ | (17) |
式中:(IL)max为一个变量固定不变。
从式(14)~(17)可以分析出,当其他条件不变,只有电流值I线性变化时,电偶极子模型和电流环模型在某一固定场点辐射的电场和磁场场强都应该随之线性变化;而当其他条件不变,只将2个电极间的间距线性变化时,电偶极子模型同样在固定场点辐射的电场和磁场场强将呈线性变化,而电流环模型的场强变化与其面积成正比,与电极间距没有直接关系。基于上面的分析,在实验室进行了试验验证。上面公式表明,频率的变化对试验定性分析2个模型的结果不会产生影响,因此,试验过程中,为了验证提出模型的有效性,还对20 kHz信号进行试验验证。
2 电流环模型试验验证为了验证通有交变电流信号的电极对在海水中辐射电磁场的辐射模型,在实验室中进行了验证试验。
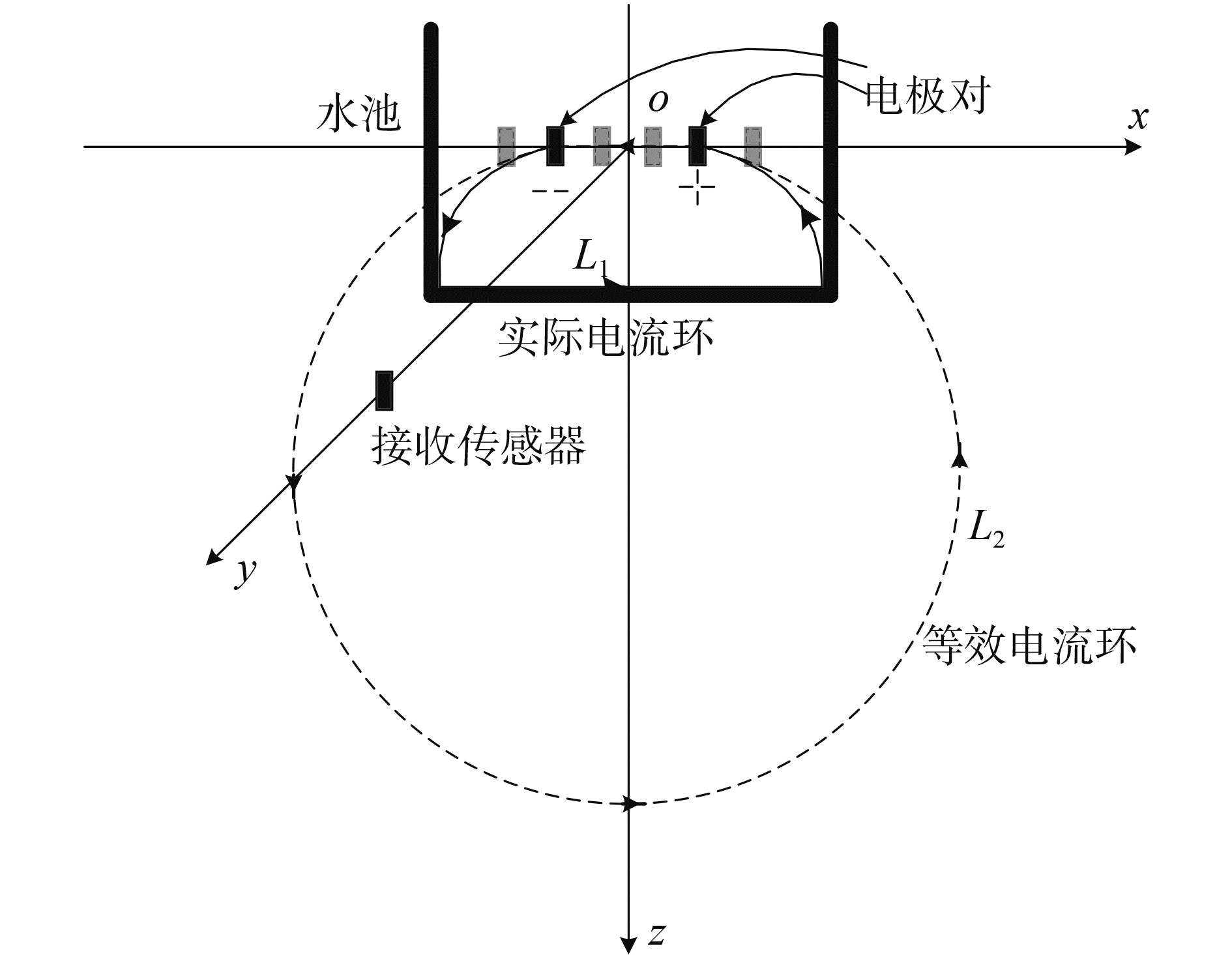
2.1 试验环境在长、宽、深分别为2.5、1.5、0.7 m的无磁性水池中模拟海洋环境,投入大量海盐溶解其中,以此来模拟海洋环境,模拟海水电导率实测值为σ=2.0 S/m,磁导率与媒质没有关系,一般取值4π×10-7。本次试验中采用的是5、20 kHz的正弦信号(5 Hz为轴频电磁场的频率范围,选择20 kHz的目的是对比分析),为了保证接收点场强变化只由电极对间距变化引起,电极对以水池宽度的中点为对称中心,在x轴上分别向左右移动,接收传感器置于y轴上,其坐标为(0 m, 2 m, 0.2 m),在整个试验过程中,接收传感器一直固定在该坐标,如图 3所示。
|
图 3 试验等效示意图 Fig.3 Schematic diagram of equivalent experiment |
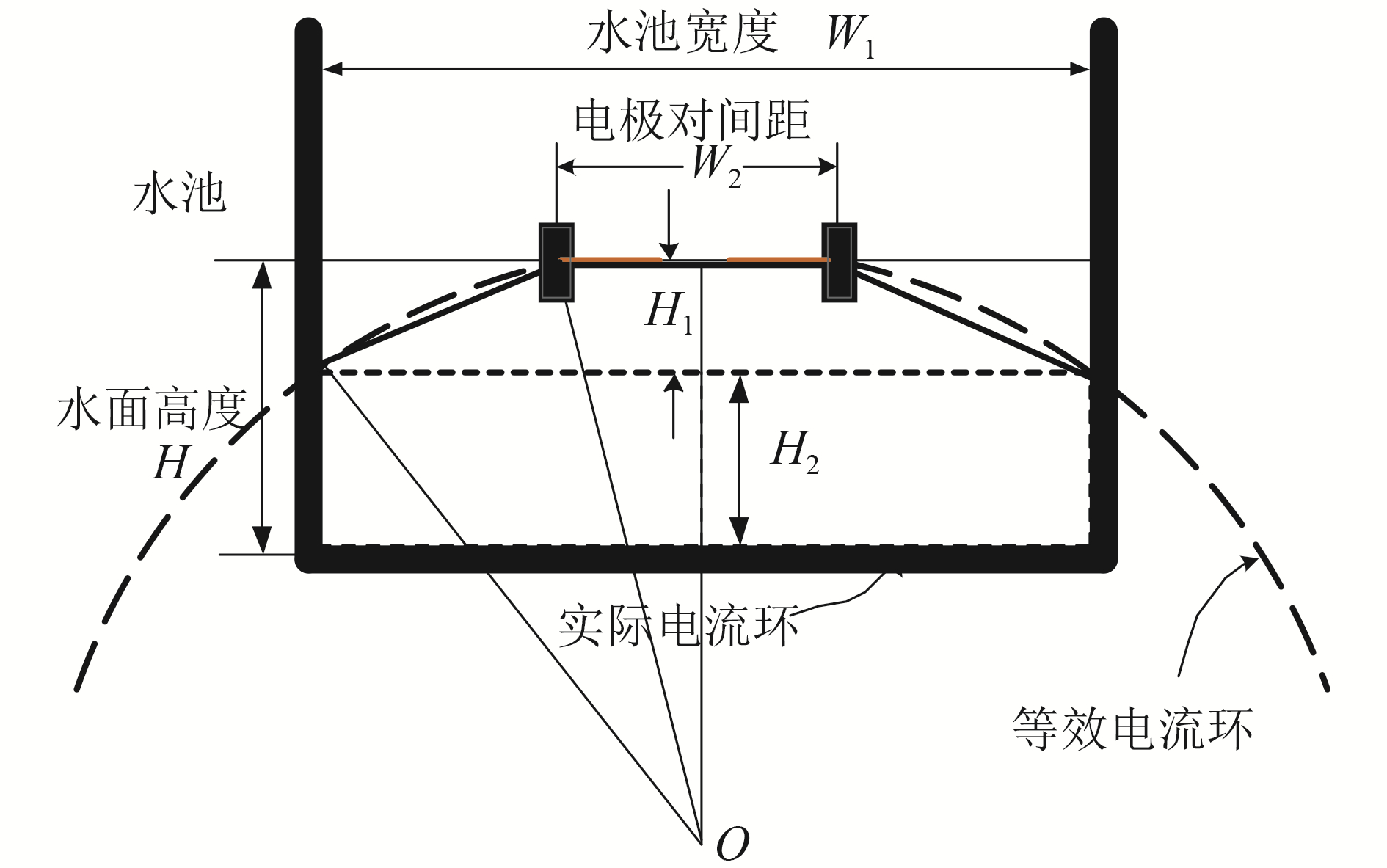
以20 kHz信号为例介绍实际电流环面积的计算方法,通过式(4)可以得到该频率的等效回流深度约为1.8 m,由于回流深度大于水池深度,等效电流由于水池尺寸的限制,将改变其路径,电流从电极对的某一极流出后沿着等效电流环到达水池侧壁,之后贴着水池侧壁,底面流回另一电极,从而形成闭合回路,如图 4所示。
|
图 4 实际电流环面积 Fig.4 Schematic diagram of actual current loop area |
在计算实际电流环的面积时,将其分解成一个梯形和一个矩形,通过2个规则图形的叠加近似得到实际环面积等效圆环半径R为
| $ R = \left( {{{\left( {\frac{\delta }{{\sqrt 2 }}} \right)}^2} + {{\left( {\frac{{{W_2}}}{2}} \right)}^2}} \right)/\left( {\frac{{2\delta }}{{\sqrt 2 }}} \right) $ |
式中:W2为电极对间距,梯形部分的高H1为
| $ {H_1} = \sqrt {{R^2} - {{\left( {\frac{{{W_2}}}{2}} \right)}^2}} - \sqrt {{R^2} - {{\left( {\frac{{{W_1}}}{2}} \right)}^2}} $ |
式中:W1为水池宽度,矩形部分高H2为
| $ {H_2} = H - {H_1} $ |
梯形部分面积S1为
| $ {S_1} = \left( {{W_2} + {W_1}} \right){H_1}/2 $ |
矩形面积为
| $ {S_2} = {W_1}{H_2} $ |
实际电流环的面积为
| $ S = {S_1} + {S_2} $ |
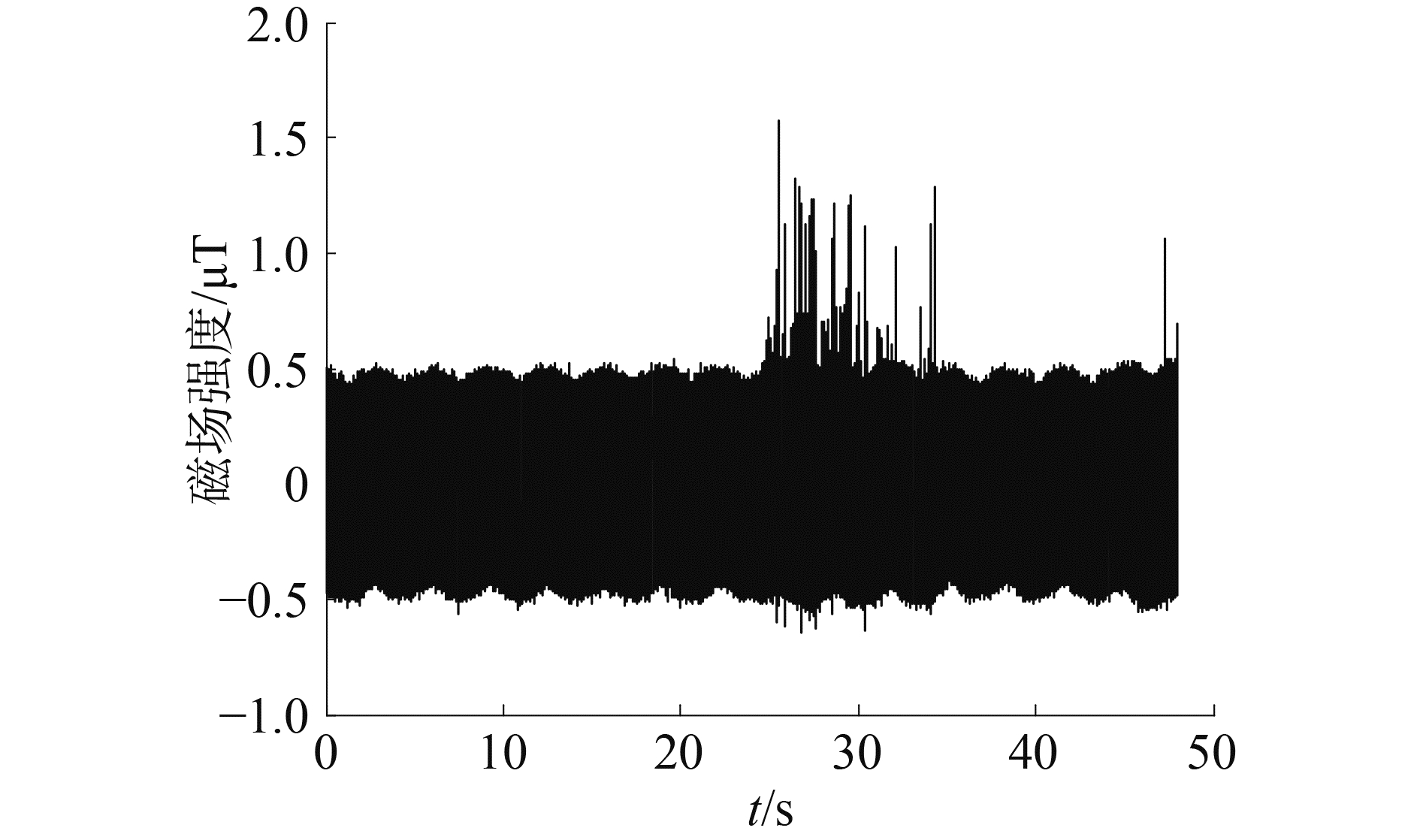
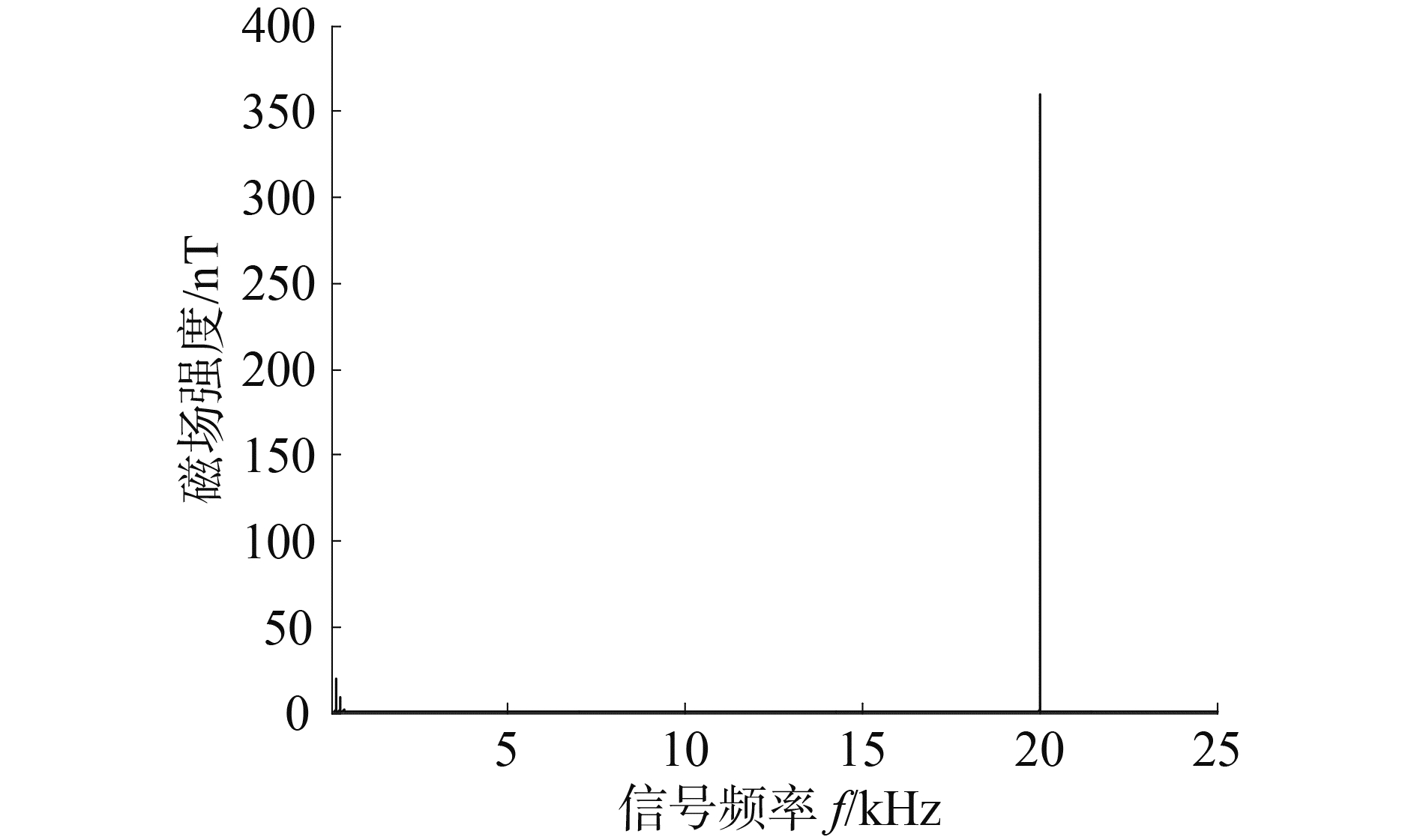
本次试验的目的是定性分析将石墨电极对置于导电媒质中时,水平电偶极子和等效电流环哪个模型更符合实际情况(该试验目的不是验证磁偶极子模型更加优于电偶极子模型,该试验只是原理性验证,由于海水是导电媒质,电偶极子模型的电偶极矩若再采用2个电极之间距离与流过电流的乘积,那么将与试验结果不符)。前面分析了2种模型与电流和电极对间距变化规律的关系(这里只需要各点之间的相对关系),因此在对试验数据分析时,将接收到的固定点的磁场信号采用了归一化处理。图 5和图 6分别是试验过程中接收到的目标信号的时域图和幅频响应图,信号的频率为20 kHz,电极对间距为1.2 m,流入石墨电极的电流为92.56 mA。
|
图 5 目标信号的时域图 Fig.5 The target signal time-domain diagram |
|
图 6 目标信号的幅频响应图 Fig.6 The target signal amplitude-frequency diagram |
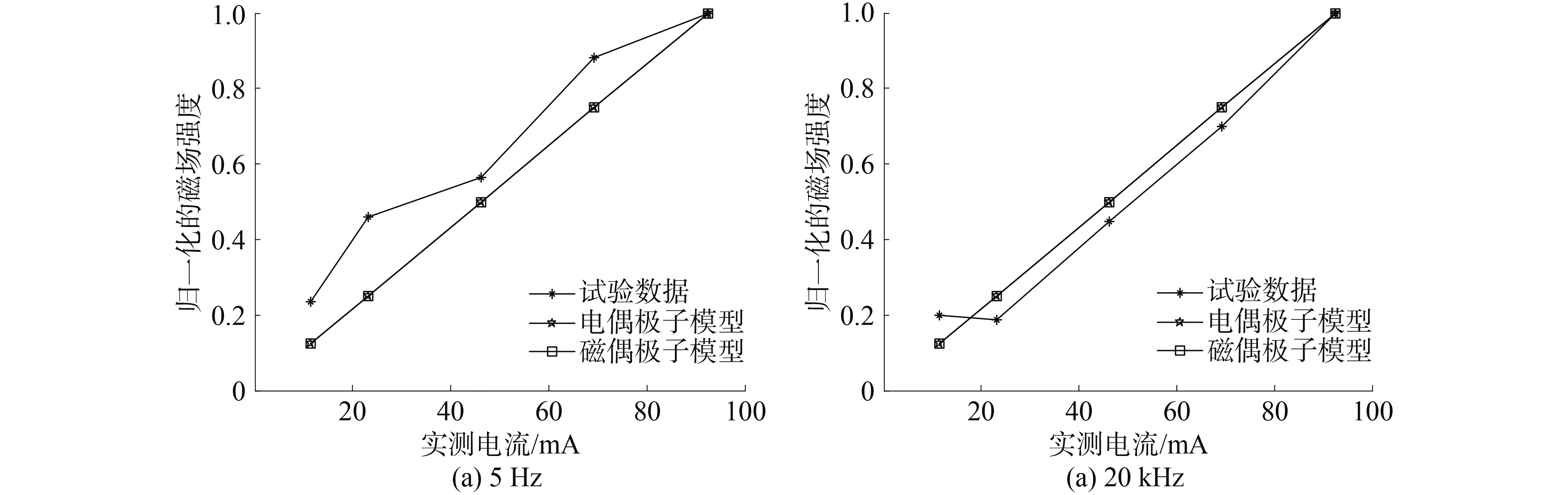
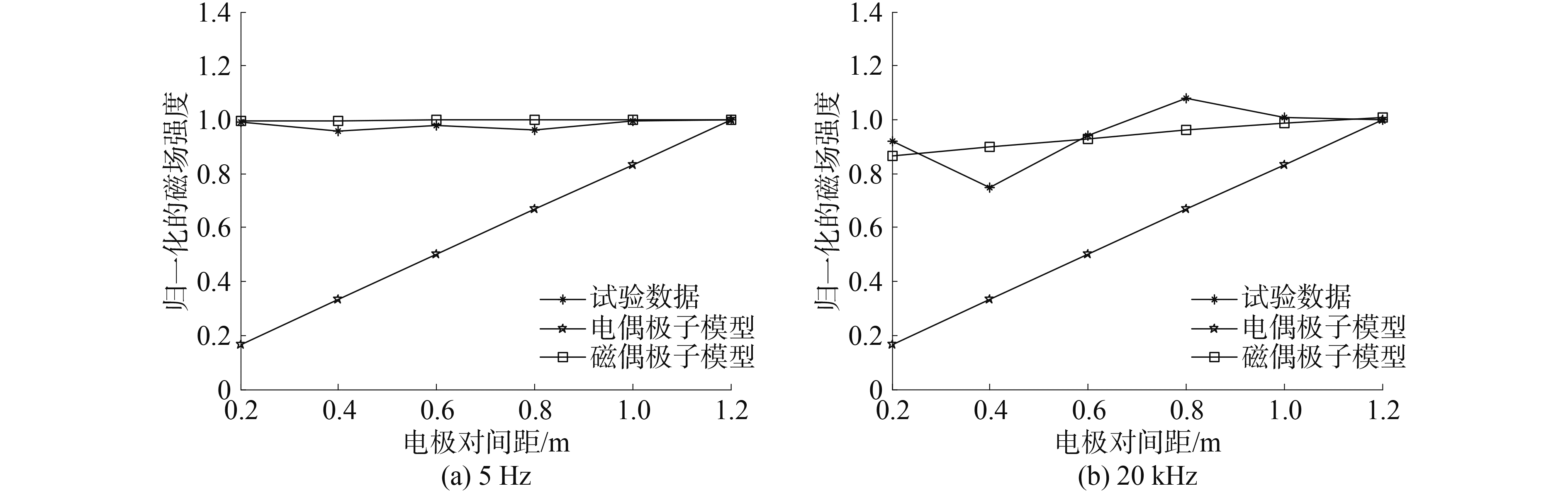
图 7是当石墨电极对间距1.2 m,电流变化时电偶极子和电流环模型与测得的磁场强度的对比关系图。这里以电流值最大(92.56 mA)时做归一化处理。从图中可以看出,电偶极子模型和电流环模型的磁场场强(由式(15)和(17)计算得出)随电流的变化呈现线性变化(两条曲线重合),且与试验测得的数据的变化规律基本吻合。图 8是当电流值92.56 mA,电极对间距变化时2个模型与测得的磁场强度的对比关系图,整个试验的过程中都在监测电极对的输入电流,当电极对间距从0.2~1.2 m变化时,电流的变化范围为94.59~ 92.56 mA,其变化很小,可忽略不计。从图中不难发现,试验测得的结果与电流环模型有较好的一致性。
|
图 7 电流变化时对比分析 Fig.7 Magnetic field intensity by different currents |
|
图 8 电极对间距变化时对比分析 Fig.8 Magnetic field intensity by different electrode pair spacing |
从图 7和图 8的对比结果可以看出,当电流变化时,2个模型都线性变化,与试验结果基本吻合;而电极对间距变化时,电流环模型与试验结果有较好一致性。与前面的理论分析基本一致,因此,采用电流环对接入导电媒质中的电极对进行建模更加准确。
3 结论1) 当电极对间距不变,电流变化时,接收到的磁场场强随着电流线性变化;
2) 当电流不变,电极对间距变化时,接收到的磁场场强只有很小的变化;
3) 电偶极子模型与试验结果差异较大;
4) 电流环模型与试验结果具有较好的一致性;
5) 对轴频电磁场场源建模时,需要考虑海水中分布电流的影响。
电流环模型与试验结果更加吻合,表明该建模方法是可行的。由于电流环模型更加接近实际情况,因此可以将该模型应用于轴频电磁场建模及传播规律研究中,为该领域的研究提供了一个新的思路和方法。
| [1] |
PROUTIERE S, FARDELLA G, SCHOM F. New concepts in mine warfare[C]//IEEE Oceanic Engineering Society. Brest, France, 2005:1408-1410.
(  0) 0)
|
| [2] |
陈聪, 李定国, 蒋治国, 等. 深海中潜艇腐蚀相关磁场全空间分布特征分析[J]. 哈尔滨工程大学学报, 2014, 35(6): 684-689. CHEN Cong, LI Dingguo, JIANG Zhiguo, et al. Research on thecorrosion-related magnetic field produced by a submarine in deep seas[J]. Journal of Harbin Engineering University, 2014, 35(6): 684-689. (  0) 0)
|
| [3] |
卢新城, 龚沈光, 孙明, 等. 轴转动调制腐蚀电流产生的极低频电场的测定[J]. 兵工学报, 2004, 25(5): 544-546. LU Xincheng, GONG Shenguang, SUN Ming, et al. Measurement of extremely low frequency field caused byshaft-ratemodulated corrosion current[J]. Acta armamentarii, 2004, 25(5): 544-546. (  0) 0)
|
| [4] |
ZHOU Xianglong, ZHAO Jingbo, GAO Feng, et al. The simulation and control of naval vessel shaft frequency electromagnetic signature[C]//Chinese Control and Decision Conference. Mianyang, China, 2011:3591-3595.
(  0) 0)
|
| [5] |
龚沈光, 卢新城. 舰船电场特性初步分析[J]. 海军工程大学学报, 2008, 20(2): 1-4. GONG Shenguang, LU Xincheng. Pilot study of electric field characteristics of warsh[J]. Journal of Naval University of Engineering, 2008, 20(2): 1-4. (  0) 0)
|
| [6] |
周骏. 海水中电磁场的特性及舰船电磁场[D]. 武汉: 海军工程大学, 1999. ZHOU Jun. The characteristics of the electromagnetic field in seawater and the electromagnetic field produced by vessels[D]. Wuhan:Navy University of Engineering, 1999. (  0) 0)
|
| [7] |
陈聪, 龚沈光, 李定国. 基于电偶极子的舰船腐蚀防腐相关静态磁场研究[J]. 兵工学报, 2010, 32(1): 113-118. CHEN Cong, GONG Shenguang, LI Dingguo. Research on the static magnetic field related with corrosion and anticorrosion of ships based on the electric dipole Model[J]. Acta armamentarii, 2010, 32(1): 113-118. (  0) 0)
|
| [8] |
IWATA M, FUJIMOTO Y. Application of BEM to design of the impressed current cathodic protection system for ship bull[J]. Journal of the society naval architects of Japan, 1992, 171: 377-380. (  0) 0)
|
| [9] |
ADEY R, BAYNHAM J. Predicing corrosion related electrical and magnetic fields using BAM[C]//Undersea Defence Technology Europe 2000. London, UK, 2000:473.
(  0) 0)
|
| [10] |
KEDDIE A J, POCOCK M D, DEGIORGI V G, et al. Fast solution techniques for corrosion and signatures modelling[C]//6th International Conference on Computer Simulation Risk Analysis and Hazard Mitigation. Brockenhurst, UK, 2008:225-234.
(  0) 0)
|
| [11] |
熊露, 姜润翔, 龚沈光. 浅海中船舶轴频电场建模方法[J]. 国防科技大学学报, 2014, 36(1): 98-103. XIONG Lu, JIANG Runxiang, GONG Shenguang. Ship modeling method ofshaft-ELFE in shallow sea[J]. Journal of National University of Defense Technology, 2014, 36(1): 98-103. DOI:10.11887/j.cn.201401018 (  0) 0)
|
| [12] |
WIMMER S A, HOGAN E A, DEGIORGI V G. Dipole modelling and sensor design[J]. Simulation of electro-chemical processes Ⅱ. WIT transactions on engineering sciences, 2007, 54: 143-152. (  0) 0)
|
| [13] |
陈聪, 魏勇, 姚陆峰, 等. 基于电流线等效的潜艇磁场估算与仿真[J]. 电子与信息学报, 2015, 37(2): 461-467. CHEN Cong, WEI Yong, YAO Lufeng, et al. Estimation and simulation analysis of the submarine magnetic field based on current-line mode[J]. Journal of electronics & information techno logy, 2015, 37(2): 461-467. DOI:10.11999/JEIT140063 (  0) 0)
|
| [14] |
王祥书. 大地电阻率在超低频/极低频电波传播技术中的作用[J]. 地震地质, 2001, 23(4): 681-687. WANG Xiangshu. Effect of earth resistivity on ELF/SLF transmission technique[J]. Seismology and geology, 2001, 23(4): 681-687. (  0) 0)
|
| [15] |
袁翊. 超低频和极低频电磁波的传播及噪声[M]. 北京: 国防工业出版社, 2011: 219-319. YUAN Xu. Propagation and noise of SLF and ELF electromagnetic waves[M]. Beijing: National Defense Industry Press, 2011: 219-319. (  0) 0)
|
| [16] |
王宏磊. 电磁波跨越海-空界面传播特性研究[D]. 西安: 西北工业大学, 2015. WANG Honglei. Study on electromagnetic wave propagation across seawater to air interface[D]. Xi'an:Northwestern Polytechnical University, 2015. http://cdmd.cnki.com.cn/Article/CDMD-10699-1016909409.htm (  0) 0)
|
| [17] |
LONG Yunliang, JIANG Hongyan, BERNHARD R. Far-region electromagnetic radiation with a certical magnetic dipole in sea[J]. IEEE transactions on antennas and propagation, 2001, 49(6): 992-996. DOI:10.1109/8.931158 (  0) 0)
|
| [18] |
谢处方, 王石安, 文希理. 加载与媒质中天线[M]. 成都: 电子科技大学出版社, 1990. XIE Chufang, WANG Shian, WEN Xili. Load the antenna with medium[M]. Chengdu: Unversity of Electronic Science and Technology Press, 1990. (  0) 0)
|
 2017, Vol. 38
2017, Vol. 38


