信源参数估计一直是阵列信号处理的重要研究方向之一,在增强有用信号、抑制干扰信号以及非合作信号侦察等方面发挥着重要的作用[1-4],主要包括空间谱估计及信源数估计等方面[5]。传统的空间谱大多以点信源模型为基础[6-7],而实际中由于多径等因素的影响接收信号往往具有一定的角度扩展特性。有学者基于接收信号特征的不同将此种具有角度扩展的接收信号模型分为相干分布源(coherently distributed, CD)和非相干分布源(incoherently distributed, ID)两种[6],国内外学者基于此种信号模型在原有点信源模型算法上进行改进创新提出了多种算法。文献[8]在分布式信源模型的基础上利用信号的非圆特征扩展了阵列的输出矩阵,同时基于回溯优化的方法快速得到信号子空间。文献[9]中提出了一种基于平行因子的低复杂度方法,在精度尚可的前提下降低了运算的复杂度。Bengtsson等[10]利用泰勒展开提出了两点近似模型,该模型在小角度扩展下忽略高阶泰勒余项,将分布源近似为2个点源表示,不需要已知角度扩展。文献[11]基于此模型提出了一种针对分布式信源的ESPRIT类算法,极大地降低了计算复杂度,但阵列结构固定。崔维嘉等[12]将非圆信号特征引入分布式信源算法中提出了基于抽样分解的非相干分布源波达方向估计(directional of arrival,DOA)方法。
由于非相干分布源的扩散特性,会导致相同阵元数时可测向目标数的减少。上述算法虽然可以很好地解决非相干分布式信源的测向问题,但并未对测向目标减少的问题进行优化,可分辨目标数急剧减少的问题依然存在。四阶累积量可以自动抑制任意加性高斯噪声并且可以扩展阵列、增加虚拟阵元,因此四阶累积量可以很好地解决非相干分布源的信号扩散带来的分辨目标减少的问题。针对经典测向模型,文献[13]类比二阶统计量的MUSIC算法提出了一种基于四阶累积量的MUSIC算法,文献[14]对上述四阶累积量方法利用波束域进行改进,通过波束输出矩阵降低了计算的复杂度。文献[15]对文献[13]算法中接收信号四阶累积量矩阵的冗余项进行了去除从而有效地降低了计算的复杂度,提高了测向的实时性。文献[16]中通过计算互质阵列接收信号的四阶协方差矩阵并利用稀疏阵列去冗余,同时利用ESPRIT类方法代替MUSIC类方法,在提升阵列自由度的前提下对复杂度进行了兼顾。但上述高阶累积量算法并未考虑多径情况,均采用点信源作为假设,不适用于非相干分布式信源。本文在非相干分布式信源模型的基础上,利用高阶累积量特性对接收信号进行阵列扩展,提高了非相干分布式信源情况下的阵列最大可识别信源个数。
1 信号模型假设空间中存在着
| $ {\boldsymbol{X}}\left( t \right) = \sum\limits_{i = 1}^K {\int_{ - \pi }^\pi {{\boldsymbol{\alpha }}\left( \theta \right)} {{s}_i}\left( {\theta ,t;{\psi _i}} \right)} {\text{d}}\theta + {\boldsymbol{N}}\left( t \right) $ |
式中:
| $ {\boldsymbol{X}}\left( t \right) = \sum\limits_{i = 1}^K {{{\boldsymbol{s}}_i}\left( t \right)} \sum\limits_{l = 1}^{{L_i}} {{\gamma _{i.l}}\left( t \right){\boldsymbol{\alpha }}\left[ {{{\bar \theta }_{i,l}}\left( t \right)} \right]} + {\boldsymbol{N}}\left( t \right) $ |
式中:
| $ {\bar \theta _{i,l}}\left( t \right) = {\theta _i} + {\varphi _{i,l}}\left( t \right) $ |
式中:
将
| $ {\boldsymbol{\alpha }}\left[ {{{\bar \theta }_{i,l}}\left( t \right)} \right] = {\boldsymbol{\alpha }}\left( {{\theta _i}} \right) + {\boldsymbol{\alpha }}'\left( {{\theta _i}} \right){\varphi _{i,l}}\left( t \right) $ |
式中:
| $ {\boldsymbol{X}}\left( t \right) \approx \sum\limits_{i = 1}^K {\left[ {{\boldsymbol{\alpha }}\left( {{\theta _i}} \right){{\boldsymbol{\upsilon }}_{i,0}}\left( t \right)} \right.} + \left. {{\boldsymbol{\alpha }}'\left( {{\theta _i}} \right){{\boldsymbol{\upsilon }}_{i,1}}\left( t \right)} \right] + {\boldsymbol{N}}\left( t \right) $ |
式中:
| $ \left\{ \begin{array}{l} {{\boldsymbol{\upsilon }}_{i,0}}\left( t \right){\text{ = }}{{\boldsymbol{s}}_i}\left( t \right)\sum\limits_{l = 1}^{{L_i}} {{\gamma _{i,l}}} \hfill \\ {{\boldsymbol{\upsilon }}_{i,1}}\left( t \right){\text{ = }}{{\boldsymbol{s}}_i}\left( t \right)\sum\limits_{l = 1}^{{L_i}} {{\gamma _{i,l}}{\varphi _{i,l}}\left( t \right)} \hfill \\ \end{array} \right. $ |
将接收信号简化为如式(1)的形式:
| $ {\boldsymbol{X}}\left( t \right) \approx {{\boldsymbol{A}}_1}\left( \theta \right){{\boldsymbol{G}}_1}\left( t \right) + {{\boldsymbol{A}}_2}\left( \theta \right){{\boldsymbol{G}}_2}\left( t \right) + {\boldsymbol{n}}\left( t \right) $ | (1) |
式中:
| $ \left\{ {\begin{array}{*{20}{c}} {{{\boldsymbol{A}}_1}\left( \theta \right) = \left[ {{{\boldsymbol{a}}_1}\left( {{\theta _1}} \right),{{\boldsymbol{a}}_1}\left( {{\theta _2}} \right), \cdots ,{{\boldsymbol{a}}_1}\left( {{\theta _{\rm{K}}}} \right)} \right] \in {{\bf{C}}^{{M} \times 1}}} \\ {{{\boldsymbol{A}}_2}\left( \theta \right) = \left[ {{{\boldsymbol{a}}_2}\left( {{\theta _1}} \right),{{\boldsymbol{a}}_2}\left( {{\theta _2}} \right), \cdots ,{{\boldsymbol{a}}_2}\left( {{\theta _{\rm{K}}}} \right)} \right] \in {{\bf{C}}^{{M} \times 1}}} \\ {{{\boldsymbol{G}}_1}\left( {\rm{t}} \right) = \left[ {{{\boldsymbol{\upsilon }}_{1,0}}\left( {\rm{t}} \right),{{\boldsymbol{\upsilon }}_{2,0}}\left( {\rm{t}} \right), \cdots ,{{\boldsymbol{\upsilon }}_{{\rm{K}},0}}\left( {\rm{t}} \right)} \right] \in {{\bf{C}}^{{K} \times 1}}} \\ {{{\boldsymbol{G}}_2}\left( {\rm{t}} \right) = \left[ {{{\boldsymbol{\upsilon }}_{1,0}}\left( {\rm{t}} \right),{{\boldsymbol{\upsilon }}_{2,0}}\left( {\rm{t}} \right), \cdots ,{{\boldsymbol{\upsilon }}_{{\rm{K}},0}}\left( {\rm{t}} \right)} \right] \in {{\bf{C}}^{{K} \times 1}}} \end{array}} \right. $ |
传统的DOA估计通常利用信号的二阶统计特性,但有时二阶统计特征不能完整地描述信号的特性,这时就需要采用高阶累积量。常用的高阶累计量通常为三阶累积量和四阶累积量,由于四阶累积量具有自动抑制加性高斯噪声和任意高斯色噪声的能力,因此阵列信号处理中通常采用四阶累积量。同时四阶累计量还可以扩展阵列孔径,因此可以实现在阵元数不变的情况下识别更多的信源。
假设信号
| $ \begin{gathered} {C_{4x}}\left( {{\tau _1},{\tau _2},{\tau _3}} \right) = {\rm{E}}\left\{ {x\left( n \right){x^*}\left( {n + {\tau _1}} \right)x\left( {n + {\tau _2}} \right){x^*}\left( {n + {\tau _3}} \right)} \right\} -\\ {\rm{E}}\left\{ {x\left( n \right){x^*}\left( {n + {\tau _1}} \right)} \right\}{\rm{E}}\left\{ {x\left( {n + {\tau _2}} \right){x^*}\left( {n + {\tau _3}} \right)} \right\} - \\ {\rm{E}}\left\{ {x\left( n \right)x\left( {n + {\tau _2}} \right)} \right\}{\rm{E}}\left\{ {{x^*}\left( {n + {\tau _1}} \right){x^*}\left( {n + {\tau _3}} \right)} \right\}- \\ {\rm{E}}\left\{ {x\left( n \right){x^*}\left( {n + {\tau _3}} \right)} \right\}{\rm{E}}\left\{ {{x^*}\left( {n + {\tau _1}} \right)x\left( {n + {\tau _2}} \right)} \right\} \\ \end{gathered} $ | (2) |
假设存在K个序列
| $ \begin{gathered} {{\boldsymbol{C}}_x}\left( {{k_1},{k_2},{k_3},{k_4}} \right) = {\rm{E}}\left\{ {{x_{{k_1}}}\left( n \right)x_{{k_2}}^*\left( n \right){x_{{k_3}}}\left( n \right)x_{{k_4}}^*\left( n \right)} \right\} - \\ {\rm{E}}\left\{ {{x_{{k_1}}}\left( n \right)x_{{k_2}}^*\left( n \right)} \right\}{\rm{E}}\left\{ {{x_{{k_3}}}\left( n \right)x_{{k_4}}^*\left( n \right)} \right\} -\\ {\rm{E}}\left\{ {{x_{{k_1}}}\left( n \right){x_{{k_3}}}\left( n \right)} \right\}{\rm{E}}\left\{ {x_{{k_2}}^*\left( n \right)x_{{k_4}}^*\left( n \right)} \right\} -\\ {\rm{E}}\left\{ {{x_{{k_1}}}\left( n \right)x_{{k_4}}^*\left( n \right)} \right\}{\rm{E}}\left\{ {x_{{k_2}}^*\left( n \right){x_{{k_3}}}\left( n \right)} \right\} \\ \end{gathered} $ | (3) |
式(3)为理论情况下的计算表达式,实际使用中也可以使用式(4)来近似估计:
| $ {{\boldsymbol{C}}_x}\left( {{k_1},{k_2},{k_3},{k_4}} \right) = \frac{1}{N}\sum\limits_{n = 1}^N {{x_{{k_1}}}\left( n \right)x_{{k_2}}^*\left( n \right){x_{{k_3}}}\left( n \right)x_{{k_4}}^*\left( n \right)} $ | (4) |
接收信号式(1)的四阶协方差矩阵可以表示为
| ${ \begin{gathered} {{\boldsymbol{C}}_X} = {\rm{E}}\left\{ {\left( {{\boldsymbol{X}} \otimes {{\boldsymbol{X}}^*}} \right){{\left( {{\boldsymbol{X}} \otimes {{\boldsymbol{X}}^*}} \right)}^{\text{H}}}} \right\}- \\ {\rm{E}}\left\{ {\left( {{\boldsymbol{X}} \otimes {{\boldsymbol{X}}^*}} \right)} \right\}{\rm{E}}\left\{ {{{\left( {{\boldsymbol{X}} \otimes {{\boldsymbol{X}}^*}} \right)}^{\text{H}}}} \right\} - \\ {\rm{E}}\left\{ {\left( {{\boldsymbol{X}}{{\boldsymbol{X}}^{\text{H}}}} \right)} \right\} \otimes {\rm{E}}\left\{ {{{\left( {{\boldsymbol{X}}{{\boldsymbol{X}}^{\text{H}}}} \right)}^*}} \right\} = \\ {{\boldsymbol{D}}_1} - {{\boldsymbol{D}}_2} - {{\boldsymbol{D}}_3} \\ \end{gathered}} $ |
式中:
| $ \left\{ \begin{array}{l} {{\boldsymbol{D}}_1} = {\rm{E}}\left\{ {\left( {{\boldsymbol{X}} \otimes {{\boldsymbol{X}}^*}} \right){{\left( {{\boldsymbol{X}} \otimes {{\boldsymbol{X}}^*}} \right)}^{\text{H}}}} \right\} \hfill \\ {{\boldsymbol{D}}_2} = {\rm{E}}\left\{ {\left( {{\boldsymbol{X}} \otimes {{\boldsymbol{X}}^*}} \right)} \right\}E\left\{ {{{\left( {{\boldsymbol{X}} \otimes {{\boldsymbol{X}}^*}} \right)}^{\text{H}}}} \right\} \hfill \\ {{\boldsymbol{D}}_3} = {\rm{E}}\left\{ {\left( {{\boldsymbol{X}}{{\boldsymbol{X}}^{\text{H}}}} \right)} \right\} \otimes E\left\{ {{{\left( {{\boldsymbol{X}}{{\boldsymbol{X}}^{\text{H}}}} \right)}^*}} \right\} \hfill \\ \end{array} \right. $ |
将式(1)带入
| $ \begin{gathered} {\boldsymbol{X}} \otimes {{\boldsymbol{X}}^*} = \left( {{{\boldsymbol{A}}_1}{{\boldsymbol{G}}_1} + {{\boldsymbol{A}}_2}{{\boldsymbol{G}}_2} + {\boldsymbol{N}}} \right) \otimes {\left( {{{\boldsymbol{A}}_1}{{\boldsymbol{G}}_1} + {{\boldsymbol{A}}_2}{{\boldsymbol{G}}_2} + {\boldsymbol{N}}} \right)^*} =\\ \left( {{{\boldsymbol{A}}_1}{{\boldsymbol{G}}_1}} \right) \otimes {\left( {{{\boldsymbol{A}}_1}{{\boldsymbol{G}}_1}} \right)^*} + \left( {{{\boldsymbol{A}}_2}{{\boldsymbol{G}}_2}} \right) \otimes {\left( {{{\boldsymbol{A}}_2}{{\boldsymbol{G}}_2}} \right)^*} + {\boldsymbol{N}} \otimes {{\boldsymbol{N}}^*}= \\ \left( {{{\boldsymbol{A}}_1} \otimes {{\boldsymbol{A}}_1}^*} \right)\left( {{{\boldsymbol{G}}_1} \otimes {{\boldsymbol{G}}_1}^*} \right) + \left( {{{\boldsymbol{A}}_2} \otimes {{\boldsymbol{A}}_2}^*} \right)\left( {{{\boldsymbol{G}}_2} \otimes {{\boldsymbol{G}}_2}^*} \right) +\\ \left( {{\boldsymbol{N}} \otimes {{\boldsymbol{N}}^*}} \right) \\ \end{gathered} $ | (5) |
将式(5)得到的
| $ \begin{gathered} {{\boldsymbol{D}}_1} = \left( {{{\boldsymbol{A}}_1} \otimes {{\boldsymbol{A}}_1}^*} \right){\rm{E}}\left\{ {\left( {{{\boldsymbol{G}}_1} \otimes {{\boldsymbol{G}}_1}^*} \right){{\left( {{{\boldsymbol{G}}_1} \otimes {{\boldsymbol{G}}_1}^*} \right)}^{\rm{H}}}} \right\}{\left( {{{\boldsymbol{A}}_1} \otimes {{\boldsymbol{A}}_1}^*} \right)^{\rm{H}}} +\\ \left( {{{\boldsymbol{A}}_2} \otimes {{\boldsymbol{A}}_2}^*} \right){\rm{E}}\left\{ {\left( {{{\boldsymbol{G}}_2} \otimes {{\boldsymbol{G}}_2}^*} \right){{\left( {{{\boldsymbol{G}}_2} \otimes {{\boldsymbol{G}}_2}^*} \right)}^{\rm{H}}}} \right\}{\left( {{{\boldsymbol{A}}_2} \otimes {{\boldsymbol{A}}_2}^*} \right)^{\rm{H}}}+ \\ {\rm{E}}\left\{ {\left( {{\boldsymbol{N}} \otimes {{\boldsymbol{N}}^*}} \right){{\left( {{\boldsymbol{N}} \otimes {{\boldsymbol{N}}^*}} \right)}^{\rm{H}}}} \right\} =\\ {{\boldsymbol{B}}_1}{{\boldsymbol{D}}_{{G_1}}}{{\boldsymbol{B}}_1}^{\rm{H}} + {{\boldsymbol{B}}_2}{{\boldsymbol{D}}_{{G_2}}}{{\boldsymbol{B}}_2}^{\rm{H}} + {{\boldsymbol{D}}_N} \\ \end{gathered} $ |
式中:
| $ \left\{ \begin{array}{l} {{\boldsymbol{B}}_1} = {{\boldsymbol{A}}_1} \otimes {{\boldsymbol{A}}_1}^* \\ {{\boldsymbol{B}}_2} = {{\boldsymbol{A}}_2} \otimes {{\boldsymbol{A}}_2}^* \\ {{\boldsymbol{D}}_{{G_1}}} = E\left\{ {\left( {{{\boldsymbol{G}}_1} \otimes {{\boldsymbol{G}}_1}^*} \right){{\left( {{{\boldsymbol{G}}_1} \otimes {{\boldsymbol{G}}_1}^*} \right)}^{\rm{H}}}} \right\} \\ {{\boldsymbol{D}}_{{G_2}}} = E\left\{ {\left( {{{\boldsymbol{G}}_2} \otimes {{\boldsymbol{G}}_2}^*} \right){{\left( {{{\boldsymbol{G}}_2} \otimes {{\boldsymbol{G}}_2}^*} \right)}^{\rm{H}}}} \right\} \\ {{\boldsymbol{D}}_N} = E\left\{ {\left( {{\boldsymbol{N}} \otimes {{\boldsymbol{N}}^*}} \right){{\left( {{\boldsymbol{N}} \otimes {{\boldsymbol{N}}^*}} \right)}^{\rm{H}}}} \right\} \\ \end{array} \right. $ |
以此方式类推可以得到:
| $ {{\boldsymbol{C}}_X} = {{\boldsymbol{B}}_1}{{\boldsymbol{C}}_{{G_1}}}{{\boldsymbol{B}}_1}^{\rm{H}} + {{\boldsymbol{B}}_2}{{\boldsymbol{C}}_{{G_2}}}{{\boldsymbol{B}}_2}^{\rm{H}} + {{\boldsymbol{C}}_N} $ | (6) |
式中
| $ \left\{ {\begin{array}{*{20}{c}} \begin{gathered} {{\boldsymbol{C}}_{{G_1}}} = {\rm{E}}\left\{ {\left( {{{\boldsymbol{G}}_1} \otimes {{\boldsymbol{G}}_1}^*} \right){{\left( {{{\boldsymbol{G}}_1} \otimes {{\boldsymbol{G}}_1}^*} \right)}^{\rm{H}}}} \right\}- \\ {\rm{E}}\left\{ {\left( {{{\boldsymbol{G}}_1} \otimes {{\boldsymbol{G}}_1}^*} \right)} \right\}E\left\{ {{{\left( {{{\boldsymbol{G}}_1} \otimes {{\boldsymbol{G}}_1}^*} \right)}^{\rm{H}}}} \right\} -\\ {\rm{E}}\left\{ {\left( {{{\boldsymbol{G}}_1}{{\boldsymbol{G}}_1}^*} \right) \otimes {{\left( {{{\boldsymbol{G}}_1}{{\boldsymbol{G}}_1}^*} \right)}^{\rm{H}}}} \right\} \\ \end{gathered} \\ \begin{gathered} {{\boldsymbol{C}}_{{G_2}}} = {\rm{E}}\left\{ {\left( {{{\boldsymbol{G}}_2} \otimes {{\boldsymbol{G}}_2}^*} \right){{\left( {{{\boldsymbol{G}}_2} \otimes {{\boldsymbol{G}}_2}^*} \right)}^{\rm{H}}}} \right\}- \\ {\rm{E}}\left\{ {\left( {{{\boldsymbol{G}}_2} \otimes {{\boldsymbol{G}}_2}^*} \right)} \right\}E\left\{ {{{\left( {{{\boldsymbol{G}}_2} \otimes {{\boldsymbol{G}}_2}^*} \right)}^{\rm{H}}}} \right\} - \\ {\rm{E}}\left\{ {\left( {{{\boldsymbol{G}}_2}{{\boldsymbol{G}}_2}^*} \right) \otimes {{\left( {{{\boldsymbol{G}}_2}{{\boldsymbol{G}}_2}^*} \right)}^{\rm{H}}}} \right\} \\ \end{gathered} \end{array}} \right. $ | (7) |
将
| $ \begin{gathered} {{\boldsymbol{B}}_1}{{\boldsymbol{C}}_{{G_1}}}{{\boldsymbol{B}}_1}^{\rm{H}} = {\boldsymbol{U\varSigma }}{{\boldsymbol{U}}^{\rm{H}}}= \\ {{\boldsymbol{U}}_{{S_1}}}{{\boldsymbol{\varSigma }}_{{S_1}}}{{\boldsymbol{U}}_{{S_1}}}^{\rm{H}} + {{\boldsymbol{U}}_{{N_1}}}{{\boldsymbol{\varSigma }}_{{N_1}}}{{\boldsymbol{U}}_{{N_1}}}^{\rm{H}} \\ \end{gathered} $ | (8) |
式中:
同理对
| $ \begin{gathered} {{\boldsymbol{B}}_2}{{\boldsymbol{C}}_{{G_2}}}{{\boldsymbol{B}}_2}^{\rm{H}} = {\boldsymbol{U\varSigma }}{{\boldsymbol{U}}^{\rm{H}}}= \\ {{\boldsymbol{U}}_{{S_2}}}{{\boldsymbol{\varSigma }}_{{S_2}}}{{\boldsymbol{U}}_{{S_2}}}^{\rm{H}} + {{\boldsymbol{U}}_{{N_2}}}{{\boldsymbol{\varSigma }}_{{N_2}}}{{\boldsymbol{U}}_{{N_2}}}^{\rm{H}} \\ \end{gathered} $ | (9) |
式中:
根据式(8)和(9),将式(6)可以转化为
| $ \begin{gathered} {{\boldsymbol{C}}_X} = \left[ {\begin{array}{*{20}{c}} {{{\boldsymbol{B}}_1}}&{{{\boldsymbol{B}}_2}} \end{array}} \right]\left[ {\begin{array}{*{20}{c}} {{{\boldsymbol{C}}_{G1}}}&{} \\ {}&{{{\boldsymbol{C}}_{G2}}} \end{array}} \right]{\left[ {\begin{array}{*{20}{c}} {{{\boldsymbol{B}}_1}}&{{{\boldsymbol{B}}_2}} \end{array}} \right]^{\rm{H}}} + {{\boldsymbol{C}}_N}= \\ {\boldsymbol{B}}{{\boldsymbol{C}}_S}{{\boldsymbol{B}}^{\rm{H}}} + {\sigma ^4}{\boldsymbol{I}}= \\ {{\boldsymbol{U}}_S}{{\boldsymbol{\varSigma }}_S}{{\boldsymbol{U}}_S}^{\rm{H}} + {{\boldsymbol{U}}_N}{{\boldsymbol{\varSigma }}_N}{{\boldsymbol{U}}_N}^{\rm{H}} \\ \end{gathered} $ |
因此可以得到:
| $ {{\boldsymbol{C}}_X}{{\boldsymbol{U}}_N} = {\boldsymbol{B}}{{\boldsymbol{C}}_S}{{\boldsymbol{B}}^{\rm{H}}}{{\boldsymbol{U}}_N} + {\sigma ^4}{{\boldsymbol{U}}_N} = {\sigma ^4}{{\boldsymbol{U}}_N} $ | (10) |
根据式(10)有:
| $ {\boldsymbol{B}}{{\boldsymbol{C}}_S}{{\boldsymbol{B}}^{\rm{H}}}{{\boldsymbol{U}}_N} = {0} $ | (11) |
矩阵
| $ {{\boldsymbol{B}}^{\rm{H}}}{{\boldsymbol{U}}_N} = {0} $ |
因此,中心DOA的估计值可以通过搜索
| $ f\left( \theta \right) = \frac{{{{\boldsymbol{B}}^{\rm{H}}}{\boldsymbol{B}}}}{{{{\boldsymbol{B}}^{\rm{H}}}{{\boldsymbol{U}}_N}{\boldsymbol{U}}_N^{\rm{H}}{\boldsymbol{B}}}} $ | (12) |
得到中心DOA的估计值后可以通过式(13)得到角度扩展
| $ \left\{ {\begin{aligned} & {{{\hat \sigma }_k} = \sqrt {\frac{{{{\left[ {{\boldsymbol{\hat \varLambda }}} \right]}_{2k,2k}}}}{{{{\left[ {{\boldsymbol{\hat \varLambda }}} \right]}_{2k - 1,2k - 1}}}}}, {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} k = 1,2, \cdots ,K} \\ & {{\boldsymbol{\hat \varLambda }} = {\boldsymbol{A}}'{{\left( {\hat \theta } \right)}^ + }\left( {{\boldsymbol{\hat R}} - \hat \sigma _n^2{{\boldsymbol{I}}_M}} \right){{\left( {{\boldsymbol{A}}'{{\left( {\hat \theta } \right)}^{\rm{H}}}} \right)}^ + }} \end{aligned}} \right. $ | (13) |
式中:
| $ \left\{ \begin{array}{l} {\boldsymbol{A}}'\left( \theta \right) = \left[ {{\boldsymbol{a}}'\left( {{\theta _1}} \right),{\boldsymbol{a}}'\left( {{\theta _2}} \right), \cdots ,{\boldsymbol{a}}'\left( {{\theta _K}} \right)} \right] \\ {\boldsymbol{a}}'\left( {{\theta _k}} \right) = \left[ {{{\boldsymbol{a}}_1}\left( {{\theta _k}} \right),{{\boldsymbol{a}}_2}\left( {{\theta _k}} \right)} \right],\;\;\;\;\;\;\;\;k = 1,2, \cdots ,K \\ \end{array} \right. $ |
算法步骤如下:
1) 利用阵列输出信号得到接收信号的四阶累积量矩阵
2) 对其进行特征值分解,对特征向量进行空间划分得到信号的四阶噪声子空间
3) 利用式(12)构造空间谱函数并计算可能入射角度的谱函数
4) 找到谱函数
5) 根据搜索得到的K个入射角,利用式(13)得到角度扩展的估计值。
4 仿真分析定义均方根误差(root mean square error, RMSE)作为衡量估计精度的指标,RMSE的计算公式为
| $ {\text{RMSE}} = \frac{1}{K}\sum\limits_{k = 1}^K {\sqrt {\frac{1}{p}\sum\limits_{p = 1}^P {\left( {{{\hat \theta }_{k,p}} - {\theta _k}} \right)} } } $ |
式中:
仿真参数设定如下:每一信源的传播路径数为100;快拍数设置为500;阵列摆放为均匀阵列;角度扩展大小设为2°;分布方式采用高斯分布。
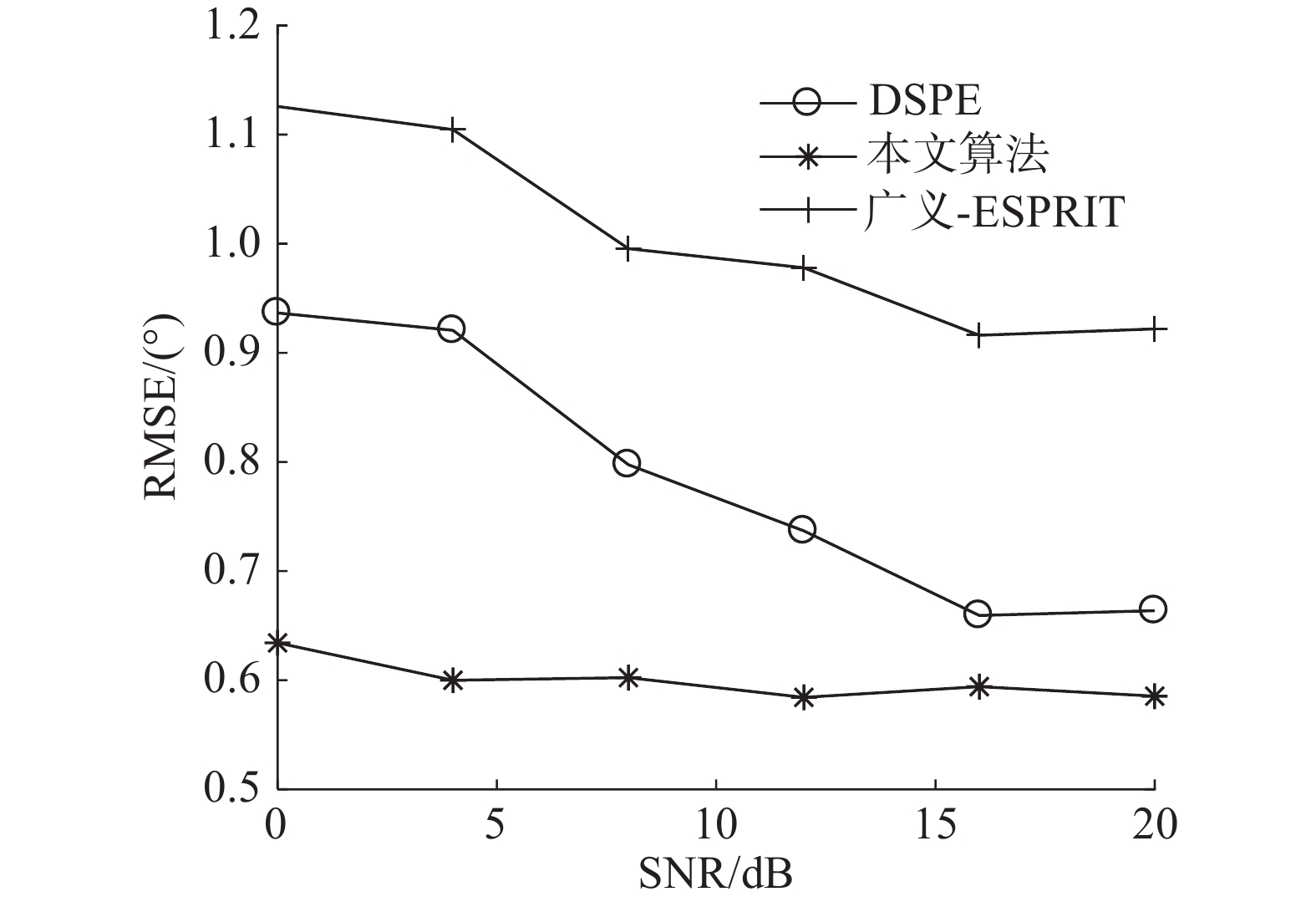
仿真 1 算法性能对比。将所提算法与广义ESPRIT算法及DSPE算法进行性能对比。对比主要针对信噪比、阵元数对测向误差的影响。对信噪比(signal to noise ratio,SNR)进行仿真时阵元数为9个;对阵元数进行仿真时信噪比为10 dB;信号的中心DOA为−10°,多次蒙特卡洛仿真后的结果如图1、图2所示。
四阶累积量可以使阵列孔径展宽从而提高测向性能。从图1可以看出,本文算法所提精度最高,DSPE算法次之,广义ESPRIT算法最差。广义ESPRIT算法采用不同子阵相对应的二阶累积量信号空间的旋转不变一致性来估计中心DOA,其数据维度最少,估计精度易受到相位影响,因此估计精度最差;DSPE算法利用二阶累积量矩阵信号空间与噪声空间的正交性来估计中心DOA,虽然最后精度受到搜索步进影响,但数据维度高于广义ESPRIT算法,因此精度较好;相比之下本文算法采用四阶累积量矩阵伪信号空间和伪噪声空间之间的正交性来估计中心DOA,由于四阶累积量扩展了虚拟阵元,因此估计精度相比DSPE算法更好。
|
Download:
|
| 图 1 RMSE随SNR变化曲线 | |
|
Download:
|
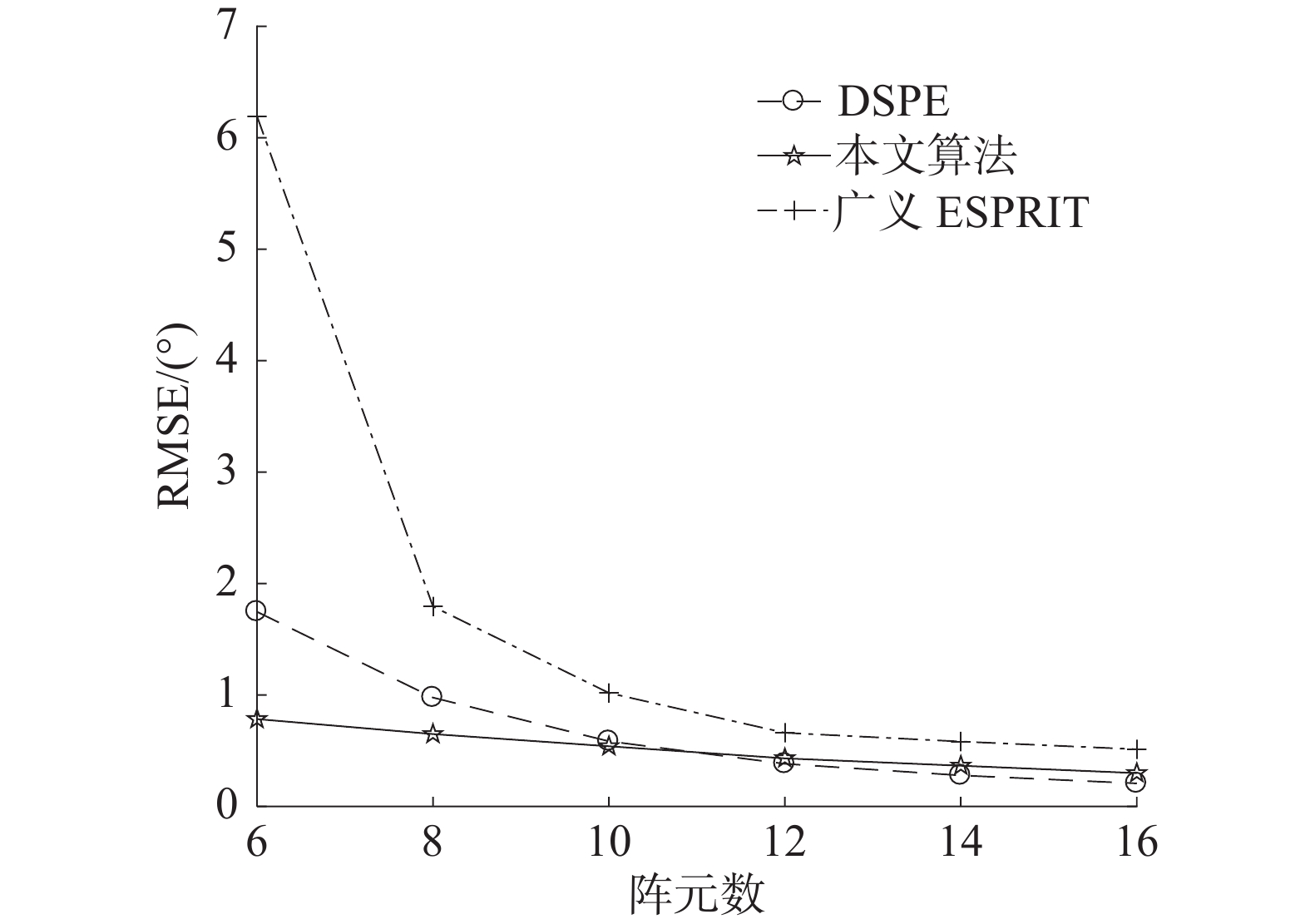
| 图 2 RMSE随阵元数变化曲线 | |
从图2可以看出本文算法在低阵元数时测向误差精度相对较高,阵元数较多时算法性能和DSPE算法相近,两者均优于广义ESPRIT算法。所提算法由于采用四阶累积量扩展了与实际阵元数相近的虚拟阵元,总阵元数(虚拟阵元数+实际阵元数)可以近似为原来的2倍,因此可以看到所提算法随阵元数的增加性能提升并不明显。而已有的2种算法由于非相干分布源的信号空间扩展特性使得低阵元数时性能较差,阵元数较少时测向性能提升较为明显,阵元数较多时与所提算法类似,测向误差趋于稳定。
仿真 2 验证最大可识别目标数。传统非相干分布式信源测向算法由于信号空间的扩展使得最大可识别目标数减少,若接收阵列的阵元个数为
|
|
表 1 可估计目标数对比 |
下面对阵列扩展的有效性进行仿真,假设阵列传感器的个数为8个,则由前面推导可以得出传统算法最大识别目标数为3个信源,本文算法的最大识别目标数为7个信源。令接收阵列阵元数为8;空间中存在7个独立的信源,信源入射方位角分别为
谱峰搜索的结果如图3所示,可以看到谱峰搜索时可以得到清晰的7个谱峰,仿真结果表明本文算法可以很好的实现最大可识别信源数的扩展。

|
Download:
|
| 图 3 最大可识别目标数 | |
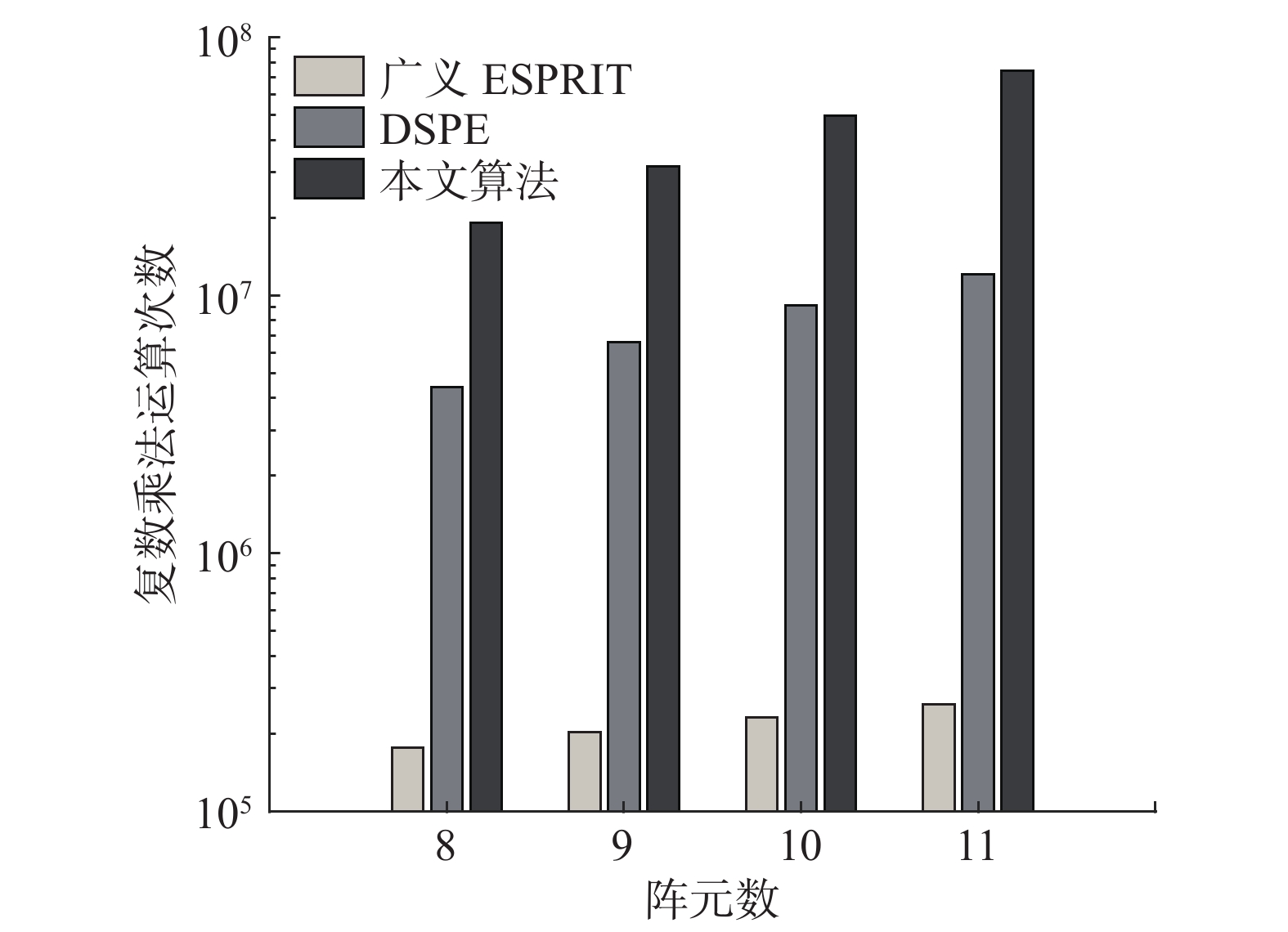
仿真 3 算法复杂度。将本文的方法与广义ESPRIT和DSPE算法进行复杂度的对比,复杂度的对比标准为复数乘法的运算次数。假设阵列个数为M,快拍数为N,信源数为K。广义ESPRIT算法主要的运算在于M阶矩阵的协方差矩阵及特征值分解运算、再加上需要进行搜索函数的构建以及谱峰搜索;DSPE算法主要运算为M阶矩阵的协方差矩阵及特征值分解运算,再加上需要进行搜索函数的构建以及谱峰搜索;本文算法主要为一个
|
|
表 2 算法复杂度对比 |
|
Download:
|
| 图 4 算法复杂度对比 | |
非相干分布式信源的信号空间扩展特性会使阵列的最大可识别目标数急剧减少。针对上述问题本文利用四阶累积量的阵列扩展特性对非相干分布式信源的测向算法进行改进,首先对基于泰勒展开的非相干分布式信源的两点近似模型对接收信号的四阶累计量矩阵处理进行简化推导,之后根据简化后的结果划分伪信号空间和伪噪声空间,最后得到非相干分布式信源模型下的四阶累积量谱峰搜索函数,仿真结果表明,该方法有效地提升了非相干分布式信源下阵列的最大可识别目标数。
本文算法由于采用了四阶累积量,在阵元数比较多时计算量的增加尤为明显。因此,本文算法在阵元数较少且需要对多目标进行位置估计的情况下优势明显。
| [1] |
XU Dazhuan, SHI Chao, ZHOU Ying, et al. Spatial information in phased-array radar[J]. IET communications, 2020, 14(13): 2141-2150. DOI:10.1049/iet-com.2019.1068 ( 0) 0)
|
| [2] |
FENG Ziang, HU Guoping, ZHOU Hao. Sparsity-based DOA estimation with gain and phase error calibration of generalized nested array[J]. Mathematical problems in engineering, 2020: 1720310. ( 0) 0)
|
| [3] |
NAZAROFF M, BYUN G, CHOO H, et al. 2-D direction-of-arrival estimation system using circular array with mutually coupled reference signal[J]. IEEE sensors journal, 2018, 18(23): 9763-9769. DOI:10.1109/JSEN.2018.2871464 ( 0) 0)
|
| [4] |
DJUROVIĆ I, SIMEUNOVIĆ M, LUKIN V V. Estimating DOA and PPS parameters of signal received by ULA in heavy noise environment[J]. Journal of electrical engineering, 2020, 71(3): 175-184. DOI:10.2478/jee-2020-0024 ( 0) 0)
|
| [5] |
张小飞, 李建峰, 徐大专. 传感器阵列信源定位[M]. 北京: 电子工业出版社, 2018: 1-4, 73-79.
( 0) 0)
|
| [6] |
VALAEE S, CHAMPAGNE B. Parametric localization of distributed sources[J]. IEEE transactions on signal processing, 1995, 43(9): 2144-2153. DOI:10.1109/78.414777 ( 0) 0)
|
| [7] |
ROY R, KAILATH T. ESPRIT-estimation of signal parameters via rotational invariance techniques[J]. IEEE transactions on acoustics, speech, and signal processing, 1989, 37(7): 984-995. DOI:10.1109/29.32276 ( 0) 0)
|
| [8] |
朝乐蒙, 邱天爽, 李景春, 等. 广义复相关熵与相干分布式非圆信号DOA估计[J]. 信号处理, 2019, 35(5): 795-801. ( 0) 0)
|
| [9] |
CHENG Qianlin, ZHANG Xiaofei, CAO Renzheng. Fast parallel factor decomposition technique for coherently distributed source localization[J]. Journal of systems engineering and electronics, 2018, 29(4): 667-675. DOI:10.21629/JSEE.2018.04.01 ( 0) 0)
|
| [10] |
BENGTSSON M, OTTERSTEN B. Low-complexity estimators for distributed sources[J]. IEEE transactions on signal processing, 2000, 48(8): 2185-2194. DOI:10.1109/78.851999 ( 0) 0)
|
| [11] |
SHAHBAZPANAHI S, VALAEE S, BASTANI M H. Distributed source localization using ESPRIT algorithm[J]. IEEE transactions on signal processing, 2001, 49(10): 2169-2178. DOI:10.1109/78.950773 ( 0) 0)
|
| [12] |
崔维嘉, 代正亮, 巴斌, 等. 基于互相关抽样分解的分布式非圆信号DOA快速估计[J]. 电子与信息学报, 2018, 40(5): 1226-1233. DOI:10.11999/JEIT170663 ( 0) 0)
|
| [13] |
杜金香, 冯西安. 基于四阶累积量的波束域MUSIC方法[J]. 西北工业大学学报, 2009, 27(5): 684-687. DOI:10.3969/j.issn.1000-2758.2009.05.019 ( 0) 0)
|
| [14] |
PORAT B, FRIEDLANDER B. Direction finding algorithms based on high-order statistics[J]. IEEE transactions on signal processing, 1991, 39(9): 2016-2024. DOI:10.1109/78.134434 ( 0) 0)
|
| [15] |
朱敏, 何培宇. 一种新的基于四阶累积量的DOA估计算法[J]. 四川大学学报(自然科学版), 2011, 48(2): 343-348. ( 0) 0)
|
| [16] |
杨松涛, 许海韵, 王大鸣, 等. 互质阵型下基于四阶累积量的高自由度低复杂波达方向估计方法[J]. 信息工程大学学报, 2019, 20(6): 647-652. ( 0) 0)
|
| [17] |
赵宇. 基于四阶统计量的虚拟天线阵波束形成及DOA估计技术研究[D]. 哈尔滨: 哈尔滨工程大学, 2018: 34-37.
( 0) 0)
|
 2021, Vol. 48
2021, Vol. 48


