2. 陕汽集团商用车有限公司,陕西 宝鸡 722405;
3. 浙江英伦汽车有限公司,浙江 义乌 321000
2. Shaanxi Automobile Group Commercial Vehicle Co., Ltd., Baoji 722405, China;
3. Zhejiang Yinglun Automobile Co., Ltd., Yiwu 321000, China
FSAE比赛发源于美国,1978年由美国汽车工程师协会(Society of Automotive Engineers,SAE)主办,目的是培养中国汽车工业技术人才和机械技术人才[1-2]。
FSAE赛车的每个系统都是整车不可或缺的一部分,任何一个系统停止工作都将会导致整项比赛退赛(did not finish,DNF),因此对整车设计仿真分析以及进行轻量化操作的研究至关重要[3-4]。随着FSAE赛车比赛的不断发展,有限元软件被大量应用在赛车设计与仿真分析中。吕绍远等[5]针对FSAE赛车利用了ANSYS workbench对所设计后轮边系统的零部件进行仿真分析,提高了赛车的瞬态响应性能。王嬿舒[6]为了找到一套适用于FSAE方程式赛车传动系统大链轮的仿真优化方法,着眼于75 m直线加速过程,计算出大链轮的最大冲击力,通过ANSYS优化校核模块,对其进行优化设计,使其对于整车的布置更加合理,尽量减重。Azmeer等[7]在SAE赛车设计中,使用ANSYS软件对后立柱进行了静态结构和状况优化分析,保证了赛车结构的同时,进行了25%、50%和75%减重操作,找到了最佳设计形状,最终实现了21%的减重,且能承受多个负载。Yadav[8]等利用了ANSYS Fluent对FSAE赛车的空气动力学相关参数进行了优化,使用了具有二阶精度的基于压力的分离求解器和K-omega SST湍流模型,以获得赛车前翼与尾翼所提供的下压力。从上述研究可以看出,多数文献均为围绕赛车的单个系统所展开的仿真分析,但是在汽车轻量化与制造生态化结合的大趋势下,拥有完整的赛车设计仿真体系学习是对未来汽车工程师的思维培养和获取汽车设计师角度的重要方针,且能使未来汽车企业整车工艺的发展变得更直观、更科学。
本文通过对参加2019年FSAE的西安航空学院的赛车总成进行了设计和仿真分析,为今后的赛车研发设计打下基础,提高了开发设计效率,且提供了较为完善的汽车知识体系和最新汽车相关技术的支持。通过使用CATIA软件对其各个系统进行建模并计算、ANSYS软件对各个系统总成以及零部件进行有限元分析,得出车身系统采用由2维到3维的单件升阻比、由前到后的整车升阻比及风压中心优化思路。对动力总成系统、悬架系统和轮边制动系统的设计也有一定的借鉴。随着汽车“五化”方向中的轻量化展开仿真实验,最终得出一种符合大赛规则且更优于此车的设计方案,达到提高整车的轻量化需求和降低赛车制造成本的目的[9-10]。
FSAE作为一项由全世界发达汽车国家共同推进的社会公益性项目,其目的是为各高校学生提供一个通过参与大赛,接触与当下汽车行业中先进的仿真—设计—制造流程的学习机会,现已成为发达国家与发展中国家挖掘和培养汽车人才的非教育领域里最重要的社会化公共平台。在参与过程中,通过学习全世界汽车设计、制造等行业广泛使用的仿真技术,能够获得宝贵的工程实践经验和相关知识。
ANSYS软件是美国ANSYS公司研制的大型通用有限元分析(finite element analysis,FEA)软件,是世界范围内增长最快的计算机辅助工程软件,是融结构、流体、电场、磁场和声场分析于一体的大型通用有限元分析软件。目前在汽车工业、航空航天和国防军工等领域有着广泛的应用[11]。
ANSYS作为大赛紧密合作伙伴已经连续赞助本项赛事8年,大赛中使用ANSYS进行赛车仿真设计的车队已达到总车队数的70%,大赛前十名车队更是绝大部分都使用了ANSYS仿真来提高赛绩。
1 整车参数与材料属性西安航空学院2019年FSAE赛车(FSCC油车)整车性能参数如表1所示。
|
|
表 1 整车性能基本参数 |
全文所设计与仿真的结构零部件材料属性均如表2所示。
|
|
表 2 7075/T6航空铝材料属性 |
车身系统的空气动力学套件能够在不同速度调整赛车底盘的下压中心,使赛车在不同时速段有更稳定的下压力,保证直线高速行驶后在降速过弯中不易出现侧滑、甩尾等不良现象。同时,配合着专业的光头胎,提供额外的抓地力,增强了高速直线或降速过弯的行驶稳定性。时速越高,下压力越大,空气阻力也会不断地增加。因此,空气动力学套件不仅要控制气动阻力,也要具备高要求的气动效率。
赛车在行驶的过程中,经过前翼的正面气流,为赛车前部提供足够的负升力,在与前翼分离时,气流会出现涡流或湍流现象,这时需要通过车身进行整流,使气流沿车身向后运动。因此车身需要采取与空气动力学套件互相配合的设计方案,以规范整车的流场。赛车设计的重点在于为赛车带来强大的负升力,减小赛车各个部件乱流的影响,适当减小风阻[12]。
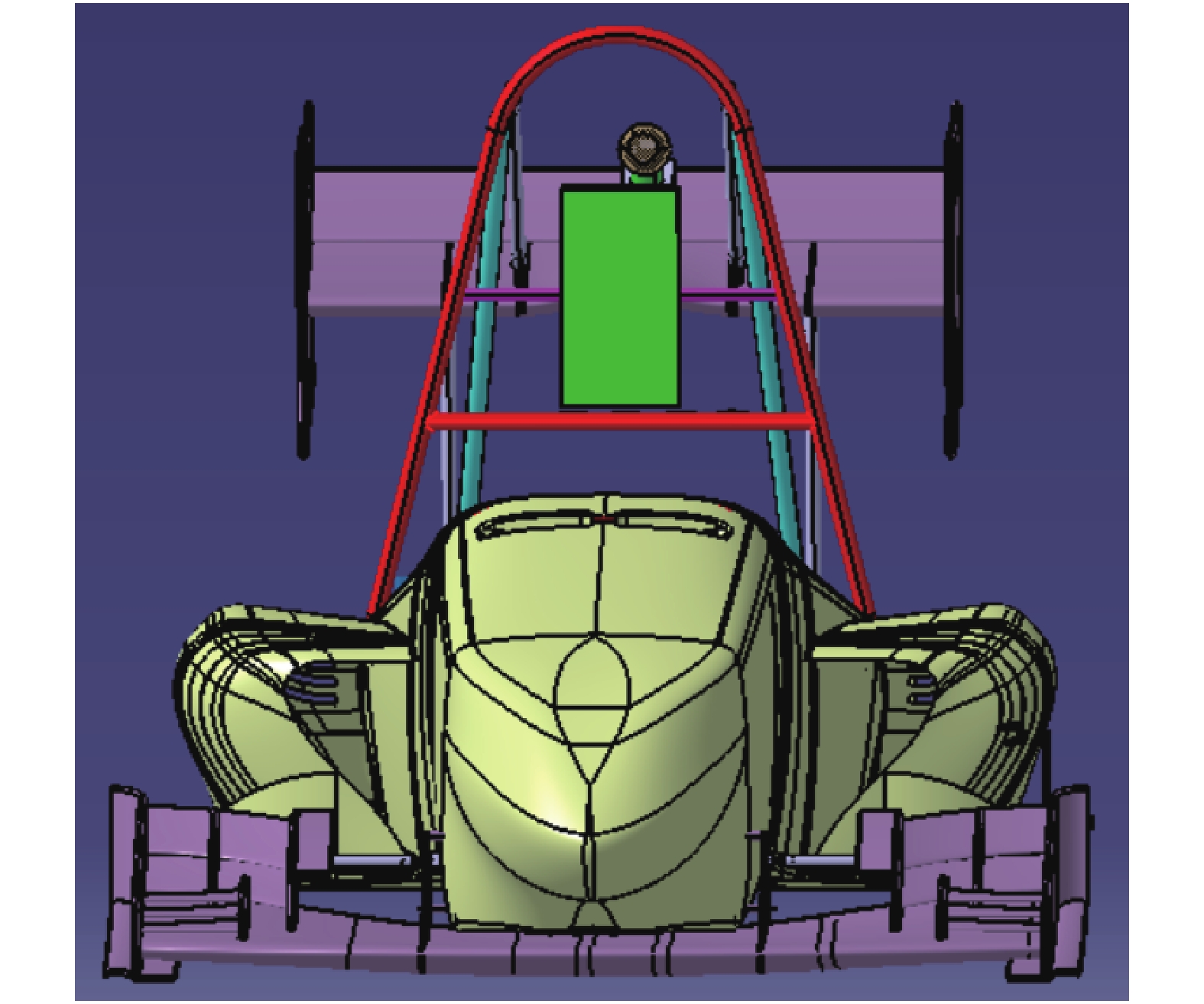
利用CATIA所建立的赛车车身系统,前翼(前导流板)、尾翼(后扰流板)、扩散器、侧箱、最终经过零部件装配模块进行总装,其三维图如图1所示。
|
Download:
|
| 图 1 CATIA建立的车身三维模型(正视图) | |
车身与空气动力学套件采用互相配合的设计方案,以规范整车流场。重点在于为赛车带来强大的负升力,减小赛车各个部件乱流的影响,适当减小风阻。经过对赛车在赛道中表现的预判,空气动力学套件设计均使用15 m/s(54 k m/h)的仿真风速,采用由2维到3维的单件升阻比、由前到后的整车升阻比及风压中心优化思路。
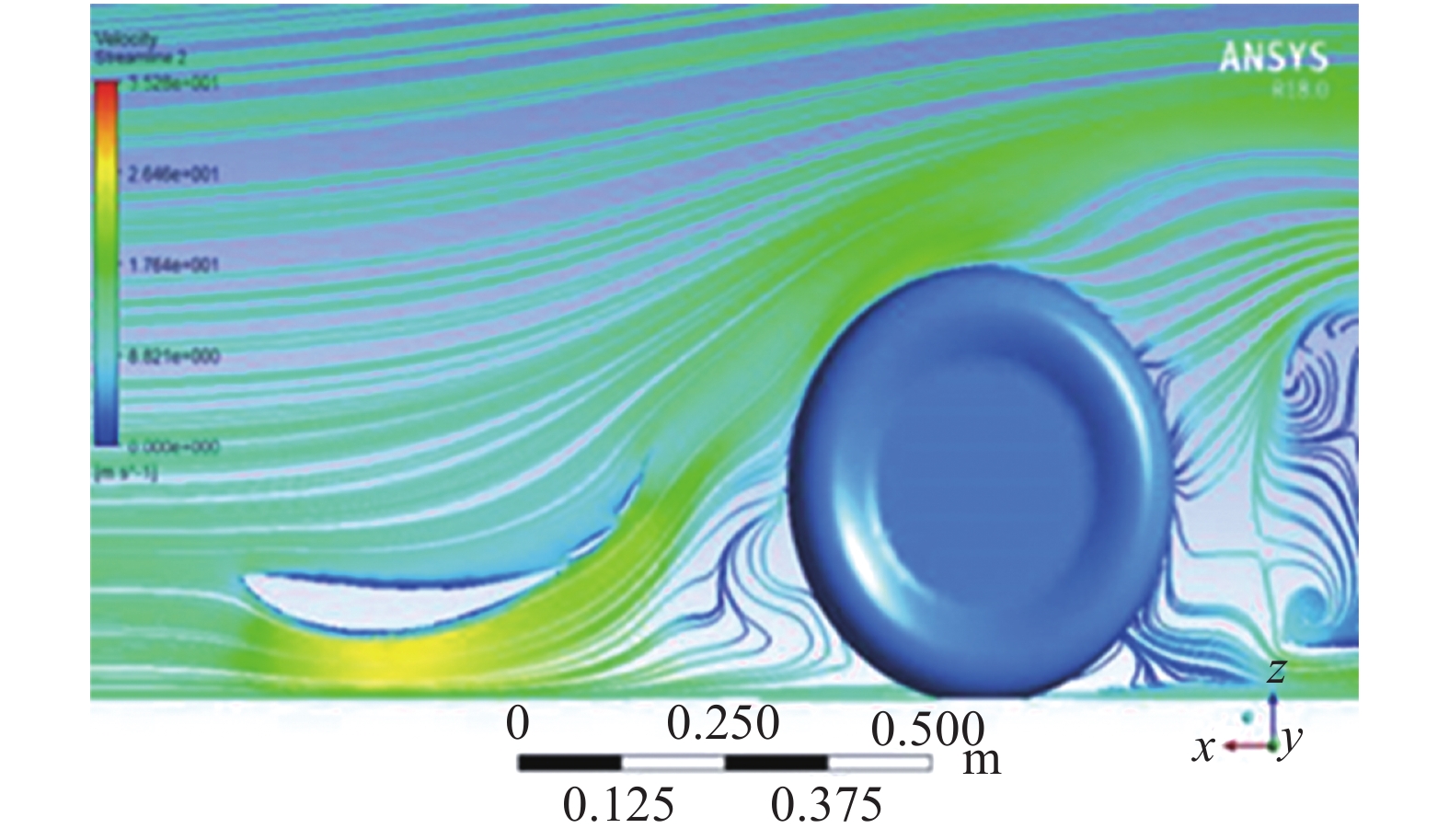
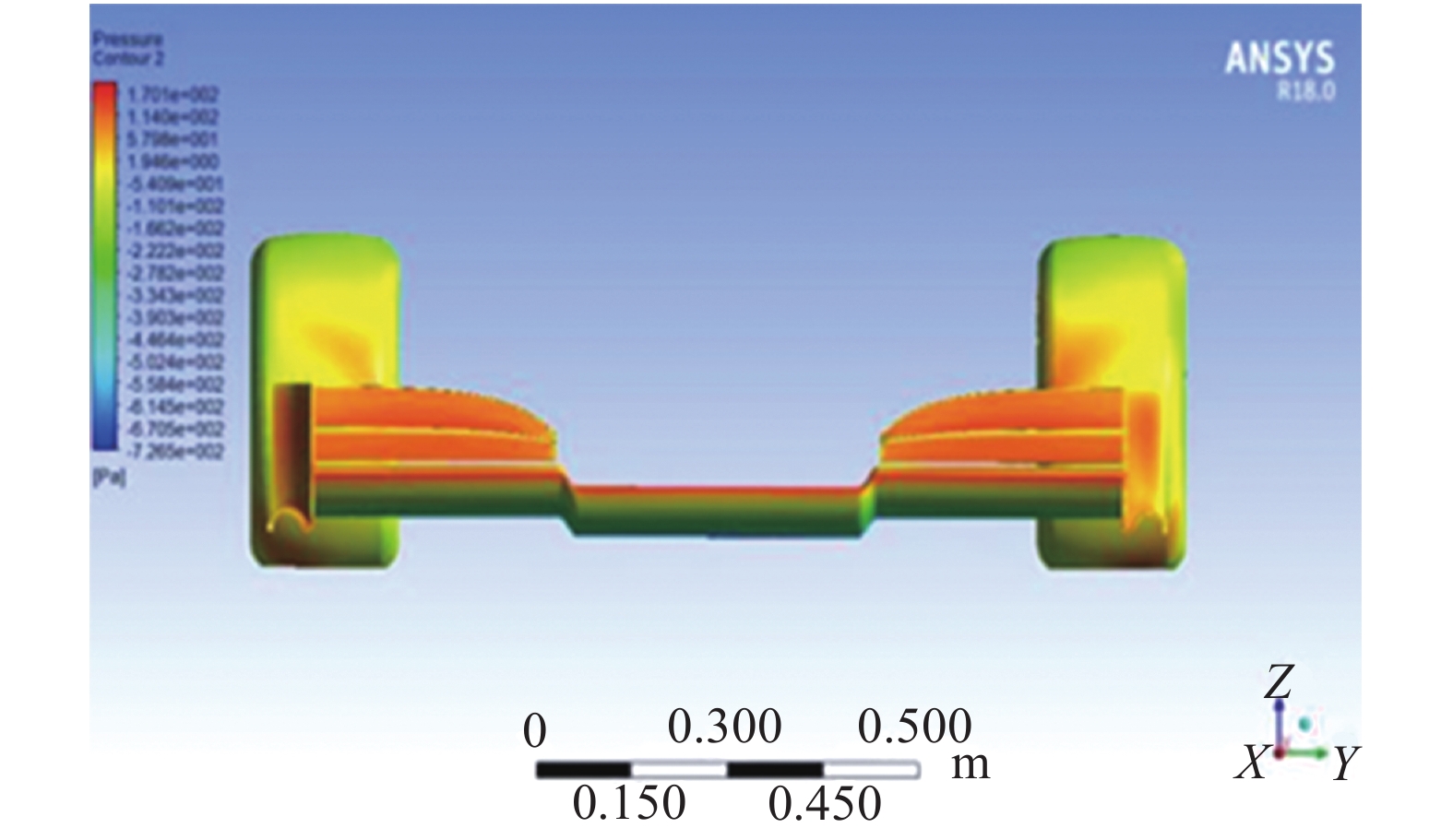
在整车流场中,前翼带来负升力约为205.46 N,阻力约27.67 N,如图2和图3所示。
|
Download:
|
| 图 2 前翼截面流线 | |
|
Download:
|
| 图 3 前翼正面压力云图 | |
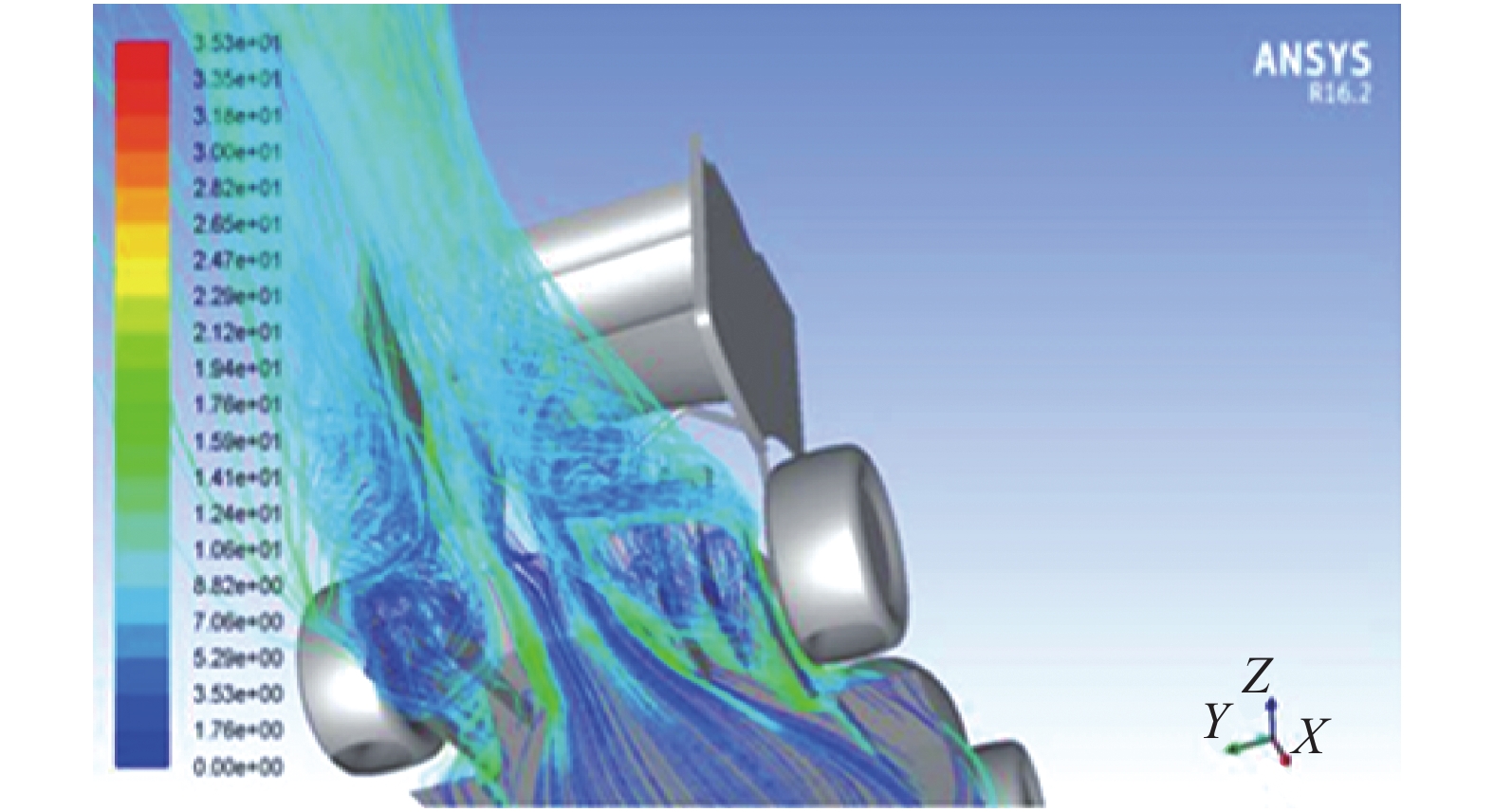
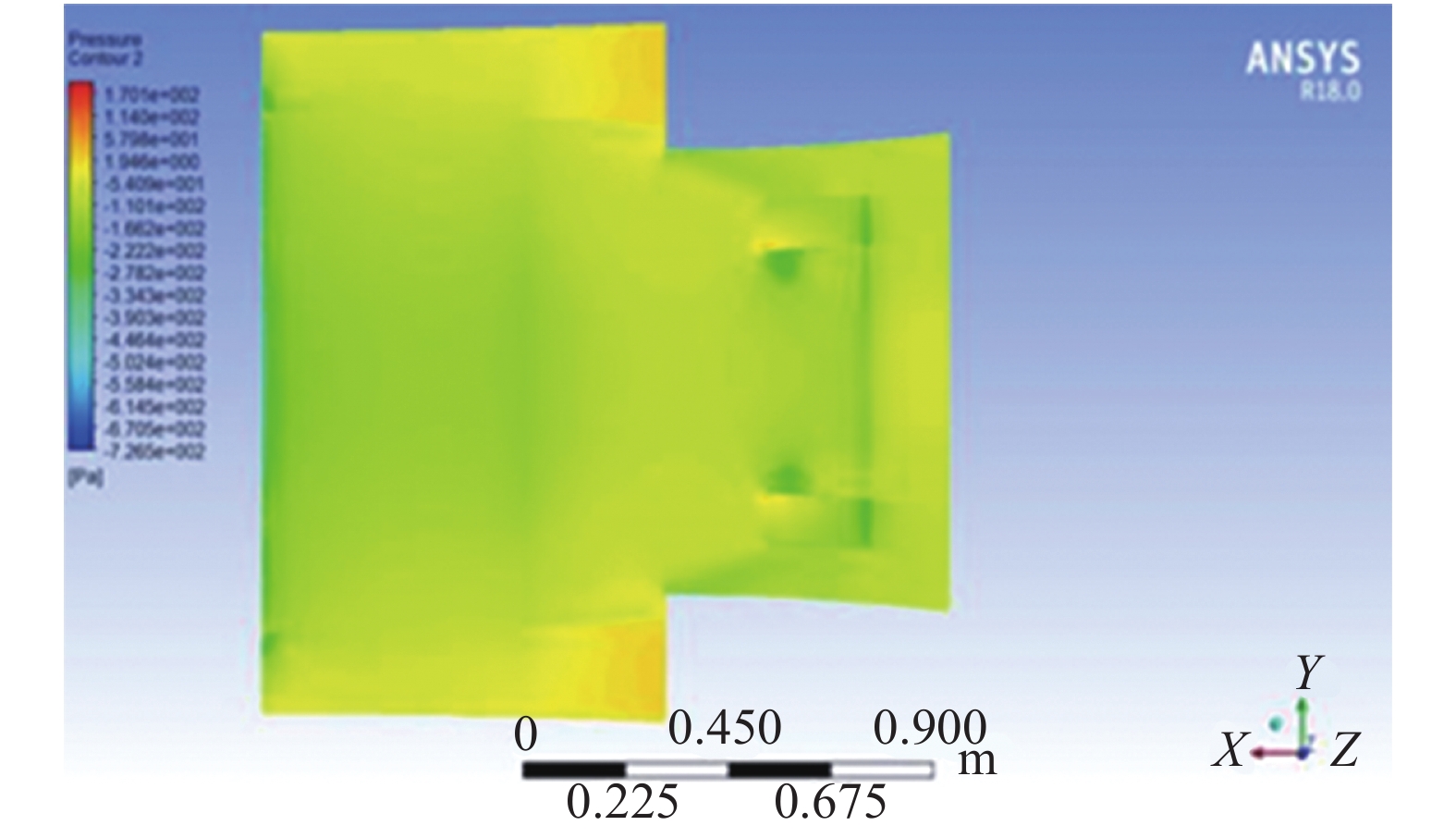
在整车流场中,扩散器带来负升力约223.22 N,阻力约8.72 N如图4和图5所示。
|
Download:
|
| 图 4 扩散器后部迹线 | |
|
Download:
|
| 图 5 扩散器底部压力云图 | |
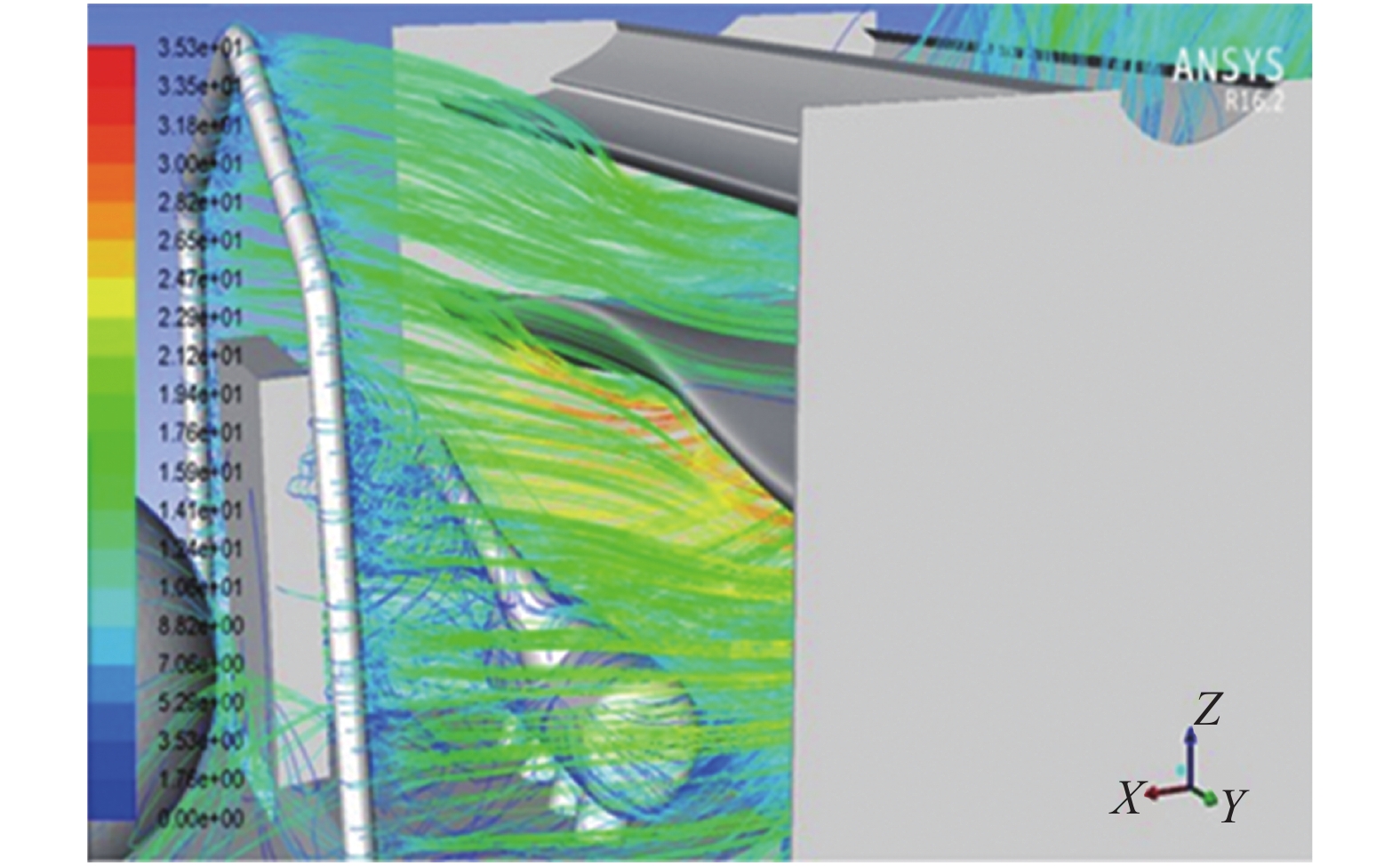
在整车流场中,尾翼带来负升力大约为316.78 N,阻力约96.82 N如图6所示。
|
Download:
|
| 图 6 尾翼气流迹线 | |
所有空气动力学套件产生约745.46 N负升力,约133.21 N阻力,升阻比约为5.6,负升力作用位置位于汽车纵向质心后约9 mm处,符合空气动力学套件的设计要求。
3 动力总成系统结构分析及拓扑优化 3.1 传动系统结构分析FSAE赛车的传动系统是整车动力传递的重要途径,为了能得到更好的赛车性能和良好的成绩,传动系统的优化能够提升赛车的动力性、燃油经济性、操纵稳定性以及行驶平顺性等性能。
要使发动机的动力发挥到最佳,FSAE赛车链传动系统的关键零部件设计及分析必不可少。一个良好的链传动系统在满足其基础安全性能以及轻量化的同时,可以促进传动效率的提升,并且对整车的操纵性有很大的影响。如设计不合理,将直接导致整车在过弯时的侧翻或者侧滑现象,会直接危及驾驶人员的生命安全。在实现汽车的最优的动力性、燃油经济性、操纵稳定性的同时,整车的动力性直接关系着驾驶人员的驾驶体验,所以大家对赛车的动力性要求也不断提高。
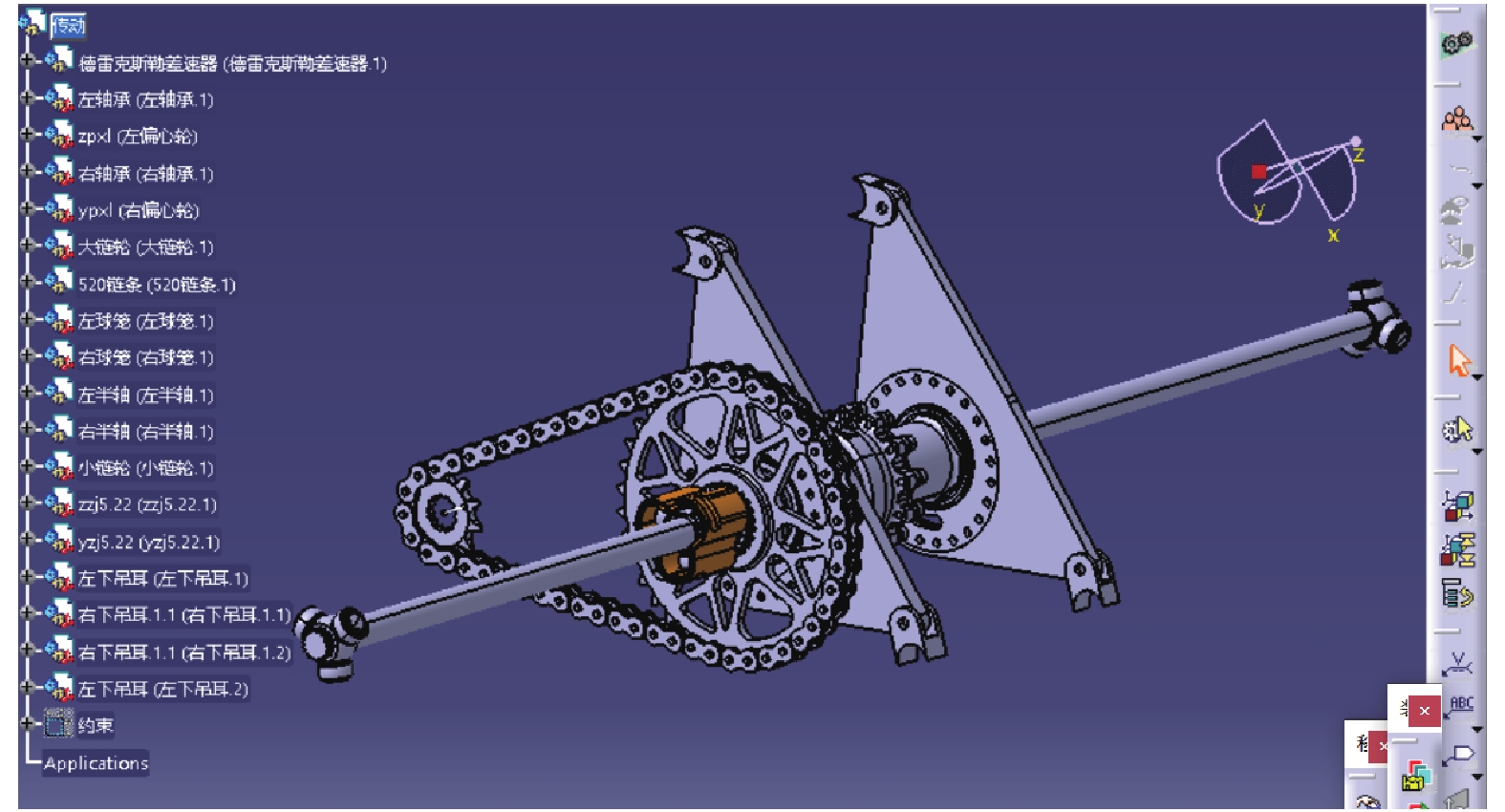
CATIA所建立的传动系统三维模型如图7所示。
|
Download:
|
| 图 7 CATIA建立的传动系统三维模型 | |
FSAE赛车链传动系统大链轮的工况分别为匀速行驶、弹射起步、停车制动。最危险工况为赛车在弹射起步时链条给大链轮所提供的紧边拉力,Drexler差速器的左端与大链轮的中心通过花键进行连接,在链条与大链轮啮合的瞬间所产生的冲击力最大,共有17个齿处于紧边拉力的状态,共有9个齿是松边拉力的状态。由于大链轮处于旋转状态,所以每个齿都会循环的受一次冲击力。
小链轮所传递的最大扭矩为
| $ {M_0} = {T_{\max }}{i_0}{i_i}\eta $ |
式中:
小链轮分度圆直径为
| $ d = \frac{P}{{\sin \left( {\dfrac{{{{180}^{\circ} }}}{z}} \right)}} $ |
式中:
大链轮的紧边拉力为
| $ {F_0} = \frac{{2{M_0}}}{d} $ |
计算得
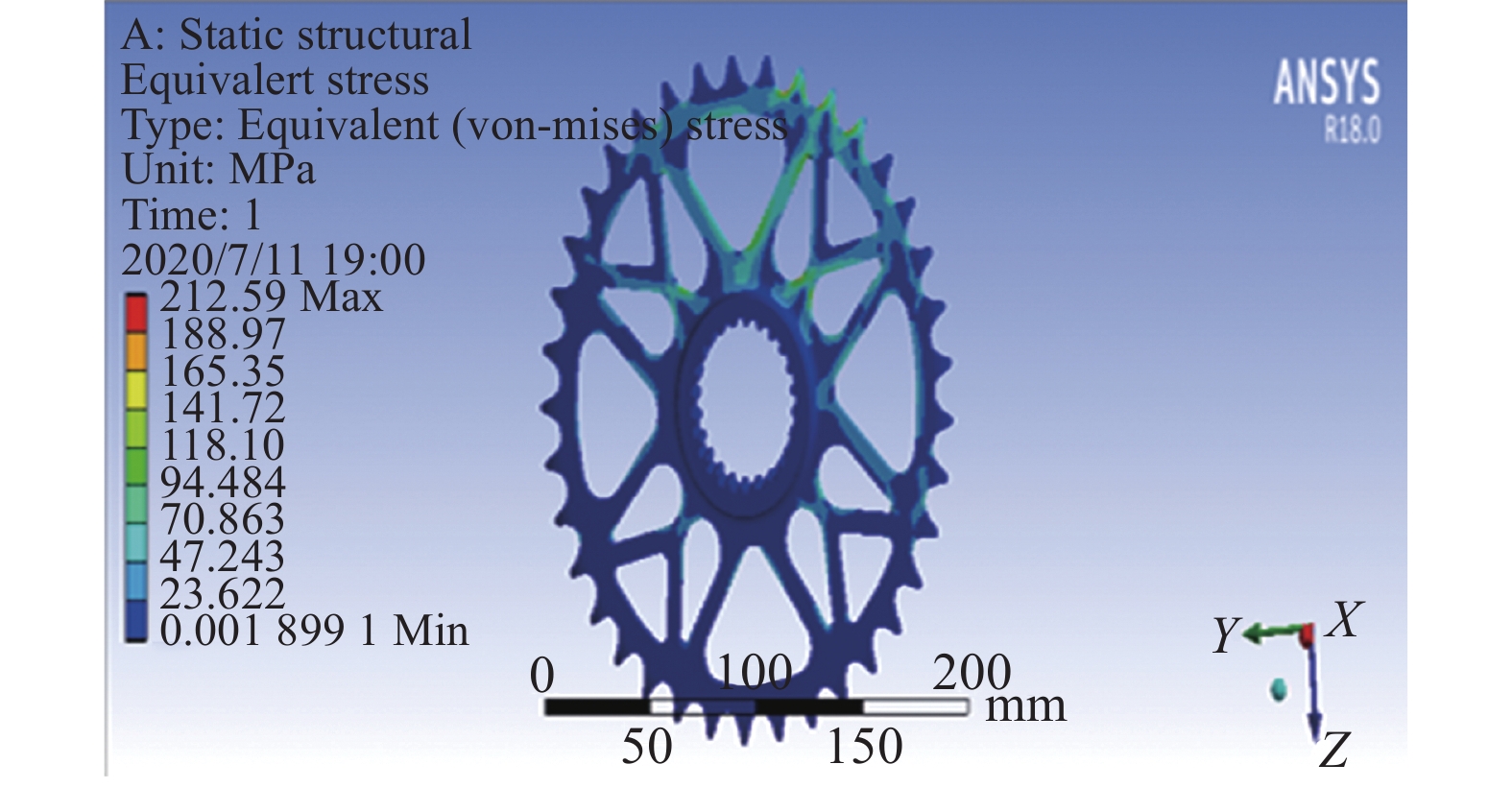
对弹射起步工况进行受力分析。由于链传动系统的大链轮为对称结构,故对其进行有限元分析时只对大链轮的3个齿上依次施加4 000、2 500、2 000 N的法向载荷,同时对其大链轮的花键部分进行固定约束,其应力与形变云图如图8所示。
|
Download:
|
| 图 8 大链轮应力云图 | |
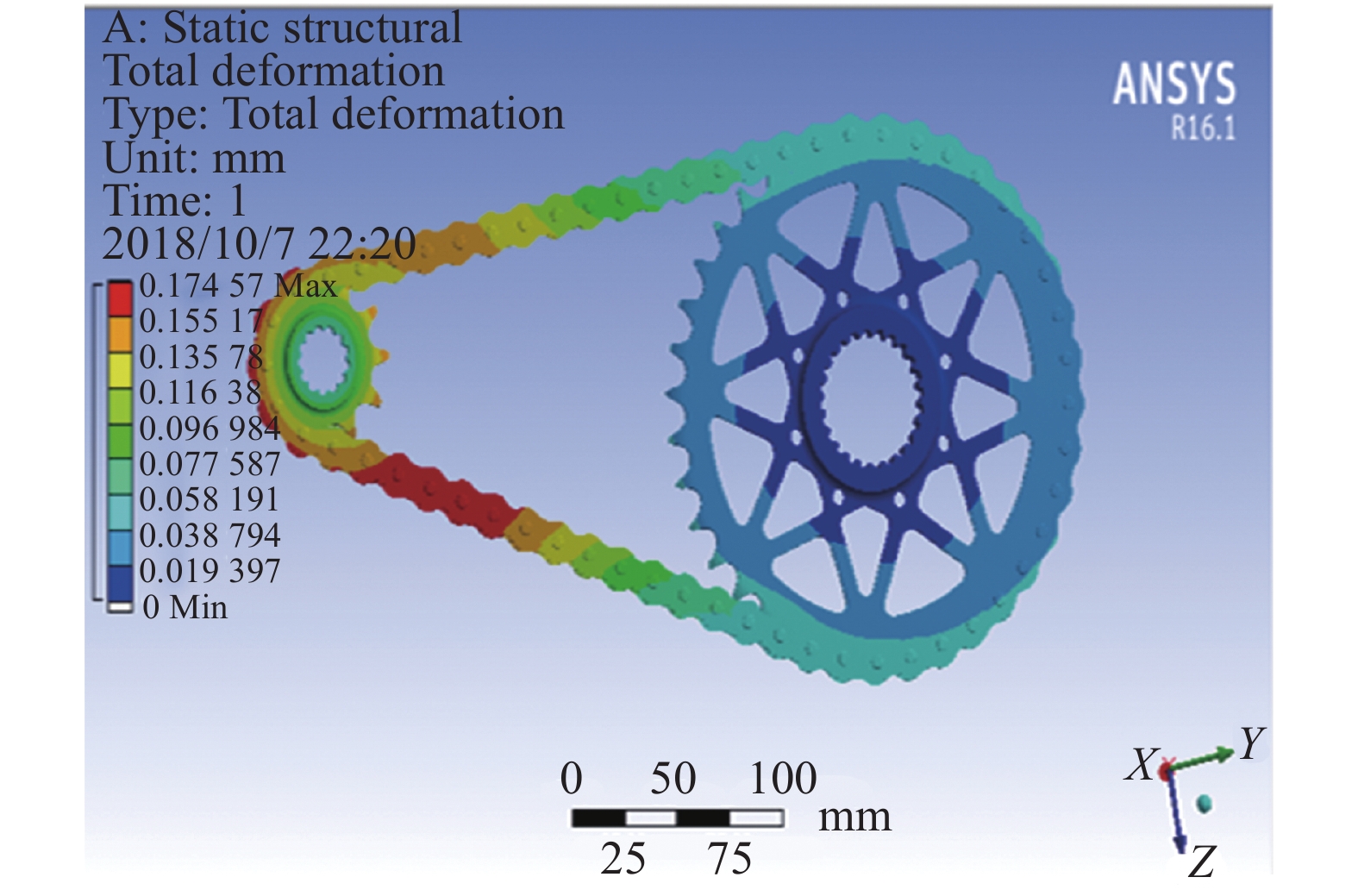
传动系统主减速器(大链轮、小链轮、链条)的总形变量分析如图9所示。
|
Download:
|
| 图 9 大小链轮及链条总形变量云图 | |
由图9可以看出大链轮所受到的最大应力是212.59 MPa,远远小于材料的许用应力505 MPa,最大变形量为0.17 mm,满足国家的标准和设计要求。
3.2 差速器支架拓扑优化拓扑优化是一种根据给定的负载情况、约束条件和性能指标,在给定的区域内对材料分布进行优化的数学方法。文章选用变密度法,变密度法即是以孔表示可以轻量化的区域,其数学模型为[13]
| $ {\rm{s}}{\rm{.t}}{\rm{.}}\left\{ \begin{array}{l} {\rm{Find}}:{\rm{ }}{{X}} = {\left[ {{x_1},{x_2}, \cdots ,{x_n}} \right]^{\rm{T}}} \\ \;\;\;\;\;\;\;\;\;\;{\rm{ }}{x_i} = \left\{ {0,\left. 1 \right\},\left({i = 1,2,\cdots ,n} \right)} \right. \\ \min :{\rm{ }}C\left(x \right) = {{{F}}^{\rm{T}}}{{U}} \\ V \leqslant {V^*} \\ {{F}} = {{KU}} \end{array} \right. $ |
式中:
差速器支架拓扑优化限制条件如表3所示。
|
|
表 3 拓扑优化限制条件 |
差速器支架拓扑优化流程如图10所示。

|
Download:
|
| 图 10 拓扑优化流程 | |
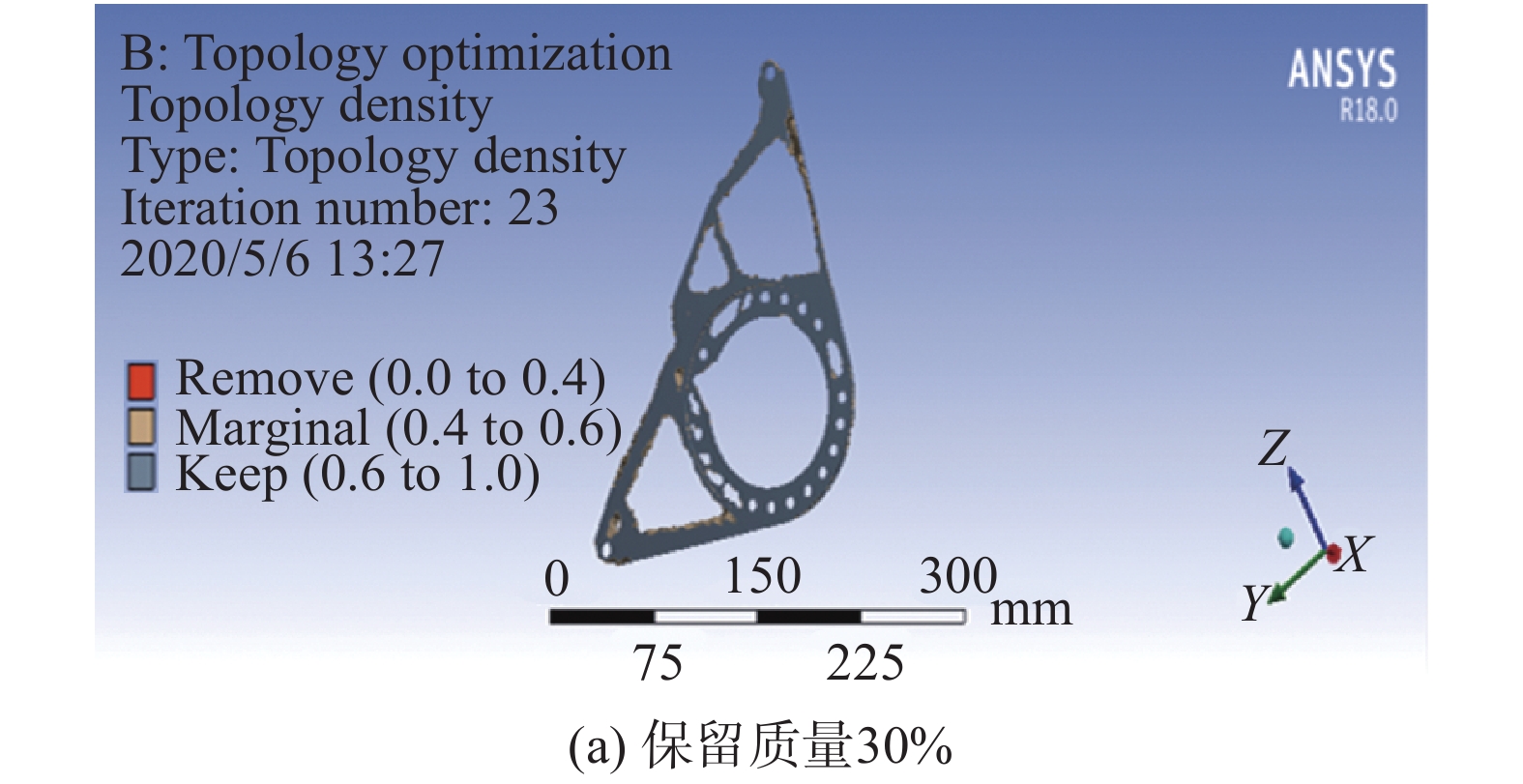
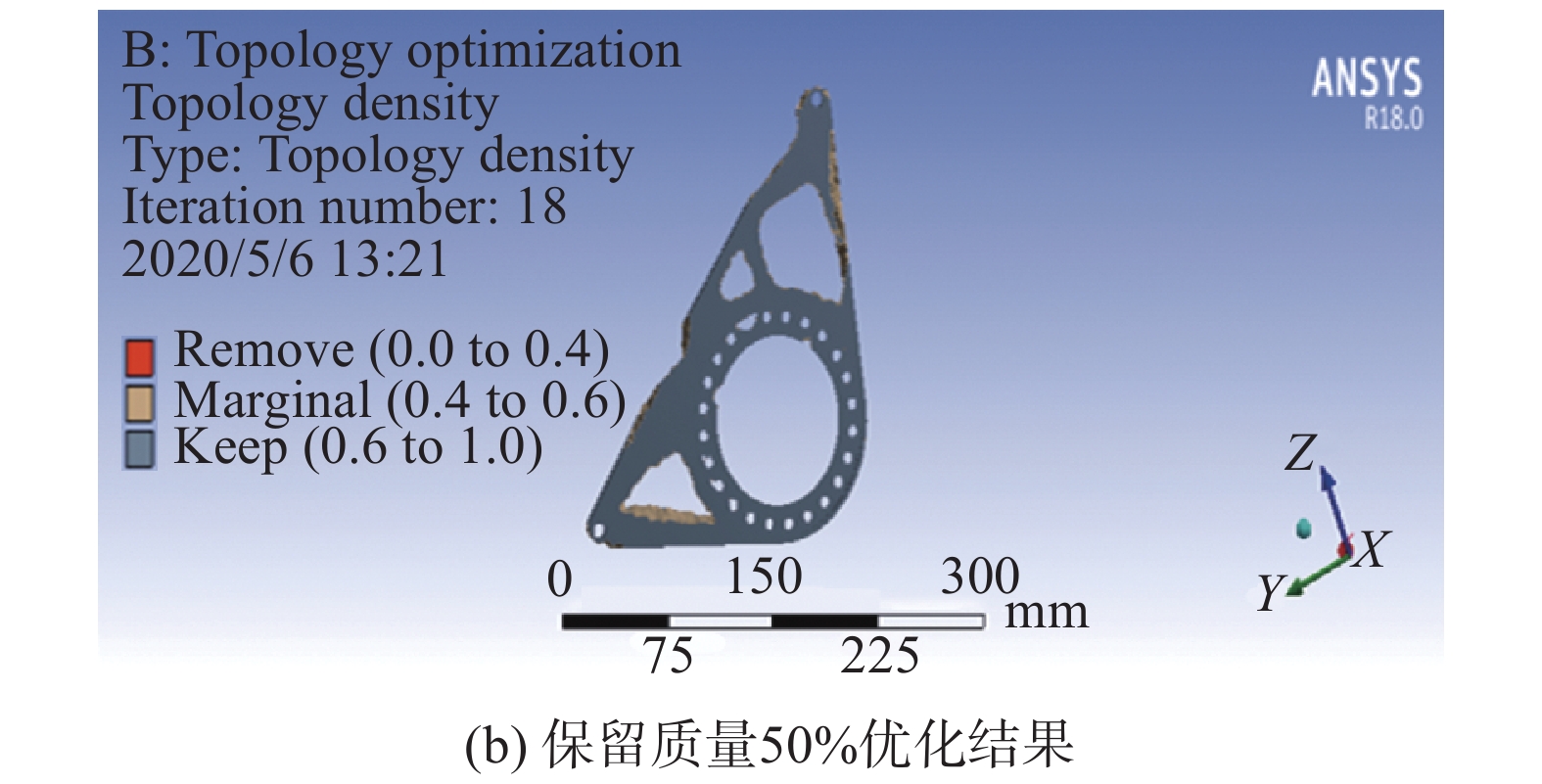
在进行拓扑优化前需先对其进行静力学分析。为了保证其网格的质量,网格选用六面体网格,网格大小为2 mm,对其两端与车架连接的固定孔进行固定约束,轴承施加的载荷为8 000 N,最终模型共分为240 699个单元和65 086个节点。完成上述所有优化设置参数,进行求解得到保留质量30%与50%的结果如图11所示。
|
Download:
|
| 图 11 | |
|
Download:
|
| 图 11 链传动支架拓扑优化结果 | |
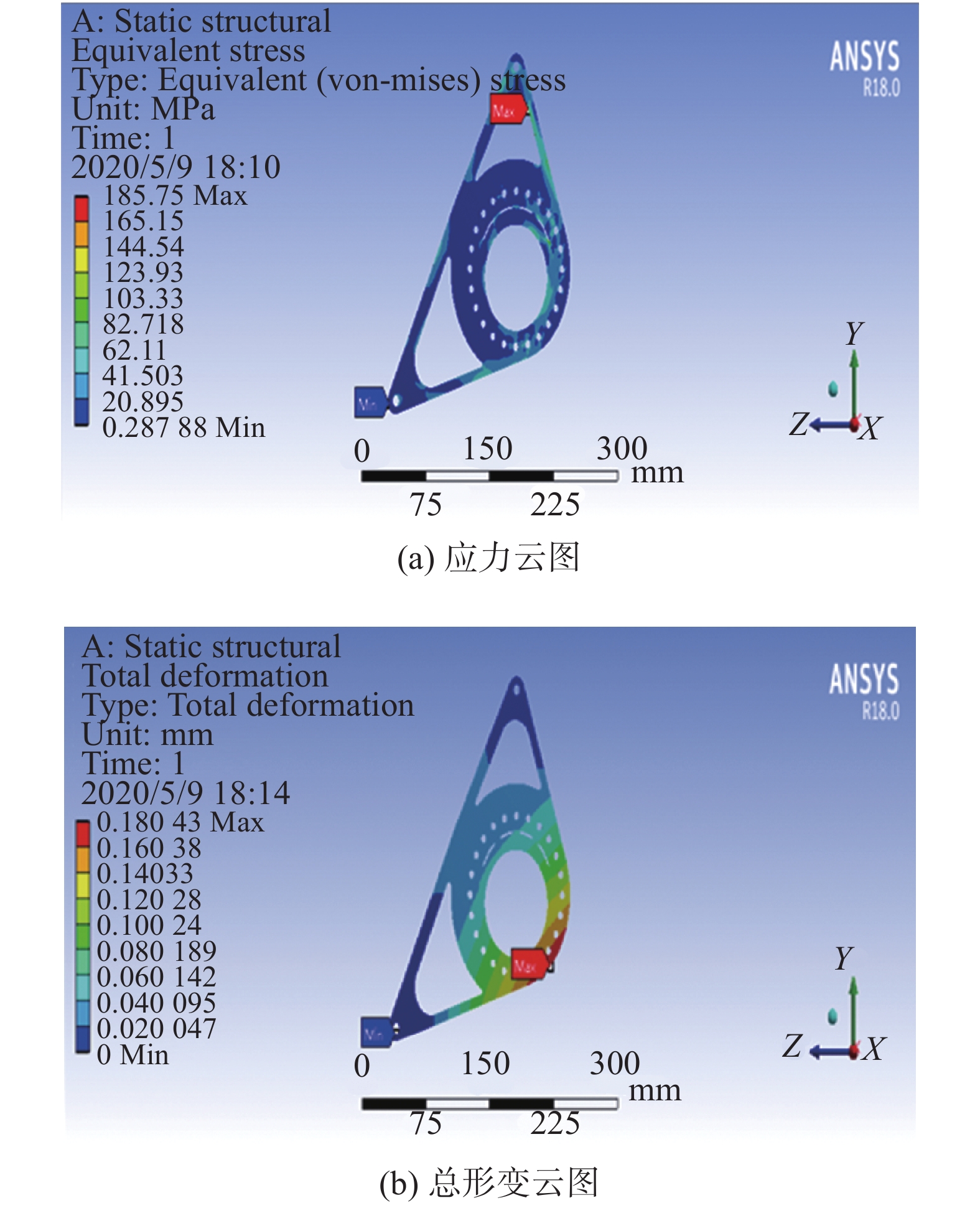
根据拓扑优化结果最终将链传动支架利用CATIA重新进行设计。拓扑优化后重新进行静力学分析其应力和应变如图12所示。
|
Download:
|
| 图 12 链传动系统支架云图 | |
表4给出优化前后性能对比情况。可以发现优化前后支架的质量和应力以及总变形都有所减小,达到了拓扑优化的目的,且满足其整车的设计需求。
|
|
表 4 优化前后结果对比 |
FSAE赛车悬架系统是FSAE赛车的车架与赛车车轮之间所有传递力矩的连接装置,也是FSAE赛车重要的总成之一。其不仅具备力矩在赛车车轮与赛车车架之间良好的传递,还要具备缓解由不同路面所传来的冲击载荷的能力,以及保证赛车车轮得到良好的运动特性,使得赛车在高速行驶中保持良好的操纵稳定性。
因此,一个高质量、高标准的FSAE赛车悬架系统,需要经过各种路况条件的严格考验,同时要确保车手与赛车的安全。本着科学严谨的态度,对关键部件及结构的设计、强度等性能要求还要更进一步的分析和优化,故接下来对悬架系统受力较大的关键部件进行结构强度分析。
FSAE赛车的摇臂是通过螺栓将避震器与拉杆进行连接而成,其中的一个螺栓连接车架系统,另外3个分别与悬架系统的推杆和减振器以及防侧倾杆进行连接。为了保证悬架摇臂的强度要求与安装精度要求,选用7075铝进行加工。利用CATIA对悬架的摇臂进行三维建模,模型如图13所示。
|
Download:
|
| 图 13 CATIA建立的悬架摇臂三维模型 | |
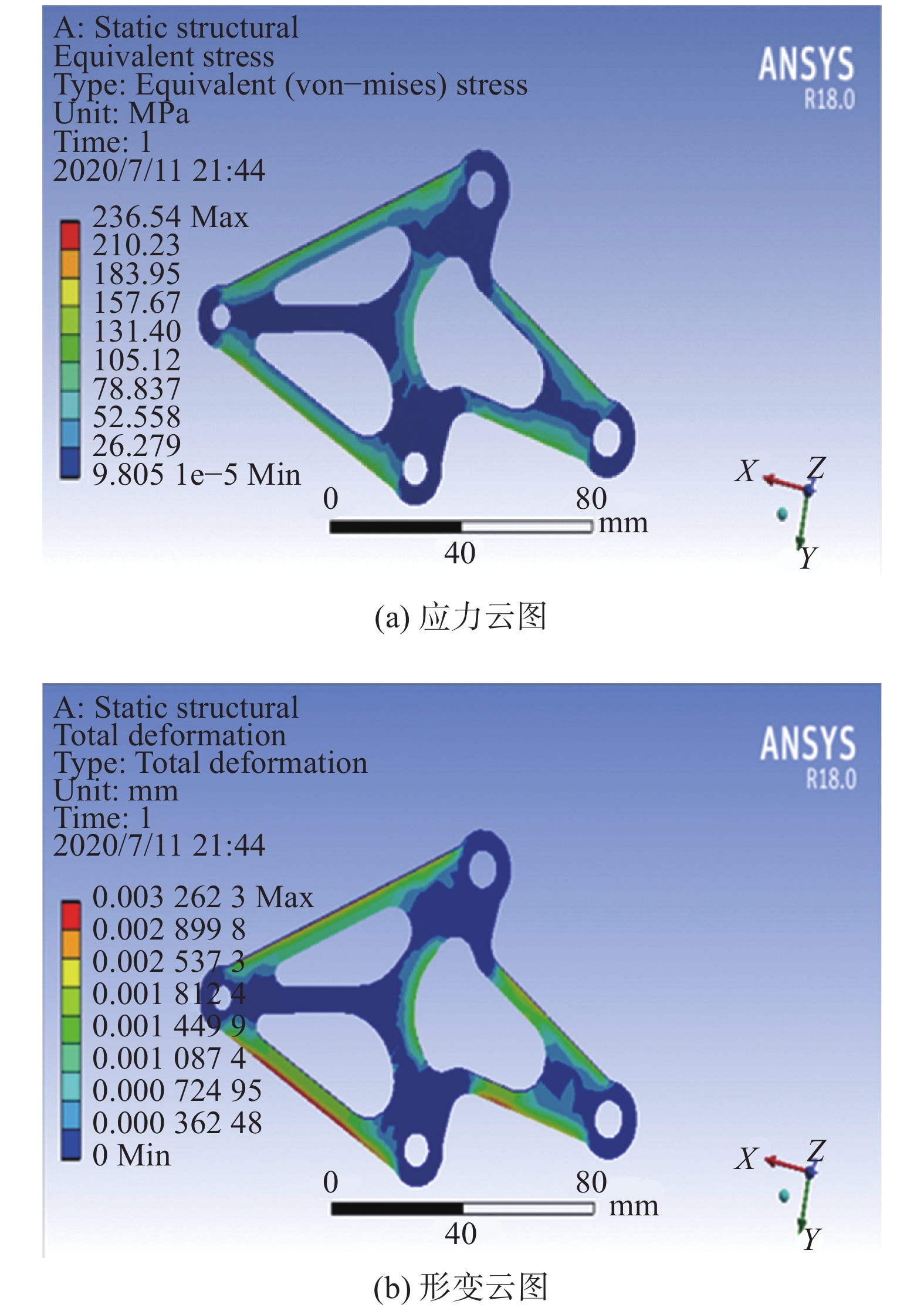
由于悬架的后摇臂厚度较薄,且受到的力在一个平面内,所以,对它进行受力分析时把它看成二维实体来进行ANSYS有限元分析,材料选用7075铝。首先进行材料属性的定义,其次进行网格的划分。后悬架受力多变,所以安全系数最好大于2.0;接下来将摇臂与车架系统的螺栓连接孔进行固定约束;最后把推杆和减震器以及防侧倾杆3个方向的力依次施加到对应位置[14],得到悬架摇臂应力图和形变如图14所示。
由图14可知,应力最大值为236.51 MPa,发生在与推杆相连接的摇臂内角点上。这个地方受到减振器和推杆2个合力的反方向作用,这样作用力相对较大。但应力最大值小于7075铝的应力极限,最大变形量为0.003,摇臂的结构强度处于安全范围之内。
|
Download:
|
| 图 14 悬架摇臂受力 | |
FSAE赛车多半采用后轮驱动的方式,且发动机布置是中置后驱。后轮将发动机的动力传递到主减速器,通过主减速器传递到差速器,差速器通过左右半轴传递到车轮两侧轮毂,最后通过轮毂传递到两侧轮胎,以实现赛车的加速、制动等[15]。
轮毂是连接传动半轴与轮辋的重要部件,轮毂的轻量化对汽车动力性的提高和油耗的降低起着重要的作用。由于赛车所用的轮辋为赛车专用轮辋,不同于普通的汽车轮毂,所以要进行轮芯的重新设计。重新设计的轮芯在满足刚度的要求下,能够和浮动制动盘配合安装,为卡钳预留足够的安装位置,并且能使轮辋通过轮辋螺栓固定在其外侧。
轮边制动系统属于赛车的底盘系统,轮毂属于赛车行驶系的重要零部件,且轮毂要用来驱动整车,实现汽车运动,故作为驱动轮时,受力较为复杂,对整车的性能及稳定性、操控性影响较大。轮毂起初的设计理念是在满足赛车的稳定性要求下,尽量达到轻量化的目的。如果想要得到理想的设计方案,需要通过ANSYS有限元分析去综合考虑赛车稳定性和轻量化的影响,最终进行优化设计[16]。
立柱(UPRIGHT)是用来连接悬架与转向和轮毂的部件,轮边系统的三维模型如图15所示。
|
Download:
|
| 图 15 CATIA建立的立柱(UPRIGHT)三维模型 | |
赛车在制动过程中载荷会发生转移,即载荷往赛车前部转移,所以制动工况中前立柱受力较大,后立柱受力较小,故只对前立柱进行制动工况下进行有限元分析。
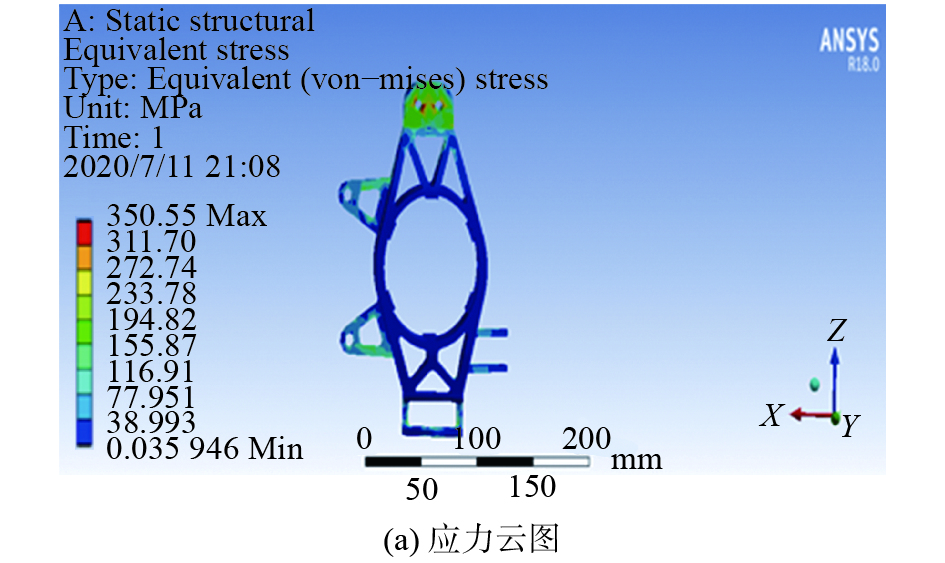
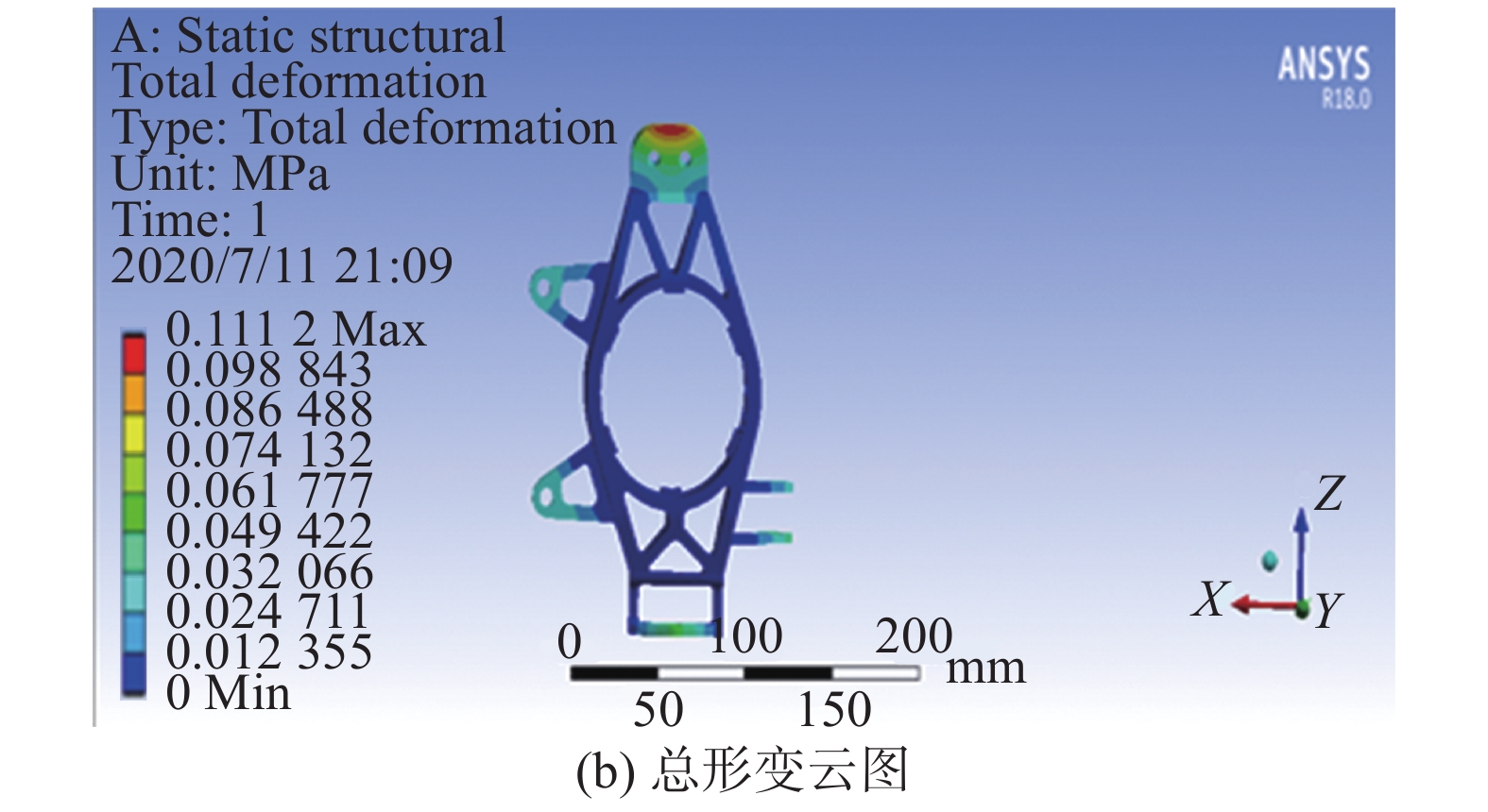
在赛车进行制动时,由于前立柱要承担转向作用,故前立柱的受力最大。在进行ANSYS有限元分析时,需要在保证安全的前提下,首先对立柱的内侧进行固定约束。在立柱轴心施加一个地球引力,其次在与悬架所连接的上吊耳处施加向后的1 000 N的力,在下轴承孔施加向前2 500 N的力,然后在制动卡钳支架连接处施加10 000 N·mm的制动力矩。最终的应力、形变如图16所示。
|
Download:
|
| 图 16 | |
|
Download:
|
| 图 16 前立柱 | |
由图16可以看出,立柱所受到的最大应力是350.65 MPa,明显小于材料的许用应力505 MPa,最大变形量为0.111 mm,满足设计要求。
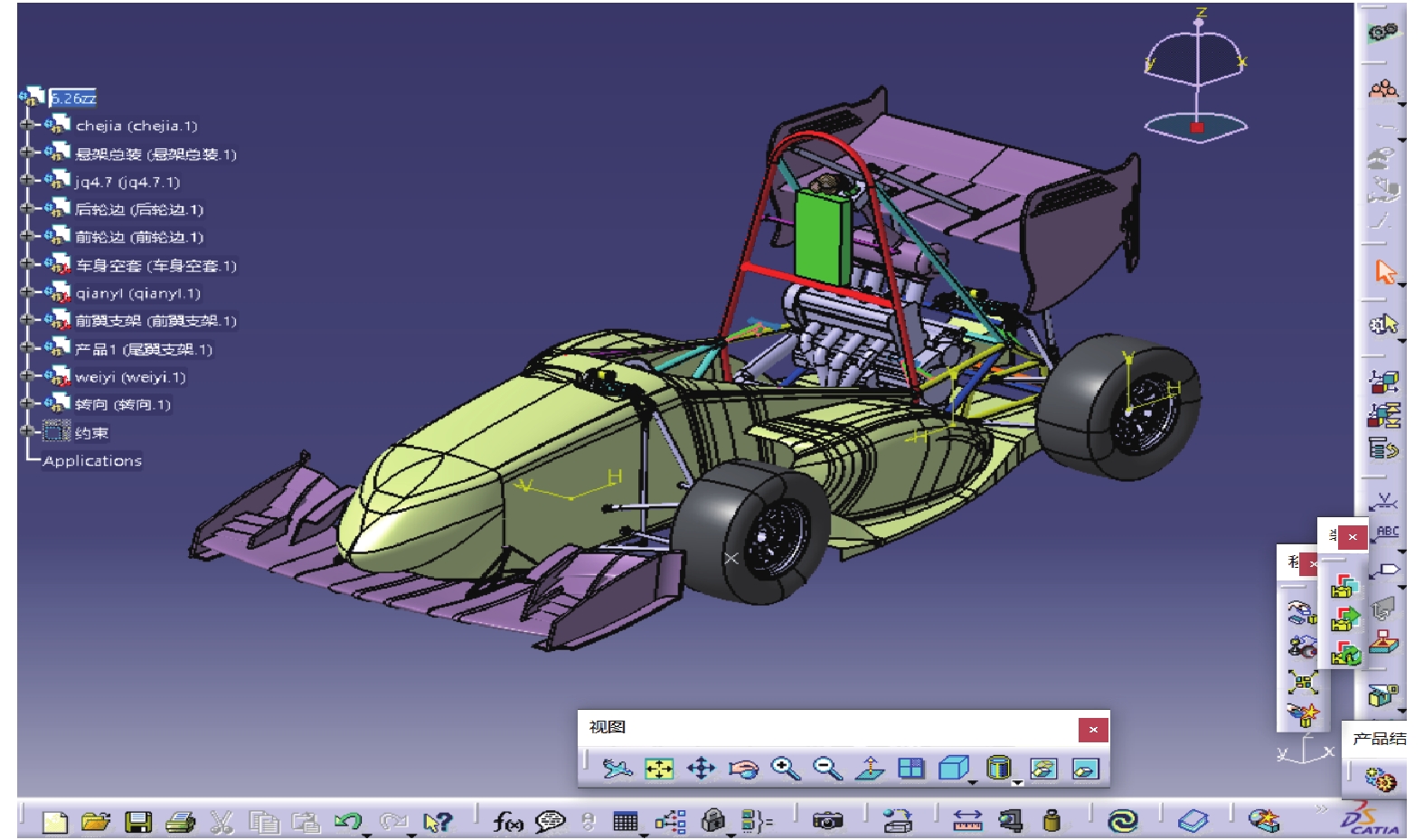
西安航空学院2019年中国大学生方程式赛车比赛用车CATIA模型与整车渲染图如图17所示。
|
Download:
|
| 图 17 CATIA建立的整车三维模型 | |
根据相关的理论计算,已知7075航空铝材料的屈服极限为505 MPa,最后通过ANSYS Workbench模块进行有限元分析,计算出各零部件的最大应力以及各部分的安全系数如表5所示。
|
|
表 5 整车各个部件安全系数表 |
1)按照《中国大学生方程式汽车大赛规则》(2019版)要求,根据大赛整车参数以及汽车理论基础等进行FSAE赛车设计,使用CATIA三维建模软件的机械设计与装配设计模块等进行了整车(悬架系统、动力总成系统、车身、轮边制动系统)模型的建立及总装。最终实车装配顺利且误差较小,满足大赛要求。
2)通过ANSYS结构静力学模块对整车的关键零部件进行了校核,在材料定义选择7075/T6航空铝材料参数,网格均采用大小为2 mm的六面体网格,确保了其分析结果的准确性。仿真分析结果显示,应力远远小于材料的屈服极限,总形变云图也满足其整车设计要求,在达到轻量化目的的同时,满足了整车成本控制的要求。
3)本文针对赛车材料选用为航空铝的零部件进行了仿真分析,根据工程图纸加工设计的要求,最后加工零部件完成整车的总装,同年此赛车参加2019中国大学生方程式汽车大赛(襄阳站)获得团体三等奖的优秀成绩,为今后国内大学生方程式赛车的设计起到了一定积极的作用。
| [1] |
ZUMBRUNN M, HESELTINE R. Italian auto legends classics of style and design[M]. [S.l.]: Merrell Publishers, 2008.
( 0) 0)
|
| [2] |
中国汽车工程学会. 中国大学生方程式汽车大赛规则(2019)[EB/OL]. [2020−08−12]. http://www.formulastudent.com.cn/.
( 0) 0)
|
| [3] |
Mohamad M L, Rahman M T A, Khan S F, et al. Design and static structural analysis of a race car chassis for Formula Society of Automotive Engineers (FSAE) event[J]. Journal of Physics: Conference Series, 2017, 908(1). ( 0) 0)
|
| [4] |
马粉粉, 崔亚辉, 王宏江. 基于ANSYS的FSAE车架轻量化研究[J]. 汽车实用技术, 2016(2): 130-132. ( 0) 0)
|
| [5] |
吕绍远, 王慰祖, 黄捷, 等. 基于ANSYS的FSAE方程式赛车后轮边系统优化设计和分析[J]. 现代农业装备, 2017(2): 39-47. DOI:10.3969/j.issn.1673-2154.2017.02.013 ( 0) 0)
|
| [6] |
王嬿舒. 基于ANSYS的方程式赛车传动系统优化设计[J]. 机械传动, 2017, 41(1): 137-141. ( 0) 0)
|
| [7] |
AZMEER M, BASHA M H, HAMID M F, et al. Design optimization of rear uprights for UniMAP automotive racing team formula SAE racing car[J]. Journal of physics: conference series, 2017, 908(1): 012051. ( 0) 0)
|
| [8] |
YADAV D, KULKARNI P S, GHIYA S. Response surface methodology based optimization of aerodynamic package of a FSAE car[C]//Proceedings of the 19th Annual CFD Symposium. Bangalore, India: National Aerospace Laboratories, 2017.
( 0) 0)
|
| [9] |
金国栋. 汽车概论[M]. 北京: 机械工业出版社, 2000.
( 0) 0)
|
| [10] |
施长政. FSAE赛车的设计与制造[D]. 青岛: 青岛大学, 2013.
( 0) 0)
|
| [11] |
蓝宇, 张连杰. 大型有限元分析软件ANSYS[J]. 应用科技, 2000, 27(6): 11-12, 15. DOI:10.3969/j.issn.1009-671X.2000.06.004 ( 0) 0)
|
| [12] |
Algorithms; Findings from H. Wang and Co-Authors Provides New Data about Algorithms (Genetic algorithm-based optimization design method of the Formula SAE racing car's rear wing)[J]. Journal of Technology & Science, 2018. ( 0) 0)
|
| [13] |
刘明, 朱瑞峰. FSAE赛车链传动张紧装置拓扑优化设计[J]. 科学技术创新, 2020(25): 154-155. ( 0) 0)
|
| [14] |
李飞, 吴华伟, 姜杰. FSAE赛车双横臂悬架系统设计[J]. 重庆理工大学学报(自然科学版), 2018, 32(5): 77-81. ( 0) 0)
|
| [15] |
BABREKAR K, BAIRAGI S, PARAJIYA J, et al. Optimization of brake pedal for FSAE vehicle[M]//NARASIMHAM G S V L, BABU A V, REDDY S S, et al. Recent Trends in Mechanical Engineering: Select Proceedings of ICIME 2019. Singapore: Springer, 2020.
( 0) 0)
|
| [16] |
李乃斌, 李耀平, 王功博. 基于ANSYS的FSAE赛车后轮芯的分析与优化[J]. 小型内燃机与车辆技术, 2016, 45(3): 69-73. DOI:10.3969/j.issn.1671-0630.2016.03.015 ( 0) 0)
|
 2021, Vol. 48
2021, Vol. 48


