系统故障演化过程存在于当今各行各业。系统指自然系统和人工系统，自然系统灾害演化过程是自然灾害按照自然规律发生发展的过程，与人是否参与无关；人工系统故障演化过程是人们根据既定目的，按照事物的自然属性所建立系统发生失效的过程。他们都可归结为系统故障演化过程。而研究系统故障演化过程主要在于过程的表示、分析和治理。但由于系统故障演化过程宏观逻辑过程和微观因果关系的复杂性，加之影响因素众多，导致演化过程具有多样性，给故障演化过程深入研究带来困难。

对系统故障演化过程的表示和分析方法研究不多，但近年来正在迅速增加。主要研究了机械系统故障^[1]、网格级联故障^[2]、多焦点策略优化^[3]、竞争故障^[4]、混合故障^[5]、多策略演化^[6]，交通系统^[7]，企业系统^[8]和行为过程^[9]等演化机理。在医疗^[10]、项目管理^[11]、软件评估^[12]、健康分析^[13]和并行结构分析^[14]等领域也出现了系统演化过程的表示方法研究。这些研究都有很强的专业背景，形成的表示分析方法都具有针对性，难以相互借鉴，更难以建立通用的系统故障演化过程表示和分析方法。

崔铁军等^[15-30]提出了空间故障树理论(space fault tree, SFT)，用于分析系统可靠性与因素关系。进一步在研究系统故障演化过程中提出了SFN^[31-35]，研究演化过程中原因事件、结果事件、因果关系和影响因素的关系。但已有研究都是将SFN根据转化规则转化为SFT，再使用SFT已有方法进行分析。但SFT方法对SFN的网络结构缺乏较好的针对性。为此又提出了SFN的结构化表示方法，借助矩阵表示SFN，这有利于计算机智能处理。在结构化表示方法中需要解决多原因事件以不同逻辑关系导致结果事件的情况。因为演化过程中事件的逻辑关系较为复杂，不止存在“与”、“或”关系，更存在其他逻辑关系。因此本文借助何华灿教授提出的柔性逻辑处理模式，转化得到事件发生逻辑关系，最终得到演化过程分析式和演化过程计算式，为SFN的结构化表示和计算机智能处理奠定基础。

1 空间故障网络及其结构化表示

SFN是SFT研究的第三阶段，用于研究系统故障演化过程。目前系统故障演化过程研究面临的问题很多，比如引起故障演化过程的原因很多，但难以确定他们之间的关系、原因事件到最终事件的演化是复杂的网络结构、网络结构不能使用化简方法删除事件及其关系、原因事件存在多种逻辑关系导致结果事件、影响演化原因和演化进程的因素很多、各种因素和各种原因是否独立或相互联系，SFN理论力求解决这些问题。由于SFN基于SFT，因此可分析多因素影响下的系统故障演化过程。通过事件间的网络结构表示他们的因果逻辑关系，可在无损状态下对网络进行化简并得到故障演化模式。虽然具有先进性，但SFN分析方法仍存在问题。

原有SFN分析方法是将得到的SFN网络，通过SFN与SFT的转化规则转化为等效SFT。虽然增加了一些表示方法，但转化SFT使用原有方法仍然存在问题。主要是SFT方法并不针对SFN网络特征，导致定性定量分布不当，效用较低。因此非常需要一种针对SFN网络特点研究的独立方法。

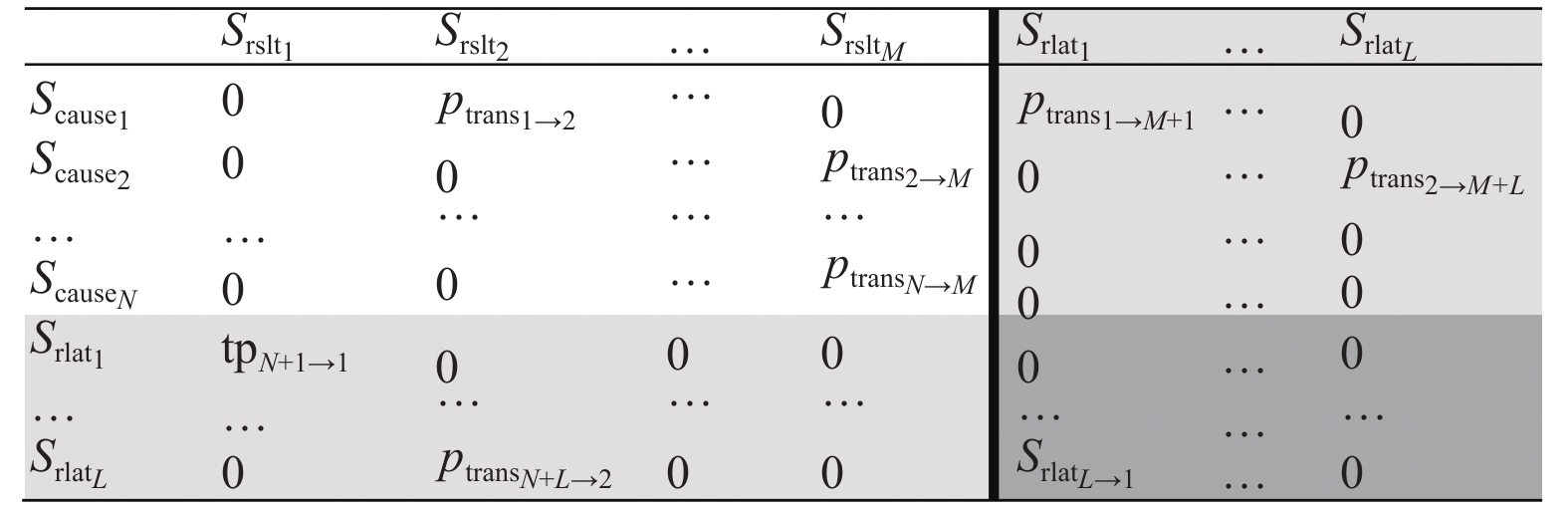
综合研究一些智能推理和数据处理方法，作者提出了SFN的结构化表示方法I。将SFN结构转化矩阵，使用矩阵操作表示故障演化过程。这样做的优势在于计算机易于对矩阵进行处理，可使用计算机智能处理SFN表示的系统故障演化过程。但其仍存在问题，即当多原因事件以不同逻辑关系导致结果事件时不易处理。由于建立的因果结构矩阵I中只有原因事件和结果事件，因此无法表示上述复杂因果关系。因此进一步对结构化表示方法进行改进，提出结构化表示方法II，添加了事件间逻辑关系，将逻辑关系等效为事件，称为关系事件。形成的因果结构矩阵II如图1所示。

定义1　因果结构矩阵(matrix of cause event and result event, CERE)(II)用于SFN的结构化表示，记为 ${{{C}}_{{\rm{CEREII}}}} = \left[ {\begin{array}{*{20}{c}} {{{{S}}_{{\rm{cause}}}}}&{{{{S}}_{{\rm{rslt}}}}}&{{{{S}}_{{\rm{rlat}}}}}&{{{{P}}_{{\rm{trans}}}}} \end{array}} \right]$ 。使用 ${s_{{\rm{caus}}{{\rm{e}}_n}}}$ 表示原因事件，n=1,2,···,N，集合 ${{{S}}_{{\rm{cause}}}} = \{ {s_{{\rm{caus}}{{\rm{e}}_n}}}\left| {n = 1,2,} \right. \cdots , N\} $ ；使用 ${s_{{\rm{rsl}}{{\rm{t}}_m}}}$ 表示结果事件，m=1,2,···,M，集合 ${{{S}}_{{\rm{rslt}}}} = \{ {s_{{\rm{rsl}}{{\rm{t}}_m}}}\left| {m = 1,2,} \right. \cdots ,M\} $ ；使用 ${s_{{\rm{rla}}{{\rm{t}}_l}}}$ 表示关系事件，l=1,2,···,L，集合 ${{{S}}_{{\rm{rlat}}}} = \{ {s_{{\rm{rla}}{{\rm{t}}_l}}}\left| {l = 1,2,} \right. \cdots ,L\} $ ；传递概率集合 ${{{P}}_{{\rm{trans}}}} = \{ {p_{{\rm{tran}}{{\rm{s}}_{n \to m}}}}\left| {n = 1,2,} \right. \cdots ,N + L;m = 1,2, \cdots M + L\} $ 。

定义2　因果关系组(II)：存储了CERE中所有事件及关系事件的逻辑关系，记为

$ \begin{array}{c} {\mathit{ \Gamma }} = \{ {s_{{\rm{caus}}{{\rm{e}}_n}}} \to {s_{{\rm{rsl}}{{\rm{t}}_m}}},{s_{{\rm{caus}}{{\rm{e}}_n}}} \to {s_{{\rm{rsl}}{{\rm{t}}_l}}},{s_{{\rm{rsl}}{{\rm{t}}_l}}} \to {s_{{\rm{rsl}}{{\rm{t}}_m}}},{s_{{\rm{rla}}{{\rm{t}}_l}}} \to {s_{{\rm{rla}}{{\rm{t}}_l}}}^\prime , \\ \;\;\;\;\;\;{S_{{\rm{cause}}}} + {S_{{\rm{rlat}}}} \to {s_{{\rm{rla}}{{\rm{t}}_l}}}|{p_{{\rm{tran}}{{\rm{s}}_{n \to m}}}} \times {s_{{\rm{caus}}{{\rm{e}}_n}}} = {s_{{\rm{rsl}}{{\rm{t}}_m}}},{p_{{\rm{tran}}{{\rm{s}}_{l \to n}}}} \times \\ \;\;\;\;\;\; {s_{{\rm{caus}}{{\rm{e}}_n}}} = {s_{{\rm{rla}}{{\rm{t}}_l}}},{s_{{\rm{rla}}{{\rm{t}}_l}}} = {s_{{\rm{rla}}{{\rm{t}}_l}}}^\prime ,{s_{{\rm{rla}}{{\rm{t}}_l}}} = {s_{{\rm{rsl}}{{\rm{t}}_m}}},{s_{{\rm{rla}}{{\rm{t}}_l}}} = \\ \;\;\;\;\;\;{{{S}}_{\rm{rslt + rlat}}} \times {{{C}}_{{\rm{CERE}}{s_{{\rm{rsl}}{{\rm{t}}_l}}}}} \\ \end{array} $

式中： ${{{S}}_{\rm{rslt + rlat}}}$ 为 ${{{S}}_{{\rm{rlslt}}}}$ 与 ${{{S}}_{{\rm{rlat}}}}$ 矩阵对应位置元素相乘的结果。

因果关系组中所有关系的前件都是原因事件，后件都是结果事件。

使用图1可表示SFN中的全部事件和全部逻辑关系。图中以粗实线为分界，左侧和右侧分析方法不同。左侧为事件关系的处理方法；右侧为关系事件的关系处理方法。最终综合整个矩阵得到因果关系组，得到最终事件演化过程分析式和计算式，请参见作者相关文献[15-30]，这里不再列出，本文主要研究多原因事件导致结果事件的逻辑关系。

2 事件逻辑关系与柔性逻辑模式

SFN的结构化表示方法基础是因果结构矩阵，用于表示所有事件和他们之间的逻辑关系。

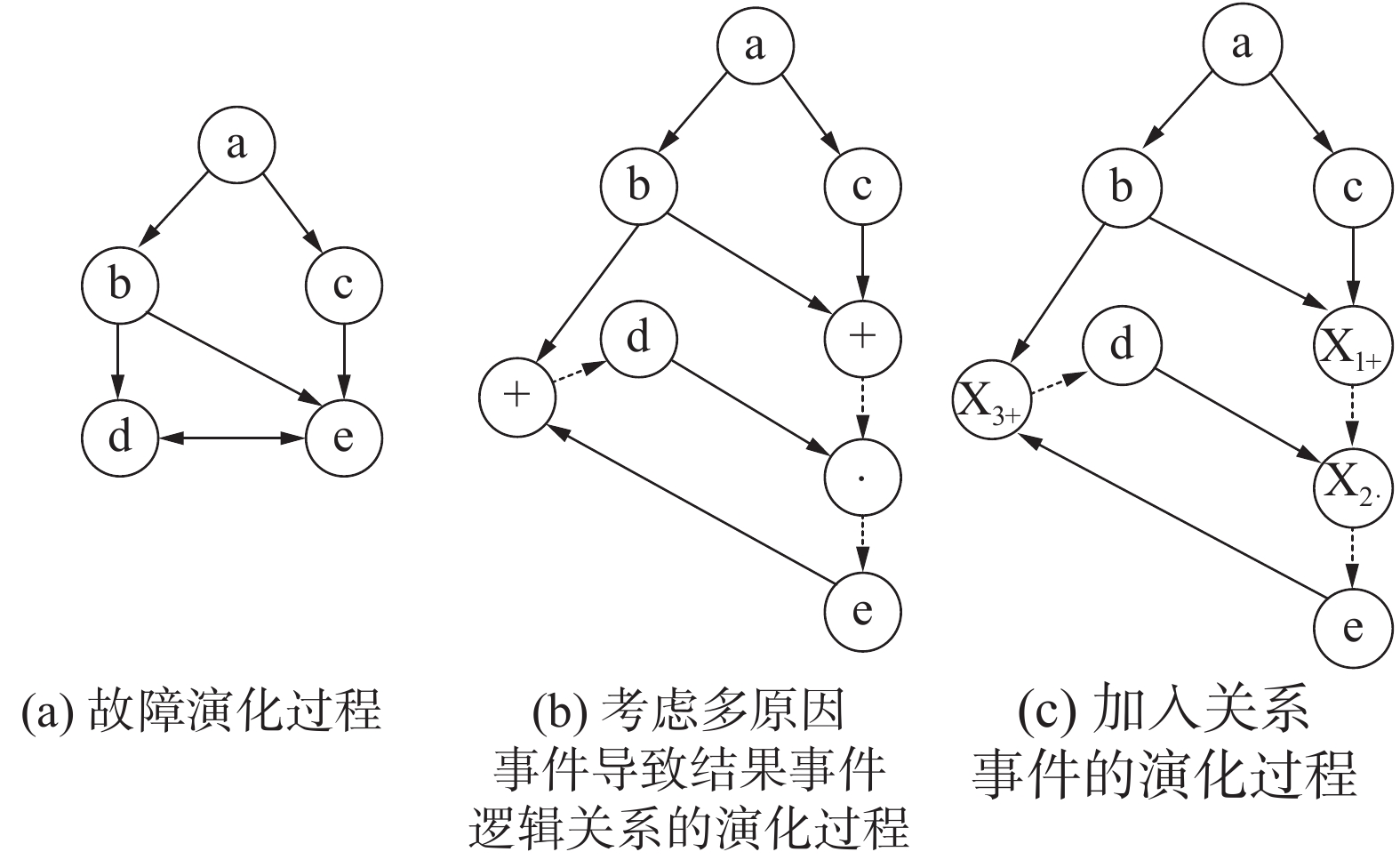
如图2表示故障演化的等效转化过程。事件为a、b、c、d、e；关系事件为X₁、X₂、X₃。事件b、c其一发生则导致下一步事件发生，是“或”关系；事件d与事件b、c结果同时发生导致事件e发生，是“与”关系。那么关键问题是类似“与”、“或”这类逻辑关系有多少种类。

根据何华灿教授提出的泛逻辑学理论，给出了柔性信息处理模式。将关系模式、关系模式分类标准及逻辑描述进行了等价研究和分析。在完备的布尔信息处理逻辑关系基础上，增加了参数 $e'$ 反应阈值。并且在经典布尔逻辑上补充了4种新逻辑关系，包括组合、平均、非组合和非平均。最终形成了20种逻辑关系，如表1所示。

表1给出了何华灿教授得到的20种不同逻辑表达形式的对应关系^[36-37]，即前4列，包括关系模式、关系模式分类标准及逻辑描述。但这些逻辑关系表示和系统故障演化过程的事件逻辑关系有所差别，不能用于SFN的结构化表示方法。因此需要解决SFN中已知事件故障概率分布(多因素下原因事件与结果事件的发生关系，即事件对象在多因素情况下发生故障的情况)情况时的最终事件故障概率计算方法。那么需要将上述20种逻辑关系等效为原因事件的故障概率分布之间的叠加关系，确定最终事件计算方法。首先需要明确的是，任何复杂的逻辑关系操作都可化简为2个事件之间的逻辑关系操作(假设为二元逻辑关系)。因此以如下2个事件为例，进行20种关系与事件故障概率之间的等效转化。

在故障演化过程中，最经典的关系是“与”、“或”关系。根据经典故障树逻辑关系与故障概率计算方法，设“与”关系：Z=x∧y $ \Rightarrow $ P(q_x,q_y)=q_xq_y；“或”关系：Z=x∧y $ \Rightarrow $ P(q_x,q_y)=1−(1−q_x)(1−q_y)。其中：P(q_x,q_y)表示原因事件x、y发生导致的结果事件故障概率分布；q_x表示原因事件x的故障概率分布与传递概率的积；q_y表示原因事件y的故障概率分布与传递概率的积。等效推导过程如下：

Z≡1 $ \Rightarrow $ P(q_x,q_y)≡1

Z=x∨y $ \Rightarrow $ P(q_x,q_y)≥1−(1−q_x)(1−q_y)=q_x+q_y−q_xq_y

Z=x®y $ \Rightarrow $ P(q_x,q_y)=q_x/2+q_y/2

Z=y→x $ \Rightarrow $ P(q_x,q_y)≥

　1−(1−q_x)(1−(1−q_y))=1−(1−q_x)q_y=1−q_y+q_xq_y

Z=x $ \Rightarrow $ P(q_x,q_y)=q_x

Z=x→y $ \Rightarrow $ P(q_x,q_y)≥

　1−(1−q_y)(1−(1−q_x))=1−(1−q_y)q_x=1−q_x+q_xq_y

Z=y $ \Rightarrow $ P(q_x,q_y)=q_y

Z=x↔y $ \Rightarrow $ P(q_x,q_y)=q_xorq_y

Z=x©^e’y $ \Rightarrow $ P(q_x,q_y)=

$ \left\{ \begin{array}{l} P \leqslant {q_x}{q_y},{q_x},{q_y} > e' \\ P \geqslant 1 - (1 - {q_x})(1 - {q_y}) = {q_x} + {q_y} - {q_x}{q_y},{q_x},{q_y} < e' \\ {q_x}{q_y} \leqslant P \leqslant {q_x} + {q_y} - {q_x}{q_y},{q_x} = {q_y} = e' \end{array} \right. $

Z=x∧y $ \Rightarrow $ P(q_x,q_y)=q_xq_y

Z=¬(x∧y) $ \Rightarrow $ P(q_x,q_y)=1−q_xq_y

Z=¬(x©^e’y) $ \Rightarrow $ P(q_x,q_y)=

$ \left\{ \begin{array}{l} P \leqslant 1 - {q_x}{q_y},{q_x},{q_y} > e' \\ P \geqslant (1 - {q_x})(1 - {q_y}) = 1 - {q_x} - {q_y} + {q_x}{q_y},{q_x},{q_y} < e' \\ 1 - {q_x}{q_y} \leqslant P \leqslant 1 - {q_x} - {q_y} + {q_x}{q_y},{q_x} = {q_y} = e' \end{array} \right. $

Z=¬(x↔y) $ \Rightarrow $ P(q_x,q_y)=1−q_xorq_y

Z=¬y $ \Rightarrow $ P(q_x,q_y)=1−q_y

Z=¬(x→y) $ \Rightarrow $ P(q_x,q_y)≤

　　1−(1−(1−(1−q_x))(1−q_y))=(1−(1−q_x))(1−q_y)=q_x−　　　q_xq_y

Z=¬x $ \Rightarrow $ P(q_x,q_y)=1−q_x

Z=¬(y→x) $ \Rightarrow $ P(q_x,q_y)≤

　1−(1−(1−(1−q_y))(1−q_x))=(1−(1−q_y))(1−q_x)=q_x−　　　q_xq_y

Z=¬(x®y) $ \Rightarrow $ P(q_x,q_y)=1−(q_x/2+q_y/2)

Z=¬(x∨y) $ \Rightarrow $ P(q_x,q_y)≤

　1−(1−(1−q_x)(1−q_y))=1−q_x−q_y+q_xq_y

Z≡□0 $ \Rightarrow $ P(q_x,q_y)≡0

在上述过程中，存在“≤”、“≥”。考虑到故障演化过程中的事件逻辑关系，事件的故障概率分布P(q_x,q_y)取极限值，即取等号情况。但由于Z=¬(x©^e'y)和Z=x©^e'y得到的P(q_x,q_y)是分段函数，保留原始推导形式。最终这20种事件发生逻辑关系如表1最后一列所示。

3 实例分析

使用图2进行上述20种事件故障逻辑关系计算举例。以原因事件b,e导致结果事件d为例进行说明。

Z=x∧y，与关系：P_d(q_b,q_e)=q_bq_e；

Z=x→y，蕴含：P_d(q_b,q_e)=1−q_b+q_bq_e；

Z=¬(x®y)，非平均：P_d(q_b,q_e)=1−(q_b/2+q_e/2)；

Z=x©^e’y，组合：设 $e'$ =0.7, q_b=0.4, q_e=0.4,

$ \begin{array}{l} {P_{\rm{d}}}\left( {{q_{\rm{b}}},{q_{\rm{e}}}} \right) \geqslant {q_{\rm{b}}} + {q_{\rm{e}}} - {q_{\rm{b}}}{q_{\rm{e}}}({q_{\rm{b}}},{q_{\rm{e}}} < e') = \\ \;\;\;\;\;\;\;\;\;0.4 + 0.4 - 0.4 \times 0.4 = 0.64。\end{array} $

当然上述关系实际上是关系事件X₃的计算，即 ${P_{{{\rm{X}}_3}}}$ (q_b,q_e)。由于X₃并不代表实体事件，而只是为了满足逻辑关系，将事件与逻辑关系分离。因此关系事件X₃到事件d之间的关系是同位关系，其传递概率为1，则 ${P_{{{\rm{X}}_3}}}$ =P_d。

在上述条件下，使用事件发生概率逻辑关系(SFN中为事件故障概率分布)进行分析。SFN可使用SFT的事件(元件)故障概率分布^[15]。那么在SFT系统中选择2个元件x₁和x₂^[15]，将他们的故障概率分布分别等同于事件b和事件e。那么b和e对于使用时间t和使用温度T的特征函数分别为 $P_{}^t(t)$ 和 $P_{}^T(T)$ 如表2所示。

根据SFT的基本事件故障发生概率，得到事件b和e的故障概率分布^[15–16]

$P(t,T) = 1 - (1 - {P^t}(t))(1 - {P^T}(T))$

(1)

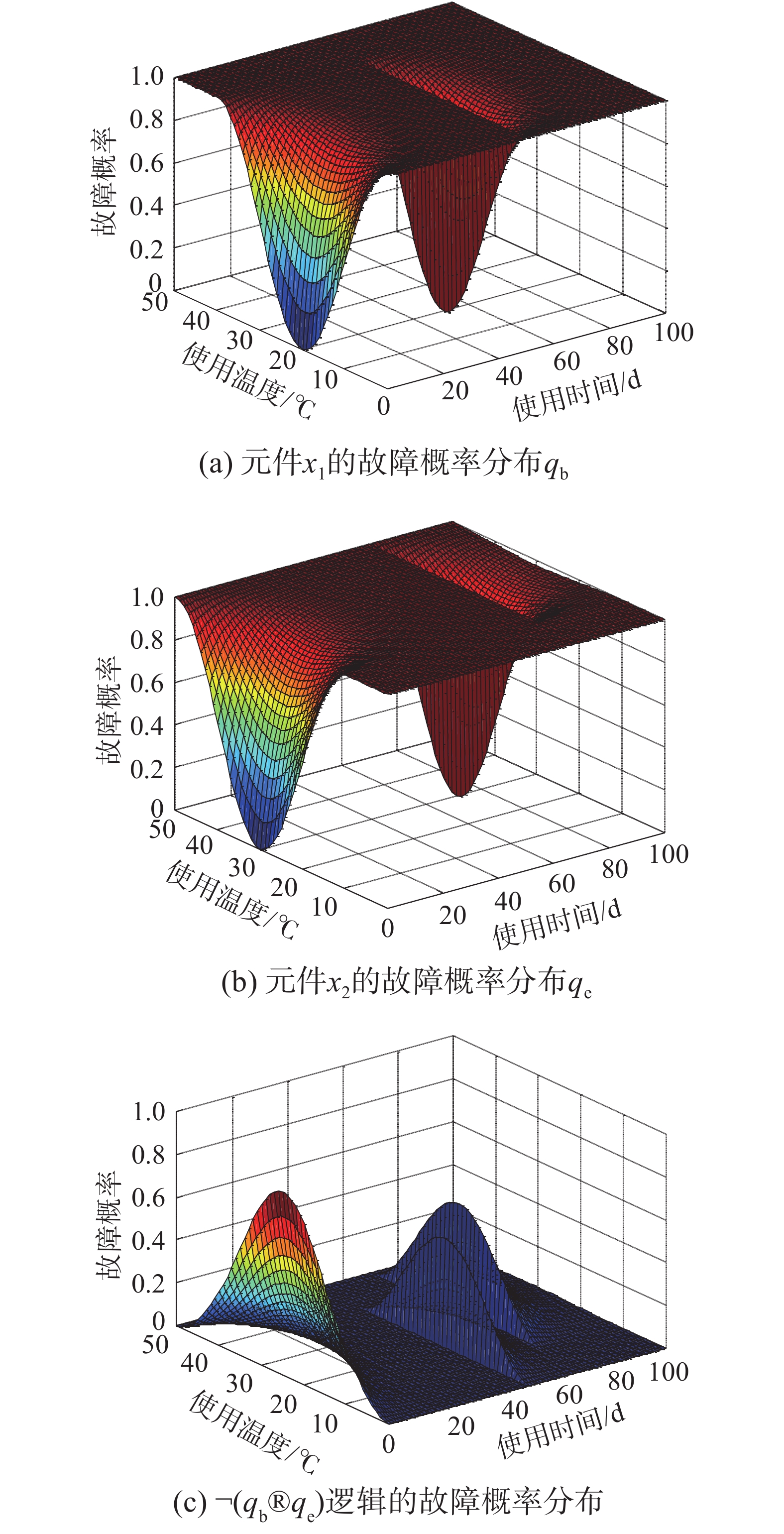
根据式(1)，在使用时间[0,100] d，使用温度[0,50]℃绘制事件b和e的故障概率分布，及他们的¬(q_b ® q_e)逻辑的故障概率分布，如图3所示。

图3(a)和(b)是由文献[15]得到的，相当于SFN的边缘事件；而图3(c)是使用¬(q_b®q_e)逻辑关系得到的结果事件故障概率分布，相当于SFN的最终事件。当然上述过程传递概率假设为1。可见不同原因事件根据不同逻辑关系导致结果事件的故障概率分布不同，可使用这20种逻辑关系配合事件故障概率分布得到。进而在演化过程中研究多因素影响下的多逻辑结果事件故障概率分布。

将这20种事件发生逻辑关系组成逻辑关系集合B。演化过程的不同层次原因事件根据这些逻辑关系得到本层次结果事件；在下层次中，将这些结果事件作为原因事件，再根据这些逻辑关系得到结果事件。以此类推，最终得到边缘事件与最终事件的演化过程分析式和演化过程计算式。

论文将柔性逻辑关系转化为事件概率逻辑关系，便于SFN演化过程的定量计算。这20种逻辑关系包括了目前已知的事件故障演化逻辑关系，为更全面地描述故障演化过程逻辑关系、SFN定性分析和定量计算奠定了坚实基础；另一方面也为SFN结构化表示方法进行智能处理奠定了逻辑关系基础。

4 结论

1)论文提出了柔性逻辑处理模式与事件发生逻辑关系的等效转化方法。考虑故障树经典“与”、“或”逻辑关系，研究认为柔性逻辑处理模式中“与”、“或”关系与故障演化过程中“与”、“或”关系是等价的。事件故障概率分布计算方式也是等价的。

2)本文推导了20种柔性逻辑在系统故障演化过程中的表达方式，并给出了过程。通过实例说明了逻辑关系的使用和计算方法。

3)本文得到了边缘事件与最终事件的演化过程分析式和演化过程计算式。为故障演化过程逻辑描述和SFN结构化方法的计算机智能处理奠定基础。