随着科学技术的的发展，电力系统结构愈发复杂，规模愈发庞大，在日常维护过程中，难免出现缺陷和问题。供电企业对电力设备进行缺陷处理，能够有效提高电力系统的安全、稳定运行^[1-4]。

针对电力系统维护过程中遇到的问题，国内外学者进行了大量的研究工作。吴丹等^[5]采用三角模糊和层次分析相结合的方法，解决了多种不确定因素影响电力负荷预测的问题，能够有效地提高电力负荷的预测精度。王文琦^[6]针对传统的人工方式消缺效率低的问题，提出将层次分析法(AHP)应用在智能缺陷识别系统中，提高了消缺效率，验证了方法的可行性。刘大伟等^[7]将云策略和微软媒体服务器协议(Microsoft media server protocol，MMS)相结合，设计自动测试系统，降低了成本，提高了调试效率。Luis Hernández-Callejo^[8]利用决策支持模型对电力设备进行检修和维护，提高了电网运行的效率。

目前，层次分析法被广泛应用在缺陷处理中。但是针对电力系统结构复杂、数据量大的问题，层次分析法也受到局限。本文将差分模型^[9]和k最邻近(k-nearest neighbor, kNN)^[10-12]算法应用到层次分析方法中，结合专家库^[13-14]进行自学习，推理出缺陷处理^[15-18]的方案，提高了缺陷处理的准确性。

1 消缺处理中的自学习方法 1.1 kNN文本分类算法

kNN是一种常用的分类算法，其核心内容为：文本信息以加权特征向量的方式作为测试文本，计算与各个训练文本的相似度，找到k个最相似的文本，根据加权距离的计算结果得到该文本所在的分类。具体步骤如下：

1)将测试文本转化成测试文本向量；

2)计算测试文本和各个训练文本的相似度，根据距离的大小顺序从小到大进行排序，找到距离最小的k个文本；

3)确定k个文本所在类的权重；

4)返回k个文本权重最大的类即为预测分类。

1.2 层次分析法

层次分析法是一种能够将复杂的决策信息按照一定的准则逐级分层，并进行定性和定量分析的决策方法。该方法无需大量的信息，即可有效地进行决策，在决策方面得到大量应用。分层模型如图1所示。

从图1可以看出，测试文本所在类别有A和B两类。当测试文本属于A类时，那么排除B类的影响，从第2层的A₁、A₂、A₃中寻找；进一步测试文本为A₁时，则排除A₂和A₃的影响，最后在第3层的A₁₁和A₁₂类中，找到测试文本所属的类别。传统方法需要逐一比较，耗费了大量的计算时间，而本文方法有效地提高计算效率。

1.3 差分模型

假设有A、B、C3个已知类别，测试文本m到3个类别的距离分别为a、b、c，当a=max{a,b,c}，b=max{b,c}，根据kNN方法，测试文本m则属于a类；根据分层思想，测试文本m再到a的子类中寻找，最后再按照kNN方法进行判断，得到所属类别；当采用差分模型的方法时，当且仅当|a|-|b|>n时，才能将测试文本m判别到a类中，否则在a和b的子类中再进行kNN算法，得到测试文本m最后的类别。

1.4 差分层次kNN算法

本文将kNN算法、层次分析法以及差分模型结合起来，得到差分层次kNN算法。改进后的算法能够综合各个算法的优点，并且能降低各个算法的缺点对缺陷处理的影响，算法的优势从以下几个方面进行阐述：

1)利用层次分析法构建层次结构。层次分析法无需大量的数据即可完成决策，解决了kNN算法因在计算过程中需要对所有文本进行计算的问题，降低了计算量，提高了计算效率。

2)差分比较。由于电力系统结构复杂，在缺陷处理方面存在类别交叉的问题，该算法能够避免经过权重比较后，直接判断测试文本所属类别的问题，能够正确判别最近邻和次近邻，提高了缺陷处理的可靠性。

3)自动添加新类别。由于电力系统数据信息较为复杂，信息量较为庞大，针对缺陷处置过程中无法给出具体的消缺方法，在算法结束的位置自动添加新类别。

2 差分层次kNN算法计算过程 2.1 算法流程

差分层次kNN算法的基本过程为：首先，文本信息以加权特征向量的方式作为测试文本；然后，利用层次分析法构建层次结构，计算每层测试文本与各个训练文本的相似度；接着，找到k个最相似的文本；最后，根据加权距离的计算结果进行差分比较，得到该文本所在的分类，算法过程结束。具体流程如下：

1)将测试文本转化成测试文本向量；

2)利用层次分析法，将训练文本集合进行分层，形成n层层次结构；

3)计算测试文本和1~n层各个训练文本的相似度，通过相似度计算公式计算相似度，第1层的计算方法如下

${\rm{si}}{{\rm{m}}_1}\left( {{{{d}}_i},{{{d}}_{1j}}} \right) = \frac{{\displaystyle\sum \limits_{k = 1}^M {W_{ik}} \times {W_{1jk}}}}{{\sqrt {\displaystyle \sum \limits_{k = 1}^M W_{ik}^2} \sqrt {\displaystyle \sum \limits_{k = 1}^M W_{1jk}^2} }}$

式中： ${{{d}}_i}$ 是测试文本向量； ${{{d}}_{1j}}$ 是第1层第 $j$ 类的中心向量； $M$ 是特征向量的维数； ${W_k}$ 则是特征向量的第 $k$ 维，一般采用一个初始值作为 $k$ 值，最后还是需要根据实验的结果来确定最终 $k$ 值的大小。

根据距离的大小顺序从小到大进行排序，找到距离最小的 $k$ 个文本。在距离最小的 $k$ 个文本中，计算各类别的权重：

${P_{1j}} = \displaystyle \sum \limits_{{d_i} \in {{L}}} {\rm{sim}}\left( {{{m}},{{{d}}_i}} \right)y\left( {{{{d}}_i},{C_j}} \right)$

式中：L代表所有测试文本向量的集合； ${{m}}$ 是测试文本的特征向量， ${\rm{sim}}\left( {{{m}},{{{d}}_i}} \right)$ 是相似度计算公式， $y\left( {{{{d}}_i},{{{C}}_j}} \right)$ 的值为0或1，当 ${{{d}}_i} \in {{{C}}_j}$ 时， $y\left( {{{{d}}_i},{{{C}}_j}} \right) = 1$ ，当 ${{{d}}_i} \notin {{{C}}_j}$ 时， $y\left( {{{{d}}_i},{{{C}}_j}} \right) = 0$ 。

对计算的权重进行排序：

${P_{11}} \geqslant {P_{12}} \geqslant {P_{13}} \geqslant \cdots \geqslant {P_{1j}} \geqslant \cdots $

利用差分模型对排序后的权重进行比较，具体方法如下。

①第1层差分公式：

${D_{12}} = {P_{11}} - {P_{12}}$

当 ${D_{12}} \geqslant {D_0}$ 时，此时的 ${D_0}$ 为阈值，则测试文本属于第1类，那么在第2层对相似度进行比较时，可排除其他类别的影响，只对第2层的第1类的子类进行比较；当 ${D_{12}} \leqslant {D_0}$ 时，则继续按照第2类、第3类等进行判断。

②第 $k$ 层差分公式：

${D_{k\left( {k + 1} \right)}} = {P_{1k}} - {P_{1\left( {k + 1} \right)}}$

当 ${D_{k\left( {k + 1} \right)}} \geqslant {D_0}$ 时，则测试文本属于第 $k$ 类，那么在第2层对相似度进行比较时，则可排除其他类别的影响，只对第2层的第 $k$ 类的子类进行比较；当 ${D_{k\left( {k + 1} \right)}} \leqslant {D_0}$ 时，则继续按照第 $k + 1$ 类、第 $k + 2$ 类等进行判断。

4)对第n层进行权重的差分比较后，如果比较的结果不唯一，还存在个别干扰性，则在第n层自动添加新类别；如果比较的结果唯一，则权重最大的类即为预测分类。

2.2 时间复杂度计算

根据差分层次kNN算法可知，计算过程中无需要将所有文本进行计算，只要对分层后该层次的子类进行计算，得到的算法复杂度^[19-20]为 $O\left( {n{\rm{log}}n} \right)$ ，而传统的kNN算法复杂度为 $O\left( {{n^2}} \right)$ ，本文方法大大降低了计算量，提高了运行效率。

3 应用实例

为了进一步验证本文方法在检修^[21-24]辅助决策系统的实用性和有效性，本文以某省电力公司的检修辅助决策系统为研究对象，将差分层次kNN算法应用到该系统中，通过系统的处理结果验证本文方法的实用价值。

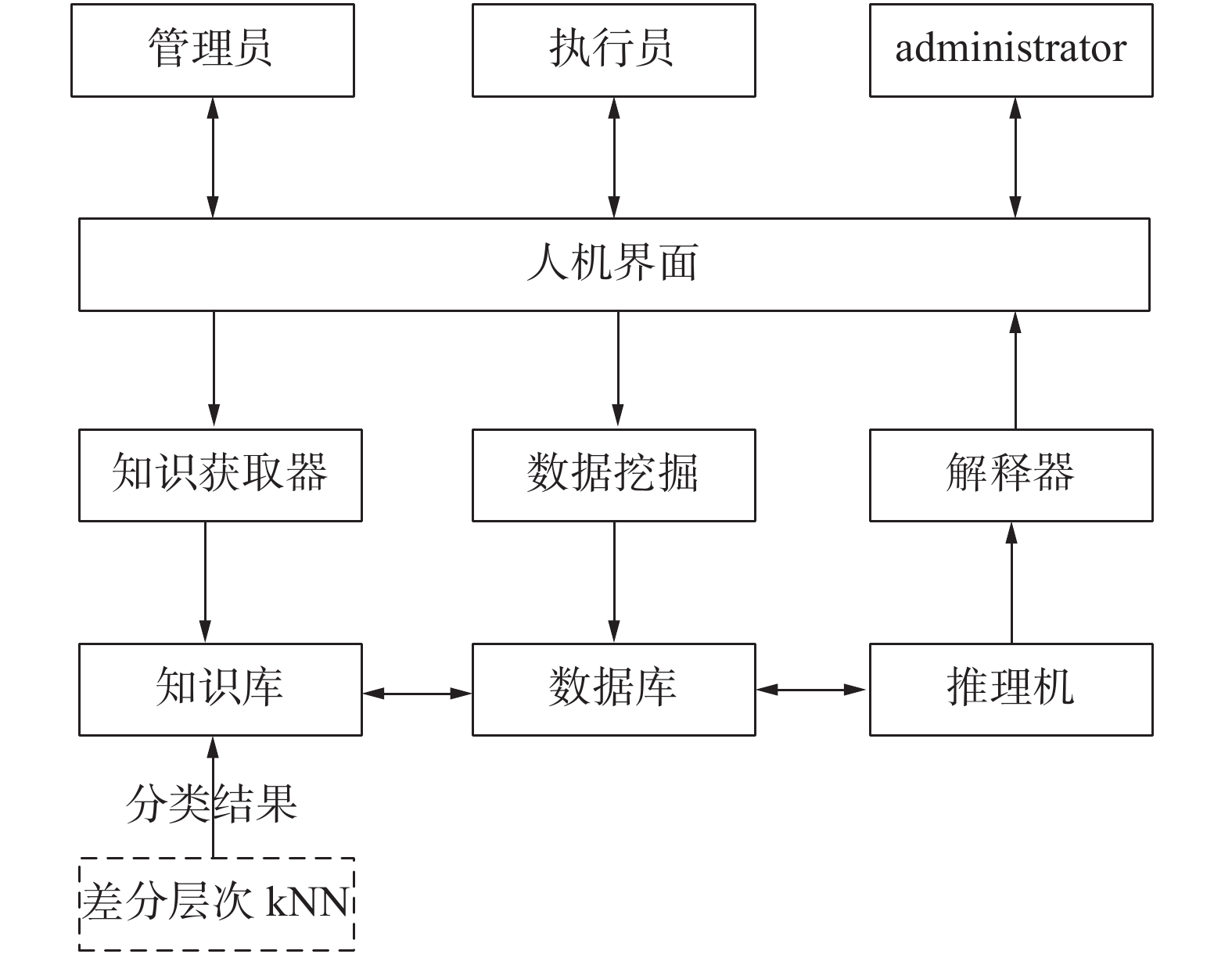
3.1 专家系统简介

在对缺陷数据进行处理和优化的基础上，构成能显示缺陷数据并且提供相应的缺陷处理方法的系统。该系统主要是知识工程师和领域专家通过获取器形成知识库，同时采用数据挖掘将信息存储到数据库中，用于匹配知识库中的条件，数据库内信息通过推理机到解释器，从而反馈到人机界面中。专家系统结构如图2所示。

系统具备常规的用户登录功能，管理员、执行员属于高级用户，administrator属于一般用户。高级用户权限较多，可对数据进行增、删、改、查等操作；一般用户只能进行基本操作。

3.2 差分层次kNN算法应用

根据差分层次kNN算法的缺陷处理模型，将每次分类的结果自动生成到知识库中，原有的知识库模板得到有效扩充，形成更新、更全面的知识库。自学习使通过差分层次kNN方法得到的分类结果自动扩充到知识库这一过程得以体现。

在检修辅助决策系统的专家库基础上，根据缺陷信息，提供详细分析结果和处理方法，提高了缺陷处理的准确性和智能性。

4 实验及结果分析

实验1　将缺陷信息形成数据集，分成6组进行测试，实验对比模型采用传统的动态时间归整(dynamic time warping，DTW)算法、最小方差匹配(minimal variance matching, MVM)算法和层次分析算法，通过对准确率进行对比，验证本文方法的有效性。其中，准确率为分类的正确文本数与实际分类文本数的比值。实验结果如表1所示。

从表1的6组实验结果可以看出，DTW算法的准确率在0.65~0.72，MVM算法的准确率在0.64~0.77，AHP算法的准确率在0.64~0.66，而本文提出的差分层次kNN算法的准确率在0.76~0.93，并且每组实验中，本文提出的方法的准确率都比DTW、MVM和AHP算法的准确率有显著提高，证明本文方法能够有效提高缺陷处理的准确性。

实验2　将数据集分成3组，采用本文提出的方法和kNN方法进行对比，计算分类所用时间，实验结果如表2所示。

从表2可以看出，第1组实验中，本文提出的查分层次kNN算法所用时间缩短了990 s；第2组实验中，本文提出算法所用时间缩短了1 230 s，接近kNN算法时间的一半；第3组实验中，本文所提算法所用时间缩短了822 s。可以看出本文算法所用时间明显缩短，能够快速对缺陷进行分类。

以220 kV母联智能终端与220 kV主变保护装置支架goose断链为例，系统给出相应的定位、建议以及影响范围，验证了方法的可行性。该系统缺陷处理的结果如图3所示。

5 结论

为了解决电力系统结构复杂、数据量过多问题，本文提出一种基于差分层次kNN算法。为了验证本文算法的有效性，开展准确率实验和分类所需时间实验，得到以下结论：

1)与层次分析算法相比，本文方法避免了缺陷处理中不能为决策提供新方案和权重难以确定等问题；通过与DTW算法、MVM算法和AHP算法的准确率进行对比，本文方法能够有效提高缺陷处理的准确性。

2)与kNN方法进行对比，本文方法能够有效缩短分类所需时间，降低了时间复杂度，提高了缺陷处理的效率。