近几年,NAND闪存因为其高存储容量、快速读写、非易失性、低成本以及体积小等优点,被广泛应用于各类电子产品和数据存储中心。随着闪存工艺水平的发展,闪存芯片的尺寸由早期的50 nm缩减到20 nm以下,使得闪存密度显著增大,相邻闪存单元距离越来越近,单元间干扰加剧[1-4]。同时,闪存在使用过程中存在不同程度的磨损,氧化层的绝缘性降低导致电子泄露从而引起持久性噪声,使得存储单元的阈值电压随时间向较低状态偏移[5-8],闪存的数据可靠性和使用寿命都不同程度降低。为了提高MLC闪存的传输完整性,可对信号进行数据后补偿或数字预失真的信号处理方式。其中,Adnan[8]利用闪存持久性噪声的特点对第一次译码错误的比特置信度进行修正,并重新译码。另一种算法[9]通过大量的译码数据样本找出更为准确的阈值量化电压。然而,这2种算法复杂度高,鉴于此,本文利用闪存读取顺序和编程顺序之间的关系,通过相邻字线低页的译码信息来辅助改善高页的纠错性能,并利用译码过程中校验信息与置信度的关系来辅助改善低页的纠错性能。
1 信道模型MLC闪存信道的建模如图1所示,数据先通过擦除与编程操作写入存储单元。不失一般性,闪存信道的干扰主要包括随机电报噪声[10-11]、持久性噪声和单元间干扰。

|
Download:
|
| 图 1 MLC闪存信道模型 | |
由于闪存的物理结构,不能直接改变闪存单元内的电子数量来完成编程,因此需要对整个闪存块进行擦除操作,再进行编程操作。处于擦除状态与编程状态下的阈值电压均服从高斯分布。
擦除状态下阈值电压概率密度函数为
| ${P_e}(v) = \frac{1}{{{\sigma _e}\sqrt {2{\rm{{\text{π}} }}} }}{{\rm{e}}^{ - \frac{{{{(v -{\mu_{_e}})}^2}}}{{2_{\sigma _e^2}}}}} = N({\mu _e},\sigma _e^2)$ |
编程状态下阈值电压概率密度函数为
| ${P_p}(v) = \frac{1}{{{\sigma _p}\sqrt {{\rm{2{\text{π}} }}} }}{{\rm{e}}^{ - \frac{{{{(v - {\mu _{_p}})}^2}}}{{2\sigma _p^2}}}} = N({\mu _p},\sigma _p^2)$ |
式中:
当前闪存采用的编程顺序为坡度编程顺序[5,12-13],如图2所示。对每个字线(记为WL i)的高页(记为MSB)与低页(记为LSB)都进行编号,并按编号从小到大的顺序进行编程。除了WL 0对应的LSB的编号为0和最后的字线WL n对应的MSB的编号为2n+1,WL i对应的LSB的编号为2i−1,对应的MSB的编号为2i+2。
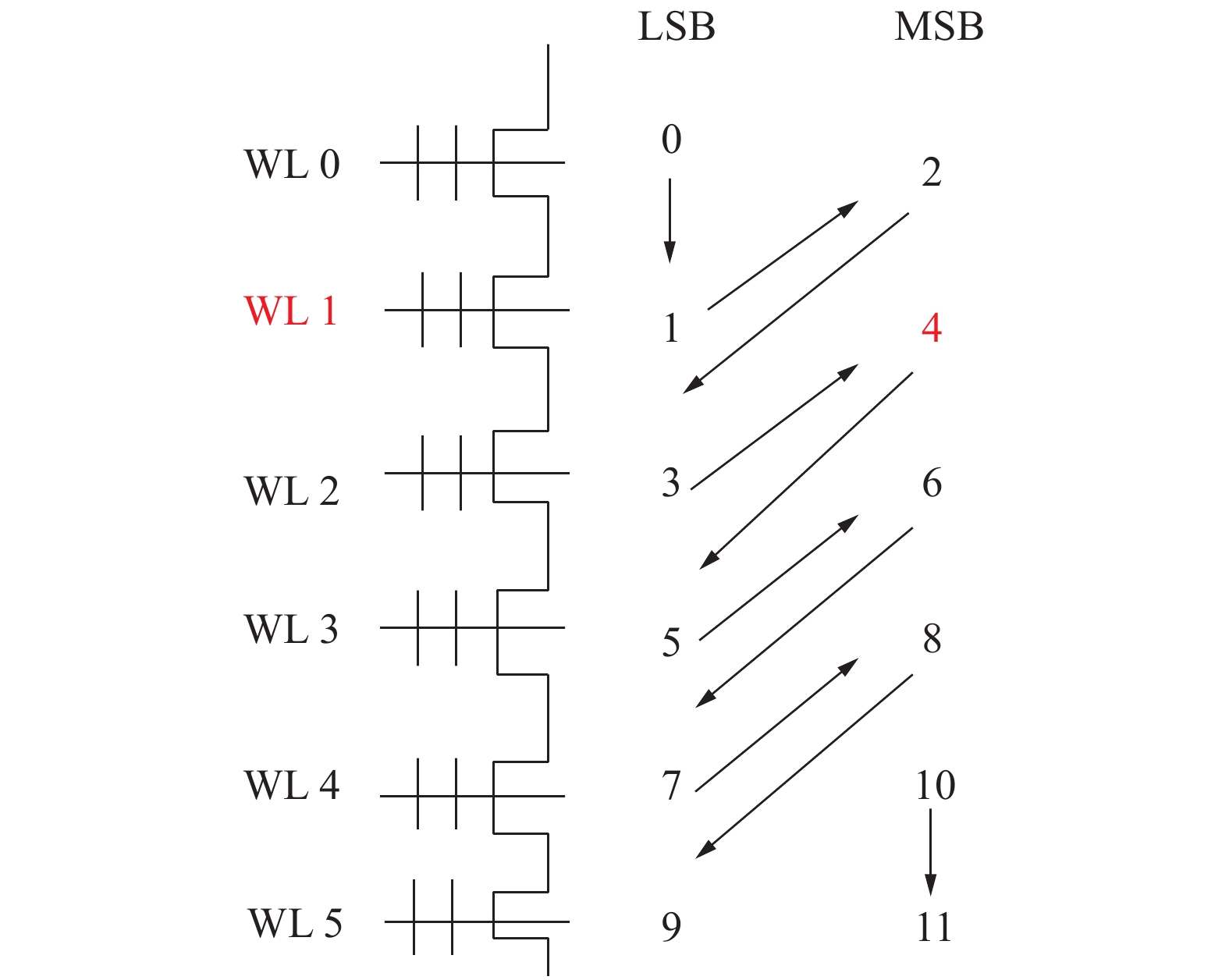
|
Download:
|
| 图 2 编程顺序 | |
随着编程和擦除次数的增加,干扰也会增加,导致阈值电压向两侧漂移,随机电报噪声服从指数分布,其概率密度函数为
| ${P_{{\rm{RTN}}}}(v) = \frac{1}{{2\lambda }}{{\rm{e}}^{ - \frac{{\left| v \right|}}{\lambda }}} = N(0,\sigma _r^2)$ |
式中:
闪存氧化层的绝缘性能会随着PE的增加而降低,使得电子泄露得更快,导致阈值电压向左偏移。持久性噪声服从高斯分布,其概率密度函数如下:
| ${P_e}(v) = \frac{1}{{{\sigma _e}\sqrt {2{\rm{{\text{π}} }}} }}{{\rm{e}}^{ - \frac{{{{(v - {\mu _{_e}})}^2}}}{{2\sigma _e^2}}}} = N({\mu _e},\sigma _e^2)$ |
式中:
当闪存结构为干扰较小的全位线结构时,由于相邻闪存单元间寄生电容耦合效应,如图3所示。因此,单元间干扰可用每个闪存单元的阈值电压变化量的线性组合来表示:
| $\Delta {V_{{\rm{CCI}}}} = \sum\limits_n {(\Delta {V^{(n)}} \times {\gamma ^{(n)}})} $ |
式中

|
Download:
|
| 图 3 全位线结构下的单元间干扰示意 | |
阈值电压的条件概率分布函数在受到随机电报噪声、持久性噪声和单元间干扰后的数学表达式为
| $\begin{array}{l} p({V_{{\rm{th}}}}|k \in \{ 11,01,00,01\} ) = \dfrac{{\rm{1}}}{{{\rm{64}}}}[N({\mu _k} - \\ \;\;\;\;\;\;\;\;\;{\mu _t},\sigma _k^2 + \sigma _t^2 + \sigma _r^2) + A + B + C] \end{array}$ |
| $\begin{array}{c} A = \displaystyle\sum\limits_{{\mu _p}} [ 2N({\gamma _{xy}}({\mu _p} - {\mu _e}) + {\mu _k} - {\mu _t},\gamma _{xy}^2(\sigma _p^2 + \\ \sigma _e^2 + 2\sigma _r^2) + \sigma _k^2 + \sigma _t^2) + N({\gamma _y}({\mu _p} - {\mu _e}) + \\ {\mu _k} - {\mu _t},\gamma _y^2(\sigma _p^2 + \sigma _e^2 + 2\sigma _r^2) + \sigma _k^2 + \sigma _t^2)], \end{array}$ |
| $\begin{array}{c} B = \displaystyle\sum\limits_{\mu _p^{(1)}} {\displaystyle\sum\limits_{\mu _p^{(2)}} {\displaystyle\sum\limits_{\mu _p^{(3)}} N } } ({\gamma _{xy}}(\mu _p^{(1)} + \mu _p^{(2)}) - 2{\mu _e}) + \\ {\gamma _y}(\mu _p^{(2)} - {\mu _e}) + {\mu _k} - {\mu _t},(2\gamma _{xy}^2 + \gamma _y^2) \cdot \\ (\sigma _p^2 + \sigma _e^2 + 2\sigma _r^2) + \sigma _k^2 + \sigma _t^2) \end{array} $ |
| $\begin{array}{c} C = \displaystyle\sum\limits_{\mu _p^{(1)}} {\displaystyle\sum\limits_{\mu _p^{(2)}} N } ({\gamma _{xy}}(\mu _p^{(1)} - {\mu _e}) + {\gamma _y}(\mu _p^{(2)} - {\mu _e}) + \\ {\mu _k} - {\mu _t},(\gamma _{xy}^2 + \gamma _y^2)(\sigma _p^2 + \sigma _e^2 + 2\sigma _r^2 + \sigma _k^2 + \sigma _t^2)) + \\ \sigma _t^2\displaystyle\sum\limits_{\mu _p^{(2)}} {\displaystyle\sum\limits_{\mu _p^{(3)}} N } ({\gamma _{xy}}(\mu _p^{(3)} - {\mu _e}) + {\gamma _y}(\mu _p^{(2)} - {\mu _e}) + \\ {\mu _k} - {\mu _t},(\gamma _{xy}^2 + \gamma _y^2)(\sigma _p^2 + \sigma _e^2 + 2\sigma _r^2) + \sigma _k^2 + \sigma _t^2) + \\ \displaystyle\sum\limits_{\mu _p^{(1)}} {\displaystyle\sum\limits_{\mu _p^{(3)}} N } ({\gamma _{xy}}(\mu _p^{(1)} + \mu _p^{(2)} - 2{\mu _e}) + {\mu _k} - \\ {\mu _t},2\gamma _{xy}^2(\sigma _p^2 + \sigma _e^2 + 2\sigma _r^2) + \sigma _k^2 + \sigma _t^2) \end{array} $ |
式中:
闪存信道参数设置如下:
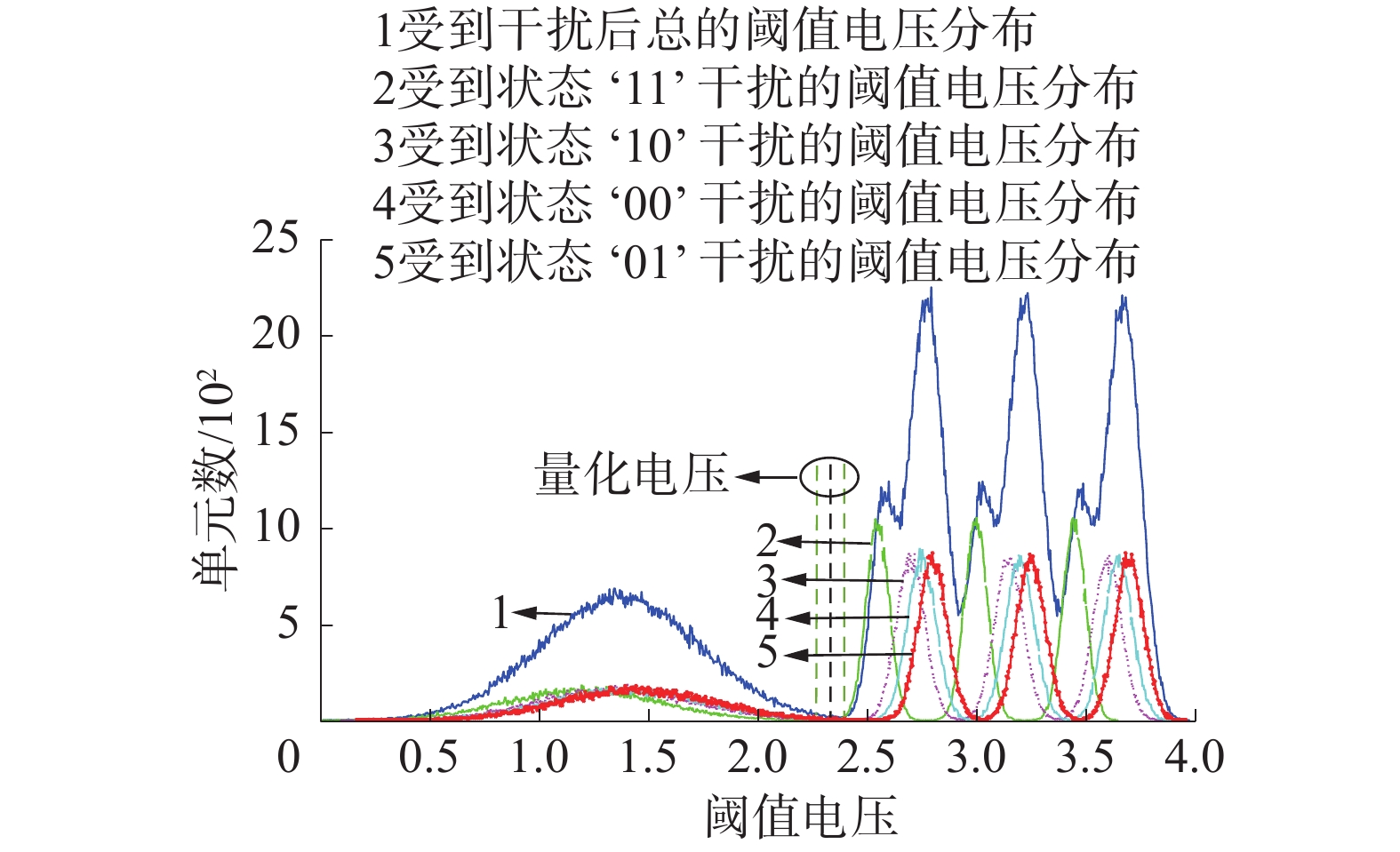
图4是MLC闪存信道在单元间干扰下的阈值电压分布图。状态‘11’为擦除状态,不对相邻单元产生单元间干扰;状态‘10’、‘00’和‘01’为编程状态,会对相邻单元造成单元间干扰,因此大部分闪存单元会受到单元间干扰,阈值电压向右移。
|
Download:
|
|
图 4 MLC闪存信道在单元间干扰下的阈值电压分布(
|
|
如图4所示,状态‘11’与‘10’的重叠区设有3个量化电压,同样地,状态‘10’与‘00’的重叠区和状态‘00’与‘01’的重叠区也设有3个量化电压,共9个量化电压
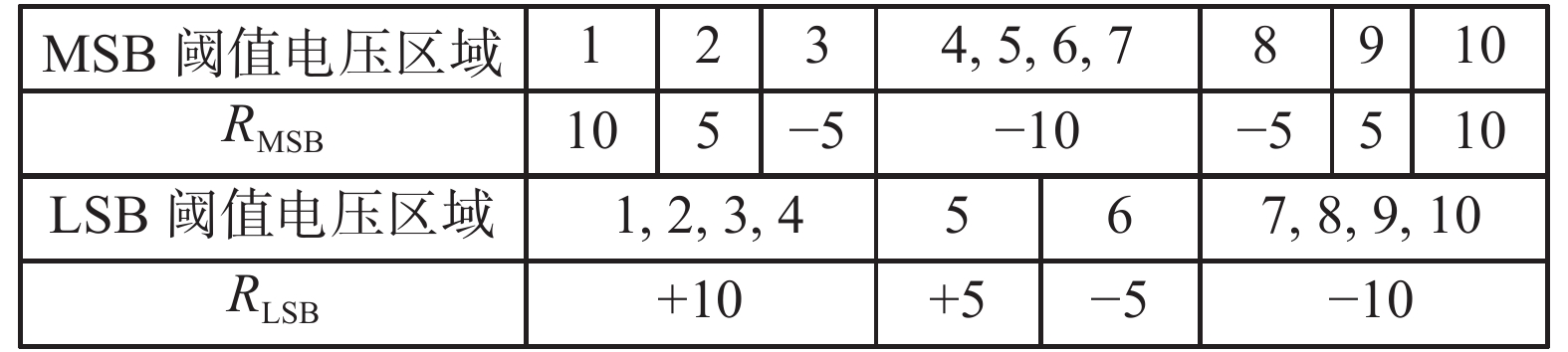
存储单元上不同页的错误概率是不平衡的,通常高页(记为MSB)的错误概率比低页(记为LSB)的错误概率高,同一个存储单元上的2个比特的可靠性不同[2],并用置信度信息表示比特的可靠性,作为译码时的初始化信息。为了减少计算复杂度,定义MSB与LSB的置信度(可靠度)信息为
|
Download:
|
| 图 5 MSB和LSB的置信度信息赋值 | |
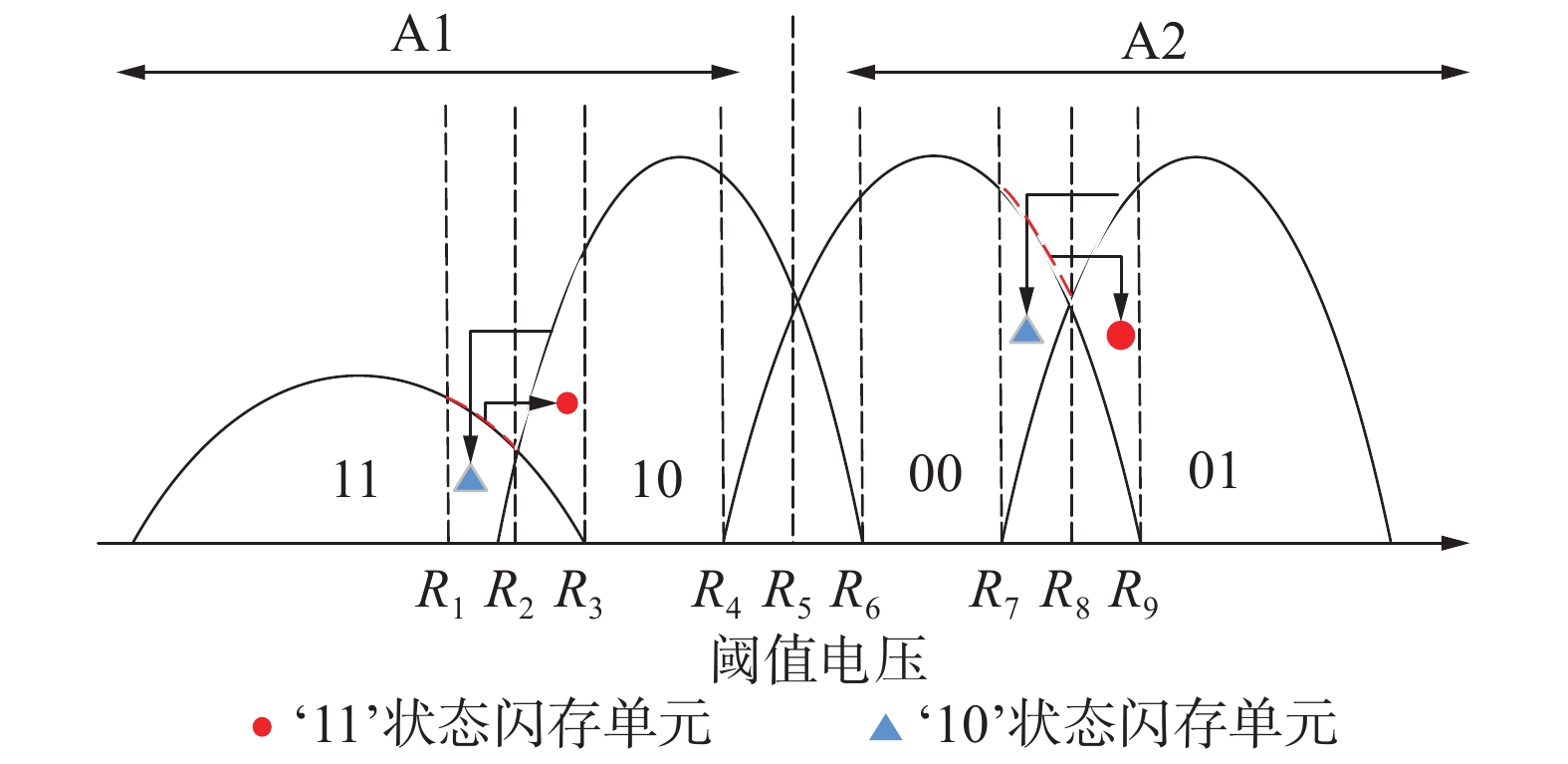
闪存在相同干扰下通过阈值量化电压对整体阈值电压进行量化,并不能确保该量化电压满足闪存每一字线的阈值电压量化,存在量化电压补偿不足和过渡补偿的可能。如图6所示。当阈值电压右移严重时,量化电压会出现补偿不足的情况,使得圆形标注的闪存单元在阈值电压量化后为‘10’状态的单元,因此其置信度信息赋值为
|
Download:
|
| 图 6 MLC闪存信道高页重叠区置信度错误分析 | |
根据闪存的读取机制[4,13-14],可同时读取到WL i的MSB和LSB,由图2可知,在WL i的MSB编程前,WL i+1的LSB已完成编程。因此,当读取到WL i的MSB时,结合闪存的编程顺序可读取到WL i的LSB(记为LLSB)和WL i+1的LSB(记为NLSB),则译码错误的MSB可利用LLSB和NLSB的译码信息。
首先找到译码失败的MSB重叠区中的闪存单元在码字中的位置U。若译码错误的MSB读取到的LLSB和NLSB都译码正确,说明LLSB和NLSB的译码信息可靠。则译码失败的MSB可利用译码成功的LLSB和NLSB在位置U上的比特值来确定MSB重叠区中置信度赋值错误的比特位,并纠正其置信度信息。比如,当
算法1 利用相邻低页信息辅助修正高页
1)若MSB译码失败,LLSB和NLSB都没有译码成功,则执行步骤5)。
2)读取LLSB和NLSB在译码后的比特信息,并分别记为
3)读取并更新MSB重叠区中错误比特的自信度信息:
if
end
if
end
if
end
if
end
4)该译码错误的MSB页重新BP译码。
5)结束。
算法1的延伸:在译码错误的MSB读取到的LLSB和NLSB中,会出现只有一个译码成功的情况,则此LLSB和NLSB并不完全可靠,在位置U上的比特值未必正确。而阈值电压区域对应的置信度信息表示该阈值电压区域的可靠性,因此可判断LLSB和NLSB在位置U上的置信度信息是否可靠,若可靠则表明LLSB和NLSB在位置U上的比特信息可靠。由已发表的大量文献[15-18]可知,LSB只有一个状态重叠区,相比LSB其他区域的可靠度要低很多。如果LLSB或NLSB在位置U上的置信度信息是LSB在状态重叠区的置信度信息,则LLSB和NLSB在位置U上的比特信息不可靠,若
由于在算法1中,找出MSB状态重叠区置信度信息赋值错误的比特需要借助LLSB和NLSB的译码信息,若LLSB和NLSB译码失败会影响MSB的修正,所以需要提高LSB的纠错性能。
在状态‘10’和状态‘00’的重叠区中,存在着少量LSB可靠性低的变量节点
| $m_{{c_i} \to {v_j}}^k = 2{\tanh ^{ - 1}}\Bigg(\prod\limits_{{v_f} \in N({c_i})\backslash {v_j}} {\tanh \Bigg(\frac{1}{2}m_{_{{v_f} \to {c_i}}}^{k{\rm{ - 1}}}\Bigg)} \Bigg)$ | (1) |
| ${\rm{ }}m_{{v_j} \to {c_i}}^k = R({v_j}) + \sum\limits_{{c_g} \in M({v_j})\backslash {c_i}} {m_{_{{c_g} \to {v_j}}}^k} $ | (2) |
| $ m_{{v_j}}^k = R({v_j}) + \sum\limits_{{c_i} \in M({v_j})} {m_{{c_g} \to {v_j}}^k} $ | (3) |
| $c = \left\{ \begin{array}{l} 1,\;\;\;\;m_{_{{v_j}}}^k < 0\\ 0,\;\;\;\;m_{_{{v_j}}}^k > 0 \end{array} \right.$ | (4) |
式中:k表示当前译码次数;
由式(1)~(4)可知,可靠性低的变量节点有可能会影响到可靠性高的变量节点总信息的计算及其向外传递信息的可靠性,从而影响硬判决,导致可靠性高的比特翻转。在闪存信道内,LSB的变量节点
|
|
表 1 BP译码算法和无译码下‘11’和‘01’的总比特错误量 |
对LSB的变量节点
| $c({v_i} \in {\rm{flag}}({\rm{1,10}})) = \left\{ {\begin{array}{*{20}{c}} {\begin{array}{*{20}{c}} \!\!\!\!\!\! {1,}&{{R_{{\rm{LSB}}}}({v_i} \in {\rm{flag}}(1,10)) < 0} \end{array}} \\ {\begin{array}{*{20}{c}} \!\!\!\!\!\! {0,}&{{R_{{\rm{LSB}}}}({v_i} \in {\rm{flag}}(1,10)) > 0} \end{array}} \end{array}} \right.$ |
经过BP译码后,LSB的变量节点
| $\left\{ {\begin{array}{*{20}{c}} {m_{{v_j}}^k > 0,}&{{R_{{\rm{LSB}}}}({{\rm{v}}_j} \in {\rm{flag}}(1,10)) < 0} \\ {m_{{v_j}}^k < 0,}&{{R_{{\rm{LSB}}}}({{\rm{v}}_j} \in {\rm{flag}}(1,10)) > 0} \end{array}} \right.$ |
因此根据式(3),可得出该错误比特的总信息与校验信息的正负关系为
| $\left\{ {\begin{array}{*{20}{c}} {m_{{v_j}}^k > 0,}&{\displaystyle\sum\limits_{{c_i} \in M({v_j})} {m_{{c_i} \to {v_j}}^k} > 0} \\ {m_{{v_j}}^k < 0,}&{\displaystyle\sum\limits_{{c_i} \in M({v_j})} {m_{{c_i} \to {v_j}}^k} < 0} \end{array}} \right.$ |
所以该错误比特的置信度与校验信息的正负关系是
| $\left\{ {\begin{array}{*{20}{c}} {\displaystyle\sum\limits_{{c_i} \in M({v_j})} {m_{{c_i} \to {v_j}}^k} > 0,}&{{R_{{\rm{LSB}}}}({v_i} \in {\rm{flag}}(1,10)) < 0} \\ {\displaystyle\sum\limits_{{c_i} \in M({v_j})} {m_{{c_i} \to {v_j}}^k} < 0,}&{{R_{{\rm{LSB}}}}({v_i} \in {\rm{flag}}(1,10)) > 0} \end{array}} \right.$ |
因此可通过
由以上推导可知,可靠性高的比特会因接收到可靠性低的校验信息而发生翻转,因此对校验信息增加可靠性权重a。为了去除可靠性低的校验信息对可靠性高的比特造成影响,令a=0;若校验信息可靠则保留,令a =1。具体过程如算法2所示。
算法2 增加LSB加权可靠度
1)初始化所有变量节点,
2)更新校验节点,计算式(1)。
3)更新变量节点,计算码字总信息。
if
更新式(2)变量节点,计算式(3)码字总信息。
else 计算式(3),并计算校正信息可靠性权重:
| ${a_{ij}} = \left\{ {\begin{array}{*{20}{c}} {\begin{array}{*{20}{c}} \!\!\!\!\!\!{0,}&{\displaystyle\sum\limits_{{c_{\rm{i}}} \in M({v_j})} {m_{{c_i} \to {v_j}}^k} \times {R_{{\rm{LSB}}}}(v_{_j}^k)} \end{array} < 0} \\ {\begin{array}{*{20}{c}} \!\!\!\!\!\! {1,}&{\displaystyle\sum\limits_{{c_i} \in M({v_j})} {m_{{c_i} \to {v_j}}^k} \times {R_{{\rm{LSB}}}}(v_{_j}^k)} \end{array} > 0} \end{array}} \right.$ |
更新变量节点:
| $m_{{v_j} \to {c_i}}^k = {R_{{\rm{LSB}}}}({v_j}) + \sum\limits_{{c_g} \in M({v_j})\backslash {c_i}} {{a_{gj}}m_{_{{c_g} \to {v_j}}}^k} $ |
计算码字总信息:
| $m_{{v_j}_i}^k = {R_{{\rm{LSB}}}}({v_j}) + \sum\limits_{{c_{\rm{i}}} \in M({v_j})} {{a_{ij}}m_{_{{c_i} \to {v_j}}}^k} $ |
end
4)硬判决式(4)。
5)若满足
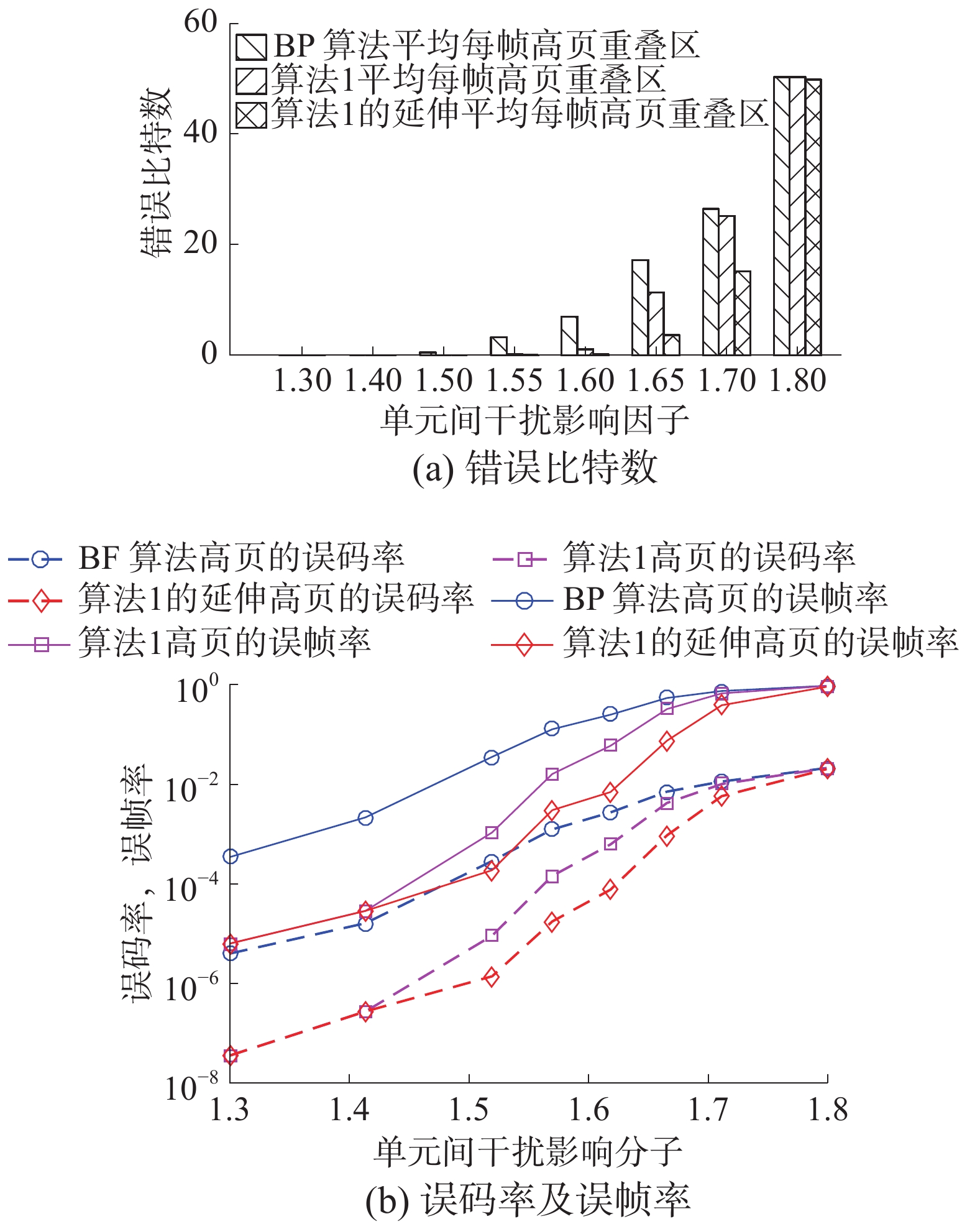
本实验仿真是在MATLAB平台上实现,所有算法都基于传统并行BP译码算法上进行改进,在每一算法中MSB和LSB同时参与译码,参数
|
Download:
|
| 图 7 BP算法和算法1及其延伸算法性能分析 | |
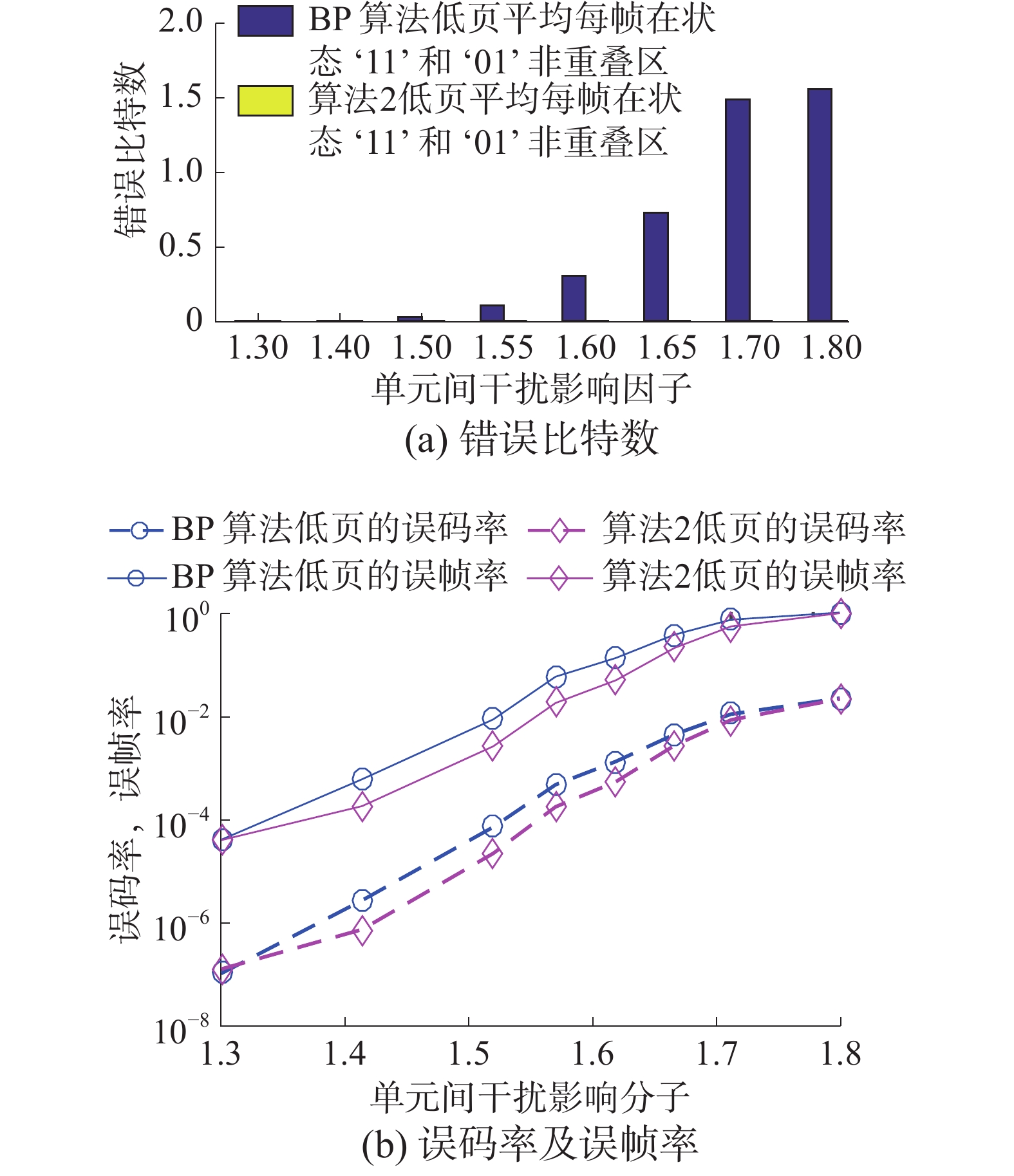
图8表示在不同的单元间干扰影响因子s下,状态‘11’和状态‘01’在LSB非重叠区下的错误比特数,以及LSB的误码率和误帧率在传统BP译码算法和算法2下的比较。可见LSB中变量节点
|
Download:
|
| 图 8 BP算法和算法2性能分析 | |
根据高密度NAND闪存数据的写入与读取机制,以及高低页比特之间的关联关系,提出了一种融合相邻单元高低页存储可靠性的BP译码算法。
1)算法1利用读取顺序与编程顺序之间的关系,通过相邻字线的译码信息来辅助改善高页的纠错性能。由于算法1性能的改进需通过相邻字线,因此提出算法2来改善相邻字线的纠错性能。
2)算法2利用了可靠性较高的比特位上的总信息求和,对该比特位接收到的校验信息增加可靠性权重,保证可靠性较高的比特位向外传递信息的可靠性,并防止可靠性较高的比特位翻转。理论分析以及数据的仿真表明该算法能够有效提高纠错性能。
| [1] |
CAI Yu, HARATSCH E F, MUTLU O, et al. Error patterns in MLC NAND flash memory: measurement, characterization, and analysis[C]//Proceedings of the Design, Automation & Test in Europe Conference & Exhibition (DATE). Dresden, German. 2012: 521–526.
( 0) 0)
|
| [2] |
CAI Yu, GHOSE S, HARATSCH E F, et al. Error characterization, mitigation, and recovery in flash-memory-based solid-state drives[J]. Proceedings of the IEEE, 2017, 105(9): 1666-1704. DOI:10.1109/JPROC.2017.2713127 ( 0) 0)
|
| [3] |
DONG Guiqiang, XIE Ningde, ZHANG Tong. On the use of soft-decision error-correction codes in NAND flash memory[J]. IEEE transactions on circuits and systems I: regular papers, 2011, 58(2): 429-439. DOI:10.1109/TCSI.2010.2071990 ( 0) 0)
|
| [4] |
PENG Zishuai, HE Ruiquan, HAN Guojun, et al. Neighbor a-posteriori information assisted cell-state adaptive detector for NAND flash memory[J]. IEEE communications letters, 2019, 23(11): 1967-1971. DOI:10.1109/LCOMM.2019.2936342 ( 0) 0)
|
| [5] |
CAI Yu, LUO Yixin, HARATSCH E F, et al. Data retention in MLC NAND flash memory: characterization, optimization, and recovery[C]//Proceedings of the IEEE 21st International Symposium on High Performance Computer Architecture (HPCA). Burlingame, USA, 2015: 551–563.
( 0) 0)
|
| [6] |
CAI Yu, YALCIN G, MUTLU O, et al. Flash correct and refresh: retention-aware error management for increased flash memory lifetime[C]//Proceedings of the IEEE 30th International Conference on Computer Design (ICCD). Montreal, Canada, 2012: 94–101.
( 0) 0)
|
| [7] |
MIZOGUCHI K, TAKAHASHI T, ARITOME S, et al. Data-retention characteristics comparison of 2D and 3D TLC NAND flash memories[C]//Proceedings of the IEEE International Memory Workshop (IMW). Monterey, USA, 2017: 1–4.
( 0) 0)
|
| [8] |
ASLAM C A, GUAN Yongliang, CAI Kui. Decision-directed retention-failure recovery with channel update for MLC NAND flash memory[J]. IEEE transactions on circuits and systems I: regular papers, 2018, 65(1): 353-365. DOI:10.1109/TCSI.2017.2714902 ( 0) 0)
|
| [9] |
FAN Zhengqin, CAI Guofa, HAN Guojun, et al. Cell state- distribution-assisted threshold voltage detector for NAND Flash memory[J]. IEEE communications letters, 2019, 23(4): 576-579. DOI:10.1109/LCOMM.2019.2900677 ( 0) 0)
|
| [10] |
DONG Guiqiang, XIE Ningde, ZHANG Tong. Enabling NAND flash memory use soft-decision error correction codes at minimal read latency overhead[J]. IEEE transactions on circuits and systems I: regular papers, 2013, 60(9): 2412-2421. DOI:10.1109/TCSI.2013.2244361 ( 0) 0)
|
| [11] |
RAY B, MILENKOVIC A. True random number generation using read noise of flash memory cells[J]. IEEE transactions on electron devices, 2018, 65(3): 963-969. DOI:10.1109/TED.2018.2792436 ( 0) 0)
|
| [12] |
CAI Yu, GHOSE S, LUO Yixin, et al. Vulnerabilities in MLC NAND flash memory programming: experimental analysis, exploits, and mitigation technique[C]//Proceedings of the IEEE International Symposium on High Performance Computer Architecture (HPCA). Austin, USA, 2017: 49–60.
( 0) 0)
|
| [13] |
SUN Hongbin, ZHAO Wenzhe, LYU Minjie, et al. Exploiting intracell bit-error characteristics to improve min-sum LDPC decoding for MLC NAND flash-based storage in mobile device[J]. IEEE transactions on very large scale integration systems, 2016, 24(8): 2654-2664. DOI:10.1109/TVLSI.2016.2535224 ( 0) 0)
|
| [14] |
ZHANG Meng, WU Fei, DU Yajuan, et al. Pair-bit errors aware LDPC decoding in MLC NAND flash memory[J]. IEEE transactions on computer-aided design of integrated circuits and systems, 2019, 38(12): 2312-2320. DOI:10.1109/TCAD.2018.2878132 ( 0) 0)
|
| [15] |
ASLAM C A, GUAN Yongliang, CAI Kui. Low-complexity quantization-aware belief-propagation (QA-BP) decoding for MLC NAND flash memory[C]//Proceedings of the 10th International Conference on Information, Communications and Signal Processing (ICICS). Singapore, 2015: 1–5.
( 0) 0)
|
| [16] |
LIU Xingcheng, YANG Guoguan, CHEN Xuechen. Variable-node-based belief-propagation decoding with message pre-processing for NAND flash memory[J]. IEEE access, 2019, 7: 58638-58653. DOI:10.1109/ACCESS.2019.2914076 ( 0) 0)
|
| [17] |
GUO Ting, LIU Xingcheng. A low latency decoding algorithm for grouping variable nodes on TLC NAND flash devices[C]//Proceedings of the IEEE International Conference on Electron Devices and Solid-State Circuits (EDSSC). Xi'an, China, 2019: 1–3.
( 0) 0)
|
| [18] |
WEI Kang, LI Jun, KONG Lingjun, et al. Page-based dynamic partitioning scheduling for LDPC decoding in MLC NAND flash memory[J]. IEEE transactions on circuits and systems II: express briefs, 2019, 66(12): 2082-2086. DOI:10.1109/TCSII.2019.2897223 ( 0) 0)
|
| [19] |
KSCHISCHANG F R, FREY B J, LOELIGER H. Factor graphs and the sum-product algorithm[J]. IEEE transactions on information theory, 2001, 47(2): 498-519. DOI:10.1109/18.910572 ( 0) 0)
|
| [20] |
BEEMANN M, SCHMALEN L, VARY P. Improved decoding of binary and non-binary LDPC codes by probabilistic shuffled belief propagation[C]//Proceedings of the IEEE International Conference on Communications (ICC). Kyoto, Japan, 2011: 1–5.
( 0) 0)
|
 2020, Vol. 47
2020, Vol. 47


