海洋立管是指用于连接水面浮体和海床井口的隔水套管系统，是深海生产系统中最复杂的一类设备。非粘结柔性立管是由柔性管发展而来的，是一种多层复合壁管，各层管壁采用不同的材料制成，且在承受外部或内部载荷时，各层管壁相互间能够发生轻微的滑动，因此具有较低的弯曲刚度。因为柔性立管具有顺应性强、便于安装与回收、设计空间很大等优点，在深海中得到了广泛的应用。非粘结柔性立管常由多层不同的结构组成^[1-2]。柔性立管所处的环境复杂，需要对于柔性管在各种荷载作用下进行分析研究，以保证立管的安全可靠。

针对柔性立管的截面静力分析，国内外学者展开了大量的研究。Felippe等^[3]和Chung等^[4]利用可以产生轴向变形、弯曲变形和扭转变形的三维梁单元来模拟管道模型，分析得出了海洋立管静态下的非线性平行构型方程。Witz等^[5]和Tan等^[6]推导出了柔性管在弯曲荷载下的临界曲率以及螺旋条带的曲率表达式，以及柔性立管在未滑移阶段和完全滑移阶段的弯曲刚度。任少飞等^[7-8]、陆钰天^[9]和陈耕^[10]根据最小势能原理推导出多层柔性立管的整体刚度矩阵。Yoo等^[11]考虑了柔性立管的非线性特性，使用整体刚度矩阵，计算了柔性立管的抗拉刚度。董磊磊等^[12]基于能量法推导出了柔性立管结构分析模型。郭有松等^[13]和陈希恰^[14]基于静力平衡、变形协调、本构关系和层间接触关系，推导出了柔性立管轴对称响应的理论模型。裴晓梅等^[15]推导了柔性立管的整体抗拉刚度和抗扭刚度计算公式。

本文基于最小势能原理推导出了柔性立管各层的刚度矩阵，并叠加得到整体刚度矩阵。使用罚函数的方法引入层间接触，并建立接触的刚度矩阵，加到整体刚度矩阵上得到考虑层间接触的柔性立管整体刚度矩阵。然后使用该矩阵计算非粘结柔性立管在拉伸、内压以及扭转作用下的变形响应。并将结果与有限元软件计算结果进行对比。

1 理论模型

根据非粘结柔性立管在在轴对称荷载作用下的力学性能研究，可以将将柔性管分为2个基本构件：圆柱层和螺旋层。螺旋层包括抗拉铠装层、抗压铠装层、骨架层，其主要为金属材料，为立管提供轴向和径向刚度。圆柱层包括防磨层、防渗漏层等，主其要材质为聚合物，为立管提供密闭性，减小层间摩擦损伤。各层之间采用非粘结的接触方式连接。典型非粘结柔性立管结构如图1所示。

为了便于推导，本文假设：

1)柔性管具有较大的轴向和径向刚度，所以各层变形均为小变形；

2)模型中的材料视为线弹性且各向同性；

3)柔性管各层的轴向变换量和绕轴向扭转角度相同。

1.1 螺旋层刚度矩阵

螺旋条带在轴对称荷载作用下可能发生轴向应变、径向应变以及弯曲和扭转变形^[9]。

1.1.1 螺旋铠装层条带的轴向和径向应变

抗拉铠装层以30°为主的角度缠绕而成，多为矩形截面，如图2所示。柔性立管长度为L；螺旋铠装层半径为R；缠绕角度为 $\alpha $ 。

螺旋条带的轴向应变为^[7-10]

$ {\varepsilon _1}{\rm{ = co}}{{\rm{s}}^2}\alpha \cdot \frac{{{\mu _Z}}}{L} + {\sin ^2}\alpha \cdot \frac{{{\mu _R}}}{R} + R\sin \alpha \cos \alpha \cdot \frac{{{\mu _\theta }}}{L} $

式中： $\;{\mu _Z}$ 为立管螺旋层轴向位移； $\;{\mu _R}$ 为径向位移； $\;{\mu _\theta }$ 轴向扭转角。

螺旋条带的径向应变为

$ {\varepsilon _2} = \frac{{\Delta t}}{t} $

式中： $\Delta t$ 为螺旋条带厚度变化； $t$ 为螺旋条带初始厚度。

根据弹性力学，应力应变关系为

$ {\sigma _1} = \frac{E}{{1 - {\nu ^2}}}\left( {{\varepsilon _1} + \nu {\varepsilon _2}} \right) $

$ {\sigma _2} = \frac{E}{{1 - {\nu ^2}}}\left( {{\varepsilon _2} + \nu {\varepsilon _1}} \right) $

式中： ${\sigma _1}$ 为螺旋条带轴向应变； ${\sigma _2}$ 为螺旋条带径向应变； $E$ 为螺旋条带材料弹性模量； $\nu $ 为螺旋条带材料泊松比。

螺旋条带在轴对称荷载作用下的应变能为

$ {U_1} = \frac{1}{2}\int {_v\left( {{\sigma _1} {\varepsilon _1} + {\sigma _2} {\varepsilon _2}} \right)} {\rm{d}}v $

式中 $v$ 为螺旋条带体积。

螺旋层在轴对称荷载作用下的外力势能为

${U_{\rm{e}}} = {P_{\rm{I}}}\Delta {V_{\rm{I}}} - {P_{\rm{O}}}\Delta {V_{\rm{O}}} + F{\mu _Z} + T{\mu _\theta }$

式中： ${P_{\rm{I}}}$ 为螺旋层受到的内压； ${P_{\rm{O}}}$ 为螺旋层受到的外压； $\Delta {V_{\rm{I}}}$ 为螺旋层内表面体积变化； $\Delta {V_{\rm{O}}}$ 为螺旋层外表面体积变化；F为螺旋层受到的轴向拉力；T为螺旋层受到的轴向扭矩。

1.1.2 螺旋层条带的弯曲和扭转

条带局部弯曲和扭转产生的应变能为

${U_2} = \frac{1}{2}\int {_v\left( {E{I_{\rm{b}}} \cdot \Delta k_{\rm{b}}^2 + GJ \cdot \Delta {\tau ^2}} \right)} {\rm{d}}s$

式中： ${I_{\rm{b}}}$ 为螺旋条带截面对副法线向量方向的惯性矩， $G$ 为螺旋条带的剪切模量， $J$ 为螺旋条带截面的极惯性矩。

螺旋层在轴对称荷载作用下的总势能为

$\varPi = n U - {U_{\rm{e}}}$

为计算方便，定义符号： ${X_Z} = \dfrac{{{\mu _Z}}}{L}$ 、 ${X_R} = \dfrac{{{\mu _R}}}{R}$ 、 ${X_\theta } = \dfrac{{{\mu _\theta }}}{L}$ 、 ${X_t} = \dfrac{{\Delta t}}{t}$ 。根据最小势能原理，螺旋层平衡时总势能最小。总势能式是关于 ${X_Z}$ 、 ${X_R}$ 、 ${X_\theta }$ 以及 ${X_t}$ 的泛函，所以对总势能式求变分，并令其等于零：

$\delta \varPi = 0$

用矩阵形式表示为

$\left[ {\begin{array}{*{20}{c}} {{K_{11}}}&{{K_{12}}}&{{K_{13}}}&{{K_{14}}} \\ {{K_{21}}}&{{K_{22}}}&{{K_{23}}}&{{K_{24}}} \\ {{K_{31}}}&{{K_{32}}}&{{K_{33}}}&{{K_{34}}} \\ {{K_{41}}}&{{K_{42}}}&{{K_{43}}}&{{K_{44}}} \end{array}} \right]\left[ {\begin{array}{*{20}{c}} {{X_Z}} \\ {{X_R}} \\ {{X_t}} \\ {{X_\theta }} \end{array}} \right] = \left[ {\begin{array}{*{20}{c}} {F + {\rm{{\text{π}}}} {P_{\rm{I}}}R_{\rm{I}}^2 - {\rm{{\text{π}}}} {P_{\rm{O}}}R_{\rm{O}}^2} \\ {2{\rm{{\text{π}}}} {P_{\rm{I}}}R_{\rm{I}}^2 - 2{\rm{{\text{π}}}} {P_{\rm{O}}}R_{\rm{O}}^2} \\ { - {\rm{{\text{π}}}} {P_{\rm{I}}}{R_{\rm{I}}}t - {\rm{{\text{π}}}} {P_{\rm{O}}}{R_{\rm{O}}}t} \\ T \end{array}} \right]$

1.2 圆柱层刚度矩阵

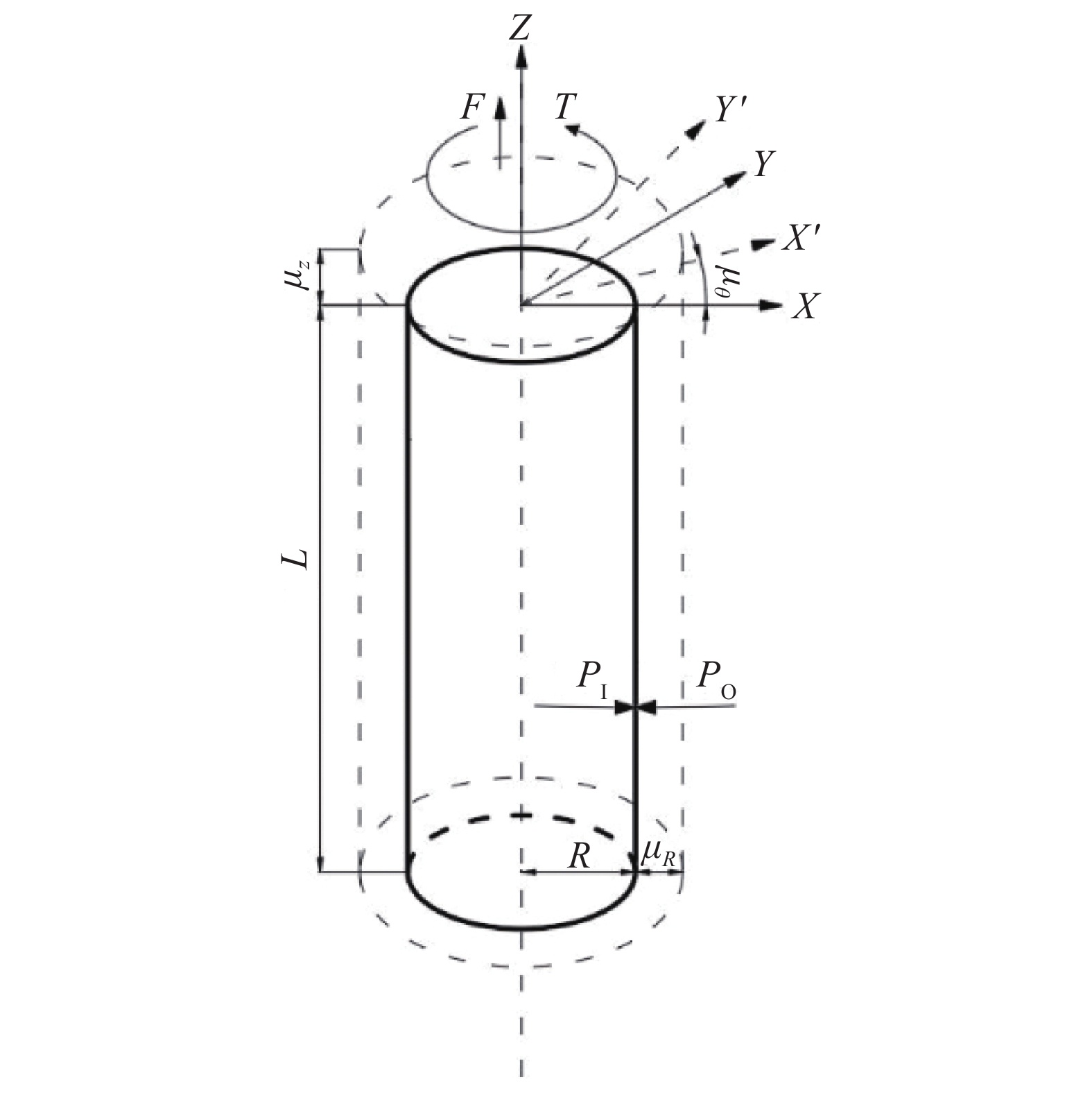
在小变形范围内，将聚合物材料视为线弹性且各向同性。对于聚合物圆柱壳采用厚壁理论分析。受力及变形图如图3所示。

由图3可知，圆柱层轴向应力和应变为 ${\sigma _1}$ 、 ${\varepsilon _1}$ ；径向应力和应变为 ${\sigma _2}$ 、 ${\varepsilon _2}$ ；环向应力和应变为 ${\sigma _3}$ 、 ${\varepsilon _3}$ ；剪切应力和应变为 ${\tau _{12}}$ 、 ${\gamma _{12}}$ ；径向位移为 ${\mu _R}$ 。其中 ${\varepsilon _1} $ 、 ${\varepsilon _2} $ 、 ${\varepsilon _3} $ 、 ${\gamma _{12}} $ 为

${\varepsilon _1} = \frac{{{\mu _{ Z}}}}{L};{\varepsilon _2} = \frac{{\partial {\mu _R}}}{{\partial R}};{\varepsilon _3} = \frac{{{\mu _R}}}{R};{\gamma _{12}} = R\frac{{{\mu _\theta }}}{L}$

弹性阶段，平面应变问题应变和应力分量之间的关系可表示为

$\left\{ {\begin{array}{*{20}{l}} {{\sigma _1} = \lambda \left( {{\varepsilon _1} + {\varepsilon _2} + {\varepsilon _3}} \right) + 2G{\varepsilon _1}} \\ {{\sigma _2} = \lambda \left( {{\varepsilon _1} + {\varepsilon _2} + {\varepsilon _3}} \right) + 2G{\varepsilon _2}} \\ {{\sigma _3} = \lambda \left( {{\varepsilon _1} + {\varepsilon _2} + {\varepsilon _3}} \right) + 2G{\varepsilon _3}} \\ {{\tau _{12}} = G{\gamma _{12}}} \end{array}} \right.$

圆柱层的外力势能计算公式和螺旋层相同，应变能可表示为

$U = \frac{1}{2}\int {_v\left( {{\sigma _1} {\varepsilon _1} + {\sigma _2} {\varepsilon _2} + {\sigma _3} {\varepsilon _3} + {\tau _{12}}{\gamma _{12}}} \right)} {\rm{d}}v$

代入势能表达式，对于圆柱壳，定义符号： ${X_Z} = \dfrac{{{\mu _Z}}}{L}$ 、 ${X_\theta } = R\dfrac{{{\mu _\theta }}}{L}$ 、 ${X_{{\varphi _{\rm{I}}}}} = \dfrac{{{\mu _{{R_{\rm{I}}}}}}}{{{R_{\rm{I}}}}}$ 、 ${X_{{\varphi _{\rm{O}}}}} = \dfrac{{{\mu _{{R_{\rm{O}}}}}}}{{{R_{\rm{O}}}}}$ ，求变分，并使其为零可以得到：

$\left[ {\begin{array}{*{20}{c}} {{K_{11}}}&{{K_{12}}}&{{K_{13}}}&{{K_{14}}} \\ {{K_{21}}}&{{K_{22}}}&{{K_{23}}}&{{K_{24}}} \\ {{K_{31}}}&{{K_{32}}}&{{K_{33}}}&{{K_{34}}} \\ {{K_{41}}}&{{K_{42}}}&{{K_{43}}}&{{K_{44}}} \end{array}} \right]\left[ {\begin{array}{*{20}{c}} {{X_Z}} \\ {{X_{{\varphi _{\rm{{\rm I}}}}}}} \\ {{X_{_{{\varphi _{\rm{O}}}}}}} \\ {{X_\theta }} \end{array}} \right] = \left[ {\begin{array}{*{20}{c}} {F + {\rm{{\text{π}}}} {P_{\rm{I}}}R_{\rm{I}}^2 - {\rm{{\text{π}}}} {P_{\rm{O}}}R_{\rm{O}}^2} \\ {2{\rm{{\text{π}}}} {P_{\rm{I}}}R_{\rm{I}}^2} \\ { - 2{\rm{{\text{π}}}} {P_{\rm{O}}}R_{\rm{O}}^2} \\ T \end{array}} \right]$

使用 ${{{k}}_{\rm{c}}}$ 表示刚度矩阵。

1.3 接触附加矩阵

非粘结柔性立管在受力情况下，各层之间可能发生接触或者分离，因此对其分析的过程中需要考虑层间接触的影响。

在柔性立管中，根据几何连续条件可得各相邻层之间的空间几何关系^[7-10]：

$ \Delta {R_{n + 1}} = \Delta {R_n} + \frac{1}{2} \left( {\Delta {t_{n + 1}} + \Delta {t_n}} \right) + {g_i} $

文献[9]将法向接触条件引入柔性管的整体刚度矩阵。由约束变分原理可知，对于有附加条件的问题可以使用罚函数法将附加条件引入泛函，构造一个新的泛函。附加泛函为

${\varPi _{{\rm{cp}}}} = \sum\limits_{j = 1}^{m - 1} {\left[ {{\omega_u}{{\left( {{\mu _{j{R_{\rm{O}}}}} - {\mu _{\left( {j + 1} \right){R_{\rm{I}}}}}} \right)}^2} + {\omega_P}{{\left( {{P_{j{\rm{O}}}} - {P_{\left( {j + 1} \right){\rm{I}}}}} \right)}^2}} \right]} $

(1)

式中： $j$ 为柔性管的层数(一共为m层)； ${\omega _{ju}}$ 和 ${\omega _{jP}}$ 为第 $j$ 层的罚参数； ${\mu _{j{R_{\rm{o}}}}}$ 为第 $j$ 层外表面的径向位移； ${\mu _{\left( {j + 1} \right){R_{\rm{I}}}}}$ 为第 $j + 1$ 层内表面的径向位移； ${P_{j{\rm{O}}}}$ 为第 $j$ 层外表面的外压； ${P_{\left( {j + 1} \right){\rm{I}}}}$ 为第 $j + 1$ 层内表面的内压。在未接触时， ${\mu _{j{R_{\rm{O}}}}} = {\mu _{\left( {j + 1} \right){R_{\rm{I}}}}} = 0$ 。

采用罚函数法将法向接触条件引入泛函，可表示为

$\varPi = {\varPi _{\rm{s}}} + {\varPi _{\rm{cp}}}$

为方便计算，直接对式(1)取变分，并使其等于零。可以得到柔性立管各层之间的接触矩阵。矩阵阶数与整体刚度矩阵相同，表示为 ${{{k}}_{\rm{cp}}}$ ，与整体刚度矩阵阶数相同。

以常见8层柔性立管结构为例，其中骨架层和抗压铠装层简化为各向异性的壳，则刚度矩阵为18阶，接触矩阵也为18阶。

${{{k}}_{\rm{cp}}} = {{w}} \cdot {{{k}}_{\rm{cpo}}}$

${{{k}}_{{\rm{cpo}}}}$ 中除以下系数外均为0： ${k_{33}} = 2R_{1{\rm{o}}}^2$ 、 ${k_{43}} =$ $ {k_{34}} = - 2{R_{1{\rm{o}}}}{R_{2{\rm{I}}}}$ 、 ${k_{44}} = 2R_{2{\rm{I}}}^2$ 、 ${k_{55}} = 2R_{2{\rm{o}}}^2$ 、 ${k_{65}} = {k_{56}} = - 2{R_{2{\rm{o}}}}{R_{3{\rm{I}}}}$ 、 ${k_{66}} = 2R_{3{\rm{I}}}^2$ 、 ${k_{77}} = 2R_{3{\rm{o}}}^2$ 、 ${k_{87}} = {k_{78}} = - 2{R_{3{\rm{o}}}}{R_{4{\rm{I}}}}$ 、 ${k_{88}} = 2R_{4{\rm{I}}}^2$ 、 ${k_{99}} =$ $ 2R_{4{\rm{o}}}^2$ 、 ${k_{109}} = {k_{910}} = - 2{R_{4{\rm{o}}}}{R_{5{\rm{I}}}}$ 、 ${k_{1010}} = {2R_{5{\rm{I}}}^2}$ 、 ${k_{1110}} = {k_{1011}} = 2{R_{5{\rm{I}}}}{t_5}$ 、 ${k_{1111}} = 2t_5^2$ 、 ${k_{1211}} = {k_{1112}} = - 2R{R_{5{\rm{I}}}}{t_5}$ 、 ${k_{1212}} = 2R_{6{\rm{I}}}^2$ 、 ${k_{1313}} = 2R_{6{\rm{o}}}^2$ 、 ${k_{1413}} =$ ${k_{1314}} = - 2{R_{6{\rm{o}}}}{R_{7{\rm{I}}}}$ 、 ${k_{1414}} = 2R_{7{\rm{I}}}^2$ 、 ${k_{1513}} = {k_{1315}} = 2{R_{7{\rm{I}}}}{t_7}$ 、 ${k_{1515}} = 2t_7^2$ 、 ${k_{1615}} = {k_{1516}} = 2{R_{8{\rm{I}}}}{t_7}$ 、 ${k_{1616}} = 2R_{8{\rm{I}}}^2$ 。

1.4 建立刚度矩阵

柔性立管各层结构的轴向变形和扭转变形是相等的，因此m层柔性立管共有2+2m个自由度：

${{{\varDelta}} _{\rm{s}}} = \left[ {{X_Z}\;\;X_R^1\;\;X_\theta ^1\;\;X_{\varphi {\rm{I}}}^2\;\;X_{\varphi {\rm{o}}}^2\;\;X_R^3\;\;X_\theta ^3\;\;X_{\varphi {\rm{I}}}^4\;\;X_{\varphi {\rm{O}}}^4 \cdots X_{\varphi {\rm{I}}}^m\;\;X_{\varphi {\rm{O}}}^m\;\;{X_\theta }} \right]$

式中：X表示自由度，上标表示层号，下标表示自由度类型。

整体刚度矩阵也应为2+2m阶。将各层的刚度矩阵以自由度为依据，组合成自由状态下的整体刚度矩阵k。最终考虑层间接触的刚度矩阵为

${{K}} = {{k}} + {{{k}}_{\rm{cp}}}$

有限元方程为

${{K}}{{{\varDelta}} _{\rm{s}}} = {{{F}}_{\rm{S}}}$

${{{F}}_{\rm{S}}}$ 为外力向量：

${{{F}}_{\rm{S}}} = \left[ {\begin{array}{*{20}{c}} {{F_Z}}&0&0&{{P_{\rm{I}}}}&0&0& \cdots &{}&0&{{P_{\rm{O}}}}&N \end{array}} \right]$

式中 ${F_Z}$ 、 ${P_{\rm{I}}}$ 、 ${P_{\rm{O}}}$ 、 $N$ 分别为轴向力、内压、外压和扭矩。

2 有限元模型 2.1 立管基本参数

本文根据de Sousa^[16]已发表的关于非粘结柔性立管的实验论文，在表1、2给出了2.5英寸柔性管各层几何参数和材料参数。

2.2 模型与网格

使用三维建模软件建立8层柔性立管三维模型，导入ABAQUS对其进行网格划分，使用C3D8R单元，如图4所示。层间接触采用库伦摩擦来模拟，摩擦系数取0.1。

2.3 分析步和边界条件

先定义一个很小的荷载的分析步，让接触关系平稳地建立起来，然后在下一个分析步中再施加真实的荷载。这样虽然分析步数目增多，但减小了收敛的困难，计算时间反而缩短^[17]。采用ABAQUS/Explicit准静态方法进行计算，采用Smoot step的加载方式^[18]。

本文先在端部截面中心设置参考点，然后对截面上所有节点的自由度与参考点进行运动学耦合。在一端参考点施加固定约束，另一端参考点施加拉伸或扭转荷载^[18]。

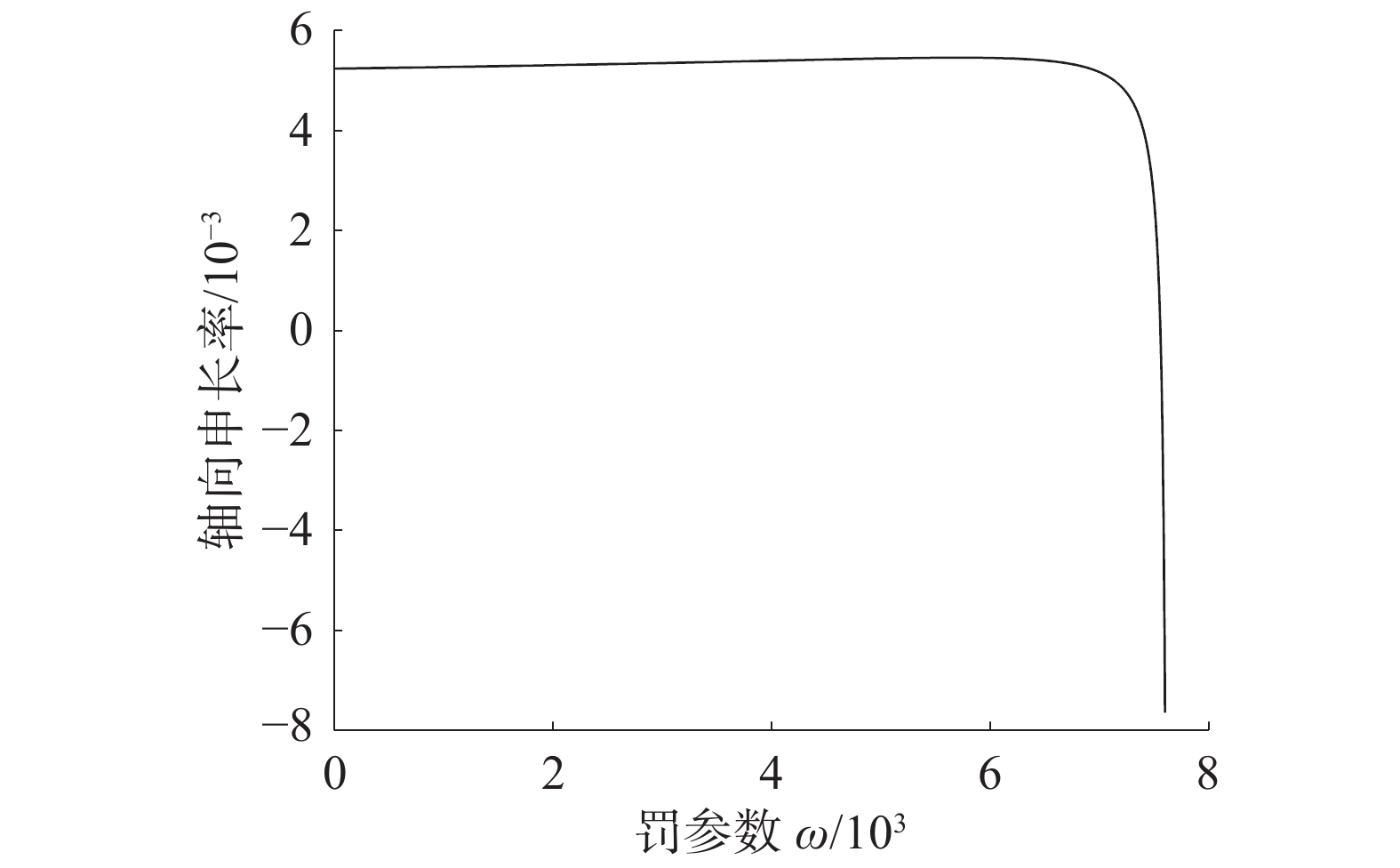
3 计算结果分析 3.1 罚参数计算

罚函数法在接触问题中可以不增加问题的自由度，所以应用较为广泛。但是求解的精度与罚参数相关。图5为在纯轴向拉伸作用下，轴向变形与罚参数w之间的关系曲线。

将结果与文献[16]中的实验结果对比，可以发现，随着罚参数的增大，计算结果越来越准确；但是当罚参数大于7 000后，轴向伸长率出现了大幅度的变化，这就是由于罚参数过大造成了方程的病态。因此本文的罚参数的选择在6 000~7 000。

3.2 拉伸工况

使用第1节中的整体刚度矩阵K_c计算轴向拉力作用下立管的受力情况。700 kN作用下各层的径向变形值可从位移理论方法计算所得的变形向量中得到，结果见表3。对比各层内外径的径向变形值，如第5层外径变化较第6层内径变化大，可以推断出层间发生了分离。从表中可以看出：第4和第5层、第6和第7层是相互接触的；但是第5和第6层、第7和第8层发生了分离。

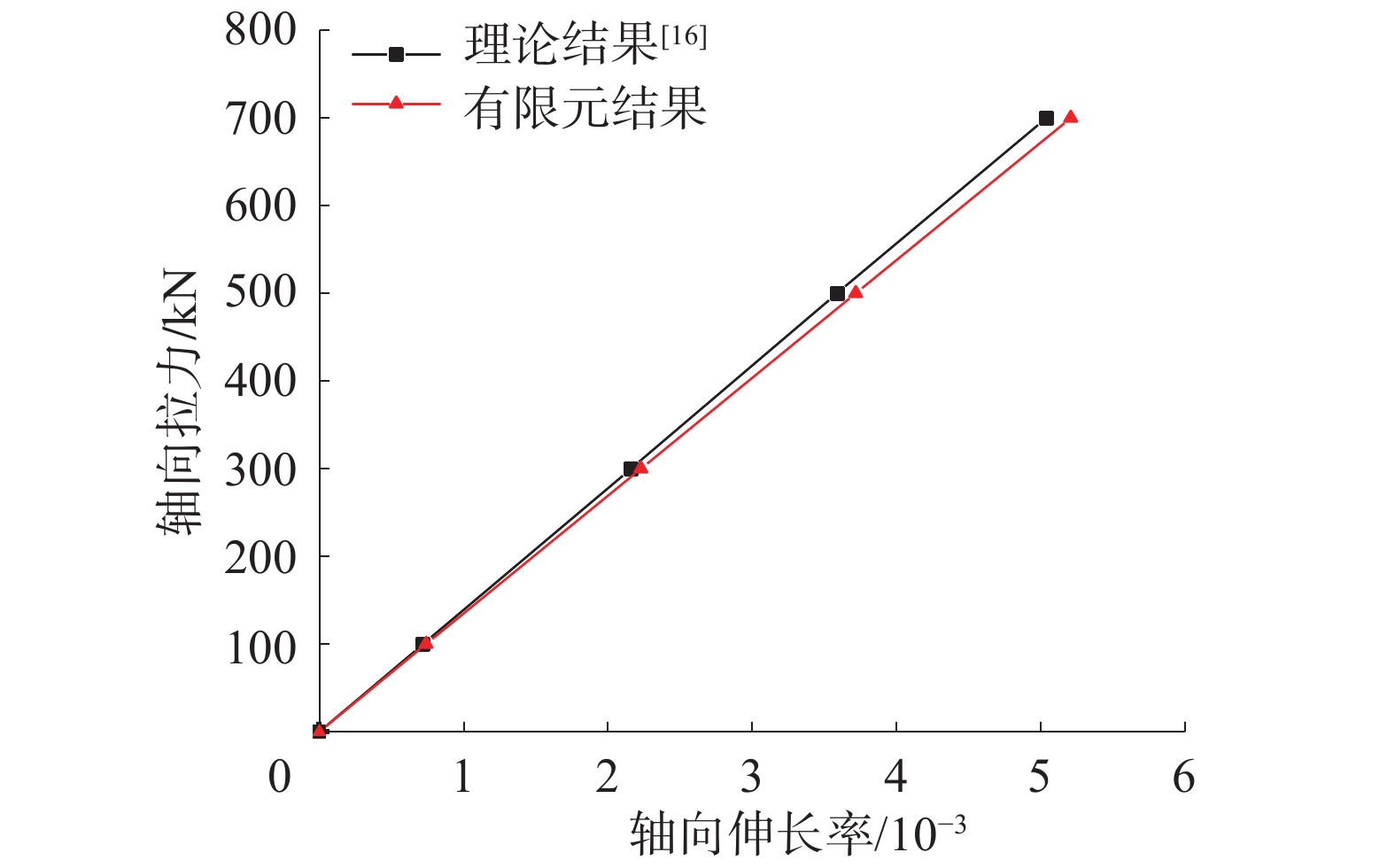
在纯拉力作用下，柔性立管的伸长率与有限元模型计算结果如图6所示。计算结果与文献[16]的实验结果相比，误差在10%以内，且数值模型误差更小。

由图6结合文献[16]可以看出，立管的轴向变形随着轴向力的增大线性增加，比较理论计算结果与数值计算结果，二者误差为5%。将位移向量中的值代入各层的计算方程中，可以得到每一层所承受的轴向拉力值。表3中给出了700 kN轴向拉力作用下的各层结构所承受的轴向拉力值。从中可以看出，第5、6层承担了柔性立管轴向拉力的84%。由此可得非粘结柔性立管的轴线刚度主要由抗拉铠装层提供。在拉伸工况下，应力较其他层大，图7为纯拉伸作用下有限元计算方法得到的抗拉铠装层应力图。

3.3 扭转工况

取内抗拉铠装层缠绕方向为顺时针方向。根据各层径向变形值，同样可以得到各层之间的接触关系。表4为柔性立管在7 kN·m的扭矩作用下，第4~8层的受扭矩情况。从表中可以看出，在立管发生扭转时，抗拉铠装层承受扭矩的86%。

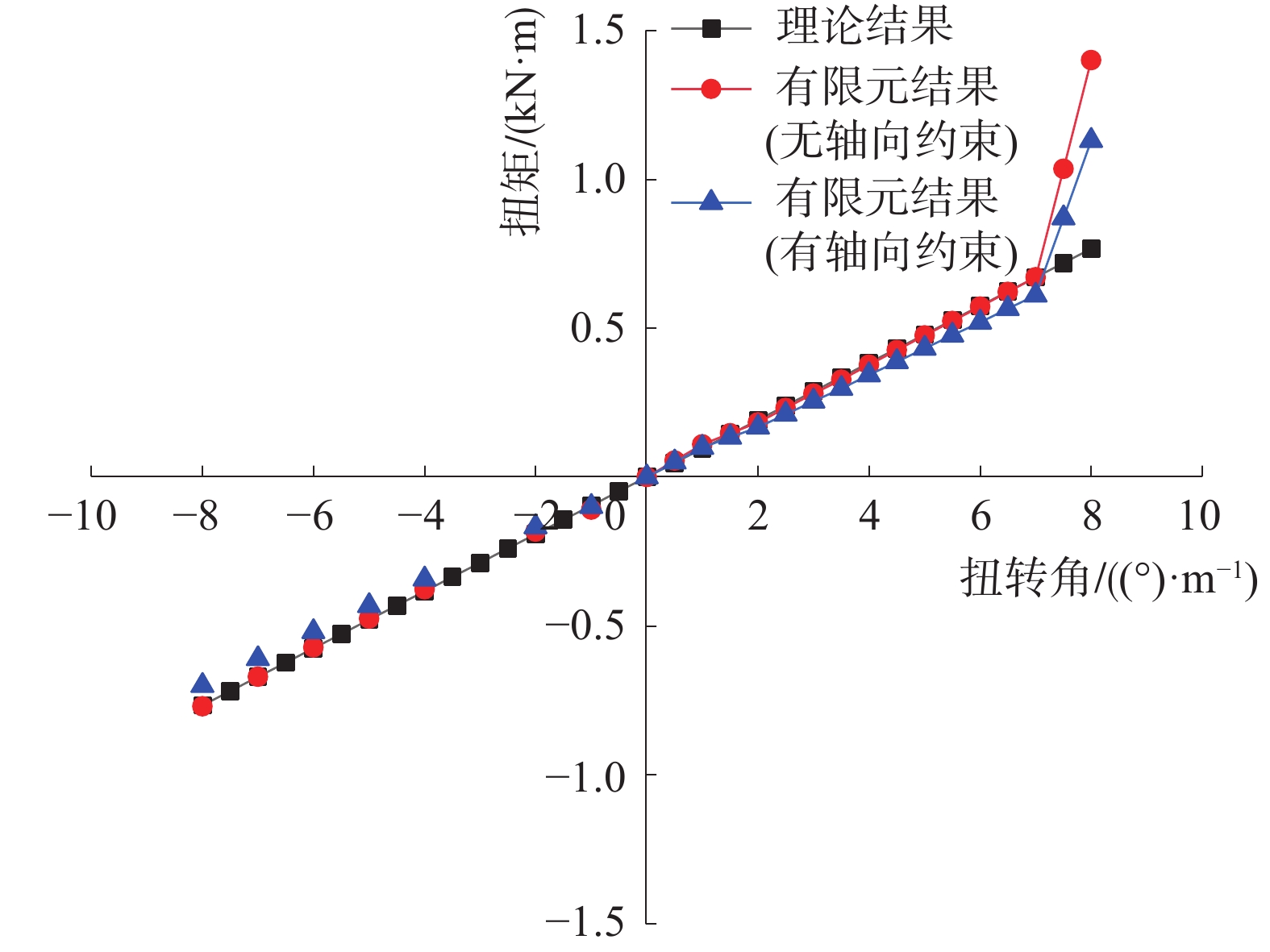
扭矩作用下的理论计算结果和有限元计算结果对比如图8所示。

从图中可以看出，柔性立管的扭转角随着扭矩的增大而线性增长。理论计算结果与无轴向约束的立管的数值模拟结果相差1.5%。而由于顺时针扭矩产生的整体刚度减小现象，理论方法无法表现出来。

4 结论

本文依据柔性立管各层的结构特性，建立了用于计算轴对称荷载作用下柔性立管各层的刚度矩阵，并将其组装得到自由状态下的刚度矩阵。通过罚函数的方法将层间法向接触引入立管整体矩阵，利用式(1)推导出接触矩阵，并加到自由状态下的刚度矩阵上，得到非粘结柔性立管的整体刚度矩阵。本文算例中计算了典型8层结构的柔性立管，并建立了三维有限元模型。讨论了接触矩阵中罚参数的取值，并对比了柔性立管在轴向拉力和扭矩作用下变形的理论解和数值模拟值。最终得出结论如下：

1) 8层柔性立管结构，罚参数可以在6 000~7 000取值。层间接触矩阵中的罚参数取值对计算结果影响较大，在不同结构参数下需要先确定罚参数的取值。

2)参考文献中的试验结果，并将本文中的理论模型与数值模型计算结果与之对比，发现误差在10%以内，证明了本文的刚度矩阵计算方法可以在设计前期使用，以便节省时间，但是在具体设计阶段，仍需要实验进行验证。