海洋平台的系统复杂，成本高昂，作业环境比较恶劣，空船重量会对作业能力起到至关重要的影响，所以对空船重量控制十分严格。有些船东甚至会直接把重量控制目标写入合同，有半潜式钻井平台达到了每超重1 t罚款20 000美元这样的超重处罚条款。另外，海工企业对海洋平台的重量控制也十分严格，尤其是对钢结构、重大设备的重量有严格要求。企业在钢结构的设计、制造环节都十分重视，也会在采购设备时把重量控制要求写入采购合同，但对于铁舾装的重量往往流于形式，并没有一个严格的考核机制。在海工企业中，铁舾装工程师往往不会进行结构强度的计算，而仅限于个人的经验，普遍参考前面的项目来进行设计。参考的链条长了以后，出于保守考虑，就自然会变得强度余量过大，从而造成超重。

如果想提升铁舾装工程师的整体设计水平，使其都具备像结构工程师一样的强度计算能力并不现实。这就需要提供一个标准的设计模板，让铁舾装工程师照模板进行设计，即能满足强度，又不会产生太大的设计余量。基于上述目的，本文以花钢板的设计为例展开铁舾装件设计研究。

1 规范设计分析研究

作者查阅了相关的船级社规范、海上人命安全公约和Mobile Offshore Drilling Units（MODU）Code的相关要求，发现对于花钢板设计，规范仅有保证安全的指导性要求。

本文参考船体结构的相关规定，研究适用于花钢板的设计标准并进行相关计算，设计出符合安全性的指导性要求数据表格，可以指导工程师对照表格进行相关材料规格的选型。

根据花钢板的实际使用位置情况分类，花钢板的使用分为室内和室外2种；根据安装形式又分为螺钉连接和焊接2种形式。而室外的花钢板，出于防腐的要求，均为焊接连接。

1.1 花钢板的规范计算依据

铺花钢板的区域均为机械区，但花钢板自身并不承受机械设备的载荷，通常花钢板厚度为4.5 mm或5.0 mm。

1.1.1 美国船级社设计依据

依据美国船级社(以下简称ABS)的MODU3-1-3/1.11.3，对于工作区域，取1.28 m的设计压头^[1]。

计算花钢板的强度参考甲板室的计算，考虑1 mm的腐蚀余量。根据MODU3-2-3/15.5计算甲板室板厚的公式^[1]为

${\rm{}}t = 3s\sqrt h + 1\;{\rm{mm}}$

(1)

根据式(1)，可以推出花钢板的间距s计算公式：

$ s=(t-1)/\left(3\sqrt{h}\right)\;\;{\rm{m}} $

(2)

由于花钢板的厚度为4.5 mm或5.0 mm，可以推导出花钢板的大支撑间距在板厚4.5 mm时为1.03 m；板厚5.0 mm时为1.18 m。如果所处的环境较好，可以不考虑腐蚀余量，则允许的最大支撑距离分别为1.33 和1.47 m。

由于式(1)的前提条件是花钢板与型材进行焊接，边界条件相当于固支；而有时是采用的螺栓连接，边界条件相当于简支。显然不能直接采用式(2)的计算结果。由于规范的板也是基于梁理论来推导的，所以对于边界条件为简支的情况可以根据梁理论进行反推^[2]。根据受均布载荷的受力模式分析，简支和固支条件下的最大弯矩分别如下文公式所示。

简支条件下，整个跨度内受均布载荷^[3]，最大弯矩和最大剪力分别为

$ {M}_{\max}=Ql/8 $

$ {F}_{\max}=0.5Q $

式中：Q为整个跨度内的总载荷； $ l $ 为跨距。

而两端固支，受均布载荷的条件下，最大弯矩在两固支点位置，最大剪力也在两固支点位置。最大弯矩和最大剪力分别为^[2]

$ {M}_{\max}=Ql/12 $

$ {F}_{\max}=0.5Q $

对比固支与简支的最大弯矩和最大剪力会发现，同等载荷同等弯矩条件下，简支的最大弯矩是固支的1.5倍。而根据参考文献[2]的推导过程可知，板厚的平方与最大弯矩成正比。所以对于螺栓连接花钢板，板厚的公式可以由式(1)演变为

$ t=3s\sqrt{1.5h}+1\;{\rm{mm}} $

(3)

根据式(3)，可以推导出螺栓连接花钢板间距s的计算公式：

$ s=(t-1)/\left(3\sqrt{1.5h}\right)\;{\rm{m}} $

(4)

可以算出花钢板的最大支撑间距在板厚4.5 mm时为0.84 m；板厚5.0 mm时为0.96 m。如果所处的环境较好，可以不考虑腐蚀余量，则允许的最大支撑距离分别为1.08 m和1.20 m。

对于花钢板下的支撑构件，通常选用工字钢。前面给定了支撑间距，后面就需要确定支撑构件的规格。为了使设计规范化，确定花钢板下的支撑构件的有效支撑距离不超过3.5 m。剖面模数(ABS标准)计算公式仍然采用甲板室的计算^[1]：

$ \mathrm{S}\mathrm{M}=3.5sh{l}^{2}\;{{\rm{cm}}^{3}} $

对于不同厚度下的间距取值由表1列出。

由于铺设花钢板的位置一般都成长条形，并且离下面的钢结构甲板很近，作为夹层使用，所以不必像常规的钢结构一样设置强梁，一般支撑到两侧的钢结构上即可。如果确实有需要提供支撑，可以设置支柱。由于支柱的高度比较小，为了采购和安装方便，采用同一规格的型材作为支柱即可。

1.1.2 中国船级社设计依据

依据中国船级社(以下简称CCS)的《海上移动平台入级规范》2-2-5/2.5.1.2规定，作业区域的设计载荷为p=9 kN/m^2[4]。

依据CCS《海上移动平台入级规范》2-3-2/3.2.7.8，板厚计算公式^[4]为

$ t=3s\sqrt{Kh}\;{\rm{mm}} $

(5)

式中K为材料系数，对于普通钢K=1。对比式(5)和(1)可以发现，CCS和ABS计算公式是完全一样的。所以型材间距的计算同样可以采用式(2)进行计算。

由于CCS规定的设计载荷为9 kN/m²，需要换算成设计压头。根据CCS《海上移动平台入级规范》2-3-2/3.2.3.2，设计载荷等效设计压头h=0.14p+0.3=1.56 m^[4]。

根据式(2)，可以算出花钢板的大支撑间距在板厚4.5 mm时为0.93 m；板厚5.0 mm时为1.07 m。如果所处的环境较好，可以不考虑腐蚀余量，则允许的最大支撑距离分别为1.20 m和1.33 m。

根据式(4)，可以计算出进行螺栓连接时的花钢板最大允许支撑间距在板厚4.5 mm时为0.84 m；板厚5.0 mm时为0.96 m。如果所处的环境较好，可以不考虑腐蚀余量，则允许的最大支撑距离分别为1.08 和1.20 m。

花钢板下的支撑构件，参考《海上移动平台入级规范》2-3-2/3.2.7.9执行^[4]，剖面模数(CCS标准)为

$ W=5sKh{l}^{2}\;{{\rm{cm}}^{3}} $

式中K为材料系数，普通钢K=1。

对于不同厚度下的间距取值由表2列出。

1.1.3 挪威−劳氏船级社设计依据

依据挪威−劳氏船级社(以下简称DNVGL)的规范DNVGL-OS-C101-Design of Offshore Steel Structures, General (LRFD Method)(2-2-4.2)规定，设备间(也称“机械区”)取设计载荷为5 kN/m^2[5]。

根据DNVGL-OS-C101中2-4-6/6.3，板厚计算公式^[5]为

$t = \frac{{15.8{k_a}s\sqrt {{p_d}} }}{{\sqrt {{\sigma _{{\rm{pd}}1}}{k_{{\rm{pp}}}}} }}\;{\rm{mm}}$

(6)

由式(6)可以推导出型材间距的计算公式：

$s = \frac{{t\sqrt {{\sigma _{{\rm{pd}}1}}{k_{{\rm{pp}}}}} }}{{15.8{k_a}\sqrt {{p_d}} }}\;{\rm{m}}$

(7)

式中：k_a为板格的比例系数，通常长宽比都大于3，取k_a=1； $ {p}_{d} $ 为设计压力，由前文可知 $ {p}_{d}=5\;{\rm{kN}}/{{\rm{m}}}^{2} $ ; $ {\sigma }_{\mathrm{p}\mathrm{d}1} $ 为设计许用弯曲应力，按静载设计，取1.67的安全系数， $ {\sigma }_{\mathrm{p}\mathrm{d}1}=141\;{\rm{MPa}} $ ； $ {k}_{\mathrm{p}\mathrm{p}} $ 为边界条件系数，对于焊接花钢板，按固支设计， $ {k}_{\mathrm{p}\mathrm{p}}=1 $ ；对于螺栓连接花钢板，按简支设计， $ {k}_{\mathrm{p}\mathrm{p}}=0.5 $ 。

根据式(7)得出最大允许支撑间距。焊接花钢板厚度为4.5 mm时允许最大支撑间距为1.51 m；板厚为5.0 mm时允许最大支撑间距为1.68 m。但是，从式(6)可以看出，并没有考虑腐蚀余量，如果考虑1 mm的腐蚀余量，厚度为4.5 mm时允许最大支撑间距为1.18 m；板厚为5.0 mm时允许最大支撑间距为1.34 m。

螺栓连接花钢板厚度为4.5 mm时允许最大支撑间距为1.07 m；板厚为5.0 mm时允许最大支撑间距为1.19 m。如果考虑1 mm的腐蚀余量，花钢板厚度为4.5 mm时允许最大支撑间距为0.83 m；板厚为5.0 mm时允许最大支撑间距为0.95 m。

花钢板下的支撑构件^[5]，参考DNVGL–OS-C101, Design of Offshore Steel Structures, General-LRFD Method 2-4-6/6.4.1执行，剖面模数(DNVGL标准)为

$ {Z}_{s}=\frac{1\;000{l}^{2}s{p}_{d}}{{k}_{m}{\sigma }_{\mathrm{p}\mathrm{d}2}{k}_{\mathrm{p}\mathrm{s}}}\;{{\rm{cm}}}^{3} $

式中：型材跨距取l=3.5 m；设计压力 $ {p}_{d}=5\;{\rm{kN}}/{{\rm{m}}}^{2} $ ；弯曲支撑的形式，焊接时按固支计算 $ {k}_{m}=12 $ ，螺栓连接时按简支计算 $ {k}_{m}=8 $ ；许用设计弯曲应力 $ {\sigma }_{\mathrm{p}\mathrm{d}2} $ 同前面的板材计算，取 $ {\sigma }_{\mathrm{p}\mathrm{d}2}=141\;{\rm{MPa}} $ ；端部形式系数 $ {k}_{\mathrm{p}\mathrm{s}} $ ，焊接时按固支计算， $ {k}_{\mathrm{p}\mathrm{s}}=1.0 $ ，螺栓连接时按简支计算， $ {k}_{\mathrm{p}\mathrm{s}}=0.9 $ 。

根据以上数据，可以计算出不同状态下的型材规格。对于不同厚度下的间距取值由表3列出。

对比表1~3分别采用3家船级社规范计算的数据可以发现，CCS的设计最为保守，DNVGL的设计安全余量最小。通常情况下无论入级是哪个船级社，可以按ABS的规格进行取值，因为这部分不需要船级社的审查。

1.2 花钢板的力学计算依据

从上面的规范计算依据来看，前提条件都是花钢板承受均布载荷，而花钢板在实际使用时承受的均布载荷只有自重，而承受人员重量、人员携带的工具重量、临时放置的小型设备重量、维修时放置的设备零部件的重量，它们的特点是接触面积较小、重量较轻，一般在9.81 kN以下。所以这一部分的载荷计算应该按接触正应力计算。

从规范来看，DNVGL也在也在Design of Offshore Steel Structures, General-LRFD Method 2-2/4.2中规定了设计点应力水平，为5 kN。由此可见，设计9.81 kN的接触点应力是足够的。但是，由于设备的放置是临时性的，放置时考虑到花钢板的强度较弱，需要进行垫钢板来加强。而经常性的载荷为人的载荷，按每个人携带工具时最大重量1 kN计算，考虑2个人站在一起协同操作的极限工况。

等厚矩形板的最大应力^[6]和最大挠度^[7]计算如下。在四边固支、中间承受集中力的情况下，受到最大应力与最大挠度分别为

$ {\sigma }_{\max}=\frac{1\;000\alpha P}{{t}^{2}}\;{\rm{MPa}} $

(8)

$ {\omega }_{\max}=\beta {\left(\frac{1\;000b}{t}\right)}^{2}\frac{1\;000P}{Et}\;{\rm{mm}} $

(9)

式中： $ \alpha $ 为系数，与长宽比相关，取1.008；P为集中压力，分P=9.81 kN和P=2 kN这2种情况； $ \beta $ 为系数，和长宽比相关，取0.079 17；b为支撑宽度，同式(2)中的s，取值按式(2)计算；E为弹性模量，取值 $ 2.1\times {10}^{5} $ MPa。

以ABS规范设计的数据为准进行计算，板厚分为4.5和5.0 mm这2种情况，每种板厚情况又分别考虑腐蚀余量和不考虑腐蚀余量，计算结果如表4所示。

从表4可以看出，在临时放置设备时，无论是最大正应力，还是最大挠度，如不垫钢板进行临时性加强，均不满足要求，会产生较大的变形，应力也远远超过许用标准，会产生塑性变形。而垫钢板满足规范要求。

四边简支的情况与四边固支的情况计算公式仍然是式(8)和(9)，但系数取值有所不同， $ \alpha $ 取1.008， $ \beta $ 取0.185 1。

由于四边简支的情况比四边固支的情况更为危险，所以放置设备时仍然需要进行垫钢板进行临时加强，在这里不进行不垫钢板的强度计算，计算结果如表5所示。

从表5可以看，最大的应力满足设计要求，最大挠度略大，为23.7 mm，但此时的最大应力为165 MPa，仍然在弹性范围内，属弹性变形，待人员离开后会恢复原样。

2 有限元校核

选用典型的设计工况进行校核，分为固支和简支2种情况。

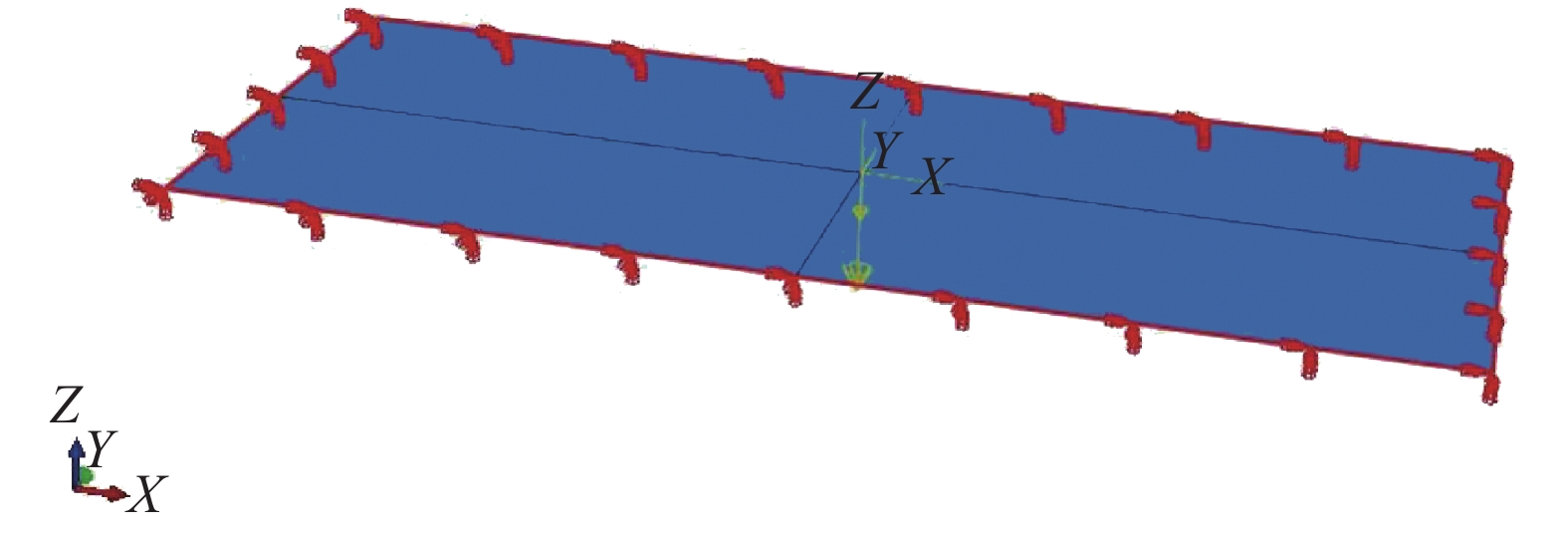
1)工况1。板厚4.5 mm，焊接，取一个板长3.5 m、宽1.03 m的板格，按四边固支计算。有限元模型如图1所示。

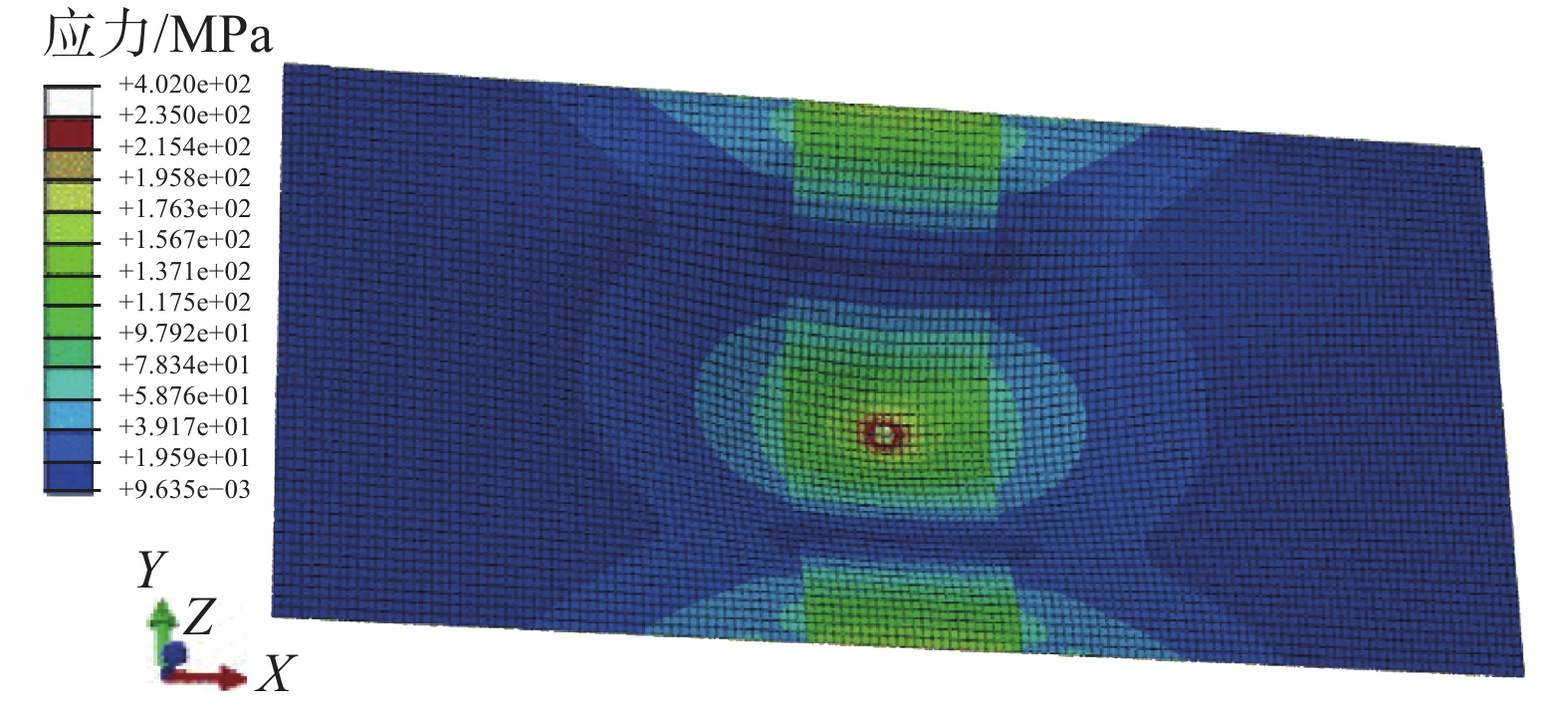
在中间施加9 810 N的集中力，应力计算结果如图2所示。

从应力云图上可以看出，除了集中力施加的中心位置有比较大的应力集中之外(这个可以忽略，因为实际的力会有一个接触面积，而不是一个点)，周围的应力在170 MPa左右，与计算的结果接近，满足要求。

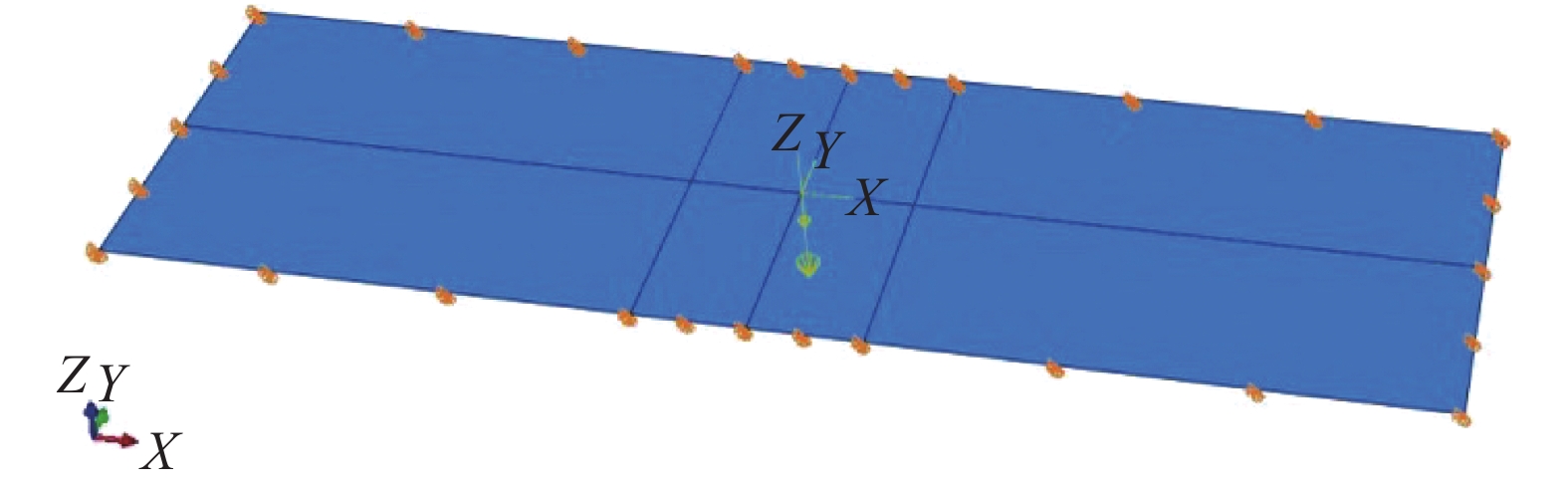
2)工况2。板厚4.5 mm，螺栓连接，取一个板长3.5 m、宽0.84 m的板格，按四边简支计算。有限元模型如图3所示。

在中间施加9 810 N的集中力，应力计算结果如图4所示。

从应力云图上可以看出，中间应力集中区域比焊接固定的范围略大，但周围的应力在170 MPa左右，与计算结果接近，满足要求。

3 花钢板设计标准

根据不同船级社的规范设计公式对比分析，以及各家的设计输入情况分析，经过强度计算，可以得出标准的花钢板设计要求。

设计标准值如表6所示。表6为标准的指导性文件，设计的最小厚度不低于表6厚度，型材间距不大于表6的值，标准的型材规格不小于表6的值。进行设计时直接查表即可，而不必进行复杂的计算。

4 结论

本文从强度和使用的根源上提出海洋平台铁舾装标准化设计方案，比现有的参考的方式更为科学。

1)根据铁舾装从业技术人员的特点，制定出标准化的设计模板，简单明了，不需要复杂的计算就可以直接掌握。

2)从材料力学的基础上，依据实际使用情况，参照各大船级社规范，如ABS、DNVGL、CCS等，又不照搬规范，从理论上给出设计依据。

依据本文的研究，可以根据船型的特点进行进一步的优化，从而符合企业的实际需求。