波浪管是一种扭曲和扩展传热表面的强化换热元件。其可在有限的空间内增加换热面积,且其特殊的几何结构可在流动阻力增加相对较少的情况下,改善管内流场分布,提高换热设备的综合换热性能。除强化换热能力较强外,波浪管加工工艺较简单,不会破坏传热管表面,且弯曲的管壁在长管路或大温差时可吸收一部分热应力引起的变形,从而省去膨胀接头等弹性连接件。因此,波浪管换热器在很多行业,尤其在对重量和尺寸非常敏感的领域有非常广泛的应用前景。
目前,用数值模拟和实验研究的方法分析换热器传热与阻力特性的方法已较为成熟[1-6],已有研究者对波浪管换热器进行了相关的研究,并通过实验[7-9]和数值仿真[10-12]的方法验证和模拟了波浪管的强化换热能力及流动参数的分布。但实验受监测手段的限制较难准确测量波浪管内的流场分布,且现有数值模拟研究成果未对垂直流动方向横截面上的二次流动进行详细分析。因此,本文通过数值分析软件Fluent对不同工况下波浪管内的流动情况进行了计算,阐述了波浪管内二次流的形成机理、发展过程、及其对阻力特性和换热特性的贡献和影响。
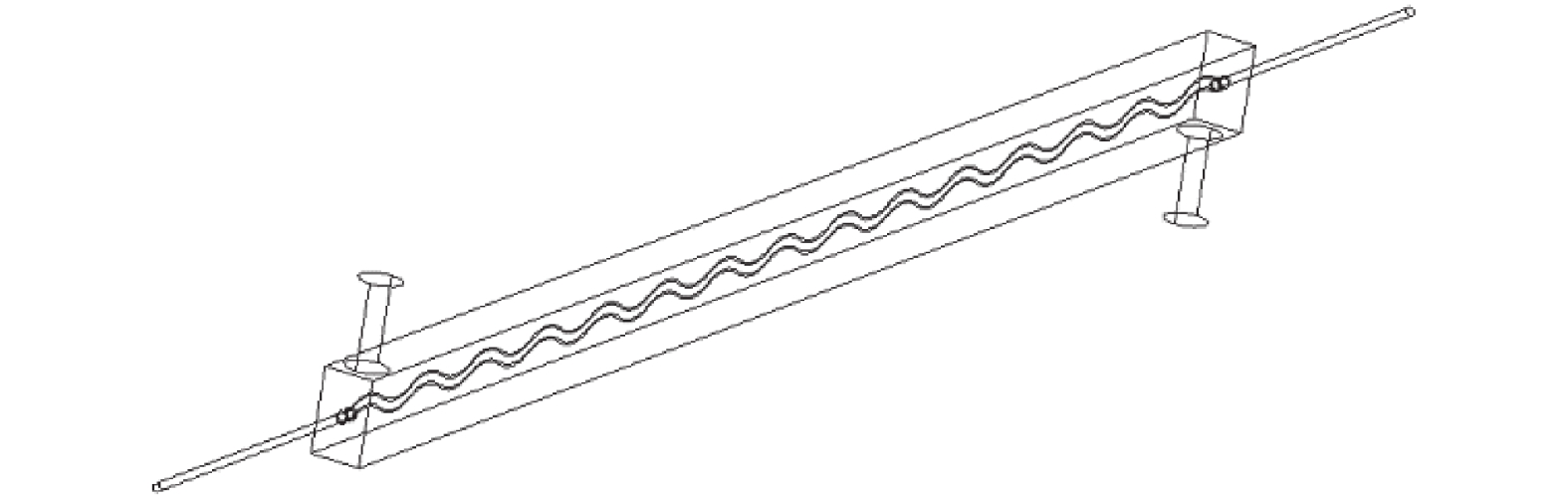
1 模型建立与网格划分本文按照实验设备尺寸[8],使用三维建模软件Unigraphics NX建立几何模型,如图1所示。实验段壳侧为30 mm×50 mm×1 000 mm的矩形通道,管侧为曲率半径33.5 mm、内径5.8 mm、角度60°的波浪管。为了消除进出口效应的影响,在波浪管实验段之外加设220 mm的直管段。
|
Download:
|
| 图 1 波浪管换热器几何模型 | |
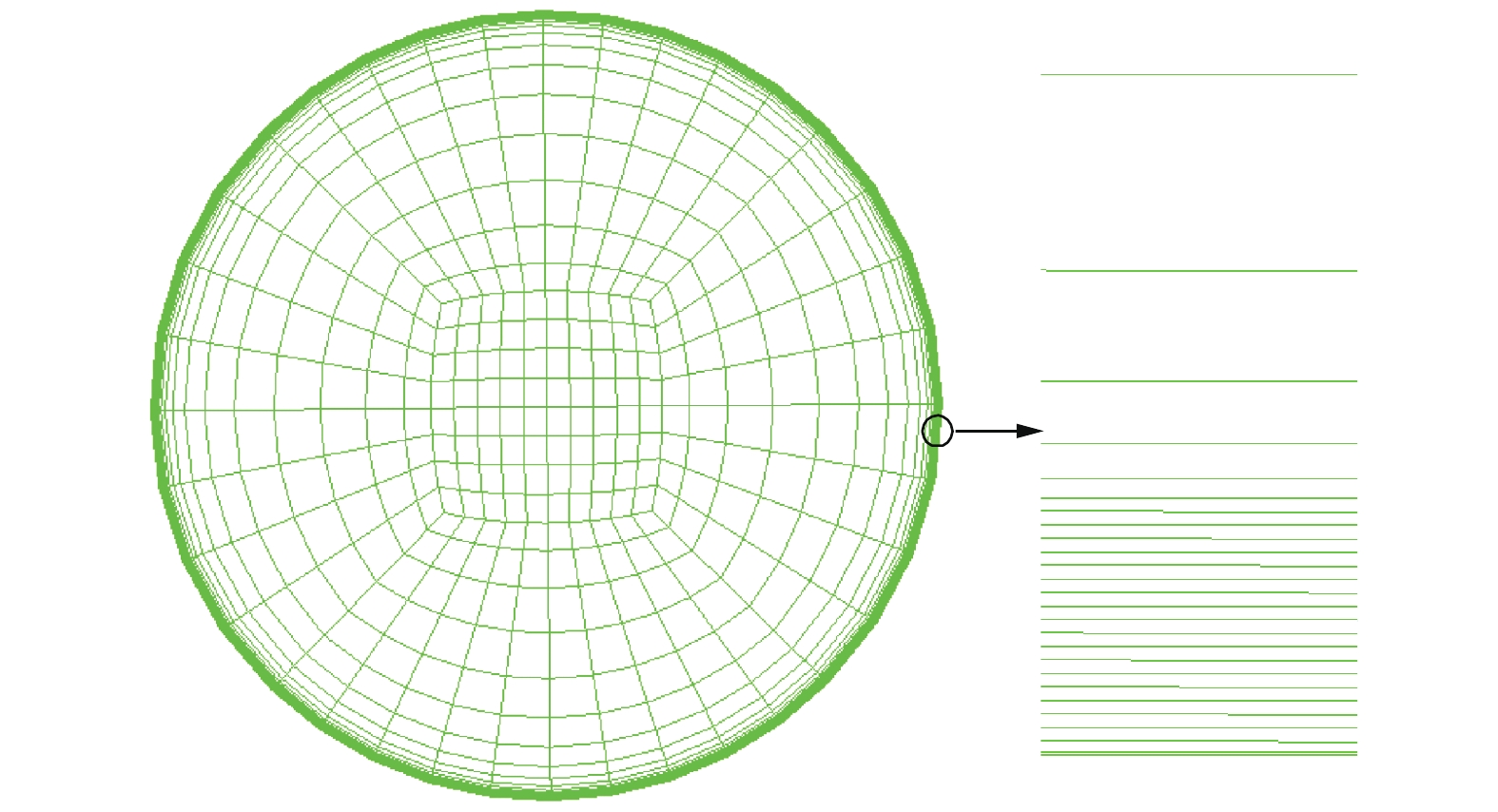
采用ICEM CFD对管壳侧流体域及管壁进行全结构化网格划分,如图2所示。为满足Enhanced Wall Treatment的使用要求,在壁面生成较细的网格,使边界层内有20层网格且y+值小于1[13-14]。生成的网格Determinant 2×2×2质量高于0.5,Equiangle Skewness质量高于0.45。
|
Download:
|
| 图 2 波浪管截面网格划分 | |
换热器管侧和壳侧的入口均设为流量入口边界条件,出口均设为压力出口边界条件,波浪管内外表面均设为coupled无滑移壁面,壳侧壁面为绝热的无滑移边界条件。
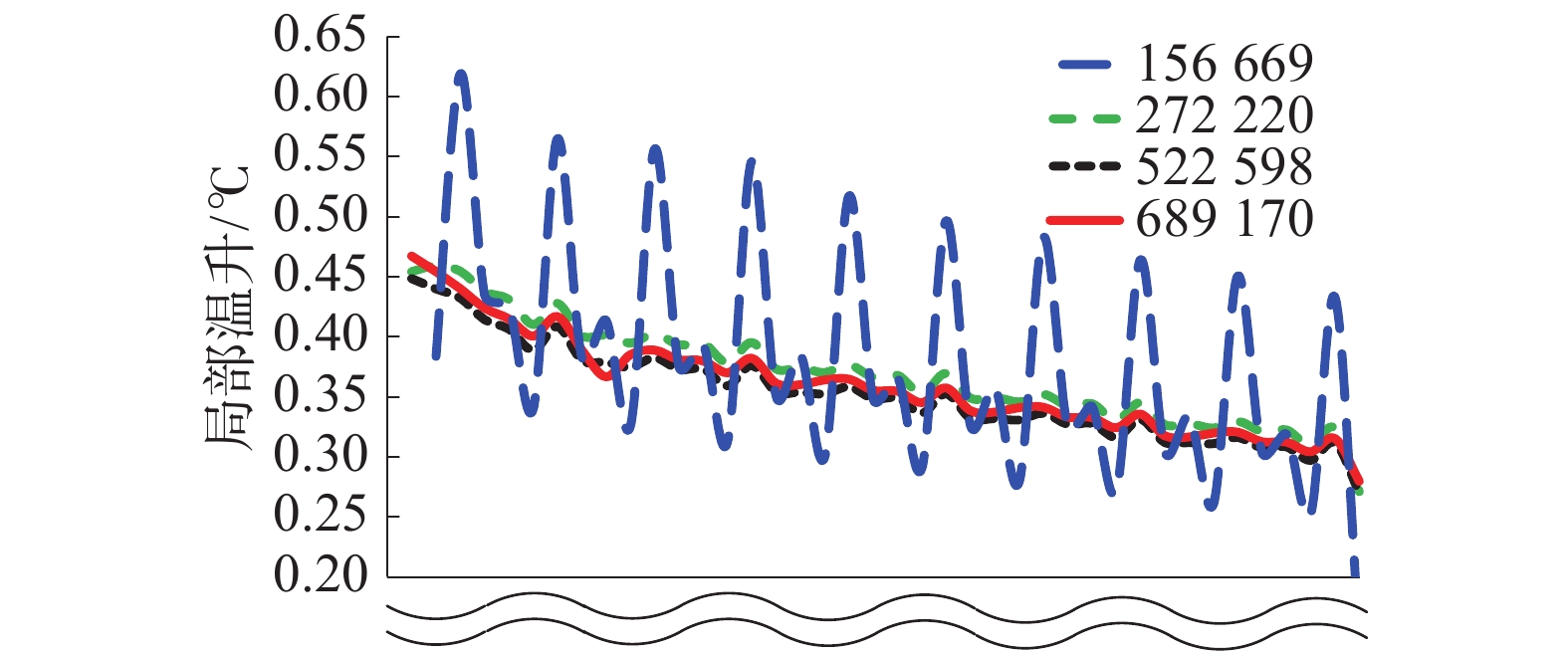
为消除网格数量对计算精度的影响[15],分别采用不同细分等级对计算模型生成了数量为156 669(1)、272 220(2)、522 598(3)、689 170(4)的4套网格。当管侧入口流量和温度分别为0.085 m3/h和7 ℃、壳侧入口流量和温度分别为9.1 m3/h和62 ℃时,4套网格对此工况下波浪管内沿程阻力损失和局部温升的计算结果分别如图3、4所示。对比不同网格数量的计算结果可以看出,网格1、2和3的计算结果相差较大,而网格3和4的计算结果几乎相同。因此,当网格数量超过522 598后,计算结果随网格数量增加而产生的变化很小,则本文采用数量为522 598的网格进行计算。
|
Download:
|
| 图 3 波浪管内沿程局部温升分布 | |

|
Download:
|
| 图 4 波浪管内沿程局部压降分布 | |
为更好地模拟波浪管内的流线弯曲、分离、二次流动和传热特性,本文采用RNG k-ε湍流模型配合Enhanced Wall Treatment壁面处理对不同工况下波浪管内流体的阻力特性和换热特性进行了计算,并与相同工况下的实验数据进行了对比[8],如表1所示。压降与换热系数的计算值均略高于实验值,其中换热系数平均误差6.8%,压降平均误差11.2%。
|
|
表 1 计算结果与实验值对比 |
从图3、4所示的局部温升及压降分布规律中还可以看出,由于波浪管周期性的几何结构,其每个周期内的流场和温度场分布趋势基本相同,且局部换热量和流动阻力最大的部位均出现在2个相邻弧段的连接处。因此本文仅对其中一段波峰至波谷之间的弯曲弧段进行分析,此弧段纵剖面和波峰及波谷处横截面上的流场及温度场分布如图5所示。

|
Download:
|
| 图 5 波浪管内流场分布 | |
由于波浪管特殊的几何结构,当流体流过如图5所示的一个弯曲弧段时,下侧和上侧流体的流动情况形成了明显差别。靠近下侧壁面流动的流体在流过弯曲弧段时处于背风侧,压力降低,流速上升;而靠近上侧壁面流动的流体在进入弯曲弧段时处于迎风侧,压力不断升高,流速逐渐下降。因而,靠近上侧壁面流动的流体压力梯度大于零,靠近下侧壁面流动的流体压力梯度小于零。在这种流动情况下,波浪管内靠上侧的高压流体产生了流动分离,形成了垂直于流动方向截面上的二次流。
不同工况下波浪管内横截面上的二次流动情况如图6所示。对于管内流动,当Re<2 000时,作用在流体上的粘性力起主导作用,直管中呈现明显的层流,各流层之间没有明显的相互掺混。而从图6中可以看出,即使在Re=18的极低雷诺数工况下,波浪管中二次流也呈现出2个明显的涡旋,这使得各流体微团之间相互掺混,提高了换热能力。由于这种涡旋在雷诺数极低的情况下就已经存在,而在相同工况下的直管中,极低的流速不足以使流体产生分离,因而此涡旋是由波浪管的特殊结构造成的,本文将其定义为二次流中的结构涡。

|
Download:
|
| 图 6 各工况二次流矢量图 | |
对于Re处于2 000~4 000的管内流动,作用在流体上的惯性力逐渐取代粘性力的主导作用,使流体分离能力变强,向湍流过渡,更易形成掺混和涡旋。在波浪管中当Re约为2 000时,靠近上侧壁面附近的二次流开始发生明显的弯转;在Re接近4 000时形成2个新的涡旋,这2个新的涡旋是由于湍流化程度升高产生的,因而本文称其为流动涡。
随着湍流化程度的升高,流动涡变得越来越明显,且向管道中心方向移动,随着流动涡的增大,结构涡变得越来越小。从图6(h)中可以看出,当雷诺数很大时,二次流中的流动涡起了主导作用,而结构涡已经变得不再明显,波浪管的结构对流动的相对影响变得越来越小。
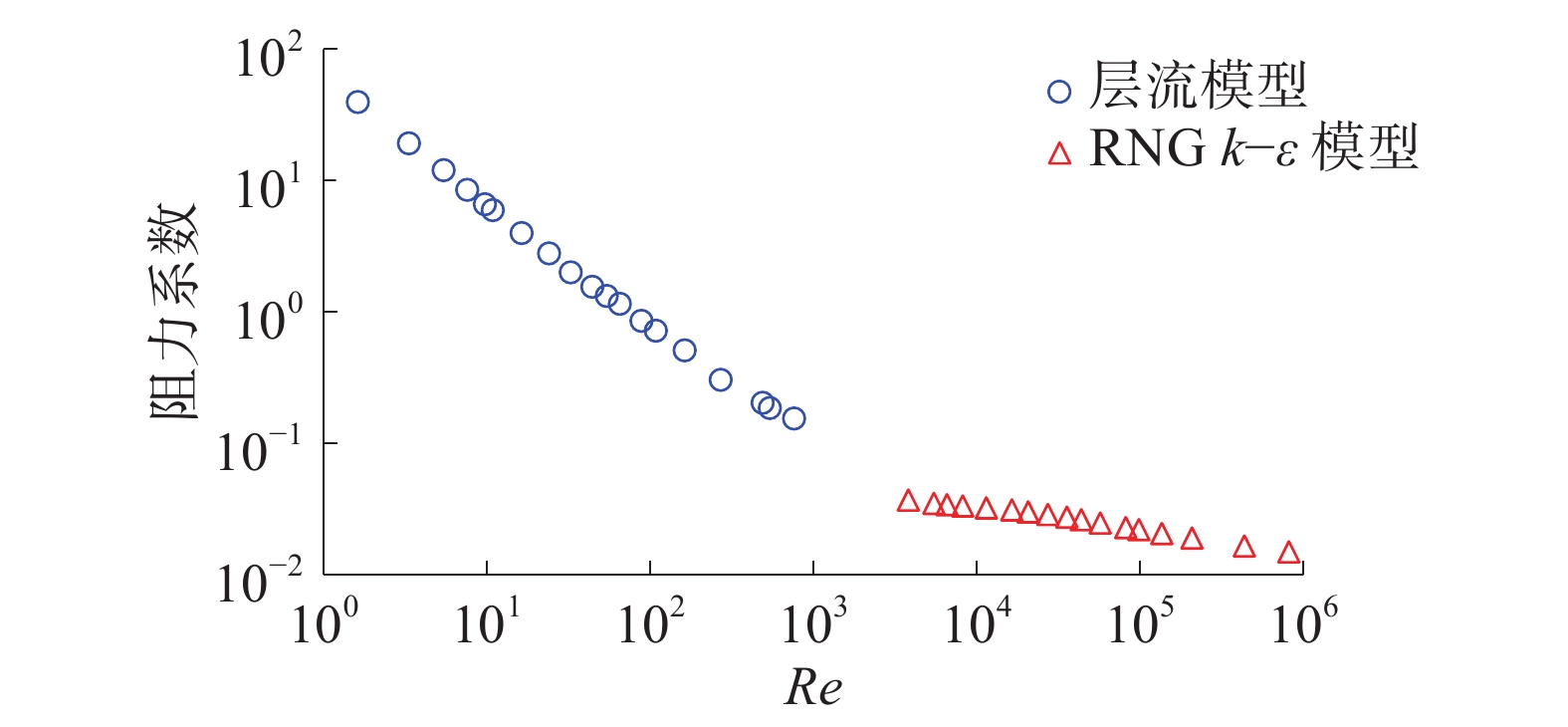
2.2 二次流对波浪管阻力特性的影响当Re<1 000时,采用层流模型进行计算;当Re>3 000时,采用RNGk-ε湍流模型进行计算,得到波浪管阻力系数随Re的分布如图7所示。
|
Download:
|
| 图 7 波浪管阻力系数分布 | |
在对数坐标下,波浪管的阻力系数随Re呈线性变化关系,但当Re<1 000和Re>3 000时斜率明显不同,因此波浪管阻力系数的变化趋势在Re处于1 000~3 000时发生了改变。结合图6也可看出,当Re在1 000~3 000时,阻力系数变化趋势发生改变的同时,流动涡也开始形成,这标志着惯性力的作用超过粘性力,波浪管内流体发生转捩并向更高湍流化程度发展。
2.3 二次流对波浪管换热特性的影响二次流的产生使得波浪管内流体的流动情况比同等情况下直管内的流动要复杂得多。波浪管中流体在二次流的作用下对壁面的冲刷能力增强,同时流体内部各微团之间的相互掺混作用也变强。这些效应都增强了波浪管的换热能力,但同时也增加了流动阻力,需要消耗更多的驱动压头。
在传热面积和流量相同的条件下,采用强化换热管综合评价系数R对波浪管换热能力的增强和流动损失的增加进行综合评价:
| $R = \frac{{N{u_{\rm{B}}}/N{u_{\rm{S}}}}}{{{{({f_{\rm{B}}}/{f_{\rm{S}}})}^{1/3}}}}$ |
式中:Nu为努塞尔数;f为阻力系数;下标B表示波浪管,下标S表示直管。
为进一步分析二次流对波浪管综合换热能力的影响,分别对不同Re下波浪管内的流动情况进行模拟,得到各Re下波浪管的强化换热综合系数R的分布如图8所示。

|
Download:
|
| 图 8 不同Re下波浪管强化换热综合系数分布 | |
在低雷诺数下,波浪管内二次流中的结构涡不仅促使了流体微团的相互掺混,而且冲刷了边界层使其变薄,因而增强了换热能力。但在低雷诺数工况下,相比换热能力的增强,流动阻力的增加并不明显,所以波浪管的强化换热综合评价系数R随雷诺数的增加明显上升。
而图8的曲线显示,Re超过约2 000后,波浪管的综合换热系数随流速的增加呈下降趋势。这从二次流的分布图中也可以得到解释。结合图5、6可以发现,二次流中的结构涡处于流速较高的位置,而流动涡处于流速较低的位置。结合图5中温度分布云图又可看出,结构涡处于温度梯度最大的位置,流动涡处于温度梯度最小的位置,且结构涡比流动涡更靠近壁面。因此,结构涡对波浪管强化换热能力的贡献要明显大于流动涡。
随着雷诺数的增加,流动涡变得越来越强,消耗的驱动压头也增加,但对换热能力的贡献相对结构涡较小。而结构涡逐渐减弱,对换热能力的贡献也明显降低。因而相比直管,波浪管换热能力的提升幅度有所减少而流动涡和结构涡消耗的总驱动压头并未减少,这导致在Re>2 000即流动涡开始形成后,波浪管的综合评价系数R开始下降。
3 结论1)波浪管内不存在严格意义上的层流,即使在极低雷诺数工况下,垂直流动方向的截面上也会产生二次流。且形成的二次流可分为2种,一种是由波浪管的特殊结构形成的结构涡,另一种是在湍流化程度升高后形成的流动涡。
2)流动涡的形成伴随着阻力系数变化趋势发生改变,标志着惯性力的作用超过粘性力,波浪管内流体发生转捩并向更高湍流化程度发展。
3)结构涡对波浪管综合换热性能的贡献明显大于流动涡。因而随着流动涡的形成和发展,波浪管的综合换热能力相比直管的提升幅度逐渐降低。
| [1] |
ABED W M, WHALLEY R D, DENNIS D J C, et al. Numerical and experimental investigation of heat transfer and fluid flow characteristics in a micro-scale serpentine channel[J]. International journal of heat and mass transfer, 2015, 88: 790-802. ( 0) 0)
|
| [2] |
李建华, 孙中宁, 吴国辉. 螺旋折流板波槽管换热器换热与阻力实验研究[J]. 应用科技, 2006, 33(8): 70-72. DOI:10.3969/j.issn.1009-671X.2006.08.020 ( 0) 0)
|
| [3] |
俞胜之, 阎昌琪, 王建军, 等. 摇摆对单相自然循环系统流动特性的影响分析[J]. 哈尔滨工程大学学报, 2017, 38(7): 1065-1071. ( 0) 0)
|
| [4] |
HAN D H, LEE K J. Single-phase heat transfer and flow characteristics of micro-fin tubes[J]. Applied thermal engineering, 2005, 25(11): 1657-1669. ( 0) 0)
|
| [5] |
吴国辉, 黄渭堂, 孙中宁. 断续螺旋折流板在管壳式换热器中的应用[J]. 应用科技, 2005, 32(4): 45-47. DOI:10.3969/j.issn.1009-671X.2005.04.016 ( 0) 0)
|
| [6] |
BHUTTA M M A, HAYAT N, BASHIR M H, et al. CFD applications in various heat exchangers design[J]. Applied thermal engineering, 2012, 32(1): 1-12. ( 0) 0)
|
| [7] |
YANG Ru, CHIANG F P. An experimental heat transfer study for periodically varying-curvature curved-pipe[J]. International journal of heat and mass transfer, 2002, 45(15): 3199-3204. DOI:10.1016/S0017-9310(02)00023-6 ( 0) 0)
|
| [8] |
朱升, 孙中宁, 范广铭. 微波浪管传热与阻力特性实验研究[J]. 原子能科学技术, 2011, 45(12): 1444-1448. ( 0) 0)
|
| [9] |
YANG R, CHANG S F, WU W. Flow and heat transfer in a curved pipe with periodically varying curvature[J]. International communications in heat and mass transfer, 2000, 27(1): 133-143. DOI:10.1016/S0735-1933(00)00092-0 ( 0) 0)
|
| [10] |
ROSAGUTI N R, FLETCHER D F, HAYNES B S. Low-Reynolds number heat transfer enhancement in sinusoidal channels[J]. Chemical engineering science, 2007, 62(3): 694-702. DOI:10.1016/j.ces.2006.09.045 ( 0) 0)
|
| [11] |
帅科, 王彤, 谷传纲. 波浪管内部流动的三维数值模拟[J]. 风机技术, 2006(2): 10-14. DOI:10.3969/j.issn.1006-8155.2006.02.003 ( 0) 0)
|
| [12] |
朱升, 孙中宁, 范广铭. 低流速时波浪管内流动与传热特性数值分析[J]. 核动力工程, 2011, 32(6): 51-55. ( 0) 0)
|
| [13] |
VERSTEEG H K, MALALASEKERA W. An Introduction to Computational Fluid Dynamics[M]. New York: Longman, 1995.
( 0) 0)
|
| [14] |
Fluent Inc. FLUENT User’s Guide[M]. Lebanon: Fluent Inc., 2003.
( 0) 0)
|
| [15] |
康顺, 石磊, 戴丽萍, 等. CFD模拟的误差分析及网格收敛性研究[J]. 工程热物理学报, 2010, 31(12): 2009-2013. ( 0) 0)
|
 2020, Vol. 47
2020, Vol. 47


