立体匹配是通过寻找同一场景在不同视角下的2幅或多副图像的像素点,逐像素点获取像素点间的二维视差,从而恢复场景深度。匹配的过程,是摄影测量和计算机视觉领域的重要研究课题,在机器人导航、无人驾驶、虚拟现实和三维重建等领域有着广泛的应用[1]。Scharstein等[2]对典型的立体匹配算法进行了研究和总结,形成了立体匹配算法的理论框架,根据优化方法的不同,将现有的立体匹配算法分为全局算法和局部算法这2类。全局立体匹配算法通过构建全局能量函数,进行最小化来求取视差值,该算法精度高但是计算复杂,常见的全局算法有置信度传播匹配算法(belief propagation, BP)[3]、图割算法(graph cut, GC)[4]和动态规划算法(dynamic programming, DP)[5]等。局部算法计算局部窗口像素的最优值,通过聚合代价进行误差值计算,具有复杂度低、效率高的特点,在实际过程中易于实现。
常见的局部立体匹配方法,主要包括自适应支持窗口法(variable support window,VSW)和自适应支持权重法(adaptive support weight,ASW)。基于VSW的方法通过图像特征来寻找最佳的支持窗口。Zhang等[6]提出了一种局域十字交叉的自适应窗口,利用相邻像素的颜色差异和空间距离的关系,在水平和垂直方向上进行像素扩展,形成一个十字交叉区域。Mei等[7]在此基础上提出了双距离阈值和双色彩阈值准则的方法来构建聚合区域,提高了匹配精度。基于ASW的方法是通过利用对固定窗口内的像素分配不同的权重来进行代价聚合。He[8]提出引导滤波的概念,Hosni等[9]将其作为代价聚合方法,引导滤波器具有计算复杂度和窗口大小无关的优点,因此在实时系统中得到广泛应用。
在实际应用过程中,边界区域部分属于容易出现深度值不连续的特殊区域,此时,所构建的区域延伸方向容易在不同深度值区域进行延伸,导致视差值不连续现象。对此,本文提出了一种基于边缘约束的自适应引导滤波的立体匹配算法解决该问题。在代价聚合过程中,将自适应区域和引导滤波算法相结合,但此时的引导滤波窗口不是固定大小的窗口,会导致边界点的交叉区域过度延伸,对此,引入边缘约束条件,使得边界点的交叉区域包含更多的有效像素点,从而提高边界区域的匹配精度,使得视差图能够更好地保持边界特征。
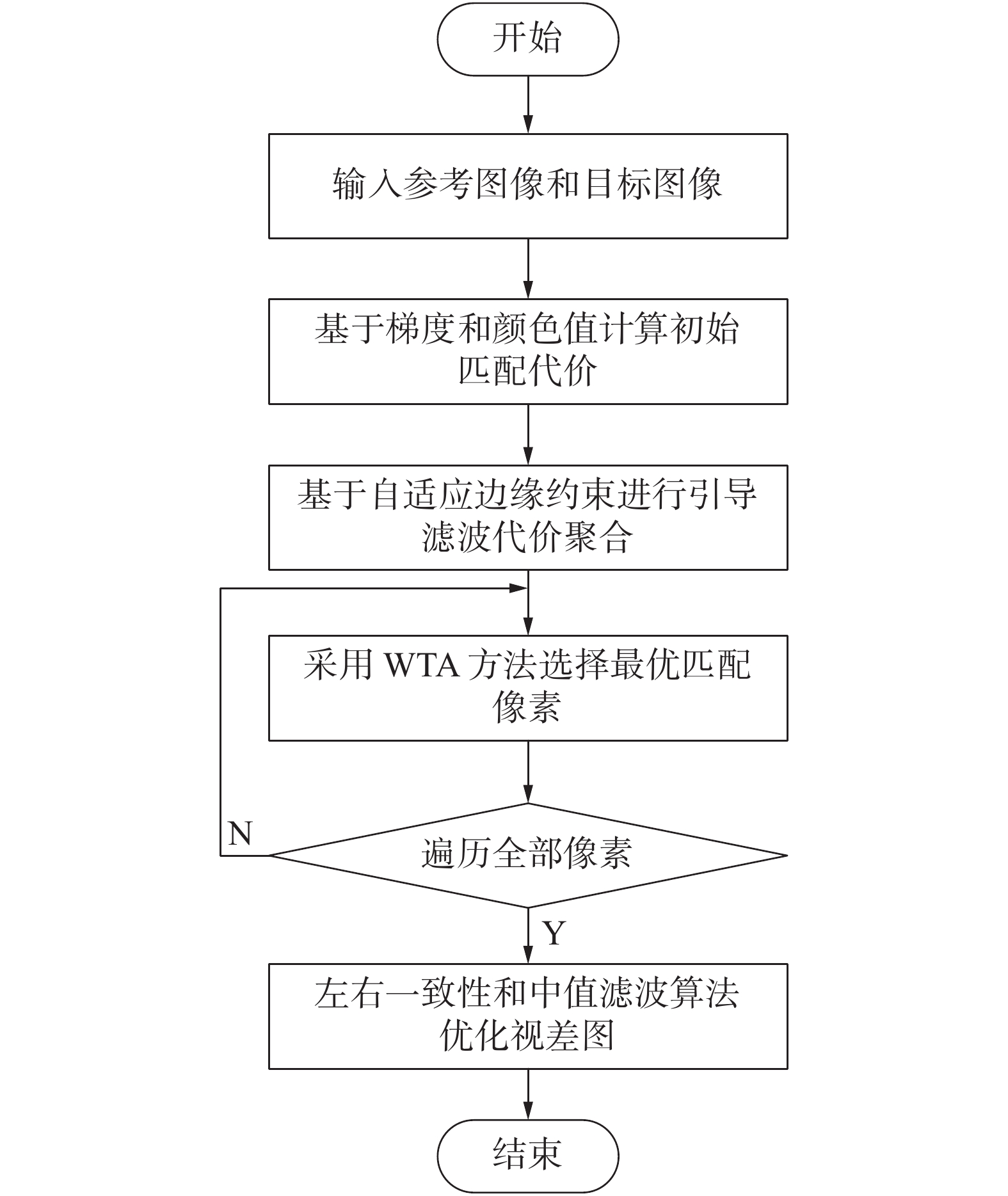
1 局部立体匹配算法框架局部匹配代价计算可以分为4步:1)匹配代价计算;2)代价聚合;3)视差计算;4)视差精细化。图1为基于边缘约束的自适应引导滤波立体匹配算法流程。
|
Download:
|
| 图 1 基于边缘约束的自适应引导滤波立体匹配算法流程 | |
常见的局部代价计算方法有绝对误差和(sum of absolute differences, SAD)、误差平法和算法(sum of squared differences, SSD)、归一化积相关算法(normalization cross-correlation, NCC)和自适应窗口等。代价聚合是局部立体匹配算法过程中最重要的一步,利用支持窗口内的初始匹配代价进行求和或者取平均值来提高匹配可靠性,最终,采用胜者为王策略取代价最低值作为该点视差值。但左右视图会由于成像视角和光照等因素影响,左右图像中均会出现无法匹配区域,在左右视差图中也会存在同一位置其视差值较大的位置,这就需要对视差图进行精细化后处理,判断寻找错误视差点,然后进行重新计算,视差图中也存在空白区域,需要进行填充操作。
2 本文立体匹配算法 2.1 匹配代价计算匹配代价是衡量左右2幅图像视差相似性的指标,通过构建一个大小为
| $\begin{array}{*{20}{c}} {C(i,d) = \alpha \min \left( {\left\| {{I_l}(i) - {I_r}\left( {{i_d}} \right),{T_1}} \right\|} \right)}+\\ {\left. { (1 - \alpha ) \min \left( {\left\| {{\nabla _x}{I_l}(i) - {\nabla _x}{I_r}\left( {{i_d}} \right),{T_2}} \right\|} \right)} \right)} \end{array}$ |
式中:
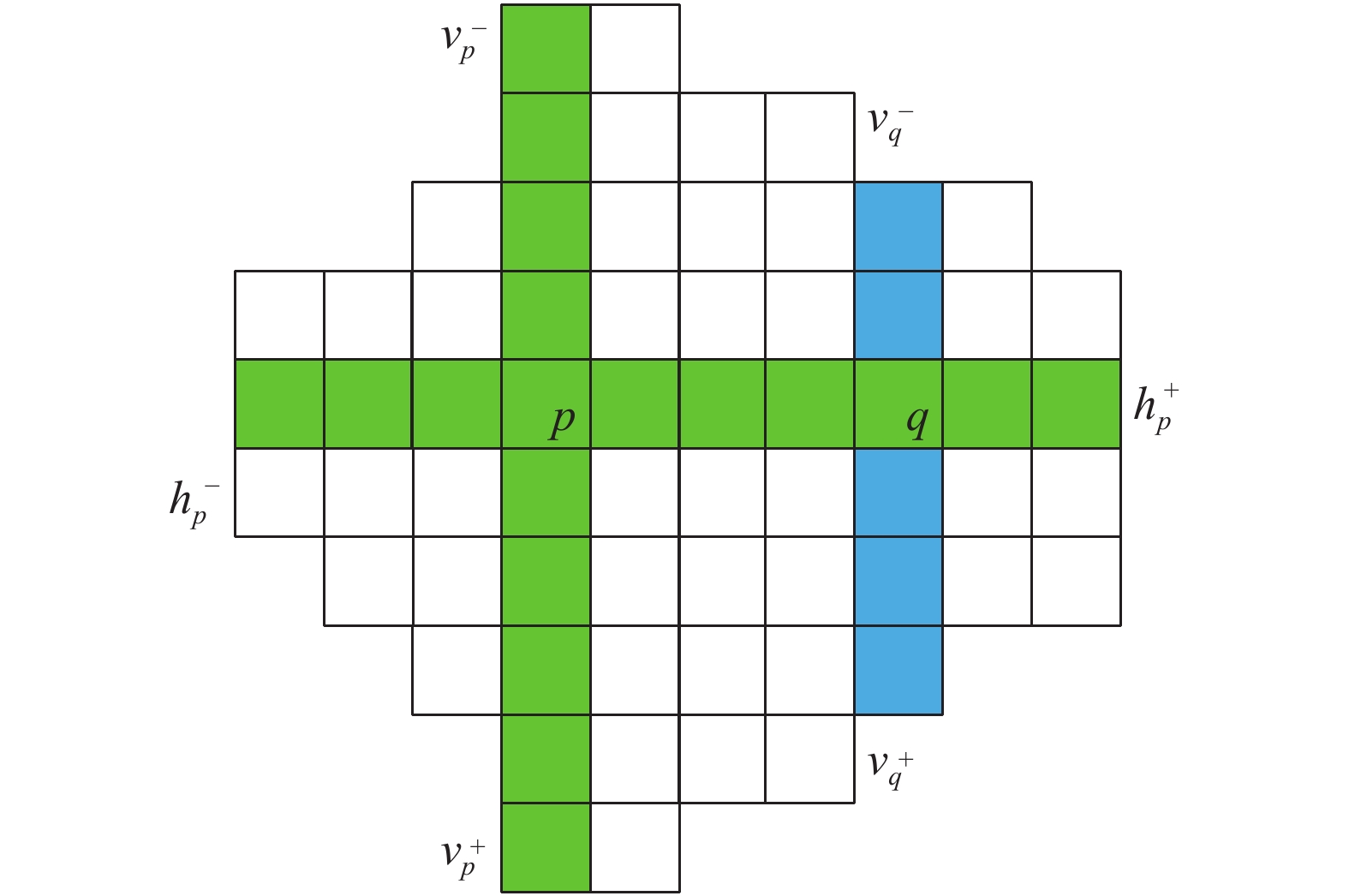
聚合窗口算法的前提条件是假设支持窗口内部的像素点具有同时视差值。基于像素点建立十字交叉的窗口进行窗口内像素聚合。核心思想是利用待匹配点的颜色信息和空间信息进行扩散约束,以此来构建符合每个像素点周围的交叉区域[11]。该算法的关键步骤是构建参考图像与目标图像中待匹配点的十字交叉结构,通过一定的判断准则分别计算得到每个待匹配像素点在水平和垂直方向上的臂长。
如图2所示,定义水平方向上臂长的最左位置为
|
Download:
|
| 图 2 十字交叉区域构建 | |
| $\delta ({p_1},{p_2}) = \left\{ {\begin{array}{*{20}{l}} {1,}\;\;{\left( {{{\max }_{i = R,G,B}}\left| {{I_i}({P_1}) - {I_i}(P)} \right|} \right) \leqslant \tau } \\ {0,\;\;{\text{其他}}} \end{array}} \right.$ | (1) |
| ${r^*} = {\max\limits_{r \in [1,L]}}\left( {1,r\prod\limits_{i \in [1,r]} \sigma \left( {p,{p_i}} \right)} \right) $ | (2) |
式中:
最后计算出像素点
| $V(p) = \{ (x,y)|x \in [{x_p} - v_p^ - ,{x_p} + v_p^ + ],y = {y_p}\} $ |
| $ U(P) = \mathop \cup \limits_{q \in V(p)} H(q) $ |
引导图滤波是常用的代价聚合计算方法,引导图滤波由于是基于盒滤波的方式实现的,整个算法的实现原理基于线性的方式,运算时间复杂度跟滤波器的大小无关,只与图像中的像素数目有关,其代价聚合为
| ${C^\prime }(p,d) = \sum\limits_q {{W_{p,q}}} (I)C(q,d)$ |
式中:
| ${Q_i} = {a_k}{I_i} + {b_k},\forall i \in {w_k}$ |
式中
通过构建损失函数来计算
| $E\left( {{a_k},{b_k}} \right) = \sum\limits_{i \in {w_k}} {\left( {{{\left( {{a_k}{I_i} + {b_k} - {p_i}} \right)}^2} + \varepsilon a_k^2} \right)} $ |
| ${a_k} = \frac{1}{{|{w_k}|}}\frac{{\displaystyle\sum\nolimits_{i \in {w_k}} {{I_i}{p_i}} - {\mu _k}{{\bar p}_k}}}{{\sigma _k^2 + \varepsilon }}$ |
| ${b_k} = {\bar p_k} - {a_k}{\mu _k}$ |
以灰度图像的计算为例,
| ${W_{p,q}} = \frac{1}{{{{\left| w \right|}^2}}}\sum\limits_{k:(p,q) \in {w_k}} {\left( {1 + \frac{{({I_p} - {\mu _k})({I_q} - {\mu _k})}}{{\sigma _k^2 + \varepsilon }}} \right)} $ | (3) |
式中:
由于传统的引导图滤波算法是基于固定窗口进行代价聚合的,匹配窗口的大小会对最终的匹配精度造成直接影响。若选用窗口过小,则会在弱纹理区域有较大的误差;若选用窗口较大,则在深度不连续区域误差较大,整个过程中没有充分考虑到窗口内部像素的差异性[14]。可以将自适应区域算法和引导滤波相结合,构建可变窗口的自适应引导滤波,充分利用各像素点的位置差异性。通过更改内核大小来对权重内核进行计算,核窗口将根据像素点的自适应区域进行调整,则式(3)的支持权重的计算方式可以变换为
| ${W_{p,q}} = \frac{1}{{\left| {{w_q}} \right|}}\sum\limits_{k \in {w_p}} {\left( {\frac{1}{{\left| {{w_k}} \right|}}\sum\limits_{q \in {w_k}} {\left( {1 + \frac{{({I_p} - {\mu _k})({I_q} - {\mu _k})}}{{\sigma _k^2 + \varepsilon }}} \right)} } \right)} $ |
式中
基于自适应区域的代价聚合方法依赖像素点之间的差异构建支持窗口,然而,在图像中,边界区域部分属于容易出现深度值不连续的特殊区域[15]。当引入了自适应区域引导滤波时,在边界上的边界点依据颜色阈值延伸臂长进行扩展,此时边界区域会沿着4个方向进行延伸,会导致部分区域的边界在进行滤波过程中分布不均衡,对于边缘区域的滤波操作会造成不同程度的影响,会产生边界不平滑现象,导致后续代价计算的匹配精度下降。因此,考虑在边缘点处添加约束条件,使得边缘处的窗口保持较小的范围,减少过多无关像素点的干扰。利用Canny[16]算法对图像处理获得其边缘图像,
| $\tau ({l_{pq}}) = - {\tau _{\max }}/{L_{\max }} \times {l_{pq}} + {\tau _{\max }}$ |
| ${D_s}(p,q) < {L_{\max }},{D_c}(p,q) < \tau \left( {{l_{pq}}} \right)$ |
| ${D_s}(p,q) = \left\{ {\begin{array}{*{20}{l}} {\min (r,{l_{pq}}),{{I}}(q) = 1} \\ {\max (r,{l_{pq}}),{\text{其他}}} \end{array}} \right.$ |
式中:
通过线性阈值进行操作,离像素点越近的位置,阈值越大;当距离像素点越远的时候,阈值变得越小。同时,在边缘点处,将该点的延伸臂长限制到一定的范围内,保证自适应区域不会包含太多的无关区域。
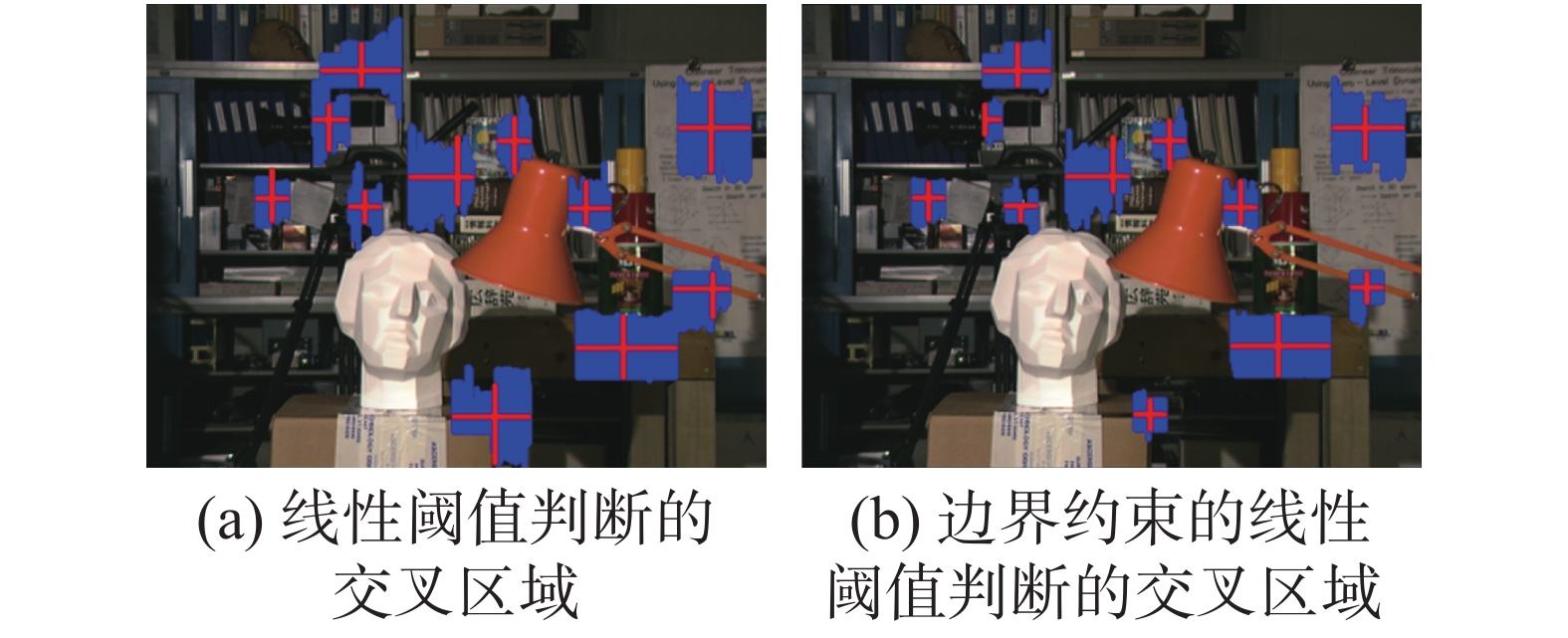
图3中是采用不同判断依据处理后得到的自适应区域,从图3(a)中看出,经过线性阈值的操作,该阈值变化受空间距离的影响,但交叉区域依然会包含过多无关像素。如图3(b)所示,经过边缘抑制,其构建的支持窗口区域明显缩小,原有的臂长延伸方向不变,但是会减小无关区域的大小,使得该区域包含了更多的有效像素,并且再也不会影响非边界区域的臂长延伸。
|
Download:
|
| 图 3 不同判决条件所构成的交叉区域 | |
图4是进行自适应引导滤波代价聚合视差图,在图4(a)中可以看出,只考虑将颜色阈值作为判断依据,由于其在边界区域的自适应区域范围过大,导致在代价聚合计算后的视差图中存在边缘过于平滑的现象。如图4(b)中的椭圆区域,将边缘约束引入之后,避免了边缘点处自适应区域的过度延伸,使得自适应区域能够包含更多的有效像素,在代价聚合过程中视差图中图像的边界区域能够更好地保持着原图的细节特征。

|
Download:
|
| 图 4 两种引导滤波算法处理后的视差 | |
经过代价聚合之后,重新计算得到的匹配代价的计算值为
| ${d_p} = \arg \mathop {\min }\limits_{d \in D} [\widehat C(p,d)]$ |
式中
| $|{d_L}(i) - {d_R}[{\rm{i}} - {d_L}(i)]| < {\delta _0}$ |
式中:
本文实验在Matlab2016a平台下进行编程实现。为验证代价计算和代价聚合的算法有效性,采用Middlebury[17]立体匹配评估测试平台提供的数据集进行实验。按照统一评价标准,设误差阈值参数为1。实验中所涉及的参数如表1所示。
|
|
表 1 实验参数设置 |
为验证边缘约束的自适应代价聚合算法的有效性,将固定窗口大小的引导滤波器立体匹配算法和改进后的代价聚合对Middlebury测试平台的标准图像进行实验。图5为Middleburry2006数据集的5组图像Baby1、Baby2、Baby3、Flowerpots和Bowling2的实验结果。

|
Download:
|
| 图 5 引导滤波算法与本文算法对比 | |
从图5中可以看出,相较于固定尺度支持窗口的引导滤波器代价聚合算法,改进算法在图像边界纹理区域的误匹配现象明显得到改善,匹配精度有所提升。这是由于在自适应引导滤波的过程中,考虑到边界像素点的特殊性,添加了阈值因子,使得原边界点按照原有的延伸方向进行伸展的过程中,包含更多的有效区域,减小了无关区域的干扰,有效减少了边界的不连续区域的产生,提高了算法的匹配精度。表2为2种聚合算法的误匹配率。
|
|
表 2 不同代价聚合算法误匹配率 |
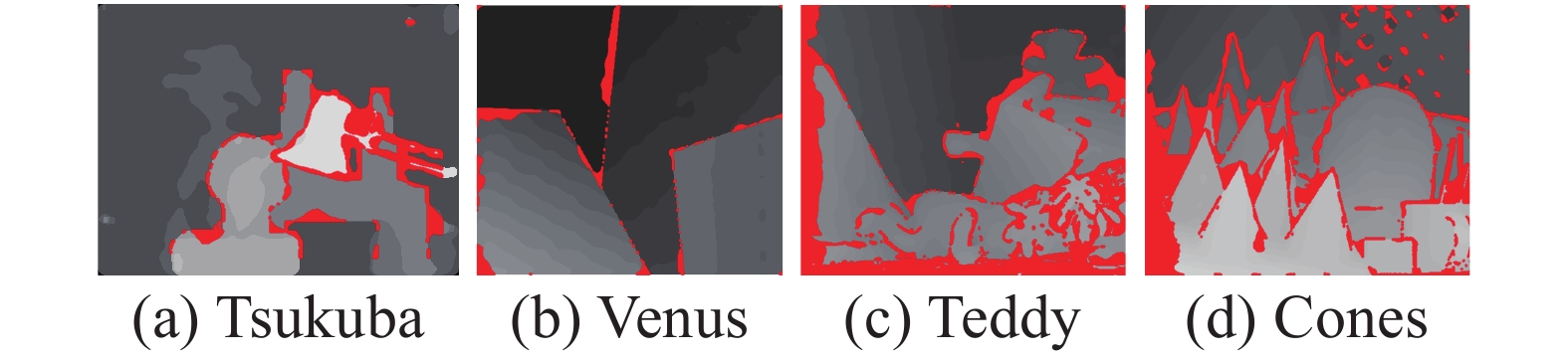
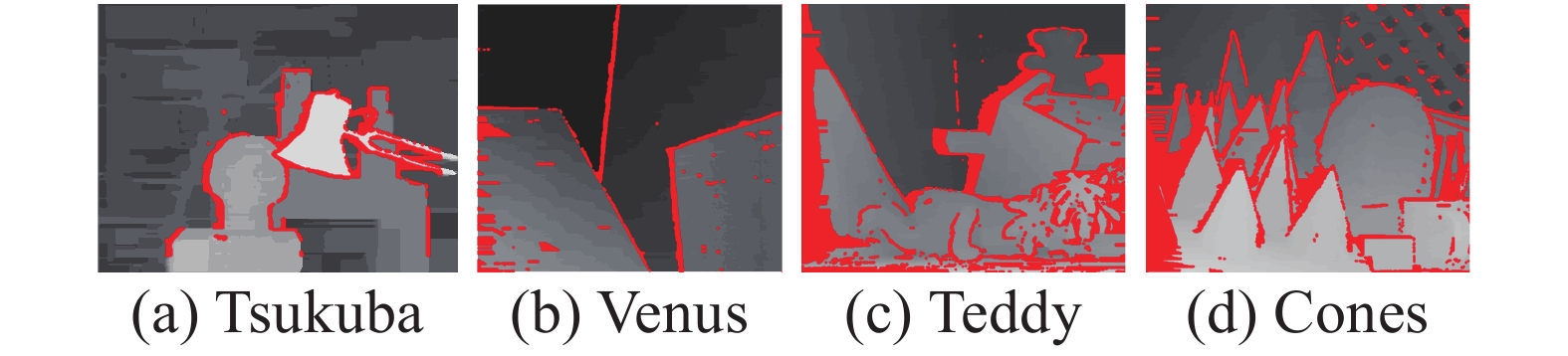
为验证本文的算法有效性能,将本文算法在Middlebury提供的4组标准测试图上进行实验,并与其它局部立体算法进行对比。其中Tsukuba、Venus、Teddy和Cones的视差搜索范围分别为[0,15]、[0,19]、[0,59]、[0,59],缩放倍数为[16,8,4,4]。本文算法分别与多种经典立体匹配算法进行对比分析,所采用的算法分别为LCVB-DEM[18]、CostFilter[9]、SMPF[19]和AdaptAggrDP[20],其中CostFilter和AdaptAggrDP均为局部立体匹配算法,比较各个算法在不同区域的误匹配率,其中误匹配视差结果如图6~11所示,红色部分表示误匹配的视差值。

|
Download:
|
| 图 6 Middlebury数据集图像 | |

|
Download:
|
| 图 7 CostFilter算法误匹配视差 | |
|
Download:
|
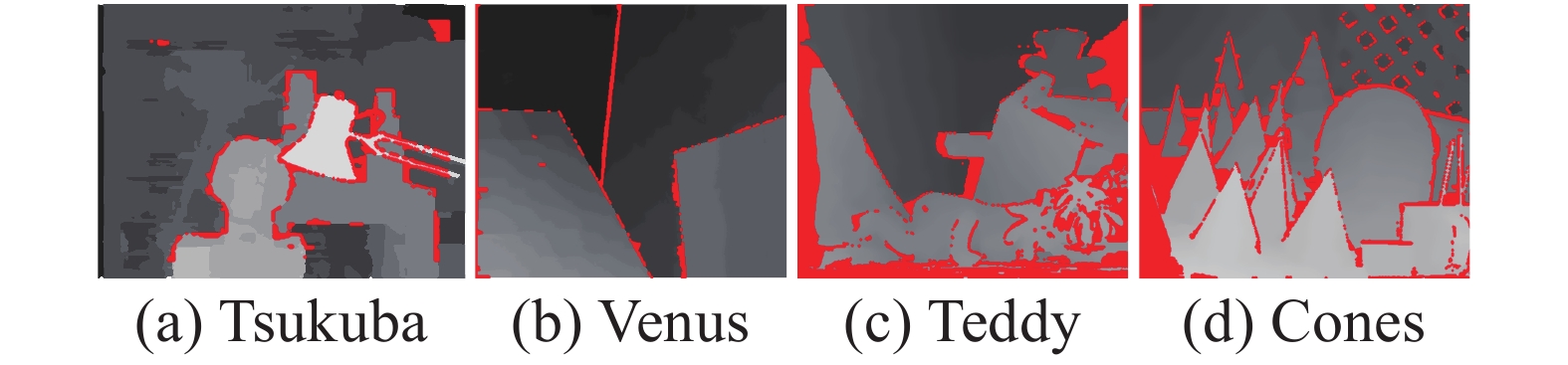
| 图 8 SMPF算法误匹配视差 | |
|
Download:
|
| 图 9 LCVB-DEM算法误匹配视差 | |
|
Download:
|
| 图 10 AdaptAggrDP算法误匹配视差 | |

|
Download:
|
| 图 11 本文算法误匹配视差 | |
在以上算法处理的结果图6~11中,红色部分均表示误匹配区域。由结果可以明显看出相较于AdaptAggrDP、SMPF算法,本文算法在各个图像中的红色区域明显减小,并且本文算法产生的深度图在边缘细节方面表现较好。在Tsukuba图像中,本文算法在台灯和人物雕塑部位有较少的误匹配点出现,而其他算法在该区域部分的误匹配点较为连续和稠密。在Vensus图像中,LCVB-DEM算法处理后的图像,在边缘处的红色误匹配点明显较多,而本文所提出的算法,在深度不连续的边缘处的误匹配点明显较少,这是由于充分利用自适应引导滤波的优势,充分利用各个像素点的交叉区域的特异性,并限制了边缘处的过度延伸,使得边缘处的细节得到更好的还原。在Cones图像中,本文算法在图像中的左区域误匹配点相较于其他算法有明显减少,其中,在深度不连续区域依然保持良好。进一步对比各算法在不同区域的误匹配率,来比较各个算法之间的差异性。表3为各个立体匹配算法的误匹配率。
|
|
表 3 立体匹配算法误匹配率比较 |
表中:N-occ表示非遮挡区域的误匹配率;
本文以局部立体匹配算法为基础,通过将自适应支持窗口算法和自适应权重算法相结合,并引入了边缘约束思想,提出了一种基于自适应边缘约束的自适应引导滤波的局部立体匹配算法。
1)与固定窗口大小的引导滤波算法相比,本文的自适应引导滤波算法可以根据各个像素点所构建的交叉区域进行滤波操作,充分利用各个像素点的差异性,并且考虑边缘点的特殊部分,使得本文算法在最终视差图中能够较好地保留边界结果。
2)自适应引导滤波由于在代价聚合过程中需要计算每个像素点的交叉区域,所以在算法的整体运算时间上会有所增加,要使立体匹配算法能够真正满足实时性的要求,可以考虑使用并行运算实现加速。
| [1] |
BLEYER M, BREITENEDER C.Stereo matching state-of-the-art and research challenges [M]. London,Springer, 2013: 143-79.
( 0) 0)
|
| [2] |
SCHARSTEIN D, SZELISKI R. Stereo matching with non-linear diffusion; proceedings of the computer vision and pattern recognition[J]. International journal of computer vision, 1998, 28(2): 155-174.
( 0) 0)
|
| [3] |
SUN J, SHUM H Y, ZHENG N. Stereo matching using belief propagation[J]. IEEE transactions on pattern analysis and machine intelligence, 2003, 25(7): 787-800. ( 0) 0)
|
| [4] |
KOLMOGOROV V, ZABIH R. Computing visual correspondence with occlusions using graph cuts[C]//Proceedings Eighth IEEE International Conference on Computer Vision. Barcelona, Spain, 2001, 2: 508-515.
( 0) 0)
|
| [5] |
VAN MEERBERGEN G, VERGAUWEN M, POLLEFEYS M, et al. A hierarchical symmetric stereo algorithm using dynamic programming[J]. International journal of computer vision, 2002, 47(1-3): 275-85. ( 0) 0)
|
| [6] |
ZHANG K, LU J, LAFRUIT G. Cross-based local stereo matching using orthogonal integral images[J]. IEEE transactions on circuits and systems for video technology, 2009, 19(7): 1073-1079. DOI:10.1109/TCSVT.2009.2020478 ( 0) 0)
|
| [7] |
MEI X, SUN X, ZHOU M, et al. On building an accurate stereo matching system on graphics hardware[C]// Proceedings of 2011 IEEE International Conference on Computer Vision Workshops . Barcelona, Spain, 2011: 467-474.
( 0) 0)
|
| [8] |
HE K, SUN J, TANG X. Guided image filtering[J]. IEEE transactions on pattern analysis and machine intelligence, 2012, 35(6): 1397-409. ( 0) 0)
|
| [9] |
HOSNI A, RHEMANN C, BLEYER M, et al. Fast cost-volume filtering for visual correspondence and beyond[J]. IEEE transactions on pattern analysis and machine intelligence, 2012, 35(2): 504-11. ( 0) 0)
|
| [10] |
闫利, 王芮, 刘华, 等. 基于改进代价计算和自适应引导滤波的立体匹配[J]. 光学学报, 2008, 38(11): 257-67. ( 0) 0)
|
| [11] |
HE K, GE Y, ZHEN R, et al. Fast adaptive support-weight stereo matching algorithm[J]. Transactions of Tianjin University, 2017, 23(3): 295-300. DOI:10.1007/s12209-017-0034-5 ( 0) 0)
|
| [12] |
葛云峰. 自适应权重立体匹配算法研究 [D].天津: 天津大学, 2017.
( 0) 0)
|
| [13] |
王志, 朱世强, 卜琰. 改进导向滤波器立体匹配算法[J]. 浙江大学学报(工学版), 2016, 50(12): 2262-2269. ( 0) 0)
|
| [14] |
黄学然. 基于双目立体视觉的三维重建技术研究 [D].西安: 西安电子科技大学, 2018.
( 0) 0)
|
| [15] |
程德强, 庄焕东, 于文洁, 等. 基于边缘加权的跨尺度局部立体匹配算法[J]. 激光与光电子学进展, 2019, 56(21): 156-64. ( 0) 0)
|
| [16] |
CANNY J. A computational approach to edge detection[J]. IEEE transactions on pattern analysis and machine intelligence, 1986(6): 679-698. ( 0) 0)
|
| [17] |
SCHARSTEIN D, PAL C. Learning conditional random fields for stereo[C]// Proceedings of 2007 IEEE Conference on Computer Vision and Pattern Recognition. Minneapolis, Minnesota, 2007: 1-8.
( 0) 0)
|
| [18] |
MARTINS J A, RODRIGUES J M, DU BUF H. Luminance, colour, viewpoint and border enhanced disparity energy model[J]. PloS one, 2015, 10(6): e0129908. DOI:10.1371/journal.pone.0129908 ( 0) 0)
|
| [19] |
PLOUMPIS S, AMANATIADIS A, GASTERATOS A. A stereo matching approach based on particle filters and scattered control landmarks[J]. Image and vision computing, 2015, 38: 13-23. DOI:10.1016/j.imavis.2015.04.001 ( 0) 0)
|
| [20] |
WANG L, YANG R, GONG M, et al. Real-time stereo using approximated joint bilateral filtering and dynamic programming[J]. Journal of real-time image processing, 2014, 9(3): 447-461. DOI:10.1007/s11554-012-0275-4 ( 0) 0)
|
 2020, Vol. 47
2020, Vol. 47


