2. 北京遥感设备研究所,北京 100854
2. Beijing Institute of Remote Sensing Equipment, Beijing 100854, China
信号的波达方向(direction of arrival, DOA)估计在阵列信号处理领域占据重要地位,广泛应用于雷达、医学诊疗等领域,近年来学者们进行了大量的研究,取得了非常显著的成果[1-3]。以MUSIC[4]和ESPRIT[5]算法为代表的经典子空间分解类算法,实现简单且分辨率高,并且在此基础上发展出了多种改进算法[6-8],但是这类算法运算量大,需要在信噪比高且快拍数多的情况下才能得到较好的估计性能。压缩感知[9-10]理论是一个新兴起的领域,它能够突破奈奎斯特采样定理的限制,压缩感知理论中的很多重构算法都被用于DOA估计中,其中平滑
针对稀疏阵列中贪婪算法DOA估计求解问题,本文引入广义正交匹配追踪(generalized orthogonal matching pursuit, GOMP)用于DOA估计,仿真表明直接将GOMP算法用于DOA估计较OMP算法性能有所提高;为了进一步提高DOA估计的精度,引入最优化理论中的最速下降法,提出基于最速下降法的改进GOMP算法。
1 基于稀疏表示的DOA估计模型假设有一个由
| ${{y}}(t) = {{Ax}}(t) + {{n}}(t)$ | (1) |
| ${{A}} = \left[ {{{a}}\left( {{\theta _1}} \right),{{a}}\left( {{\theta _2}} \right), \cdots ,{{a}}\left( {{\theta _N}} \right)} \right]$ | (2) |
| ${{a}}\left( {{\theta _n}} \right) = {\left[ {1,{{\rm{e}}^{{\rm{j}}{\varphi _1}}}, \cdots ,{{\rm{e}}^{{\rm{j}}(M - 1){\varphi _n}}}} \right]^{\rm{T}}}$ |
| ${\varphi _n} = 2{\text{π}}d\sin {\theta _n}/\lambda ,n \in \left\{ {1,2, \cdots ,N} \right\}$ |
式中:
稀疏表示的DOA估计就是在已知阵列接收矢量
由式(1)、(2)可知,
为了找出
基于OMP算法的DOA估计方法,耗时比较长且估计的精度不高,为了提高DOA估计精度,采用广义正交匹配追踪算法来求解DOA估计。
OMP算法和GOMP算法均是通过贪婪迭代从阵列流型矩阵
最速下降法基于最优化理论[20],从梯度的角度来求解最优化问题。函数
| $f({{x}}) = f({{{x}}_k}) + \nabla f{({{{x}}_k})^{\rm{T}}}({{x}} - {{{x}}_k}) + o({{x}})$ |
式中:
由柯西−施瓦兹不等式可知:
| $\left| {{{d}}_k^{\rm{T}}{{{g}}_k}} \right| \leqslant \left| {{{{d}}_k}} \right|\left| {{{{g}}_k}} \right|$ |
当且仅当
最速下降法在每次迭代时选择一个合适的步长,使得目标函数每次减小的程度最大,即每次得到的值和目标函数值之间的差距最小。用
| ${a_k} = \arg \min f\left( {{{{x}}_k} - a{{{g}}_k}} \right)$ |
梯度的迭代为
| ${{{x}}_{k + 1}} = {{{x}}_k} - a{{{g}}_k}$ |
因此计算步长的公式就是为找到最好的点
最速下降法的过程可以表示为在每次迭代中,从
将函数的类型扩展至二次型,设函数为
| $f({{x}}) = \frac{1}{2}{{{x}}^{\rm{T}}}{{Q}}{{x}} - {{{b}}^{\rm{T}}}{{x}}$ |
式中:
| ${{{g}}_k} = \nabla f({{x}}) = {{Q}}{{x}} - {{b}}$ |
迭代表示为
| ${{{x}}_{k + 1}} = {{{x}}_k} - a{{{g}}_k}$ |
步长为
| ${a_k} = \arg \min f\left( {{{{x}}_k} - a{{{g}}_k}} \right)$ |
在
| ${{{\varphi}}'}_k(a) = {({{{x}}_k} - a{{{g}}_k})^{\rm{T}}}{{Q}}( - {{{g}}_k}) - {{{b}}^{\rm{T}}}( - {{{g}}_k})$ |
当
将最速下降法和GOMP相结合得到改进GOMP算法,改进算法在信号重构时不使用计算量大的最小二乘法,而是沿着负梯度方向进行搜索而得到最优解。
改进算法中迭代选择原子及更新索引集的过程和GOMP算法相一致,在恢复信号过程中,GOMP等贪婪算法均使用最小二乘法进行重构,其矩阵公式为
用
| $ \begin{array}{c} {a_i} = \dfrac{{\left\langle {{{{g}}_i},{{{g}}_i}} \right\rangle }}{{\left\langle {{{{g}}_i},{{{\varPsi }}_i}^{\rm{T}}{{{\varPsi }}_i}{{{g}}_i}} \right\rangle }} = \dfrac{{\left\langle {{{{\varPsi }}_i}^{\rm{T}}{{{r}}_i},{{{g}}_i}} \right\rangle }}{{\left\langle {{{{g}}_i},{{{\varPsi }}_i}^{\rm{T}}{{{\varPsi }}_i}{{{g}}_i}} \right\rangle }} =\\ \dfrac{{\left\langle {{{{r}}_i},{{{c}}_i}} \right\rangle }}{{\left\langle {{{{\varPsi }}_i}{{{g}}_i},{{{\varPsi }}_i}{{{g}}_i}} \right\rangle }} = \dfrac{{\left\langle {{{{r}}_i},{{{c}}_i}} \right\rangle }}{{\left\| {{{{c}}_i}} \right\|_2^2}} \end{array} $ | (3) |
式中
| ${{{x}}_i} = {{{x}}_{i - 1}} + {a_i}{{{g}}_i}$ |
最后更新残差:
| ${{{r}}_i} = {{{r}}_{i - 1}} - {a_i}{{{c}}_i}$ | (4) |
完成循环,判断是否满足迭代停止条件。
改进后的GOMP算法步骤可总结如下:
1)初始化残差
2)计算残差和测量矩阵
3)更新索引集
4)利用
5)利用式(4)更新残差;
6)若满足迭代停止条件,根据索引集
本文通过MATLAB仿真验证所提算法的可行性,并与
| ${\rm{RMSE}} = \sqrt {\frac{1}{{MK}}{{\sum\limits_{m = 1}^M {\sum\limits_{k = 1}^K {\left( {{{\hat \theta }_{km}} - {\theta _{km}}} \right)^2} } }}} $ | (5) |
式中:
实验1 残差二范数对比实验。设2个信号源以入射角10°、30°入射到均匀直线阵列上,对结合最速下降法的改进GOMP算法和原始GOMP算法进行性能对比,在单快拍条件下,比较2种情况下的残差二范数,进行500次蒙特卡洛实验,仿真结果如图1所示。

|
Download:
|
| 图 1 改进GOMP算法与GOMP算法残差比较 | |
通过图1可以看出,改进GOMP算法比GOMP算法的残差值小,随着信噪比的提升,改进算法的残差值下降更快,可见对GOMP算法的优化是有效的。
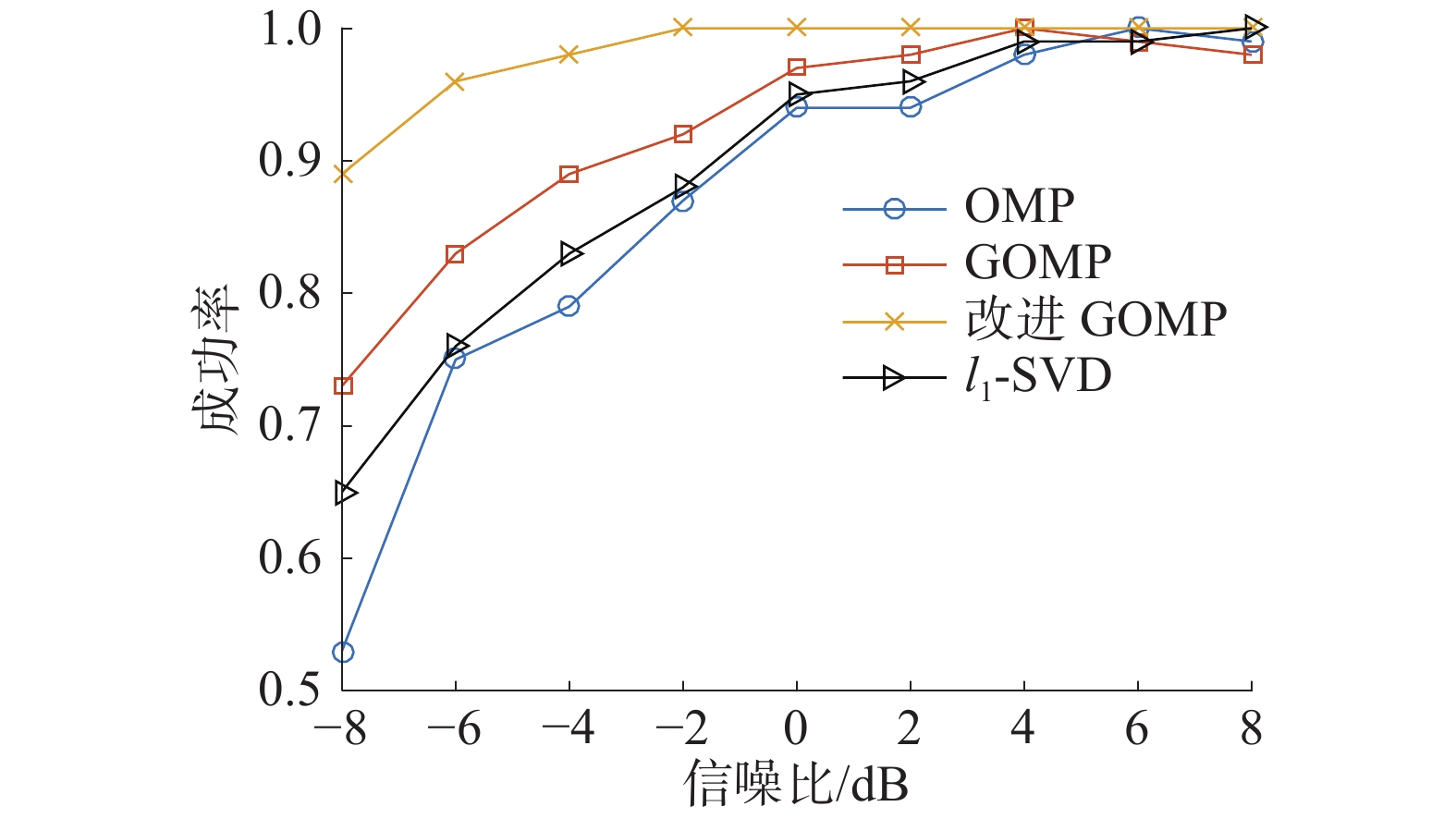
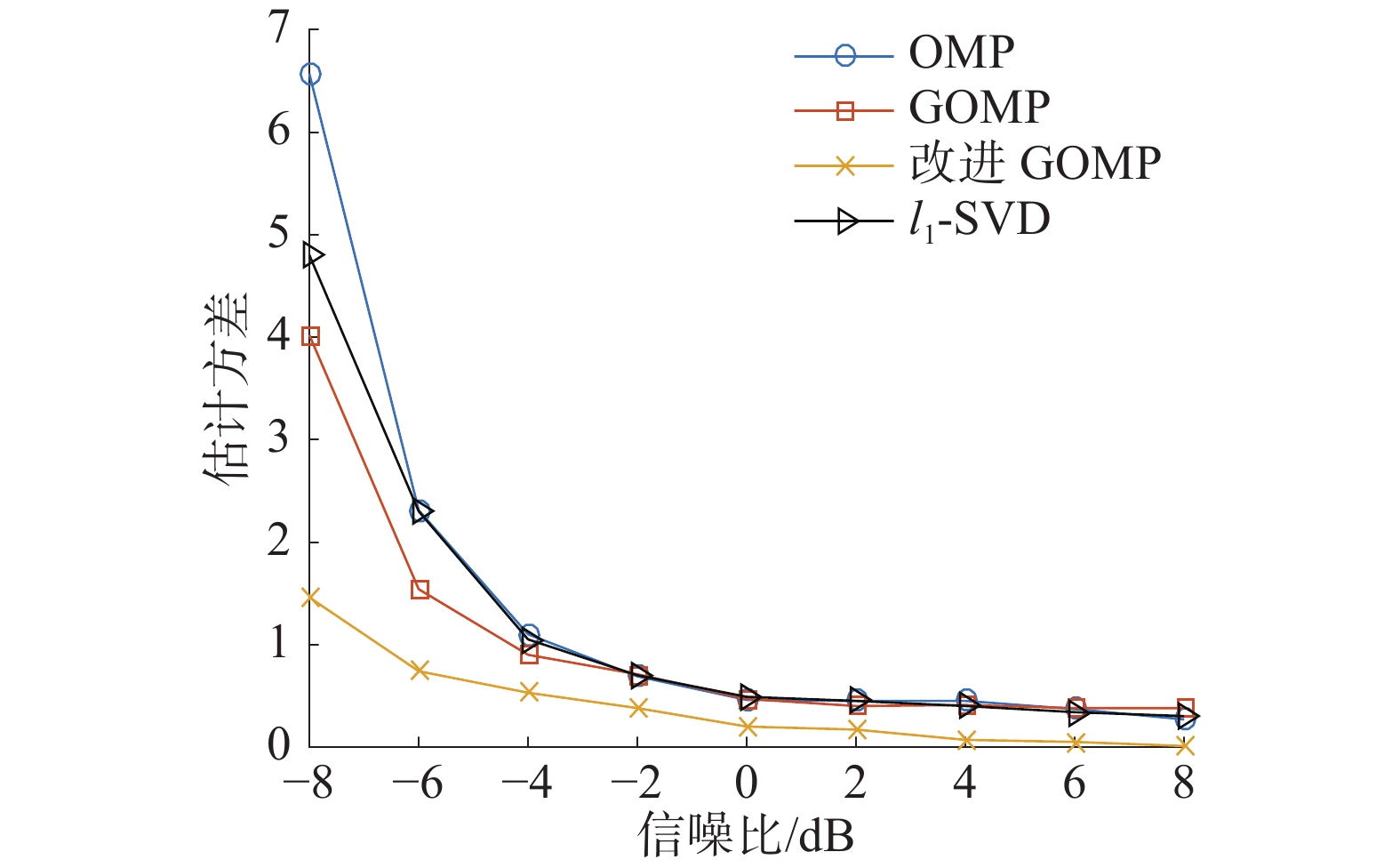
实验2 不同信噪比下DOA估计的性能对比实验。设2个信号源以入射角10°、30°入射到均匀直线阵列上,均匀线阵阵元数为12,快拍数为8,信噪比以2 dB为步进从−8 ~8 dB变化,在相同的实验条件下进行500次蒙特卡洛实验。当估计偏差小于或等于1°时,认为估计成功,在不同信噪比条件下,统计各个条件下的成功概率和均方根误差,仿真结果如图2、3所示。
|
Download:
|
| 图 2 不同信噪比下DOA估计成功概率 | |
|
Download:
|
| 图 3 不同信噪比下DOA估计均方根误差 | |
在不同信噪比条件下,由图2可以看出,与其他3种算法相比,改进GOMP算法具有更高的估计成功概率,在信噪比为−2 dB时估计成功概率接近100%。由图3可以看出,在高信噪比情况下,4种算法均趋于稳定,改进GOMP算法具有更小的均方根误差,特别是在低信噪比情况下,改进GOMP算法具有明显的优势。
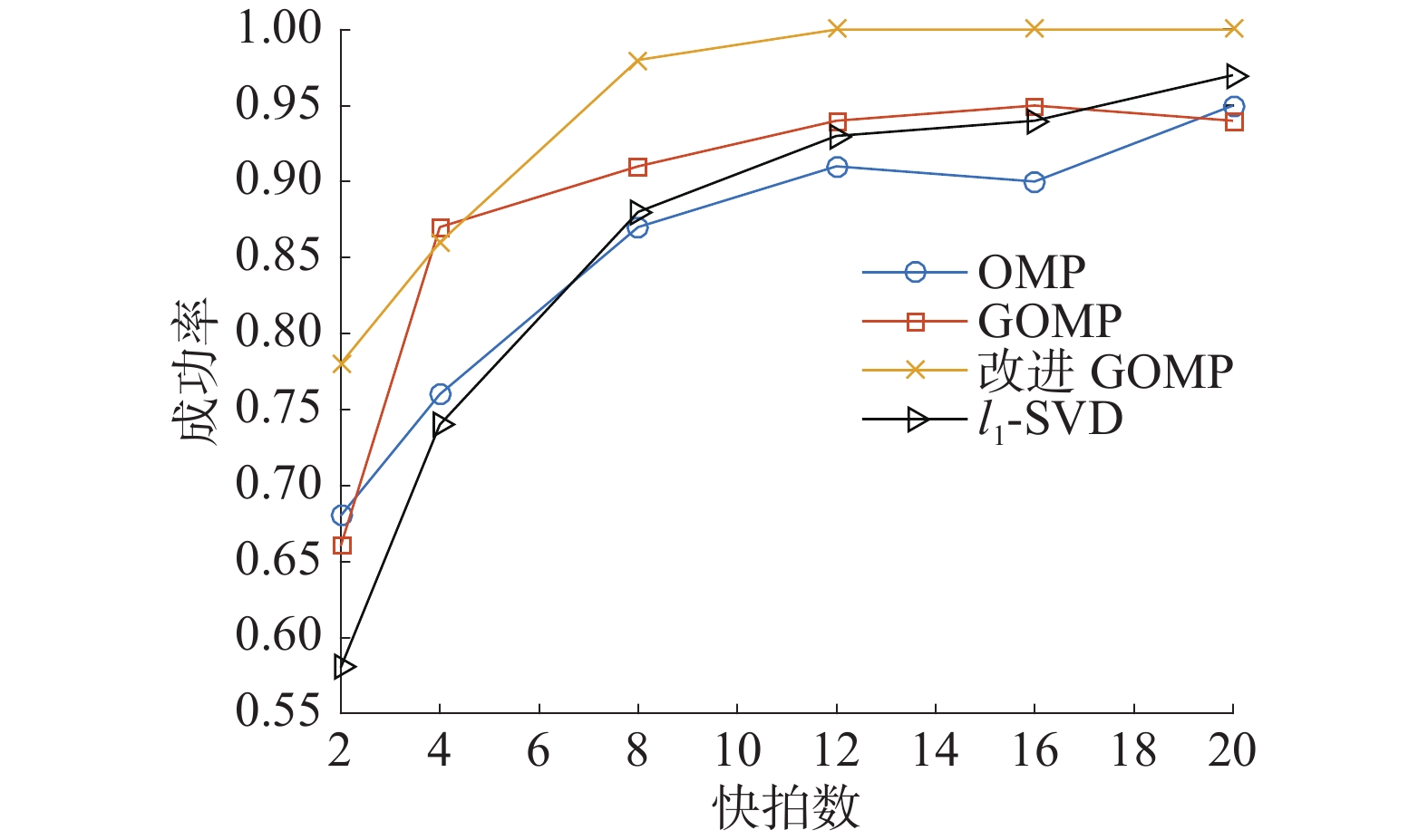
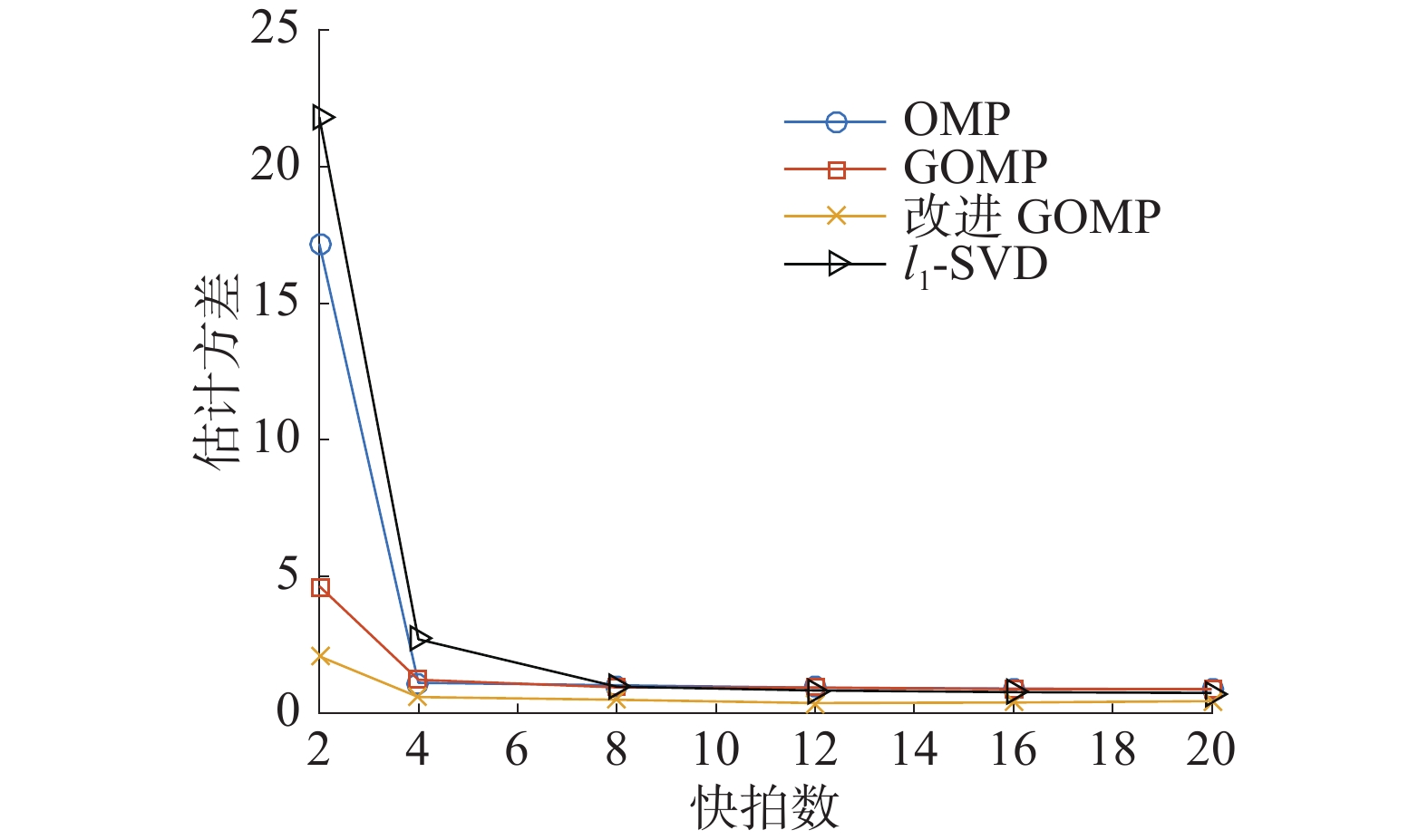
实验3 不同快拍数下的DOA估计的性能对比实验。设2个信号源以入射角10°、30°入射到均匀直线阵列上,均匀线阵阵元数为12,信噪比为−4 dB,在相同的实验条件下进行500次蒙特卡洛实验。当估计偏差小于或等于1°时,认为估计成功,在快拍数不同的情况下,统计各个条件下的成功概率和均方根误差,仿真结果如图4、5所示。
|
Download:
|
| 图 4 不同快拍数下DOA估计成功率 | |
|
Download:
|
| 图 5 不同快拍数下DOA估计均方根误差 | |
在不同快拍数情况下,由图4可以看出,改进GOMP算法具有更高的估计成功概率,且具有很高的稳定性。在快拍数为12时,已经达到以100%的概率估计出信号的DOA。随着快拍数的增加,其他3种算法的成功率缓慢增加至趋于平稳。由图5可以看出,4种算法的均方根误差均随着快拍数的增加逐渐减小,改进GOMP算法一直保持着较小的均方根误差,特别是在低快拍数情况下,改进GOMP算法具有明显的优势。
实验4 不同快拍数情况下算法运行时间对比实验。由于l1-SVD算法运行时间相对于贪婪类算法运行时间长,所以只比较另外3种算法的运行时间。由图6可以看出,随着快拍数的增加,3种算法的运行时间均逐步上升,且改进GOMP算法相较于其他2种算法的运行时间相对较短;在相同的条件下,同其他2种算法相比,改进GOMP算法具有更短的运算时间。因此从整体上看改进GOMP算法的运行时间相对偏低,相比于其他2种算法具有运行时间上的优势。
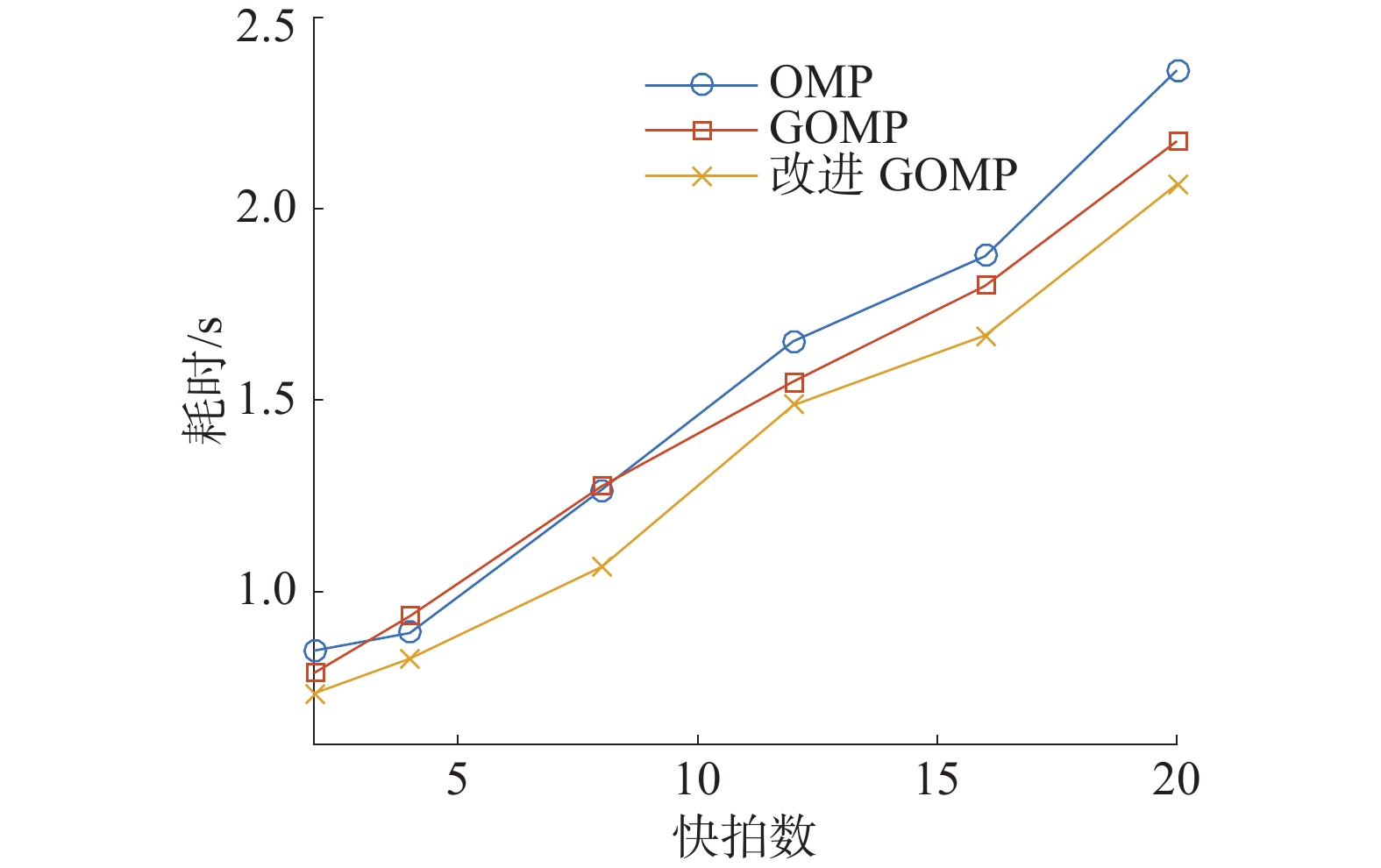
|
Download:
|
| 图 6 不同快拍数下算法运行时间比较 | |
本文提出了一种新的贪婪DOA估计方法,该方法可有效提高DOA估计的精度。GOMP是一种改进的贪婪恢复算法,其利用更好的原子选择方式,提高了贪婪算法的稳定性和角度估计精度。
1)利用GOMP算法求解DOA问题,相较于原有贪婪DOA估计方法提高了估计精度和成功率。
2)引入最速下降法对GOMP算法进行优化,并通过仿真验证了改进方法具有更高的估计精度和成功率,降低了算法的运行时间,相对于原有贪婪DOA估计方法的性能有一定的提升。
| [1] |
汤永涛, 林鸿生, 陈春. 现代导弹导引头发展综述[J]. 制导与引信, 2014(1): 12-17. DOI:10.3969/j.issn.1671-0576.2014.01.003 ( 0) 0)
|
| [2] |
王永良, 陈辉, 彭应宁. 空间谱估计理论与算法[M]. 北京: 清华大学出版社, 2004.
( 0) 0)
|
| [3] |
张小飞. 阵列信号处理的理论与应用[M]. 北京: 国防工业出版社, 2013.
( 0) 0)
|
| [4] |
SCHMIUDT R. Multiple emitter location and signal parameter estimation[J]. IEEE transactions on antennas and propagation, 1986, 34(3): 276-280. DOI:10.1109/TAP.1986.1143830 ( 0) 0)
|
| [5] |
ROY R, KAILATH T. ESPRIT-estimation of signal parameters via rotational invariance techniques[J]. IEEE transactions on acoustics speech and signal processing, 1989, 37(7): 984-995. DOI:10.1109/29.32276 ( 0) 0)
|
| [6] |
JIANG Guojun, MAO Xingpeng, LIU Yongtan. Reducing errors for root-MUSIC-based methods in uniform circular arrays[J]. IET signal processing, 2018, 12(1): 31-36. DOI:10.1049/iet-spr.2016.0576 ( 0) 0)
|
| [7] |
LIU Lutao, LIU Huan. Joint estimation of DOA and TDOA of multiple renections in mobile communications[J]. IEEE access, 2016, 4: 3815-3823. ( 0) 0)
|
| [8] |
YAN Fenggang, LIU Shuai, WANG Jun. Real-valued root-MUSIC for DOA estimation with reduced-dimension EVD/SVD computation[J]. Signal processing, 2018, 152: 1-12. DOI:10.1016/j.sigpro.2018.05.009 ( 0) 0)
|
| [9] |
DONOBO D L. Compressed sensing[J]. IEEE transactions on information theory, 2006, 52(4): 1289-1306. DOI:10.1109/TIT.2006.871582 ( 0) 0)
|
| [10] |
WEI Jingbo, HUANG Yukun, KE Lu. Nonlocal low-rank-based compressed sensing for remote sensing image reconstruction[J]. IEEE geoscience and remote sensing letters, 2017, 13(10): 1557-1561. ( 0) 0)
|
| [11] |
冯俊杰, 张弓, 文方青. 基于SL0范数的改进稀疏信号重构算法[J]. 数据采集与处理, 2016, 31(1): 178-183. ( 0) 0)
|
| [12] |
单泽涛, 刘小松, 单泽彪, 等. 基于改进平滑l0范数的DOA估计算法
[J]. 吉林大学学报(信息科学版), 2017(6): 22-26. ( 0) 0)
|
| [13] |
MALIOUTOV D, CETIN M, WILLSKY A S. A sparse signal reconstruction perspective for source localization with sensor arrays[J]. IEEE transactions on signal processing, 2005, 53(8): 3010-3022. DOI:10.1109/TSP.2005.850882 ( 0) 0)
|
| [14] |
燕学智, 温艳鑫, 刘国红. 基于稀疏表示和近似l0范数约束的宽带信号DOA估计
[J]. 航空学报, 2017(6): 221-228. ( 0) 0)
|
| [15] |
刘晓, 吴明儿, 张华振. 基于最速下降法的可展开索网天线型面调整方法[J]. 中国空间科学技术, 2018, 38(3): 1-7. ( 0) 0)
|
| [16] |
TROPP J A, GILBERT A C. Signal recovery from random measurements via orthogonal matching pursuit[J]. IEEE transactions on information theory, 2007, 53(12): 4655-4666. DOI:10.1109/TIT.2007.909108 ( 0) 0)
|
| [17] |
NEEDELL D, VERSKYNIN R. Signal recovery from incomplete and inaccurate measurements via regularized orthogonal matching pursuit[J]. IEEE journal of selected topics in signal processing, 2010, 4(2): 310-316. DOI:10.1109/JSTSP.2010.2042412 ( 0) 0)
|
| [18] |
蔡盛盛, 张佳维, 冯大航. 改进正则化正交匹配追踪波达方向估计方法[J]. 声学学报, 2014(1): 39-45. ( 0) 0)
|
| [19] |
王军, 孔令斌, 赵洁. 基于压缩感知的OMP改进重构算法[J]. 光通信研究, 2016(1): 74-78. ( 0) 0)
|
| [20] |
DEHGHANI M, AGHABABAIYAN K. FOMP algorithm for direction of arrival estimation[J]. Physical communication, 2018, 26: 170-174. DOI:10.1016/j.phycom.2017.12.012 ( 0) 0)
|
 2020, Vol. 47
2020, Vol. 47


