波达方向(direction of arrival，DOA)估计是阵列信号处理的重要课题之一，在天线、通信和雷达等领域有着广泛的应用^[1-2]。近几十年来，人们先后提出了多种DOA估计方法，包括波束形成、基于子空间的算法和最大似然(maximum likelihood，ML)估计等。其中子空间类算法^[3-5]有着优秀的超分辨能力，作为代表的MUSIC方法是传统DOA估计技术中最成功的方法，然而子空间类算法需要大量的快拍才能获得高分辨的性能，且当信号由于多路径传播而高度相关或相干时，这些方法可能无法工作。加权子空间拟合(weighted subspace fitting,WSF)是一种参数化的DOA估计方法，该方法原理简单且具有较高的估计精度，因此受到了广泛的关注^[6-7]。

近年来，空间的稀疏性引起了人们对信号处理的兴趣，极大地促进了稀疏表示方法在DOA估计^[8-10]中的应用，这些方法，都展现出了许多优秀的特性，如提高了信号的分辨率、对噪声的鲁棒性等，其中，稀疏贝叶斯学习^[11-15]是最流行的稀疏恢复方法之一。出色的DOA估计性能取决于一个假设，即真正的信号位于预定义的离散空间网格上，然而，实际信号的到达角与其最临近的网格点之间总是存在间隔，即网格失配问题，如果减小离散网格的间距，会带来计算量的大幅增加，而增大离散网格的间距，则算法的估计性能也会因此而变差。为了减小网格失配带来的建模误差，研究者们提出了一些改进的方法来处理离网的DOA估计^[16-19]，文献[16]采用一阶泰勒模型对真实DOA进行了线性逼近，提出了一种离网SBL方法，有效地解决了网格失配的问题，获得了更优的估计性能。文献[17]利用样本协方差矩阵，进一步提出了一种改进的离网SBL方法来减小噪声方差的影响。文献[18]通过使用相邻的2个网格点，提出了一种线性插值方法对真实DOA线性逼近，这些线性逼近方法确实可以减小离网间隙引起的建模误差，但不能完全消除，如果使用较粗的离散网格，在实际应用中仍然会有较大的建模误差。为此，文献[19]提出了一种基于动态网格的求根SBL算法，该算法在计算复杂度和估计精度之间取得了平衡，即使采用粗网格，也能获得较好的估计性能，对网格间距具有较好的鲁棒性，但是在低信噪比等条件下估计有效性不足。

1 子空间拟合模型

假设K个远场窄带信号以角度 ${{\theta }} = [{\theta _1},{\theta _2}, \cdots , {\theta _K}]^{\rm{T}}$ 入射到M元均匀天线阵列上，入射信号的波长为 $\lambda $ ，相邻天线间距离为 $d = \lambda /2$ ，那么在t时刻天线阵列的输出可以写成：

${{X}}(t) = {{A}}(\theta ){{S}}(t) + {{N}}(t),t = 1,2, \cdots ,L$

式中： ${{N}}(t) = {\left[ {{n_1}(t),{n_2}(t), \cdots ,{n_M}(t)} \right]^{\rm{T}}}$ 是均值为零的加性平稳高斯白噪声； ${{S}}(t) = {\left[ {{s_1}(t),{s_2}(t), \cdots ,{s_K}(t)} \right]^{\rm{T}}}$ 为入射信号，并假设入射信号与噪声相互独立；入射角 ${{\theta }}$ 定义为信号与阵列法线的夹角；L表示快拍数； ${{A}}(\theta ) = \left[ {{{a}}({\theta _1}),{{a}}({\theta _2}), \cdots ,{{a}}({\theta _K})} \right] \in {{\bf{C}}^{M \times K}}$ 为阵列的流型矩阵； ${{a}}({\theta _k}) = {[1,{{\rm{e}}^{ - {\rm{j}}2{\rm{{\text{π}} }}d\sin ({\theta _k})/\lambda }}, \cdots ,{{\rm{e}}^{ - {\rm{j}}2{\rm{{\text{π}} }}(M - 1)d\sin ({\theta _k})/\lambda }}]^{\rm{T}}}$ 表示阵列的方向矢量。则阵列接收数据的协方差矩阵定义为

${{{R}}_X} = {{E}}[{{X}}(t){{{X}}^{\rm{H}}}(t)] = {{A}}(\theta ){{{R}}_s}{{{A}}^{\rm{H}}}(\theta ) + \sigma _n^2{{I}}$

对矩阵 ${{{R}}_X}$ 进行特征分解可以得到：

${{{R}}_X} = \sum\limits_{i = 1}^M {{\mu _i}{{{v}}_i}{{v}}_i^{\rm{H}} = {{{U}}_s}{{{\varLambda }}_s}{{U}}_s^{\rm{H}}} + {{{U}}_n}{{{\varLambda }}_n}{{U}}_n^{\rm{H}}$

式中： ${\mu _1}$ ≥ ${\mu _2}$ ≥ $ \cdots > {\mu _{K + 1}} = \cdots = {\mu _M}$ 为 ${{{R}}_X}$ 的特征值；由特征向量构成的矩阵 ${{{U}}_s}$ 和 ${{{U}}_n}$ 分别定义为信号子空间和噪声子空间。理想情况下，信号子空间 ${{{U}}_s}$ 与阵列流型矩阵 ${{A}}$ 具有相同的张成子空间，即存在一个列满秩矩阵 ${{T}}$ 使得

${{{U}}_s} = {{AT}}$

然而实际中，由于有限的采样数及噪声的存在，阵列流型张成的子空间与信号子空间并不完全相同，为了解决这个问题，经典WSF算法^[4]通过构造一个拟合关系，使得两者在最小二乘意义下拟合得最好，即

${{\hat \theta }} = \arg \mathop {\min }\limits_{{\theta }} \left\| {{{{U}}_s}{{{W}}^{1/2}} - {{AT}}} \right\|_F^2$

式中 ${{W}}$ 为权矩阵。当 ${{W}} = {({{{U}}_s} - \sigma _n^2{{I}})^2}{{\varLambda }}_s^{ - 1}$ 时为最优权，则信号的加权子空间与阵列流型之间的线性关系为

${{Y}} = {{AT}} + {{E}}$

(1)

式中： ${{Y}} = {{{U}}_s}{{{W}}^{1/2}}$ ；等价噪声矩阵 ${{E}}$ 近似服从均值为0的高斯分布。

2 子空间拟合块稀疏贝叶斯算法 2.1 稀疏模型

为了将式(1)纳入稀疏贝叶斯学习框架求解，首先需要构造稀疏模型。将空间以角度为单位等间隔划分成N份，假设离散网格的间隔足够小，则能保证所有入射信号都落在这N个离散角度上，每一个离散角度都对应一个空间信号 ${{{\hat T}}_n}(n = 1, 2, \cdots, N)$ ，便构造了一个稀疏度为K的信号矢量，然后计算离散网格点对应的导向矢量，即可得到稀疏化后的阵列流型矩阵 ${{\varPhi }}(\hat \theta ) = [ {{a}}({{\hat \theta }_1}),{{a}}({{\hat \theta }_2}), \cdots , {{a}}({{\hat \theta }_N}) ] \in {{\bf{C}}^{M \times N}}$ ，则稀疏表示下的信号模型为

${{Y}} = {{\varPhi \hat T}} + {{E}}$

(2)

根据式(2)中 ${{\hat T}}$ 的统计假设， ${{{\hat T}}_{n }}$ 服从复高斯分布，即 $p(\left. {{{{{\hat T}}}_{n }}} \right|{\gamma _n},{{B}}) = {\rm{CN}}(0,{\gamma _n}{{B}})$ ，其中矩阵 ${{B}}$ 为包含时间相关信息的正定矩阵， ${\gamma _n}$ 为控制 ${{{\hat T}}_{n }}$ 稀疏性的非负参数，当 ${\gamma _n}$ 趋近于0时，相对应的 ${{{\hat T}}_{n }}$ 也趋近于0。为了便于对每个信源的时间相关性进行建模，根据块稀疏贝叶斯理论，式(2)可以转换成如下SMV模型^[20]：

${{y}} = {{Ds}} + {{n}}$

(3)

式中： ${{y}} = {\rm{vec}}({{{Y}}^{\rm{T}}})$ ； ${{D}} = {{\varPhi }} \otimes {{{I}}_K}$ ； ${{s}} = {\rm{vec}}({{{\hat T}}^{\rm{T}}})$ 且 ${{n}} = {\rm{vec}} ({{{E}}^{\rm{T}}})$ 。根据 ${{\hat T}}$ 的统计假设， ${{s}}$ 的先验分布为 $p(\left. {{s}} \right|{{\gamma }}, {{B}}) = {\rm{CN}}(0,{{{\varSigma }}_0})$ ，其中 ${{{\varSigma }}_0} = {{\varGamma }} \otimes {{B}}$ ； ${{\varGamma }} = {\rm{diag}}({{\gamma }})$ ； ${{\gamma }} = {[{\gamma _1},} {{\gamma _2}, \cdots ,{\gamma _N}]^{\rm{T}}}$ 。

在实际情况下，入射信号都位于网格点上是不现实的，真实DOA与空间离散网格点之间的间隔不可避免地会导致较大估计误差，针对此网格失配问题，本文将在后面内容提出一种多项式求根方法解决建模误差，将采样网格点作为动态参数，然后通过迭代更新离散网格。

2.2 块稀疏贝叶斯学习

由稀疏模型式(3)可知 ${{s}}$ 的后验概率密度分布可以表示为

$p(\left. {{s}} \right|{{y}};{{\gamma }},{{B}},\lambda ) = {\rm{CN}}({{{\mu }}_s},{{{\varSigma }}_s})$

式中： ${{{\mu }}_s} = \dfrac{1}{\lambda }{{{\varSigma }}_s}{{{D}}^{\rm{T}}}{{y}}$ ； ${{{\varSigma }}_s} = {\Bigg({{\varSigma }}_0^{ - 1} + \dfrac{1}{\lambda }{{{D}}^{\rm{T}}}{{D}}\Bigg)^{ - 1}}$ 。定义超参数 ${{\varTheta }} = \left\{ {{{\gamma }},{{B}},\lambda } \right\}$ ，为了获得该参数的估计，采用EM算法求解 ${E_{\left. {{s}} \right|{{y}};{{{\varTheta }}^{{\rm{old}}}}}}\left[ {\log p({{y}},{{\gamma }},{{B}},\lambda )} \right]$ ，其中 ${{{\varTheta }}^{{\rm{old}}}}$ 表示上一次迭代得到的超参数，则超参数的学习规则为

${\gamma _i} = {{{\rm{tr}}\left[ {{{{B}}^{ - 1}}({{\varSigma }}_s^i + {{\mu }}_s^i{{({{\mu }}_s^i)}^{\rm{H}}})} \right]}/K},i = 1,2, \cdots ,N$

(4)

${{B}} = \left\{ {\sum\limits_{i = 1}^N {{{({{\varSigma }}_s^i + {{\mu }}_s^i{{({{\mu }}_s^i)}^{\rm{H}}})}/{{\gamma _i}}}} } \right\}$

(5)

$\lambda = \frac{{\left\| {{{y}} - {{D}}{{{\mu }}_s}} \right\|_2^2 + \lambda \left[ {NK - {\rm{tr}}({{{\varSigma }}_s}{{\varSigma }}_0^{ - 1})} \right]}}{{MK}}$

(6)

式中： ${{\mu }}_s^i \triangleq {{{\mu }}_s}((i - 1)K + 1:iK)$ ； ${{\varSigma }}_s^i \triangleq {{{\varSigma }}_s}((i - 1)K + 1:iK, (i - 1)K + 1:iK)$ 。

值得注意的是，学习规则式(4)、(5)的维数很高，算法速度不快。文献[14]指出可以通过合理地近似降低学习规则的维度，即利用MSBL算法来简化上述规则，其中MSBL算法为

${{\hat T}} = {{\varGamma }}{{{\varPhi }}^{\rm{H}}}{(\lambda {{I}} + {{\varPhi \varGamma }}{{{\varPhi }}^{\rm{H}}})^{ - 1}}{{Y}}$

(7)

${{{\varSigma }}_{\hat T}} = {\Bigg({{{\varGamma }}^{ - 1}} + \frac{1}{\lambda }{{{\varPhi }}^{\rm{H}}}{{\varPhi }}\Bigg)^{ - 1}}$

(8)

将式(7)、(8)及近似公式 ${({{I}} + {{D}}{{{\varSigma }}_0}{{{D}}^{\rm{H}}})^{ - 1}} \approx {({{I}} +} { {{\varPhi }}{{{\varSigma }}_0}{{{\varPhi }}^{\rm{H}}})^{ - 1}} \otimes {{B}}$ 代入学习规则，则超参数学习规则可以简化为

${\gamma _i} = \frac{1}{K}{{{\hat T}}_{i }}{{{B}}^{ - 1}}{{\hat T}}_{i }^{\rm{H}} + {({{{\varSigma }}_{\hat T}})_{ii}}$

(9)

${{B}} = \sum\limits_{i = 1}^N {\frac{{{{\hat T}}_{i }^{\rm{H}}{{{{\hat T}}}_{i }}}}{{{\gamma _i}}}} + \eta {{I}}$

(10)

$\lambda {\rm{ = }}\frac{1}{{MK}}\left\| {{{Y}} - {{\varPhi \hat T}}} \right\|_F^2 + \frac{\lambda }{M}{\rm{tr}}\left[ {{{\varPhi \varGamma }}{{{\varPhi }}^{\rm{H}}}{{(\lambda {{I}} + {{\varPhi \varGamma }}{{{\varPhi }}^{\rm{H}}})}^{ - 1}}} \right]$

(11)

式中 $\eta $ 是正数。式(10)的正则化形式保证了 $B$ 是正定的。

2.3 网格更新

在本节中，针对网格失配问题带来的建模误差，将离散网格点作为动态参数，然后通过多项式求根来更新离散网格。设空间离散角 ${{\hat \theta }}$ 为动态参数。根据EM(expectation maximization)算法，首先对式(5)中的似然函数进行数学期望运算，忽略独立常数项即可得到目标函数：

$\begin{array}{l} {\kern 1pt} {\kern 1pt} {{ E}_{p({{y}}|{{\hat s}},\lambda ,{{\gamma }},{{B}})}}\left\{ {\ln (p({{y}}|{{\hat s}},\lambda ))} \right\} = - ||{{y}} - {{D\mu }}||_2^2 - {\rm{tr}}({{D\varSigma }}{{{D}}^{\rm{H}}}) = \\ - \displaystyle\sum\limits_{k = 1}^K {||{{{Y}}_k} - {{\varPhi }}{{{{\hat T}}}_k}||_2^2} - {\rm{tr}}\left( {{{\varPhi }}{{{\varSigma }}_{\hat T}}{{{\varPhi }}^{\rm{H}}}} \right){\rm{tr}}\left( {{B}} \right) \end{array}\!\!\!\!\!\!\!\!$

(12)

为了更新每个离散的空间网格 ${\hat \theta _i},i = 1,2, \cdots , N$ ，或者它的指数形式 ${{{v}}_{{{\hat \theta }_i}}} = {{\rm{e}}^{ - {\rm{j}}2 {\text{π}} d/\lambda \sin ({{\hat \theta }_i})}}(i = 1,2, \cdots ,N)$ ，计算式(12)对 ${{{v}}_{{{\hat \theta }_i}}}$ 的微分，并令其结果为0，可得：

$\frac{{\partial \displaystyle\sum_k {\left\| {{{{Y}}_k} - {{\varPhi }}{{{{\hat T}}}_k}} \right\|} _2^2}}{{\partial {{{v}}_{{{\hat \theta }_i}}}}} = {({{{{{\alpha}} '}}_i})^{\rm{H}}}\left( {{{{\alpha }}_i}\sum\limits_{k = 1}^K {{{\left| {{{{{\hat T}}}_{ki}}} \right|}^2} - \sum\limits_{k = 1}^K {\left| {{{\hat T}}_{ki}^*} \right|{{{Y}}_{k - i}}} } } \right)$

(13)

$\frac{{\partial {\rm{tr}}\left( {{{\varPhi }}{{{\varSigma }}_{\hat T}}{{{\varPhi }}^{\rm{H}}}} \right)}}{{\partial {{{v}}_{{{\hat \theta }_i}}}}} = {({{{\alpha '}}_i})^{\rm{H}}}\left( {{\varepsilon _{ii}}{{{\alpha }}_i} + \sum\limits_{j \ne i} {{\varepsilon _{ji}}{{{\alpha }}_j}} } \right)$

(14)

令式(12)的导数为0，可以得到：

$\begin{array}{l} {({{{{\alpha '}}}_i})^{\rm{H}}}\left( {{{{\alpha }}_i}\underbrace {\left( {\sum\limits_{k = 1}^K {{{\left| {{{{{\hat T}}}_{ki}}} \right|}^2}} + {\varepsilon _{ii}}{\rm{tr}}\left( {{B}} \right)} \right)}_{ \buildrel \Delta \over = {\phi ^{(i)}}}} + \right.\\ \;\;\;\;\;\;\;\;\left. { \underbrace {{\rm{tr}}\left( {{B}} \right)\sum\limits_{j \ne i} {{\varepsilon _{ji}}{{{\alpha }}_j}} - \sum\limits_{k = 1}^K {\left| {{{\hat T}}_{ki}^*} \right|{{{y}}_{k - i}}} }_{ \buildrel \Delta \over = {\varphi ^{(i)}}}} \right)=0 \end{array}$

(15)

式中： ${{{\alpha }}_i}$ 、 ${{{\hat T}}_{ki}}$ 、 ${\varepsilon _{ij}}$ 分别表示 ${{\varPhi }}$ 的第 $i$ 列、矩阵 ${{\hat T}}$ 以及 ${{{\varSigma }}_{\hat T}}$ 的第 $(i,j)$ 个元素，且 ${{{Y}}_{k - i}} = {{{Y}}_k} - \sum\nolimits_{j \ne i} {{{{{\hat T}}}_{kj}}{\alpha _j}} $ ， ${{{\alpha '}}_i} \triangleq {{{\rm{d}}{{{\alpha }}_i}}/ {{\rm{d}}{v_{{{\hat \theta }_i}}}}}$ 。

则式(15)可以写成如下多项式形式：

$\left[ {{v_{{{\hat \theta }_i}}},1,v_{{{\hat \theta }_i}}^{ - 1}, \cdots ,v_{{{\hat \theta }_i}}^{ - (M - 2)}} \right]\left[ {\begin{array}{*{20}{c}} {\dfrac{{M(M - 1)}}{2}{\phi ^{(i)}}} \\ {\varphi _2^{(i)}} \\ {2\varphi _3^{(i)}} \\ \vdots \\ {(M - 1)\varphi _M^{(i)}} \end{array}} \right] = 0$

(16)

式中 $\varphi _m^{(i)}$ 为 ${{{\varphi }}^{(i)}}$ 的第m个元素。显然，式(16)一共有M−1个根，需要从中挑选出一个来更新离散网格，根据 ${{{v}}_{{{\hat \theta }_i}}}$ 的定义可知，待选取的根的模应为1，然而由于噪声的存在，根可能不在单位圆上，因此，在实际情况下，选取最接近单位圆的根 ${z_i}$ 来细化网格：

$\hat \theta _i^{{\rm{new}}} = \arcsin \left( { - \frac{\lambda }{{2 {\text{π}} d}} {\rm{angle}}\left( {{z_i}} \right)} \right)$

(17)

需要注意的是，在每次迭代过程中，并不需要更新所有的离散网格点，选择更新 ${{\gamma }}$ 中与K个较大极值点对应的网格点即可保证算法的性能，这将大大提高算法的运算效率。

2.4 算法步骤

综上所述，基于子空间拟合和块稀疏贝叶斯学习的离网DOA估计算法步骤如下：

1)对阵列接收数据的协方差矩阵特征分解，构造信号的加权子空间 ${{Y}}$ ；

2)初始化参数 ${{\gamma }}$ 、 ${{B}}$ 、 $\lambda $ 以及 ${{\hat \theta }}$ ，设定收敛条件；

3)迭代；

a)利用式(7)、(8)计算 ${{\hat T}}$ 和 ${{{\varSigma }}_{\hat T}}$ ；

b)利用式(9)、(10)、(11)、(17)更新 ${{\gamma }}$ 、 $B$ 、 $\lambda $ 及 ${{\hat \theta }}$ ；

c)若 ${{||{{{\gamma }}^{i + 1}} - {{{\gamma }}^i}|{|_2}}/{||{{{\gamma }}^i}|{|_2}}} < \tau $ 成立或达到最大迭代次数，则退出迭代；反之，则重复步骤a)、b)，其中 $\tau $ 为收敛判决门限。

4)根据 ${{\gamma }}$ 中极值点的位置，即可得到相应信号的DOA估计。

3 仿真实验与性能分析

为了验证所提出算法的有效性，在本节中，进行了一些仿真实验来验证所提方法的性能，将所提出的算法与OGSBI(off-grid sparse bayesian inference)算法以及rootSBL(root sparse bayesian learning)算法进行了比较。仿真实验中，天线阵列设定为8元均匀线阵，迭代次数最大值设定为1000次，误差判决门限设置为 $\tau {\rm{ = }}{10^{{\rm{ - }}3}}$ ，蒙特卡洛实验次数设置为500次。

3.1 均方根误差

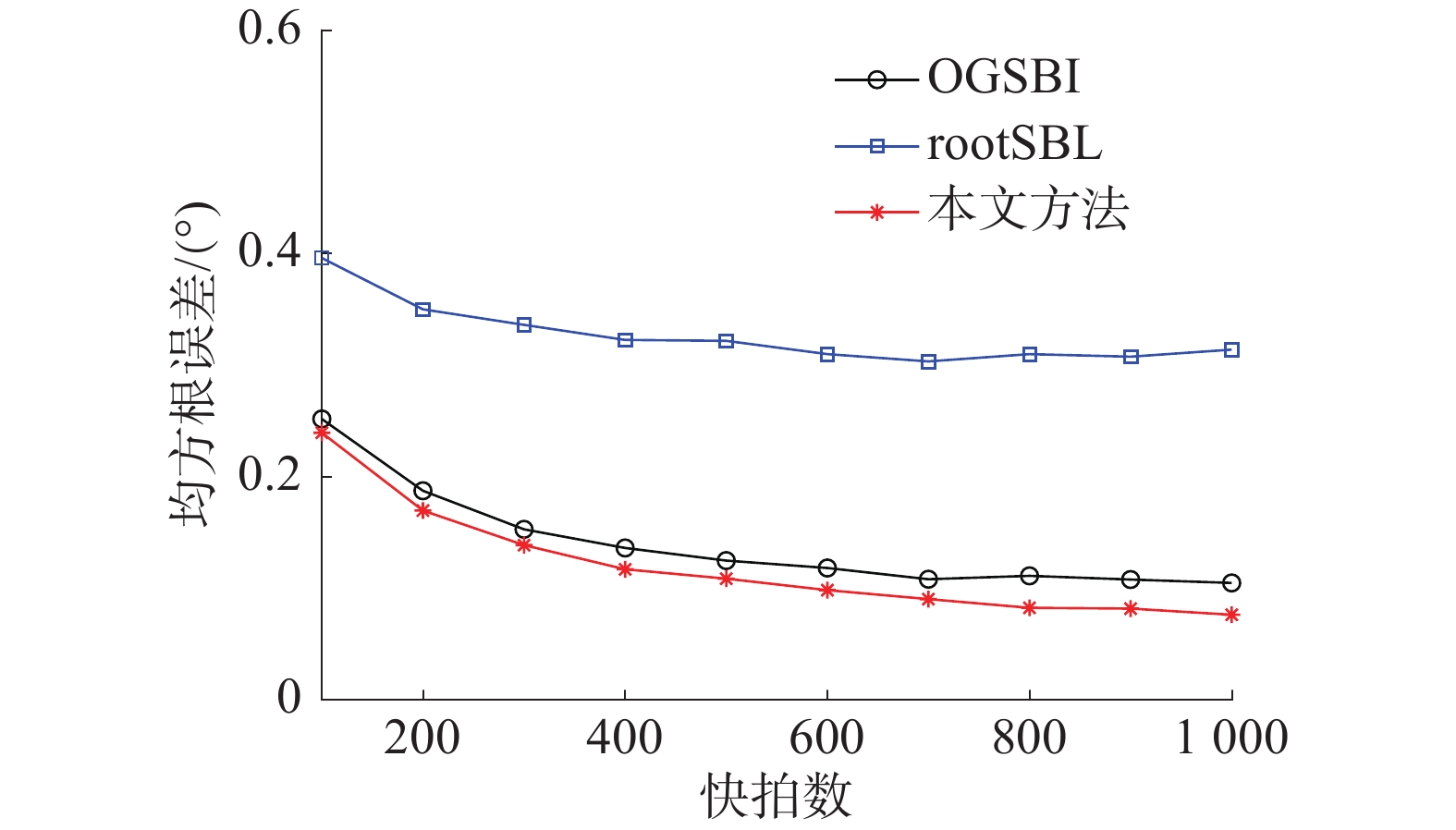
实验1设置快拍数为100，离散网格的间隔为2°，仿真实验比较了3种算法的均方根误差随信噪比变化的结果；实验2设置信噪比为0 dB，离散网格的间隔为2°，仿真实验比较了在不同快拍数下3种算法的均方根误差。

图1表明，当信噪比提高时，3种算法的均方根误差均有所减小，其中相比较rootSBL算法，在较低信噪比下OGSBI算法的估计精度更高，而当信噪比较高时，rootSBL算法的均方根误差能收敛到更小的值，相比较这2种算法，本文所提出的算法在不同信噪比条件下均具有更高的估计精度。由图2可以看出，当快拍数逐渐增大时，3种算法的均方根误差均不断降低，相比较2种对比算法，本文所提出的算法由于采用了子空间拟合，因此随着快拍数的增加，均方根误差能收敛到更小的值，具有更高的估计精度。

3.2 离散网格间隔

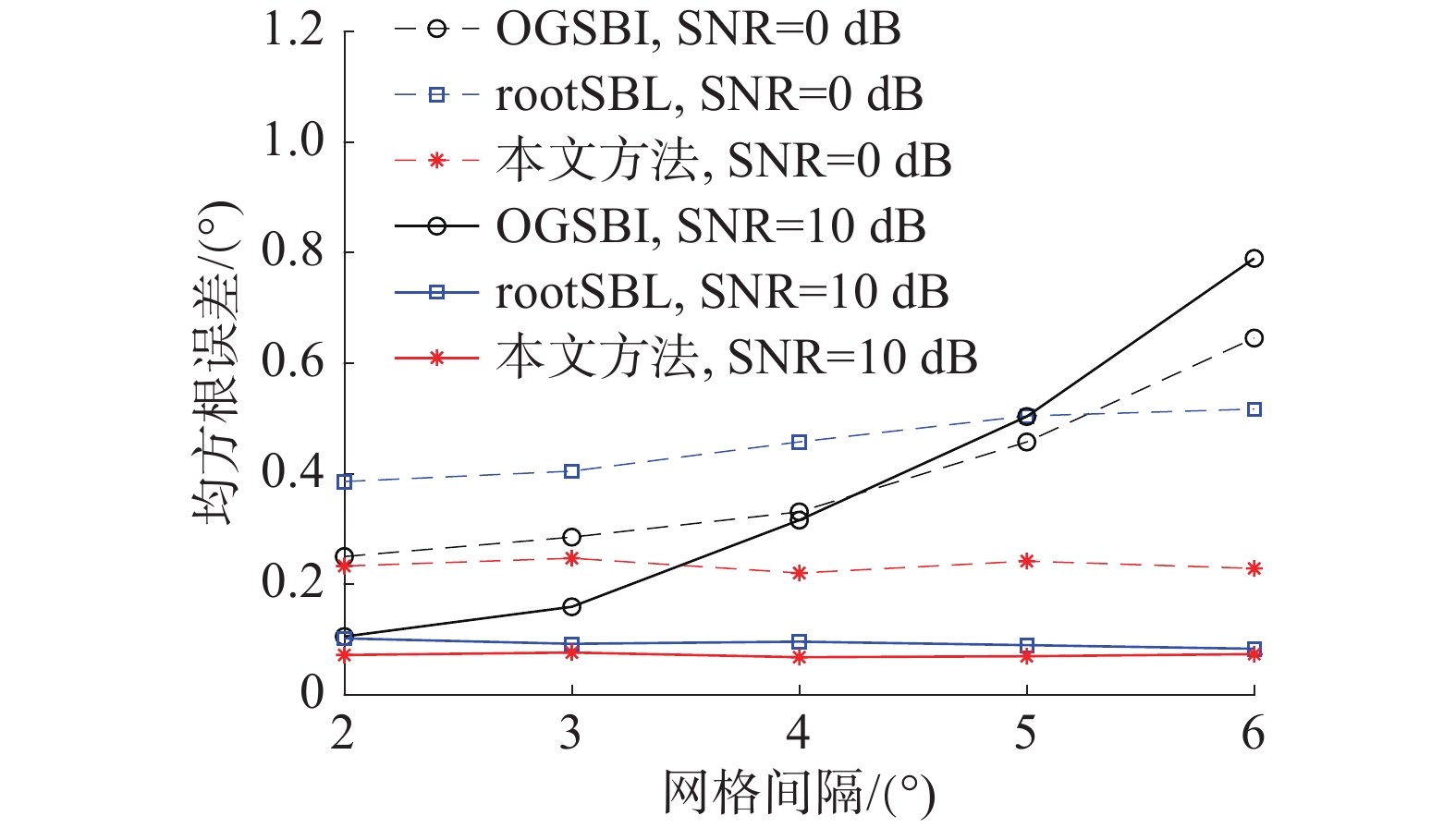
设置采样数为100，仿真实验3比较了在不同网格间隔下3种算法的均方根误差。由图3可以看出，随着网格间隔增大，OGSBI算法均方根误差增大较为明显，而rootSBL算法及本文提出的算法均方根误差变化较小。由于OGSBI算法中采用了线性逼近方法，因此当使用粗网格时会导致较大的建模误差，从而带来较大的均方根误差，而本文提出的算法将粗网格中的采样点作为可调参数，可以很好地减小网格失配带来的误差，具有较强的鲁棒性。

3.3 空间分辨率

设置信噪比为10 dB，采样数为100，离散网格的间隔为2°，空间2入射信号的角度间隔分别为4°~10°，仿真实验4比较了3种算法在不同角度间隔下的均方根误差。图4表明，当空间2角度间隔较近时，OGSBI算法及rootSBL算法均具有较大的均方根误差，当角度间隔逐渐增大，3种算法的均方根误差均有所减小并趋于稳定，相比较这两种算法，本文所提出的算法在不同角度间隔的条件下均具有更小的均方根误差，具有更好的空间分辨率。

4 结论

1)本文将加权子空间拟合引入块稀疏贝叶斯学习，提出了一种新的离网DOA估计方法。

2)针对建模带来的网格失配问题，将离散网格中的采样点作为动态可调参数，然后对网格进行迭代更新来消除建模误差。

3)通过实验仿真分析，相对于传统稀疏贝叶斯算法，本文算法在相同条件下能很好地改善离格误差，具有更高的DOA估计精度和空间分辨率，因而在实际应用中具有更高的可靠性。

为了提高算法的实时性，将本文算法应用于实数域是下一步的研究工作。