配电网重构是通过改变配电网的联络开关和分段开关的组合来改变网络拓扑,从而达到配电网优化运行目的的一种自愈控制手段[1-2]。该方法在20世纪70年代由Merlin提出,早期主要应用于规划配电线路、降低供电成本等方面。近年来,随着电网规模的不断扩大和分布式电源(distributed generation,DG)比例的增加,配电网重构还要考虑提高供电质量、减少网络损耗、均衡负荷等保障系统安全、经济运行的因素[3-5]。
配电网重构是一个多约束的多目标优化问题,文献[6]利用联络开关的环网编码来判断网络的连通性和辐射性,具有较快的计算速度但是容易陷入局部最优。文献[7]基于前推回代法,对各种DG的潮流计算数学模型进行了分析研究,为含DG的配电网重构的研究提供了理论依据,但没有提出求解方法。文献[8]基于二进制粒子群优化(binary particle swarm optimization,BPSO)算法和禁忌搜索算法提出了一种具有不需进行网络辐射结构判断的新型算法,提高了计算速度,但存在局部收敛的问题。文献[9]基于BPSO提出了可以降低问题维度的分层分布式优化算法,降低了问题求解的难度,但是迭代次数比较多。文献[10]提出了能克服局部收敛问题的自适应交叉率和变异率遗传算法(genetic algorithm, GA),提高了解的精度,但也存在计算时间长的问题。
配电网重构包括系统故障前的优化重构和故障后的恢复重构2种情况[11]。本文对前一种情况进行分析研究,采用随机权重方法建立了可根据配电网的运行状态进行动态调整的数学模型。为克服传统BPSO算法存在的收敛速度慢和局部收敛问题,提出了改进型BPSO算法,可快速调整拓扑结构,具有操作损耗小、供电能力高、计算速度快的优点,显著提高了系统在风险状态下的稳定性。
1 配电网重构数学模型 1.1 问题目标函数为保证系统的经济和可靠运行,配电网重构要考虑减少系统网损、提高负荷均衡性、减少开关操作次数、提高最大供电能力等问题[12]。本文在构建目标函数时,为达到多目标优化的目的,采用随机权重的方法对上述4个指标进行归一化处理,通过对各指标的重要程度排序来得到相应目标函数的权重[13],所得目标函数表达式为
| $\min F = {w_{\rm{1}}}{f_1} + {w_{\rm{2}}}{f_2} + {w_{\rm{3}}}{f_3} + {w_{\rm{4}}}{f_4}$ | (1) |
式中:f1是最小网损的目标函数[14];f2是负荷均衡性的目标函数;f3是最小开关操作次数目标函数[15];f4是系统最大供电能力的极小值型目标函数;w1~w4分别是上述4个指标在目标函数中的权重系数。各指标的目标函数具体表达式为
| $\min {f_1} = \sum\limits_{i = 1}^n {\frac{{{P_i}^2 + {Q_i}^2}}{{{U_i}^2}}{s_i}{r_i}} $ |
式中:n代表网络的馈线总数;i代表支路编号;Ui代表线路i末端的节点电压;Pi和Qi分别为流经线路i的有功和无功功率;si表示线路分合状态,si = 0表示线路i断开,si = 1表示线路i闭合;r为等效支路的电阻。
| $\min {f_2} = \mathop {\max }\limits_{i \in n} \left( {\frac{{{I_i}}}{{{I_{{N_i}}}}}} \right) - \mathop {\min }\limits_{i \in n} \left( {\frac{{{I_i}}}{{{I_{{N_i}}}}}} \right) $ |
式中Ii和INi分别表示支路i的实际负载和额定容量。
| $\min {f_3} = \sum\limits_{i = 1}^N {\left| {{x_i} - {x_{i_0}}} \right|} $ |
式中:N表示开关总数;
| $\max {f_4} = - \left( {\sum\limits_{i = 1}^N {{S_i}} + \sum\limits_{j \in D} {k{S_j}} } \right)$ |
式中:右边括号内第1项为整个系统重构前的实际负荷总量;第2项为重构之后负荷的增加量;N表示节点的总数;Si表示节点i的负荷;D表示所有的负荷区域;k表示负荷增加的倍数。
1.2 约束条件在求解重构的目标函数时,需满足的约束条件如下所示[16]:
| $\left\{ \begin{array}{l} {P_i} = {P_{L_i}} + {V_i} \displaystyle\sum\limits_{j = 1}^{N_b} {{V_j}\left( {{G_{ij}}\cos {\delta _{ij}} + {B_{ij}}\sin {\delta _{ij}}} \right)} \\ {Q_i} = {Q_{L_i}} + {V_i}\displaystyle\sum\limits_{j = 1}^{N_b} {{V_j}\left( {{G_{ij}}\sin {\delta _{ij}} - {B_{ij}}\cos {\delta _{ij}}} \right)} \\ \end{array} \right.$ |
式中:Pi和Qi分别表示节点i注入的有功和无功功率;
| $\left\{ {\begin{array}{*{20}{l}} {{V_{i,\min }} \leqslant {V_i} \leqslant {V_{i,\max }}} \\ {{I_i} \leqslant {I_{i,\max }}} \\ {{S_{G,\min }} \leqslant {S_G} \leqslant {S_{G,\max }}} \end{array} } \right.$ |
式中:第1个式子表示节点电压约束,Vi表示节点i的电压幅值;Vi,min和Vi,max分别表示节点i的电压限值;第2个式子表示线路容量约束,Ii和Ii,max分别为支路i流过的电流和该支路允许流过的最大电流;第3个式子表示分布式电源的限制。网络拓扑约束为
| $t \in T$ |
式中:t表示配电网重构之后的拓扑结构;T表示满足连通辐射状要求的拓扑集合。
2 配电网重构控制模型选择当配电网处于不同的运行状态时,它的风险等级是不同的,重构的目标也会有所不同。当系统的风险等级较低时,重构策略对经济性的要求比较高。而当系统风险程度较高时,重构策略对安全性和控制速度的要求会高于经济性的要求。配电网重构的控制目标和风险等级的关系如图1所示。

|
Download:
|
| 图 1 配电网重构目标 | |
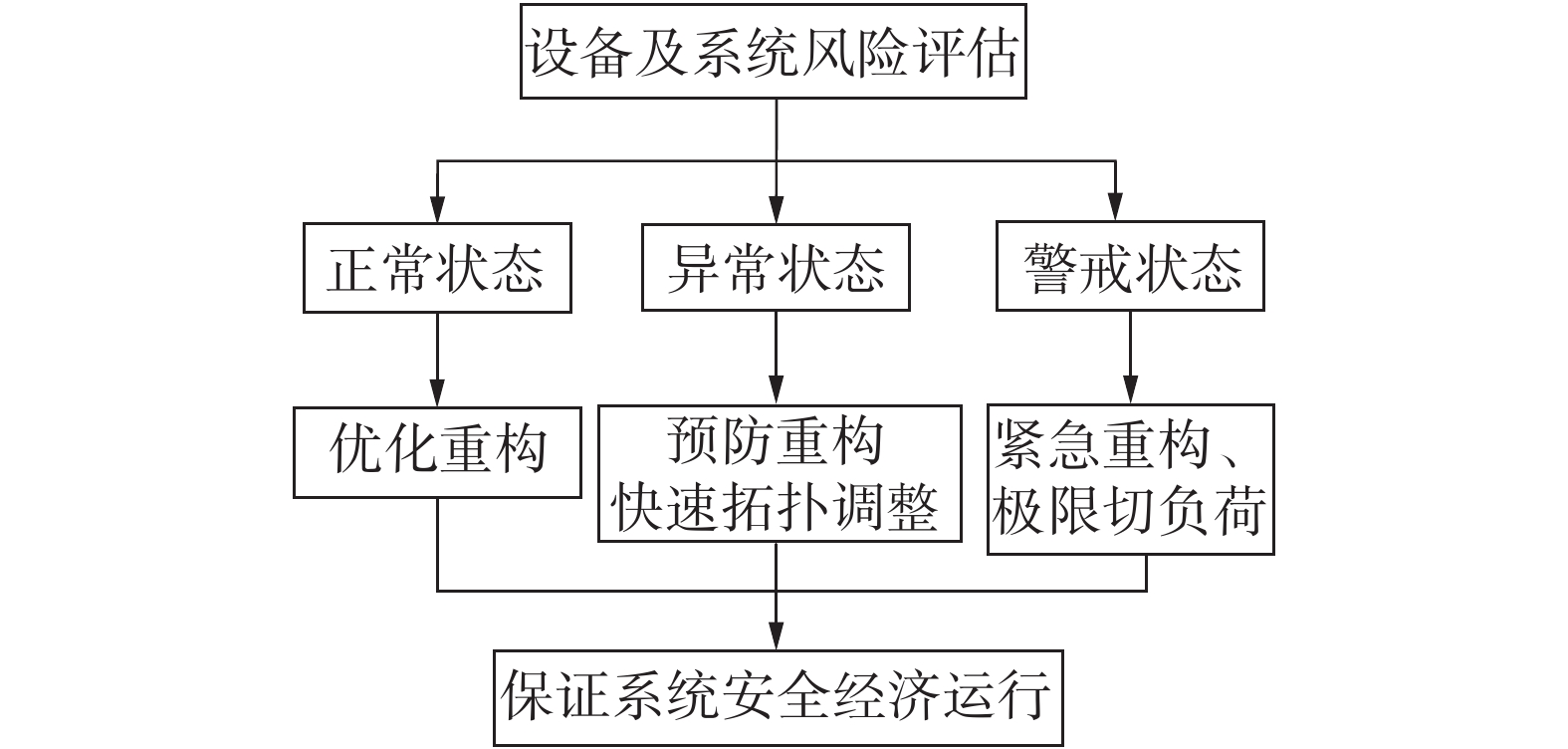
在实际运行中,要根据系统的运行状态来衡量经济性、安全性和控制速度的重要程度,从而选择最优的重构方案。根据在线监测和风险评估结果,配电网的运行状态可以分为正常状态、异常状态和警戒状态,这3种状态下的重构控制目标如图2所示。
|
Download:
|
| 图 2 配电网重构方案 | |
本文在构建配电网重构的目标函数时,采用了随机权重的方法,如式(1)所示,其中,w1~w4分别表示最小网络损耗、最大负荷均衡性、最大供电能力和最少开关操作次数在目标函数中的比重。合理选择系统在不同运行状态下的权重,有利于提高重构方案的有效性。通过衡量各指标在系统3种运行状态下的重要程度,可以得到不同运行状态下目标函数的权重系数配置,如表1所示。
|
|
表 1 随机权重系数 |
BPSO算法是粒子群优化(particle swarm optimization,PSO)算法在离散问题中的应用。BPSO算法将粒子的位置信息用二进制变量“0-1”表示,粒子的速度大小用来表示粒子位置为“1”的概率,且粒子速度越大,粒子位置为“1”的概率越大;粒子速度越小粒子位置为“1”的概率越小[17-19]。BPSO算法中粒子的速度和位置信息迭代过程为
| $O_{iv}^{h + 1} = \alpha O_{iv}^h + a{}_1{r_1}(p_{iv}^h - X_{iv}^h) + {a_2}{r_2}(g_v^h - X_{iv}^h)$ |
| $\left\{ \begin{array}{l} S(X_{iv}^{h + 1}) = {1 / {1 + {{\rm{e}}^{ - O_{iv}^{h + 1}}}}} \\ X_{iv}^{h + 1} = 1,\quad \quad {{r}} < {\rm{Sig}}(X_{iv}^{h + 1}) \\ X_{iv}^{h + 1} = 0,\quad \quad {{r}} > {\rm{Sig}}(X_{iv}^{h + 1}) \end{array} \right.$ |
| ${\rm{Sig}}(X) = \left\{ \begin{array}{l} 0.99,\quad \quad \quad \quad \quad X > 5 \\ \dfrac{1}{{1 + {{\rm{e}}^{ - X}}}},\quad \quad - 5 < X < 5 \\ - 0.99,\quad \quad \quad \quad X < - 5 \end{array} \right.$ |
式中:h、i、v分别表示迭代次数、第i个粒子、第v维空间;Oiv、Xiv分别表示粒子i在v维空间的速度和位置信息;piv、gv分别表示个体最优值和全局最优值;r1、r2是[1,2]之间的随机数;a1、a2表示加速度系数;r是一阶向量,其每一维分量都是在[0,1]之间的随机数;Sig(X)表示Sigmoid函数。
在迭代过程中,函数饱和会导致“早熟”和局部收敛的问题。为了避免这类问题,本文将粒子的速度限制在[−5,5]范围内。
3.2 改进型BPSO算法BPSO算法虽然具有精确度高、收敛性好的优点,但是求解的速度普遍较慢,当应用在系统对求解速度要求比较高的异常或警戒状态时,效果不好。为此,本文提出改进BPSO算法,该方法根据系统运行特点和规则进行求解,不仅能快速找到问题可行解,还保留了传统BPSO算法精确度高的优点,适用于系统处于风险状态的情况。
当配电网处于风险状态时,可通过调整网络的拓扑提高系统的稳定性。具体思路是将高风险设备通过控制开关通断的手段转移到供电路径的末端,并把原高风险设备的下游负荷转移至其他线路。具体调整步骤如下:
1)采用动态规划法找到高风险设备所在的最短供电线路及其下游负荷;
2)若高风险设备处在供电路径的上游,则通过控制联络开关及分段开关的通断状态,将其转移至供电路径末端或直接退出运行;
3)将原高风险设备的下游负荷转移至剩余容量大的可行供电路径或直接退出运行。
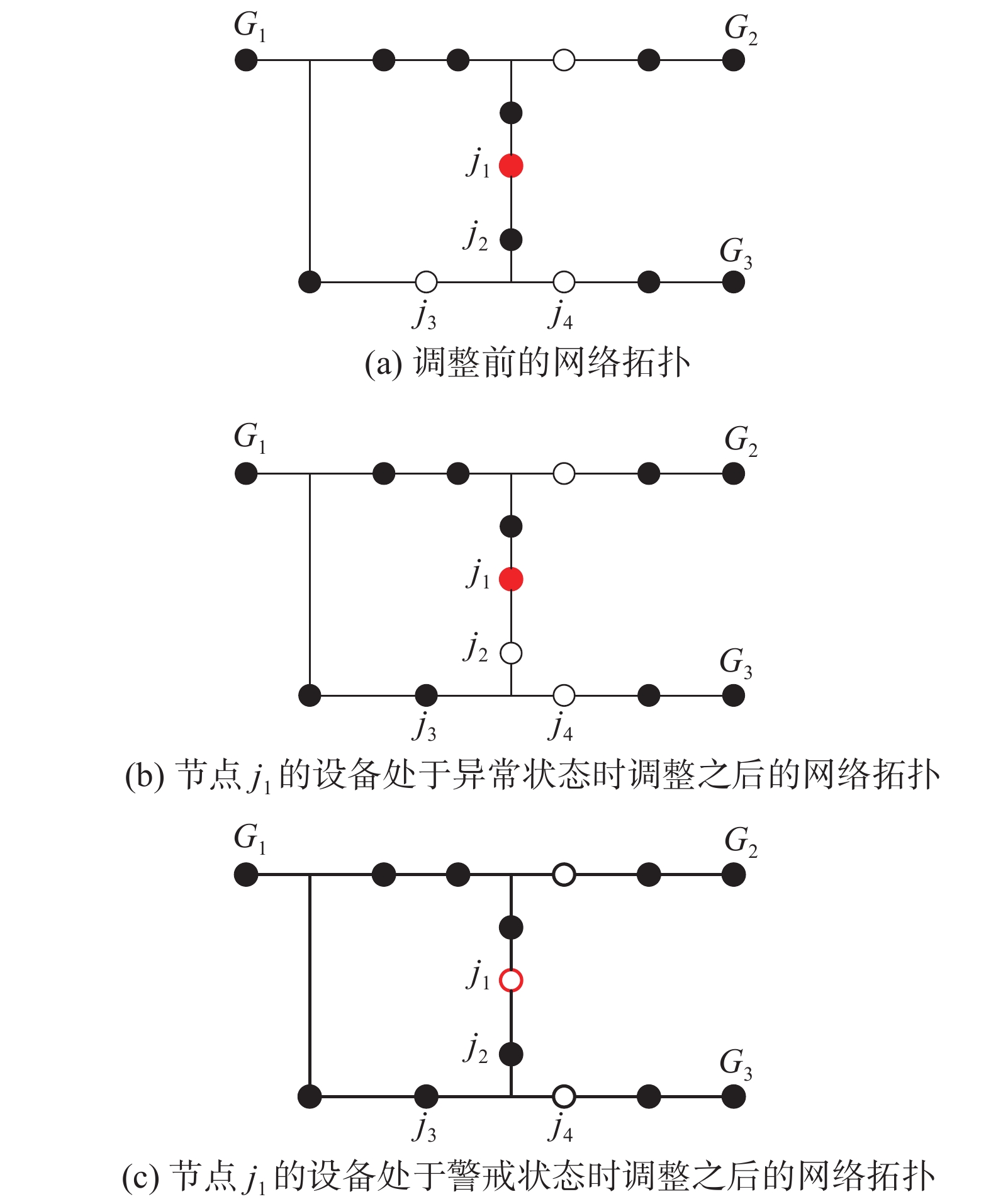
图3以14节点网络为例,说明改进型BPSO的快速拓扑调整流程。
|
Download:
|
| 图 3 快速拓扑调整过程 | |
图3中G节点表示电源,其余节点表示负荷。假设拓扑调整之前节点j1的设备处于高风险状态,分别讨论j1处于异常状态和脆弱状态2种情况下系统的调整方案。
1)当节点j1的设备处于异常状态时,节点j2设备退出运行,节点j3(或j4)设备投入运行。将j1设备转移至供电路径末端,将由j1供电的下游负荷转移到由节点j3(或j4)供电。此调整策略不仅提高系统的安全性,还有提高负载的均衡性、保证辐射状网络结构的特点。拓扑调整结果如图3(b)所示。
2)当节点j1的设备处于警戒状态时,系统处于故障和事故的临界处,节点j1设备需退出运行以提高系统安全性。将节点j3(或j4)设备投入运行,使节点j2的负荷由电源G1(或G2)经过节点j3(或j4)供电。拓扑调整结果如图3(c)所示。
经上述对14节点网络的分析可知,改进型BPSO算法首先采用动态规划法找到高风险设备所在的最短供电线路及其下游负荷;然后根据设备的风险程度选择是否切除设备。在异常状态下,不切除高风险设备,通过将其下游部分负荷转移至其它电源馈线供电,来提高负载均衡性。而在设备和系统风险等级更高的脆弱状态下,选择将高风险设备直接切除,并将其下游供电区域转由其他电源供电。因此,改进型BPSO算法可以快速提高系统的稳定性,并尽可能地保证负载的均衡性和系统的带负荷能力。
快速拓扑调整的流程图如图4所示。

|
Download:
|
| 图 4 快速拓扑调整流程 | |
采用IEEE 33节点配电系统[20]来验证所提算法,如图5所示。该系统共有37条线路和1个电源,其中5条线路配置联络开关。系统的基准电压为12.66 kV,三相功率基准值为10 MVA,当前工况下的总负荷为5084.26+j2547.32 kVA。仿真环境为Matlab2015a,CPU为i7-6700、3.40 GHz,内存为16 GB。

|
Download:
|
| 图 5 IEEE 33节点配电系统 | |
假设系统运行于异常状态,采用随机权重的方法构建目标函数,其中,w1~w4的值分别为0.5、0.25、0.15和0.1。分别使用本文提出的改进型BPSO算法、传统BPSO算法、文献[8]的分层优化算法和文献[9]的GA算法对同一目标函数进行优化求解。4种算法的加速度系数均为a1=a2=2,种群数均为30,最大迭代次数均为200,收敛精度为10−6,重复实验20次,得到平均运行结果如表2所示,将重构后网络损耗和节点电压与重构之前的网络损耗和节点电压进行对比,如表3。
|
|
表 2 4种算法的求解结果对比 |
|
|
表 3 重构结果比较 |
由表2、3可知,采用本文提出的改进BPSO算法对系统进行重构之后,配电网兼具较低的有功损耗、最大的供电能力、最少的迭代次数和负荷均衡性最好这几个优点,这说明采用随机权重的方法构建目标函数是合理的。
改进型BPSO算法通过将处于风险状态的设备快速转移到供电线路末端,提高了系统的稳定性,使得系统具有最大的供电能力和良好的负荷均衡性。由表2可知,在4种方法中,本文所提算法的平均最大供电能力分别比传统BPSO算法、分层优化算法和GA算法增加了33.98%、49.48%和12.13%。同时,改进的BPSO算法的迭代次数最少,具有较快的寻优能力,也说明了算法设计的合理性。
传统BPSO算法不能将处于风险状态的设备快速转移到供电线路末端,当系统处于高风险状态时,动作时长过长,不利于系统的稳定。分层优化算法的有功损耗也比较低,但是迭代次数太多,所需计算时间较长,当系统处于风险状态时效果不佳。GA算法的各项指标均弱于改进型BPSO算法。由仿真结果和分析可知,本文所提算法的迭代次数最少,具有较快的计算速度;有功损耗最低、最大供电能力最高,具有较好的经济性,验证了本文所提算法的合理性及有效性。
5 结论本文首先建立了配电网重构的多目标优化数学模型,然后介绍了BPSO算法原理并提出一种改进型BPSO算法。该方法根据系统运行特点和规则进行求解,不仅保留了传统BPSO算法精确度高的优点,还大大降低了计算时间。通过IEEE 33节点标准算例测试,得到如下结论:
1)本文建立的数学模型,综合考虑了配电网重构的各项优化指标,包括网络损耗、负荷均衡性、开关操作次数、最大供电能力等,达到了多目标优化的目的。
2)重构之后配电网的有功损耗降低,节点最低电压有了很大提升,说明配电网重构可以达到优化系统运行的目的。
3)相比于其他3种算法,改进型BPSO算法的有功损耗最小、最大供电能力最高、计算速度最快,适用于系统处于风险状态的情况,满足系统安全经济运行的要求。
| [1] |
TALESKI R, RAJICIC D. Distribution network reconfiguration for energy loss reduction[J]. IEEE transactions on power systems, 1997, 12(1): 398-406. DOI:10.1109/59.575733 ( 0) 0)
|
| [2] |
李振坤, 路群, 符杨, 等. 有源配电网动态重构的状态分裂多目标动态规划算法[J]. 中国电机工程学报, 2019, 39(17): 5025-5036, 5284. ( 0) 0)
|
| [3] |
吴泓俭, 雷霞, 刘斌, 等. 基于遗传膜算法的含风电机组和电动汽车的配电网分时段动态重构[J]. 电工技术学报, 2016, 31(2): 196-205, 220. DOI:10.3969/j.issn.1000-6753.2016.02.025 ( 0) 0)
|
| [4] |
曹昉, 张姚, 李赛. 基于网架结构相似性和适应性的主动配电网动态重构[J]. 电力系统自动化, 2019, 43(16): 78-86. ( 0) 0)
|
| [5] |
张沈习, 袁加妍, 程浩忠, 等. 主动配电网中考虑需求侧管理和网络重构的分布式电源规划方法[J]. 中国电机工程学报, 2016, 36(S1): 1-9. ( 0) 0)
|
| [6] |
麻秀范, 丁宁, 李龙. 配电网重构中网络辐射形与连通性的判断[J]. 电工技术学报, 2014, 29(8): 289-293. DOI:10.3969/j.issn.1000-6753.2014.08.037 ( 0) 0)
|
| [7] |
张立梅, 唐巍. 计及分布式电源的配电网前推回代潮流计算[J]. 电工技术学报, 2010, 25(8): 123-130. ( 0) 0)
|
| [8] |
DENG Lihua, FEI Juntao, BAN Cuiren. The simulation of self-healing restoration control for smart distribution network[C]//2015 6th IEEE International Conference on Software Engineering and Service Science (ICSESS). Beijing, China, 2015: 482–485.
( 0) 0)
|
| [9] |
WANG Chaoxue, GUO Shihong, LI Changhua. Application of genetic algorithm based on gene therapy theory for distribution network reconfiguration[C]// 2008 4th International Conference on Natural Computation. Jinan, China, 2008: 551–556.
( 0) 0)
|
| [10] |
NEMATSHAHI S, MASHHADI H. Distribution network reconfiguration with the application of DLMP using genetic algorithm[C]//2017 IEEE Electrical Power and Energy Conference (EPEC). Saskatoon, Canada, 2017: 1–5.
( 0) 0)
|
| [11] |
袁玉松, 钟建伟, 李沁, 等. 混合型粒子群算法在含分布式电源配电网重构中的应用[J]. 电气自动化, 2019, 41(6): 55-57,99. ( 0) 0)
|
| [12] |
李晏君. 考虑可靠性的含风电配电网多目标快速重构研究[D]. 杭州: 浙江大学, 2019.
( 0) 0)
|
| [13] |
俞隽亚. 基于恶劣气候条件的城市配电网风险评估及应用[D]. 北京: 华北电力大学, 2015.
( 0) 0)
|
| [14] |
ZHENG Ruiguan, ZHANG Zhiya, WANG Haiming, et al. Economical research of distribution network reconstruction in emigration areas[C]//2011 IEEE Power Engineering and Automation Conference. Wuhan, China, 2011: 67–70.
( 0) 0)
|
| [15] |
李振坤, 路群, 符杨, 等. 有源配电网动态重构的状态分裂多目标动态规划算法[J]. 中国电机工程学, 2019, 39(17): 5025-5036, 5284. ( 0) 0)
|
| [16] |
杨明, 翟鹤峰, 马嘉翼, 等. 计及分布式电源发电不平衡度约束的三相不对称配电网动态重构[J]. 中国电机工程学报, 2019, 39(12): 3486-3499. ( 0) 0)
|
| [17] |
KENNEDY J, EBERHART R. A discrete binary version of the particle swarm algorithm[C]//1997 IEEE International Conference on Systems, Man, and Cybernetics. Computational Cybernetics and Simulation. Orlando, FL, USA, 1997: 4104–4108.
( 0) 0)
|
| [18] |
徐义春, 肖人彬. 一种改进的二进制粒子群算法[J]. 模式识别与人工智能, 2007, 20(6): 788-793. DOI:10.3969/j.issn.1003-6059.2007.06.011 ( 0) 0)
|
| [19] |
YANG Guangyou. A modified particle swarm optimizer[C]// 2007 8th International Conference on Electronic Measurement and Instruments. Xi'an, China, 2007: 675–679.
( 0) 0)
|
| [20] |
刘路宁, 彭春华, 温泽之, 等. 基于配电网动态重构的分布式光伏消纳策略[J]. 电力自动化设备, 2019, 39(12): 56-62. ( 0) 0)
|
 2020, Vol. 47
2020, Vol. 47


