低截获概率(low probability of intercept,LPI)雷达具有低截获、高分辨率和抗干扰能力强等特点,传统的非合作截获接收机探测更加困难,所以明显提高了战场的生存能力,是军事领域反侦察、抗干扰的最有效技术之一。所以对LPI雷达信号波形如何进行有效识别便成了非合作雷达信号处理研究的重点工作[1-3]。对于LPI雷达信号波形识别的重点在于选取有效的信号特征和识别算法。早在20世纪90年代,A.K.Nandi等[4-5]提出了一种基于时域瞬时和统计特征提取的雷达信号识别算法,当信噪比在10 dB的情况下,对PSK、FSK等信号的识别准确率达到了90%。但是对于多相码调制(如P1码),则无法进行有效识别。Barbarossa S等[6-7]用Pseudo-Wigner分布和Wigner-Ville分布识别了线性调频信号和多种频率调制信号,对于相位调制类型的信号并没有进行研究。Lunden等[8]提出基于CWD和Wigner-Ville 分布(Wigner-Ville distribution, WVD)进行雷达信号识别的算法,识别了8种雷达信号波形,信噪比在6 dB的情况下,总体的识别准确率达到98%。但是在复杂的噪声环境下,由于算法对载波频率以及子脉冲宽度估计不准确导致了识别成功率的下降。文献[9]提出基于CWD时频变换和图像处理等方法提取雷达信号波形特征,并结合ENN神经网络分类识别,在信噪比−2 dB条件下,对8种雷达波形(LFM、BPSK、Costas、Frank码、P1~P4码)识别率为94.7%,但是在工程实现上较为困难。戴亮军等[10]提出利用瞬时频率以及频谱的方法对信号进行分类,通过信号特征间的差异进行识别。文献[11]提出了基于频谱复杂度的识别方法,该方法使用信号的频谱复杂度的差异进行分类识别,但是在将信号进行平方后计算频谱复杂度进行信号区分的过程中,受噪声影响很大。
综上所述,为解决传统方法LPI雷达波形特征提取困难、时频图像预处理过程复杂、低信噪比下多种类波形识别率低以及工程实现较为困难的问题,本文提出一种基于分数阶傅里叶变换和循环谱的方法。该方法利用分数阶傅里叶变换特征、频谱复杂度特征以及循环谱等特征实现几种常用雷达信号的分类识别。通过与文献[10]和[11]对比,结果显示识别率有很大提高,在低信噪比下仍然有很好的识别效果。
1 信号特征分析雷达信号不同的调制方式可以体现在不同域中,如时域、频域以及时频域,由于信号的时域波形很容易受噪声的影响,根据信号的时域特征很难区分,所以,接下来利用信号在分数阶域上的特征,以及循环谱和频谱复杂度特征实现对雷达信号不同调制方式的分类。接下来针对NS、BPSK、QPSK、2FSK、LFM和NLFM这6种常用的雷达信号进行研究。
1.1 分数阶傅里叶变换的基本理论分数阶傅里叶变换表达式为
| ${X_p}(u) = {F^p}[s(t)] = \int_{ - \infty }^\infty {s(t){K_p}} (t,u){\rm{d}}t$ |
转换内核是
| $\begin{array}{c} {K_P}(t,u) = \\ \;\;\left\{\!\!\!\begin{array}{l} \sqrt {(1 - {\rm{j}}\cot \alpha )} \exp {\rm{j{\text{π}} }}[({t^2} + {u^2})\cot\alpha - 2tu \csc\alpha ],\;\alpha \ne n{\rm{{\text{π}} }} \\ \delta (t - u),{\rm{ }}\;\alpha = 2n{\rm{{\text{π}} }} \\ \delta (t + u),{\rm{ }}\;\alpha = (2n + 1){\rm{{\text{π}} }} \\ \end{array} \right. \end{array} $ |
式中:P是FRFT的变换阶数;
FRFT用于信号识别,我们必须使用DFRFT数值运算。通过采样类型的Ozaktas算法[12]映射时间的n个采样点域原始功能,实现FRFT快速算法,重写FRFT表达式如下:
| $\begin{array}{c} {X_p}\Bigg(\dfrac{m}{{2\Delta x}}\Bigg) = \dfrac{{{A_\alpha }}}{{2\Delta x}} \cdot x\Bigg(\dfrac{n}{{2\Delta x}}\Bigg) \cdot \\ \displaystyle\sum\limits_{n = - N}^N {\exp } \left( {{\rm{j{\text{π}} }}\gamma {{\Bigg(\dfrac{m}{{2\Delta x}}\Bigg)}^2} - {\rm{j}}2{\rm{{\text{π}} }}\beta \dfrac{{mn}}{{{{(2\Delta x)}^2}}} + {\rm{j{\text{π}} }}\gamma {{\Bigg(\dfrac{n}{{2\Delta x}}\Bigg)}^2}} \right) \\ \end{array} $ |
式中
FRFT可用于信号识别的最重要原因是它对于LFM具有出色的检测性能,因为FRFT是线性的,而且可以进行旋转任何角度操作,LFM在分数阶傅里叶域具有独特的能量聚集[13],LFM和编码信号可以通过在分数阶傅里叶域做二维峰值搜索进行区分。
下面对几种典型的调制信号及其FRFT结果进行分析,仿真如图1所示。

|
Download:
|
| 图 1 6种雷达信号的分数阶域曲线 | |
仿真结果表明,编码信号的模量一定在P=1的位置,而LFM信号的模量在P=1.25的位置,不等于1。由于调频斜率的不同,对于不同的调频斜率,LFM的峰值会出现在不同的值上,从而可以识别出LFM信号和编码信号[14]。
在上述分析的基础上,总结了识别LFM信号和编码信号的方法:将信号转换成分数阶傅里叶域,然后提取每个信号的最大模量对应的旋转角度;由此得到傅里叶变换的阶数,并根据阶数的不同位置对不同的信号进行区分;编码信号的模量在P=1时出现峰值,而调频信号的模量在调频斜率匹配时出现峰值,即P≠1[15]。
从图1可以看出,NS、BPSK、QPSK和2FSK信号通过分数阶傅里叶变换后,在分数阶P=1时模值会出现尖峰;而LFM信号和NLFM信号经分数阶傅里叶变换后,在P=1处不会出现模值尖峰。所以以尖峰对应P值是否为1作为标准,可以将6种信号识别为两大类[16],即LFM、NLFM调频信号为一类,NS、BPSK、QPSK、2FSK非调频信号为另一类。
1.2 谱峰特征对于2FSK信号,利用其在频域上有2个明显谱峰的特点将该信号与其他信号进行分类。为了减小噪声的影响,通过对信号频谱{s(k)}进行平滑操作处理,得到平滑后频谱{S(k)},设定平滑步长是sstep,得:
| $S\left( k \right) = \frac{1}{{{s_{{\rm{step}}}}}}\sum\limits_{m = k}^{k + {s_{{\rm{step}}}} - 1} {s\left( m \right)} ,k = 1,2, \cdots ,N - {s_{{\rm{step}}}}$ |
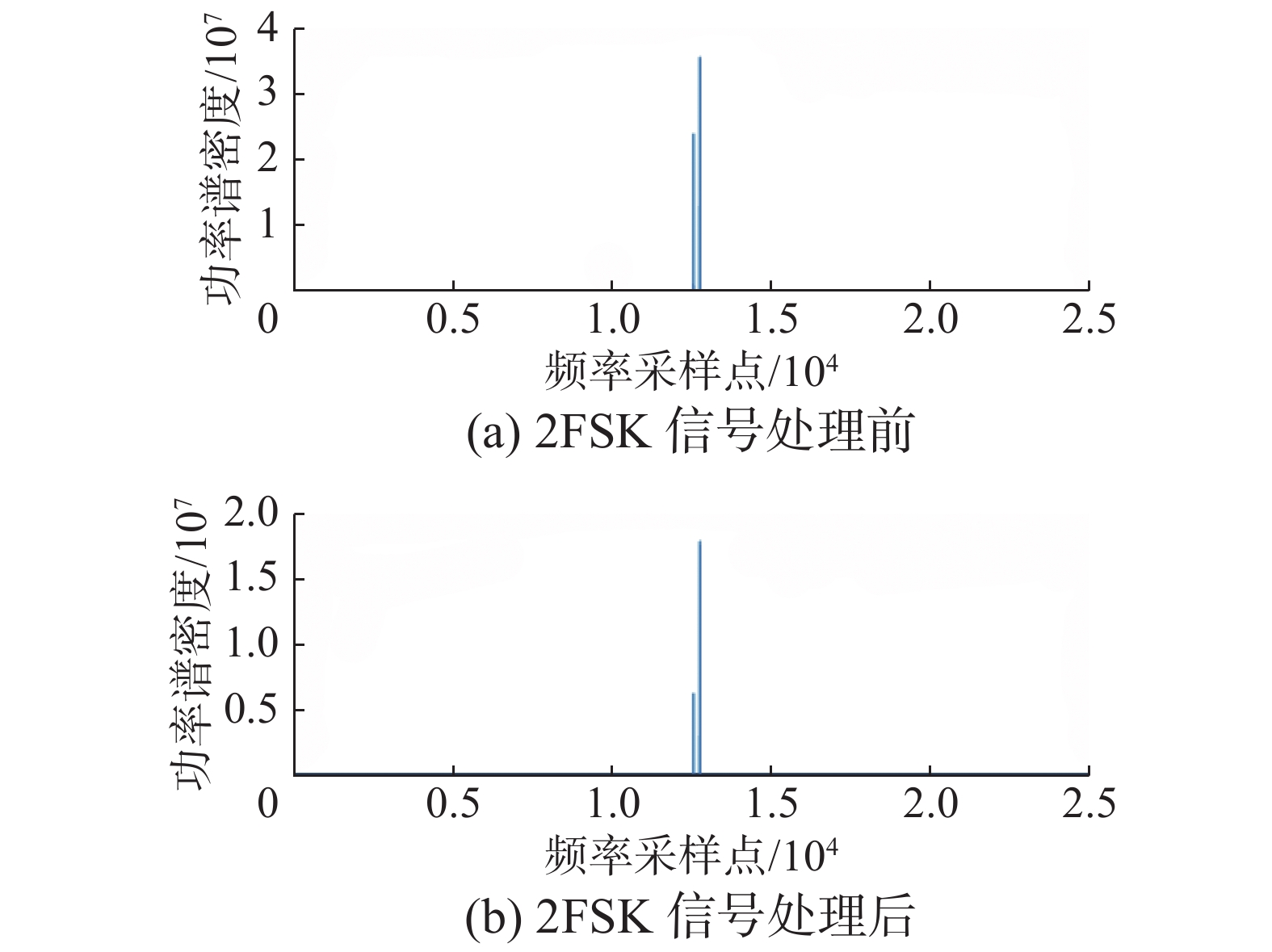
对平滑处理后的频谱{S(k)}进行谱峰搜寻,其过程如图2所示,最终得到2FSK信号处理前后的功率谱密度如图3所示。

|
Download:
|
| 图 2 2FSK识别流程 | |
|
Download:
|
| 图 3 平滑功率谱密度 | |
从图3可以看出,2FSK信号的谱峰数为2,利用谱峰特征可以实现2FSK信号与NS、BPSK、QPSK信号的区分。
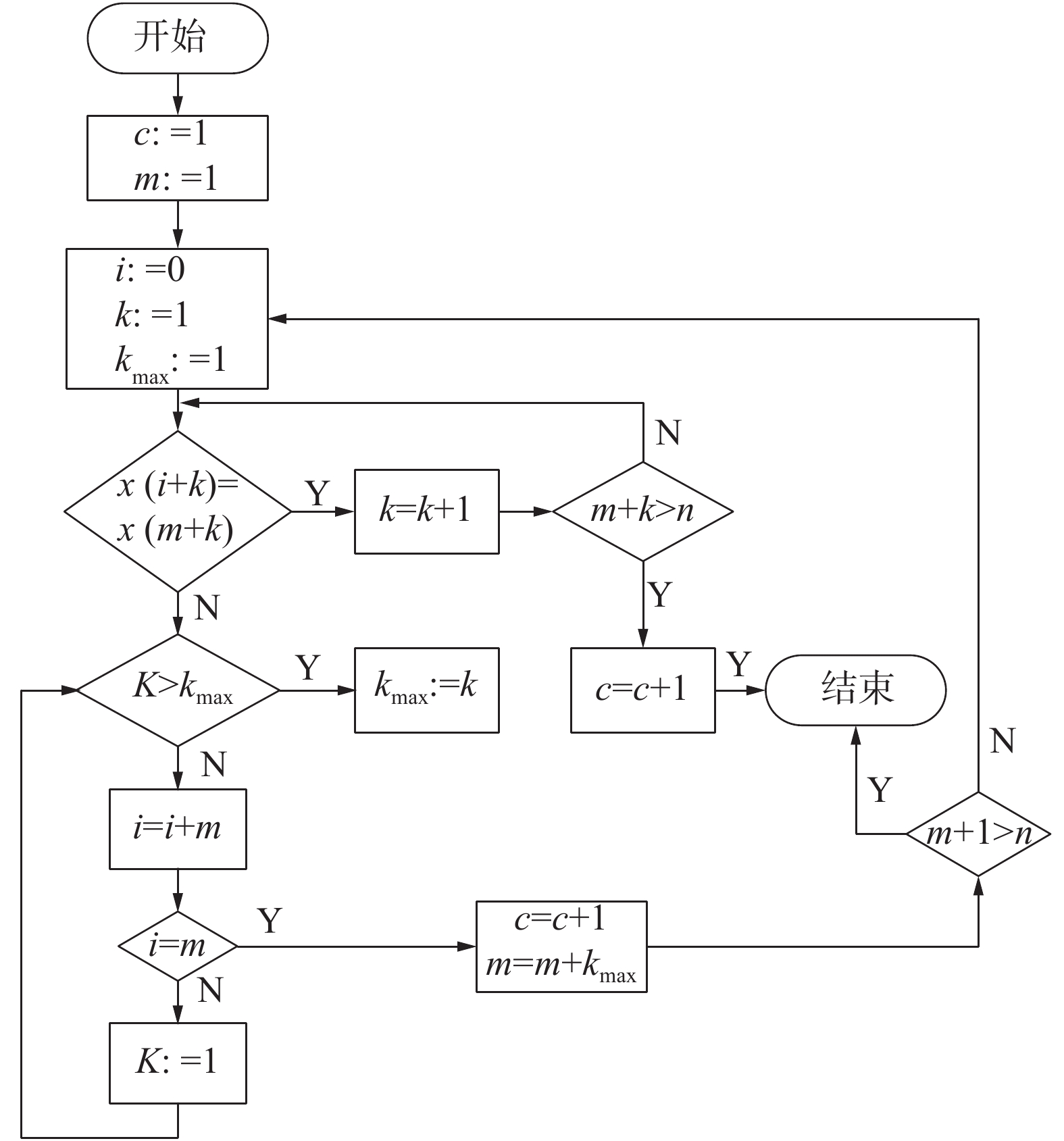
1.3 Lempel-Ziv(L-Z)复杂度特征L-Z复杂度用2个简单的操作(复制和插入)表示序列特征,插入时间是复杂度,计算流程如图4所示。
|
Download:
|
| 图 4 L-Z复杂度计算过程的流程 | |
图4中,c为添加时间,即复杂度;m是符号的个数,i和k是自然变量。
假设给定的字符串x(1),x(2),…,x(M)已由程序重建至数字x(M),并且新插入了x(m) (即不通过简单地复制从x(1),x(2),…,x(M))。至x(m)的字符串将会用Y=x(1),x(2),…,x(m)表示,x(m)是新插入的。为了检验剩下的Y,即x(m+1),x(m+2),…,x(M)是否可以通过简单的复制(或者是否需要插入新的数字)来重建,Lempel和Ziv[17]进行了以下步骤:
1)集合Z=x(m+1),确定是否可以从YZπ中复制(YZπ表示连接Y和Z新的字符串,然后删除最后一个符号)。
2)如果答案是肯定的,y不变,但需要将下面的数字x(m+2)插入Z中,则Z=x(m+1),x(m+2);如果答案是否定的,Z=x(m+2),Y=x(1),x(2),…,x(m),x(m+1),继续判断。
3)重复步骤2),直到Y包含所有重建的数字,插入时间为L-Z复杂度,表示为c(M)。但是,如果最后一个操作是复制的,则需要添加一个插入次数。
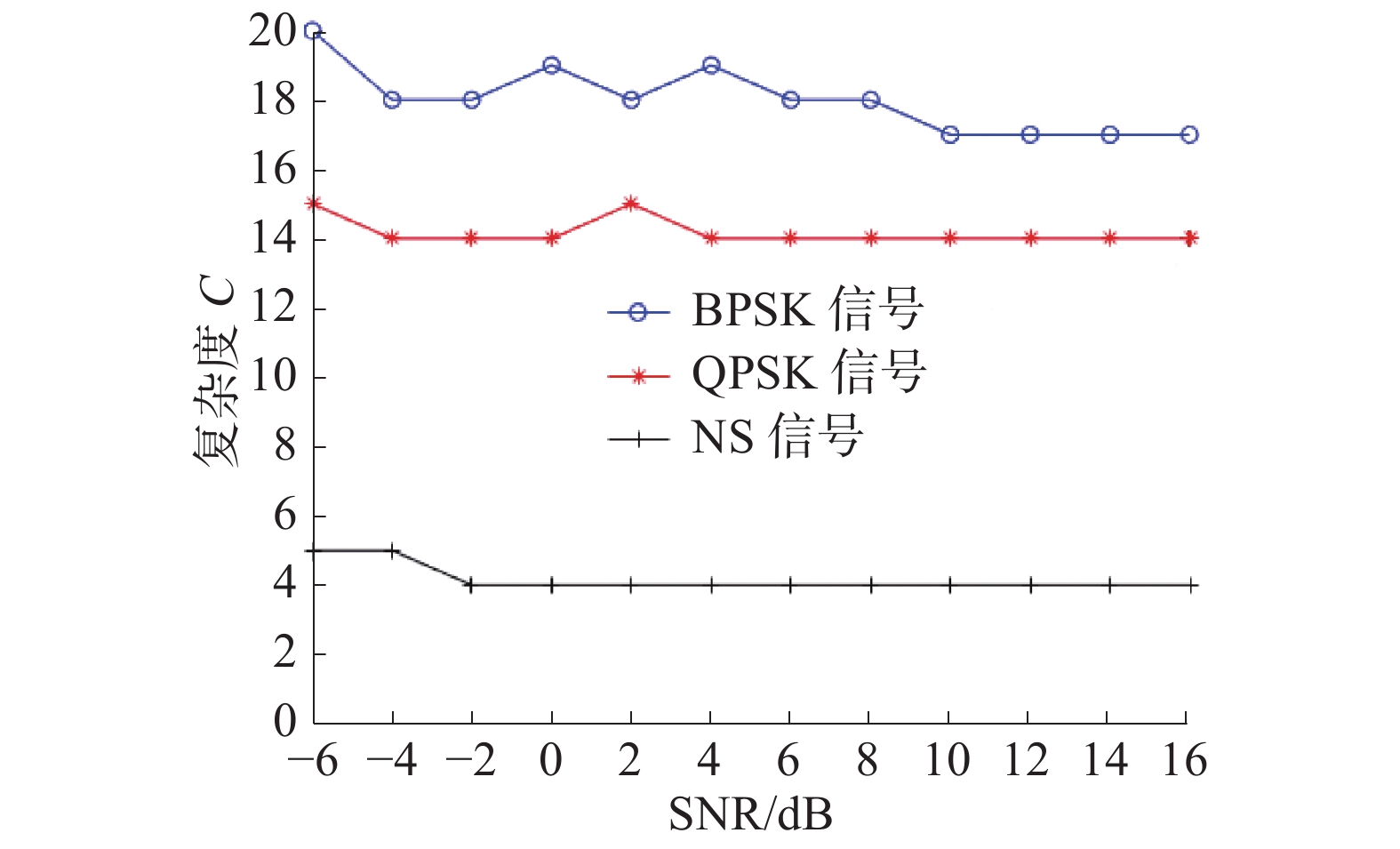
对于NS信号,频谱中是一个离散的单频谱线,因此其信号频谱复杂度最低。而BPSK和QPSK信号的相位在码元之间会发生变化,如BPSK信号会发生180°的跳变,QPSK信号会发生90°的跳变,最终造成频谱复杂度的不同。BPSK信号平方后变为一个NS信号,只是信号载频变成了原来的2倍。也就是说,BPSK信号的频谱复杂度通过平方变换后,频谱复杂度和常规雷达信号频谱复杂度相同。对于QPSK信号来说,对信号进行2次平方可以变成一个四倍载频的常规雷达信号,从而使频谱复杂度达到最低。从理论上讲利用频谱复杂度可以实现NS、BPSK、QPSK信号的细分类,如图5。但是在低信噪比情况下信号平方后频谱复杂度不够稳定,所以在实际应用中,会造成BPSK信号和QPSK信号难以区分。
|
Download:
|
| 图 5 BPSK、QPSK、NS信号的频谱复杂度 | |
从图5可以看出,利用频谱复杂度可以实现NS信号与BPSK和QPSK信号的区分。
1.4 循环谱针对在低信噪比下对信号平方后频谱复杂度不够稳定、难以实现BPSK信号与QPSK信号的分类的问题,提出了循环谱的方法实现对BPSK和QPSK信号的细分类。
对于循环平稳信号而言,其循环谱密度函数为循环自相关函数的的傅里叶变换[18],表达式如下:
| $S_x^\alpha (f) = F[R_x^\alpha (\tau )] = \int_{ - \infty }^\infty {R_x^\alpha (\tau ){{\rm{e}}^{ - {\rm{j}}2{\rm{{\text{π}} }}f\tau }}{\rm{d}}\tau } $ | (1) |
对于离散信号而言,式(1)又可以写为
| $S_x^\alpha (k) = \sum\limits_{n = 0}^{N - 1} {R_x^\alpha (\tau )} {{\rm{e}}^{ - {\rm{j}}2{\rm{{\text{π}} }}kn/N}}$ | (2) |
对于式(2)而言,当α=0时,
|
Download:
|
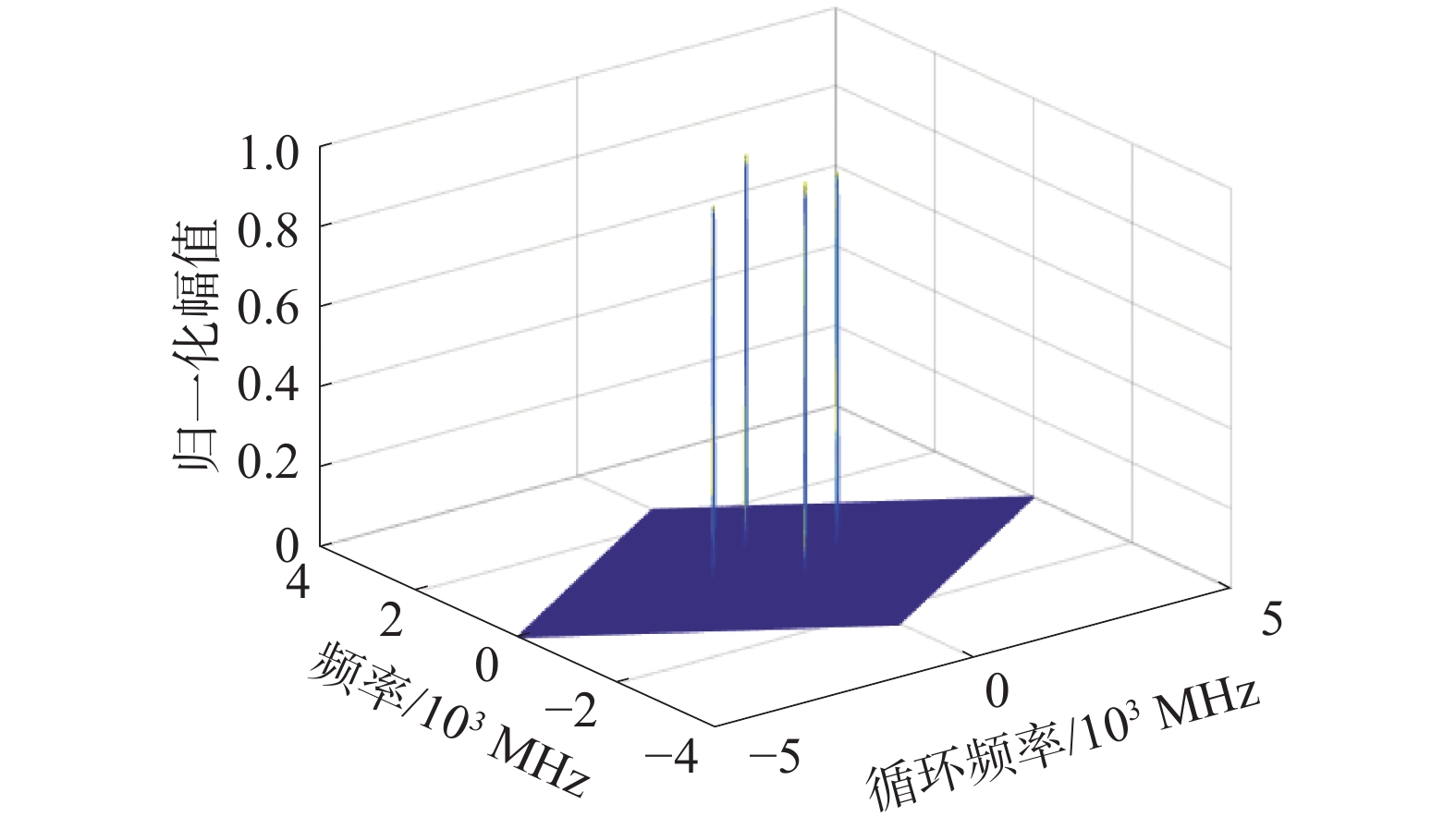
| 图 6 BPSK信号循环谱三维图 | |
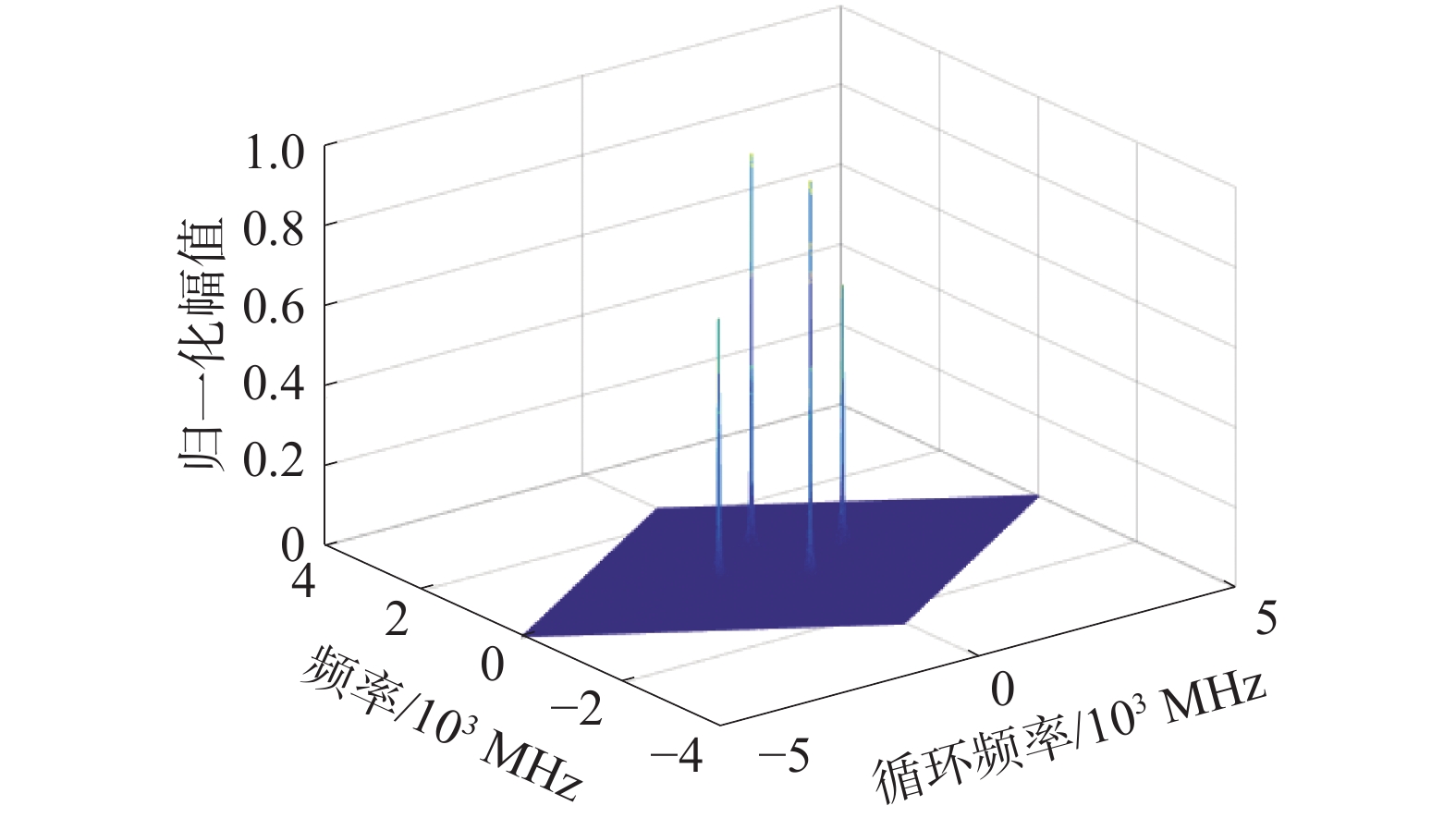
|
Download:
|
| 图 7 QPSK信号循环谱三维图 | |
1)BPSK信号的循环谱密度函数峰值出现在f=0循环频率轴截面和α=±2f0上,而QPSK信号的峰值不会出现在在α=±2f0处。
2)BPSK信号循环谱密度函数的f=0循环频率轴截面的最大值和在α=0频率轴截面的最大值的比值非常接近1;而QPSK信号两者之间的比值与1相差很大。
所以根据结论2,定义循环谱在f=0循环频率轴截面的最大值和α=0频率轴截面的最大值的比值为λ,当比值λ小于阈值时,判断为QPSK信号,反之为BPSK信号,如图8所示。

|
Download:
|
| 图 8 BPSK和QPSK信号的λ值 | |
从图8可以看出,利用循环谱的方法,在低信噪比仍然可以实现BPSK信号和QPSK信号的准确识别。
1.5 调频信号信号功率谱非线性调频信号可以表示为
| $s\left( t \right) = A{{\rm{e}}^{{\rm{j2{\text{π}} }}\left( {{a_1}t + {a_2}{t^2} + {a_3}{t^3}} \right)}}$ |
对信号做瞬时自相关得:
| $\begin{array}{c} x\left( t \right) = s\left( {t + \tau } \right) \cdot {s^ * }\left( t \right) = \\ {A^2}{{\rm{e}} ^{\left( {{\rm{j2{\text{π}} }}\left( {{a_1}\tau + {a_2}{\tau ^2} + {a_3}{\tau ^3} + \left( {2{a_2}\tau + 3{a_3}{\tau ^2}} \right)t + 3{a_3}\tau {t^2}} \right)} \right)}} \\ \end{array} $ | (3) |
式中τ为固定值。
式(3)变换为一个LFM信号,如图9中所示,其功率谱密度的外形特征近似为一个矩形。当信号s(t)为LFM信号,此时a3=0,式(3)将转化为一个单载频信号,其功率谱密度在频域的外形特征表现为一根冲击谱线,所以,通过观察调频信号(LFM、NLFM)在瞬时自相关后的功率谱如图9,可以实现LFM和NLFM的细分类。
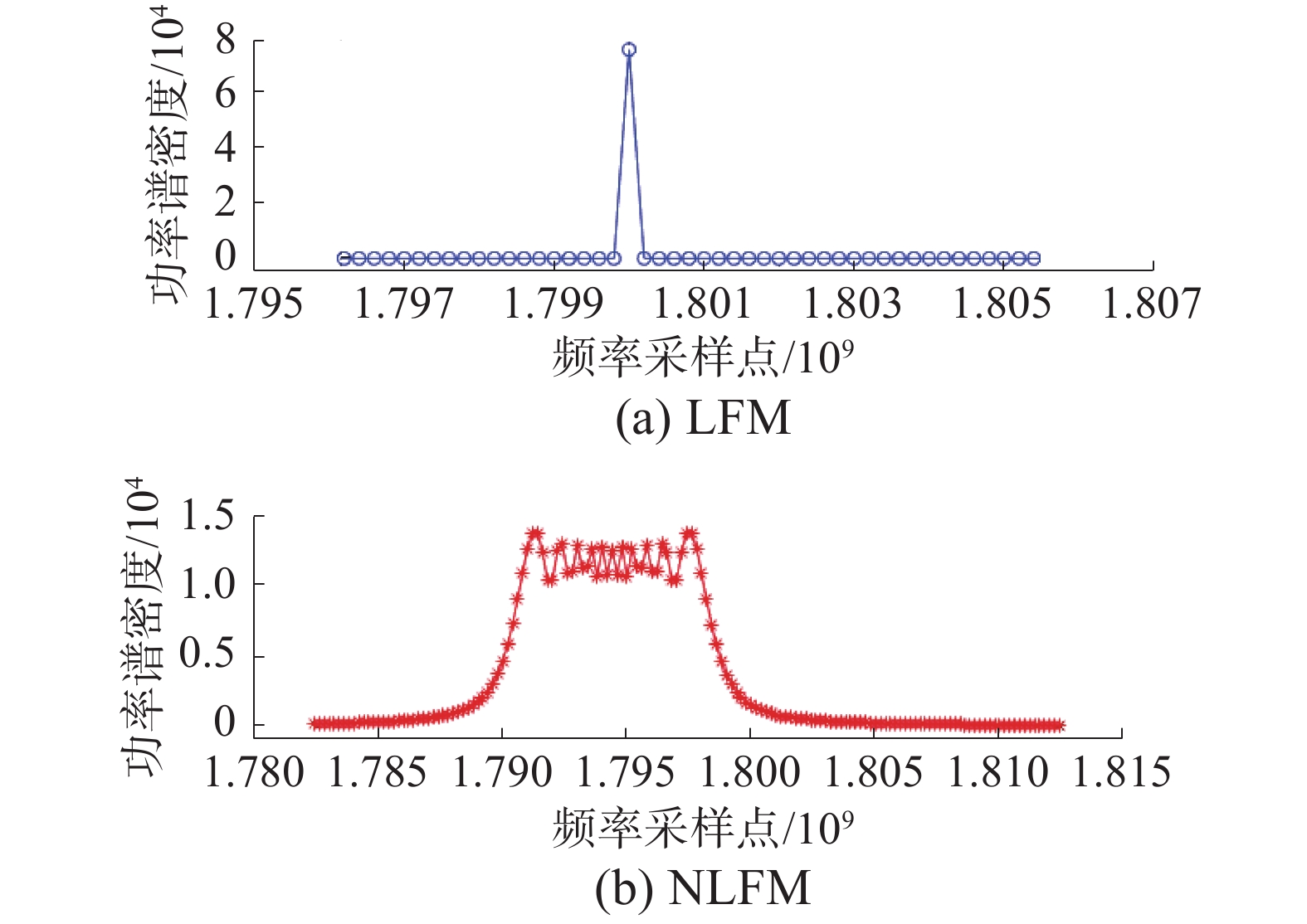
|
Download:
|
| 图 9 瞬时自相关功率谱 | |
通过对调频信号以及非调频信号的特征分析,结合信号的分数阶傅里叶变换最大峰值对应的分数阶、信号复杂度和循环谱特征以及功率谱特征,设计如图10所示的识别流程。

|
Download:
|
| 图 10 雷达信号识别流程 | |
1)对接收信号进行分数阶傅里叶变换(FRFT),分数阶记为P,P∈[0,2],搜索出最大峰值对应的分数阶,记为P0。
2)根据P0是否等于1,将信号分为调频信号和非调频信号两大类[19],调频信号包含LFM、NLFM信号,非调频信号包含NS、BPSK、QPSK和2FSK信号。
3)对于非调频信号类进行处理。
①进行傅里叶变换,并对功率谱进行平滑去噪操作。搜索功率谱的谱峰个数n1,利用n1的值对信号进行判断,根据前文特征分析可知,2FSK信号的谱峰个数n1为2,所以判断为2FSK信号,不然即为其他信号,再通过步骤②进行处理。
②对处理后的信号功率谱进行L-Z复杂度计算,根据复杂度C的大小,设定阈值为4。当C=4,判断为常规信号;否则判断为其他信号,再通过步骤③进行处理。
③计算循环谱在f=0循环频率轴截面的最大峰值和在α=0频率轴截面的最大峰值的比值为λ,当比值λ小于阈值时,判断为QPSK信号;否则为BPSK信号。
4)对调频信号类进行处理。进行自相关傅里叶变换,求得其功率谱。由特征分析可知,线性调频信号会变换为单载频信号,其功率谱密度在频域的外形特征表现为一根冲击谱线,对功率谱进行谱峰搜索,当谱峰数n2等于1,即为线性调频信号;否则为非线性调频信号。
3 仿真结果与分析实验参数的设定:信号的调制类型包括2FSK、BPSK、NS、LFM、QPSK和NLFM这6种信号;脉冲宽度为5~30 µs;采样频率为500 MHz;载波频率为10~100 MHz;相位编码信号码元数为7~100;码元宽度为300~1 000 ns;频率编码信号的频率差为40 MHz;线性调频信号的带宽为5~100 MHz。通过1 000次蒙特卡洛实验,绘制了在不同信噪比条件下的信号识别准确率图,如图11所示。

|
Download:
|
| 图 11 不同信噪比下的信号识别准确率 | |
由图11可以看出,BPSK和QPSK信号的识别效果最佳,信噪比在0 dB时就达到了100%识别率,这是因为它的循环谱特征在噪声情况下表现稳定;NS在低信噪比下识别率较低,因为频谱复杂度特征在低信噪比下不够稳定,但当信噪比为0 dB时,识别率也达到了100%;当信噪比大于4 dB时,LFM信号和NLFM信号以及2FSK信号的识别准确率都能够达到90%以上。因此可以说明利用谱峰搜索的方法进行识别是可行的,有着比较好的识别效果,将实验仿真结果通过与文献[10]比较,在低信噪比下,NS、BPSK、QPSK信号识别率均大幅提升,其他不同调制类型信号在不同信噪比下也有所提高。
4 结论1)根据信号的分数阶傅里叶变换最大峰值所对应分数阶以及雷达信号频谱等特点,设计了一个基于分数阶傅里叶变换及循环谱的雷达信号识别方法。实验结果显示,在信噪比为2 dB的情况下,信号的总体识别准确率可以到达90%,所以该方法有很好的识别效果。
2)针对BPSK及QPSK信号,平方后利用频谱复杂度的方法受噪声影响太大,提出了利用循环谱的特征进行区分,在低信噪比下依然可以区分。
3)本文所用到的信号都是变化的,更接近于实际信号,具有较好的工程应用价值,虽然针对这6种常用信号有着很好的识别效果,但过程较为复杂,如果要识别更多的信号,接下来需要研究更具有普适性的算法。
| [1] |
王星, 周一鹏, 周东青, 等. 基于深度置信网络和双谱对角切片的低截获概率雷达信号识别[J]. 电子与信息学报, 2016, 38(11): 2972-2976. ( 0) 0)
|
| [2] |
呙鹏程, 王星, 田元荣. 基于CEEMDAN-ASVM的低截获概率雷达信号识别[J]. 现代雷达, 2018, 40(3): 27-32. ( 0) 0)
|
| [3] |
LIU Yongjian, XIAO Peng, WU Hongchao, et al. LPI radar signal detection based on radial integration of Choi-Williams time-frequency image[J]. Journal of systems engineering and electronics, 2015, 26(5): 973-981. DOI:10.1109/JSEE.2015.00106 ( 0) 0)
|
| [4] |
NANDI A K, AZZOUZ E E. Algorithms for automatic modulation recognition of communication signals[J]. IEEE transactions on communications, 1998, 46(4): 431-436. DOI:10.1109/26.664294 ( 0) 0)
|
| [5] |
NANDI A K, AZZOUZ E E. Automatic analogue modulation recognition[J]. Signal processing, 1995, 46(2): 211-222. DOI:10.1016/0165-1684(95)00083-P ( 0) 0)
|
| [6] |
BARBAROSSA S. Analysis of multicomponent LFM signals by a combined Wigner-Hough transform[J]. IEEE transactions on signal processing, 1995, 43(6): 1511-1515. DOI:10.1109/78.388866 ( 0) 0)
|
| [7] |
BARBAROSSA S, LEMOINE O. Analysis of nonlinear FM signals by pattern recognition of their time-frequency representation[J]. IEEE signal processing letters, 1996, 3(4): 112-115. DOI:10.1109/97.489064 ( 0) 0)
|
| [8] |
LUNDEN J, KOIVUNEN V. Automatic radar waveform recognition[J]. IEEE journal of selected topics in signal processing, 2007, 1(1): 124-136. DOI:10.1109/JSTSP.2007.897055 ( 0) 0)
|
| [9] |
ZHANG Ming, LIU Lutao, DIAO Ming, et al. LPI radar waveform recognition based on time-frequency distribution[J]. Sensors, 2016, 16(10): 1682. DOI:10.3390/s16101682 ( 0) 0)
|
| [10] |
戴亮军. 基于频谱和瞬时频率特征的雷达信号识别[J]. 哈尔滨商业大学学报(自然科学版), 2018, 34(5): 568-572, 587. DOI:10.3969/j.issn.1672-0946.2018.05.013 ( 0) 0)
|
| [11] |
刘鲁涛, 戴亮军, 陈涛. 基于频谱复杂度的雷达信号调制方式识别[J]. 哈尔滨工程大学学报, 2018, 39(6): 1081-1086. ( 0) 0)
|
| [12] |
OZAKTAS H M, ARIKAN O, KUTAY M A. Digital computation of the fractional Fourier transform[J]. IEEE transactions on signal processing, 1996, 44(9): 2141-2150. DOI:10.1109/78.536672 ( 0) 0)
|
| [13] |
KWOK H K, JONES D L. Improved instantaneous frequency estimation using an adaptive short-time Fourier transform[J]. IEEE transactions on signal processing, 2000, 48(10): 2964-2972. DOI:10.1109/78.869059 ( 0) 0)
|
| [14] |
段皓楠. 基于分数阶傅里叶变换的线性调频信号估计与分离研究[D]. 南京: 南京理工大学, 2017.
( 0) 0)
|
| [15] |
王彦欢. 基于FRFT的信号识别与参数估计方法研究[D]. 哈尔滨: 哈尔滨工程大学, 2016.
( 0) 0)
|
| [16] |
XIA Jie, ZHANG Jianyun, LI Xiaobo, et al. Weak signal detection based on FRFT-domain adaptive filtering algorithm[C]//Proceedings of 2016 CIE International Conference on Radar. Guangzhou, China: IEEE, 2016.
( 0) 0)
|
| [17] |
LEMPEL A, ZIV J. On the complexity of finite sequences[J]. IEEE transactions on information theory, 1976, 22(1): 75-81. DOI:10.1109/TIT.1976.1055501 ( 0) 0)
|
| [18] |
熊达福. 基于信道化的LPI雷达侦察技术研究与实现[D]. 哈尔滨: 哈尔滨工程大学, 2018.
( 0) 0)
|
| [19] |
戴亮军. 雷达信号脉内调制特征识别的研究与实现[D]. 哈尔滨: 哈尔滨工程大学, 2018.
( 0) 0)
|
 2020, Vol. 47
2020, Vol. 47


