设计谱作为舰载设备抗冲击的考核输入，其合理性决定着舰载设备的设计成本与抗冲击性能之间的均衡。目前的设计谱方法是基于谱跌效应提出的，对此O’Hara做出了卓越的贡献，其研究成果至今仍然在美国海军抗冲击设计中广泛应用。1989年，O’Hara和Cunniff^[1-3]通过简单的多自由度系统解释了海军设计谱值的由来，并对其有效性进行了验证。国内也开展了相应的研究，2009年，姜涛等^[4]从理论上采用简化设备——基础的二自由度模型分析了设备质量、安装频率对谱跌效应的影响，得出二者安装频率相近或前者的质量超过0.2倍的后者时，设计谱值必须考虑谱跌效应。2010年，何少华等^[5]从理论上采用四自由度系统阐述谱跌的原理，并对其设计谱的建立提出参考方法。2016年，于博文等^[6]分析了圆盘−悬臂梁的谱跌效应，发现结构的应力响应与伪速度规律一致，增加上层设备的质量和刚度，会使设计谱值降低。谱跌效应产生机理已经得到理论上的证明，但其在舰船实际水下爆炸中的影响规律是否与理论一致有待研究。基于此，本文将简化设备安装于舰船的甲板上，通过改变设备的安装参数来研究实船的谱跌效应及其对设备的设计谱值影响。

1 谱跌效应及其影响因素 1.1 理论计算模型

在本次研究中，根据线性理论将舰载设备等效为拥有3个自由度的弹簧−质量系统；基础（甲板或者基座）等效为单自由度系统，其底部受到F的作用，如图1所示。

根据多自由度系统的理论求解方法，假设质量 ${m_1} = 100\;{\rm{ kg}}$ 、 ${m_2} = 50\;{\rm{ kg}}$ 、 ${m_3} = 30\;{\rm{ kg}}$ 、 ${m_4} = 20\;{\rm{ kg}}$ ，弹簧刚度 ${k_1} = 1.5 \times {10^8}\;{\rm{ N/m}}$ 、 ${k_2} = 7.5 \times {10^7}\;{\rm{ N/m}}$ 、 ${k_3} = $ $3.75 \times$ $ {10^7}\;{\rm{ N/m}}$ 、 ${k_4} = 1.5 \times {10^7}\;{\rm{ N/m}}$ ，得到设备−基础耦合系统的前四阶固有频率，分别为 ${f_1} = 84.3\;{\rm{ Hz}}$ 、 ${f_2} = 157.4\;{\rm{ Hz}}$ 、 ${f_3} = 232.1\;{\rm{ Hz}}$ 、 ${f_4} = 302.6\;{\rm{ Hz}}$ ，单独设备系统的前三阶固有频率为 ${f_{31}} = 93.0\;{\rm{ Hz}}$ 、 ${f_{32}} = 184.6\;{\rm{ Hz}}$ 、 ${f_{33}} = 278.6\;{\rm{ Hz}}$ ，对质量 ${m_1}$ 施加如下载荷激励：

$F = {10^5} \times {{\rm e} ^{- 20t}}$

(1)

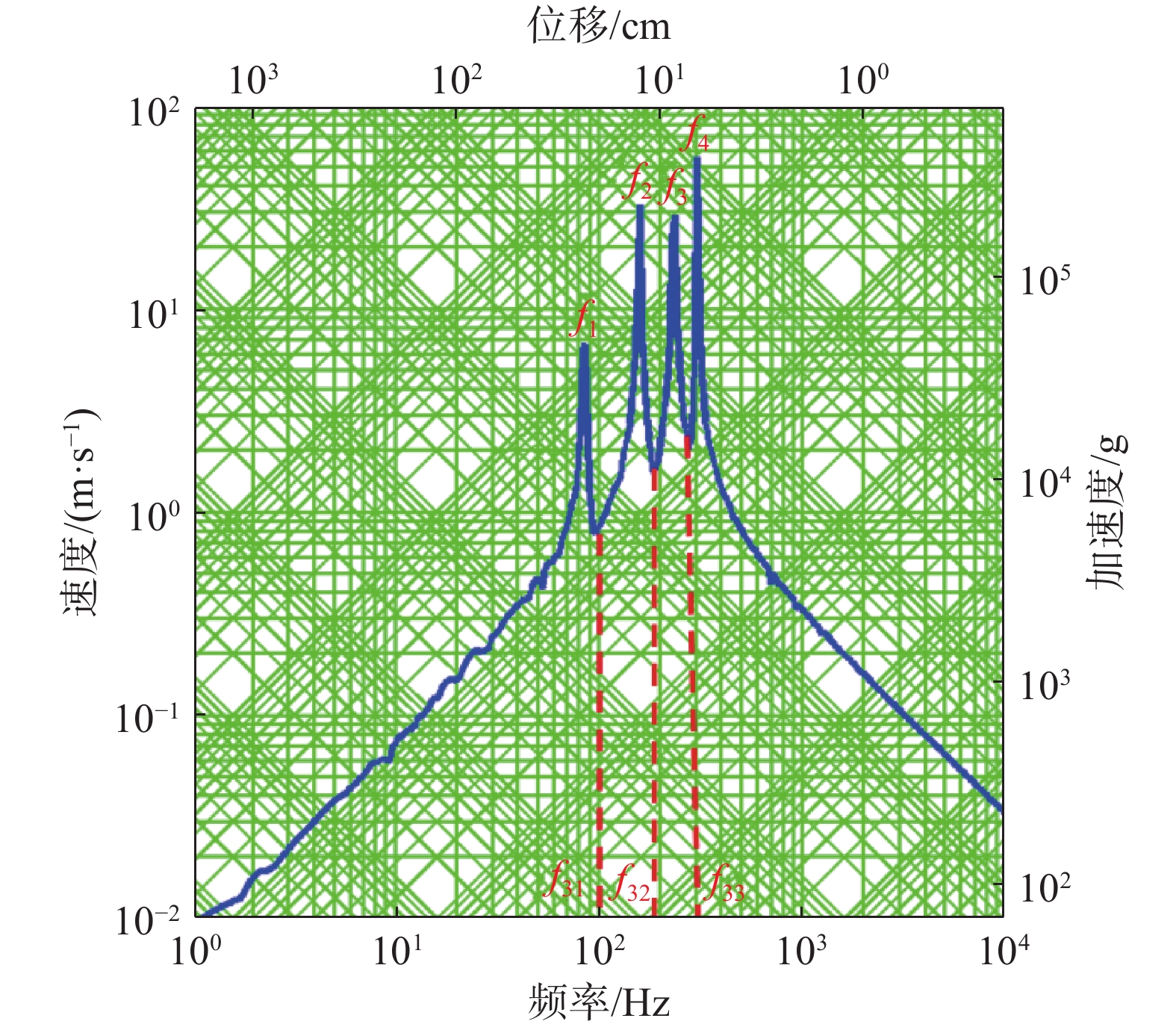
如图2所示， ${m_1}$ 处的冲击谱曲线出现4个波峰，分别对应设备−基础耦合系统的前四阶固有频率；而在单独设备子系统的前三阶固有频率处出现波谷，称为谱跌现象，表现为在设备安装频率下的冲击谱值会出现明显下降的现象。

1.2 谱跌产生的机理

谱跌现象是设备与基础之间相互作用的结果，类似于机械上的动力吸振，可以通过机械阻抗法进行解释。机械阻抗的定义为简谐激振力与其所引起的稳态响应的复数比^[7]。

因此可以得到设备−基础四自由度系统的阻抗矩阵 ${{Z}}(\omega )$ 为

${{Z}}(\omega ) = {{K}} - {\omega ^2}{{M}}$

(2)

式中： ${{K}}$ 为刚度阵； ${{M}}$ 为质量阵。

设备−基础系统的频响函数 ${{H}}(\omega )$ 为

$ {{H}}(\omega ) = {{{Z}}^{ - 1}}(\omega ) = \left[ {\begin{array}{*{20}{c}} {{H_{11}}(\omega )}&{{H_{12}}(\omega )}&{{H_{13}}(\omega )}&{{H_{14}}(\omega )} \\ {{H_{21}}(\omega )}&{{H_{22}}(\omega )}&{{H_{23}}(\omega )}&{{H_{24}}(\omega )} \\ {{H_{31}}(\omega )}&{{H_{32}}(\omega )}&{{H_{33}}(\omega )}&{{H_{34}}(\omega )} \\ {{H_{41}}(\omega )}&{{H_{42}}(\omega )}&{{H_{43}}(\omega )}&{{H_{44}}(\omega )} \end{array}} \right] $

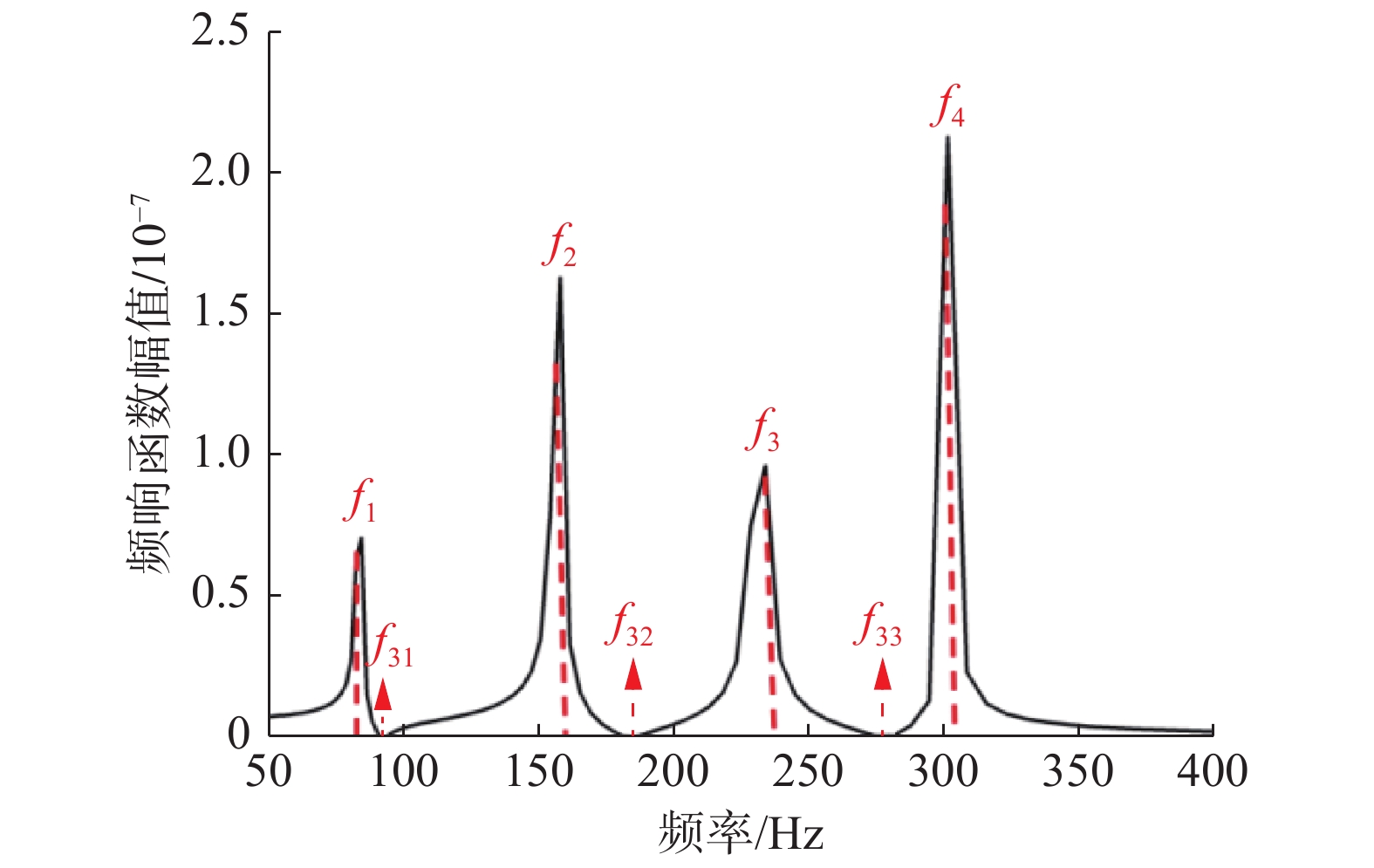
通过对原点频响函数 ${H_{11}}(\omega )$ 分析即可得到 ${m_1}$ 的响应特性，作出 ${H_{11}}(\omega )$ 随 $\omega $ 的变化曲线如图3所示。当外部激励力的主频率与设备−基础系统的耦合频率接近时，频响幅值曲线在耦合频率处出现峰值，即外部激励载荷与设备−基础系统发生共振，同时该频率下的冲击谱曲线表现为波峰。而当外部激励载荷与设备系统的安装频率相近时，频响幅值曲线在安装频率处出现极小值，即外部激励载荷与设备系统发生反共振，同时该频率下冲击谱曲线出现谱跌现象，这与动力消声器的原理有类似之处^[8]。

1.3 谱跌的控制因素

考虑一个单自由度系统，基础受到 $\ddot y(t)$ 作用。则质量 $m$ 与基础的相互作用力为

$F(t) = kz = - \frac{k}{\omega }\int\limits_0^t {\ddot y(\tau )} \sin \omega (t - \tau ){\rm{d}}\tau $

(3)

式中： $z$ 为单自由度系统的位移； $k$ 为单自由度系统的刚度； $\omega $ 为单自由度系统的的圆频率； $t$ 为时间； $\tau $ 为积分变量。

已有文献[9]证明在低频段 $z(t) \to - y_0(t)$ ，即

$F(t) = m{\omega ^2}y_0(t)$

(4)

从式（4）可以看出，外部激励不变的情况下，在低频段时，设备所受到的最大动态力与设备安装频率的平方成正比例关系；与质量成反比例关系。同理在高频段时， ${\omega ^2}z(t) \to - \ddot y_0(t)$ ，因此：

$F(t) = m\ddot y_0(t)$

(5)

在高频段，设备所受的动态力与安装频率无关，与质量成正比例。上面的假设建立在基础所受载荷不变的前提下，实际情况下由于设备与基础之间的相互作用会使得基础的冲击输入改变，为此本文将简化设备安装于实际舰船来验证理论结果的正确性。

2 实际舰船设备设计谱及其影响因素 2.1 有限元模型

舰船模型是依据千吨级实际舰船的中间舱段进行拉伸处理得到的简化模型，船长48 m、船宽9.4 m、吃水2.84 m、排水量900 t，如图4所示。采用声固耦合法对水下非接触爆炸下舰载设备基础下的冲击环境进行计算^[10]。

对船体−流场有限元模型进行模态分析得到舰船的前三阶模态频率分别为1.4、3.1、3.9 Hz，可以代表实际舰船的阵型。

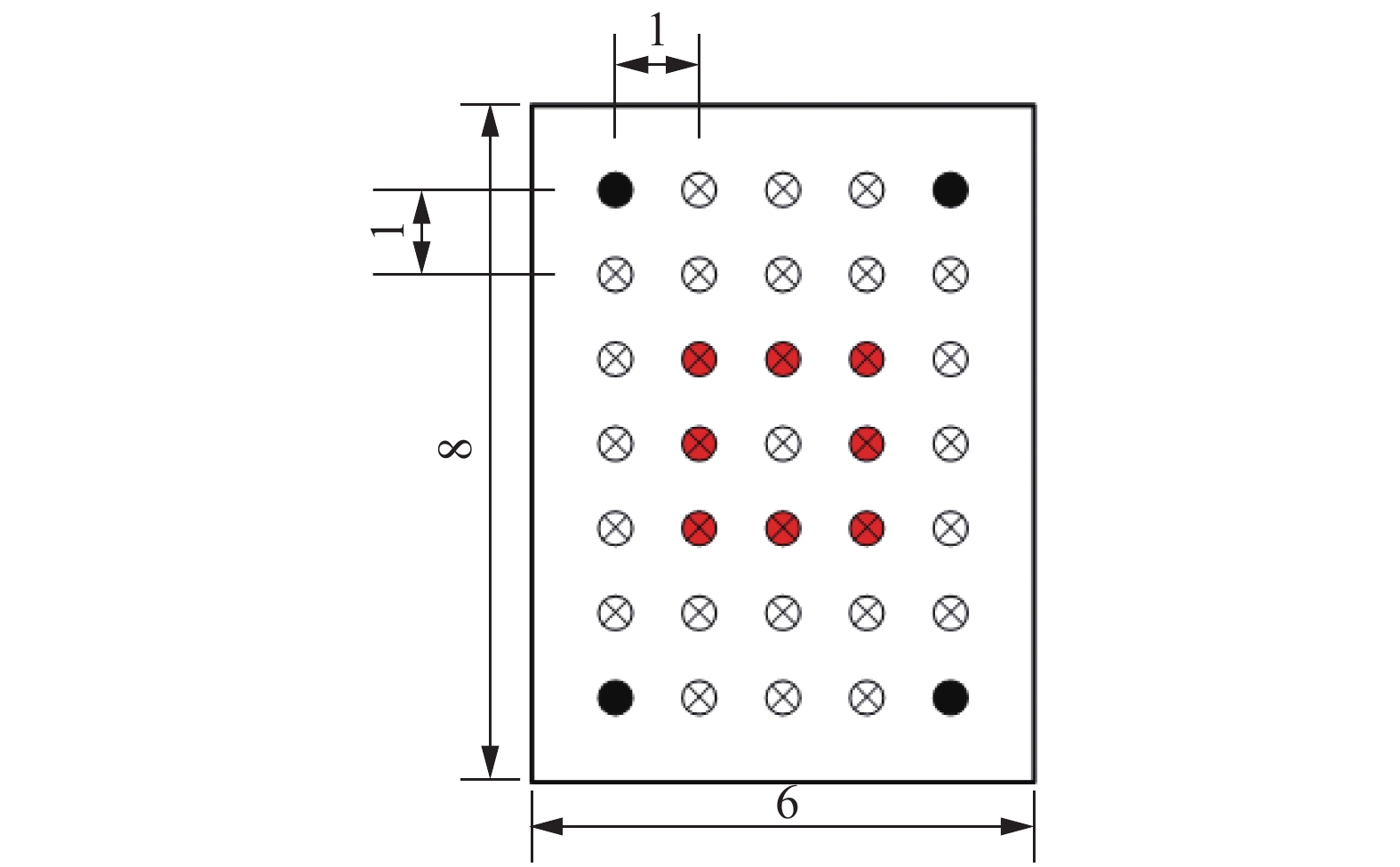
2.2 设备简化模型

为研究不同设备参数对设计谱的影响规律，本文采用简化的设备模型，在仿真计算中用刚体代替，长6 m、宽8 m。隔振器布置示意图如图5所示，中间代表8根隔振器布置的情况，总共可以布置35根隔振器。

2.3 工况设置

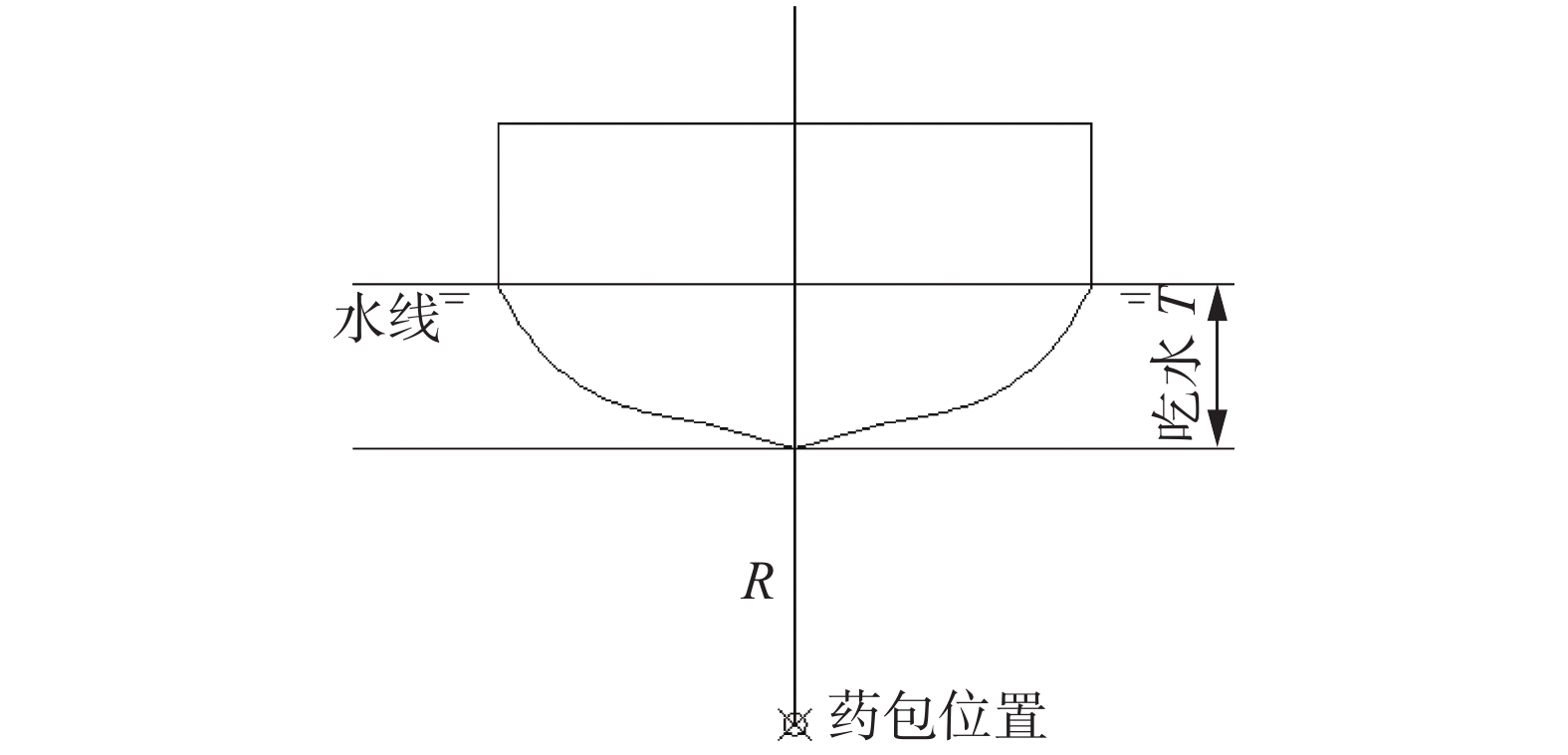
水面舰船通常选用龙骨冲击因子来衡量冲击波能量^[11]，本文计算中采用冲击因子0.3，药包位于舰船中横剖面的正下方，药包质量为1 000 kg、攻角90°、爆距105 m，具体位置如图6所示。

2.4 不同参数对设计谱的影响分析 2.4.1 设备安装频率对设计谱的影响

将简化设备通过隔振器安装于舰船的中间甲板上。由于常见设备的安装频率在10 Hz左右，一般不超过25 Hz^[12]，故本论文中选取设备安装频率为10~25 Hz，设备的质量为10~100 t，共5种工况，具体工况参数如表1所示。

由于不同工况下的曲线变化规律一致，因此只列出工况1下的冲击谱曲线，如图7所示。

从图7中可以看出：所有设备基础处的冲击谱曲线在设备安装频率处都发生明显的谱跌现象，与理论计算结果现象一致；所有设备基础处的冲击谱曲线在低频段基本重合，与自由甲板具有相同的波峰频率；在中高频段，设备基础处的冲击谱曲线具有明显的波谷，极小值与安装频率反相关。

为方便建立统一的标准，工程上常用伪速度表示的设计谱曲线来衡量冲击载荷的强弱，按照相关标准将冲击谱曲线进行圆整得到不同测点的设计谱值。由于测点的冲击环境不同，因此将不同工况的设计谱值进行平均处理，得到不同工况下舰载设备的设计值如表2所示。

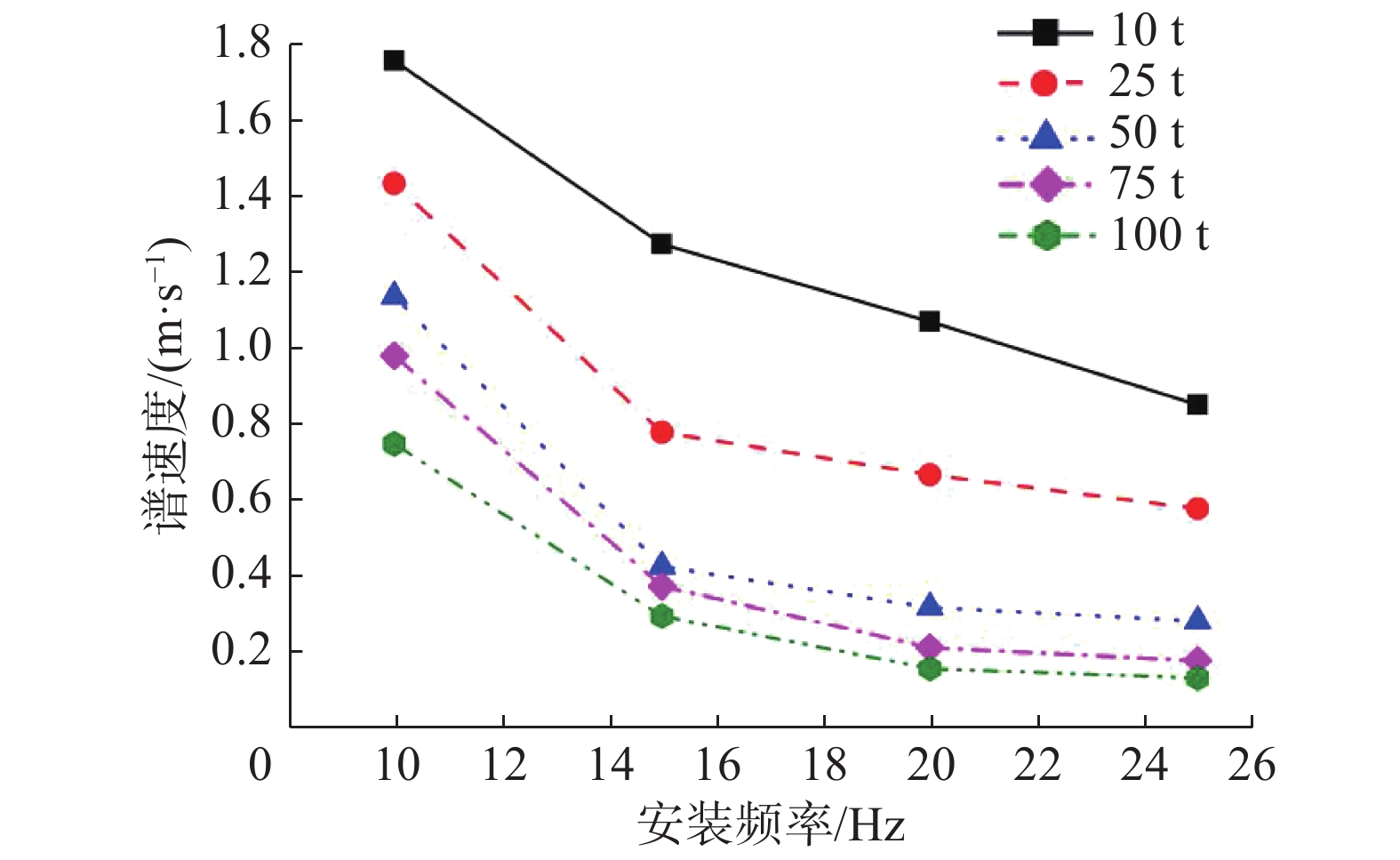
不同设备质量下的伪谱速度随安装频率的变化曲线如图8所示。

从图8中可以看到，舰载设备的谱速度与安装频率成反相关。由前面的理论推导可知，低频段时设备与基础之间的动态力与安装频率成正比例关系，安装频率越大，动态力越大，意味着设备基础处的伪速度越小，与理论计算结果一致。对比分析表2，设备质量10 t、安装频率10 Hz下的谱速度为1.76 m/s，而设备质量10 t、安装频率25 Hz下的谱速度为0.85 m/s，前者是后者的2倍。同样设备质量100 t、安装频率10 Hz下的谱速度是同样设备质量安装频率为25 Hz的近5倍，说明安装频率对于设计谱有着重要的影响，必须予以考虑。

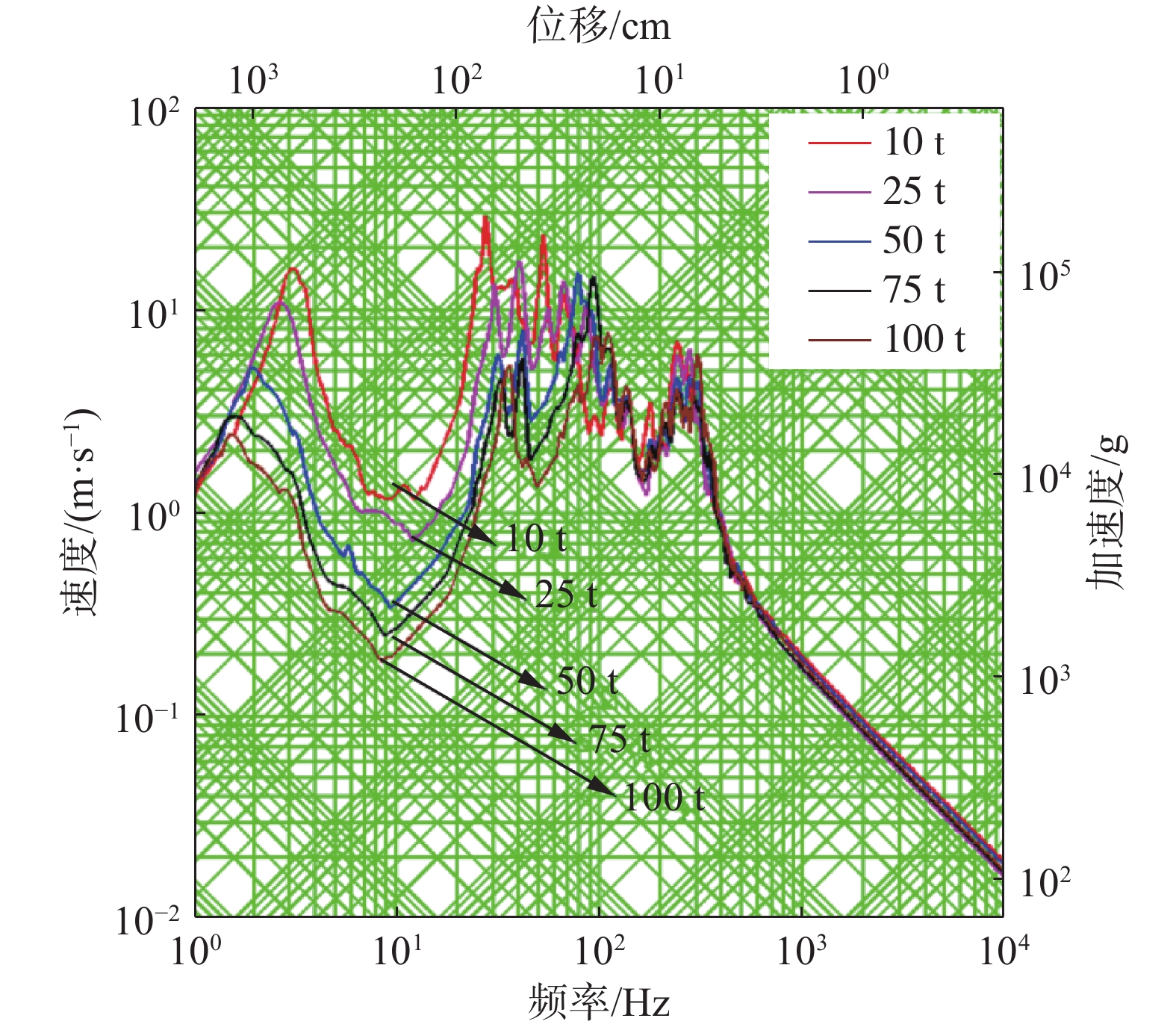
2.4.2 设备质量对设计谱的影响

保持设备的安装频率不变，改变设备的质量，得到设备质量10 t、安装频率10 Hz下的冲击谱曲线如图9所示。由于不同工况的冲击谱曲线规律一致，只给出工况1的曲线，其他工况不做叙述。

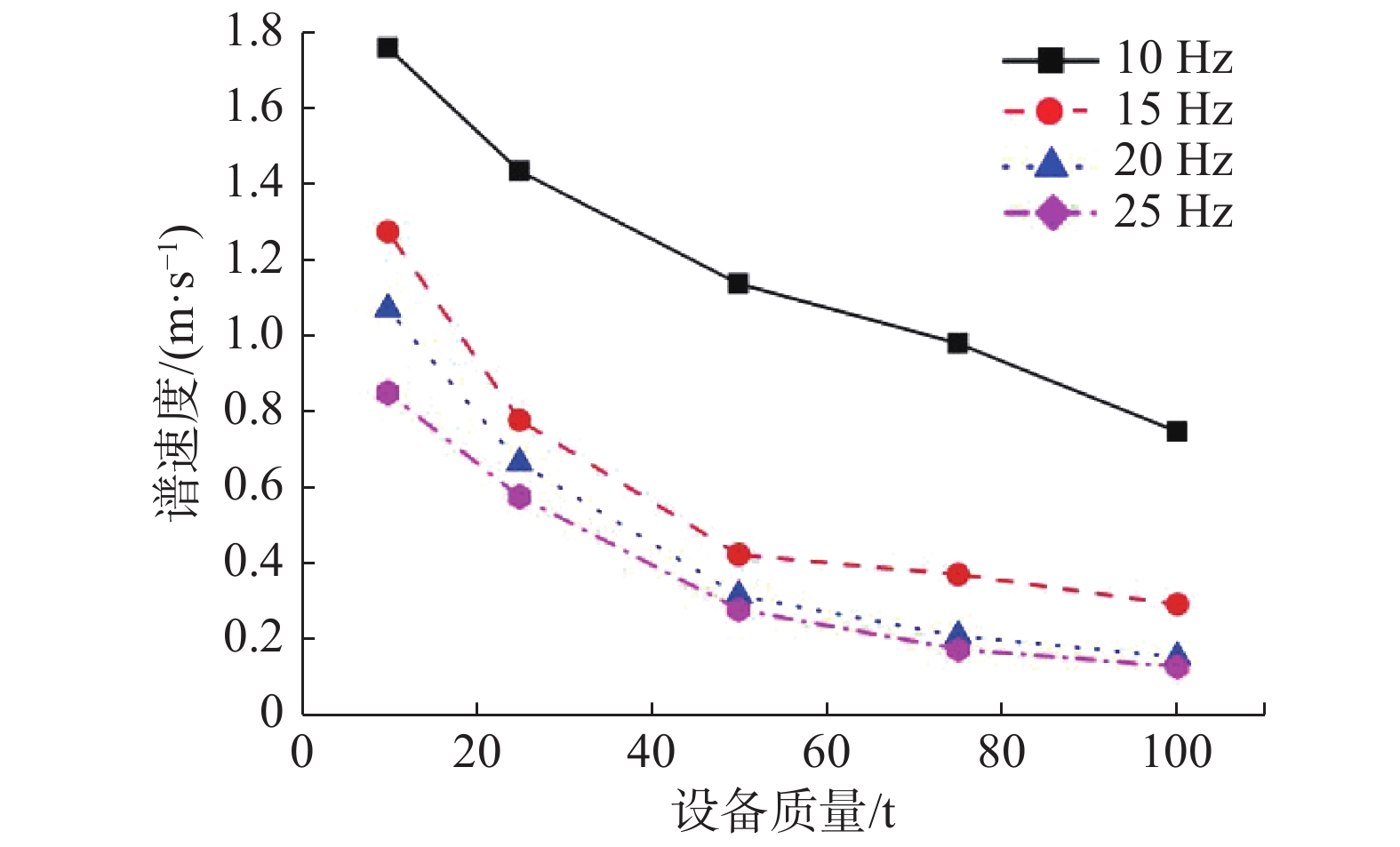
从图9中可以看到，安装频率一定时，设备基础处的冲击谱曲线在中频率有着明显的谱跌现象，并且极小值与设备质量成反比例关系。将表2以设备质量为横坐标得到不同工况下的设计谱曲线如图10所示。

从设计谱值曲线上，当设备的安装频率保持不变时，设计谱速度与设备质量反相关。由前面的理论推导可知，无论是低频段还是高频段，设备与基础之间的动态力与质量成正比，质量越大，动态力越大。意味着设备基础处的伪速度越小，结论与理论一致，说明设备质量对于谱速度有着显著的影响。

2.4.3 隔振器数量对设计谱的影响

前面的理论计算将设备假设为线性系统，而实际的结构具有无限的模态，存在设备与基础之间多模态耦合的问题，为研究结构模态对设计谱的影响，本文采用改变隔振器数量的方法，以此提高设备与基础之间的耦合程度。保持总的隔振器刚度不变，分别采用不同的隔振器数量来代表着设备与基础之间的耦合程度，测得的冲击环境如图11所示。

25根与35根隔振器的冲击谱基本重合，并且在低中频段高于8根代表的冲击谱曲线。从耦合程度上看，三者隔振器形成的面积对应于船体甲板面积的1/12，1/3，1/2。将设备安装于船体上，从某种意义上来说相当于船体甲板的固有频率改变，刚度更大，使得二者之间的耦合减弱。因此，缩小隔振器的布置面积可以减小设备的响应。

3 结论

本文通过将设备安装于实际舰船上，计算其水下非接触爆炸下的冲击环境，得到如下规律:

1）在低频段设备的谱速度与设备的安装频率反相关，与理论推导规律一致；同时设备质量100 t、安装频率10 Hz下的谱速度是同样设备质量安装频率为25 Hz的近5倍，因此设备的安装频率在舰船设计中必须考虑。

2）设备的谱速度与设备的质量反相关，与理论推导规律一致。

3）将隔振器的布置面积从1/2减少到1/12，设备所受的冲击力减少近一倍，因此可通过减少隔振器相对安装部位的面积来减少冲击输入。