2. 大连船舶重工集团有限公司,辽宁 大连 116005
2. Dalian Shipbuilding Industry Co., Ltd., Dalian 116005, China
海洋平台在遭受海上恶劣作业环境和进行油气开采时,可能发生火灾或爆炸等严重事故,造成重大的安全和财产损失[1]。为了提高海洋平台的安全性,防止舱室内油气爆炸带来二次危害,防爆门和防爆墙等结构在设计时,重点要考虑其抗爆性能。在防爆门研究设计中,陆新征等[2]对防爆门被破坏过程进行了动态模拟计算与分析,并根据数值模拟分析的特点,修改相关参数以改变爆炸冲击载荷的压力随时间变化曲线,对防爆门在承受不同程度爆炸载荷时的抗爆性能进行了评估。郭东[3]根据对典型梁板式钢结构防护门的数值模拟,结合量纲分析理论,提出了合理的工程计算模型,推导出了防爆门在承受爆炸冲击时门扇在弹性阶段的反弹力解析解。宋祥[4]、任涛[5]、赵应许[6]、谭朝明等[7]分别针对加腹板工字钢骨架结构防爆门、拱形防爆门等典型防爆门结构,采用单自由度等效静载和动态模拟方法,得到在不同程度爆炸荷载下的动态响应,比较了各个防爆门结构参数对动态响应的影响。张晓峰[8]对某海洋平台波纹板防爆墙设计了多种结构形式,用ANSYS分别建立整体有限元模型进行分析,对比了线性静力分析和弹塑性分析对计算结果产生的影响,总结了防爆墙的设计理念,得出了防爆墙的优化设计参数和结构形式。叶昊[9]对海洋平台舱壁的槽形构架进行了非线性动态分析,并根据规范和非线性有限元方法对结构进行了强度评估。目前,对于防爆门的研究取得了一定的成果,但海洋平台的蒸汽云团爆炸如何简化载荷仍不明确,防爆门的各结构参数对其性能的影响仍不清晰。在此背景下,本文以某型海洋平台舱室防爆门为研究对象,确定防爆门承受的爆炸载荷,并探究防爆门防爆性能影响因素,以期为该类结构的设计与生产提供一定的参考。
1 舱室可燃物爆炸载荷在海洋平台舱室中发生的爆炸事故通常是由舱室内的油气泄漏形成蒸汽云团引发的。相对于空气中固态炸药的爆炸,蒸汽云团爆炸源的密度往往较小,爆炸过程和爆炸载荷更为复杂。为了确定爆炸载荷,可采用等效TNT法来量化爆炸能量,以爆炸能量相当为原则,将大范围的蒸汽云团混合爆炸简化为固定爆源的TNT炸药爆炸,参与爆炸的可燃物质释放的能量换算成释放出同等能量的炸药的量,然后用炸药爆炸的数据来代替蒸汽云爆炸。在海洋平台爆炸事故中,蒸汽云爆炸的载荷取决于爆炸时云团中可燃物质的量,即舱室中石油天然气的泄漏量。因此,需首先得知海洋平台上储存舱室的大小以及空气中的可燃气体浓度,假设舱室尺寸为10 m×8 m×2.5 m,弥漫的天然气浓度为10%(既大于天然气爆炸浓度下限5%,又小于爆炸上限15%),天然气密度为0.7 kg/m3,经过计算得到泄漏可燃气体的质量为14 kg。则参与爆炸的蒸汽云团中可燃物的等效TNT当量计算公式为[10]
| ${W_{{\rm{TNT}}}} = aW{{{H_f}} / {{H_{{\rm{TNT}}}}}}$ |
式中:
TNT炸药爆炸冲击载荷的超压峰值与时间关系式为
| $p\left( t \right) = {p_0} + {p_m}\left( {1 - \dfrac{t}{{{t_d}}}} \right){{\rm{e}}^{{{ - ct} / {{t_d}}}}}$ |
式中:
目前国内外的相关爆炸理论认为爆炸载荷主要与炸药的量、爆炸距离有关,因此常采用定义折合距离的方式来表示爆炸过程中各项参数的关系,即
| $r = \frac{R}{{\sqrt[3]{W}}}$ |
式中:
对于球形TNT炸药在无限空气中的爆炸,目前存在多个可用来计算冲击波超压峰值的经验计算公式,本文采用Henrych经验公式[11],即
| $\left\{ \begin{array}{l} p = \dfrac{{1.379}}{r} + \dfrac{{0.543}}{{{r^2}}} - \dfrac{{0.035}}{{{r^3}}} + \dfrac{{0.000\;6}}{{{r^4}}},\;0.05 \leqslant r \leqslant 0.3\\ p = \dfrac{{0.607\;6}}{r} - \dfrac{{0.032}}{{{r^2}}} + \dfrac{{0.209}}{{{r^3}}},\;0.3 \leqslant r \leqslant 1\\ p = \dfrac{{0.064\;9}}{r} + \dfrac{{0.397\;3}}{{{r^2}}} + \dfrac{{0.322\;6}}{{{r^3}}},\;1 \leqslant r \leqslant 10 \end{array} \right.$ |
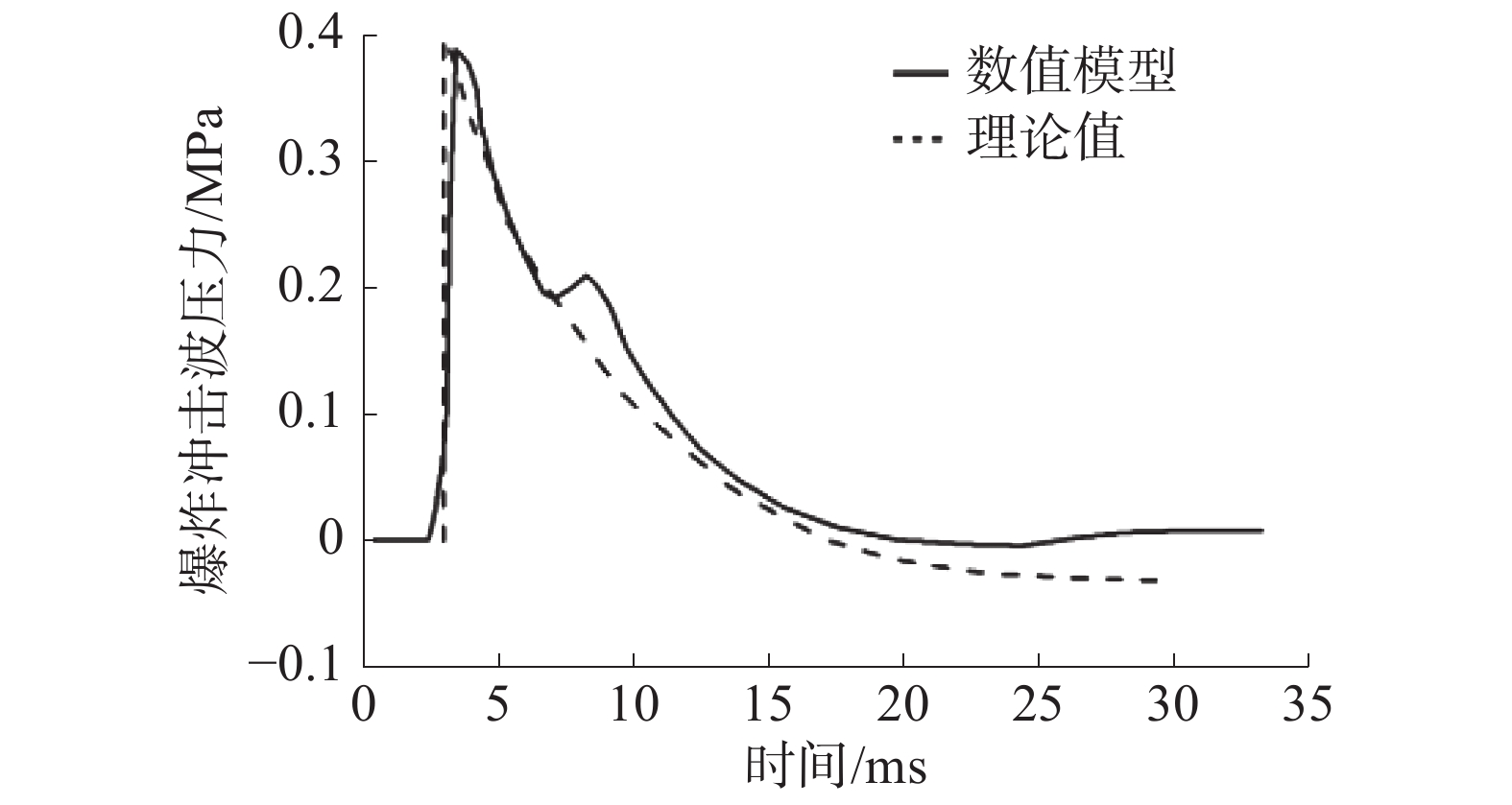
根据ABAQUS中的体积分数模拟方法,得到空气场中的爆炸冲击波传递过程如图1所示。提取距离爆源6.5 m处的爆炸载荷和理论压力−时间曲线进行对比,如图2所示。根据经验公式和数值模拟方法所得的不同距离下的冲击波峰值对比如图3所示。

|
Download:
|
| 图 1 空气场中的爆炸冲击波传播云图 | |
|
Download:
|
| 图 2 冲击波压力−时间曲线 | |

|
Download:
|
| 图 3 不同距离下的冲击波超压峰值 | |
由图2、3可知,本文通过数值模拟得到的爆炸冲击波压力时程曲线和理论曲线拟合较好,当测点距离爆源3 m以上时,冲击波超压峰值的经验公式值和数值模拟值也十分接近。因此,本文根据数值模拟方法所得的爆炸载荷可作为防爆门抗爆研究的施加载荷。
2 海洋平台防爆门结构设计目前的防爆门研究一般着眼于平板式防爆门,对于拱形防爆门的研究十分少见。本文以拱形防爆门为研究对象,设计其结构形式如图4所示,有限元模型如图5所示。防爆门整体高1 800 mm、宽1 200 mm、厚100 mm,迎爆面凸起,形成一定程度的拱高,防爆门内部均匀布置m×n形式骨架梁(即m道横梁,n道纵骨)。本文考虑到防爆门的塑性,其材料属性如表1所示。

|
Download:
|
| 图 4 防爆门结构示意(单位:mm) | |

|
Download:
|
| 图 5 防爆门有限元模型 | |
|
|
表 1 防爆门模型材料属性 |
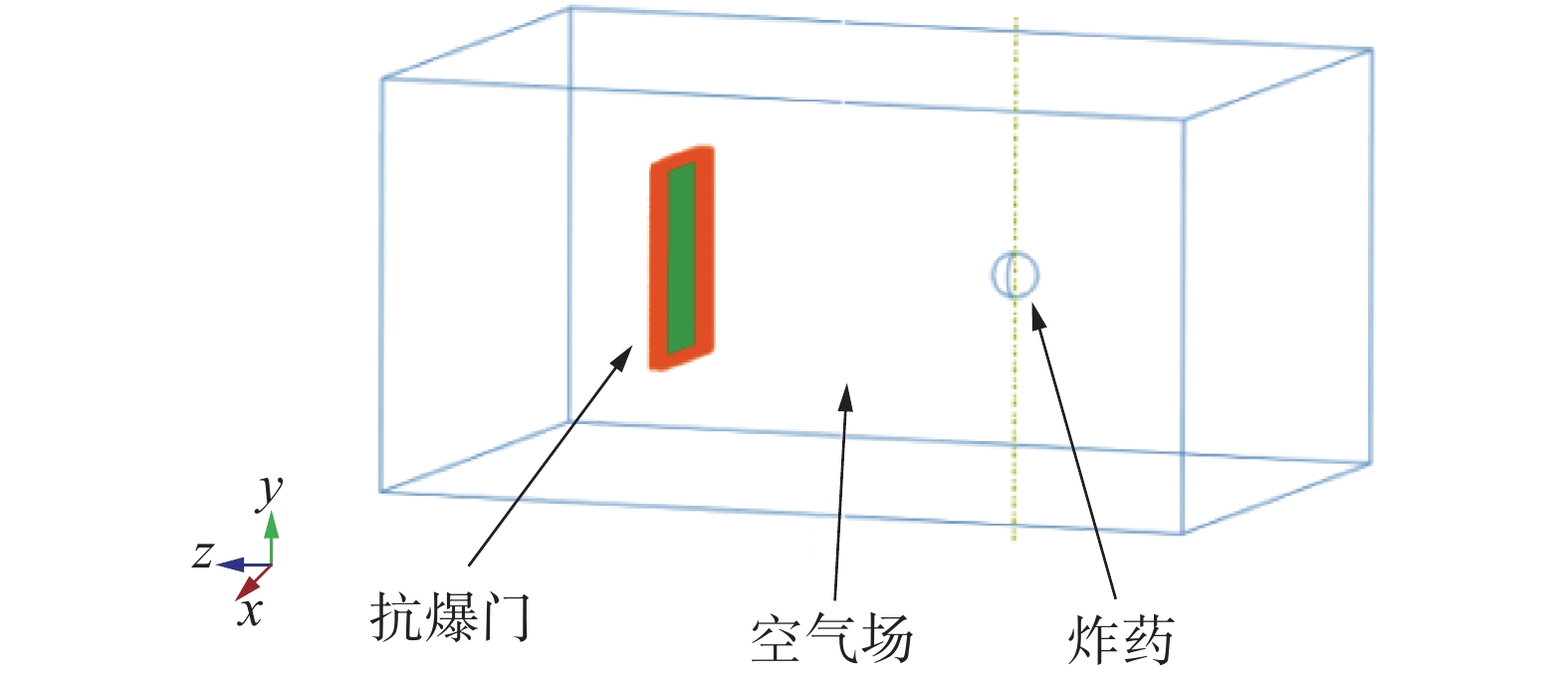
本文采用ABAQUS/Explicit计算方法,建立炸药−空气场−防爆门的一体化计算模型,如图6所示。防爆门四周简支[12],空气场边界无反射。
|
Download:
|
| 图 6 炸药−空气场−防爆门一体化计算模型 | |
根据以往研究及工程经验可知,防爆门的防护性能主要与其结构参数息息相关。为了开展防爆门的优化设计,研究防爆门的抗爆性能与骨架形式、拱高、面板厚度和骨架厚度的关系,明确了其影响程度,为该类防爆门的设计提供参考。
3.1 骨架形式的影响骨架梁作为防爆门内部的主要支撑结构,其数量会对防爆门的抗爆性能产生较大的影响。本文分别计算了1×1,2×2,3×3骨架形式下的防爆门的动态响应,其等效塑性应变云图如图7所示。

|
Download:
|
| 图 7 防爆门等效塑性应变云图 | |
由图7可知,在1×1,2×2,3×3不同骨架布置形式下,防爆门均在面板与骨架的连接处出现屈服,产生的等效塑性应变值分别为31.9、17.7和6.25 mm,减小幅度较大。
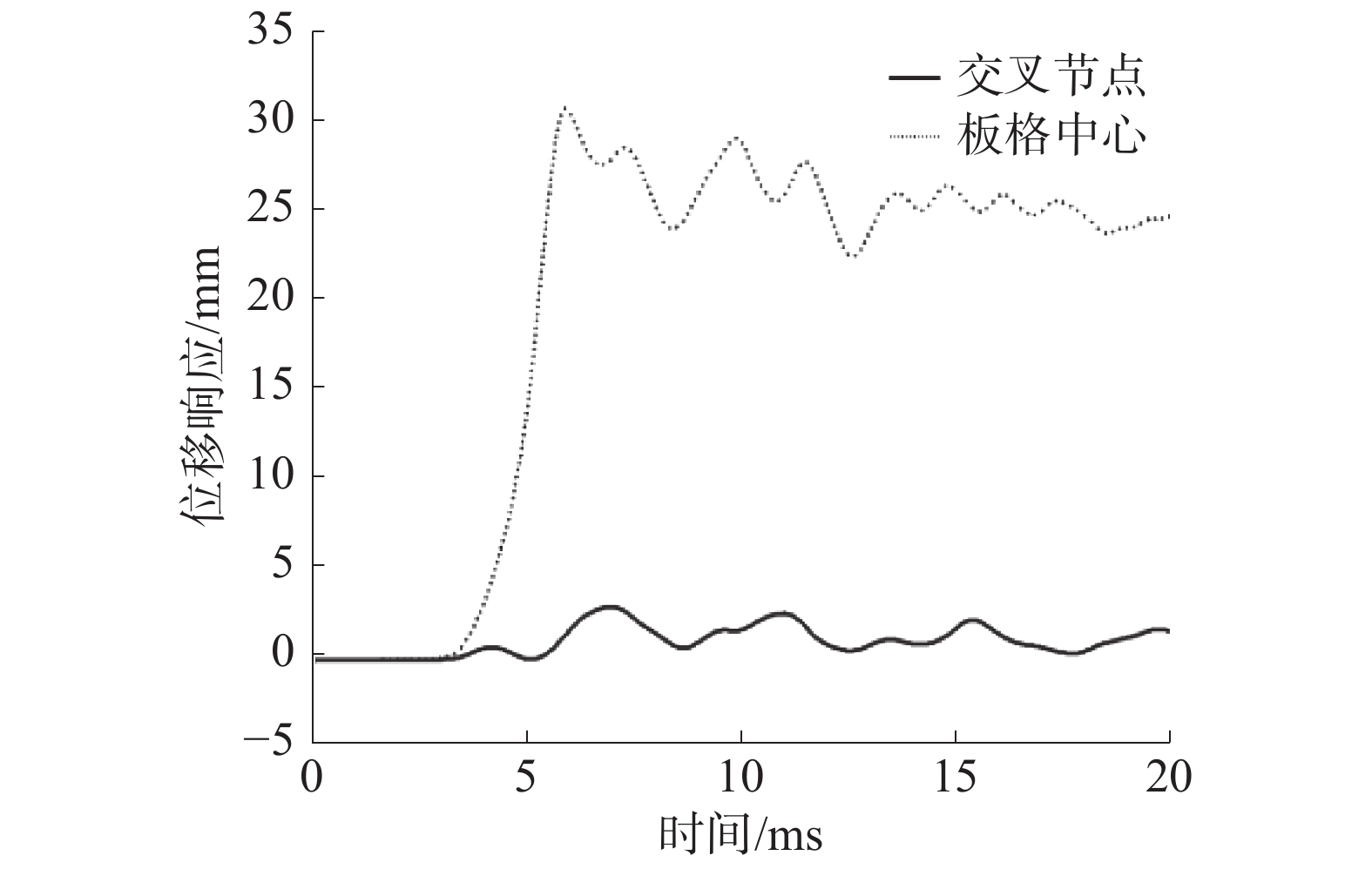
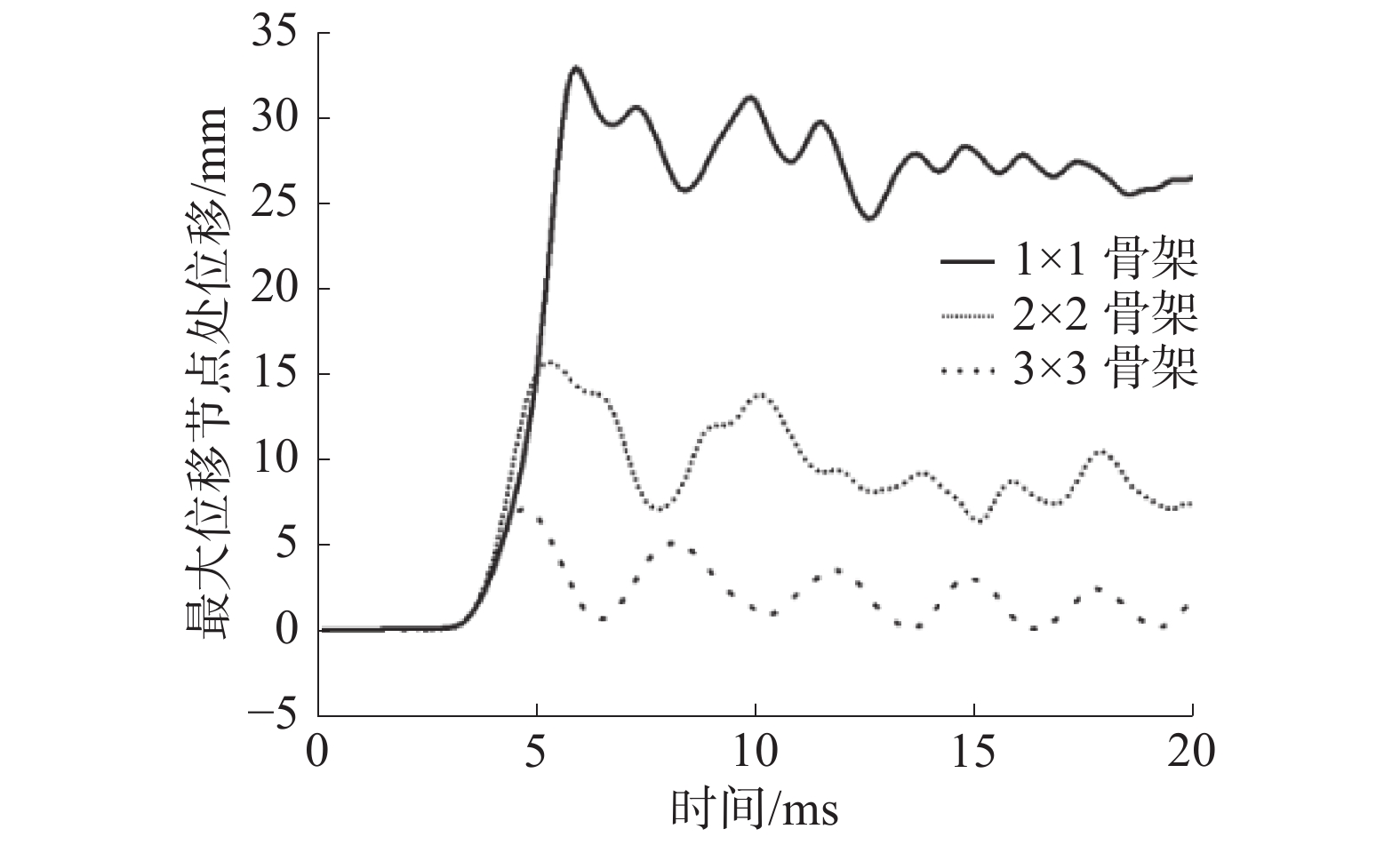
2×2形式防爆门中的中心位置为板格中心,同时也是最大位移出现的位置。但在1×1和3×3式防爆门中,防爆门中心为骨架梁的交叉节点,最大位移出现在附近板格区域中心,对比该两点的位移响应,如图8、9所示。3种结构形式下的防爆门最大位移节点处的响应对比如图10所示。
|
Download:
|
| 图 8 1×1骨架形式防爆门上不同位置响应 | |

|
Download:
|
| 图 9 3×3骨架形式防爆门上不同位置响应 | |
|
Download:
|
| 图 10 不同骨架形式下的最大位移节点响应 | |
由图8、9可知,对于同一骨架结构形式的防爆门而言,不同位置处的位移响应具有较大差异,板格中心位置的位移响应比骨架交叉节点处大。3×3骨架形式下,骨架分布较为密集,防爆门的整体刚度较大,位移达到峰值后的衰减速度较快。由图10可知,防爆门内部骨架梁数量增加后,防爆门的最大位移响应大幅度降低,因此适当增加骨架梁数量是提高防爆门抗爆性能的有效方式。
3.2 拱高的影响在拱形防爆门的设计中,拱高是一个相当重要的结构参数,但是以往对于防爆门的研究中却均未涉及到拱高对于抗爆性能的影响研究,如何确定拱高是一个尚不明确的问题。本文以2×2骨架形式防爆门为研究对象,分别计算了防爆门在拱高为0(此时防爆门为平板式)、2、4、6、8和10 mm下的动态响应,得到其跨中(即防爆门迎爆面中心位置)位移时程曲线如图11所示,位移峰值与拱高的关系如图12所示。

|
Download:
|
| 图 11 不同拱高下的跨中位移变化曲线 | |
|
Download:
|
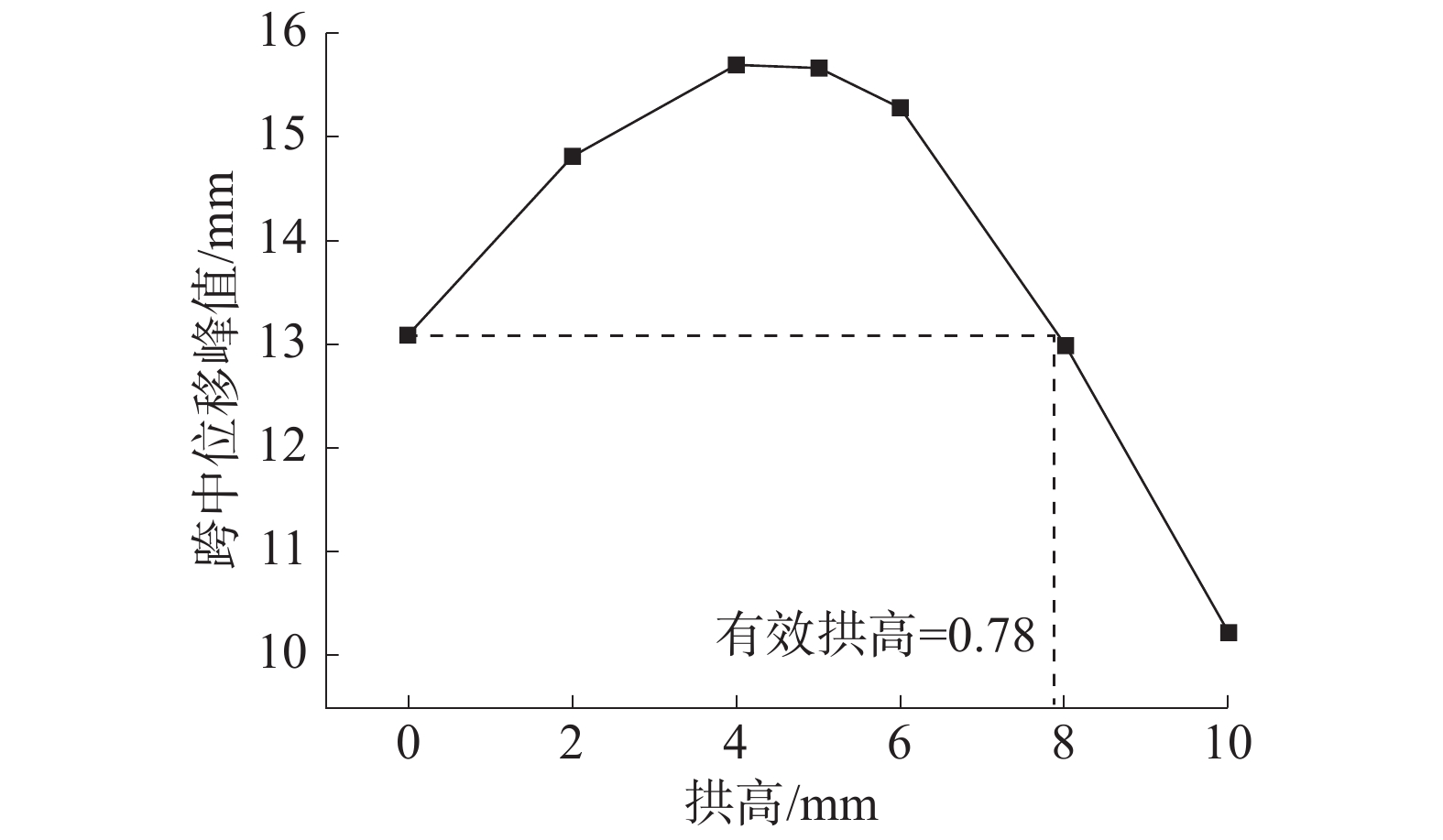
| 图 12 跨中位移峰值与拱高的关系曲线 | |
由图11可知,在拱高不同时,防爆门的跨中位移响应变化趋势接近,但在数值上存在较大的差异。由图12可知,随着拱高的不断增大,防爆门的最大位移响应呈现先增大再减小的趋势,只有在拱高与防爆门厚度的比值即有效拱高大于0.78时,拱形防爆门的抗爆性能才会优于平板式防爆门。在工程实际中,由于空间和制造成本的限制,防爆门的拱高存在上限,因此,需要根据实际情况选择适当的拱高。
3.3 面板厚度的影响迎爆面的面板厚度是影响防爆门性能的关键参数之一。本文分别计算了防爆门在面板厚度为4、5、6和8 mm时的动态响应,得到跨中位移时程曲线如图13所示,位移峰值随面板厚度的关系如图14所示。

|
Download:
|
| 图 13 不同面板厚度下的跨中位移变化曲线 | |
|
Download:
|
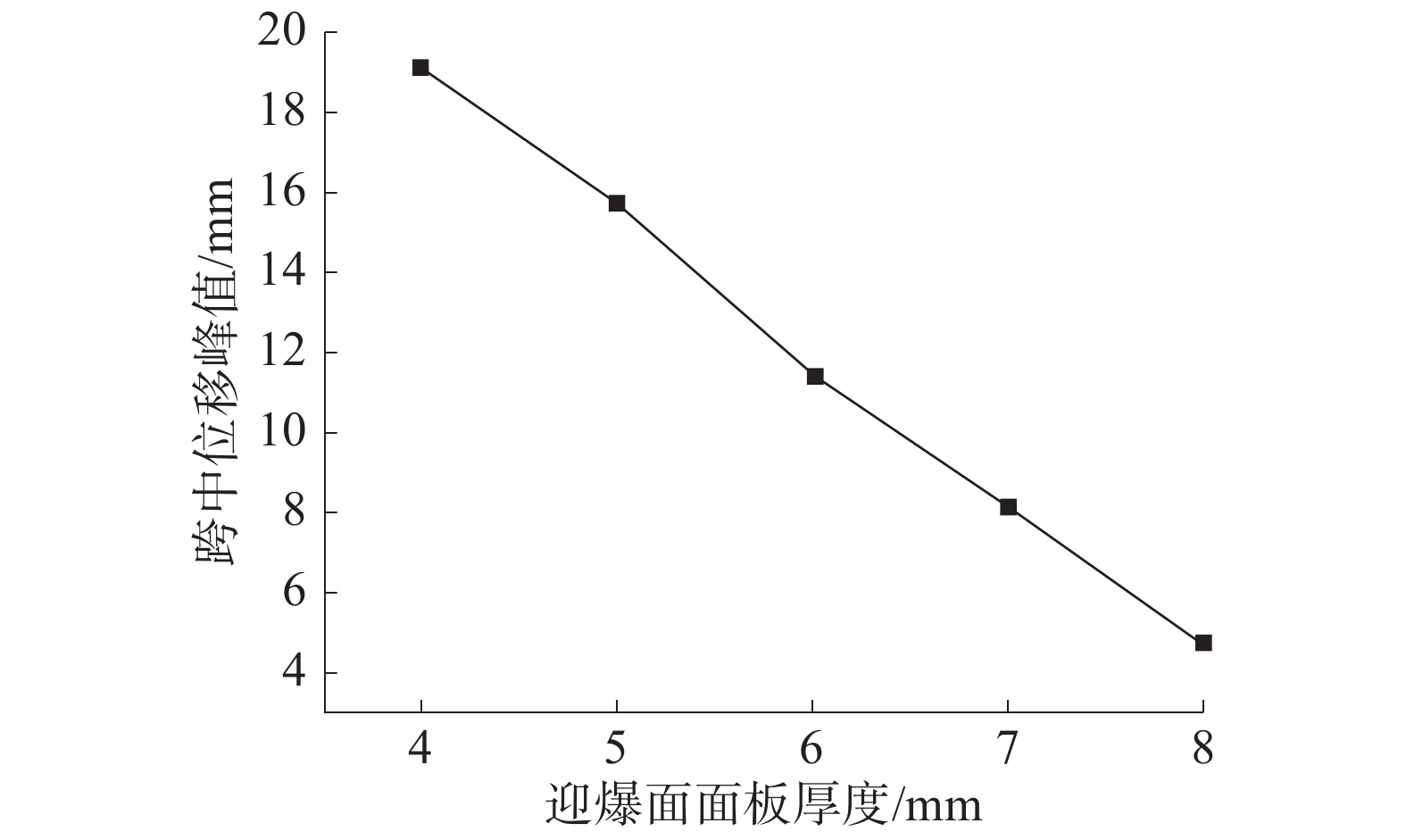
| 图 14 跨中位移峰值与面板厚度关系曲线 | |
由图13可知,增大迎爆面面板厚度后,防爆门的跨中位移随时间变化的趋势基本一致,但在数值上降低幅度显著。由图14可知,跨中位移峰值与面板厚度呈近似线性关系,适当增加面板厚度,可显著增强防爆门的抗爆性能。
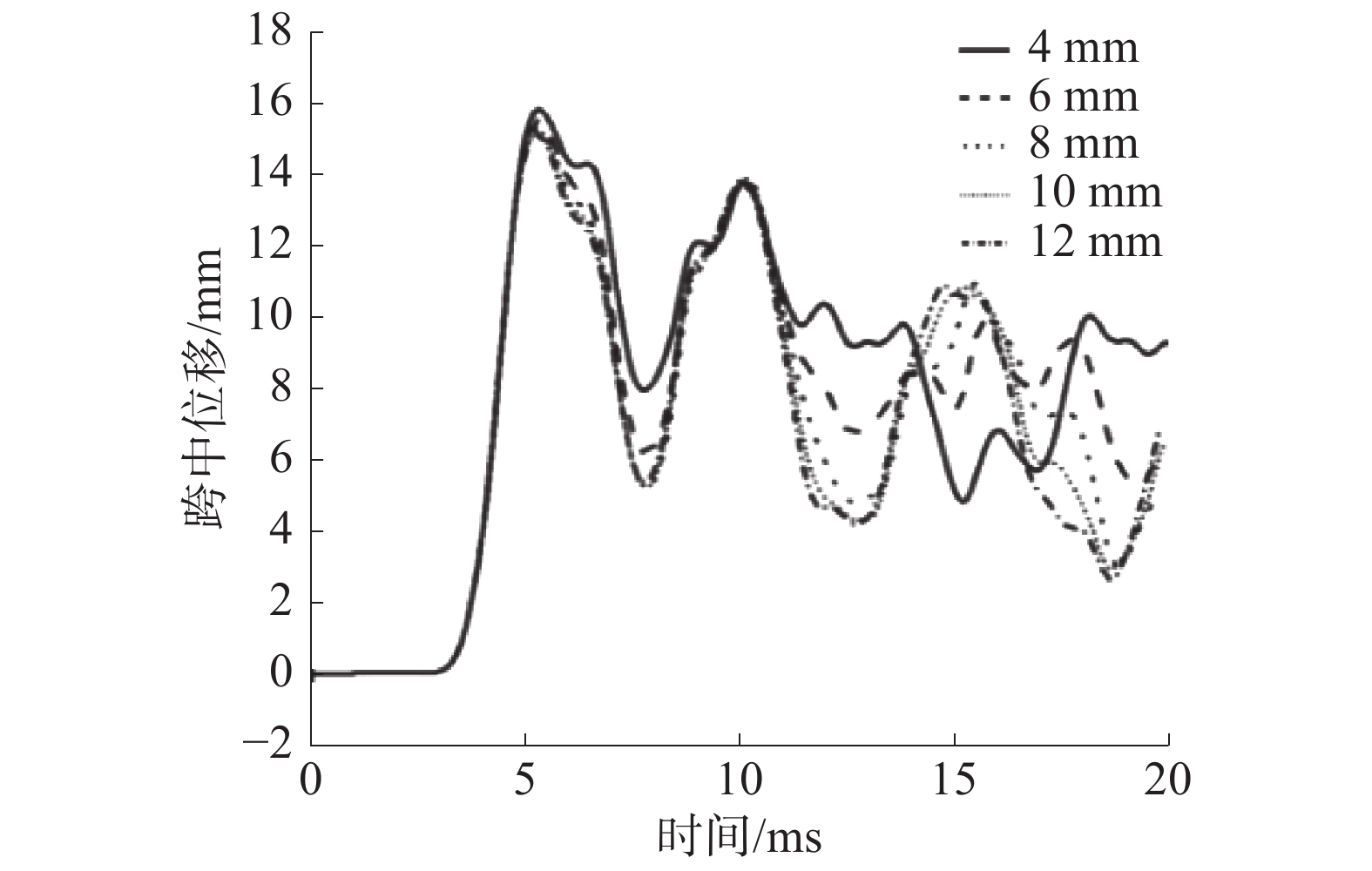
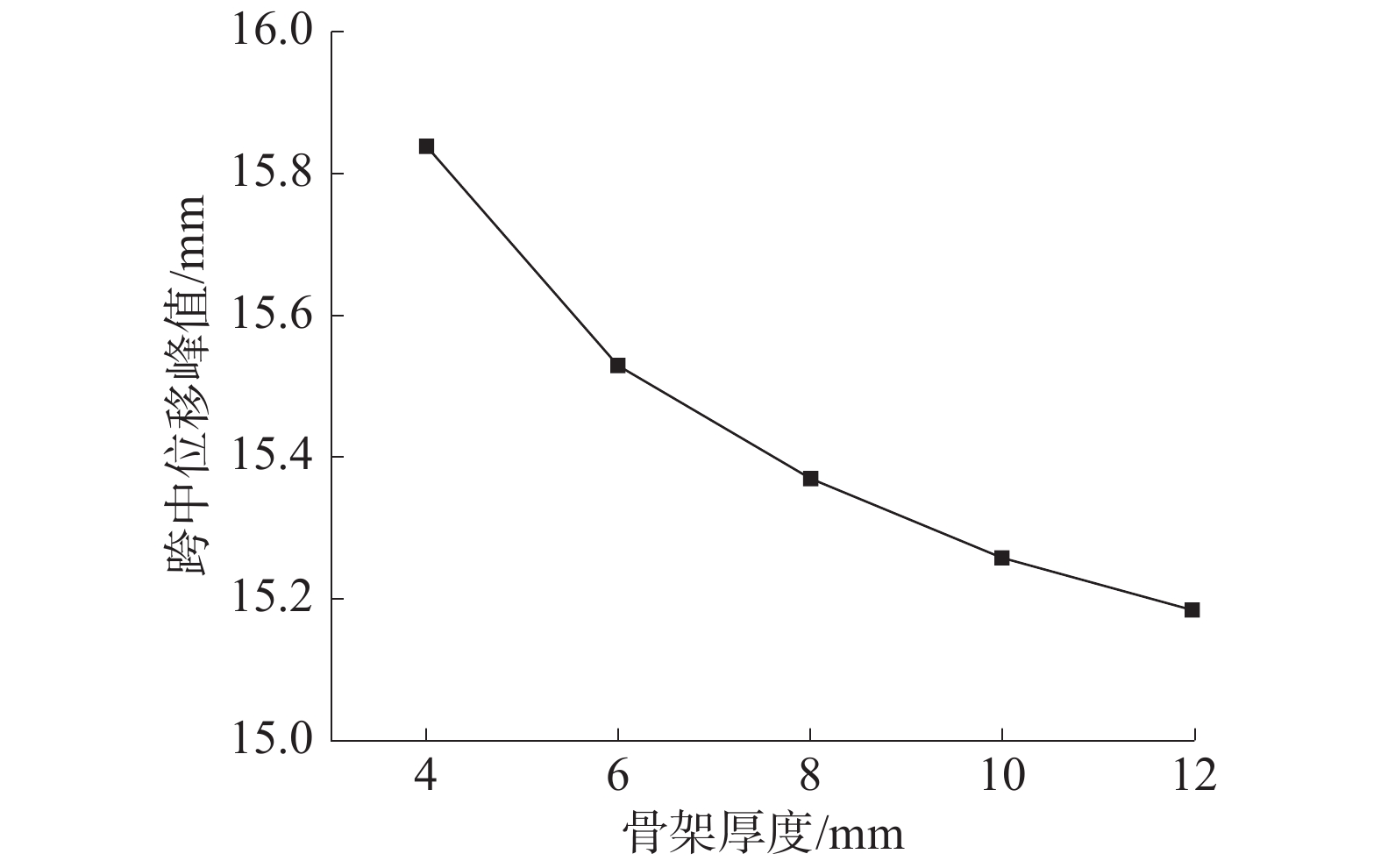
3.4 骨架厚度的影响为了研究防爆门骨架厚度对其抗爆性能的影响,本文分别计算了防爆门在骨架厚度为4、6、8、10和12 mm时的动态响应,得到不同骨架厚度下的跨中位移时程曲线如图15所示,位移峰值随骨架厚度的关系如图16所示。由图15、16可知,改变防爆门的骨架厚度后,防爆门的位移响应在初始阶段基本一致,仅在后续强迫振动阶段趋势不同,位移峰值基本没有变化,因此可认为骨架厚度对防爆门的抗爆性能影响较小。
|
Download:
|
| 图 15 不同骨架厚度下的跨中位移变化曲线 | |
|
Download:
|
| 图 16 跨中位移峰值与骨架厚度关系曲线 | |
本文为了提高海洋平台舱室在燃气爆炸环境下的安全性,针对防爆门的结构形式设计与抗爆性能影响因素开展了研究。改变拱形防爆门的骨架形式、骨架厚度、拱高和迎爆面面板厚度,对比各种不同防爆门的动态响应,得到以下结果和结论:
1)防爆门的等效塑性应变出现在面板与骨架交接处,最大位移出现在防爆门面板上的板格区域中心,增加防爆门内部的骨架数量可明显减小其动态响应;
2)对于海洋平台舱室拱形防爆门,随着拱高的不断增大,防爆门的位移响应呈现先增加再减小的趋势,只有当拱高与门厚的比值大于0.78时,拱形防爆门的抗爆性能才会优于平板式防爆门;
3)增加防爆门的迎爆面厚度可显著增强其抗爆性能,但是增加防爆门内部骨架梁的厚度却对其抗爆性能几乎没有影响。
| [1] |
闫会宾. 海洋平台结构与设备的可靠度与风险评估[D]. 杭州: 浙江大学, 2016.
( 0) 0)
|
| [2] |
陆新征, 江见鲸. 抗爆门结构考虑接触影响的动力有限元分析[J]. 力学与实践, 2003, 25(2): 24-26. DOI:10.3969/j.issn.1000-0879.2003.02.007 ( 0) 0)
|
| [3] |
郭东. 爆炸荷载作用下防护门的动态响应行为与反弹机理研究[D]. 北京: 清华大学, 2012.
( 0) 0)
|
| [4] |
宋祥. 加腹板工字钢骨架结构抗爆门的抗爆性能研究[D]. 西安: 长安大学, 2014.
( 0) 0)
|
| [5] |
任涛. 抗爆门有限元分析及优化设计[D]. 西安: 长安大学, 2011.
( 0) 0)
|
| [6] |
赵应许. 爆炸冲击荷载作用下抗爆门的动力响应分析[D]. 西安: 长安大学, 2013.
( 0) 0)
|
| [7] |
谭朝明, 吕贝贝. 平板抗爆门动力响应有限元分析[J]. 橡塑技术与装备, 2017, 43(12): 57-60. ( 0) 0)
|
| [8] |
张晓峰. 海洋平台防爆墙计算方法及结构型式研究[J]. 工程建设, 2015, 47(6): 27-29, 33. ( 0) 0)
|
| [9] |
叶昊. 海洋平台防爆墙的分析与设计[D]. 哈尔滨: 哈尔滨工程大学, 2008.
( 0) 0)
|
| [10] |
谭朝明. 拱形抗爆门的动力响应分析及优化设计[D]. 西安: 长安大学, 2015.
( 0) 0)
|
| [11] |
杨鑫, 石少卿, 程鹏飞, 等. 爆炸冲击波在空气中传播规律的经验公式对比及数值模拟[J]. 四川建筑, 2007, 27(5): 71-73. DOI:10.3969/j.issn.1007-8983.2007.05.033 ( 0) 0)
|
| [12] |
杨心宇, 赵跃堂, 周泽鑫. 平板防护门不同约束形式下的动力响应[J]. 爆破, 2014, 31(2): 47-50, 56. DOI:10.3963/j.issn.1001-487X.2014.02.010 ( 0) 0)
|
 2020, Vol. 47
2020, Vol. 47


