随着计算机硬件设施的发展,计算流体力学(computational fluid dynamics,CFD)在船舶与海洋结构物的性能预报中得到了广泛的应用。传统的船模拖曳水池试验,往往只能对阻力、倾角等单一的水动力性能进行测试,其对于船舶精细流场很难做到全方位的捕捉。而基于CFD的数值研究能够在节约时间、财力的同时,获得相对准确的力学及流场信息。目前,CFD技术不仅应用在传统的阻力试验模拟中[1],在船舶操纵性[2]、耐波性[3]以及自航性能[4]等诸多领域也得到了相应的开展。
丁科等[5]通过RANS和VOF方法,对船+桨自航状态下的螺旋桨激振力进行了数值预报,未考虑舵的影响。Chang等[6]基于CFD软件STAR-CCM+对安装扇形节能导管的船舶航行性能进行研究,计算未计及舵的干扰。Duman等[7]基于RANS方法对DTMB5512船模的船桨干扰进行了研究,但文中的螺旋桨用虚拟盘模型替代,未考虑真实的螺旋桨形状。同样,Jasak等[8-9]选用虚拟盘模型进行了实尺度船舶自航计算,在与实海域测量结果对比的基础上,阐述了网格的验证及确认过程。Dhinesh等[10]对某双桨船进行了试验及数值研究,探讨了自航数值模拟的流程,并分析了螺旋桨对船舶尾流场的影响。李亮等[11]、朱芳艳[12]以KCS船和KP505桨为研究对象,研究了单桨集装箱船的航行性能。
目前,学者们对于船模自航数值模拟进行了较多的研究分析,但大多数研究未考虑舵对船舶航行性能的影响,且相当一部分研究是基于虚拟盘模型进行的,研究船型也多为单桨船舶。因此,本文基于真实螺旋桨模型,计及舵的影响,对大型水面舰艇的DTMB5415模型进行自航数值研究,分析船体、螺旋桨、舵之间的相互干扰及流场变化,为双桨推进船舶航行性能的研究提供参考。
1 数值计算方法 1.1 湍流模型及离散格式本文所有的研究工作(船模阻力计算、螺旋桨敞水计算、船−桨−舵耦合自航计算)均是基于STAR-CCM+进行的。采用SST k-w湍流模型对其进行求解并封闭方程组。控制方程采用基于压力的耦合求解,其中对流项采用二阶迎风格式进行空间离散,耗散项采用二阶中心差分格式进行离散,利用VOF模型进行自由液面的捕捉,基于滑移网格实现螺旋桨的旋转。
1.2 几何模型本文所使用的的船舶模型为美国驱逐舰DDG−51母型船的缩尺模型,该船具有球鼻艏以及方形尾特征,是典型的的中高速船舶水面舰艇,被国际拖曳水池会议(ITTC)推荐作为船舶水动力性能研究的三大基准模型之一。由于该船原配桨公开的试验资料极少,本文计算所使用的的桨为DTMB5415−M船模操纵性试验[13]中所用的P4508库存桨。图1为装配完成的船−桨−舵一体化计算模型。表1给出了文中所使用的模型的主要参数。

|
Download:
|
| 图 1 自航计算船舶模型 | |
|
|
表 1 模型主尺度 |
船模自航数值计算共包含阻力计算、螺旋桨敞水计算以及自航模拟3部分。图2(a)为螺旋桨敞水计算时的计算域,其分为旋转域和背景域2部分,中间通过Interface交界面实现物质交换。背景域的形状为直径等于8D的圆柱,螺旋桨距离进流口和出口的长度分别为3D和8D。阻力和自航计算时的计算域如图2(b)所示,自航计算时包含旋转域部分,背景域为长宽高分别为4.5LPP、1.5LPP、3LPP的长方体。
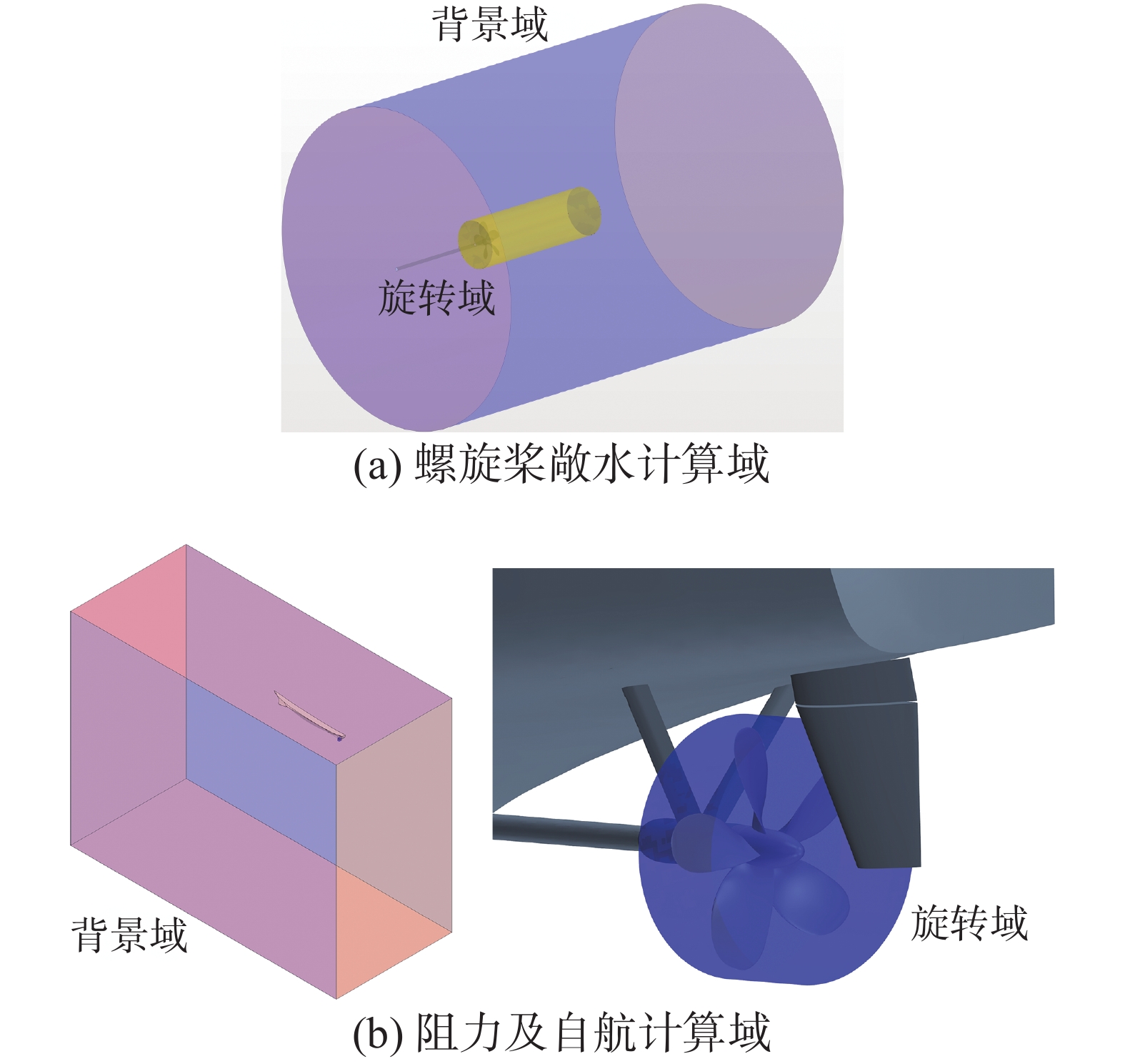
|
Download:
|
| 图 2 计算域的划分 | |
为了提高非均匀流场的模拟精度,对流场信息进行更加精确的捕捉,需要对计算域特定区域进行加密。本文采用切割体网格进行计算域网格的划分,利用不同尺寸的加密体对船艏、附体、螺旋桨等表面曲率变化较大,以及开尔文波系、螺旋桨尾迹等重点关注的区域进行加密。螺旋桨敞水计算时,对梢涡、毂涡等区域进行网格加密。图3为不同工况时的网格划分情况。裸船体船模阻力计算、全附体船模阻力计算、螺旋桨敞水计算以及船模自航计算的最终网格数分别为253万、281万、420万、710万。

|
Download:
|
| 图 3 网格划分 | |
对DTMB5415船模在巡航速度(Fr=0.28)以及最高航速下(Fr=0.41)的阻力进行计算,计算中允许船模做纵倾及深沉运动。阻力计算结果与INSEAN水池试验值的对比如表2所示。由表可知,2种航速下的阻力计算值值与试验值的误差均在4%以内,具有较好的求解精度。
|
|
表 2 阻力结果对比 |
图4、5分别为Fr=0.28时的波形、伴流场计算结果与INSEAN水池试验结果的对比。由图可知,波形计算结果与试验结果吻合良好,对船艏艉等波形变化剧烈的区域进行了良好的捕捉。同样,伴流场计算结果的等值线轮廓也和试验结果较为接近。船舶精细流场的准确捕捉,为后续的分析结论提供支撑。

|
Download:
|
| 图 4 Fr=0.28时波形计算与试验结果对比 | |

|
Download:
|
| 图 5 Fr=0.28时伴流场计算与试验结果对比 | |
将螺旋桨的转速设定为22 r/s,通过调整螺旋桨的来流速度,来改变进速系数J的大小。当模型桨的最低雷诺数大于临界雷诺数时,螺旋桨的性能几乎与雷诺数无关,ITTC规程将临界雷诺数的值设定为3×105,其定义为
| $Re = \frac{{{b_{0.75R}}\sqrt {{V_A}^2 + {{(0.75{\text{π}} nD)}^2}} }}{\upsilon }$ |
式中:VA为进速;b0.75R为0.75半径处的叶切面弦长;n为螺旋桨转速;
本文进行螺旋桨敞水计算时的最低临界雷诺数为3.635×105,满足ITTC规程要求。
图6为P4508桨敞水特性计算值与试验值的对比,图中进速系数J的考察范围为(0.2~0.9)。由图可知:在低进速系数时,计算得到的推力、扭矩系数偏小;随着进速系数的增大,扭矩系数计算值增大,推力系数计算值减小。当J≤0.7时,螺旋桨的效率计算值与试验值吻合良好,误差在5%以内;当J>0.7时,误差有增大的趋势,但仍在可接受的范围内。

|
Download:
|
| 图 6 P4508桨敞水性能 | |
自航试验之前,对DTMB5415全附体船模的阻力及航行姿态进行了预报。在进行船模自航模拟时,基于前期预报得到的船舶航行姿态数据进行展开,即在计算之前将计算模型预先调整到所对应的阻力试验船模姿态,忽略螺旋桨对船体姿态的微量影响。
在自航试验中,对DTMB5415船模在Fr=0.28和Fr=0.413(MARIN水池公布有Fr=0.413时的试验数据)的自航特性进行数值研究。自航点的求解过程与船模自航试验相同,最终使螺旋桨发出的推力来克服阻力(Rm−FD)。FD为摩擦阻力修正值,其定义为
| ${F_D} = {R_m} - \frac{{{\rho _m}}}{{{\rho _s}}}\frac{{{R_s}}}{{{\lambda ^3}}}$ |
式中:Rm和ρm分别为模型尺度下的阻力和水密度;Rs和ρs分别为实尺度下的阻力和水密度。
表3为船桨舵耦合计算得到的Fr=0.413航速下的实船自航点与MARIN试验值的对比,两者的差值为−5.3%,满足计算精度需求。自航点转速计算值较低的原因可能在于本研究未安装舭龙骨、减摇鳍等附体,进而在一定程度上降低了船体阻力,从而降低了自航点螺旋桨转速。
|
|
表 3 Fr=0.413时的船−桨−舵耦合自航点 |
表4为船+桨+舵耦合计算得到的实船性能预报结果,船舶的推力减额分数t、伴流分数w与双桨快速船的经验值相吻合[14]。表中,VS为实船航速,ηH和ηD分别为船身效率和船舶推进效率。
|
|
表 4 船−桨−舵耦合计算时的实船推进性能 |
为了分析螺旋桨对船体阻力的影响,对船+舵、船+桨+舵状态下的阻力系数Ct、摩擦阻力系数Cf以及剩余阻力系数Cv进行分析,结果如图7所示。由图可知,螺旋桨工作状态下,船模的总阻力出现了一定程度的增大,2种航速下的阻力增幅在11%~12%;螺旋桨对船舶的摩擦阻力影响不大,尤其是当Fr=0.28时,剩余阻力的增大才是螺旋桨引起船体阻力增大的原因。
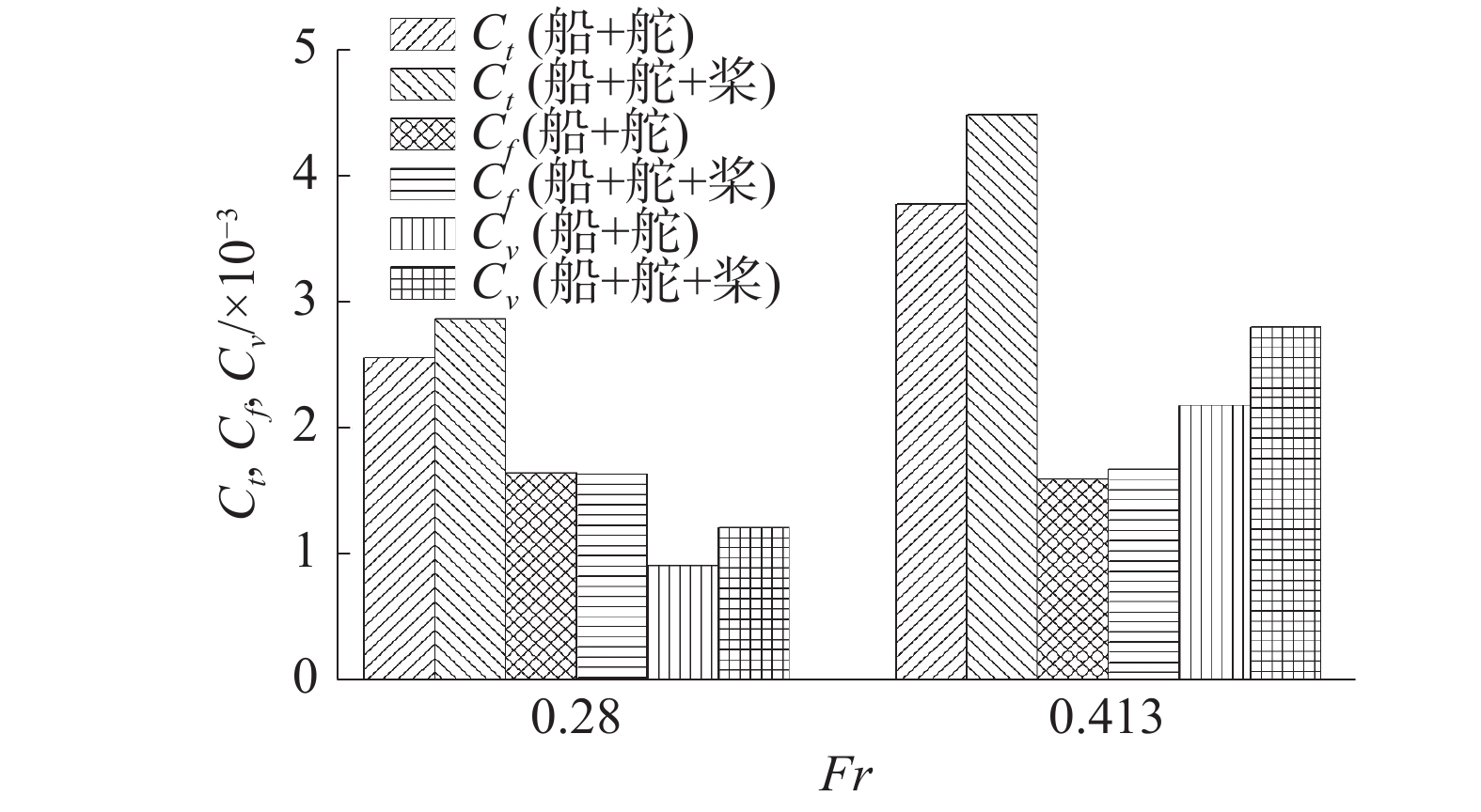
|
Download:
|
| 图 7 螺旋桨对船体阻力的影响 | |
当船后安装螺旋桨时,螺旋桨旋转会引起其周围流场的变化,而导致上述所说的船体阻力的改变。图8为安装螺旋桨前后的船艉区域压力系数分布的变化。压力系数为
| ${C_P} = \frac{{P - \rho gh}}{{\dfrac{1}{2}\rho V_0^2}}$ |
式中:P为总压力;ρ为水密度;h为水深;V0为轴向速度。
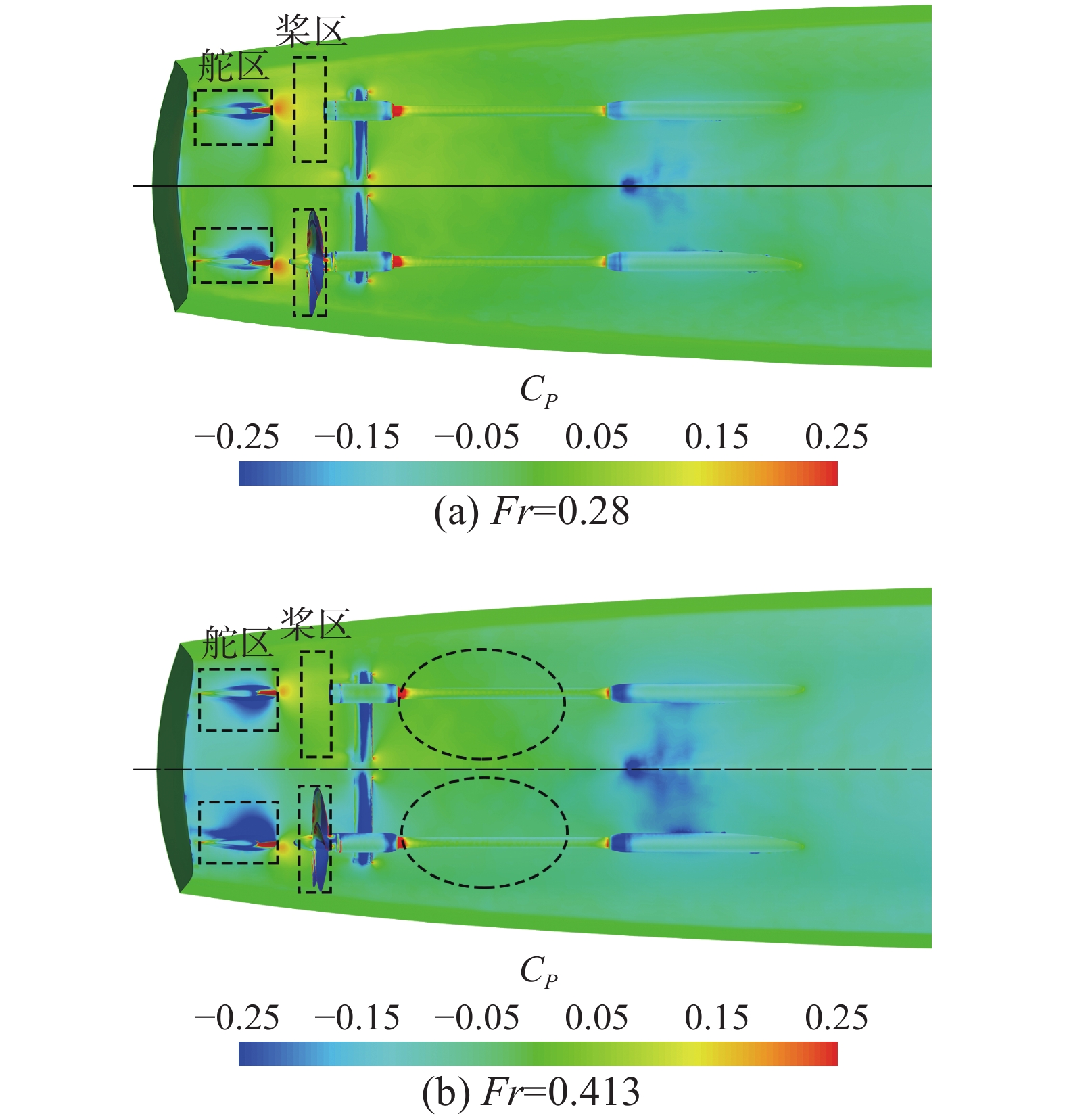
|
Download:
|
| 图 8 螺旋桨对船体压力的影响 | |
由图8可知,对于Fr=0.28时,螺旋桨安装后的“舵区”以及“桨区”的低压区域明显增大,船艉区域的降低就意味着船舶艏艉压力差的增大,进而导致了船体黏压阻力的增大;当Fr=0.413时,船尾低压区域面积的增幅更大,除了“舵区”以及“桨区”,轴支架附近区域的压力也出现了明显的降低,这解释了此航速下推力减额分数较大的原因。
4.3 螺旋桨对自由表面波形的影响图9为安装螺旋桨前后,自由液面波形的变化。由图可知,2种航速下的船+桨+舵耦合计算时的波高值都要比船+舵计算时的波高值大很多,特别是针对船艉波系的波高值;波高值的增大就意味着兴波阻力的增大,这也是图7中船体剩余阻力增大的主要原因。
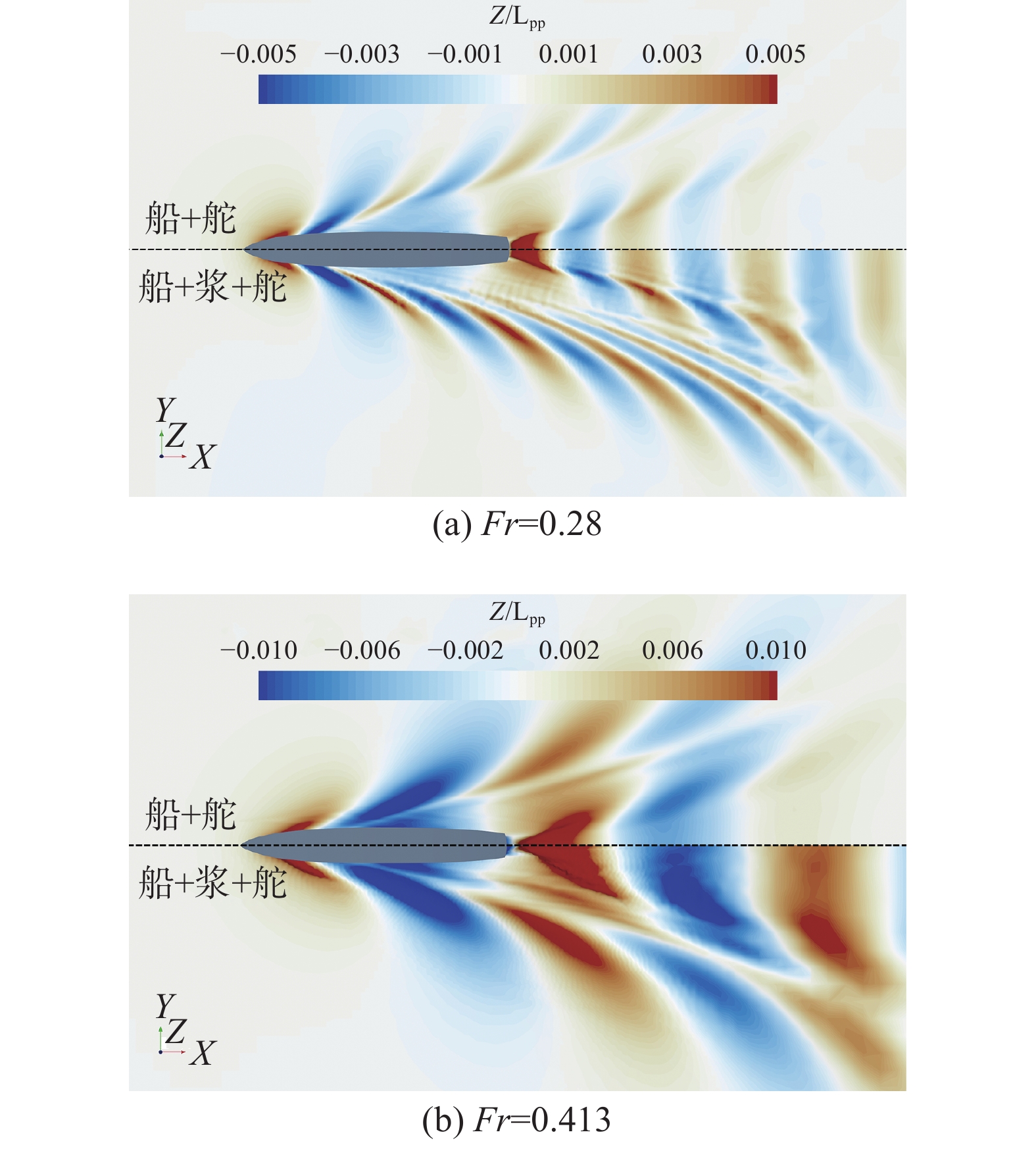
|
Download:
|
| 图 9 螺旋桨对自由液面波形的影响 | |
图10表示Fr=0.413时的螺旋桨尾涡结构。由图可知,螺旋桨的梢涡、毂涡与舵相遇后进行重构,并在舵后进行传递演化。舵处在螺旋桨不断演化的周期性尾流中,在吸收螺旋桨尾流动能的同时,其受力势必会具有强烈的非定常性。
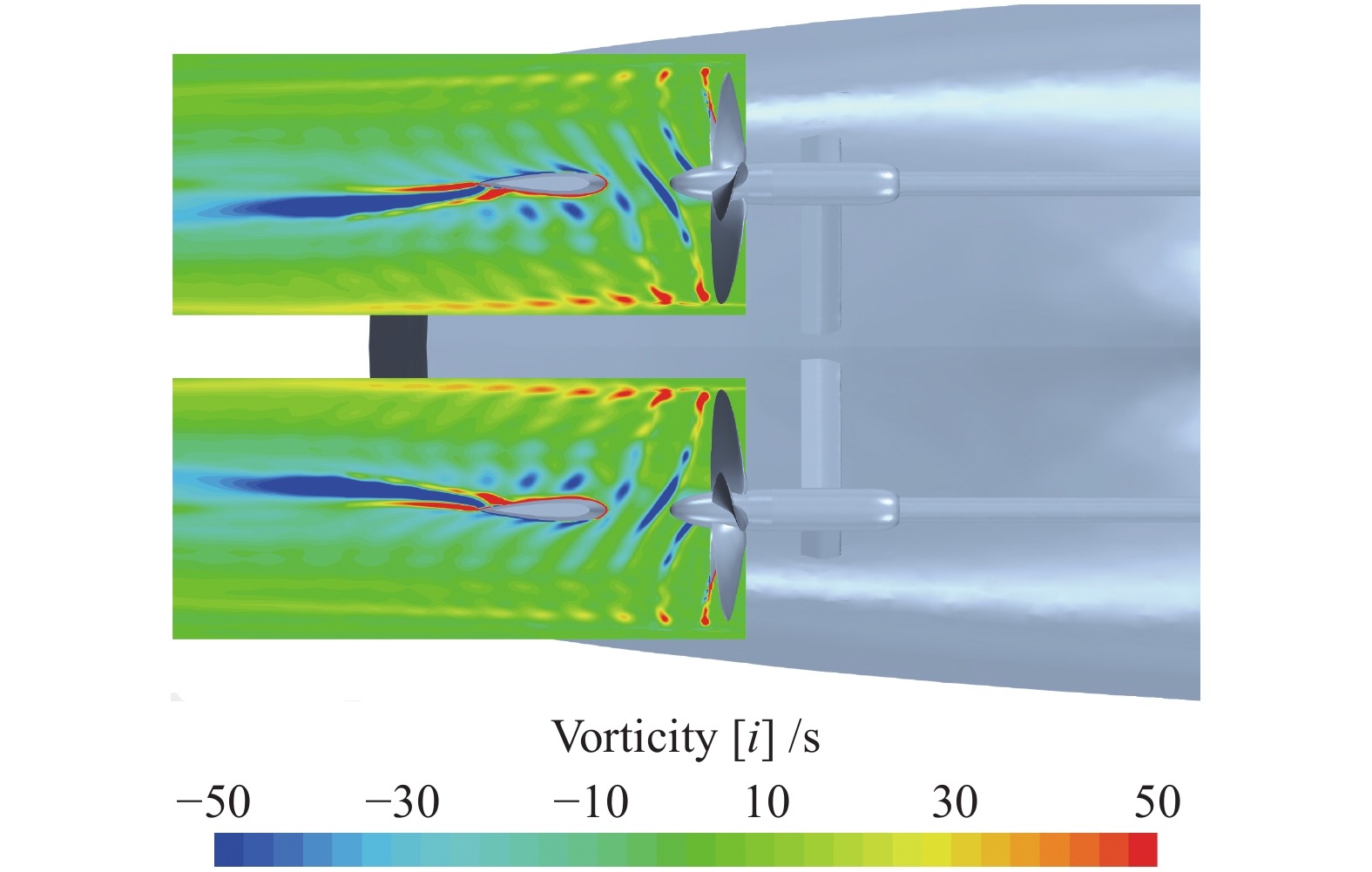
|
Download:
|
| 图 10 Fr=0.413时的螺旋桨涡结构 | |
对计算稳定状态下X方向的非定常舵力(记为Rx)进行监测,并基于时域结果进行快速傅里叶变换(FFT),得到的结果在图11给出。由图可知:舵力在螺旋桨的尾流中呈现出明显的周期性变化特征;非定常舵力在轴频(axis passing frequency,APF)以及叶频(blade passing frequency,BPF)处为明显的脉动峰值;高航速下(Fr=0.413)非定常舵力的时域曲线表现出锯齿状特征,对应的频域结果除了在轴频以及叶频处出现明显的峰值外,在高频处也存在一定的峰值,说明高频脉动舵力的分量是不能忽略不计的。

|
Download:
|
| 图 11 非定常舵力 | |
基于数值方法,对船−桨−舵一体化耦合下的双桨船自航特性进行模拟,并分析了船体、螺旋桨以及舵之间的相互影响,可得出的结论如下:
1)螺旋桨的工作使船尾区域的压力降低,并且随着航速的增大,压力的降低幅度更大,从而导致推力减额分数的增大;
2)螺旋桨工作状态下的自由液面波高值明显增大,这是船体剩余阻力增大的重要原因;
3)舵力在螺旋桨的尾流中呈现出规律的周期性变化特征,并在轴频和叶频处出现明显的脉动峰值。
| [1] |
SONG K W, GUO C Y, GONG J, et al. Influence of interceptors, stern flaps, and their combinations on the hydrodynamic performance of a deep-vee ship[J]. Ocean engineering, 2018, 170: 306-320. DOI:10.1016/j.oceaneng.2018.10.048 ( 0) 0)
|
| [2] |
WANG J H, ZOU L, WAN D C. CFD simulations of free running ship under course keeping control[J]. Ocean engineering, 2017, 141: 450-464. DOI:10.1016/j.oceaneng.2017.06.052 ( 0) 0)
|
| [3] |
SADAT-HOSSEINI H, WU P C, CARRICA P M, et al. CFD verification and validation of added resistance and motions of KVLCC2 with fixed and free surge in short and long head waves[J]. Ocean engineering, 2013, 59: 240-273. DOI:10.1016/j.oceaneng.2012.12.016 ( 0) 0)
|
| [4] |
程宣恺, 周志勇, 陈康, 等. 船模自航试验数值模拟研究[J]. 船舶与海洋工程, 2013(3): 10-15. DOI:10.3969/j.issn.2095-4069.2013.03.003 ( 0) 0)
|
| [5] |
丁科, 王永生, 魏应三. 船艉螺旋桨激振力的数值预报[C]//第十一届全国水动力学学术会议暨第二十四届全国水动力学研讨会并周培源诞辰110周年纪念大会文集(下册). 无锡, 中国, 2012: 887-893.
( 0) 0)
|
| [6] |
CHANG X, SUN S, ZHI Y C, et al. Investigation of the effects of a fan-shaped Mewis duct before a propeller on propulsion performance[J]. Journal of marine science and technology, 2019, 24(1): 46-59. DOI:10.1007/s00773-018-0530-x ( 0) 0)
|
| [7] |
DUMAN S, SEZEN S, BAL S. URANS approach in hull-propeller-rudder interaction of a surface combatant at high speed[C]//Proceedings of the 11th Symposium on High Speed Marine Vehicles. Naples, Italy, 2017: 131–139.
( 0) 0)
|
| [8] |
JASAK H, VUKČEVIĆ V, GATIN I, et al. CFD validation and grid sensitivity studies of full scale ship self propulsion[J]. International journal of naval architecture and ocean engineering, 2019, 11(1): 33-43. DOI:10.1016/j.ijnaoe.2017.12.004 ( 0) 0)
|
| [9] |
VUKČEVIĆ V, JASAK H, GATIN I, et al. Ship scale self propulsion CFD simulation results compared to sea trial measurements[C]//Proceedings of the VII International Conference on Computational Methods in Marine Engineering. Nantes, France, 2017.
( 0) 0)
|
| [10] |
DHINESH G, MURALI K, SUBRAMANIAN V A. Estimation of hull-propeller interaction of a self-propelling model hull using a RANSE solver[J]. Ships and offshore structures, 2010, 5(2): 125-139. DOI:10.1080/17445300903231109 ( 0) 0)
|
| [11] |
李亮, 王超, 孙帅, 等. 实船自航试验数值模拟及尺度效应分析[J]. 哈尔滨工程大学学报, 2016, 37(7): 901-907. ( 0) 0)
|
| [12] |
朱芳艳. 船模自航试验的数值模拟[D]. 武汉: 武汉理工大学, 2013.
( 0) 0)
|
| [13] |
STERN F, AGDRUP K, KIM S Y, et al. Experience from SIMMAN 2008-the first workshop on verification and validation of ship maneuvering simulation methods[J]. Journal of ship research, 2011, 55(2): 135-147. ( 0) 0)
|
| [14] |
盛振邦, 刘应中. 船舶原理(下)[M]. 上海: 上海交通大学出版社, 2015.
( 0) 0)
|
 2020, Vol. 47
2020, Vol. 47


