2. 贵州电网有限责任公司电力科学研究院,贵州 贵阳 550002
2. Electric Power Research Institute of Guizhou Power Grid Co., Ltd, Guiyang 550002, China
近年来无人机应用的领域越来越广泛,产生了不少的特种作业无人机,称为空中机器人[1-2]。空中机器人有着体积小、机动性强、能够定点悬停等优点,成为了优秀的空中作业平台。空中机器人作业时,负载经常会固定在机身下方,但由于机身下方负载摆放空间有限以及负载外形与机身不匹配的问题,负载的选择存在着大量的限制,而将负载悬挂在机身下方则不再需要考虑这些问题,在货物运输[3-4]、喷洒农药[5]等应用领域有着较大的应用前景。但是空中机器人悬挂负载飞行时,系统的稳定性会受到负载摆动的影响,极大地限制了该方式的应用,所以研究悬挂负载空中机器人的控制器设计有着重要意义。
无人机悬挂飞行研究一直受到国内外研究团队的关注,国内外针对无人机悬挂飞行的问题提出了很多有效的控制方法。文献[6]设计了一种基于反步控制算法的非线性控制器,使得无人机可以在悬挂负载大幅度摆动时仍然能进行很好的轨迹跟踪,但是其并没有对悬挂负载的位置进行控制,飞行过程中存在负载剧烈摆动的情况;文献[7]运用了微分平滑方法设计了针对平面四旋翼无人机悬挂系统的控制器,实现了针对四旋翼无人机悬挂系统的轨迹生成和跟踪;文献[8]中,研究人员使用迭代线性二次型最优控制器,实现了无人机的轨迹跟踪控制并抑制了悬挂负载的摆动,虽然控制效果显著,但是控制器复杂,需要复杂的运算,现有无人机上的机载微处理器不一定能达到要求的运算速度;在文献[9]中,研究人员采用了强化学习的方法,对特定负载的直升机飞行控制系统进行训练,达到了对悬挂负载的轨迹进行规划的目的,但只能在特定重量的负载下才能使用,当改变负载需要重新进行训练,适用性不强;在文献[10]中,研究人员对带挂负载的四旋翼无人机起飞过程进行了研究;文献[11]解决了四旋翼无人机在悬挂负载未知的情况下实现安全起飞的问题,并通过仿真结果证实了其算法的有效性。
综上所述,近年来对无人机悬挂系统的研究成果显著,但是许多方法仍存在一些局限性。针对这些问题,本文设计的位置控制器,既不依赖于模型的线性化,也无需复杂的结构,而是采用了滑模(sliding mode, SM)变结构控制方法,并加入了可变厚度的边界层法,有效地进行了抗摆控制,降低了抖震现象。
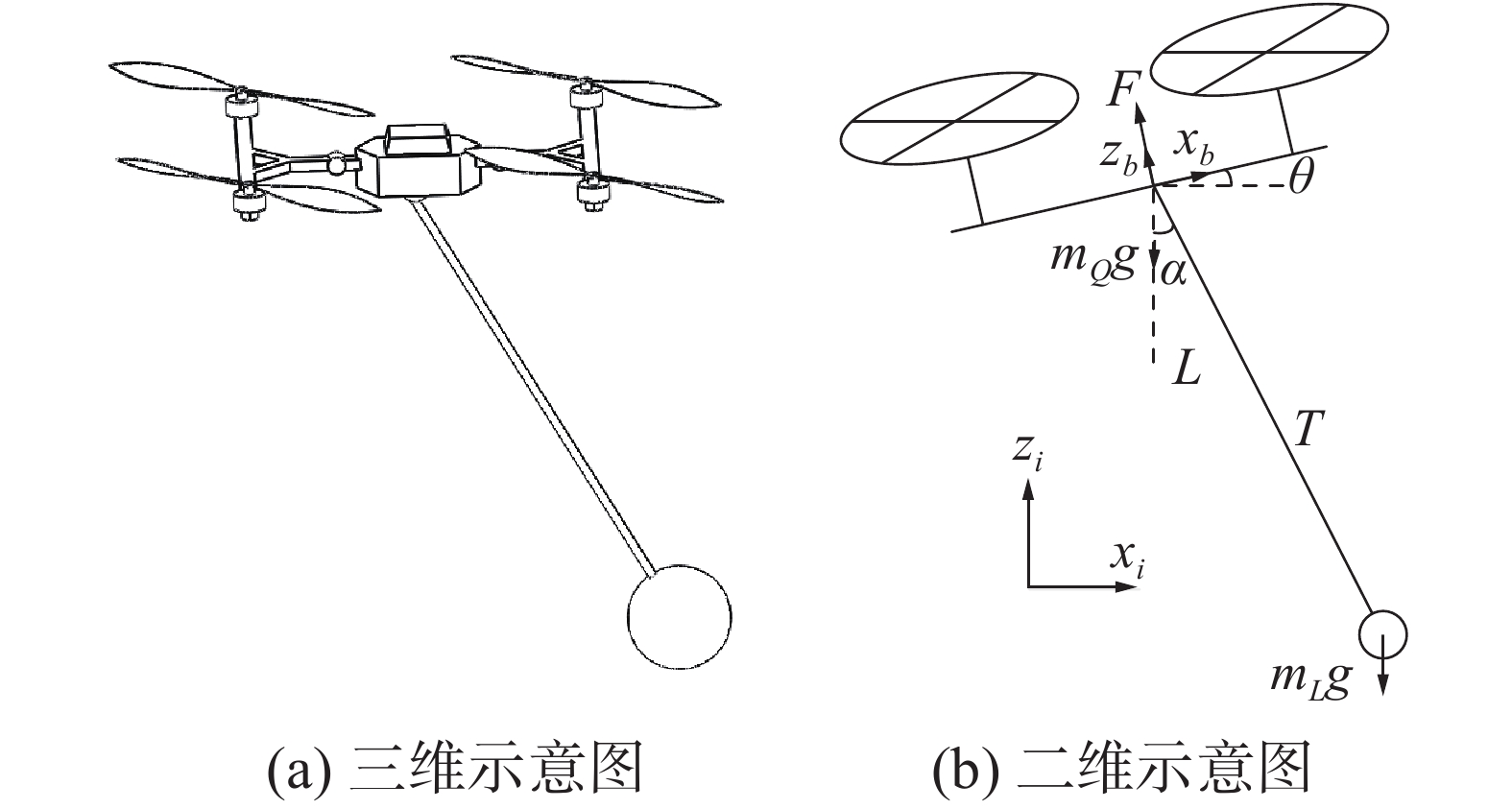
1 数学模型悬挂负载的空中机器人的结构示意图如图1所示。
|
Download:
|
| 图 1 悬挂负载的空中机器人结构 | |
图1(a)是悬挂负载空中机器人的三维示意图,图1(b)是与其对应的二维模型示意图。由于悬挂负载在水平方向的2个自由度相互解耦,研究悬挂负载空中的高度控制和抗摆控制,可在其对称面内简化为二维模型,采用图1(b)作为本文的控制模型。
首先建立2个坐标系[11],惯性坐标系I和机体坐标系B,图中
假设1 空中机器人为刚性且对称的;
假设2 机体坐标系的原点、质心以及几何中心是重合的;
假设3 负载始终处于空中机器人的下方,即α−θ∈(−90°, 90°),图中所示位置
假设4 绳索的质量不计,且是刚性、不可伸缩的。
假设1和假设2简化了问题的分析,保证了二维示意图以及下面推导的正确性。
假设3成立的前提是无人机的俯仰角
假设4成立的前提是绳索的弹性系数较大,从而可以忽略绳的张力T带来的伸长量,而确保绳索是刚性不可收缩的。只要保证绳的张力T始终是大于0的,由式(5),T的数学表达式可推导出,只要α−θ∈(−90°, 90°),那么T是始终大于0的。
将总升力F按照图1(b)中惯性坐标系的
| $\left\{ {\begin{array}{*{20}{c}} {{F_X} = - F\sin \theta } \\ {{F_Z} = F\cos \theta } \end{array}} \right.$ |
根据假设2和3,可以得到悬挂负载与空中机器人的相对位置:
| $\left\{ {\begin{array}{*{20}{c}} {{x_L} = {x_Q} + L\sin \alpha } \\ {{z_L} = {z_Q} - L\cos \alpha } \end{array}} \right.$ | (1) |
式中:
同时对式(1)两边求对时间的二阶导数,可以得到负载的加速度在水平和竖直2个方向的分量:
| $\left\{ {\begin{array}{*{20}{c}} {{{\ddot x}_L} = {{\ddot x}_Q} - L\dot \alpha \sin \alpha + L\ddot \alpha \cos \alpha } \\ {{{\ddot z}_L} = {{\ddot z}_Q} + L\dot \alpha \cos \alpha + L\ddot \alpha \sin \alpha } \end{array}} \right.$ | (2) |
如图1(b)所示,对空中机器人和悬挂负载进行牛顿第二定律分析可以得到:
| $\left\{ \begin{array}{l} {m_Q}{{\ddot x}_Q} = {F_X} + T\sin \alpha \\ {m_Q}{{\ddot z}_Q} = {F_Z} - T\cos \alpha - {m_Q}g \\ {m_L}{{\ddot x}_L} = - T\sin \alpha \\ {m_L}{{\ddot z}_L} = T\cos \alpha - {m_L}g \\ \end{array} \right.$ | (3) |
将式(3)代入到式(2)可以得到绳中的张力T和负载摆动的角加速度
| $\left\{ \begin{array}{l} T = \dfrac{{{m_L}( - {F_X}\sin \alpha + {F_Z}\cos \alpha + L{M_Q}{{\dot \alpha }^2})}}{{{m_Q} + {m_L}}} \\ \ddot \alpha = - \dfrac{1}{{{m_Q}L}}({F_X}\cos \alpha + {F_Z}\sin \alpha ) \\ \end{array} \right.$ | (4) |
将式(4)回代到式(3),可以就得到悬挂负载的空中机器人的动力学模型:
| $\left\{ {\begin{array}{*{20}{l}} {\begin{array}{*{20}{c}} {{{\ddot x}_Q} = \dfrac{{{m_Q} + {m_L}{{\cos }^2}\alpha }}{{({m_Q} + m){m_Q}}}{F_X} + \dfrac{{{m_L}\sin \alpha \cos \alpha }}{{({m_Q} + {m_L}){m_Q}}}{F_Z} + } \\ {{\rm{ }}\dfrac{{{m_L}L}}{{{m_Q} + {m_L}}}{{\dot \alpha }^2}\sin \alpha {\rm{ }}} \end{array}} \\ {{{\ddot z}_Q} = \dfrac{{{m_L}\sin \alpha \cos \alpha }}{{({m_Q} + {m_L}){m_Q}}}{F_X} + \dfrac{{{m_Q} + {m_L}{{\sin }^2}\alpha }}{{({m_Q} + {m_L}){m_Q}}}{F_Z} - } \\ \quad \quad \quad {\dfrac{{{m_L}L}}{{{m_Q} + {m_L}}}{{\dot \alpha }^2}\cos \alpha - g{\rm{ }}} \\ {\ddot \alpha = - \dfrac{{\cos \alpha }}{{{m_L}L}}{F_X} - \dfrac{{\sin \alpha }}{{{m_L}L}}{F_Z}{\rm{ }}} \end{array}} \right.$ | (5) |
滑模变结构控制[12-15]因为滑动模态对于参数摄动和外界扰动等不确定因素具有不敏感性,并且滑动模态的动态品质可以预先设计,成为一种有效的鲁棒控制方法,已经在很多领域得到广泛应用。近年来,滑模变结构控制大量的应用在欠驱动系统上,而悬挂负载空中机器人是一个典型的欠驱动系统,所以本文采用滑模变结构的方法来设计空中机器人的位置控制器及抗摆控制器,并在此基础上采用了改进过的边界厚度可变的边界层法[16],有效地降低了滑模控制器固有的抖震现象。
首先对模型可以进行简化,由于摆角
| $\left\{ {\begin{array}{*{20}{l}} {\dfrac{{{m_L}\sin \alpha \cos \alpha }}{{({m_Q} + {m_L}){m_Q}}}{F_Z} \ll \dfrac{{{m_Q} + {m_L}{{\cos }^2}\alpha }}{{({m_Q} + m){m_Q}}}{F_X}} \\ {\dfrac{{{m_L}\sin \alpha \cos \alpha }}{{({m_Q} + {m_L}){m_Q}}}{F_X} \ll \dfrac{{{m_Q} + {m_L}{{\sin }^2}\alpha }}{{({m_Q} + {m_L}){m_Q}}}{F_Z}} \\ {\dfrac{{\sin \alpha }}{{{m_L}L}}{F_Z} \ll \dfrac{{\cos \alpha }}{{{m_L}L}}{F_X}} \end{array}} \right.$ |
所以式(5)可简化为:
| $\left\{ \begin{array}{l} {{\ddot x}_Q} = \dfrac{{{m_Q} + {m_L}{{\cos }^2}\alpha }}{{({m_Q} + m){m_Q}}}{F_X} + \dfrac{{{m_L}L}}{{{m_Q} + {m_L}}}{{\dot \alpha }^2}\sin \alpha \\ {{\ddot z}_Q} = \dfrac{{{m_Q} + {m_L}{{\sin }^2}\alpha }}{{({m_Q} + {m_L}){m_Q}}}{F_Z} - \dfrac{{{m_L}L}}{{{m_Q} + {m_L}}}{{\dot \alpha }^2}\cos \alpha - g \\ \ddot \alpha = - \dfrac{{\cos \alpha }}{{{m_L}L}}{F_X} \end{array} \right.$ |
该模型自动解耦成2部分,一部分是只与水平方向分力
悬挂负载的空中机器人的高度模型为
| ${\ddot z_Q} = \frac{{{m_Q} + {m_L}{{\sin }^2}\alpha }}{{({m_Q} + {m_L}){m_Q}}}{F_Z} - \frac{{{m_L}L}}{{{m_Q} + {m_L}}}{\dot \alpha ^2}\cos \alpha - g$ |
模型可写成如下形式:
| $\left\{ \begin{array}{l} {x_2} = {{\dot x}_1} \\ {{\dot x}_2} = {f_1}({{x}}) + {b_1}({{x}}){F_Z} \\ \end{array} \right.$ |
式中:
由上述模型可以看出,该模型是单自由度和单控制输入的非欠驱动系统,只需要设计一级滑模面即可。所以构造如下的滑模面:
| ${s_1} = {c_1}{e_z} + {\dot e_z}$ |
式中:
对
| ${\dot s_1} = {c_1}{\dot x_1} + {\dot x_2} = {c_1}{x_2} + {f_1}({{x}}) + {b_1}({{x}}){F_Z}$ |
定义如下的李雅普诺夫函数:
| ${V_1} = \frac{1}{2}{s_1}^2$ | (6) |
对式(4)求导可得:
| ${\dot V_1} = {s_1}({c_1}{x_2} + {f_1}({{x}}) + {b_1}({{x}}){F_Z})$ |
| $ - {\varepsilon _1}{\rm{sgn}} ({s_1}) - {K_1}{s_1} = {c_1}{x_2} + {f_1}({{x}}) + {b_1}({{x}}){F_Z}$ |
于是可以得到高度控制器的控制率:
| ${F_Z} = \frac{{ - {c_1}{x_2} - {f_1}({{x}}) - {\varepsilon _1}{\rm{sgn}} ({s_1}) - {K_1}{s_1}}}{{{b_1}({{x}})}}$ | (7) |
此时,构造的李雅普诺方程的导数为
| ${\dot V_1} = - {\varepsilon _1}\left| {{s_1}} \right| - {K_1}{s_1}^2 \leqslant 0$ |
所以高度跟踪误差是渐近稳定的。
2.2 抗摆控制器设计悬挂负载空中机器人的摆动模型为
| $\left\{ {\begin{array}{*{20}{l}} {{{\ddot x}_Q} = \dfrac{{{m_Q} + {m_L}{{\cos }^2}\alpha }}{{({m_Q} + {m_L}){m_Q}}}{F_X} + \dfrac{{{m_L}L}}{{{m_Q} + {m_L}}}{{\dot \alpha }^2}\sin \alpha } \\ {\ddot \alpha = - \dfrac{{\cos \alpha }}{{{m_L}L}}{F_X}} \end{array}} \right.$ | (8) |
式(8)可以改写成如下形式:
| $\left\{ \begin{array}{l} {x_4} = {{\dot x}_3} \\ {{\dot x}_4} = {f_2}({{x}}) + {b_2}({{x}}){F_X} \\ {x_6} = {{\dot x}_5} \\ {{\dot x}_6} = {f_3}({{x}}) + {b_3}({{x}}){F_X} \\ \end{array} \right.$ |
式中:
由式(8)可以看出,摆动模型部分是一个具有2个自由度一个控制输入的欠驱动系统,所以采用分层滑模控制的方法进行控制器的设计。首先将系统模型化成以下2个子系统:
| $A:\left\{ {\begin{array}{*{20}{l}} {{x_2} = {{\dot x}_1}} \\ {{{\dot x}_2} = {f_1}({{x}}) + {b_1}({{x}}){F_X}} \end{array}} \right.$ |
| $B:\left\{ {\begin{array}{*{20}{l}} {{x_4} = {{\dot x}_3}} \\ {{{\dot x}_4} = {f_2}({{x}}) + {b_2}({{x}}){F_X}} \end{array}} \right.$ |
然后构造第一级滑模面:
| ${s_2} = {c_2}{e_x} + {\dot e_x}$ |
| ${s_3} = {c_3}{e_\alpha } + {\dot e_\alpha }$ |
式中:
根据等效控制理论[16],可以得到每个子系统的等效控制率:
| ${u_{{\rm{eq}}_{\rm{1}}}} = - \frac{{{c_1}{x_2} + {f_1}({{x}})}}{{{b_1}({{x}})}}$ |
| ${u_{{\rm{eq}}_2}} = - \frac{{{c_2}{x_4} + {f_2}({{x}})}}{{{b_2}({{x}})}}$ |
由于摆动模型是一个欠驱动系统,控制量的数量少于状态量的数量,总的控制率必须包含每个子系统的控制量,所以定义总的控制量为
| ${F_X} = {u_{{\rm{e}}{{\rm{q}}_{\rm{1}}}}} + {u_{{\rm{e}}{{\rm{q}}_2}}} + {u_{{\rm{SW}}}}$ |
式中
设计第二层滑模面:
| $S = {a_1}{s_2} + {a_2}{s_3}$ |
式中a1、a2为常数。定义李雅普诺夫函数:
| $V = \frac{1}{2}{S^2}$ |
对
| $\begin{split} \dot V = & S\dot S = S[{a_1}({c_1}{{\dot x}_1} + {{\dot x}_2}) + {a_2}({c_2}{{\dot x}_3} + {{\dot x}_4})] = \\ & {\rm{ }}S[{a_1}({c_1}{x_2} + {f_1} + {b_1}({u_{{\rm{e}}{{\rm{q}}_{\rm{1}}}}} + {u_{{\rm{e}}{{\rm{q}}_2}}} + {u_{{\rm{SW}}}})) + \\ & {\rm{ }}{a_2}({c_2}{x_4} + {f_2} + {b_2}({u_{{\rm{e}}{{\rm{q}}_{\rm{1}}}}} + {u_{{\rm{e}}{{\rm{q}}_2}}} + {u_{{\rm{SW}}}}))] = \\ & {\rm{ }}S[{a_1}{b_1}({u_{{\rm{e}}{{\rm{q}}_2}}} + {u_{{\rm{SW}}}}) + {a_2}{b_2}({u_{{\rm{e}}{{\rm{q}}_{\rm{1}}}}} + {u_{{\rm{SW}}}})] \end{split} $ |
| $ - {\varepsilon _2}{\rm{sgn}} (S) - {K_2}S = {a_1}{b_1}({u_{{\rm{e}}{{\rm{q}}_2}}} + {u_{SW}}) + {a_2}{b_2}({u_{{\rm{e}}{{\rm{q}}_1}}} + {u_{{\rm{SW}}}})$ | (9) |
式中:ε2、K2均为正数。由式(9)可以求出
| $\begin{array}{l} {u_{{\rm{SW}}}} = {({a_1}{b_1} + {a_2}{b_2})^{ - 1}}[ - {a_2}{b_2}{u_{{\rm{e}}{{\rm{q}}_1}}} - {a_1}{b_1}{u_{{\rm{e}}{{\rm{q}}_2}}} - \\ \quad {\rm{ }}{\varepsilon _2}{\rm{sgn}} (S) - {K_2}S] \end{array} $ |
于是可以得到总的控制率为
| $\begin{split} & \quad \quad \quad \quad \quad {F_X} = {u_{{\rm{e}}{{\rm{q}}_{\rm{1}}}}} + {u_{{\rm{e}}{{\rm{q}}_2}}} + {u_{SW}} = \\ & {u_{{\rm{e}}{{\rm{q}}_1}}} + {u_{{\rm{e}}{{\rm{q}}_2}}} + \dfrac{{ - {a_2}{b_2}{u_{{\rm{e}}{{\rm{q}}_1}}} - {a_1}{b_1}{u_{{\rm{e}}{{\rm{q}}_2}}} - {\varepsilon _2}{\rm{sgn}} (S) - {K_2}S}}{{{a_1}{b_1} + {a_2}{b_2}}} = \\ & \dfrac{{{a_1}{b_1}}}{{{a_1}{b_1} + {a_2}{b_2}}}{u_{{\rm{e}}{{\rm{q}}_1}}} + \dfrac{{{a_2}{b_2}}}{{{a_1}{b_1} + {a_2}{b_2}}}{u_{{\rm{e}}{{\rm{q}}_2}}} + \dfrac{{ - {\varepsilon _2}{\rm{sgn}} (S) - {K_2}S}}{{{a_1}{b_1} + {a_2}{b_2}}} \end{split} $ | (10) |
此时李雅普诺夫函数的导数为
| $\dot V = S( - {\varepsilon _2}{\rm{sgn}} (S) - {K_2}S) = - {\varepsilon _2}\left| S \right| - {K_2}{S^2} \leqslant 0$ | (11) |
由式(11)可知,系统总滑模面满足李雅普诺夫意义下的稳定,是渐近稳定的。对于2个子滑模面,可以通过式(10)所设计的总控制输入使其能够渐近稳定,一旦任意一个状态脱离滑模面,总的切换控制
由于滑模控制器自身存在抖震现象,为了减少这种现象,本文采用边界层法,用饱和函数
| ${\rm{sat}}(S) = \left\{ {\begin{array}{*{20}{c}} {1{\rm{ , }}S > \mathit{\Delta} } \\ {kS{\rm{ , }}\left| S \right| \leqslant \mathit{\Delta} } \\ { - 1{\rm{ , }}S < \mathit{\Delta} } \end{array}} \right.,k = 1/\mathit{\Delta} $ |
式中
| $\mathit{\Delta} {\rm{ = }}\left\{ {\begin{array}{*{20}{l}} {{\mathit{\Delta} _1},{\rm{ }}\left| e \right| < {e_{\min }}} \\ {{\mathit{\Delta} _2},{\rm{ }}\left| e \right| > {e_{\max }}} \\ {\dfrac{{({e_{\max }} - \left| e \right|){\mathit{\Delta} _1} + (\left| e \right| - {e_{\min }}){\mathit{\Delta} _2}}}{{{e_{\max }} - {e_{\min }}}},\;\;\;{\text{其他}}} \end{array}} \right.$ |
式中:
在实际使用中,悬挂负载空中机器人的主要任务是带着负载飞行到指定的位置,并要求整个飞行过程中负载的摆角要尽可能小,到达指定位置后负载应无残余震荡。所以设计以下实验:让空中机器人从惯性坐标系的原点
采用控制律式(7)和(10)进行控制,控制器的参数分别为:c1=5、c2=20、c3=13、a1=12、a2=10、K1=3、K2=0.8、ε1=0.5、ε2=0.8、
为了验证本文设计的控制器的有效性,下面使用基于积分反步(integral backstepping, IB)法设计的控制器与本文设计的控制器的控制效果进行对比。
为了比较算法的抗扰能力,在仿真实验中将反馈给控制器的信号加入了幅值为0.01的高斯白噪声,仿真结果如图2~8所示。
|
Download:
|
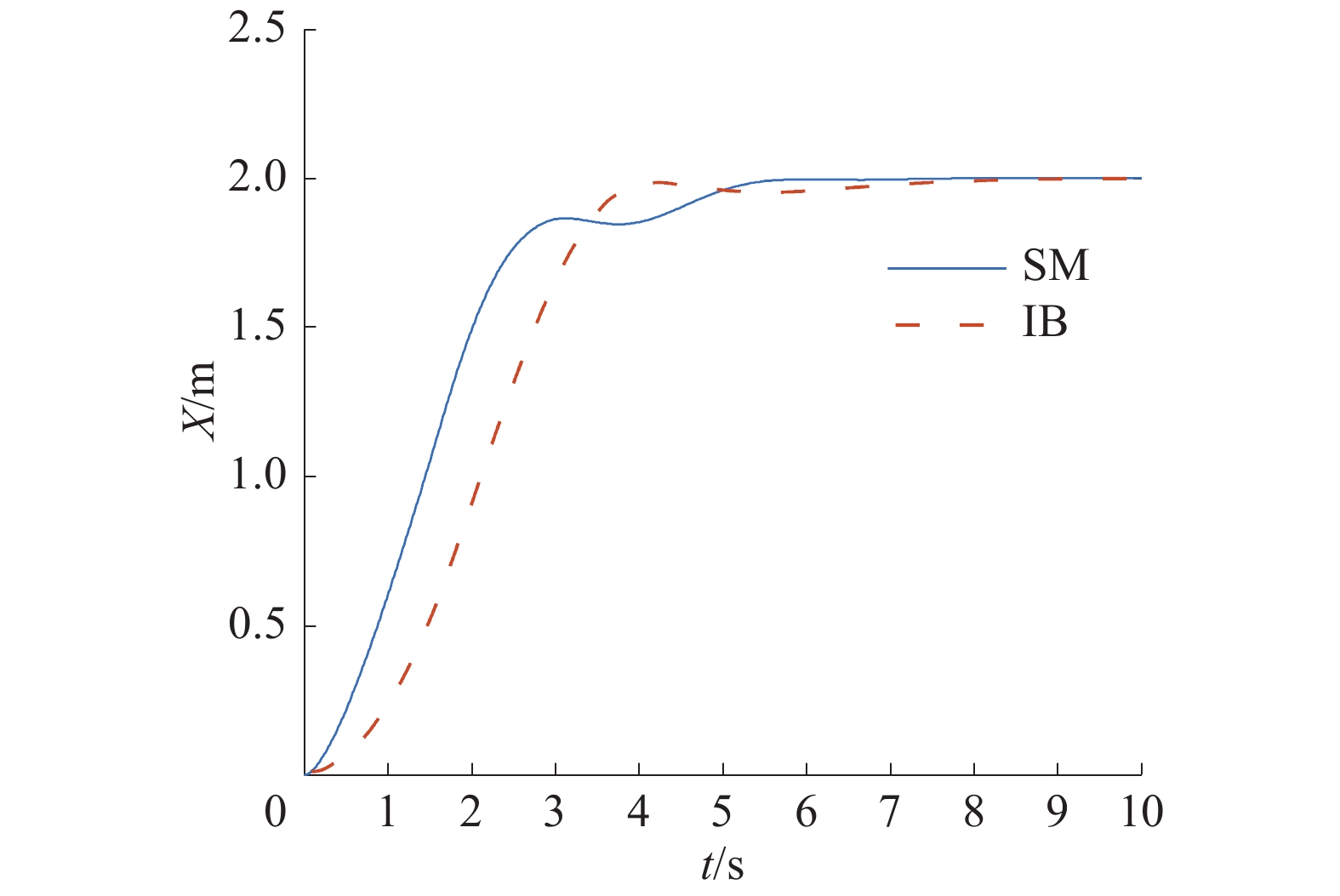
| 图 2 IB控制与SM控制下的水平位置响应 | |
|
Download:
|
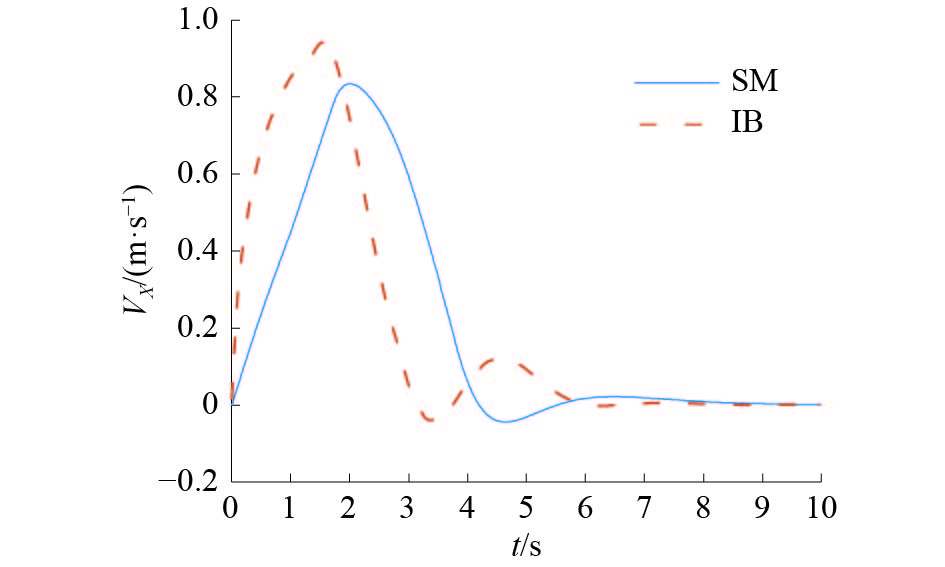
| 图 3 IB控制与SM控制下的水平速度响应 | |
|
Download:
|
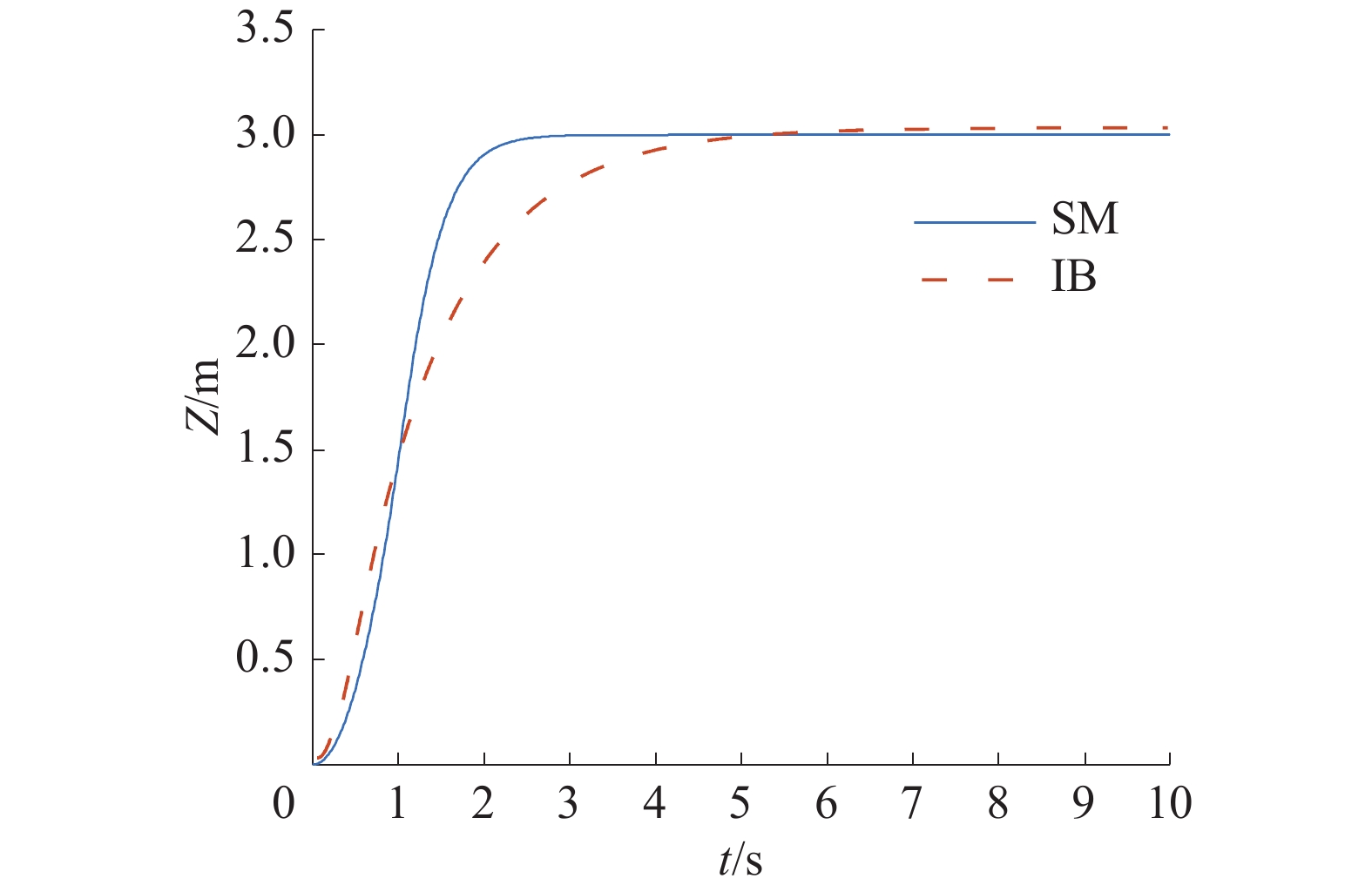
| 图 4 IB控制与SM控制下的高度位置响应 | |

|
Download:
|
| 图 5 IB控制与SM控制下的高度速度响应 | |
|
Download:
|
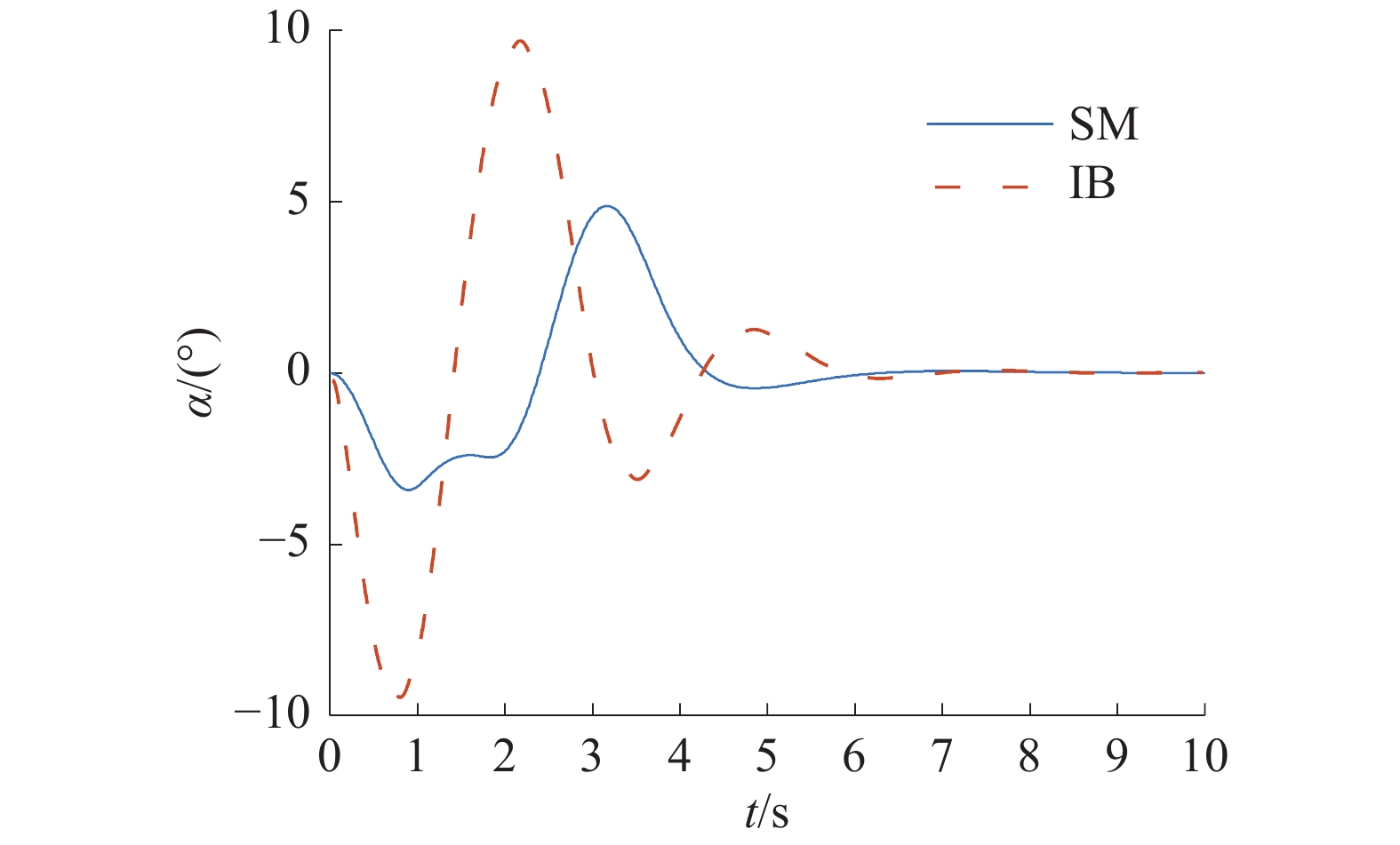
| 图 6 IB控制与SM控制下的摆角响应 | |
|
Download:
|
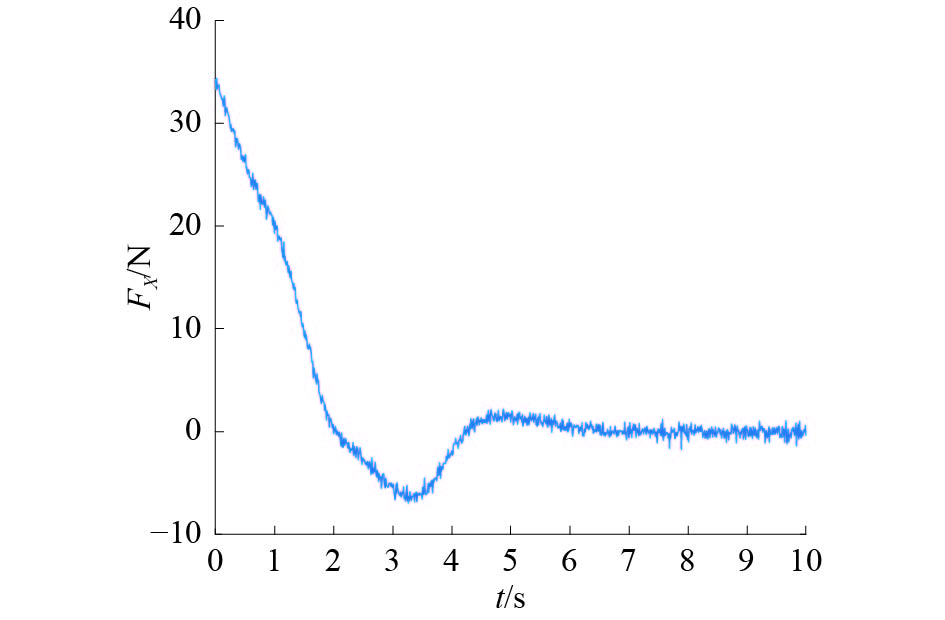
| 图 7 SM控制器水平方向的控制输入 | |

|
Download:
|
| 图 8 SM控制器竖直方向的控制输入 | |
图2~6为在本文设计的控制器和IB控制器的作用下空中机器人的响应曲线。由仿真曲线可以看出:本文设计的控制器在水平位置和高度位置响应上都要比IB控制器要快;并且在抗摆的效果上也比IB控制器好,在整个飞行过程,响应曲线都很平稳,摆角始终控制在±5°以内,并且到达指定位置之后没有残余震荡;空中机器人和负载同时达到稳定的时间比IB控制的时间少。图7、8为本文设计的控制器输出的控制信号曲线,可以看出设计的控制器输出变化平稳,输出的幅值也在合理范围之内,并且在加入了可变厚度的边界层之后,有效地降低了抖震现象。
通过以上分析可以看出,本文设计的控制器具有较好的控制效果,能够很好地完成控制任务。
4 结论本文设计的控制器,很好地解决了悬挂负载空中机器人飞行运动时产生的负载摆动和残余振荡问题。根据仿真结果与分析可以得出如下结论:
1)采用分层滑模控制方法能够解决驱动量少于自由度的控制问题,值得其他欠驱动系统推广使用;
2)本文针对悬挂负载空中机器人的二维模型进行了控制器设计,仿真结果说明了控制算法的有效性,可以考虑将本方法进一步运用到三维模型中;
3)本文设计的边界层厚度可变的边界层法能够有效降低滑模控制存在的抖震现象,值得深入研究;
4)仿真结果表明,本文所设计的控制器能够将负载摆角始终控制在±5°以内,控制效果较好,具有实际应用价值,可应用于货物运输等领域。
| [1] |
TOGNON M, FRANCHI A. Nonlinear observer-based tracking control of link stress and elevation for a tethered aerial robot using inertial-only measurements[C]//Proceedings of 2015 IEEE International Conference on Robotics and Automation. Seattle, USA, 2015: 3994–3999.
( 0) 0)
|
| [2] |
王冠林, 朱纪洪. 空中机器人系统及关键技术[J]. 飞航导弹, 2009(6): 52-59. ( 0) 0)
|
| [3] |
MENOUAR H, GUVENC I, AKKAYA K, et al. UAV-enabled intelligent transportation systems for the smart city: applications and challenges[J]. IEEE communications magazine, 2017, 55(3): 22-28. DOI:10.1109/MCOM.2017.1600238CM ( 0) 0)
|
| [4] |
MO Rigen, GENG Qingbo, LU Xin. Study on control method of a rotor UAV transportation with slung-load[C]//Proceedings of the 2016 35th Chinese Control Conference. Chengdu, China, 2016: 3274–3279.
( 0) 0)
|
| [5] |
刘泽锋, 唐宇, 骆少明, 等. 多旋翼植保无人机变量喷洒系统设计[J]. 农机化研究, 2018, 40(12): 47-54. DOI:10.3969/j.issn.1003-188X.2018.12.009 ( 0) 0)
|
| [6] |
KLAUSEN K, FOSSEN T I, JOHANSEN T A. Nonlinear control of a multirotor UAV with suspended load[C]//Proceedings of 2015 International Conference on Unmanned Aircraft Systems. Denver, CO, USA, 2015: 176–184.
( 0) 0)
|
| [7] |
SREENATH K, MICHAEL N, KUMAR V. Trajectory generation and control of a quadrotor with a cable-suspended load - A differentially-flat hybrid system[C]//Proceedings of 2013 IEEE International Conference on Robotics and Automation. Karlsruhe, Germany, 2013: 4888–4895.
( 0) 0)
|
| [8] |
ALOTHMAN Y, GU Dongbing. Quadrotor transporting cable-suspended load using iterative Linear Quadratic regulator (iLQR) optimal control[C]//Proceedings of the 2016 8th Computer Science and Electronic Engineering. Colchester, UK, 2017: 168–173.
( 0) 0)
|
| [9] |
FAUST A, PALUNKO I, CRUZ P, et al. Learning swing-free trajectories for UAVs with a suspended load[C]//Proceedings of 2013 IEEE International Conference on Robotics and Automation. Karlsruhe, Germany, 2013: 4902–4909.
( 0) 0)
|
| [10] |
PALUNKO I, FIERRO R, CRUZ P. Trajectory generation for swing-free maneuvers of a quadrotor with suspended payload: a dynamic programming approach[C]//Proceedings of 2012 IEEE International Conference on Robotics and Automation. Saint Paul, MN, USA, 2012: 2691–2697.
( 0) 0)
|
| [11] |
高皜, 曹琳, 曹茂永. 倒立摆系统基于能量控制的起摆控制策略研究[J]. 山东科技大学学报(自然科学版), 2016, 35(6): 95-100. DOI:10.3969/j.issn.1672-3767.2016.06.015 ( 0) 0)
|
| [12] |
XIA Yuanqing, FUMengyin, DENG Zhihong, et al. Recent developments in sliding mode control and active disturbance rejection control[J]. 控制理论与应用, 2013, 30(2): 137-147. DOI:10.7641/CTA.2013.20498 ( 0) 0)
|
| [13] |
LEVANT A. Higher-order sliding modes, differentiation and output-feedback control[J]. International journal of control, 2003, 76(9/10): 924-941. ( 0) 0)
|
| [14] |
YANG Liang, YANG Jianying. Nonsingular fast terminal sliding-mode control for nonlinear dynamical systems[J]. International journal of robust and nonlinear control, 2011, 21(16): 1865-1879. DOI:10.1002/rnc.1666 ( 0) 0)
|
| [15] |
彭继慎, 刘盼, 宋立业. 倒立摆的神经网络自适应滑模控制[J]. 控制工程, 2018, 25(11): 1976-1981. ( 0) 0)
|
| [16] |
赵文杰, 刘吉臻. 一种改进的边界层滑模控制方法[J]. 系统仿真学报, 2005, 17(1): 156-158, 180. DOI:10.3969/j.issn.1004-731X.2005.01.040 ( 0) 0)
|
| [17] |
张翔, 王德石, 李景熹. 滑模控制器趋近律仿真研究[J]. 微处理机, 2008, 29(1): 80-81. DOI:10.3969/j.issn.1002-2279.2008.01.027 ( 0) 0)
|
| [18] |
王健, 蔡宇萌. 主动悬架的滑模控制指数趋近率参数优化[J]. 重庆理工大学学报(自然科学版), 2017, 31(9): 15-21. DOI:10.3969/j.issn.1674-8425(z).2017.09.003 ( 0) 0)
|
 2020, Vol. 47
2020, Vol. 47


