天然气是当今世界最为绿色、高效的优质能源之一，被世界各国人民广泛使用^[1]。随着全球经济的快速发展和人类生存环境的不断恶化，人类对天然气的需求量急剧提升^[2]。因此，对城市燃气负荷进行预测显得尤为重要^[3]。本文主要对城市燃气日负荷进行短期预测。由于在全年范围内，每2个月内的温度和人口等因素变化范围不大。因此，将某市某年的燃气日负荷历史数据分为6组，以每2个月为1组进行建模，利用广义动态模糊神经网络（GD-FNN）对燃气日负荷进行组合预测，得到预测精度（平均）和预测时间。

1 基于广义回归神经网络的城市燃气日负荷预测 1.1 数据预处理

数据预处理的作用主要是防止异常数据的波动而引起训练时间的增加，严重时可能会导致广义回归神经网络(GRNN)无法收敛，需要对原始数据进行归一化处理。在训练样本中采用式（1）将参数归一化到[0, 1]：

${X_i} = \frac{{\left( {X - {X_{\min }}} \right)}}{{\left( {{X_{\max }} - {X_{\min }}} \right)}}$

(1)

而在输出层中，用式（2）换算得到的数值就是燃气日负荷预测值：

$X = {X_{\min }} + \left( {{X_{\max }} - {X_{\min }}} \right){X_i}$

(2)

式中：X_max为训练样本的最大值；X_min为训练样本的最小值；X_i为归一化后的数据；X为反归一化后得到的燃气日负荷预测值^[4]。

为了避免不稳定数据对网络训练的干扰，可以在归一化前留出余量，使其归一化后的数值落在[0.1, 0.9]中，对归一化公式重新进行推导，由于 $\ln 0.1 = - 2.302 \;6 $ ， $\ln 0.9 = - 0.105\;4$ ，使

$0.1 \leqslant {X_i} = \frac{{\left( {X - {X_{\min }}} \right)}}{{\left( {{X_{\max }} - {X_{\min }}} \right)}} \leqslant 0.9$

可以推导出新的归一化公式：

${X_i}{\rm{ = 1}} - \frac{1}{{\exp \left[ {0.105 \;4 + \dfrac{{\left( {2.302 \;6 - 0.105 \;4} \right)\left( {X - {X_{\min }}} \right)}}{{{X_{\max }} - {X_{\min }}}}} \right]}}$

(3)

反归一化公式为

$X \!=\! \frac{{{X_{\max }} - {X_{\min }}}}{{\left( {2.302 \;6 - 0.105 \;4} \right)}}\left[ {\ln \left( {\frac{1}{{\left( {1 - {X_i}} \right)}}} \right) - 0.105 \;4} \right] + {X_{\min }}\!\!$

(4)

根据式(3)和(4)可将数据归一化到[0.1, 0.9]，有利于加快神经网络训练^[5]。

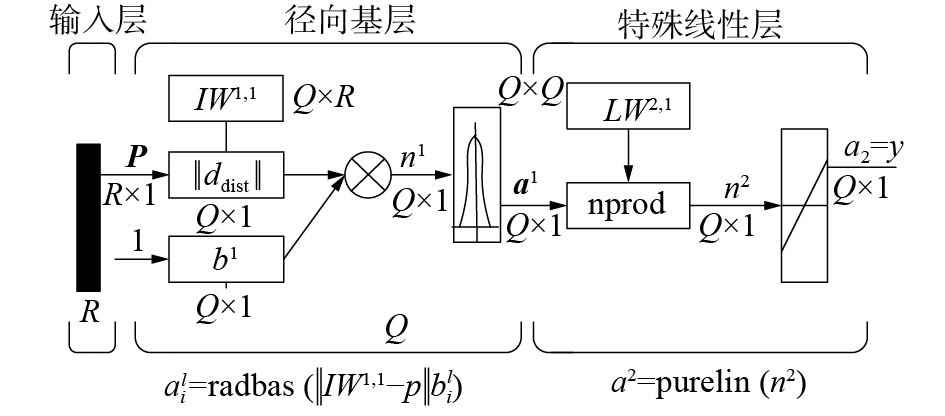
1.2 GRNN和预测结果及分析

GRNN的结构如图1所示^[6]。图中 ${{P}}$ 为输入向量， $a_i^1$ 是向量 ${{{a}}^1}$ 的第 $i$ 个元素， ${W^{1,1}}$ 和 ${W^{2,1}}$ 分别是第一层和输出层的权值矩阵， $R$ 为输入向量元素的数目， $Q$ 为输入输出样本的数目，nprod模块表示计算径向基层输出矢量 ${{{a}}^1}$ 和输出层权值矩阵的规则化内积， ${b^1}$ 为平滑系数， $\left\| {d_{\rm{dist}}} \right\|$ 为输入向量与权值向量的距离，purelin为线性函数， ${\rm{radbas}}$ 为高斯函数。

对某市的燃气日负荷历史数据进行训练建模。神经网络输入节点取4个（预测日前3 d的燃气日负荷数据和一周前1 d的日负荷数据）；输出节点取1个，即预测日燃气负荷。本文中，限于篇幅，仅列出12月25日至31日（以下同）的燃气日负荷预测结果及误差，见表1及图2、3。预测的相对误差公式如式（5）所示：

${\text{相对误差}}{\rm{ = }}\frac{{{\text{预测值}} - {\text{真实值}}}}{{\text{真实值}}} \times 100{\rm{\% }}$

(5)

在GRNN中，平滑系数^{[5] $\sigma = 0.12$} 。由表1可知，GRNN燃气日负荷预测数据在12月27日的相对误差较大，超过20%，可能是由于燃气日负荷数据不准确或预测模型故障导致的预测精度降低。可以通过其他预测模型的预测精度进行验证或进行组合预测提高其预测精度。在全年范围内，GRNN最大预测误差为26.707%，平均预测精度达到81.838%。

2 基于灰色−广义回归神经网络建立预测模型 2.1 灰色理论法

灰色理论法是一门研究信息部分清楚，部分不清楚并带有不确定性现象的应用数学。其主要工作原理是对燃气日负荷数据进行整理和分析，发现其中的规律性，通过其中的规律对燃气日负荷进行预测，其核心是对数的操作，主要是为了减小数据的干扰性和随机性，增加数据的规律性^[7]。

灰色理论首先要求历史数据必须具有序列走势平缓的特点，并且在经过一次累加后的数据序列必须具有指数增长的规律性，否则无法建立灰色预测模型。但是可以利用灰色理论对燃气日负荷的历史数据进行预处理，减少错误数据的干扰以提高预测模型的精度^[8]。

灰色−GRNN共有3种网络结构，主要包括串联型结构、并联型结构和嵌入式型结构。本文主要采用嵌入式型网络结构进行神经网络的建模工作。嵌入式型灰色−GRNN模型如图4所示。

灰化层的作用主要是用来减少原始数据的随机性，由于原始数据中可能存在异常的坏数据，这样会增加训练时间或使神经网络无法收敛，灰化层主要是对数值的运算，一般是对原始数据进行至少一次的累加，使经过累加的数据具有单调递增的特性，这样可以有效地减少原始数据的随机性，显著提高预测精度。

白化层的作用是对灰化层的逆运算，是对已经通过GRNN预测得到的预测值进行累减操作，最后得到的结果就是灰色−GRNN的预测值。

2.2 预测结果及分析

灰色−广义回归神经网络（灰色−GRNN）的建模流程与GRNN相似，主要是在灰化层和白化层的处理上与单独使用GRNN有所不同。

2.2.1 输入/输出设计

由于燃气日负荷的真实值中就包括了各种影响因素对燃气日负荷的作用，所以建模时输入（输出）向量设置为经过灰色生成（白化）处理的燃气日负荷历史真实值。灰色−GRNN输入节点取4个（预测日前3 d的数据和预测日前7 d的数据累加生成数据）；输出节点取1个,即预测日燃气负荷。

2.2.2 灰化层处理

对原始的燃气日负荷数据采用一次累加的方法进行灰色生成，这样可以大大减少燃气日负荷的不平稳性。首先给定原始时间序列X⁽⁰⁾={X⁽⁰⁾(0), X⁽⁰⁾(1),···,X⁽⁰⁾(n)}，对其进行一次累加后，得到灰化处理值X⁽¹⁾={X⁽¹⁾(0), X⁽¹⁾(1),···,X⁽¹⁾(n)}，其中

${X^{(1)}}\left( k \right) = \sum\limits_{i = 1}^k \{{{x^{(0)}}}, \left( i \right)\} (k = 1,2, \cdots ,n)$

(6)

根据式（6）得到燃气日负荷灰化值，x⁽⁰⁾(i)为燃气日负荷历史数据；x⁽¹⁾(i)为经过一次累加生成的燃气日负荷值。在经过白化层处理后可得到燃气日负荷预测值。白化公式如下

${X^{(0)}}\left( {k + 1} \right) = {X^{(1)}}\left( {k + 1} \right) - {X^{(1)}}\left( k \right)$

式中：X⁽¹⁾(k+1)为第（k+1） d的燃气日负荷灰化值预测；X⁽⁰⁾(k+1)为第（k+1） d的燃气日负荷预测值。

2.2.3 数据的预处理

为了进一步减少原始数据对燃气日负荷预测的影响，对已经经过灰色生成的数据再进行归一化处理，这样能够有效减少历史数据的随机性带来的影响，防止异常数据的波动引起训练时间的增加及GRNN发散，通过式（3）使最后的预处理数值在[0.1, 0.9]。

2.2.4 网络训练

在GRNN中，进行网络训练最重要的是找到系统的平滑系数 $\sigma $ ，同样在MATLAB中采用试验法确定 $\sigma $ 的值，通过不断变换 $\sigma $ 的值进行测试，最终找到误差最小的 $\sigma $ 值作为系统的平滑系数，经过最终测试，确定灰色−GRNN的平滑系数 $\sigma {\rm{ = }}0.35$ 。

2.2.5 基于灰色−GRNN模型进行燃气日负荷预测

通过已经搭建好的灰色−GRNN预测模型进行燃气日负荷预测，再将得到的预测值进行反归一化处理，利用式（4）得到反归一化数据，随后再进行白化层处理。白化层处理的主要作用是为了抵消灰化层的影响，经过一系列的处理后得到的数值就是最终的燃气日负荷预测值，预测结果见表1及图2、3。

由表1可见，灰色−GRNN在12月27日的预测精度为8.133%，由此说明GRNN模型在12月27日的预测中发生了故障。在全年范围内，灰色−GRNN的最大预测误差为20.215%，平均预测精度为83.982%。

3 基于梯度−广义回归神经网络建立预测模型 3.1 梯度神经网络法

1996年，Mulgrew.B提出了一种用于消除时间序列不平稳性的非线性神经网络建模方法，称为梯度神经网络法，可以利用这种梯度神经网络建模法进行燃气日负荷原始数据的预处理工作^[9]。

梯度神经网络法主要是通过对时间序列的差分来去除非平稳性的^[10]。在经过梯度处理后，能够有效减少由于原始数据的不平稳性和随机性所导致的误差，十分有利于提高预测的准确性，具体的处理方式如下：

设原始时间序列为 ${X_1},{X_2}, \cdot \cdot \cdot ,{X_n}$ ，按照公式：

$\Delta {X_m} = {X_{m + 1}} - {X_m},(m = 1,2, \cdots ,n - 1)$

(7)

得到新的数据序列 $\Delta {X_1},\Delta {X_2}, \cdots ,\Delta {X_{n - 1}}$ ，并将得到的新数据序列作为广义回归神经网络的输入。

3.2 预测结果及分析

基于梯度−GRNN的燃气日负荷预测步骤与灰色−GRNN相似，其主要不同之处在于使用的是梯度神经网络法对燃气日负荷历史数据进行处理，再进行归一化操作，在得到梯度−GRNN的预测值后，同样要进行反归一化和反梯度化处理，才能得到最终的燃气日负荷预测值。

3.2.1 梯度神经网络法消除误差

首先使用梯度神经网络法对原始数据进行处理，利用式（7）对原始数据进行梯度处理，得到新的数据序列，再将得到的新的数据序列进行归一化操作。

3.2.2 归一化处理

将通过梯度神经网络法得到的新数据序列进行归一化处理，利用式（3）进行归一化处理，将数据归一化到[0.1, 0.9]。归一化处理能够有效减少异常数据的波动，加快梯度−GRNN的训练。

3.2.3 平滑系数 $\sigma $ 的确定

通过试验法确定神经网络的平滑系数 $\sigma $ ，平滑系数 $\sigma $ 的选取过程与GRNN的平滑系数 $\sigma $ 的选取过程相同，最终确定平滑系数 $\sigma = 0.27$ 。

3.2.4 反归一化与反梯度化处理

在得到梯度−GRNN的预测值后，需要进行反归一化处理和反梯度化处理。利用式（4）进行反归一化处理，将得到的数值再进行反梯度化处理，相当于进行一次累加操作，最后得到的就是燃气日负荷预测值。梯度−GRNN输入节点取3个（预测日前3 d的数据和预测日前7 d的数据的一阶差分），输出节点取1个（燃气日燃气负荷的一阶差分）。预测结果见表1及图2、3。

由表1可知，梯度−GRNN在1月27日的预测精度没有像GRNN那样出现较大的误差，这同样可以证明使用GRNN进行建模在27日发生故障，才导致它在27日的预测中出现非常大的误差。在全年范围内，梯度−GRNN燃气日负荷预测的最大预测误差为18.232%，平均预测精度为85.963%。

4 基于广义动态模糊神经网络（GD-FNN）建立组合预测模型

GD-FNN的结构如图5所示。设r是输入变量数，并且每个输入变量 ${x_i}(i = 1,2, \cdots ,r)$ 有 $u$ 个隶属函数 ${A_{ij}}(j = 1,2, \cdots ,u)$ ，它们位于第2层，这些隶属函数都是如下形式的高斯函数：

${\mu _{ij}}({x_i}) = \exp \left[ { - {{{{({x_i} - {c_{ij}})}^2}}/{{\sigma ^2}_{ij}}}} \right]$

式中： ${\mu _{ij}}$ 是 ${x_i}$ 的第 $j$ 个隶属函数； ${c_{ij}}$ 和 ${\sigma _{ij}}$ 分别为 ${x_i}$ 的第 $j$ 个高斯隶属函数的中心和宽度； $i = 1,2, \cdots ,r;$ $j = 1,2, \cdots ,u$ 。

输入层中第0个节点的输入值 ${x_0}$ =1，它的作用是提供模糊后件中的常数项。第3层的每个结点代表一条模糊规则，它的作用是用来匹配模糊规则的前件，计算出每条规则的适用度^[11]：

${\varphi _j} = \mathop \prod \limits_{i = 1}^r {A_{ij}},\left( {j = 1,2, \cdots ,u} \right)$

后件网络中第2层的作用是计算每一条规则的后件，即

${w_j} = {\alpha _{0j}} + {\alpha _{1j}}{x_1} + \cdots + {\alpha _{rj}}{x_r},\left( {j = 1,2, \cdots ,u} \right)$

后件网络中的第3层计算系统的输出为

$y({x_1},{x_2}, \cdots ,{x_r}) = \mathop \sum \limits_{j = 1}^u {w_j} \cdot {\varphi _j}$

GD-FNN学习算法的基本步骤为^[12]：

1）初始化系统预定义参数 ${\varepsilon _{\min }}$ 、 ${\varepsilon _{\max }}$ 、 ${e_{\min }}$ 、 ${e_{\max }}$ 、 ${k_{{\rm{mf}}}}$ 、 ${k_s}$ 、 ${k_{{\rm{eer}}}}$ ，其含义见文献[11]。

2）由第1组样本数据产生第一条规则，其参数的确定采用误差反传法^[13]。

3）从第2组样本数据开始，每来一组样本，分别计算系统误差 ${e^k}$ 和马氏距离 $d_{\rm{m}}^k(j)$ 。

设 ${{{X}}_k}$ 是第k个输入样本向量， ${t_k}$ 是第k个期望的输出，计算当前结构下的GD-FNN输出 ${y_k}$ 。定义系统误差为

$\left\| {{e_k}} \right\| = \left\| {{t_k} - {y_k}} \right\|$

如果 $\left\| {{e_k}} \right\| > {k_e}$ ，则应该考虑增加一条新的模糊规则。这里 ${k_e}$ 是预先定义的一个阈值，它在学习过程中按以下准则逐渐变化：

${k_e} = \left\{ \begin{array}{l} {e_{\max }},\quad 1 < k < n/3\\ \max [{e_{\max }} \times {\beta ^k},{e_{\min }}],\;\quad n/3 \leqslant k \leqslant 2n/3\\ {e_{\min }},\quad 2n/3 < k \leqslant n \end{array} \right.$

式中： $k$ 是学习的次数； $\;\beta \in (0,1)$ 为收敛常数，可以很容易推导出 $\beta = {\left( {{{{e_{\min }}}/{{e_{\max }}}}} \right)^{3/n}}$ ；马氏距离：

${d^k}(j) = \sqrt {{{({{X}} - {{{C}}_j})}^{\rm{T}}}\sum\limits_{}^{} {{{_j}^{ - 1}}({{X}} - {{{C}}_j})} } $

式中： ${X} = {[{x_1},{x_2}, \cdots ,{x_r}]^{\rm{T}}} \in {\bf{R}}^r$ ； ${{{C}}_j} = {[{c_{1j}},{c_{2j}}, \cdots ,{c_{rj}}]^{\rm{T}}} \in {\bf{R}}^r$ ；同时 $\sum\nolimits_ {j}^{ - 1} $ 为 $\sum\nolimits_{j}^{ - 1} = {\rm{diag}}\left[ {{1/{{\sigma ^2}_{1j}}}{{,1}/{{\sigma ^2}_{2j}}}, \cdots ,{1/{{\sigma ^2}_{rj}}}} \right]$ , $j = 1,$ $2, \cdots ,u$ ，找到 $J = \mathop {\arg \min }\limits_{1 \leqslant j \leqslant u} ({d^k}(j))$ 。

4）如果满足 ${d^k}(j) > {k_d}$ ，应该考虑产生一条新规则。 ${k_d}$ 是一个预先设定并与 $\varepsilon $ 相关联的阈值， ${k_d}$ 在学习的过程中按式（8）变化：

${k_d} = \left\{ \begin{gathered} {d_{\max }} = \sqrt {\ln ({1/{{\varepsilon _{\min }}}})} ,\quad \quad 1 < k < {n/3} \\ \max [{d_{\max }} \times {\gamma ^k},{d_{\min }}]\;,\quad {n/3} \leqslant k \leqslant {{2n}/3} \\ {d_{\min }} = \sqrt {\ln ({1/{{\varepsilon _{\max }}}})} ,\quad \quad {{2n}/3} < k \leqslant n \end{gathered} \right.$

(8)

式中 $\gamma \in (0,1)$ 称为衰减常数，它可以由式（9）推算出来：

$\gamma = {\left( {{d_{\min }}/{d_{\max }}} \right)^{3/n}} = {\left( {\sqrt {\ln (1/{\varepsilon _{\max }})} /\sqrt {\ln (1/{\varepsilon _{\min }})} } \right)^{3/n}}$

(9)

5）若满足 ${e_k} > {k_e}$ ，则产生新规则，决定该规则的参数，计算出误差减小率 ${\rho _j}$ 和第j条规则的重要性 ${\eta _j}$ (j=1,2 $, \cdots ,$ u)^[11]，否则自动调整已存在的规则的后件参数。新规则参数的确定方法如下：

计算数据 $x_i^k$ 和边界 ${\varPhi _i}$ 之间的欧式距离：

$d_i^{\rm{e}}(j) = \left| {x_i^k - {\varPhi _i}(j)} \right|,\left( {j = 1,2, \cdots ,u + 2} \right)$

式中 ${\varPhi _i} \in \left\{ {{x_{{i_{\min }}}},{c_{{i_1}}},{c_{{i_2}}}, \cdots ,{c_{{i_u}}},{x_{{i_{\max }}}}} \right\}$ ，同时找到：

${j_n} = \arg \mathop {\min }\limits_{j = 1,2, \cdots ,u + 2} (d_i^{\rm{e}}(j))$

如果 $d_i^{\rm{e}}({j_n}) > {k_{{\rm{mf}}}}$ ，则高斯函数的中心和宽度设置如下

${c_{i(u + 1)}} = x_i^k$

${\sigma _i} = \max \{ \left| {{c_i} - {c_{i - 1}}} \right|,\left| {{c_i} - {c_{i + 1}}} \right|\} /\sqrt {\ln (1/\varepsilon )} $

式中： ${c_{i - 1}}$ 和 ${c_{i + 1}}$ 是与第 $i$ 个隶属函数临近的2个隶属函数的中心； $i = 1,2, \cdots ,u$ 。

后件参数的调整采用自适应学习律^[13]。

6）若满足 ${e^k} < ke$ ,则调整已存在规则前件参数中的宽度，再调整规则的后件参数，否则自动调整已存在的规则的后件参数。

前件参数宽度作如下调整：

$\sigma _{ij}^{{\rm{new}}} = \xi \times \sigma _{ij}^{{\rm{old}}}$

式中 $\xi \in (0,1)$ 是衰减因子，它由式（10）决定：

$\xi = \left\{ \begin{array}{l} {k_s}/{k_s} + {r^2}(1 - {k_s}){({B_{ij}} - 1/r)^2},\quad {B_{ij}} < 1/r\\ 1,\quad {B_{ij}} \geqslant 1/r \end{array} \right.$

(10)

定义

$\left\{ \begin{gathered} {B_j} = \sum\limits_{k = 2}^{r + 1} {{\rho _j}(k)} ,\quad j = 1,2, \cdots ,u \\ {B_{ij}} = {{{\rho _{ij}}}/{{B_j}}},\quad i = 1,2, \cdots ,r \end{gathered} \right.$

式中 ${\rho _{ij}}$ 是与第 $j$ 个规则中的第 $i$ 个输入变量对应的误差减少率。

7）如果满足 ${\eta _j} > {k_{{\rm{eer}}}}$ ,则删除第 $j$ 条规则，否则自动调整已有规则的后件参数。

8）判断观察是否结束，若没有，返回步骤3)，否则结束整个学习过程。

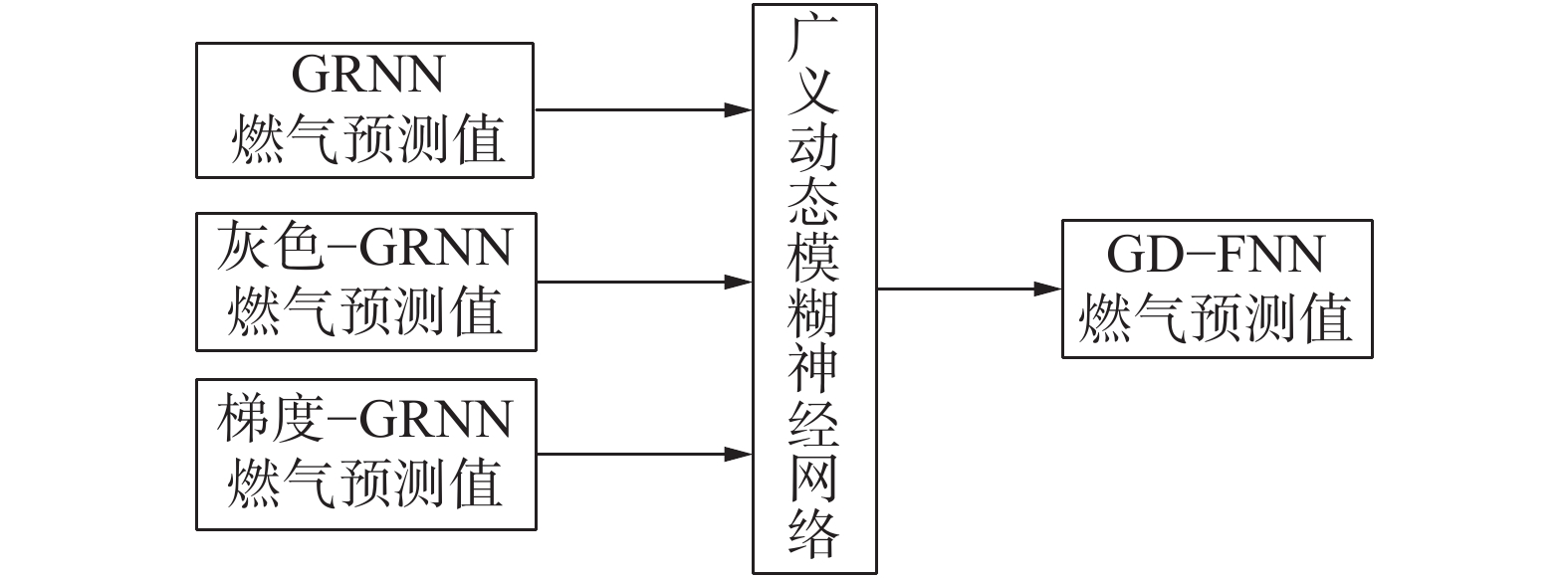
使用GD-FNN进行组合预测，首先要确定输入向量。前面已经将全年6组燃气日负荷历史数据分别作为GRNN、灰色−GRNN和梯度−GRNN的训练样本，通过各自的模型得到了相应的燃气日负荷预测值，本节分别将GRNN、灰色−GRNN、梯度−GRNN所得燃气日负荷预测值作为GD-FNN的输入向量，通过GD-FNN进行组合预测。GD-FNN预测流程如图6所示。

经过反复试验，最终确定GD-FNN^[14]初始化参数为ε_min=0.5，ε_max=0.8，e_min=0.009，e_max=0.02，k_mf=0.015，k_s=0.9，k_eer=0.001。基于GD-FNN模型进行燃气日负荷预测结果见表1及图2、3。

预测结果表明，GD-FNN在1月27日的相对误差为7.028%，与前面的GRNN相比有明显提高，同样可以证明GRNN在1月27日的预测过程中发生了故障，并且通过GD-FNN组合预测模型的预测，1月27日的预测精度也要高于灰色−GRNN和梯度−GRNN。全年预测值相对误差及平均精度如表2所示。在全年范围内，GD-FNN组合预测方法的最大预测误差为9.619%，平均预测精度为93.637%，预测平均使用时间为7.668 s。

可以看出，在预测精度方面，GD-FNN组合预测模型的预测精度明显要高于GRNN、灰色−GRNN和梯度−GRNN的预测模型精度，而且GD-FNN所用的预测时间也较短，综上，采用GD-FNN进行燃气日负荷预测效果最佳。

5 结论

设计了一种短期燃气日负荷的智能组合预测方法，将燃气日负荷一年的历史数据分为6组分别建立预测模型，利用模型切换预测城市燃气日负荷值。

1）由于广义回归神经网络具有良好的非线性逼近功能。所以，分别采用GRNN、灰色−GRNN和梯度−GRNN对燃气日负荷数据进行预测，仿真表明，预测模型总体上可行，但预测精度并不是很高，而且无法处理预测过程中出现的预测模型故障现象。因此，采用组合预测模型对燃气日负荷进行进一步的预测。

2）针对城市燃气日负荷预测的随机性和不确定性，采用广义动态模糊神经网络（GD-FNN）进行组合预测，将GRNN、灰色−GRNN和梯度−GRNN的预测数据作为组合预测模型的数据基础，通过MATLAB平台仿真，结果表明：从预测精度上看，组合预测模型的预测精度要明显高于单一预测模型的预测精度，预测时间也在合理范围内，并且能解决单一预测模型发生故障情况。