非能动安全壳冷却技术(passive containment cooling system, PCCS)主要依靠水膜的蒸发换热以及逆流空气的自然对流等共同作用,将反应堆在发生事故过程中产生的热量排出到环境中。为了保证安全壳有足够的冷却能力,需要对水膜在逆向空气剪切力作用下的降膜流动规律有比较深刻的认识,进而为CAP1400的PCCS系统设计提供理论支撑。
由于PCCS结构为尺寸较大的双层圆柱罐体,因此可简化为大尺度矩形通道。众多学者采用实验[1-3]和数值[4-5]方法研究矩形通道内的降膜流动特性,包括降膜厚度、降膜覆盖宽度、降膜表面波形态、降膜表面波波速以及降膜流动的演变过程。但是在这些研究中,主要考虑水膜的流动,而忽略了空气和液膜相界面的剪切力。Huang等[6]指出在较大速度的逆向空气气流作用下,降膜流动会受到破坏,出现液滴夹带的现象。为克服试验研究中仅能获取局部位置的液膜参数信息,采用数值模拟手段来解决。但是在模拟过程中,水膜通常被假定为定常层流流动,忽略其表面波动。目前普遍认为即使再小的液膜雷诺数,也会发生波动,暂时没有波动出现可能是由于在降膜流动中平板倾角过小,或者研究中的流动距离过短等原因造成的[7]。田瑞峰等[8]在对水膜表面进行受力分析的基础上,建立二维板壁水膜波动流动模型,并讨论了液膜入口扰动频率以及扰动振幅对降膜波动情况的影响。黄磊等[9]在研究板式海水淡化降膜吸收装置时,建立三维平板降膜流动数值模型,考虑了气液剪切力作用;但是他们研究的计算域尺寸较小,尤其在降膜流动方向上。就现有相关研究工作而言,降膜流动方向上的长度最多为厚度方向的200倍[4]。卢涛等[10]研究表明在降膜流动过程中,同一高度处的液膜厚度差别不大。另外,在实际PCCS系统内,水膜流量随着重力水箱液位的下降而不断减小,在钢制安全壳壁面上形成的水膜厚度也逐渐减薄,水膜厚度占整个通道高度尺寸的比例是变化的。
因此,在文献[10-11]基础上,考虑空气和液膜相界面剪切力,建立二维单侧矩形通道降膜流动的数值模型,其中入口水膜宽度也被当作水膜在入口位置的厚度。为使降膜流动充分发展,同时尽量减少计算域中划分的网格数量,需先将PCCS环形通道的实际高度进行缩小;接着采用固定通道高度而改变液膜入口宽度的办法,分析通道高度对水膜厚度沿流动方向变化的影响。此外,还考察不同边界条件(液膜入口速度分布、液膜入口雷诺数、空气入口速度以及空气流动方向等)对液膜形态以及液膜平均厚度变化的影响,为进一步分析PCCS系统降膜蒸发传热传质特性提供基础。
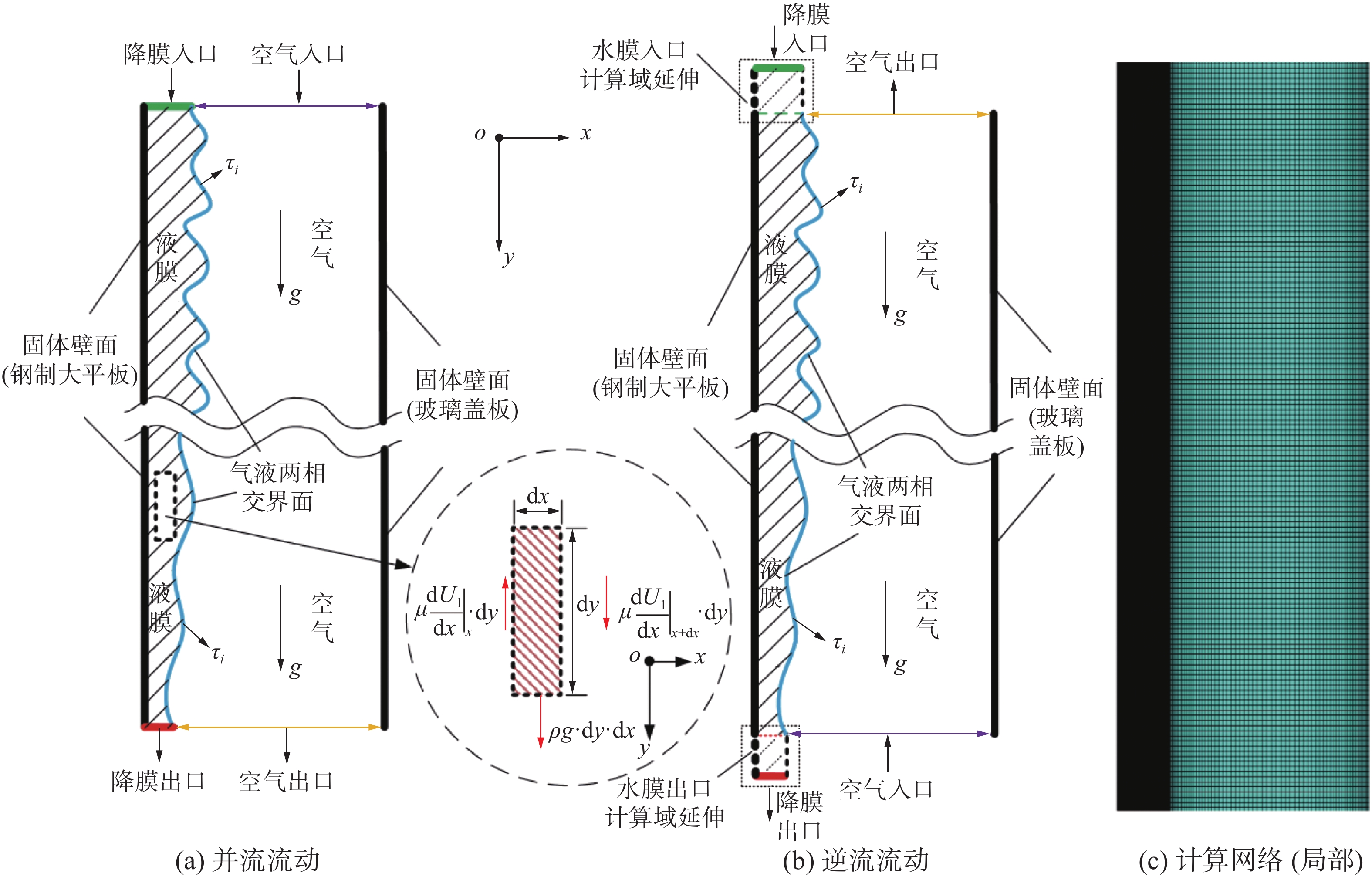
1 模型及求解方法 1.1 物理对象描述如图1所示,PCCS流道被简化成一个高度为25 mm(x轴,即降膜厚度),长度为800 mm(y轴)的二维矩形通道,流动介质为水和空气。水膜在重力作用下始终沿固体壁面(钢制大平板)由上而下形成降膜流动,而空气则以一定的速度从入口位置进入计算域,跟水膜形成并流(图1(a))和逆流(图1(b))2种情形。水膜和空气的相交界面将整个通道的高度分成2部分,采用3个不同的水膜入口宽度(分别为1、3、5 mm),以研究水膜入口宽度对降膜流动行为的影响。
|
Download:
|
| 图 1 物理模型及数值计算网格 | |
液膜和空气的进口设置为速度入口;液膜和空气的出口设置为压力出口;左侧接触水膜的钢制大平板设置为无滑移壁面,接触角为45°;而右侧玻璃盖板也设置为无滑移壁面,接触角为90°。空气的入口指定为均匀速度,而液膜的入口有均匀入口、准对数分布、对数分布3种方式,如图2所示。其中图2(b)、(c)的边界条件通过Fluent用户自定义函数(UDF)实现。整个计算域的初始速度为0,只有紧贴钢制大平板壁面的一薄层区域设置为水膜,该薄层厚度可由式(1)确定,其余部分均为空气:
| $ \delta = {(0.75)^{{1 / 3}}}{({{{\nu ^2}} / g})^{{1 / 3}}}R{e^{{1 / 3}}} $ | (1) |
式中:δ为平均液膜厚度;ν为液膜的运动黏度;g 为重力加速度;Re为液膜雷诺数,满足Re=4Γ/μ;μ为液膜的动力黏度;Γ为水膜入口质量流量,kg/(m·s−1),满足Γ=

|
Download:
|
| 图 2 液膜入口速度分布示意 | |
另外,本文中液膜雷诺数和空气流速等参数范围主要依据文献[12]进行选取。
1.2 数值求解采用计算流体力学软件Fluent15.0研究空气剪切力作用下垂直钢板表面水膜流动行为。其中空气和水膜两相界面通过几何重构两相流模型——流体体积函数(volume of fluid,VOF)捕捉,同时耦合连续表面张力(continuum surface force,CSF)模型求解表面张力;湍流模型选择可实现的k-ε模型,并采用增强近壁面处理方法。气液界面剪切力τi根据式(2)确定,通过UDF实现:
| $ {\tau _i}{\rm{ = }}0.5f{\rho _{\rm{g}}}u_{\rm{g}}^2 $ | (2) |
式中:
| $ f = 0.005(1 + 300{\delta / {{D_h}}}) $ |
| $ f{\rm{ = }}0.079R{e_{\rm{g}}}^{ - 0.25}\left[ {1 + 115{{\left( {{\delta ^*}} \right)}^N}} \right] $ |
式中:δ*=δ/LL;N=3.95/[1.8+3(LL/Dh)];LL=[(ρl−ρg)g/σ]−0.5;σ为气液两相之间的表面张力系数;Dh为水力直径。
选取液膜内一微元体(如图1),进行受力分析,可推导出:
| $ {U_{\rm{l}}} = \frac{{g{\delta ^2}}}{\nu }\left[ {\frac{x}{\delta } - \frac{1}{2}{{\left( {\frac{x}{\delta }} \right)}^2}} \right] + \frac{{{\tau _{\rm{i}}}}}{\mu }x $ | (3) |
利用
采用基于压力的瞬态求解器,为提高解的收敛性,开启隐式体积力选项。时间项采用一阶隐式格式,动量和湍流项采用二阶迎风离散,压力项采用PRESTO算法,压力和速度的耦合方式选择PISO方法。质量、动量及湍流等控制方程迭代残差的收敛标准设为10−4。时间步长设为10−4 s,总模拟时间为1.0 s。当空气和水膜逆流流动时,为了防止水膜直接从气相出口流出,对计算域中水膜入口和出口位置进行延伸,延长的长度均为100 mm,同时计算过程改为稳态计算。
由于降膜流动瞬态发展过程中的平均液膜厚度是一个非常关键的参数,该参数决定了降膜流动传热传质的阻力。因此,本文主要对流动稳定阶段的液膜厚度进行统计,具体按下式进行计算
| $ \overline \delta {\rm{ = }}\frac{1}{n}\sum\limits_{i{\rm{ = }}1}^n {{\delta _i}} $ | (4) |
式中n为流动稳定区域沿流动方向的网格节点总数。
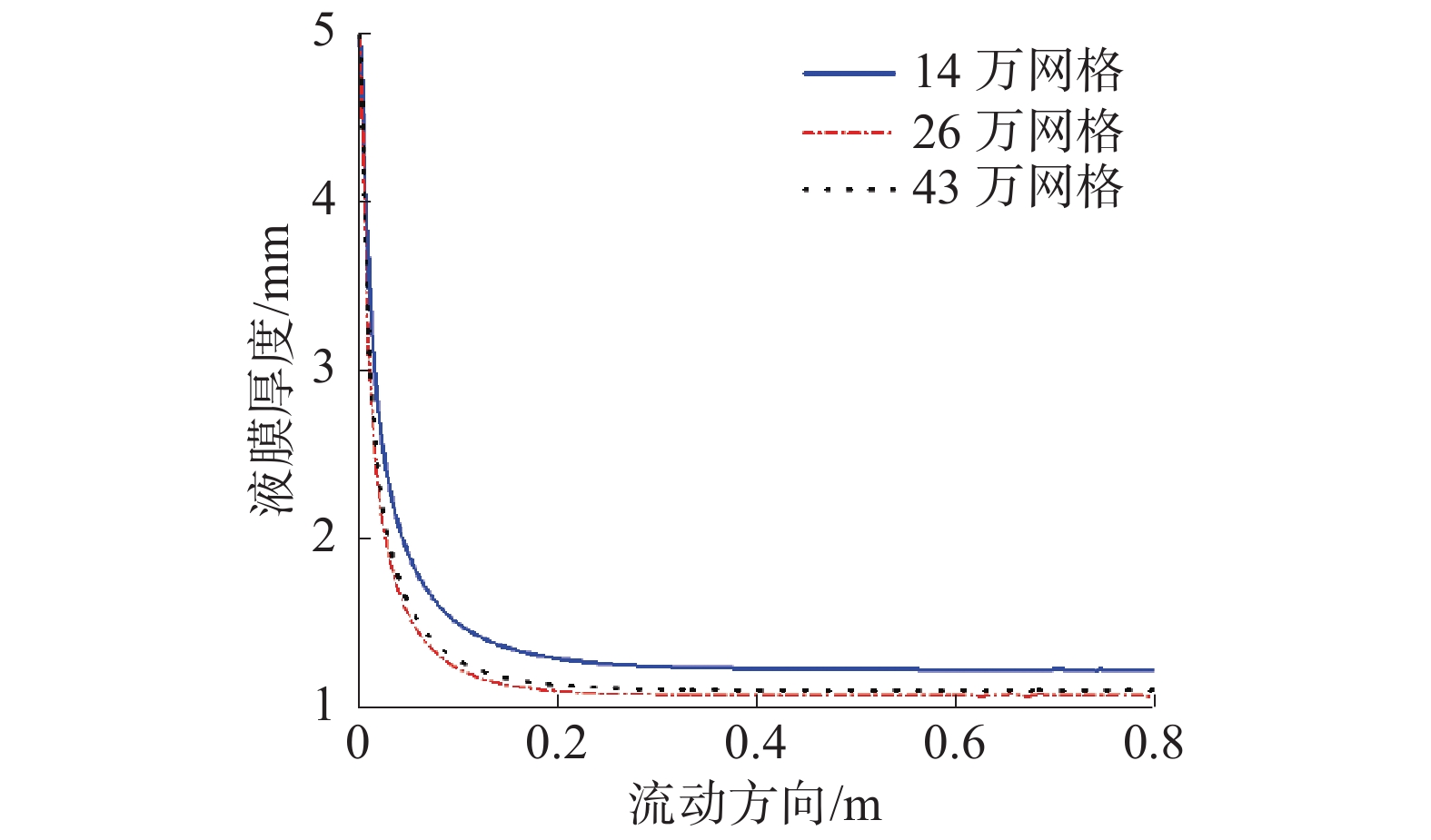
1.3 网格无关性分析及数值模型验证采用分区划分网格的方法,对液膜区域进行加密,选择结构化网格,如图1(c)所示,网格在x方向上的分布是不均匀的,尤其是靠近气液相交界面以及壁面的地方,网格较密集。使用3种不同数量网格,最小网格尺寸分别为0.05、0.1、0.2 mm(对应网格总数量为43万、26万、14万),以液膜雷诺数Rel=300(均匀入口速度)、空气雷诺数Reg=0、液膜入口宽度为5 mm的工况进行网格无关性分析。提取网格单元中液体体积份额等于0.5时所对应的x坐标值作为液膜厚度。从图3看出,当网格总数为26万和43万时,水膜厚度随流动方向的变化趋势是一致的,即沿着降膜流动方向,液膜厚度越来越小,最大偏差不超过4%。因此,为节约计算成本,本文选择网格总数量为26万的模型进行模拟。
|
Download:
|
| 图 3 网格无关性分析 | |
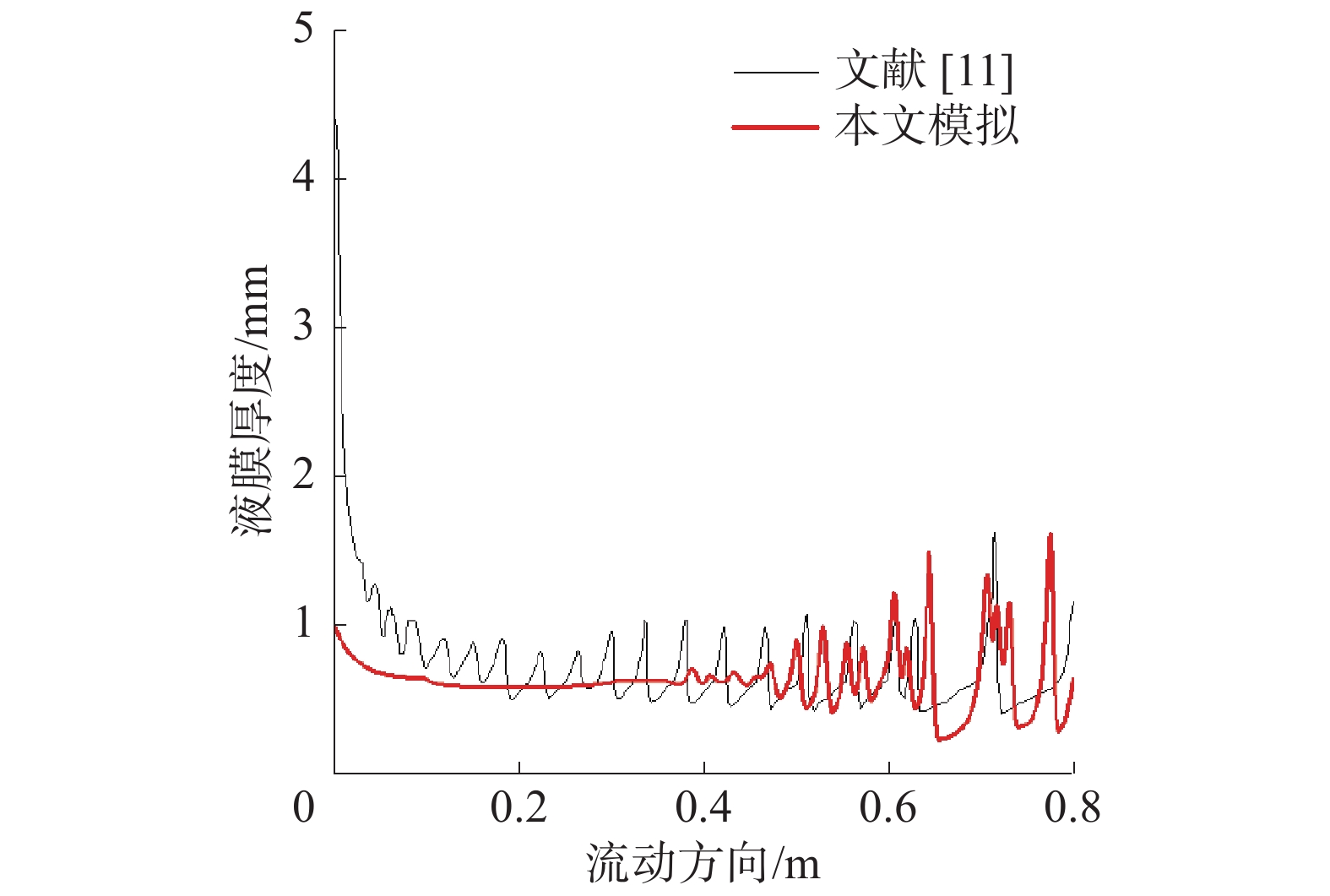
为验证该数值模型有效性,选择文献[11]中的工况进行比较,主要参数为:Rel=750(均匀入口速度)、Reg=0、入口宽度为1 mm。从图4看出,本文所计算的液膜厚度沿流动方向的变化趋势跟文献预测结果是比较吻合的,当流动距离超过0.5 m后,降膜的波动频率和波动幅值都很接近,该段流动距离内液膜平均厚度的最大偏差不超过8%。由此可见,本文所建的数值模型是合理的。
|
Download:
|
| 图 4 数值模型验证 | |
图5为3种不同入口速度分布条件下钢板表面水膜厚度沿流动方向的变化情况,其中水膜入口宽度5 mm,空气雷诺数为0,液膜雷诺数分别为300、900、1 500、2 700。

|
Download:
|
| 图 5 入口速度分布对液膜厚度沿流动方向变化的影响 | |
从图5(a)~(d)看出,当计算时间为0.25 s时,液膜在均匀分布条件下流动最慢,而在对数分布条件下流动最快;而当计算时间为1.0 s时,液膜厚度沿流动方向的变化趋势处于稳定,并且在均匀和准对数2种分布条件下液膜厚度的变化规律是重合的,液膜厚度均小于对数速度分布条件下的数值。这主要与液膜入口质量流量有关。从图2可知,在均匀分布和准对数分布条件下,液膜入口质量流量是相等的,并且小于对数分布条件下的值。另外,当液膜入口雷诺数在300~1 500递增时,准对数分布和均匀分布条件下液膜y方向流动速度差值在不断减少,甚至超过液膜在对数分布条件下y向的流动速度,如图5(c)所示。这是由于液膜产生较明显的x方向的流动速度,引起表面波动增强,进而使y向的流动速度减小。如果液膜雷诺数继续增大,将产生如图5(d)中所示的液膜“托举”现象,导致大部分液膜脱离钢板壁面而沿对侧玻璃壁面流动。尹涌澜[15]认为液膜在重力作用下聚集使其前段速度大于下部的气相速度,导致液膜产生偏转。
此外,在相同的液膜入口宽度条件下,入口速度分布的影响作用可能被放大,因为还受到液膜入口质量流量的影响。从图2可知,需增大均匀和准对数分布中液膜入口宽度方向上的液膜入口速度,或者减小对数分布中液膜入口宽度方向上的液膜入口速度,从而保证均匀、准对数以及对数分布这3个工况具有相同的液膜入口质量流量,这样也就更能评估入口速度分布的影响。图5(e)和(f)中均匀和准对数分布算例增加了液膜入口宽度方向上的液膜入口速度,从而保证图5(e)和(f)中的均匀、准对数和对数分布中液膜具有相同的入口质量流量,都等于图5(a)中对数分布工况下的值。分析图5(e)、(f)中数据可知,对数分布和均匀分布对平均液膜厚度产生的影响在8%以内,要小于图5(a)中对数和均匀分布的影响(约22%);而图5(e)、(f)和图5(a)中准对数分布和均匀分布对平均液膜厚度产生的影响均小于1%。另外,在图5(c)看到,当液膜雷诺数增大到1 500时,准对数分布和均匀分布对平均液膜厚度产生的影响将变大(接近5%)。我们比较液膜波动出现的位置、频率以及产生的波幅,发现液膜波动现象在准对数分布条件下比在均匀条件下明显。
综上所述,速度分布对液膜厚度变化规律的影响主要是通过液膜入口质量流量变化来反映。如果液膜入口宽度越小,越接近经典的Nusselt值,那么速度分布对液膜厚度变化规律的影响可忽略不计。
2.2 液膜入口宽度的影响图6为3种不同水膜入口宽度(1、3、5 mm)下水膜厚度沿流动方向的变化情况,其中液膜和空气的雷诺数分别为300和0,水膜入口速度为准对数分布。当降膜流动时间为0.25 s时,液膜沿y方向的流动速度随液膜入口宽度的减小而增加,而最大液膜厚度却随入口宽度的增加而增加。可见,液膜在较小的入口宽度下主要表现出沿通道长度方向上的铺展流动,此时,对应的液膜厚度较薄,所受黏性力作用较弱。随着液膜入口宽度的增加,液膜在x方向的堆积作用增强,导致液膜明显增厚,所受的黏性力也逐渐增加。因此,当流动时间增至1.0 s时,流动已处于稳定,液膜表面在入口宽度为3、5 mm时比较平坦,而在1 mm时则呈现出波动。另外,根据式(4),很容易得到跟文献[10]相同的结论,即液膜平均厚度随入口宽度增大而增大。

|
Download:
|
| 图 6 液膜入口宽度对液膜厚度沿流动方向变化的影响 | |
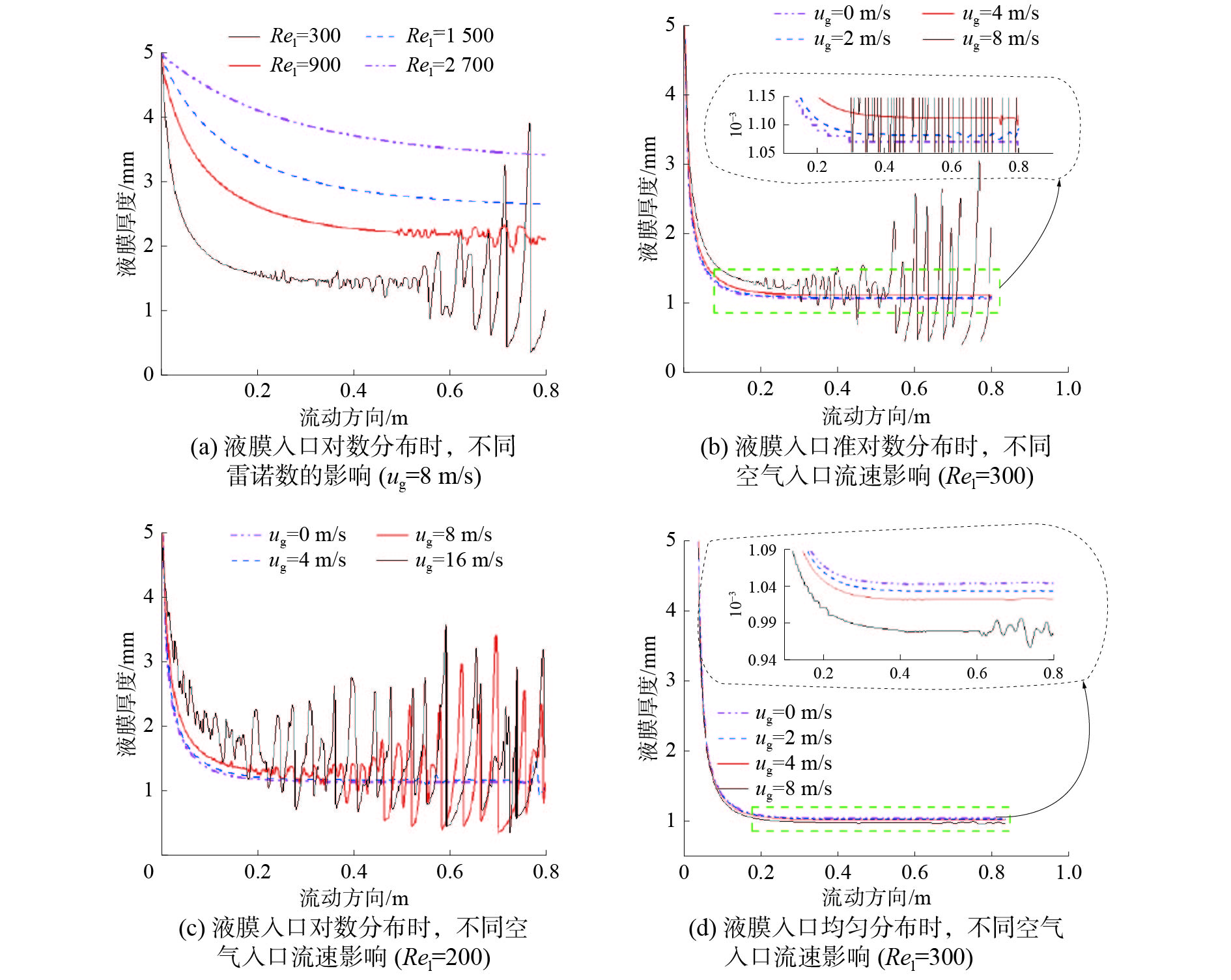
设计4组空气和水膜并流流动计算工况,关键参数见表1,相应的计算结果如图7所示。
|
|
表 1 数值计算工况关键参数 |
|
Download:
|
| 图 7 空气入口流速及液膜入口雷诺数对液膜厚度沿流动方向变化曲线(液膜入口宽度5 mm) | |
图7(a)主要描述了液膜入口雷诺数的影响,从该图可知,在液膜入口宽度为5 mm,并流空气流速为8 m/s时,随着液膜入口雷诺数的增加,液膜平均厚度在不断增加,这与自由降膜流动条件下(图5)得到的结论是一致的。但也有不同的地方,特别是液膜表面的波动情况。在自由降膜流动条件下,液膜表面波动表现出随液膜入口质量流量增加而增强的状态;然而,在较大的空气剪切力作用下,随液膜雷诺数增加,液膜表面的波动是逐渐减弱的,甚至消失。这是因为当空气入口流速固定不变时,液膜表面的流动速度随液膜入口质量流量的增加而增加,从而导致了气液两相之间的速度差减小,因此,在较高的液膜雷诺数下,液膜表面波动不断减弱。
图7(b)~(d)主要展示了空气入口流速的影响,从图7(b)、(c)中均能看出,液膜表面波动随着空气入口流速的增加而显著增强,这与空气和水膜两相之间的速度差有关。然而,平均液膜厚度随气流速度增加而增加,这与卢涛等[10]得出液膜平均厚度随气流速度增加而减薄的结论相悖,主要是由边界条件不同所引起的。据式(3)可推知,图7(b)、(c)中的液膜质量流量是在文献[10]的基础上叠加了气液波动界面剪切力作用而引起液膜质量流量变化。另外,图7(d)中的结果是在保证液膜入口总的质量流量不变的条件下得出的,相当于仅考虑式(3)右边第一项的影响。从图7(d)中也恰好发现液膜平均厚度随气流速度增加而减小。因此,当ug增大时,首先,根据式(2)计算,τi会逐渐增大;接着,由式(3)计算Ul的平均值也会增加。在相同的液膜入口宽度条件下,总的液膜质量流量增加,所以,图7(b)、(c)中液膜平均厚度随气流增加而变大。但是Ul的增加值相对于ug而言是比较小的。那么,两相间的速度差就会随空气流速的增大而增大,液膜的波动现象就会变得强烈。在图7(d)中也发现液膜波动随空气流速的增大而增大,但波动幅度明显小于图7(b)、(c)。
此外,由于液膜表面流动速度随液膜入口雷诺数的减少而减慢,当液膜雷诺数减少至200时,液膜在1.0 s 还没抵达通道出口位置,所以实际计算的流动时间取2.0 s。
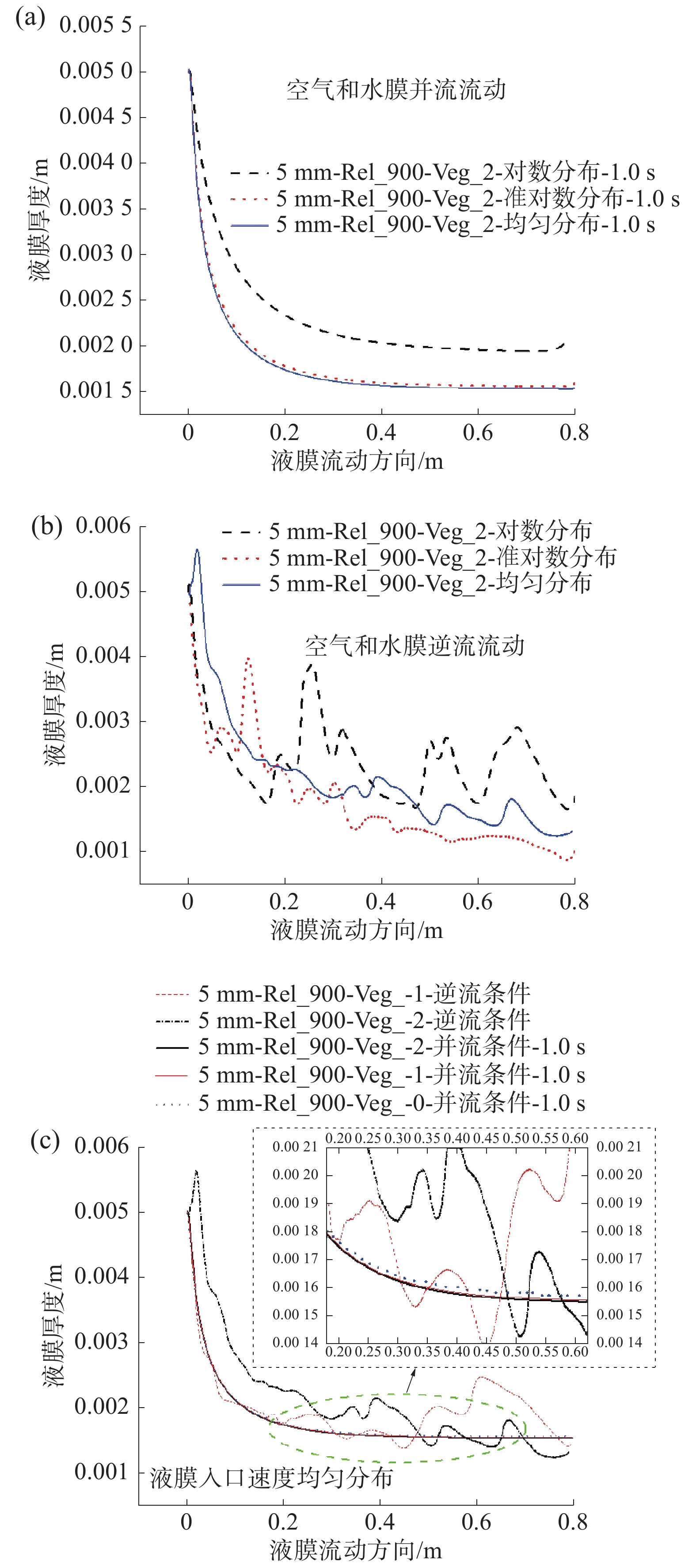
2.4 气体流动方向的影响图8为液膜入口宽度为5 mm,雷诺数为900,空气入口速度分别为0、1、2 m/s 时,气体流动方向对液膜厚度沿流动方向变化的影响。由图8可知,空气流动方向对液膜厚度沿流动方向的变化影响较大,即在逆流条件下,液膜表面处于波动状态,并且平均液膜厚度要比并流条件下的大。这种影响在较大的逆向空气流速条件下会更加明显。因为剪切力τi与气流速度ug2相关,且随气流速度增加而增加,它迫使液膜在逆流条件下做减速运动,而在并流条件下做加速运动。另外,在图8(a)中得到和图5(b)相同的结果,即并流液膜厚度在对数分布条件下要比准对数分布以及均匀分布条件下的大。但是在逆流情况下,如图8(b)所示,对数分布条件下液膜平均厚度跟准对数条件下的差值在逐渐减少,准对数条件下的液膜平均厚度比均匀条件下的小,主要原因是剪切力τi在逆流条件下为负值。
|
Download:
|
| 图 8 空气流动方向对液膜厚度沿流动方向变化的影响 | |
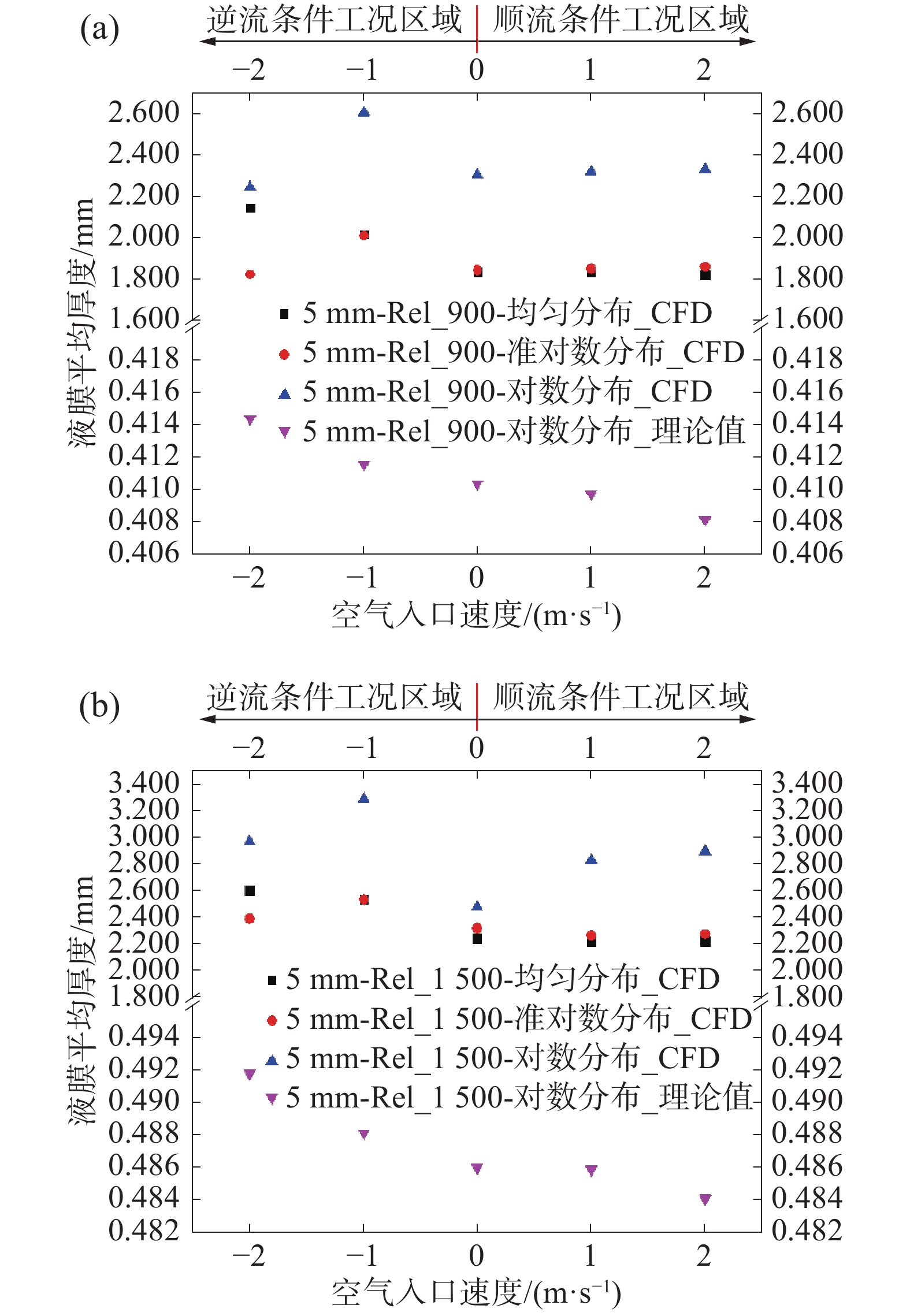
图9为平均液膜厚度在液膜入口宽度为5 mm、雷诺数为900和1 500时随气流速度的变化,从图9中看出,不同入口条件下液膜平均厚度随入口空气流速的变化趋势是完全相同的,并且液膜雷诺数较大时,液膜的平均厚度也会越大。另外,还给出理论预测值(基于Nusselt液膜平均厚度,详细推导方法参见文献[12]),结果表明理论预测值和CFD计算结果的变化趋势相同,但理论预测值明显小于CFD计算值。
|
Download:
|
| 图 9 不同空气流速条件下平均液膜厚度的变化 | |
主要原因是Nusselt是基于层流条件而提出的,在大流量下这种平均液膜厚度假设会形成越来越大的偏差[9]。此外,还发现当液膜入口雷诺数和逆向气流速度较大时,液膜平均厚度在对数分布条件下随气流速度的变化也越大,主要原因与气液界面剪切力的大小和方向相关。
3 结论本文对二维矩形通道内不同的初边值条件下降膜流动行为进行了数值研究,主要分析了相应条件下液膜厚度沿流动方向的变化趋势,得到以下结论:
1)速度分布对液膜厚度沿流动方向的影响主要是通过液膜入口质量流量变化来反映的。对于瞬态流动模拟来说,可用入口准对数速度分布来减少常规均匀分布中流动发展所需的模拟时间。当入口质量流量比较小时,速度分布的影响可以忽略。随着液膜入口流量增加,准对数分布条件下的液膜波动现象比均匀分布条件下显著。
2)液膜在较大的入口宽度下呈现出向壁面法向上的堆积,使液膜增厚,所受黏性力增大;而在较小的入口宽度下表现出沿通道长度方向上的铺展流动,液膜减薄,流速加快,导致液面波动增强。
3)在空气和水膜并流流动条件下,液膜表面波动现象跟气液两相间的速度差有关,两相间速度差越大,液膜表面波动越剧烈。在液膜入口速度分布为对数分布和准对数分布条件下,气液波动界面剪切力作用引起液膜入口质量流量的增加对平均液膜厚度的影响较大。
4)气体流动方向对液膜厚度沿流动方向的变化趋势影响较大。在并流条件下,重力和界面剪切力合力大于壁面黏性力,导致液膜做加速运动,液膜减薄;而在逆流条件下,壁面黏性力和界面剪切力的合力大于重力,导致液膜做减速运动,液膜增厚。
| [1] |
韦胜杰, 宋建, 胡珀, 等. 竖壁冷态降液膜流动统计特性实验研究[J]. 原子能科学技术, 2012, 46(6): 674-678. ( 0) 0)
|
| [2] |
宋建, 胡珀, 韦胜杰, 等. 竖直平板降水膜表面波波动特性实验研究[J]. 原子能科学技术, 2012, 46(6): 679-683. ( 0) 0)
|
| [3] |
袁猛, 胡剑光, 陈剑佩, 等. 微结构壁面降膜波动的统计特性[J]. 华东理工大学学报(自然科学版), 2012, 38(3): 293-300. ( 0) 0)
|
| [4] |
于意奇, 杨燕华, 程旭, 等. 降膜流动行为的数值模拟研究[J]. 原子能科学技术, 2012, 46(10): 1207-1211. ( 0) 0)
|
| [5] |
潘新新, 宋春景, 邱健. 水分配围堰的水膜流动特性数值模拟[J]. 核科学与工程, 2016, 36(4): 482-486. DOI:10.3969/j.issn.0258-0918.2016.04.007 ( 0) 0)
|
| [6] |
HUANG X G, YANG Y H, HU P, et al. Experimental study of water–air countercurrent flow characteristics in large scale rectangular channel[J]. Annals of nuclear energy, 2014, 69: 125-133. DOI:10.1016/j.anucene.2014.02.005 ( 0) 0)
|
| [7] |
石玉琦. 降膜吸收传热传质理论与实验研究[D]. 杭州: 浙江大学, 2018.
( 0) 0)
|
| [8] |
田瑞峰, 李兆俊, 张庆武. 板壁水膜波动流动数值研究[J]. 核动力工程, 2006, 27(5): 29-32. DOI:10.3969/j.issn.0258-0926.2006.05.006 ( 0) 0)
|
| [9] |
黄磊, 李明春, 陈冬, 等. 降膜流动及膜破裂特性的三维数值模拟[J]. 能源工程, 2015(2): 13-20. DOI:10.3969/j.issn.1004-3950.2015.02.003 ( 0) 0)
|
| [10] |
卢涛, 张蔷. 非能动安全壳竖直平板降膜流动特性数值模拟[J]. 热科学与技术, 2016, 15(5): 345-351. ( 0) 0)
|
| [11] |
赵婵. 垂直降液膜的流体力学研究[D]. 天津: 天津大学, 2014.
( 0) 0)
|
| [12] |
于意奇. 大尺度平板水膜流动行为的数值模拟和试验研究[D]. 上海: 上海交通大学, 2012.
( 0) 0)
|
| [13] |
WALLIS G B. One-dimensional two-phase flow[M]. New York: McGraw-Hill, 1969.
( 0) 0)
|
| [14] |
STEPHAN M, MAYINGER F. Experimental and analytical study of countercurrent flow limitation in vertical gas/liquid flows[J]. Chemical engineering & technology, 1992, 15(1): 51-62. ( 0) 0)
|
| [15] |
尹涌澜. 沉降膜换热器基础研究及其复合源热泵系统应用分析[D]. 长春: 吉林大学, 2012.
( 0) 0)
|
 2020, Vol. 47
2020, Vol. 47


