目前，人们对于经典的通信方式如二进制相移键控(binary phase shift keying, BPSK)、正交相移键控(quadrature phase shift keying, QPSK)、正交频分复(orthogonal frequency division multiplexing, OFDM）、正交振幅调制(quadrature amplitude modulation, QAM)等都有了深入的研究，这些通信方式本身不具有隐匿信息的能力，需靠码加密技术来保证通信安全。由于混沌信号并非随机却貌似随机，具有非周期性、连续宽带频谱、类噪声的特性，具有异常复杂的运动轨迹和不可预测性，使它具有天然的隐蔽性，适合作为保密通信的载体^[1]。现阶段，已经构造出较多的混沌通信系统，如混沌掩蔽、混沌键控、混沌调制、混沌密码系统等，这些通信系统的研究均取得了较多的成果。文献[2]提出了一种使用Duffing振子提取混沌掩盖的正弦信号的方法；文献[3]提出了一种无信号间干扰的相关延迟−差分混沌键控(correlation delay-differential chaos shift keying, CD-DCSK)通信方案，传输速率有所提升；文献[4]给出了新的全局混沌同步通用准则及其理论证明，研究了一种基于混沌掩蔽的高幅信息信号传输的安全通信方法。目前FPGA技术在电子通信领域得到了越来越广泛的应用，并已逐渐成为电子产品实现的首选方案。现阶段，已有一些使用FPGA实现混沌通信系统的研究：文献[5]介绍了一种基于新型三涡卷混沌吸引子的混沌发生器的实时FPGA实现方法；文献[6-7]使用FPGA完成了一个混沌通信系统；文献[8]提出了一种直接使用Verilog硬件描述语言和四阶Runge-Kutta算法在FPGA上实现Duffing振荡器的有效方法；文献[9]提出一种基于该超混沌系统非线性同步的混沌掩盖保密视频通信方案，并使用FPGA实现出来。但是，混沌通信系统仍有一些亟待解决的问题，如混沌同步的制约，实际系统误码率性能不高，传输速度不高，且混沌通信系统关于硬件实现的研究较少、大部分研究停留在理论研究软件仿真方面。本文借鉴文献[10]中使用混沌Duffing振子振列检测常规信号的方法，提出了一种基于FPGA硬件平台的使用Duffing阵列接收四进制混沌信号的可实行方案。该方案检测的是Duffing振子产生的混沌信号，信号较为安全；且传递的信息为四进制信号，一定程度上提升了传输效率；解调时，使用Duffing阵列检测信号，采取的是非相干解调，回避了混沌同步的难题，提高了检测性能。

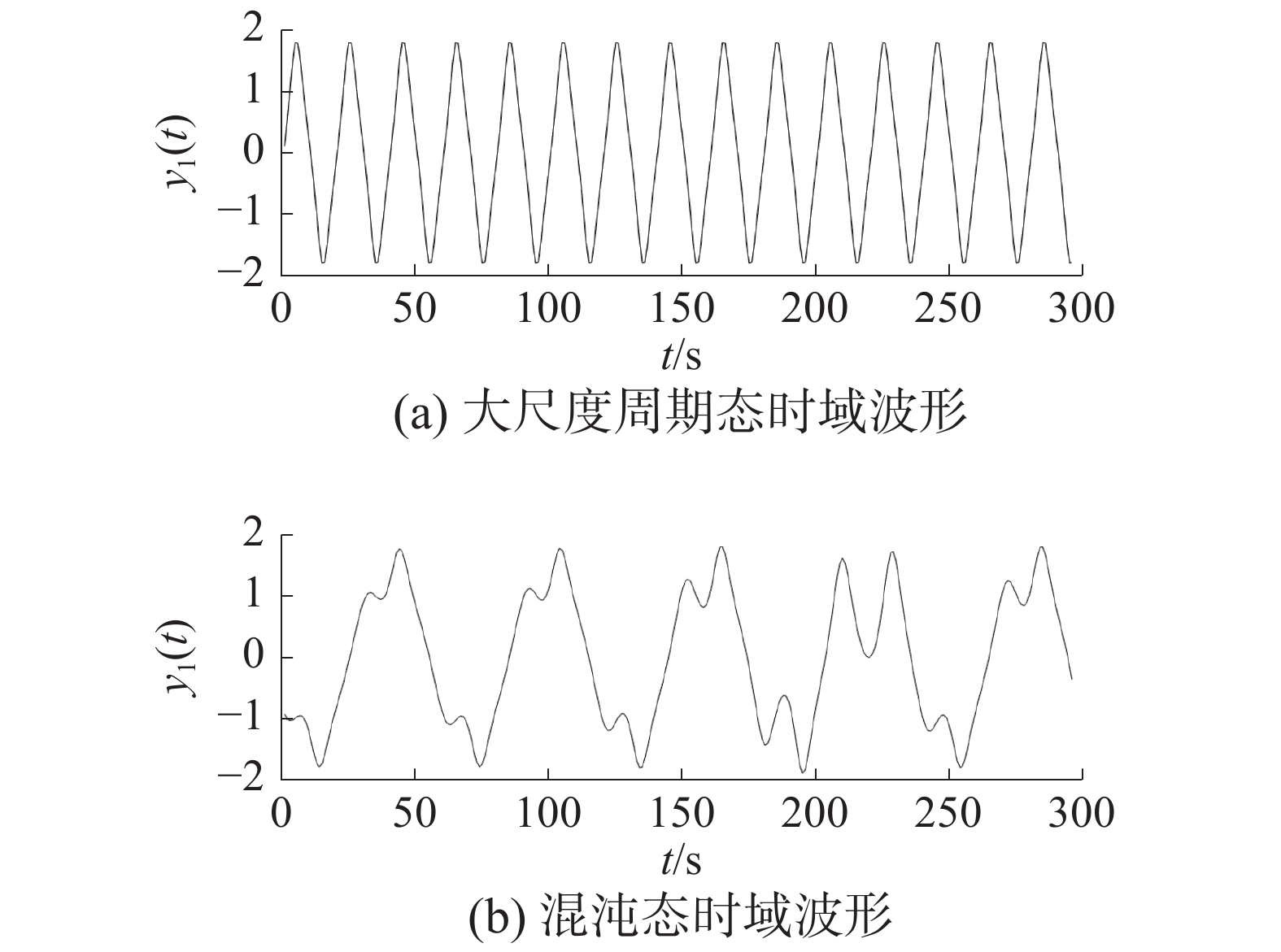
1 四进制混沌信号调制原理

因为混沌Duffing振子不同状态时对应的时域信号之间存在着明显且稳定的差异，本文运用了映射的原理，来进行信号的传递。当基带信号为1时，使Duffing振子处于大尺度周期态，其时域信号为正弦信号，其频率与Duffing振子内部驱动力频率相同；当基带信号为0时，Duffing振子处于混沌态，其时域信号为不规则类噪声信号，幅度略小于大尺度周期态的时域信号。具体如图1所示。

因此可以利用Duffing振子时域信号的差异，进行混沌信号的调制。由此可得，四进制混沌调制的具体流程如图2所示。

如图2所示，先对基带码元信号进行串并转换，将信号转换为2路并行的码元分别控制2个Duffing振子，对2路信号分别进行混沌映射。进行混沌映射的信号再经过QAM调制后即可得到混沌调制信号。本次设计中使用的Dudding振子的内部驱动力频率为0.9 MHz，进行QAM混沌调制后的信号如图3所示。

2 四进制混沌接收机的系统设计 2.1 下变频模块

经过接收到的射频信号需要进行下变频后方可以进行后续的处理。在本方案中使用射频前端对信号进行下变频及滤波处理，设计中制作射频前端的核心芯片为AD831。AD831由混频器、限幅放大器、低噪声输出放大器和偏置电路等组成，主要用于接收机中射频到中频的频率转换等场合。具体的硬件连接图如图4所示。

图4中右侧为±5 V的供电模块；左边为AD831模块，天线是用来接收射频信号，本振由信号发生器供给，进行混频后的信号经过AD831中自带的滤波器可得到下变频后的信号。在本设计中，射频调制的频率为100 MHz，所以信号发生器给出的本振信号也为100 MHz，经过下变频的信号即为中心频率为3 MHz的混沌调制信号，然后送入到FPGA开发板中进行后续处理。

2.2 四进制混沌接收机的FPGA设计

经过射频前端下变频并放大的信号将会直接送入到FPGA开发板中进行后续的处理。在FPGA中实现混沌接收机的功能主要需要A/D转换、正交解调、基带信号检测、并串转换及抽样判决等模块。具体流程如5所示。

本设计所采用的开发板为Altera公司提供的Stratix ii-EP2S180，其板上具有丰富的资源，使用的软件环境为Quartus ii 13.0。开发板实物如图6所示。

经过下变频的信号要经过模数转换后再进行后续处理，本方案中使用的是Stratix ii-EP2S180开发板中自带的AD9433模块进行模数转换处理。AD9433是一种12位单片采样的A/D转换器，本方案中使用的采样速率为18 MHz。因为进行下变频的信号仍然携带有载波分量，所以需要进行正交解调，这里使用的是常规的Costas环进行正交解调^[11]。经过正交解调的信号需要经过梳状滤波器恢复出采样率为9 MHz的混沌信号，经过一个中心频率为0.9 MHz，带宽为0.4 MHz的FIR滤波器后进行后续的基带信号检测。

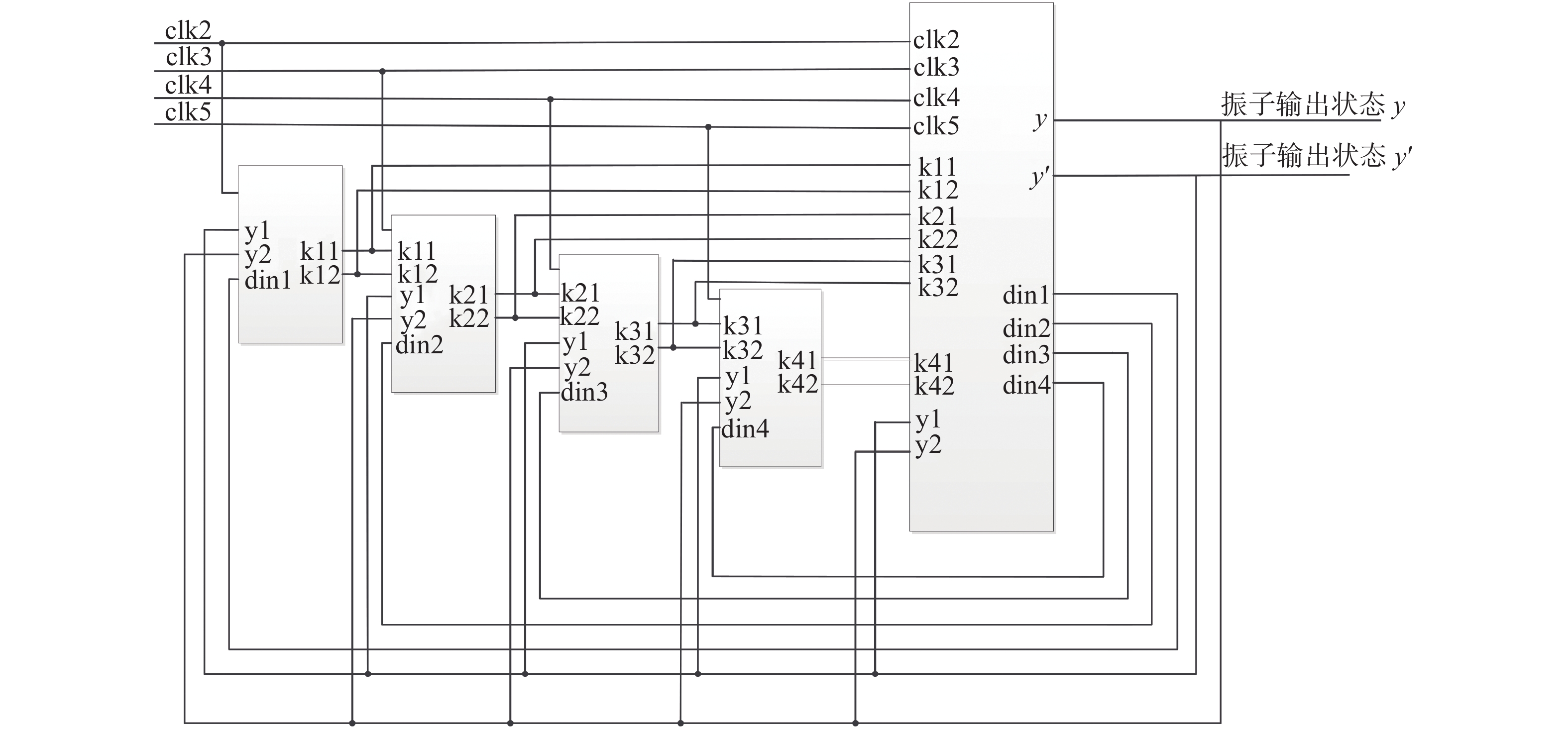
其中基带信号检测模块是核心部分，它主要由四阶龙格库塔法解Duffing方程、区域分割器、积分清洗滤波器以及求和模块组成。采用Duffing阵列检测信号的主要目的是屏蔽相位敏感性，利用Duffing振子的幅度敏感性来检测信号。

2.2.1 四阶龙格库塔解Duffing方程

Duffing方程属于二阶微分方程，本课题中选择使用四阶龙格库塔法进行求解^[12]，Duffing方程可写成：

$\left\{ {\begin{array}{*{20}{l}} {{{\dot y}_1} = \omega {y_2}} \\ {{{\dot y}_2} = \omega \left[ { - k{y_2} + {y_1} - y_1^3 + \gamma \cos (\omega {{t}} + {\varphi _0}) + ax(t)} \right]} \end{array}} \right.$

(1)

使用四阶龙格库塔法求解二阶微分方程：

${y_{n + 1}} = {y_n} + \frac{h}{6}({K_1} + {K_2} + {K_3} + {K_4})$

(2)

式中： ${y_n}$ 为微分方程的前一时刻的状态值； ${y_{n + 1}}$ 微分方程的当前时刻的状态值；h为四阶龙格库塔的运算步长； ${K_1}$ 、 ${K_2}$ 、 ${K_3}$ 、 ${K_4}$ 是4个相邻时间段的斜率，经过迭代计算便可以求出下一状态的数值，

$\left\{ {\begin{array}{*{20}{l}} {{K_1} = f({t_n},{{Y} _{{n}}})} \\ {{K_2} = f\Bigg({t_n} + \dfrac{h}{2},{Y_n} + \dfrac{h}{2}{K_1}\Bigg)} \\ {{K_3} = f\Bigg({t_n} + \dfrac{h}{2},{Y_n} + \dfrac{h}{2}{K_2}\Bigg)} \\ {{K_4} = f\Bigg({t_n} + \dfrac{h}{2},{Y_n} + h{K_3}\Bigg)} \end{array}} \right.$

(3)

式中： $f$ 为式(1)中所示的Duffing方程的函数； ${t_n} = n \times h,n = 1,2, \cdots $ ，为时间的离散状态变量； $h$ 为计算时采用的迭代步长。本次设计选择的迭代步长为 $h = 1/10{f_0}$ ，其中 ${f_0}$ 为Duffing振子的内部驱动力的频率，0.9 MHz。在Duffing振子的四阶龙格库塔法展开式之中，每一步计算中均用到了外部输入信号的分量，分别为 $ax({t_n})$ 、 $ax({t_n} + h/2)$ 和 $ax({t_n} + h)$ 。其中 $ax({t_n} + h)$ 为当前输入信号的数值， $ax({t_n})$ 为前一时刻输入信号的数值， $ax({t_n} + h/2)$ 则为时间区间 $({t_n},{t_n} + h)$ 内的斜率。使用四阶龙格库塔法求解Duffing方程的流程如图7所示。

由图7可知，各个阶段K值内部的计算是并行运行的，但每一个K值的计算都会用到上一阶K值的运算结果。为了保证在一个采样时钟内完成一次四阶龙格库塔法的迭代计算，在本设计中，产生了6个频率同为9 MHz，初始相位相差60°且占空比为1∶5的时钟信号分别控制不同K值模块及加法模块的运算。同时，外部输入信号的分量需要用对应的时钟进行同步处理，送到相应的模块之中进行运算。

本文设计中采用Verilog硬件描述语言将上述的RK模块进行实现，用Quartus II软件进行编译通过的并用Modelsim进行功能仿真。x_com与y_com为Duffing振子的时域分量和微分分量。可以看出外部输入信号为高时，Duffing振子处于大尺度周期态，对应的时域分量为周期为0.9 MHz的正弦信号；反之，Duffing振子处于混沌态，对应的时域分量为无规则类噪声信号，如图8所示。

2.2.2 域分割器及积分清洗滤波器

上面讲述了Duffing振子检测器FPGA实现的具体过程，输入信号经过Duffing振子阵列信号检测器后输出2个状态变量，需要在每一路Duffing振子后加上区域分割器及积分清洗滤波器。根据文献[1]，将圆域分割器及积分清洗滤波器进行组合简化设计，可以得到的圆域分割器及积分清洗滤波器的实现结构如图9所示。

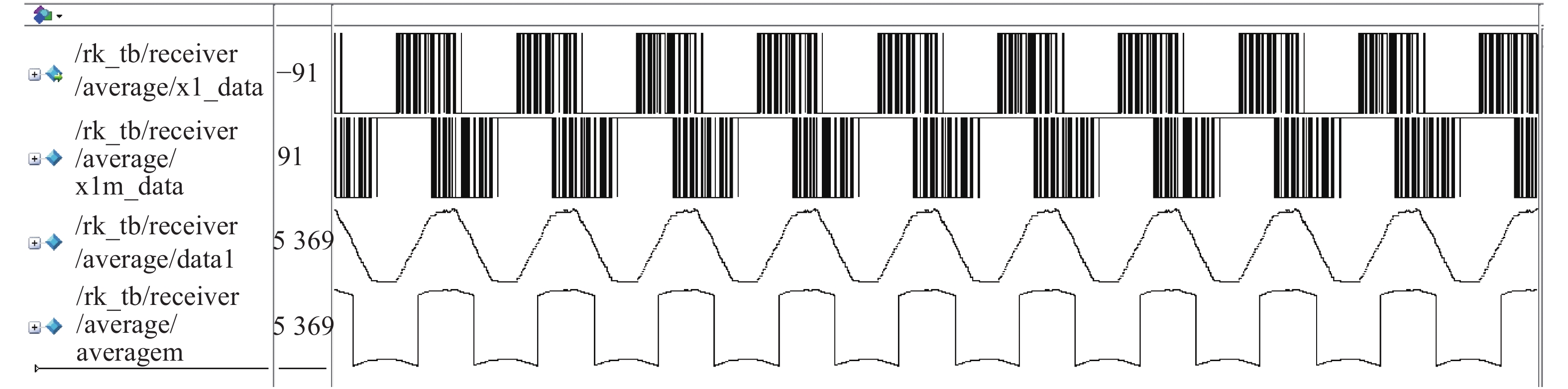
此种结构下的圆域分割器及积分清洗滤波器的结构简单，运算复杂度较低，便于在FPGA上实现。使用Verilog语言编写的圆域分割器包含可平方运算、求和运算、fifo延时模块及阈值比较的模块。根据上面对圆域分割器及积分清洗滤波器描述，编写程序可以得到如图10的Modelsim仿真图。

由图10可知，经过平方运算、求和运算的信号被分为2路。第一路当输入信号为高时，Duffing振子处于大尺度周期态，Duffing振子不会穿过圆域分割器，比较器将会输出持续为低的信号；当输入信号为低时，Duffing振子处于混沌态，Duffing振子不断穿过圆域分割器，则其会输出为高低不断变化的信号，如图10中x1_data所示。同样的，另一路信号经过fifo延时器延时半个时钟周期后，经过与第一路相反的比较器，即输入信号为高时，比较器将会输出持续为高的信号；输入信号为低时，输出为高低不断变化的信号，如图10中x1m_data所示。将2路信号进行累加，可以实现积分清零的功能，这样就可以得到滤波后的波形，经过低通滤波器的信号averagm则是恢复出的基带波形。

3 四进制混沌接收机的联合调制

根据上述的参数进行设计，将各个模块进行级联并使用QuartusⅡ进行全编译，可以得到如图11的RTL视图。

由图11所示，pll_1模块为时钟分频模块，可以将来自于板上晶振的100 MHz的时钟分频以供后续的工作使用；AD9433为AD转换模块，用来将模拟信号转化为数字信号；fir_qianduan为前端的带通滤波器，其主要作用是滤除带外噪声；polarcatas为正交解调模块，恢复出发射机产生的调制信号；Sigcic为梳状滤波器，可以将信号转化成9 MHz；reciver1与reciver2为信号的基带检测模块，用来恢复基带信号；基带信号检测模块之后再进行串并转换便可以得到恢复出的基带信息。

在本设计之中，进行混沌调制时，基带信号的码元速率为50 kHz，混沌调制的Duffing振子内部驱动力频率为0.9 MHz，幅度 $\gamma = 0.6$ ，阻尼系数k为0.5，进行QAM调制时的载波频率为3 MHz，然后再进行射频调制，射频信号的频率为100 MHz。在接收端，信号经过天线后使用AD831模块下变频至中心频率为3 MHz的调制信号，然后送入到AD转换模块，经过A/D转换的速率为18 MHz，数据位宽为12位。进行基带检测时，使用了2条完全相同的Duffing阵列进行信号解调。Duffing阵列是同时使用了4个内部驱动力初始相位不同（0°，90°，180°，270°）、内部驱动力幅度为0.19、频率为0.9 MHz的4个Duffing振子组成的Duffing阵列检测信号。使用四阶龙格库塔法求解Duffing振子时，使用了18位定点数进行计算，计算时的采用的步长为9 MHz。同时，进行域分割及积分清洗滤波时，使用的都是9 MHz的系统时钟；进行位同步时，系统时钟为36 MHz。使用上面的参数完成对整个程序的编写并进行了系统验证。

3.1 联合仿真验证

为了测试整个程序的性能，使用MATLAB仿真产生待接收的数据，将其作为输入信号送混沌通信系统之中。编译后经过Modelsim得到仿真图如图12所示，其中dout1与dout2为经过正交解调与带通滤波器的待检测信号，qq与qq1为I路与Q路恢复出的基带信号，base为发射机发送的原始的基带信号，sda为接收机检测到的基带码元信号。对比base与sda信号可以看出，接收机可以正确接收发射机发出的信号。

3.2 基于Stratix ii-EP2S180开发板的下载与测试

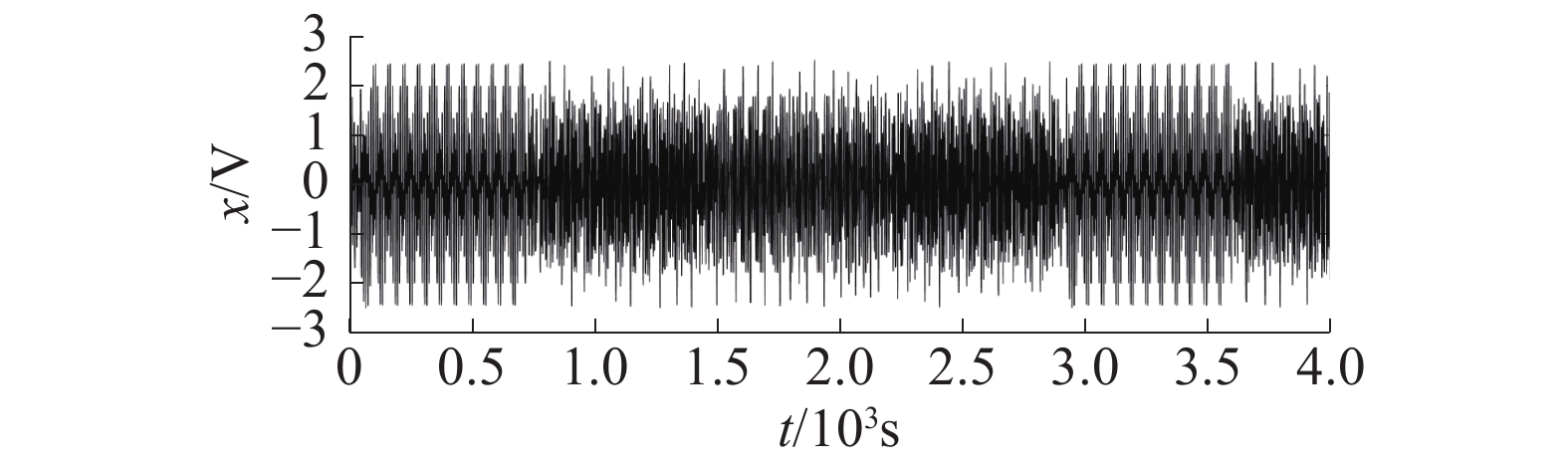
将整个程序进行时序约束及引脚分配，编译后下板验证，实验使用的示波器为泰克科技TDS220。图13中示波器通道1为发射的伪随机码，通道2为混沌振子接收机解调的基带信号，对比2路的信号，虽然有一定延迟，但该数字接收机的FPGA实现了预期的功能，完成了基于Duffing振子的混沌数字接收机的设计。证明了该混沌接收机的可行性及有效性。

4 结论

本文的四进制混沌接收机主要由射频前端，AD转换模块、正交解调模块、基带信号检测模块及并转串模块构成，可以实现对具有任意相位的四进制混沌调制信号的接收。从以上的研究可以得到如下结论：

1）此混沌接收机接收的信号为Duffing振子的时序信号，更具有隐蔽性，通信系统更加安全；

2）本次设计使用四进制混沌调制，一定程度提升了信号传递的速度；

3）利用了Duffing振子阵列的幅度敏感性检测信号，且屏蔽了其相位的敏感性，使其可以接收具有任意相位的混沌信号，并且回避了混沌同步的难题；

4）本文使用了Modelsim功能仿真及下板验证证明了该方案的可行性。