2. 武汉第二船舶设计研究所,湖北 武汉市 430000
2. Wuhan Second Ship Design Institute, Wuhan 430000, China
随着当今世界海洋开发的逐渐深入,各种类型的海洋平台数量也逐年上涨,大型海洋结构物之间的碰撞事故的发生频率也越来越高,其中大部分为海洋供应船与海洋平台之间的碰撞,而对于海洋平台之间的碰撞,由于碰撞物的吨位更大,碰撞位置更多变,碰撞角度更灵活,因此可能造成更为严重的后果。目前,国内外大多学者更关注船舶与海洋平台间的碰撞问题。金伟良等[1]采用非线性弹簧来模拟受损构件的内凹特性,计算分析了船舶侧向撞击导管架平台结构在不同的碰撞接触时间下的构件损伤情况。王自力等[2]结合理论分析与数值仿真研究了船舶碰撞外部机理与内部机理之间的滞后效应。他指出,这种滞后效应与撞击速度相关,用于分析高速撞击问题。叶文兵[3]比较了3种数值仿真方法,研究了舱内液体、撞击位置与撞击速度对船舶耐撞性的影响。Amante 等[4]考虑几何非线性与材料非线性,研究受供应船撞击后的半潜式平台圆筒的抗弯强度,并与完整的半潜式平台的极限抗弯强度进行比较分析。高振国等[5]模拟了3种工况,即供应船船侧沿横向、纵向、斜向撞击半潜式平台立柱时,研究立柱结构的抗撞特性,并评估了撞击对平台整体强度的影响。Martin Storheim 等[6]运用非线性数值仿真分析了7 500 t带有球鼻艏的供应船撞击固定管架海洋平台的损伤情况,主要关注损坏行为和管架是否会刺入船舶及对碰撞的影响。本文对支持平台和钻井生产平台之间的碰撞展开研究,主要关注碰撞后平台结构的碰撞力、损伤、能量转化情况,为平台的损伤评估提供一定参考。
1 支持平台与钻井平台的有限元模型支持平台与生产平台之间的碰撞一般发生在支持平台靠泊生产平台进行补给作业的过程中,如图1所示。半潜式支持平台处于靠泊连接就位位置,和生产平台之间通常保持数十米距离。此时,支持平台在自身系泊系统作用下,和生产平台近距离靠泊连接,以进行人员和物资的转运。在此靠泊过程中,由于操作失误或在强烈的风、浪、流作用下,支持平台可能会以一定速度和一定角度撞向被补给平台,从而产生严重后果。

|
Download:
|
| 图 1 支持平台靠泊生产平台示意 | |
支持平台和钻井平台的结构尺寸有所差异,但整体结构组成相似。平台的下浮体采用简单箱形,下浮体主要由外板和内结构组成;上船体也采用规则的箱形结构,上船体下部有4个高度相等的方立柱,立柱主要由外板、水密平台、非水密平台、水密通道围壁、水密舱室、垂向加强筋和水平加强筋组成。支持平台和钻井平台的主要结构参数如表1所示。
|
|
表 1 支持平台和钻井平台的主要结构参数 |

|
Download:
|
| 图 2 支持平台有限元模型 | |
|
Download:
|
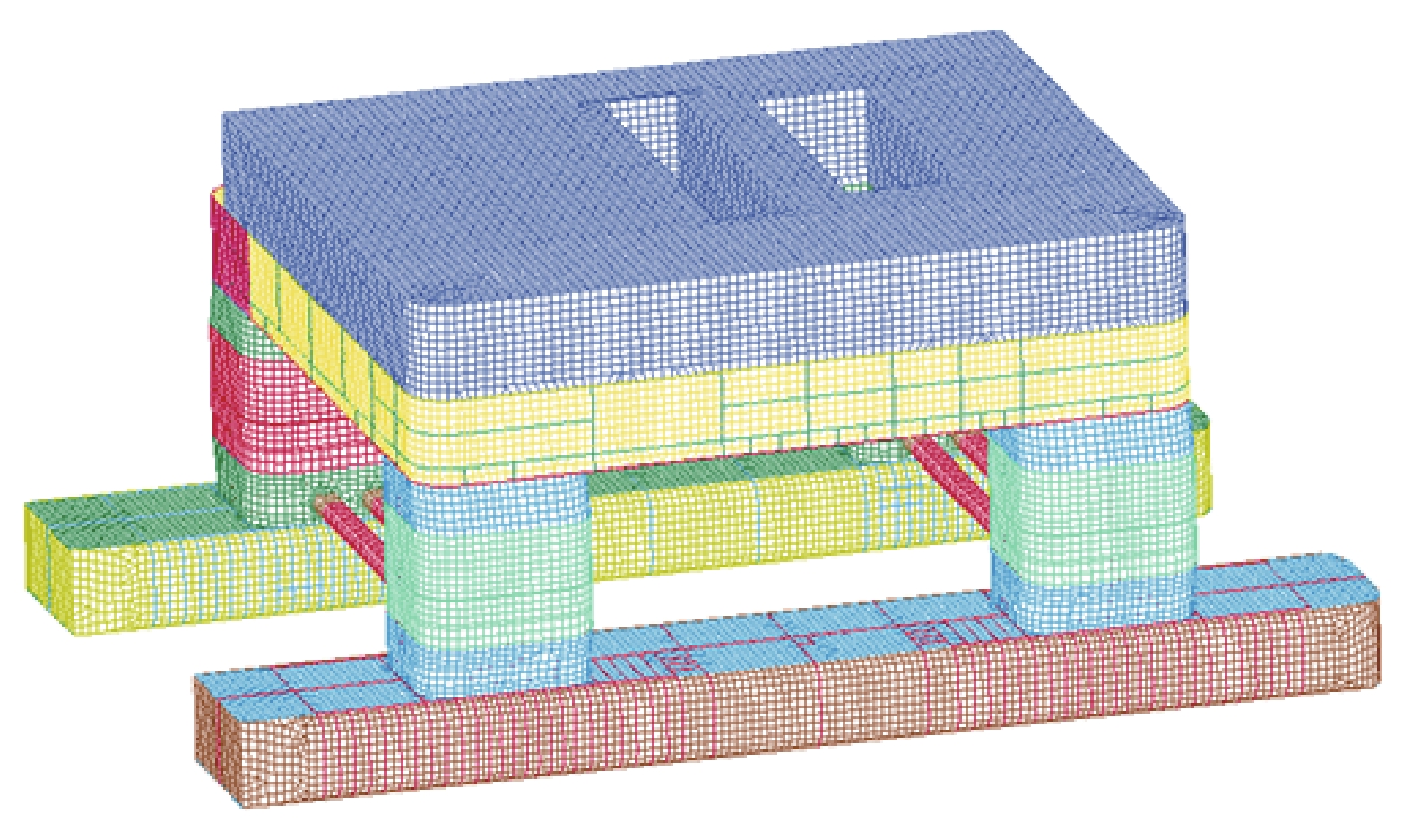
| 图 3 钻井平台有限元模型 | |
网格划分和网格尺寸对有限元分析计算的精度和计算时间影响较大,根据Kõrgesaar 等[7]得到的结论:碰撞区域网格尺寸与结构厚度的比值在2~20结果可靠。为提高计算速度,将碰撞区的网格细化为0.03 m,可以在保证计算精度的基础上提高计算效率,最终建立的支持平台和钻井平台的节点数约为80 000个,单元数约为90 000个。
1.2 支持平台和钻井平台的碰撞工况图4为两平台相撞的示意图,碰撞角度分别为0°、30°和90°。考虑到正常海况下平台的运动和恶劣海况下海洋平台间相接触时风、浪、流等对海洋平台运动的影响,碰撞速度分别为3和0.6 m/s,分别对应高能碰撞情况和低能碰撞情况。本文将2个平台的吃水高度均设置在作业吃水状态,2个平台相撞的6个具体工况如表2所示。

|
Download:
|
| 图 4 碰撞工况示意 | |
|
|
表 2 支持平台撞击钻井平台工况 |
支持平台−钻井平台的撞击区材料模型采用双线性弹塑性动态模型即Cowper-Symonds(MAT24)弹塑性材料,材料参数如表3所示[8]。
|
|
表 3 弹塑性材料参数 |
在碰撞过程中,周围流体在短时间内将产生较大的阻力阻碍平台的运动响应。在数值仿真时,对这一现象的描述一般有2种方法,一是准确建立流体模型,采用流固耦合算法计算;二是采用附加质量法。王自力等[9]通过对两船相撞的数值模拟,得出流固耦合算法的计算时间几乎占用了整个计算时间的98%,而应用附加质量法会使计算时间大大减少,且最大误差不超过10%。本文采用附加质量法来描述结构周围流体的作用,选取的附连水质量系数如表4所示[10]。其中斜角度撞击时的附连水质量系数按照差值方法取为0.17。
|
|
表 4 附连水质量系数 |
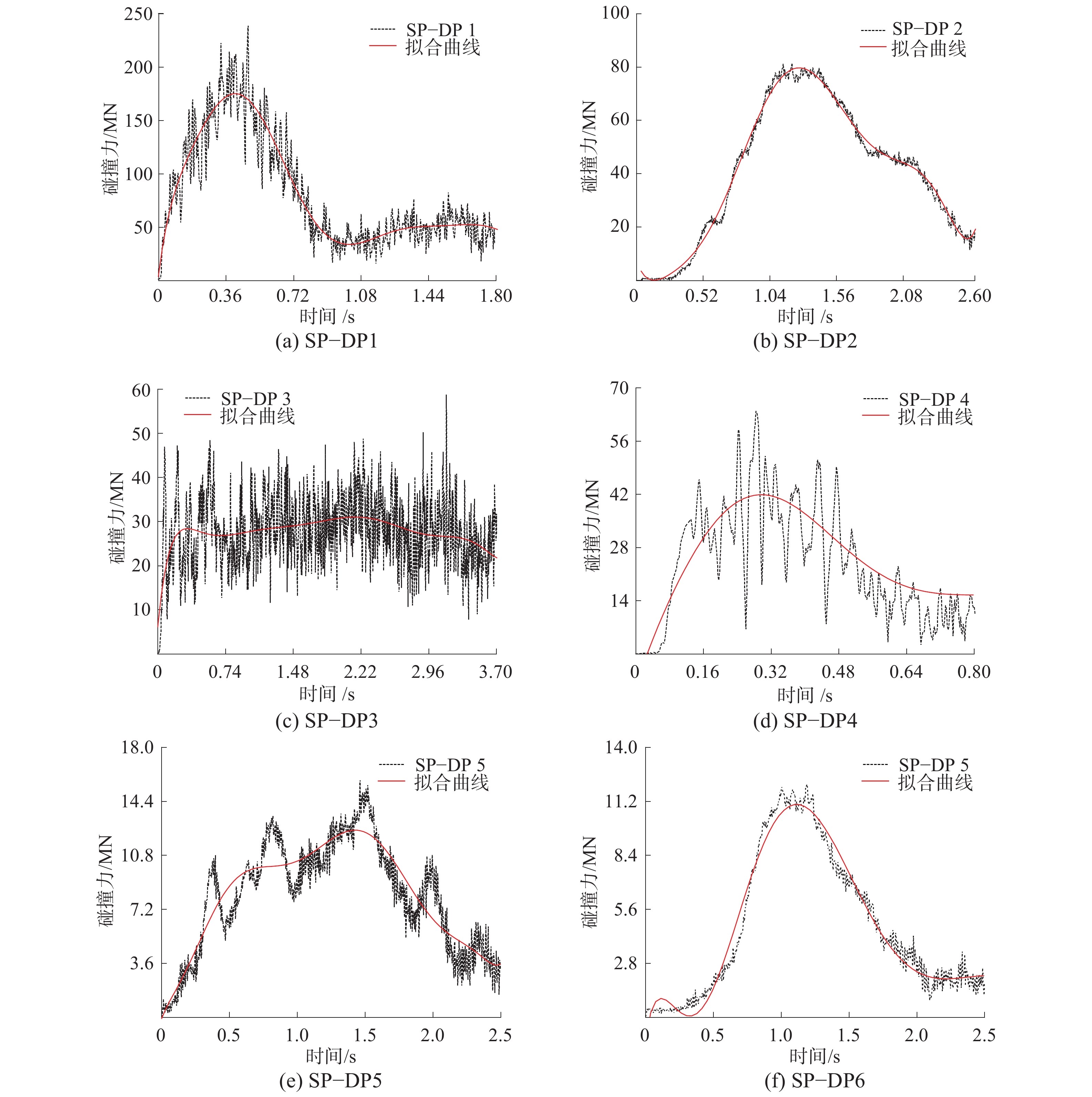
SP−DP1~SP−DP6这6种工况包含0.6和3 m/s 2种初始碰撞速度,3种平台撞击角度。图5为SP−DP1至SP−DP6的撞击力时历曲线,其中(a)、(b)、(c)为碰撞速度为3 m/s时碰撞力时历曲线,(d)、(e)、(f)为碰撞速度为0.6 m/s时碰撞力时历曲线。
|
Download:
|
| 图 5 碰撞力时历曲线 | |
从图5可以看出碰撞力曲线呈现明显振动,这是由于碰撞时结构存在局部振动,其拟合曲线可以代表碰撞力的发展趋势。从碰撞时间来看,碰撞时间大致在1~4 s。碰撞速度越大,两平台的碰撞接触时间越长。对于大型海洋平台来说,其自摇周期大致在20 s左右,因此碰撞时间大致为平台自摇周期的1/20~1/5。在碰撞速度相同时,平台间呈0°夹角时碰撞力的曲线最陡峭,碰撞力峰值也最大;30°角次之;90°夹角相撞碰撞力最小。这是由于SP−DP1和SP−DP4碰撞属于正碰,在水平面内不发生旋转,所有耗散能量都需要正面碰撞消耗;其他工况平台在碰撞发生后会以碰撞接触点为圆心在水平面内发生旋转,动能有很大一部分由平动动能转化为转动动能,因此碰撞力较小。图5(c)曲线中SP−DP3的撞击力在碰撞初期迅速增加,当撞击力维持一段时间,原因是支持平台尖艏结构强度不足,在此碰撞力下持续变形。
2.2 结构损伤对比分析碰撞角度决定了平台之间的碰撞区域,使两平台接触面积和接触结构均不相同,图6为支持平台撞钻井平台的损伤变形云图,其中图6(a)、(b)为SP−DP1下结构的变形云图,(c)、(d)为SP−DP2下结构的变形云图,(e)、(f)为SP−DP3下结构的变形云图。

|
Download:
|
| 图 6 支持平台撞钻井平台的应力云图 | |
从图6(a)、(b)中可知,SP−DP1下支持平台涉及到的主要变形为下浮体外板面的拉伸变形和内部桁材的褶皱变形。钻井平台下浮体外板变形的位置是与支持平台的舱壁板和强框等桁材相碰的位置。由于重心高于撞击区,碰撞后上船体相互靠拢,故下浮体上边缘成为支点,其应力值更高,是结构发生破坏的主要位置。
如图6(c)、(d)所示,两平台以30°角发生碰撞后,支持平台的下浮体艏侧面产生凹陷变形,随着碰撞区域逐渐扩大,应力集中在凹陷区边缘,凹陷区中心不再直接与钻井平台发生接触,碰撞后期下浮体艏侧板完全内凹后,碰撞应力主要由艏侧板四周相邻的外板结构承担。钻井平台的应力集中在碰撞区的4个角处。原因是支持平台产生内凹后,4个角的结构刚度最大,构成4个尖角,钻井平台在这4个角对应位置处出现穿透失效。
SP−DP3的两平台结构应力及变形情况如图6(e)、(f)所示,SP−DP3钻井平台和支持平台的结构变形和失效形式与SP−DP2类似,区别在于SP−DP3碰撞区域较小,应力更集中。
2.3 能量转化对比分析表5为各种工况下碰撞结束后系统的总能量、摩擦能和系统动能、内能占总能量比例分配情况。支持平台动能的耗散主要转化为钻井平台的动能和两平台结构变形吸收的内能。其中动能占比超过一半,内能占比较小。说明碰撞后两平台仍继续运动一段时间直到动能完全耗散。在0°角正碰时,由于两平台接触面积更大,参与吸能的构件更多,所以吸能比例更高;而在斜角度撞击时,平台结构吸能比例更小;90°角撞击时,接触面积最小,因此形成更严重的局部损伤。
|
|
表 5 碰撞结束后系统能量分配情况 |
图7为钻井平台的下浮体外板、下浮体内结构和立柱结构吸能时历曲线。

|
Download:
|
| 图 7 钻井平台碰撞区域各结构吸能情况 | |
从图中可知,只有平台侧面正碰的时候平台下浮体的外板和内结构变形所吸收的能量是相近的,并且内结构吸收的能量更多一些。而另外2种工况下,均是外板吸收了更多的能量,尤其是夹角为30°时,二者相差接近5倍。这说明平台碰撞时各结构的变形吸能情况由碰撞区域范围和碰撞位置结构决定。
3 结论本文应用LS-DYNA软件对支持平台与钻井生产平台间的碰撞过程进行了数值模拟,分析得到了碰撞力、结构损伤、结构吸能等碰撞响应特性,总结规律如下:
1)当碰撞速度一定时,两平台以0°角正碰时碰撞力最大,30°角时次之,90°角时最小,说明平台间碰撞的碰撞力随碰撞角度的增大而增大。
2)平台的初始动能主要由碰撞后两平台的变形损伤所吸收,其中0°角正碰时,两平台接触面积更大,吸能比例更高,而在斜角度撞击时,平台结构吸能比例更小,但局部损伤更为严重。
| [1] |
金伟良, 龚顺风, 宋剑, 等. 大型船舶碰撞引起的海洋导管架平台结构损伤分析[J]. 海洋工程, 2003, 21(2): 20-25. DOI:10.3969/j.issn.1005-9865.2003.02.004 ( 0) 0)
|
| [2] |
王自力, 顾永宁. 船舶碰撞运动的滞后特性[J]. 中国造船, 2001, 42(2): 56-62. DOI:10.3969/j.issn.1000-4882.2001.02.009 ( 0) 0)
|
| [3] |
叶文兵. 典型船舶舷侧结构耐撞性能研究[D]. 武汉: 华中科技大学, 2008.
( 0) 0)
|
| [4] |
DO AMARAL AMANTE D, TROVOADO L, ESTEFEN S F. Residual strength assessment of semi-submersible platform column due to supply vessel collision[C]//Proceedings of the 27th International Conference on Offshore Mechanics and Arctic Engineering. Estoril, Portugal, 2008: 779–789.
( 0) 0)
|
| [5] |
高振国, 胡志强, 王革. FPSO舷侧结构抗撞性能的解析计算研究[J]. 工程力学, 2014, 31(S1): 155-160, 176. ( 0) 0)
|
| [6] |
STORHEIM M, AMDAHL J. Design of offshore structures against accidental ship collisions[J]. Marine structures, 2014, 37: 135-172. DOI:10.1016/j.marstruc.2014.03.002 ( 0) 0)
|
| [7] |
KÕRGESAAR M, ROMANOFF J. Influence of mesh size, stress triaxiality and damage induced softening on ductile fracture of large-scale shell structures[J]. Marine structures, 2014, 38: 1-17. DOI:10.1016/j.marstruc.2014.05.001 ( 0) 0)
|
| [8] |
Det Norske Veritas. DNV-RP-C208, Determination of structural capacity by non-linear FE analysis methods[S]. Høvik, Norway: Det Norske Veritas, 2013.
( 0) 0)
|
| [9] |
王自力, 蒋志勇, 顾永宁. 船舶碰撞数值仿真的附加质量模型[J]. 爆炸与冲击, 2002, 22(4): 321-326. DOI:10.3321/j.issn:1001-1455.2002.04.006 ( 0) 0)
|
| [10] |
程正顺, 胡志强, 杨建民. 半潜式平台结构抗撞性能研究[J]. 振动与冲击, 2012, 31(4): 38-43. DOI:10.3969/j.issn.1000-3835.2012.04.008 ( 0) 0)
|
 2019, Vol. 46
2019, Vol. 46


