2. 哈尔滨工程大学 船舶工程学院,黑龙江 哈尔滨 150001
2. School of Shipbuilding Engineering, Harbin Engineering University, Harbin 150001, China
随着船舶向大型化、高速化方向发展以及高功率主机的使用,船后伴流场的不均匀程度和螺旋桨的负荷加重,出现了尾振、结构损坏、噪音及剥蚀等现象。在开展螺旋桨设计时,未考虑伴流场的影响,将可能导致所设计的螺旋桨所在伴流场不匹配,出现振动、噪声、推力不符合要求,耗能增大等现象。船舶螺旋桨适伴流设计的目的就是考虑船桨一体的相互影响,在船舶艉后伴流场条件下,选择合适的直径及拱度、螺距、纵斜和侧斜的分布,尽量减小桨引起的振动、空泡及噪声等一系列问题。开展螺旋桨的适伴流设计需预报船后伴流场以设计适合于所在伴流场条件下运转的螺旋桨。
舰艇艉后为以湍流脉动、黏性效应和漩涡运动为特征的复杂流场区域,导致艇艉后伴流严重不均匀[1−2]。由于潜艇螺旋桨实际上都是工作于艇艉后伴流中,螺旋桨空化、噪声性能受到艇艉后不均匀伴流的影响十分严重,在对螺旋桨设计时必须考虑艇艉后不均匀伴流场的影响。1963年,Beveridge等[3]基于Lerps理论采用Eckhardt-Morgan方法设计适伴流螺旋桨,在敞水和伴流条件下进行试验,均得到很好的性能。Donald MacPherson[4]分析舰船适伴流螺旋桨设计时,认为随着越来越多螺旋桨建造厂能够实现数字化建造,舰船量身定制或半定制合适的推进器成为可能。丁举等[5−6]比较单桨与双桨船的流场不同特点,计及切向伴流影响,开展双桨船适伴流桨设计。罗晓园等[7]针对传统舵桨实际运行中出现的螺旋桨振动、低速等问题,给出开展全回转舵桨适伴流设计概念。侯立勋等[8]以实现节能为目标,以螺旋桨环流理论分别对前桨和后桨进行实桨适伴流设计,建立了一种高效对转桨适伴流设计方法。宋才生等[9]研究船舶艉型与适伴流螺旋桨的一体化匹配设计,并将设计结果与实船实验数据进行比较,验证优化设计结果。但是以往学者都是将螺旋桨理论设计与优化设计分开研究,可能造成理论设计得到的螺旋桨各方面性能不能达到最优,或者开展优化设计时缺少母型桨。因此本文将螺旋桨适伴流的理论设计和优化设计相组合,形成一套比较完整的螺旋桨设计系统。
螺旋桨适伴流理论设计及参数优化设计的目的是在舰艇艉后伴流场的条件下,合理地设计螺旋桨的几何参数分布,使设计桨适合于所在伴流场下的运转,满足水动力性能方面要求,而且对空化、噪声性能有利,实现为舰艇量身定制螺旋桨。本文首先介绍了船用螺旋桨适伴流理论设计及参数优化设计流程;然后,介绍螺旋桨参数化表达的方法;最后,通过对HSP桨重新设计,验证螺旋桨适伴流理论设计及参数优化设计的可行性。
1 螺旋桨适伴流理论设计及参数优化设计流程本文将螺旋桨适伴流的理论设计和优化设计相组合,形成一套比较完整的螺旋桨设计系统。该系统包含了伴流场的谐振分析方法、螺旋桨理论设计前桨叶数、纵倾分布和侧斜分布的选择方法、考虑纵倾侧斜影响的升力线设计程序、升力面设计程序、非定常面元法预报螺旋桨水动力性能程序和以设计桨为母型的适伴流参数优化设计程序。该系统全面考虑了适伴流设计桨的水动力性能、非定常推力的脉动、强度条件,而且操作简单,可自动完成各程序之间的数据传输,大大减少人工的介入。该系统运行的过程中可输出文档和设计桨模型,便于设计者对设计进程进行观察和控制。
具体流程如下:
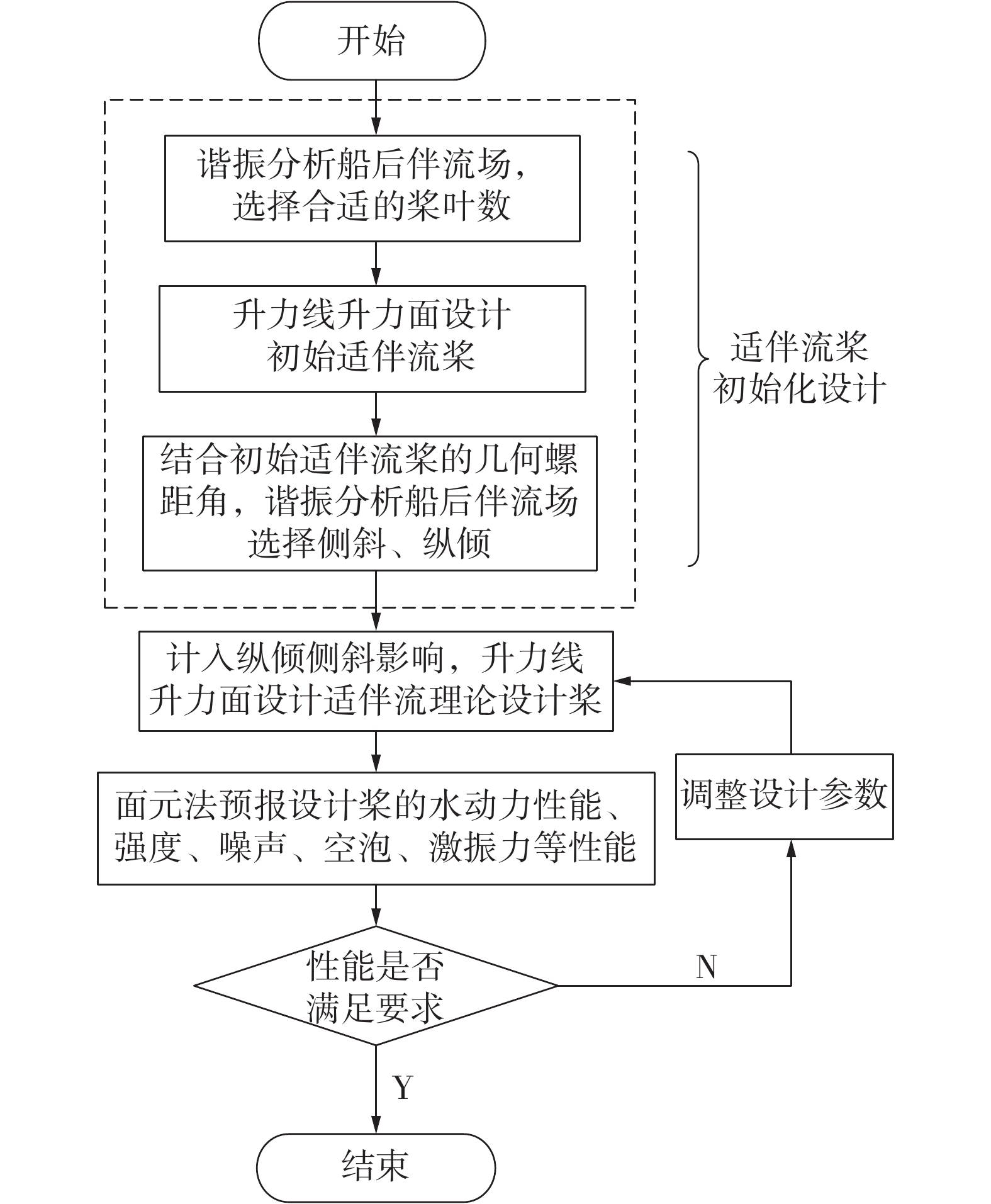
1)螺旋桨适伴流桨的初始化理论设计。根据舰艇的船型特点和设计要求,确定升力线输入参数,包括螺旋桨转速、直径,推力,螺旋桨收到的马力、伴流分数等。其中,伴流分数可根据船型特点和经验公式估算,开展不考虑纵倾侧斜的螺旋桨适伴流初始化理论设计,根据侧斜纵倾的选择原则,结合初始化适伴流桨的几何螺距角、谐振船后伴流场选择合适的侧斜分布和纵倾分布。
2)螺旋桨适伴流理论设计。在船后伴流场条件下,采用考虑纵倾和侧斜分布的升力线和升力面设计程序开展螺旋桨适伴流理论设计。采用非定常面元程序预报适伴流设计桨的性能,判断适伴流设计桨水动力性能、激振力是否满足要求,否则,重新进行螺旋桨适伴流理论设计。
3)螺旋桨适伴流优化设计。这一步骤是为了进一步提高适伴流理论设计桨的各方面性能而开展的。以适伴流理论设计桨为母型,探索设计变量空间,确定设计变量的变化范围。结合优化算法和非定常面元法程序,采用悬臂梁法预报设计桨的应力分布,限制其最大应力值小于材料的许用应力6.37
螺旋桨适伴流理论设计部分的流程如图1所示,螺旋桨适伴流参数优化设计部分的流程如图2所示。
|
Download:
|
| 图 1 螺旋桨适伴流理论设计流程 | |

|
Download:
|
| 图 2 螺旋桨适伴流优化设计流程 | |
B样条曲线对曲线控制灵活[10]。如果用基于B样条曲线参数来表达桨的几何参数,可用较少的控制点得到光顺半径方向的几何参数分布。螺旋桨几何参数径向分布的B样条曲线的具体表达如下:
| $p\left( u \right) = \sum\limits_{i = 0}^n {{d_i}{N_{i,k}}\left( u \right),0 \leqslant u \leqslant 1} $ |
式中:p(u)为几何参数分布;
在螺旋桨的几何参数优化设计中,螺旋桨的几何参数在不同的径向处有不同的值,进行几何参数优化时,需要重新获得不同径向处的几何参数值,其表现为一条曲线。通过改变控制顶点得到新的几何参数分布不能很好地控制几何参数的变换范围。因此,对设计人员来说,应该直接考虑曲线上的几何参数分布而不是控制多边形的形状。从初始曲线,反算出控制多边形,求出合理的曲线形状[10]。具体来讲,就是已知B样条曲线上沿径向的几何参数,取其中的
本文采用反求控制点的三次B样条曲线求解方法如下:已知三次B样条曲线上的分段点
| $\frac{{\left( {{d_i} + {d_{i + 1}} + {d_{i + 2}}} \right)}}{6} = {p_i}\left( {i = 1,2, \cdots ,n} \right)$ | (1) |
式(1)有n个方程及n+2个未知量,因此只需2个边界条件即可求解。沿径向分布的螺旋桨几何参数为不封闭的曲线,对此需补充如下边界条件:
| ${d_0} = {d_2};{d_{n - 1}} = {d_{n + 1}}$ |
结合上述反求控制点的B样条曲线方法理论,作者基于FROTRAN语言编译了相关程序用于表达螺旋桨几何参数。以P4382桨为例,验证本程序表达的可行性。用反求B样条曲线的程序对P4382桨的沿径向的分布弦长、螺距、厚度、拱度、纵倾和侧斜进行参数化表达。
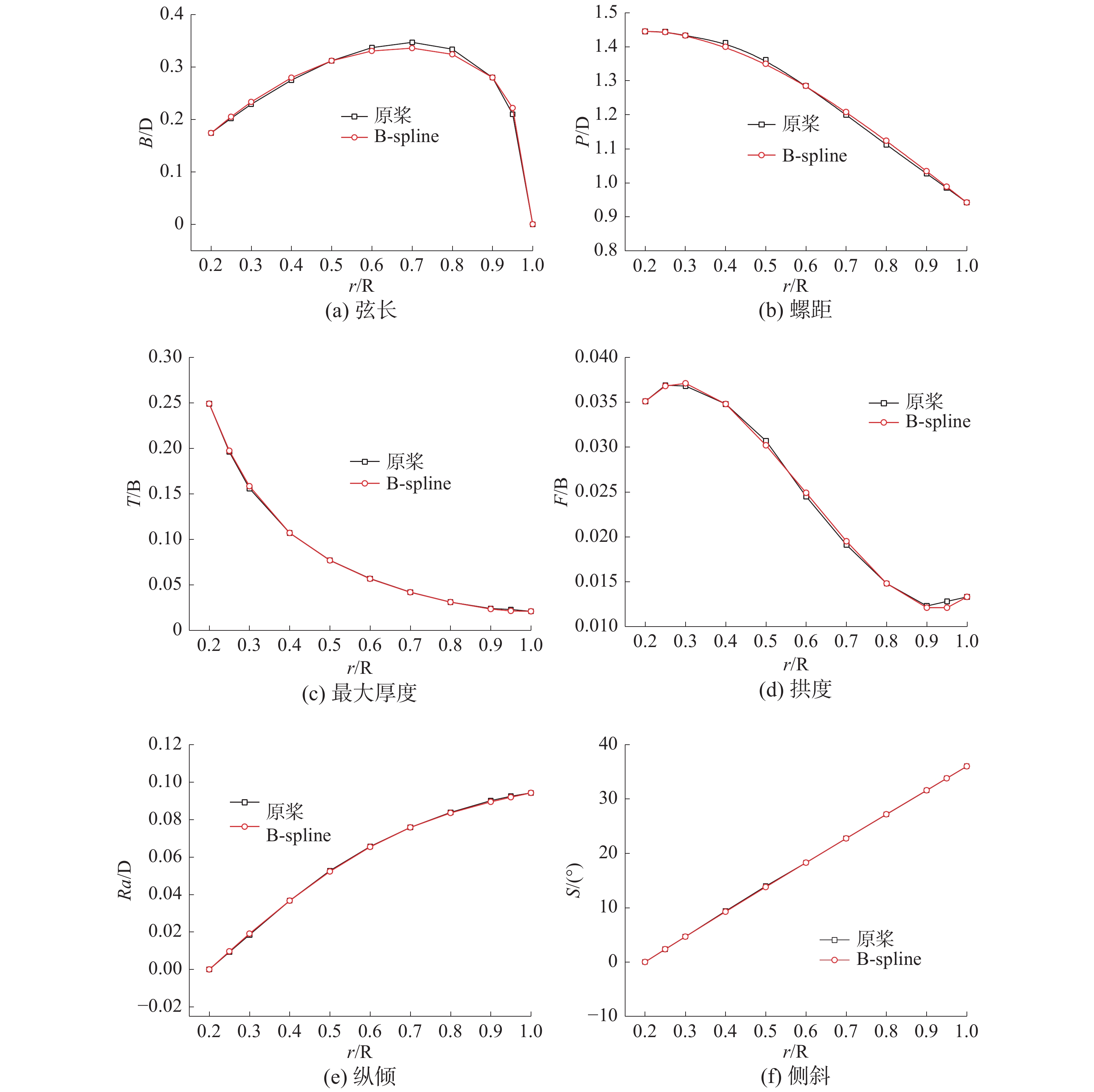
鉴于B样条曲线的优点,本文选了4个控制点。4个控制点的具体位置需根据几何参数的分布情况而定。如图3所示,P4382桨沿径向的弦长、螺距、厚度、拱度、纵倾和侧斜经参数化表达后基本与原桨相吻合。
|
Download:
|
| 图 3 原桨与参数化表达后桨的几何参数对比 | |
计算出经参数化表达后桨的水动力性能,并将其与原桨的水动力性能相比较。如图4所示,图中KT、KQ分别为螺旋桨的推力系数与扭矩系数,原P4382桨与参数化表达后的桨的敞水性能曲线基本一致。可见,本文的反求B样条曲线参数化表达程序是可用于表达螺旋桨的几何参数。因此,在以下开展螺旋桨适伴流优化设计过程中可以通过调整控制点来改变螺旋桨的几何形状。

|
Download:
|
| 图 4 原桨与参数化表达后桨的敞水性能曲线对比 | |
为验证本文所述船用螺旋桨适伴流理论设计及优化设计系统的有效性,以对HSP桨再设计为例。HSP桨的几何参数、伴流场以及水动力性能的实验值见文献[12]。根据HSP桨的试验条件,给出HSP桨部分升力线设计的初始输入参数,如表1所示。根据HSP桨轴向伴流分布如图5所示,得到每个半径处的轴向伴流周向平均值,如表2所示。
|
|
表 1 HSP桨升力线输入参数 |

|
Download:
|
| 图 5 HSP桨轴向伴流分布 | |
|
|
表 2 HSP桨轴向伴流的周向平均值 |
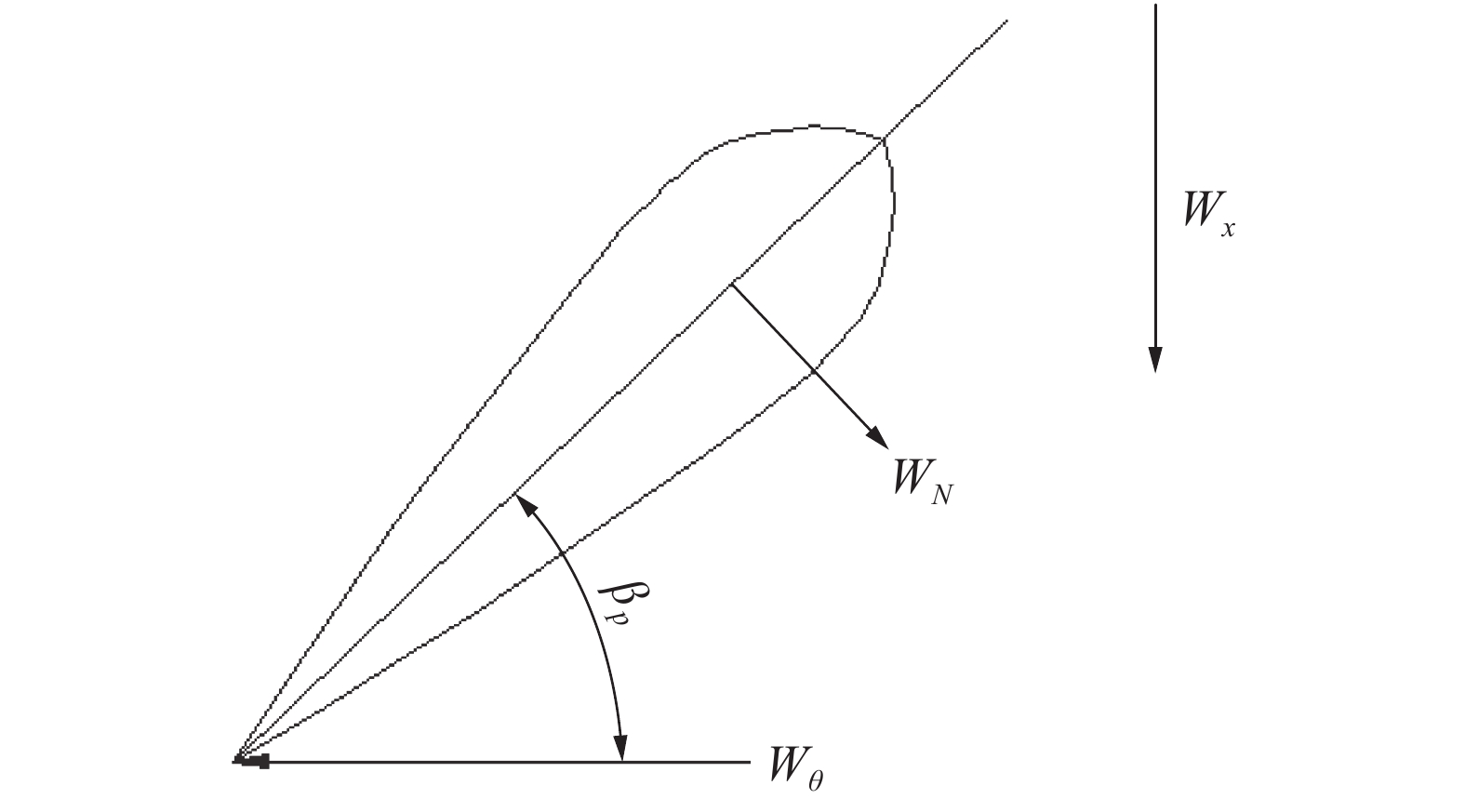
由于不同舰艇艉后伴流场是不同的,需要根据船舶伴流的具体情况选择螺旋桨合适的侧斜分布。在螺旋桨适伴流理论设计前,采用谐调分析法分析舰艇艉后法向伴流(如图6所示),合理的选择侧斜分布,目的是避开桨各个剖面同时转动到高伴流区。侧斜分布必须与伴流场的各谐调分量一起考虑,不计径向伴流影响,各个剖面的法向伴流为:
| ${W_N} = {W_x}\cos {\beta _p} - {W_\theta }\sin {\beta _p}$ |
|
Download:
|
| 图 6 桨叶剖面法向伴流 | |
螺旋桨适伴流理论设计前,需要初始化设计螺旋桨,得到设计桨的几何螺旋桨角,以便开展法向伴流场的谐振分析。由于原HSP桨的几何螺距角已知,本文省去了该步骤。通过对HSP桨的法向伴流场协调分析,得到5阶最大法向相位角如表3所示。
|
|
表 3 HSP桨伴流场最大法向相位及3种侧斜分布 |
表3同时给出了HSP桨的原侧斜分布。为了方便理解,图7给出了3种侧斜分布的螺旋桨正投影图。侧斜分布设计原则是初步确定的螺旋桨侧斜分布要尽量使得侧斜分布线与法向伴流相位的分布曲线存在比较大的交角。根据该原则,作者初步选定平衡式和后侧斜形式这2种方式的HSP桨沿径向的侧斜分布形式进行探讨。

|
Download:
|
| 图 7 3种不同侧斜分布桨的正视图 | |
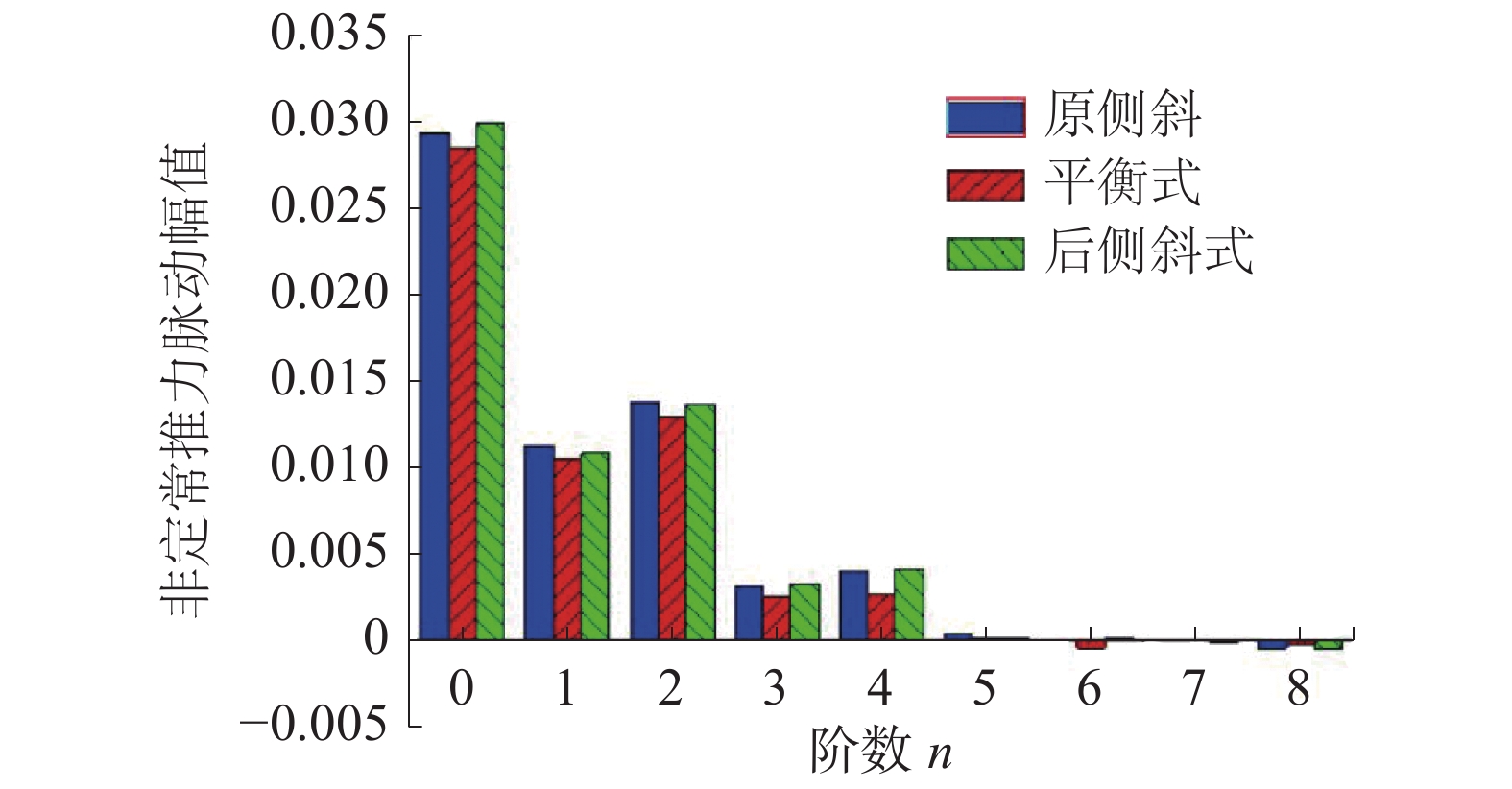
在其他几何参数不变条件下,分别预报了原侧斜、平衡式以及后侧斜形式的不同HSP桨的非定常的水动力性能。基于傅里叶分析法频谱分析3种侧斜方式的HSP桨主桨叶的非定常推力系数,可得到主桨叶的各阶力的幅值。由图8可知,平衡式和后侧斜式的侧斜分布对应的HSP桨的非定常推力主要脉动幅值均比原桨减小了,其中平衡式减小的幅度更大。另外,后侧斜式的HSP桨主桨叶平均推力系数(0阶推力幅值)比原桨增大了,而平衡式的HSP桨的主桨叶平均推力幅值比原桨减小了,但是减小的幅度不大。因此,为了保证强度特性,在满足螺旋桨的推力条件下,尽量选择平衡式侧斜分布形式。若桨的强度可保证,为提高螺旋桨的推力系数,可选择后侧斜式的侧斜分布形式。
|
Download:
|
| 图 8 不同侧斜分布桨非定常推力系数各阶幅值 | |
纵倾设计主要目的是增加桨叶和船艉板之间的间隙,降低桨的尾流对船艉的冲刷,从而降低振动,而设计者通常是孤立进行螺旋桨设计,并通过船后伴流场来计入船体艉后速度场对螺旋桨的作用。纵倾的分布形式有桨叶纵倾内半径前置外半径后置分布、前置纵倾以及后置纵倾等。从强度角度考虑,后置纵倾不宜过大,以减小纵倾引起的离心力弯矩;前置纵倾对大侧斜螺旋桨强度有利,能有效降低桨的应力水平。从水动力性能角度考虑,后倾桨随着纵倾角度增加,其推力系数和扭矩系数都会提高;而前置纵倾能够提高螺旋桨的效率。从空泡角度考虑,后置纵倾能改善梢部的三维绕流,从而推迟梢涡空泡起始。综合考虑螺旋桨的水动力性能、空泡、噪声和强度,可以选用桨叶纵倾内半径前置外半径后置的分布方式,内半径区内纵倾分布前置螺旋桨的效率有所增加,外半径稍后置对其效率影响较小。
本算例以HSP桨再设计选择五叶桨,纵倾和侧斜分布选择如表4所示,作为升力线的输入参数。
|
|
表 4 HSP桨升力线侧斜纵倾输入参数 |
完成了设计桨的侧斜和纵倾选择后,即可开展HSP桨的适伴流理论设计。表5给出了适伴流理论设计桨的几何参数,该桨的叶根和叶梢处的螺距比原桨小,对减小螺旋桨的毂涡和梢涡有利。
|
|
表 5 适伴流理论设计桨几何参数 |
图9给出了螺旋桨的三维模型,几何外形比较光顺。采用本实验室开发的基于面元法和悬臂梁法的螺旋桨应力预报方法对该设计桨的应力分布进行预报,如图10所示。该桨的最大应力值为2.5×107 Pa,小于材料的许用应力6.37×107 Pa,强度满足要求。
|
Download:
|
| 图 9 设计桨示意 | |

|
Download:
|
| 图 10 设计桨应力分布 | |
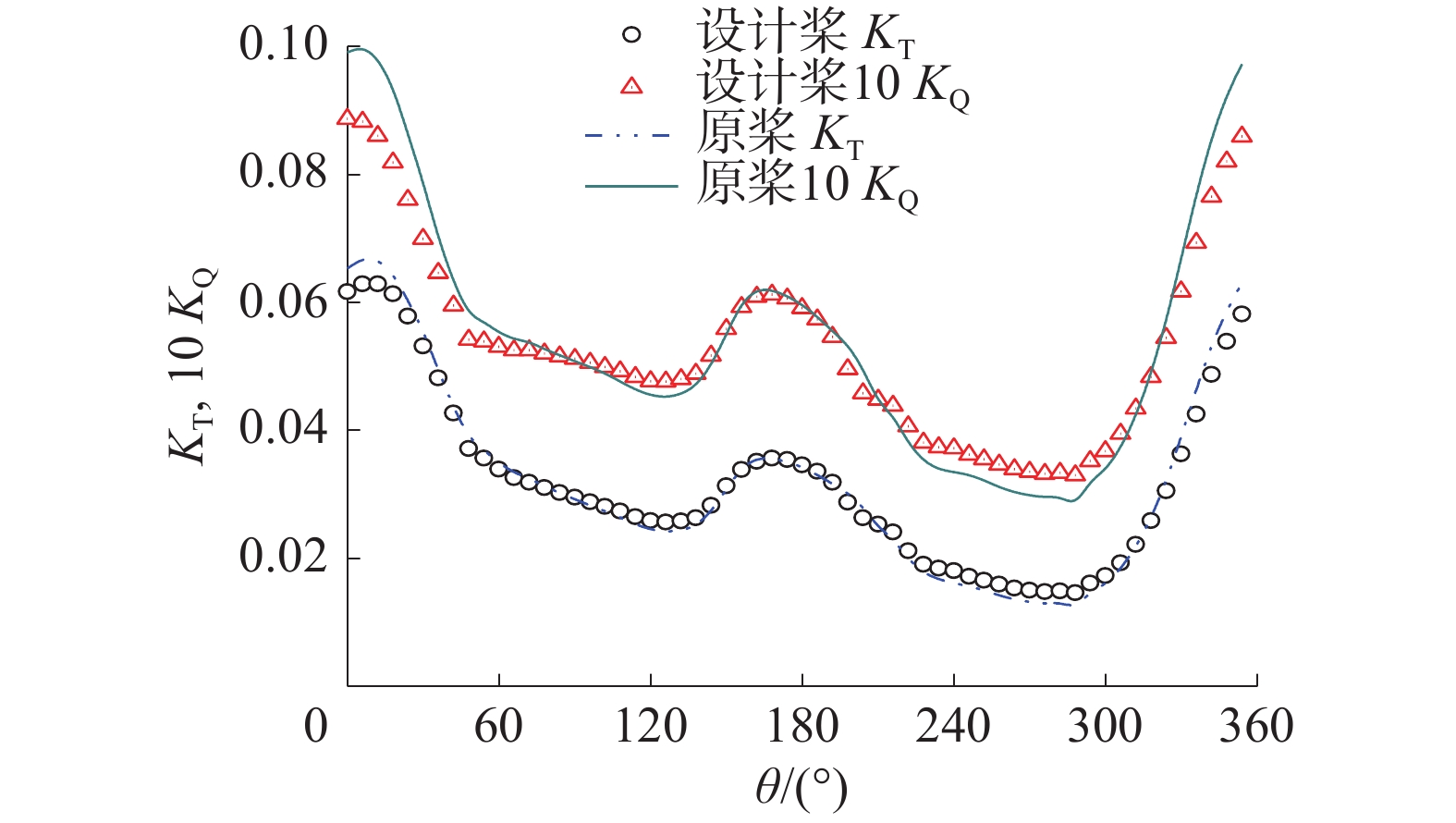
为了对适伴流理论设计桨进行更好地分析,采用非定常面元法对其性能进行预报,并与原HSP桨的性能进行对比,如表6和图11所示。
|
|
表 6 原HSP桨与设计桨水动力性能均值对比 |
|
Download:
|
| 图 11 主桨叶旋转一周过程中的推力系数和转矩系数 | |
由表6可知,原HSP桨和设计桨的推力系数与扭矩系数的误差均控制在3%以内。可见,设计桨的水动力性能与原HSP桨一致。由图11可知,原桨和设计桨的主桨叶在旋转一周过程中的推力系数和转矩系数比较吻合。同时,由图12可知,原桨和设计桨的主桨叶在旋转一周过程中的推力系数各阶幅值基本一致,但是设计桨的推力幅值要比原桨小。有利于减小螺旋桨的振动与噪声。

|
Download:
|
| 图 12 主桨叶一周旋转得到的推力系数各阶幅值 | |
本算例以文中HSP桨的适伴流理论设计桨为母型,验证建立的螺旋桨适伴流优化设计方法的可行性。在设计进速系数下,以提高平均推力系数和降低主桨叶最大非定常推力幅值为目标,将螺旋桨最大应力限制在6.37×107 Pa以下,对适伴流设计桨沿径向的分布的弦长、螺距、纵倾、侧斜、拱度进行优化设计。其中,螺旋桨应力计算采用悬臂梁法计算得到。为了节省优化设计的时间,搜索目标桨时将种群数目设为30,迭代次数12次。
以优化后的适伴流设计桨的最大主桨叶非定常推力幅值为横坐标和平均推力系数为纵坐标,组成了Pareto前沿。如图13所示,优化前的适伴流设计桨的主桨叶最大非定常推力幅和平均推力系数的坐标点离Pareto前沿有段距离。可见,经过螺旋桨适伴流优化设计后,将会进一步提高螺旋桨适伴流理论设计桨的性能。Pareto前沿的每个坐标点代表一个设计方案,船舶设计人员可以根据不同的船舶需求来权衡各方面因素,选择合适的方案桨。

|
Download:
|
| 图 13 螺旋桨适伴流优化设计桨Pareto前沿 | |
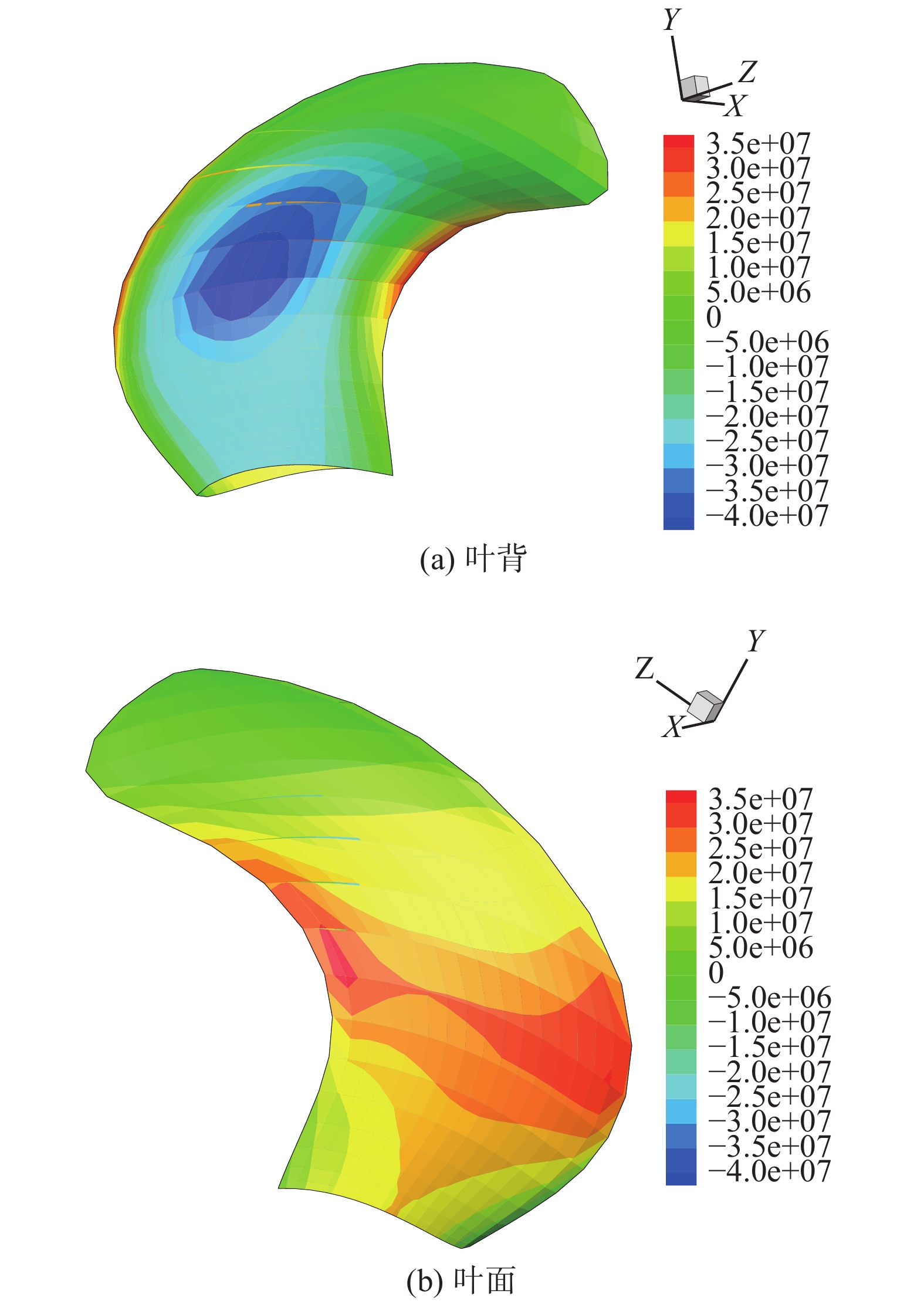
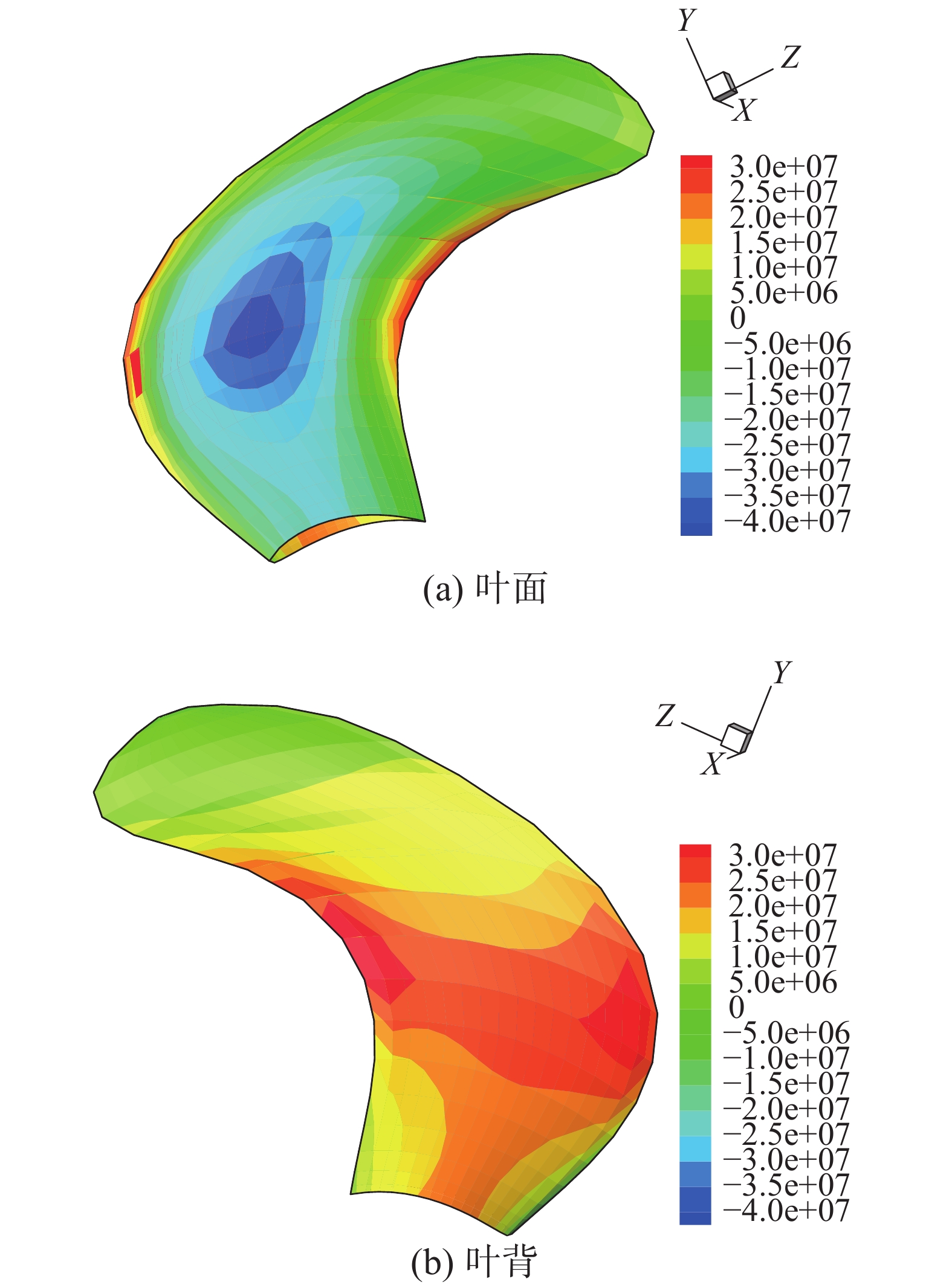
从Pareto前沿上选择2个适伴流优化设计桨进行分析,以下简称方案桨。图14、15给出了2个方案桨的应力预报结果,方案桨1的最大应力为3.5×107 Pa,方案桨2的最大应力为3×107 Pa。可见,2个方案桨的最大应力均未超过6.37×107 Pa,强度符合要求。
|
Download:
|
| 图 14 方案1桨的桨叶应力分布 | |
|
Download:
|
| 图 15 方案2桨的桨叶应力分布 | |
表7给出了2个方案桨、适伴流理论设计桨和原桨的最大主桨叶非定常推力幅值和平均推力系数。由表7和图16可知,方案桨1和方案桨2的最大主桨叶非定常推力幅值均低于原HSP桨;方案桨1、2均高于原HSP桨的平均推力系数。因此,在HSP桨船后伴流场下,方案桨1和方案桨2的快速性和振动性能要比原HSP桨更优。
|
|
表 7 设计桨与原桨水动力性能对比 |

|
Download:
|
| 图 16 主桨叶非定常推力系数各阶幅值 | |
图17给出了原桨、适伴流理论设计桨和2个方案桨的弦长、螺距、拱度、侧斜以及纵倾沿径向的分布。与原桨相比,方案桨的这些几何参数的分布曲线均比原桨要光顺且分布趋势与原桨有较大不同。适伴流理论设计桨和2个方案桨的内半径处的弦长与原桨相比有所减小,从而提高了设计桨的敞水效率;叶根处和叶梢处的螺距均比原桨小,桨叶中部的螺距比原桨大,这对减小螺旋桨的毂涡和梢涡是有利的。2个方案桨沿径向的螺距分布与适伴流理论设计桨有较大不同,推断螺距分布对螺旋桨的最大主桨叶非定常推力幅值和平均推力系数影响较大。拱度决定叶剖面的负荷沿弦向的分布,拱度增大能避免导边附近出现负压峰,推迟空泡的发生,但对整个桨叶的强度不利,适伴流理论设计桨和2个方案桨的叶根处的拱度比原HSP桨要小很多,这对叶根处的强度和毂涡是有利的;2个方案桨桨叶中部的拱度分布均比适伴流理论设计桨大,对提高螺旋桨的推力有利。原HSP桨、适伴流理论设计桨和2个方案桨的侧斜分布变化趋势比较类似,但是适伴流理论设计桨和2个方案桨在叶梢处的侧斜要比原HSP桨大,这对减小最大主桨叶非定常推力幅值有利。对于纵倾,方案桨的桨叶叶根处纵倾减小而叶梢附近的纵倾增加,适伴流理论设计桨和两2个方案桨的纵倾分布与原桨有较大不同,这种分布形式对螺旋桨的强度是有利的。

|
Download:
|
| 图 17 原桨和设计桨的几何参数对比 | |
本文将伴流场的谐振分析方法、螺旋桨理论设计前桨叶数、纵倾分布和侧斜分布的选择方法、考虑纵倾侧斜影响的升力线设计程序、升力面设计程序、非定常面元法预报螺旋桨水动力性能程序和以适伴流理论设计桨为母型的适伴流参数优化设计程序等组合,形成了一套比较完整的螺旋桨适伴流理论设计及参数优化设计系统,分析得到以下结论:
1)采用B样条曲线的螺旋桨参数化表达方法,通过合理的选择控制点,可实现以较少的控制点得到光顺螺旋桨的几何参数分布,并且沿径向的弦长、螺距、厚度、拱度、纵倾和侧斜经参数化表达后分布曲线与原桨是一致的,可应用于螺旋桨的参数优化设计。
2)螺旋桨适伴流理论设计要求螺旋桨的水动力性能与原桨一致,强度满足要求,而振动、噪声性能优于原桨,而本文所述的螺旋桨适伴流理论设计实现了这一目的,验证了该方法的有效性。
3)螺旋桨适伴流理论设计要达到的效果是在原适伴流理论设计桨的基础上,限制强度条件,进一步提高设计桨的各方面性能。而本文所述的螺旋桨适伴流参数优化设计,使得优化后的适伴流设计桨的推进性能和振动性能比适伴流理论设计要好,强度满足要求。
| [1] |
刘志华, 熊鹰, 王展志, 等. 潜艇新型整流方法的设计与试验研究[J]. 中国造船, 2010, 51(3): 47-55. DOI:10.3969/j.issn.1000-4882.2010.03.006 ( 0) 0)
|
| [2] |
黄振宇, 周连第. 带全附体潜艇尾流场的数值预报研究[J]. 中国造船, 2001, 42(4): 6-11. DOI:10.3969/j.issn.1000-4882.2001.04.002 ( 0) 0)
|
| [3] |
BEVERIDGE J L. Performance of wake-adapted propellers in open-water and propulsion conditions as determined by theory and experiment[R]. Washington DC: David Taylor Model Basin, 1963.
( 0) 0)
|
| [4] |
MACPHERSON D. Wake-adapted design and propeller analysis for naval architects[J]. The naval architect, 2010: 50-54. ( 0) 0)
|
| [5] |
丁举, 郭永崧. 双桨船螺旋桨的适伴流设计[J]. 中国造船, 2011, 52(2): 40-46. DOI:10.3969/j.issn.1000-4882.2011.02.006 ( 0) 0)
|
| [6] |
丁举, 陈红梅, 于海. 大型LNG船螺旋桨设计研究[J]. 船舶工程, 2011, 33(3): 9-12. DOI:10.3969/j.issn.1000-6982.2011.03.003 ( 0) 0)
|
| [7] |
罗晓园, 李新, 郑锐聪, 等. 基于内河运输船的新型全回转舵桨设计研究[J]. 船舶, 2013, 24(4): 39-43. ( 0) 0)
|
| [8] |
侯立勋, 汪春辉, 胡安康. 对转桨适伴流设计方法研究[J]. 中国造船, 2015, 56(4): 1-7. DOI:10.3969/j.issn.1000-4882.2015.04.001 ( 0) 0)
|
| [9] |
宋才生, 张华, 陈林, 等. 基于数值模拟的艉型及适伴流高效桨优化设计[J]. 中国水运, 2017, 17(8): 9-10. ( 0) 0)
|
| [10] |
PARIDA L. A computational technique for general shape deformations for use in font design[J]. Computers & graphics, 1993, 17(4): 349-356. ( 0) 0)
|
| [11] |
胡志刚, 余周, 丛晓霞. 反算控制点的三次均匀B样条闭曲线插值功能模块的设计[J]. 河南职技师院学报, 2000, 28(1): 44-46. DOI:10.3969/j.issn.1673-6060-B.2000.01.015 ( 0) 0)
|
| [12] |
胡健. 螺旋桨空泡性能及低噪声螺旋桨设计研究[D]. 哈尔滨: 哈尔滨工程大学, 2006: 6.
( 0) 0)
|
 2019, Vol. 46
2019, Vol. 46


