2. 北京航空航天大学 航空科学与工程学院,北京 100191
2. School of Aeronautic Science and Engineering, Beihang University, Beijing 100191, China
电动汽车作为新能源汽车的一种,具有使用过程中污染低、结构简单、维护方便等优点[1],目前在北京的纯电动汽车数量已经接近20万辆。相较于传统燃油汽车的加油站,电动汽车充电站操作简单、安全性高,但使用时间较长,一般直流充电桩充电时间为1~2 h左右,交流充电桩充电时间可达8 h以上,充电桩的建设是电动汽车中远途出行的最大制约条件之一[2]。这也导致了电动汽车用户的充电习惯与燃油车用户的加油模式存在非常大的区别。大型电动汽车充电站的选址亦与加油站存在区别,一般选择建设在住宅区停车场、大型商业区、企业园区内部或其他公共设施内部[3],以降低用户充电等待的时间成本。
由于充电桩单用户占用时间长的特点,充电站建设时必须对潜在的用户数量具有较为精确的估计,充电桩过少可能无法满足周边用户充电需求而导致大量排队,充电桩过多时则会加剧电网负荷峰谷差,影响电网运行的经济性和安全可靠性[4]。目前的优化方法包括充电桩软、硬件改进和通过模型预测充电站的负载量等[5]。其中充电站负载量预测研究主要针对大型公共充电站或出租车充电站[6−7],通过地区总用户数量估算充电站单位时间平均用户数量和平均充电时间。对于用户的到达间隔一般近似服从负指数分布,对于平均充电时间,选取分布包括负指数分布[8−9]、正态分布等[10−11],基于排队模型可求解充电站的平均排队人数、平均负载率等关键指标。对于建立在商业区、工业园区内部的充电站,其平均用户数量随时间变化较大,使用平均值进行分析难以反映其最恶劣情况下的排队状态。针对企业园区内部的充电桩,为了考虑冬季最恶劣工况,本文选取了2017年12月—2018年2月间某大型工业园区内部的充电桩使用记录,统计了不同时段用户数量、平均负载率等参数。基于统计数据建立了不同用户数量下的排队模型,通过蒙特卡洛方法对不同用户数量的工况进行了仿真,对比了不同充电时间分布对排队关键参数的影响,并给出了排队长度、排队时间等关键指标。最后,本文通过建立的排队模型对未来更大客流量情况的排队进行了仿真分析,给出了排队基本参数。
1 用户充电习惯统计本文选取某大型工业园区内部充电站作为研究对象,其主要原因在于:1)该充电站位于某大型工业园区内部,充电用户较为固定;2)该充电站具有专人管理维护,故障率低;3)该充电站具有完善规章条例,能最大限度降低设备故障、燃油车占位等可能对数据分析产生干扰的因素。充电站共有电动汽车充电桩16个,其中直流充电桩15个,交流充电桩1个。为了减少新用户注册对统计数据的影响,仅考虑注册后充电次数>4的用户,共计170名用户。本文统计的2017年12月—2018年2月用户充电周期的分布图1所示。
|
Download:
|
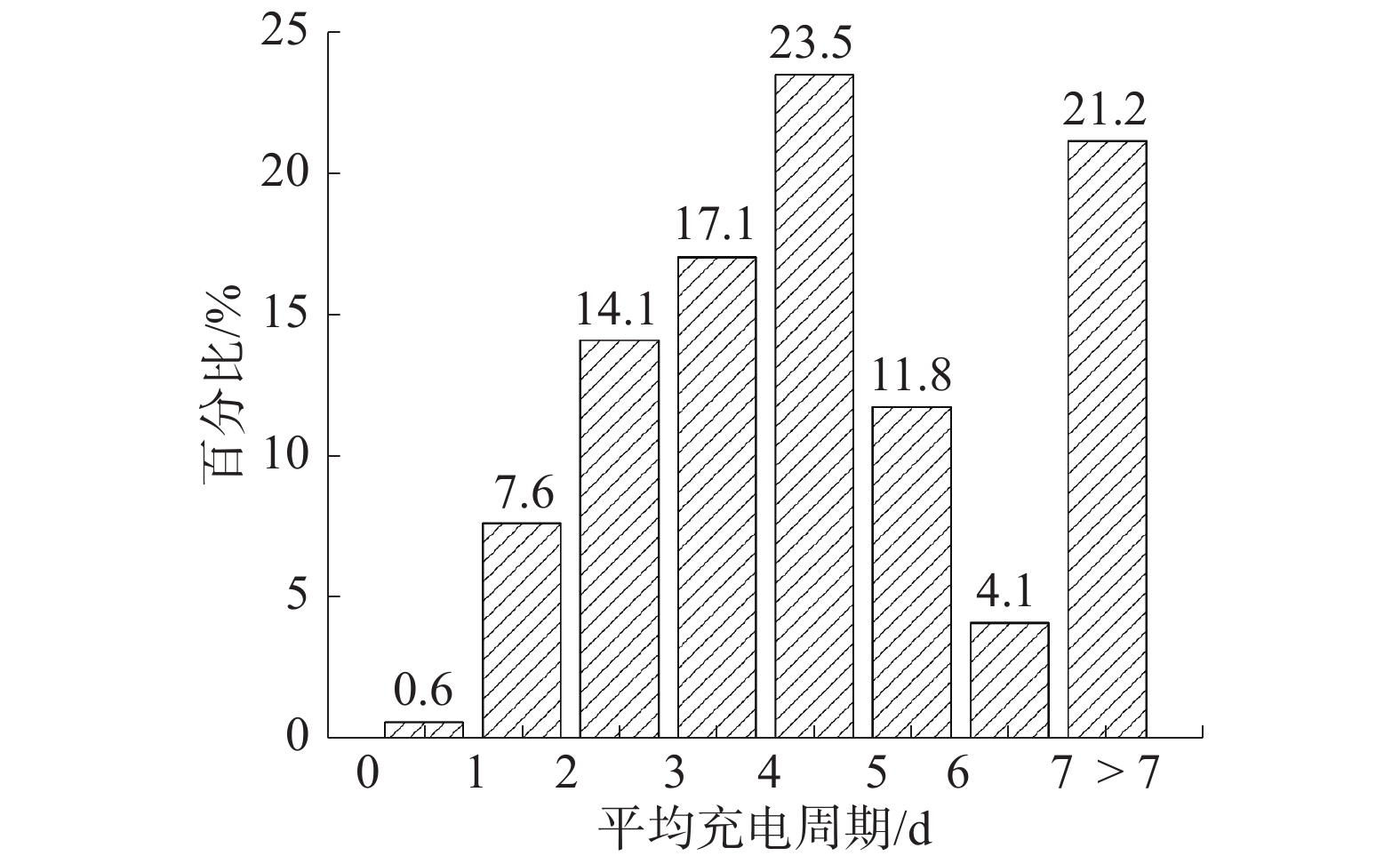
| 图 1 平均充电周期分布 | |
如图中所见,在该充电站充电周期2~6 d的用户占据了70%以上,充电周期7 d以上的用户亦占据了21.2%左右,可认为这部分用户亦有在其他充电站或家用充电桩进行充电的习惯。当仅考虑充电间隔1~7 d的用户时,用户的平均充电间隔为3.81 d。如图2为充电桩每次服务充电量分布。
|
Download:
|
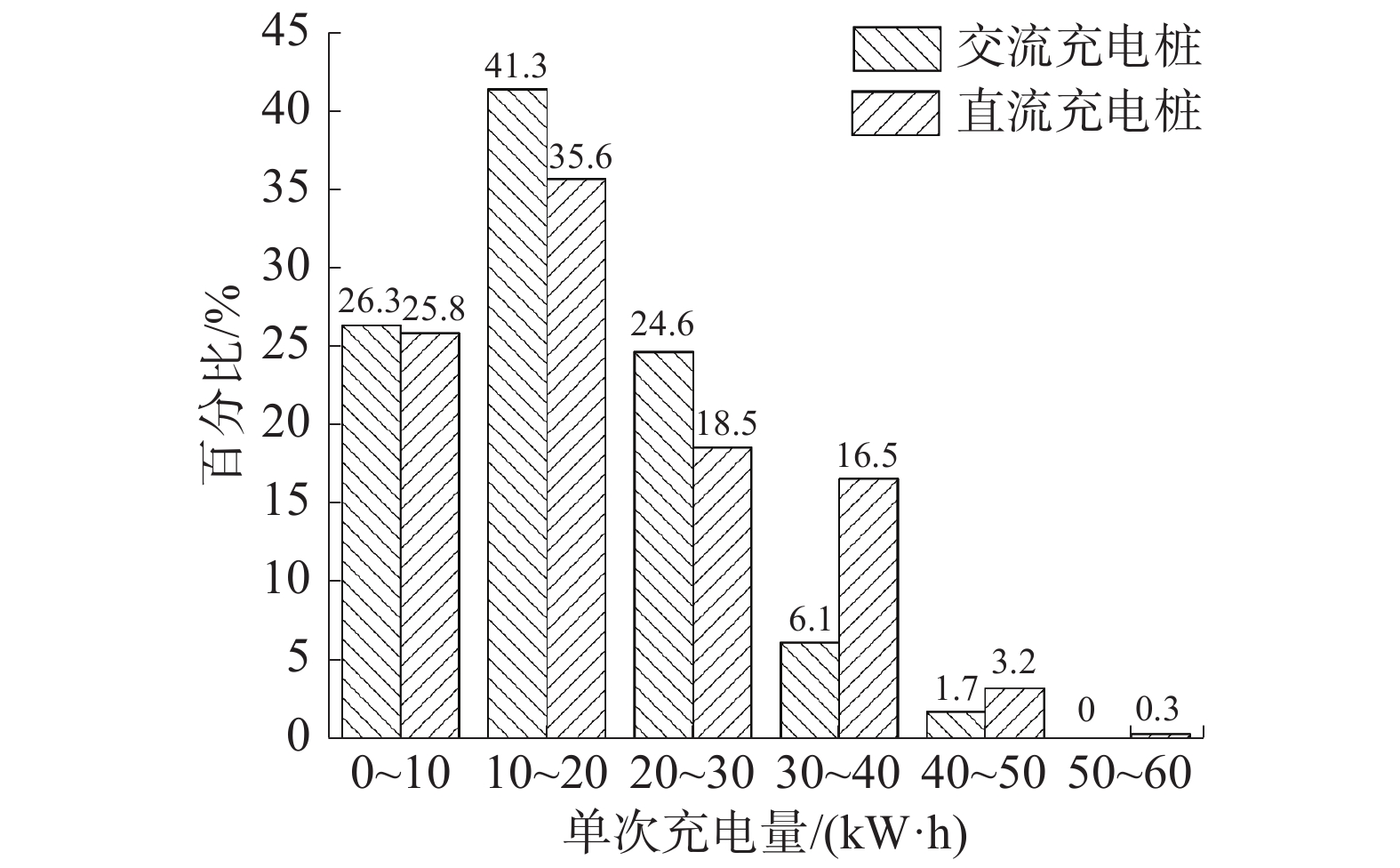
| 图 2 充电量分布 | |
如图中所见,选择每次充电10~20 kW·h的用户达到了40%以上,而用户的平均充电量为18.1 kW·h。根据统计数据,目前北京平均通勤单程距离为17.4 km[12],而一般小型纯电动汽车耗电量在0.15 kW·h·km−1左右[13],平均充电周期内的电量消耗E可以表示为
| $E{\rm{ = }}\frac{{n \times s \times t}}{w}$ | (1) |
式中:s为用户日平均单程通勤距离,km/次;t为平均充电周期,d;w为小型纯电动汽车单位里程耗电量,kW·h·km−1;n为用户单日通行次数,次/d,考虑用户主要为上下班通勤用途,n取2 次/d。由此可得平均充电周期内的电量消耗约为19.9 kW·h,与该充电站的统计数据偏差约为10%左右。考虑到大型园区在地理分布上的差异性和离散性,这个偏差是可以接受的。
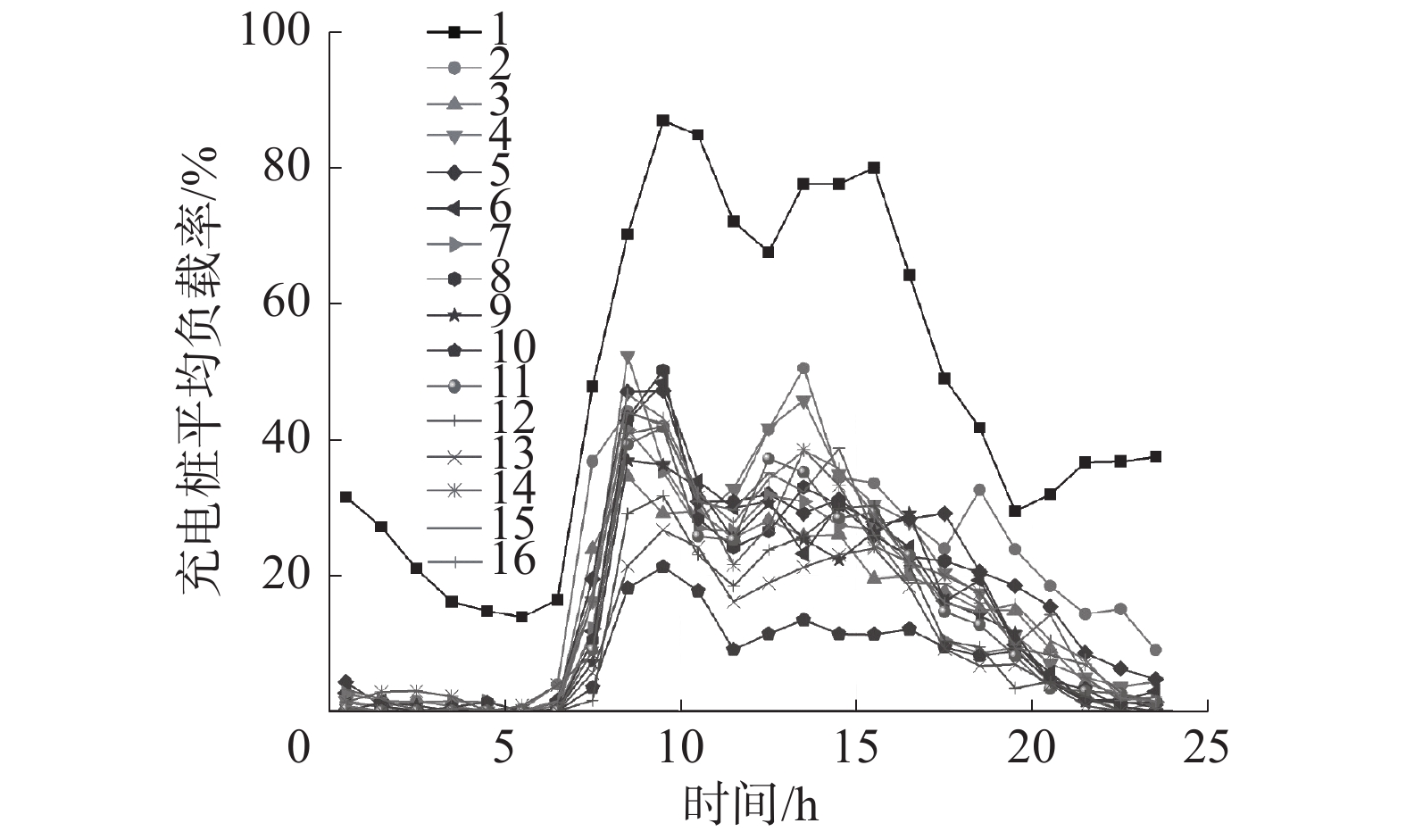
对于用户在充电时间上的选择,充电桩在一天内的平均占用率变化曲线如图3所示,其中1号为交流充电桩,2~16号为直流充电桩。
|
Download:
|
| 图 3 充电桩平均占用率 | |
如图3所示,在工业园区内部的充电站负载率呈现了非常强的时间相关性,即在昼间负载率较高,夜间负载率较低。本文对67 d内充电站在工作日昼间、工作日夜间、非工作日昼间、非工作日夜间的抵达人数进行了统计,发现在工作日昼间(7:00—19:00),平均抵达人数约为3.99 人/h,占据一周内总抵达人数的80.0%。同时,如图中所见,目前直流充电桩在高峰时间占用率仅为20%~50%,用户到达充电站后往往可以立即开始充电而不需要进行排队,即系统记录的开始充电时间可以代表用户的到达时间。但对于用率较高的交流充电桩,后台往往存在多位用户对其状态进行监视,并准备前往充电。无法获得后台排队的用户数量将大大降低模型的精确度,故本文对排队模型的仿真主要针对直流充电桩进行。
2 充电桩排队模型 2.1 排队模型建立用户在充电站排队充电的事件可以使用排队模型进行仿真,一般而言,用户到达充电站的时间间隔服从负指数分布,其概率密度为
| ${{f}}(x) = \left\{ {\begin{array}{*{20}{l}} {\dfrac{1}{\theta }{{\rm{e}}^{ - \frac{1}{\theta }x}},x \geqslant 0} \\ {0,x < 0} \end{array}} \right.$ | (2) |
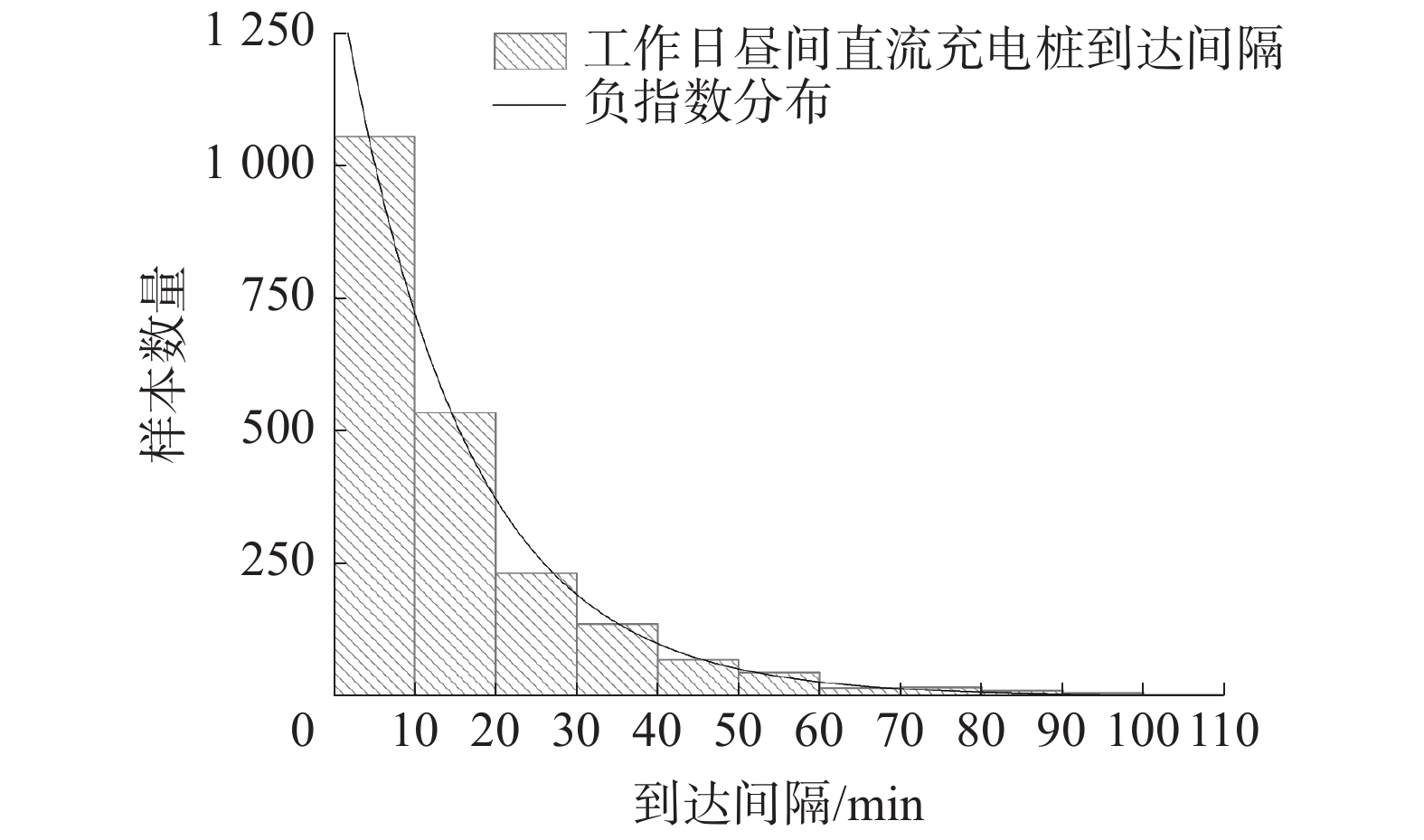
式中θ为负指数分布的尺度参数,min,即排队模型中用户到达的平均间隔。图4为工作日昼间的用户到达直流充电桩的间隔分布与负指数分布对比。
|
Download:
|
| 图 4 用户到达间隔分布 | |
如表1所示为对工作日昼间(7:00—19:00)、工作日夜间(19:00—0:00)、非工作日昼间、非工作日夜间用户到达时间负指数分布拟合参数和K−S检验结果,其中N为样本量,E、SE分别为负指数分布尺度参数θ的估计值和估计值标准误差,p为显著性水平,h为检验结果。
|
|
表 1 用户到达间隔时间负指数分布拟合与K−S检验结果 |
如表中所见,在显著性水平0.05的情况下,不能拒绝数据服从负指数分布的假设。
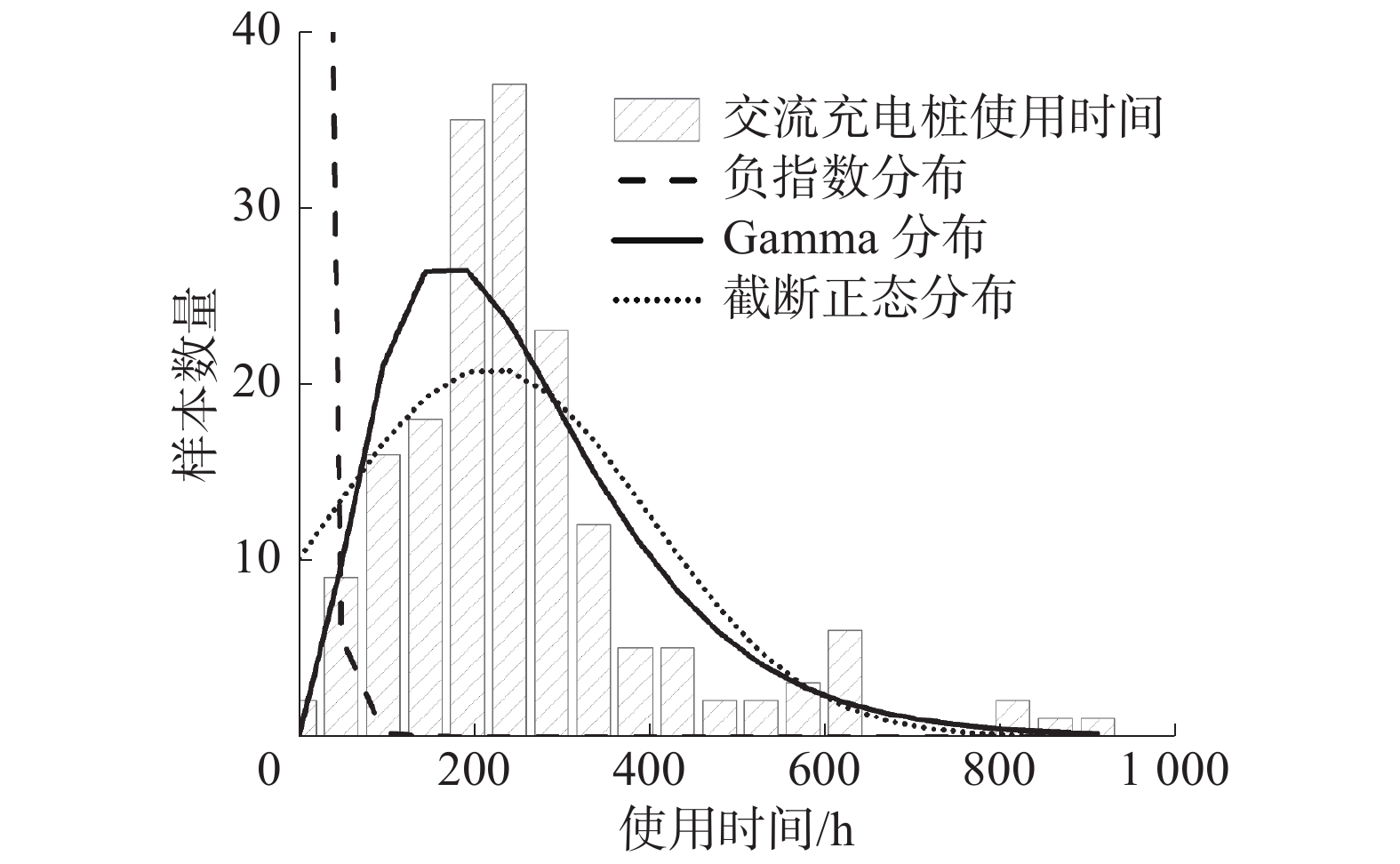
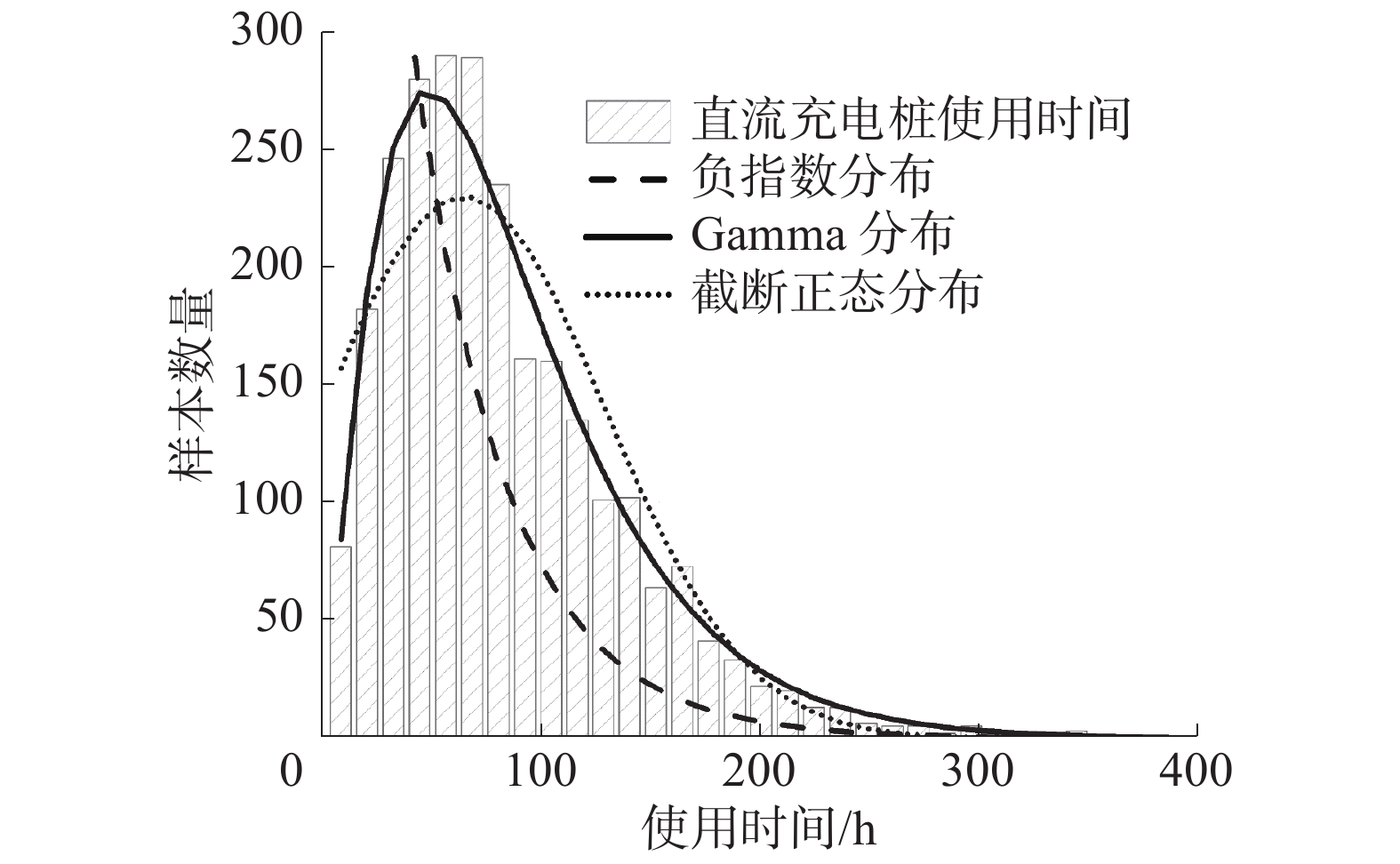
针对充电桩的平均服务时间,目前研究选择的分布包括负指数分布、正态分布等。本文对交流充电桩、直流充电桩平均服务时间进行了统计,图5、6为该充电站交流、直流充电桩的使用时间分布与几种典型分布的对比。
|
Download:
|
| 图 5 交流充电桩服务时间分布 | |
|
Download:
|
| 图 6 直流充电桩服务时间分布 | |
表2、3为交流、直流充电桩使用时间分布拟合参数和K−S检验结果,其中Exp、Norm、Gamma分别为负指数分布、截断正态分布和Gamma分布,E、SE、M分别为分布参数的估计值、估计值标准误差和分布均值,θ为负指数分布的尺度参数,μ、σ为截断正态分布的位置参数和尺度参数,α、β为Gamma分布的形状参数和尺度参数,p为显著性水平,h为检验结果。
|
|
表 2 交流充电桩充电时间分布的K−S检验结果 |
|
|
表 3 直流充电桩充电时间分布的K−S检验结果 |
如表2、3所见,在显著性水平0.05的条件下,该充电站内充电桩的服务时间长度近似服从Gamma分布,其概率密度函数为
| ${{f}}(x) = \frac{{{\beta ^\alpha }}}{{\mathit{\Gamma} (\alpha )}}{x^{\alpha - 1}}{{\rm{e}}^{ - \beta x}},x > 0$ | (3) |
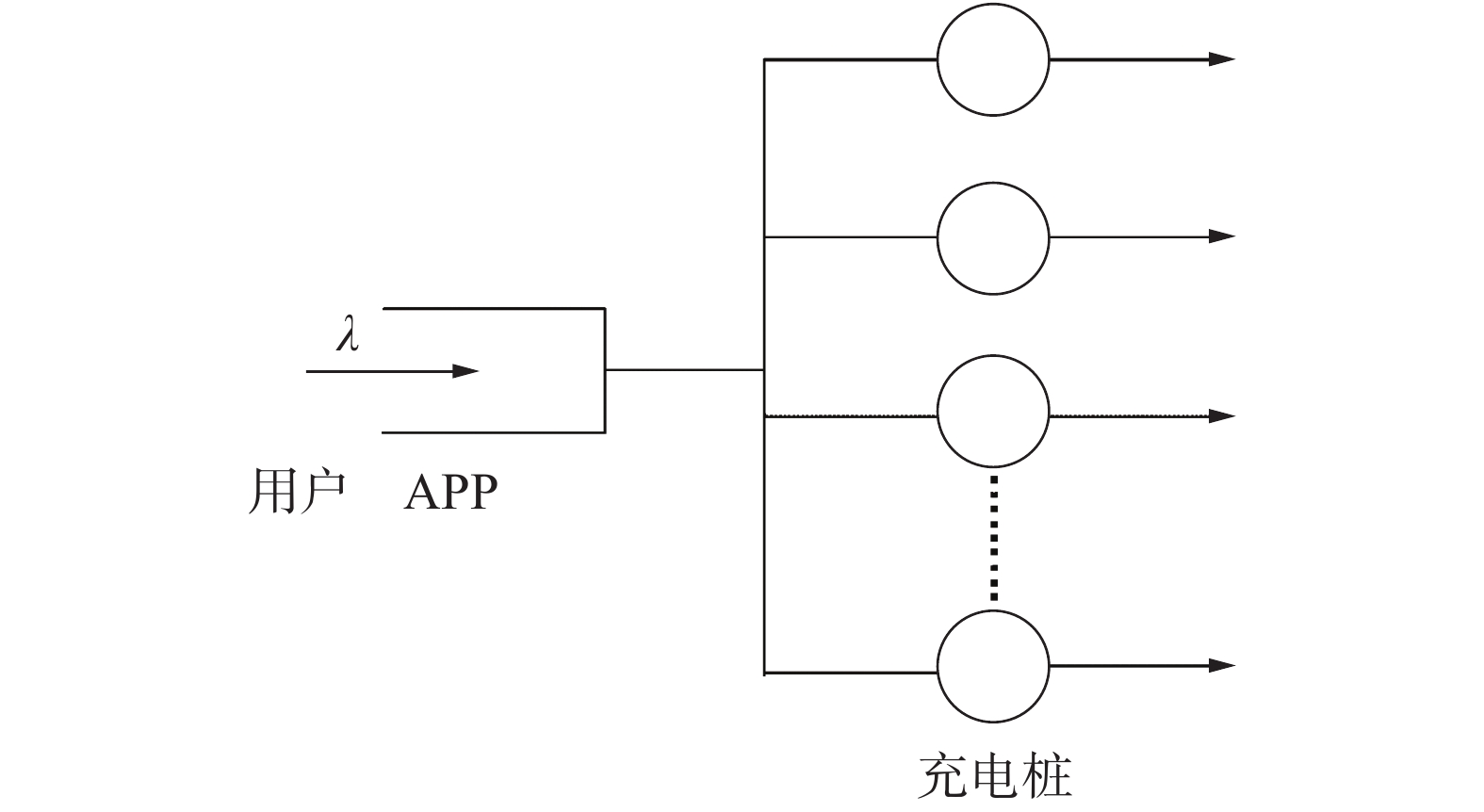
式中:α为Gamma分布的形状参数;β为Gamma分布的尺度参数。本文基于分布拟合数据建立了M/G/k排队模型,即到达时间间隔服从负指数分布,平均服务时间为一般分布的多服务台模型,如图7所示。用户通过客户端APP程序查看充电站是否有空闲充电桩(单队列),并抵达充电站寻找空闲充电桩进行充电(多服务台)。
|
Download:
|
| 图 7 充电站排队模型 | |
目前对于M/G/k排队模型尚没有公式化的推导过程,平均等待时间和平均排队长度等指标没有明确的数学表达式,可采用近似公式给出[14]。但对于不同队长的概率,则较难通过经验公式求解。本文基于MATLAB对M/G/k排队过程进行了蒙特卡洛仿真。为了对不同服务时间分布对排队模型的影响进行分析,除对现有4个时段的工况进行仿真外,本文还对用户持续增长后工作日昼间、工作日夜间和非工作日昼间的工况进行了仿真,仿真工况如表4所示。
|
|
表 4 仿真工况 |
其中仿真工况1~4基于现有统计数据,对不同时段的排队状态进行模拟,仿真工况5~10为用户增长后的工作日昼间工况,仿真工况11~16为用户增长后的工作日夜间工况,仿真工况17~22为用户增长后的非工作日昼间工况。假设用户的充电习惯不随用户数量增长发生改变,客流量随用户数量线性增长,则可建立5~22工况用户到达时间间隔分布的尺度参数θ与对应工况当前参数间的联系:
| $\frac{n}{{{n_0}}}{\rm{ = }}\frac{\lambda }{{{\lambda _{\rm{0}}}}}{\rm{ = }}\frac{\theta }{{{\theta _{\rm{0}}}}}{\rm{ = }}\alpha $ | (4) |
式中:
本文分别对服务时间服从负指数分布、截断正态分布、Gamma分布的条件进行了40次仿真,为了对蒙特卡洛模型的收敛性进行评估,应对多次仿真结果的关键参数离散度进行分析。由于各参数量纲、均值不同,选用离散系数Cν作为收敛判据,其可以对量纲、均数不同的多个数据集的离散程度进行比较[15],表达式为
| ${C_\nu }{\rm{ = }}\sigma {\rm{/}}\mu $ | (5) |
式中:σ为样本的标准差;μ为样本的平均值。
当客流量较低时,排队时间、排队人数、无空闲充电桩概率接均接近于0,无法对收敛程度进行反映,选取其中数值大于10−4的参数进行统计。表5为1~4工况排队关键参数的离散系数,其中W为用户在充电站平均停留时间,Wq为用户在充电站的平均排队时间,Ws为用户在充电站的平均服务时间,L为系统中平均人数,Lq为平均排队人数,P为无空闲充电桩的概率。
|
|
表 5 关键参数的离散系数Cν |
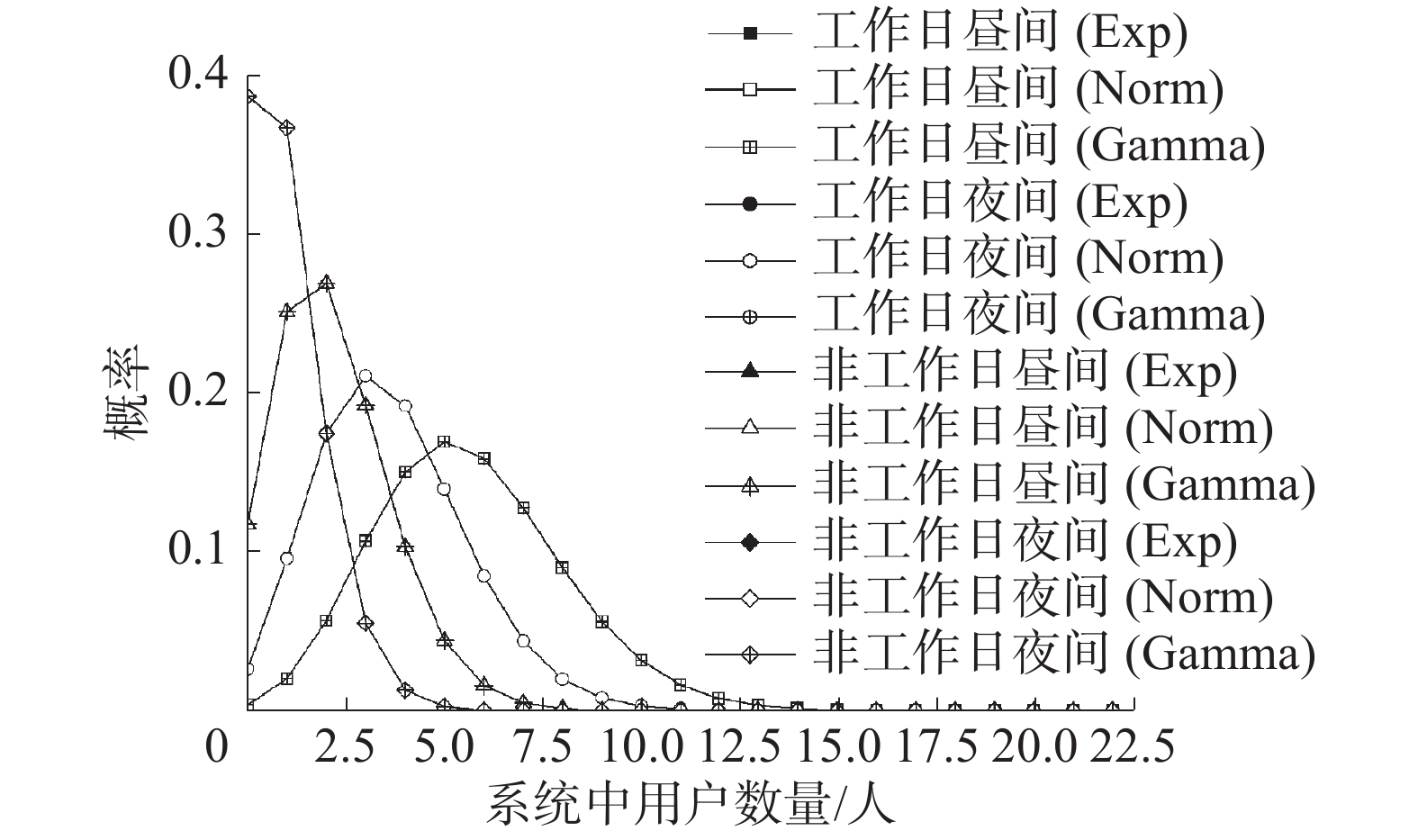
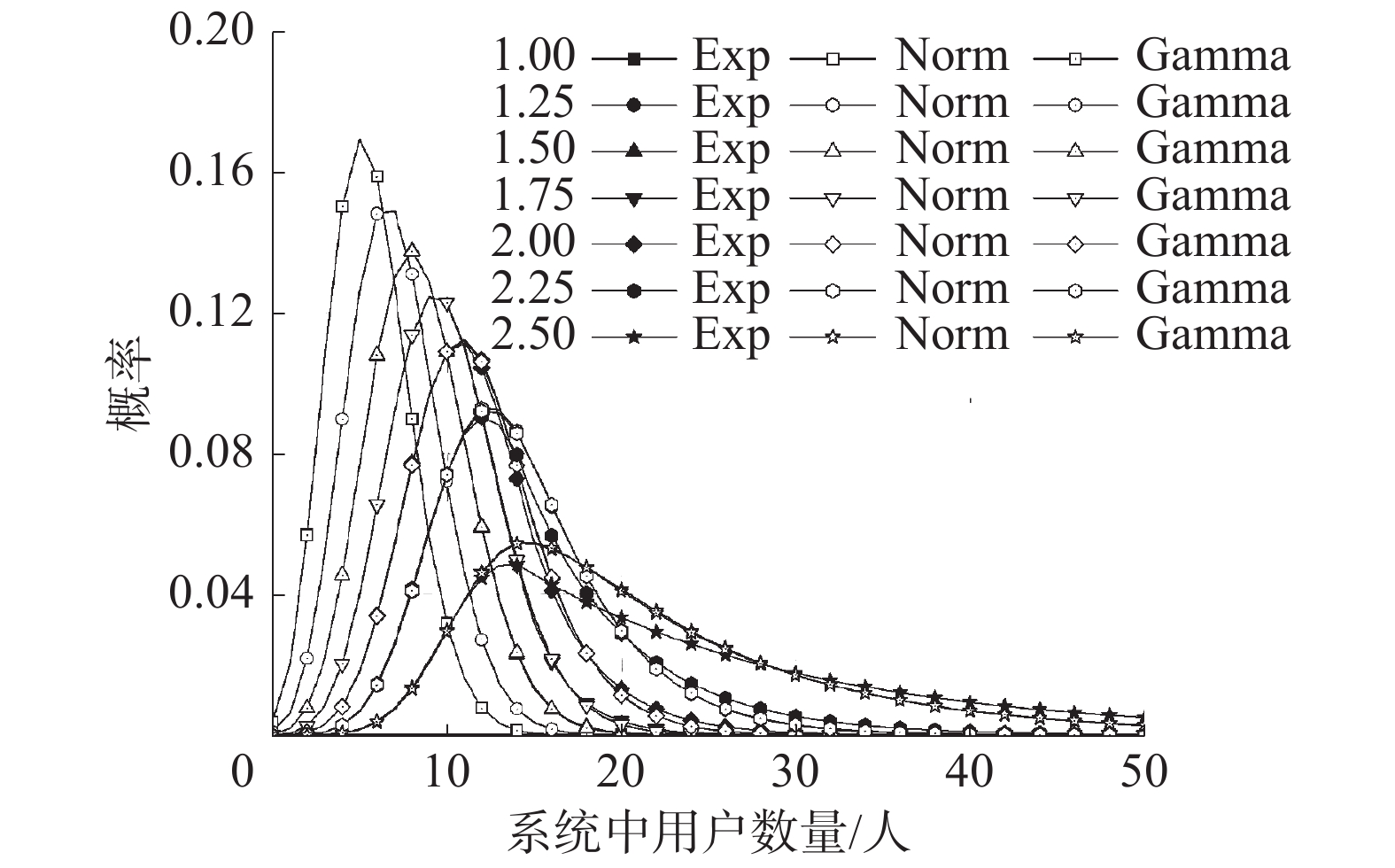
如表中所见,统计参数的离散系数均在0.05以下,即多次蒙特卡洛仿真获得的结果非常接近,可以代表该排队模型的关键参数。图8为通过蒙特卡洛仿真方法模拟的排队过程中,不同工况条件下稳态时系统内用户数量的概率分布;图9为客流量继续增加时系统内用户数量概率分布。
|
Download:
|
| 图 8 不同时段系统内用户数量分布 | |
|
Download:
|
| 图 9 不同客流量下系统内用户数量分布 | |
如图中所见,对于系统负载率较低的工况,即平均排队长度较小时,由于用户发现空闲充电桩的几率较高,充电服务时间的分布形式对系统中用户数量影响很小。随着充电人数的增加,服务时间服从截断正态分布与Gamma分布计算结果较为接近,负指数分布则产生了较大差异。表6为工作日昼间用户数量继续增长时的排队关键参数列表。
|
|
表 6 不同用户数量时排队模型的关键参数 |
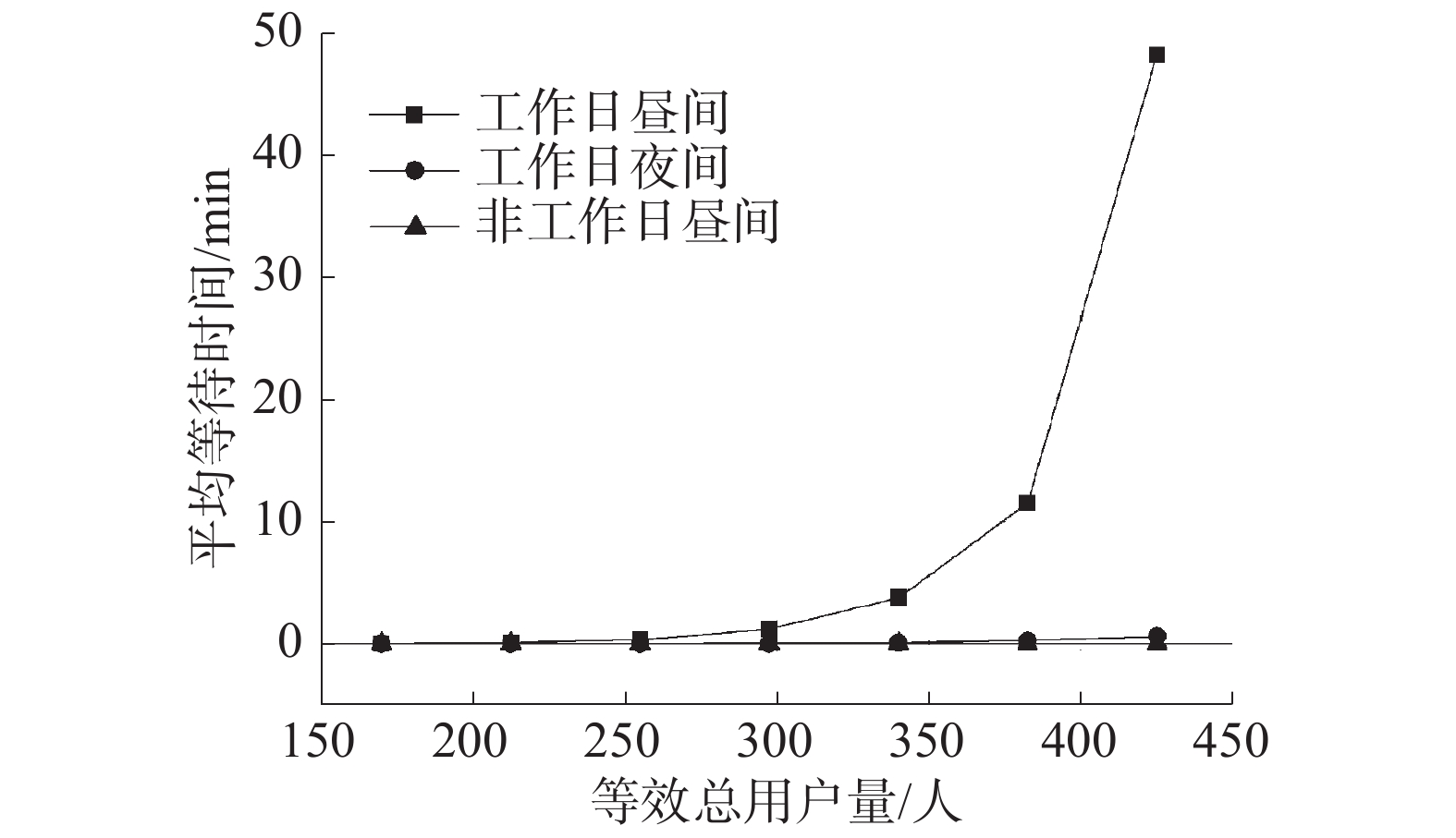
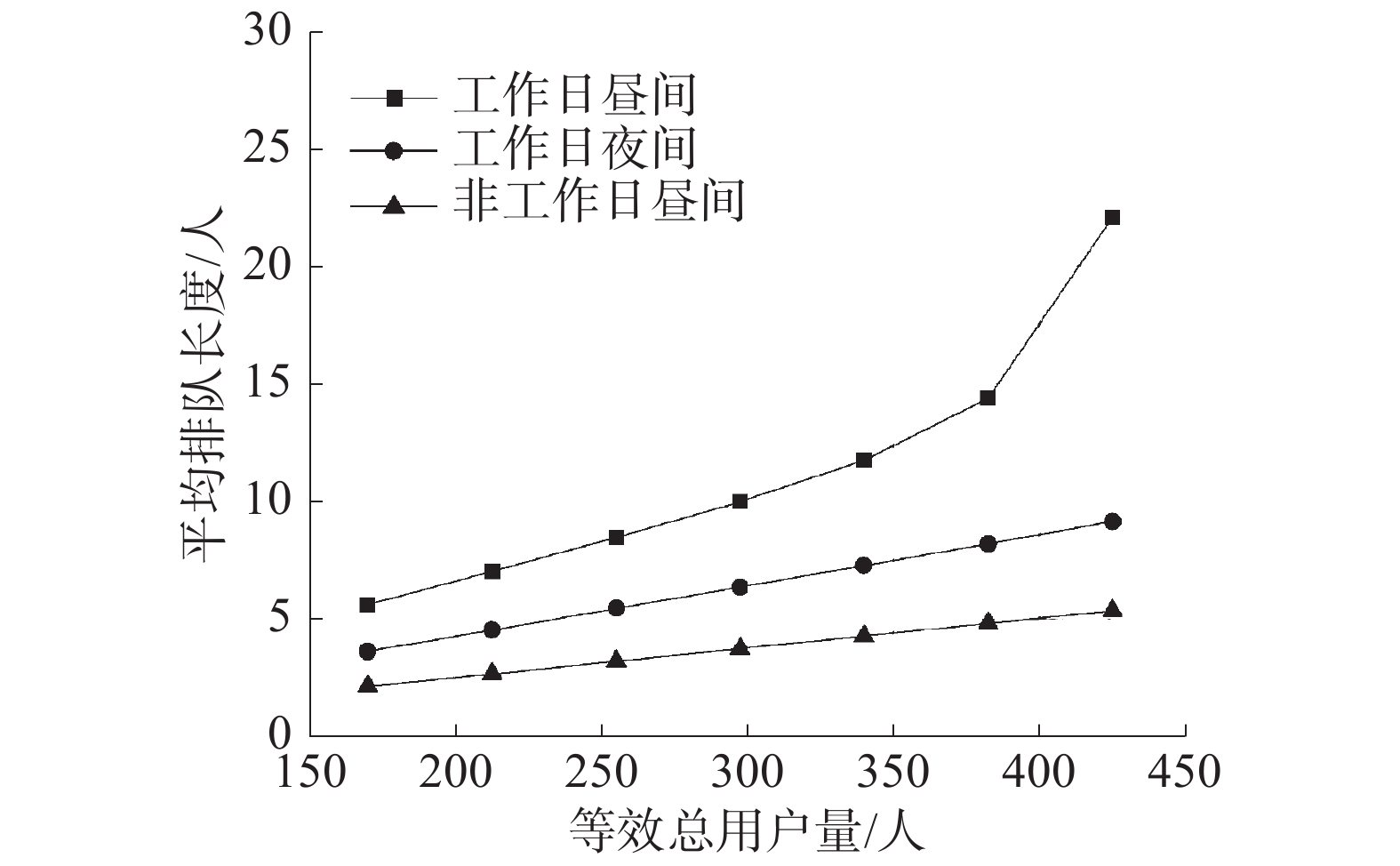
如表中所见,在充电桩客流量较低时,由于不同服务时间分布的数学期望一致,排队时间等关键指标差异不大。随着客流量增大,服务时间的分布对平均排队长度、平均排队时间均会产生影响,其中截断正态分布与Gamma分布的计算结果较为接近,负指数分布的计算结果则偏差较大,这与文献[10]的结论是相似的。即针对电动汽车充电桩排队优化的问题中的服务时间分布,应选取与实际情况最为接近的Gamma分布或截断正态分布。如图10、11为用户数量增长时,工作日昼间、工作日夜间、非工作日昼间的排队平均等待时间和平均排队长度变化趋势。
|
Download:
|
| 图 10 平均等待时间 | |
|
Download:
|
| 图 11 平均排队长度 | |
如图中所见,对于工作日夜间、非工作日昼间的关键参数随总户数量的增加而平稳增长;对于工作日昼间工况,当总用户达到383人以上时,平均等待时间和平均排队长度迅速增加,可能达到40 min以上。即针对大型园区内部充电桩建设数量问题,当用户充电习惯和现有情况一致时,充电桩数量不应低于0.04桩/人,否则可能导致高峰时段充电等待时间过长。
3 结论本文针对大型园区内部电动汽车充电站的规划、建设问题,整理了3个月间某大型工业园区内部充电站的使用信息,统计了用户在充电周期、充电量、服务时间上的习惯;在现有用户负荷的基础上,基于M/G/k排队模型,建立了大型园区内部直流充电桩的排队仿真模型;通过蒙特卡洛方法给出了不同时段充电站的平均人数、排队长度等参数;分析了不同服务时间分布所带来的影响,并对未来客流量进一步增加时的关键参数进行了仿真,得出如下的结论:
1)大型园区内部充电桩使用率随时间变化存在较大波动,平均充电人数可相差10倍以上,当计算充电站对于区域电网负载影响时,应当考虑其工作日昼间的工况。
2)充电桩服务时间近似服从Gamma分布,充电桩负载较低(排队时间Wq≈0)时,排队模型的关键参数仅和分布的数学期望有关,此时各种分布计算结果很接近。随着客流量增大,模型间差异逐渐增大,选取与实际情况最接近的Gamma分布或截断正态分布计算结果较为接近,均可用于对充电站的排队估算。
3)针对大型工业园区内部的充电桩规划、建设问题,当仅考虑直流充电桩时,若用户充电习惯不发生明显变化时,充电桩的建设数量不应低于0.04桩/人,否则可能导致高峰时段排队时间长于30 min以上。对于其他情况下的充电桩占用率估算,可使用本文建立排队模型进行计算。
| [1] |
张文亮, 武斌, 李武峰, 等. 我国纯电动汽车的发展方向及能源供给模式的探讨[J]. 电网技术, 2009, 33(4): 1-5. DOI:10.3969/j.issn.1674-0629.2009.04.001 ( 0) 0)
|
| [2] |
肖湘宁, 温剑锋, 陶顺, 等. 电动汽车充电基础设施规划中若干关键问题的研究与建议[J]. 电工技术学报, 2014, 29(8): 1-10. DOI:10.3969/j.issn.1000-6753.2014.08.001 ( 0) 0)
|
| [3] |
王姝凝, 杨少兵. 居民小区电动汽车充电负荷有序控制策略[J]. 电力系统自动化, 2016, 40(4): 71-77. DOI:10.7500/AEPS20150429013 ( 0) 0)
|
| [4] |
刘文霞, 刘流, 赵天阳. 变电站区域充电桩接入控制模式及策略[J]. 电力系统自动化, 2013, 37(16): 66-72. DOI:10.7500/AEPS201209081 ( 0) 0)
|
| [5] |
赵明宇, 王刚, 汪映辉, 等. 电动汽车充电设施监控系统设计与实现[J]. 电力系统自动化, 2011, 35(10): 65-69, 98. ( 0) 0)
|
| [6] |
贾龙, 胡泽春, 宋永华. 考虑不同类型充电需求的城市内电动汽车充电设施综合规划[J]. 电网技术, 2016, 40(9): 2579-2587. ( 0) 0)
|
| [7] |
张帝, 姜久春, 张维戈, 等. 电动出租车充电桩优化配置[J]. 电工技术学报, 2015, 30(18): 181-188. DOI:10.3969/j.issn.1000-6753.2015.18.022 ( 0) 0)
|
| [8] |
周雪会, 王希平. 考虑顾客满意度的电动汽车充电桩规划策略[J]. 可再生能源, 2017, 35(6): 933-939. DOI:10.3969/j.issn.1671-5292.2017.06.021 ( 0) 0)
|
| [9] |
李建军, 刘力维, 黄振生. 基于排队模型的电动汽车充电桩数量优化设计[J]. 数学的实践与认识, 2017, 47(9): 212-218. ( 0) 0)
|
| [10] |
张维戈, 陈连福, 黄彧, 等. M/G/k排队模型在电动出租汽车充电站排队系统中的应用[J]. 电网技术, 2015, 39(3): 724-729. ( 0) 0)
|
| [11] |
孟旭瑶, 张维戈, 鲍谚, 等. 考虑充电功率的电动汽车快充站充电设施优化配置[J]. 电力自动化设备, 2018, 38(7): 28-34. ( 0) 0)
|
| [12] |
报告: 北京居民上班路途全国最远平均17.4公里[N/OL]. 中国新闻网. (2018−01−27). https://wemedia.ifeng.com/46763100/wemedia.shtml.
( 0) 0)
|
| [13] |
许挺, 张磊, 梁一桥. 电动汽车的能耗效率分析及提高能耗经济性的研究[J]. 能源工程, 2011(2): 1-5. DOI:10.3969/j.issn.1004-3950.2011.02.001 ( 0) 0)
|
| [14] |
KIMURA T. Diffusion approximation for an M/G/m queue
[J]. Operations research, 1983, 31(2): 304-321. DOI:10.1287/opre.31.2.304 ( 0) 0)
|
| [15] |
刘杰. 基于变异系数的COD行业优化分配模型研究[J]. 数学的实践与认识, 2015, 45(8): 172-178. ( 0) 0)
|
 2019, Vol. 46
2019, Vol. 46


