单通道干涉仪测向系统中，需要一个高精度的数字移相器对天线信号在0°～360°（步进小于1°）内进行多次移相^[1]。系统中移相器的误差，会引起天线阵元间的相位差测量结果附加误差，进而影响测向精度^[2]，因此对移相器的研究有着重要的意义。传统的移相器多采用单片数字移相器芯片或模拟移相器芯片结合外围控制电路设计实现^[3-5]。目前，数字移相器芯片的精度可以达到6位，最小步进为5.625°，但工作频段范围主要为1 GHz以上；而模拟移相器芯片的精度受控制电压精度的影响，且移相相位与电压改变是非线性关系，要实现0°～360°的数字移相较困难^[6]。本文所研究的基于直接频率合成、混频技术的数字移相器，可以实现单通道干涉仪测向系统对移相器的要求。

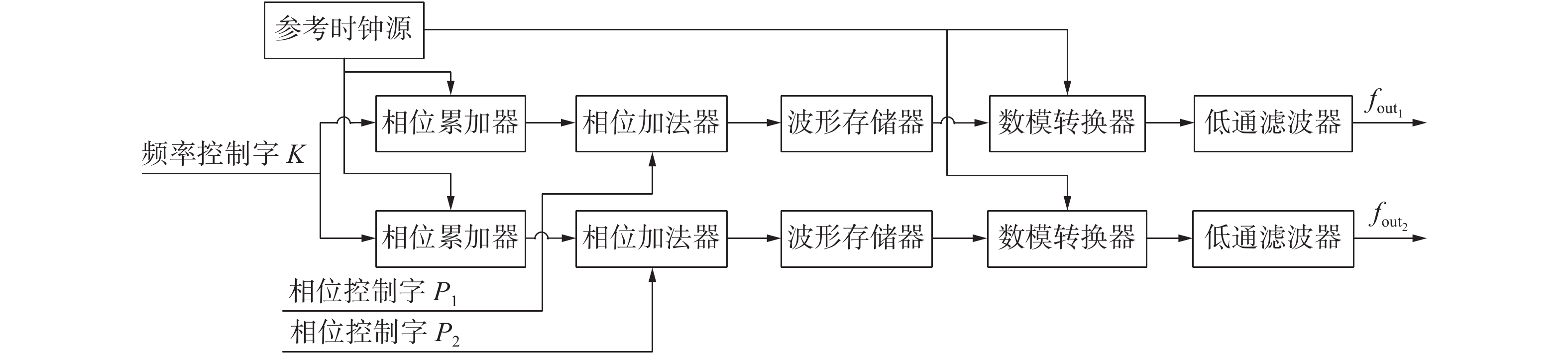
1 移相器的工作原理 1.1 DDS信号发生器

直接数字频率合成^[7]（DDS）信号发生器的原理框图如图1所示。它由1个参考时钟源、2个相位累加器、2个数字加法器、2个波形存储器、2个数模转换器以及2个低通滤波器等组成。2个波形存储器中存储的是同一余弦波的归一化空间采样。2个相位累加器由同一个参考时钟源驱动，且由同一个频率控制字控制。2个数字加法器由2个不同的相位控制字控制。根据DDS的原理，DDS信号发生器输出的信号的频率和频率分辨率、相位分辨率可以表示如下^[8]：

$ \begin{array}{l} {f_{{\rm{out}}}} = K \times {f_c}/{2^N} \\ \Delta f = {f_c}/{2^N} \\ \Delta \theta = 2{\text{π}}/{2^N} \end{array} $

式中： ${f_{{\rm{out}}}}$ 为输出信号频率；K为频率控制字；N为相位累加器字长； $\Delta f$ 为频率分辨率； ${f_c}$ 为系统参考时钟； $\Delta \theta $ 为相位分辨率。

如图1所示，该DDS信号发生器的功能是通过输入1个频率控制字和2个相位控制字，实现输出2路同频信号。通过不同的相位控制字使数字加法器的值不同，实现两路信号在同一时刻始终出现固定的相位偏移。相位控制字的字长P小于或等于相位累加器的字长N且与相位累加器输出的高位对齐。DDS信号发生器输出信号的最小相位差 $\Delta \theta '$ 可以表示为

$\Delta \theta ' = 2{\text{π}}/{2^P}$

(1)

式中P为相位控制字字长。

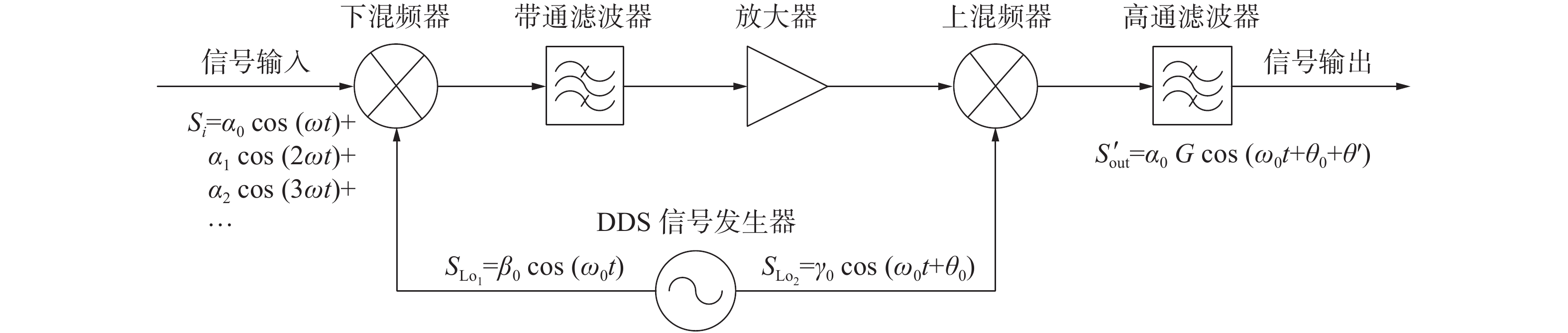
1.2 移相器

移相器的原理框图如图2所示。它主要由2个混频器、1个带通滤波器、1个高通滤波器、1个DDS信号发生器组成。DDS信号发生器的两路输出作为2个混频器的本振输入信号。2个混频器分别进行下混频和上混频^[9]，带通滤波器的中心频率为输入信号频率减去本振频率，带宽约为本振信号频率的一半。由于下混频器的本振信号和上混频器的本振信号同步，且频率相同，相位有固定偏差，因此输出信号与输入信号频率相同，且存在固定的相位差。通过控制两本振信号的相位差，即可实现对输入射频信号移相。

根据图2的原理，在不考虑传输路径和器件本身延迟的条件下，包含有谐波分量的射频输入信号 ${s_i}$ 、下混频器本振信号 ${S_{{\rm{L}}{{\rm{o}}_1}}}$ 和上混频器本振信号 ${S_{{\rm{L}}{{\rm{o}}_2}}}$ 可以表示为：

$\begin{split} & {S_i} = {\alpha _0}\cos (\omega t){\rm{ + }}{\alpha _1}\cos (2\omega t){\rm{ + }}{\alpha _2}\cos (3\omega t){\rm{ + }} \cdots \\ & {S_{{\rm{L}}{{\rm{o}}_1}}} = {\beta _0}\cos ({\omega _0}t) + {\beta _1}\cos (2{\omega _0}t) + {\beta _2}\cos (3{\omega _0}t) + \cdots \\ & {S_{{\rm{L}}{{\rm{o}}_2}}} = {\gamma _0}\cos ({\omega _0}t + {\theta _0}) + \;{\gamma _1}\cos (2{\omega _0}t + {\theta _1}) + \; \\ & \;\;\;\;\;\;\;\; {\gamma _3}\cos (3{\omega _0}t + {\theta _2}) + \cdots \end{split} $

(2)

式中：t为时间； $\omega $ 为输入信号基波频率； ${\omega _0}$ 为本振信号基波频率； ${\alpha _0}$ 、 ${\alpha _1}$ 、 ${\alpha _2}$ 为输入信号基波、一次谐波、二次谐波的幅度系数； ${\beta _0}$ 、 ${\beta _1}$ 、 ${\beta _2}$ 为下混频器本振信号的基波、一次谐波、二次谐波的幅度系数； ${\gamma _0}$ 、 ${\gamma _1}$ 、 ${\gamma _2}$ 为上混频器本振信号的基波、一次谐波、二次谐波的幅度系数^[10-11]。

由于信号发生器的输出端有匹配的低通滤波器，因此本振信号的谐波幅度很小，可以忽略，即式（2）中的 ${\beta _1}$ 、 ${\beta _2}$ 和 ${\gamma _1}$ 、 ${\gamma _2}$ 等系数为0。

经过下混频之后，输出信号主要有输入信号频率的基频分量，输入信号基频分量和输入信号谐波分量与本振信号的和频、差频分量，可以表示为

$ \begin{array}{l} {S_{{\rm{I}}{{\rm{F}}_1}}} = {\alpha _0}{a_0}\cos [(\omega + {\omega _0})t + {\phi _{{a_0}}}] + \;{\alpha _0}{b_0}\cos [(\omega - {\omega _0})t + {\phi _{{b_0}}}] + \\ \;\;\;\;\;\;\;\;{\alpha _0}{c_0}\cos (\omega t + {\phi _{c_0}}) + {\alpha _1}{a_1}\cos [(2\omega + {\omega _0})t + {\phi _{{a_1}}}] + \\ \;\;\;\;\;\;\;\;{\alpha _1}{b_1}\cos [(2\omega - {\omega _0})t + {\phi _{{b_1}}}] + {\alpha _1}{c_1}\cos (2\omega t + {\phi _{{c_1}}}) + \\ \;\;\;\;\;\;\;\;{\alpha _2}{a_2}\cos [(3\omega + {\omega _0})t + {\phi _{{a_2}}}] + {\alpha _2}{b_2}\cos [(3\omega - {\omega _0})t + {\phi _{{b_2}}}] + \\ \;\;\;\;\;\;\;\;{\alpha _2}{c_2}\cos (3\omega t + {\phi _{c_2}}) + \cdots \\ \end{array} $

式中： ${S_{{\rm{I}}{{\rm{F}}_1}}}$ 为下混频器输出的信号； ${a_0}$ 、 ${b_0}$ 、 ${c_0}$ 、 ${a_1}$ 、 ${b_1}$ 、 ${c_1}$ 、 ${a_2}$ 、 ${b_2}$ 、 ${c_2}$ 等为下混频器在相应频率成分上的幅度衰减系数； ${\phi _{a_0}}$ 、 ${\phi _{b_0}}$ 、 ${\phi _{c_0}}$ 、 ${\phi _{a_1}}$ 、 ${\phi _{b_1}}$ 、 ${\phi _{c_1}}$ 、 ${\phi _{a_2}}$ 、 ${\phi _{b_2}}$ 、 ${\phi _{c_2}}$ 等为下混频器在相应频率上引入的相位差。

由于除了输入信号基频与下混频器本振信号的差频信号以外的信号都位于带通滤波器的阻带处，因此带通滤波器的输出信号 ${S_{{\rm{I}}{{\rm{F}}_2}}}$ 可以表示为

$ {S_{{\rm{I}}{{\rm{F}}_{\rm{2}}}}} = {\alpha _0}{b_0}{G_0}\cos [(\omega - {\omega _0})t + {\phi _{{b_0}}} + {\phi _{{G_0}}}] $

式中：G₀为带通滤波器的带内衰减系数； ${\phi _{{G_0}}}$ 为带通滤波器引入的相位差。

通过上混频器后的信号可表示为

$\begin{array}{l} {S_{{\rm{I}}{{\rm{F}}_{\rm{4}}}}} \!=\! {\alpha _0}{b_0}{G_0}{G_1}{G_{{m_0}}}\cos (\omega t \!+\! {\theta _0} \!+\! \;{\phi _{{b_0}}} \!+\! {\phi _{{G_0}}} \!+\! {\phi _{{G_1}}} \!+\! {\phi _{{m_0}}}) + \\ \;\;\;\;\;\;\;\;{\alpha _0}{b_0}{G_0}{G_1}{G_{{m_1}}}\cos [(\omega \!-\! 2{\omega _0})t \!-\! {\theta _0} \!+\! {\phi _{{b_0}}} \!+\! {\phi _{{G_0}}} \!+\! {\phi _{{G_1}}} \!+\! {\phi _{{m_1}}}] + \\ \;\;\;\;\;\;\;\;{\alpha _0}{b_0}{G_0}{G_1}{G_{{m_2}}}\cos [(\omega \!-\! {\omega _0})t \!+\! \;{\phi _{{b_0}}} \!+\! {\phi _{{G_0}}} \!+\! {\phi _{{G_1}}} \!+\! {\phi _{{m_2}}}] \\ \end{array} $

式中： ${G_{{m_0}}}$ 、 ${G_{{m_1}}}$ 、 ${G_{{m_2}}}$ 为混频器在相应频率成分上的幅度衰减； ${\phi _{{m_0}}}$ 、 ${\phi _{{m_1}}}$ 、 ${\phi _{{m_2}}}$ 为混频器在相应频率上引入的相位差。

通过高通滤波器后的信号可表示为

$ \begin{array}{l} {S_{{\rm{out}}}} = {\alpha _0}{b_0}{G_0}{G_1}{G_{{m_0}}}{G_2}\cos (\omega t + {\theta _0} + \\ \;\;\;\;\;\;\;\;{\phi _{{b_0}}} + {\phi _{{G_0}}} + {\phi _{{G_1}}} + {\phi _{{m_0}}} + {\phi _2}) \\ \end{array} $

式中： ${G_{{m_0}}}$ 为上混频器的衰减系数；G₂为高通滤波器的带内衰减系数；ϕ₂为高通滤波器引入的相位差； ${\phi _{{m_0}}}$ 为上混频器引入的相位差。

当移相器的硬件确定后，传输路径和器件本身延迟导致的固有相位偏移为一固定值，即 ${\phi _{{b_0}}}$ 、 ${\phi _{{G_0}}}$ 、 ${\phi _{{G_1}}}$ 、 ${\phi _{{m_0}}}$ 、 ${\phi _2}$ 均为确定值，可以通过在 ${\theta _0} = 0$ 的条件下进行测量获得。各器件的增益和衰减也为确定值，即G为确定值，假设 ${\phi _{{b_0}}} + {\phi _{{G_0}}} + {\phi _{{G_1}}} + {\phi _{{m_0}}} + {\phi _2}{\rm{ = }}\theta '$ ， ${b_0}{G_0}{G_1}{G_{{m_0}}}{G_2}{\rm{ = }}G$ ，则移相器的输出可以表示为

$ {S'_{{\rm{out}}}} = {\alpha _0}{{G}}\cos (\omega t + {\theta _0} + \theta ') $

(3)

由式（3）可知，输入输出信号的相位差只与两本振信号相位差、移相器固有相位差有关，因此可通过控制两本振信号的相位差，即通过控制DDS信号发生器的相位控制字，实现对输入信号移相。移相器实际移相角度 $\theta $ 与两本振信号相位差 ${\theta _{{\rm{LO}}}}$ 的关系为

$ \theta = \Delta {\theta _{{\rm{LO}}}} + \theta ' $

式中 $\theta '$ 为移相器的固有相位差。

2 移相器样机的设计与实现

根据上述工作原理，搭建了移相器的原理样机，如图3所示。移相器中DDS信号发生器的DDS部分用FPGA实现，硬件由Xilinx公司的SP605评估板和自研的D/A FMC子卡组成。

DDS信号发生器的参考时钟频率为204.8 MHz，相位累加器字长为32位，频率控制字为6位，相位控制字为12位。根据奈奎斯特采样定理，理论上，DDS信号发生器可以输出频率不大于102.4 MHz的信号，但考虑到输出频率高时输出信号相位抖动比较大，而DDS信号发生器的输出信号频率主要影响移相器中的滤波器设计，与移相器的功能和移相精度无关。考虑到移相器中滤波器的实现难度^[12]，输出频率固定设置为10 MHz。由于相位控制字为12位，由式（1）可知，移相步进小于0.09°。

移相器样机的工作频率为432~434 MHz。两级混频电路的混频器和滤波器根据此频段进行选择，混频器的型号为Mini-Circuits公司的ZX05-25MH-S+，带通滤波器的通带频率为421~425 MHz^[13]，高通滤波器的截止频率为430 MHz，放大器的增益约为15 dB。

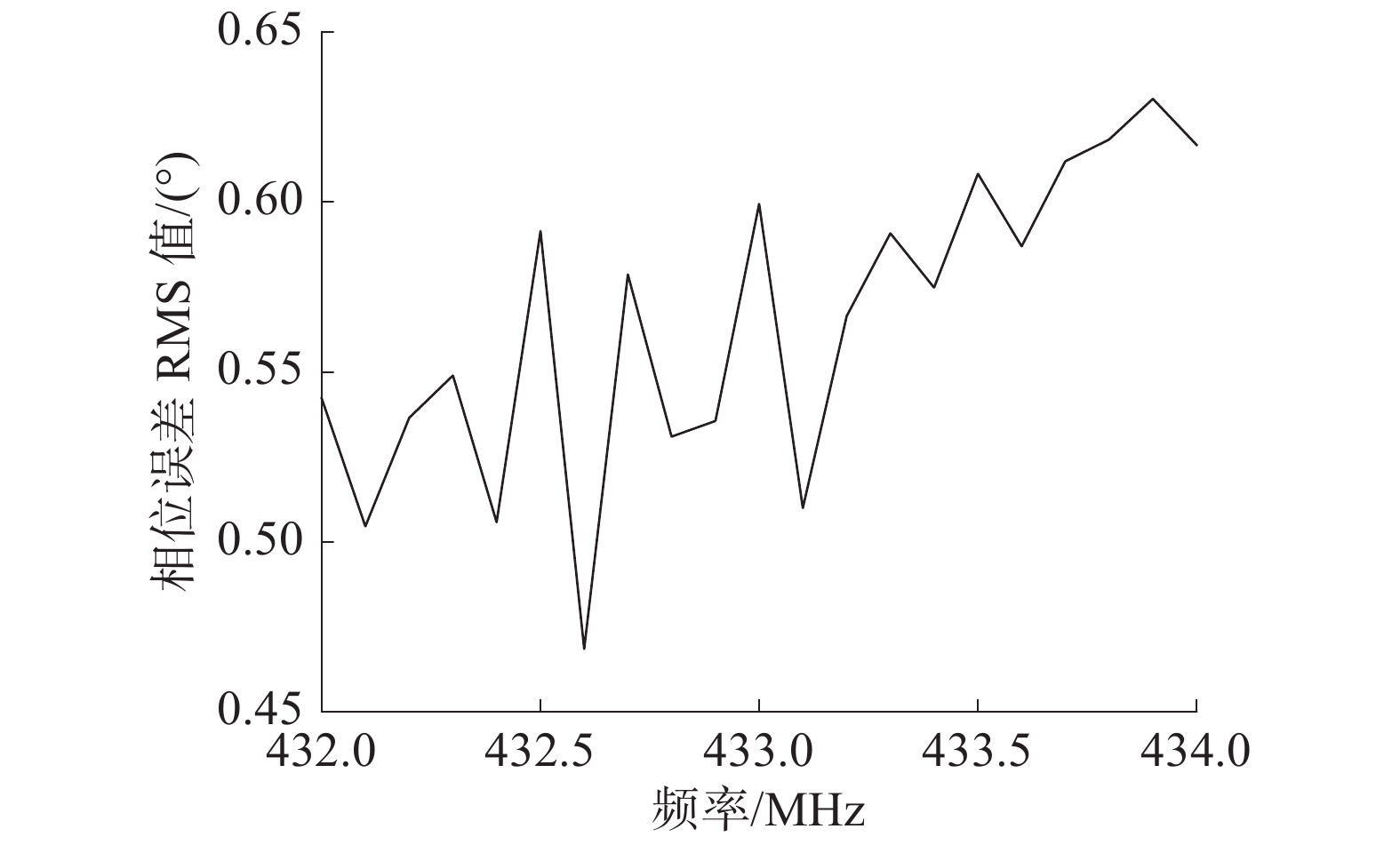
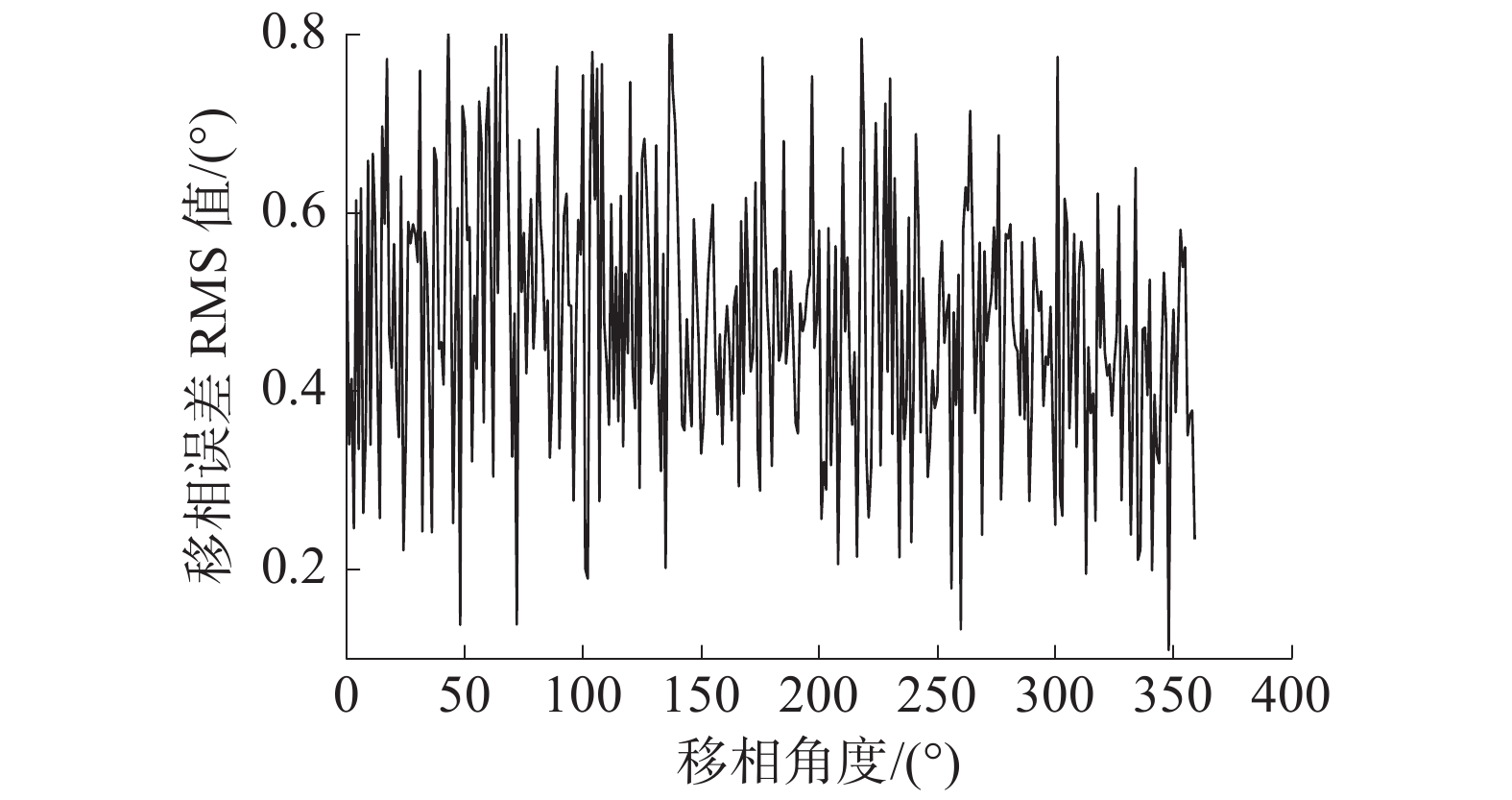
3 测量结果

采用Agilent公司的E5071C矢量网络分析仪按照频率步进0.1 MHz和移相角度步进约0.088°（对应DDS信号发生器的两路信号相位控制字相差1）对移相器进行了测试，并对移相器实测移相角度与理论移相角度之差（误差）的RMS值进行了统计。移相器在不同频率处的移相角度均方根误差数据见图4，移相器在不同移相角度处的移相角度均方根误差数据见图5。

4 结论

实验结果表明：1）移相器样机实现了432~434 MHz频率范围内的非同步输入信号0°～360°移相，且在频段内移相器的RMS误差小于0.65°；2）移相器在0°～360°的各个移相角度上的RMS误差均小于0.8°；3）移相器的步进小于0.09°。

通过本文的分析可知，提高移相器中DDS信号发生器的输出频率，并选择合适的中频滤波器，可以实现更大频率范围的输入信号移相；选用不同的中频滤波器，可以实现对不同频源的输出信号的功率有一定的要求，输入信号有能段的信号移相，具备较大的灵活性。同时，本移相器也存在一些缺点，电路相对复杂，对DDS信号量损失、系统噪声会引起输入信号信噪比下降。