图像拼接技术即通过校准融合,拼接若干存在重叠区域且视角和色彩差异不大的图像,从而获得高分辨率的全景图像。应用这种技术可以消除传统相机成像中高分辨率和广视角不可兼得的弊端[1]。凭借这一优势,该技术已广泛应用于现代研究的多个领域,不仅与人们的生活息息相关,也为科学研究和生产实践带来了便利。
图像拼接主要分为图像采集、图像预处理、图像配准和图像融合4个步骤,其中关键步骤为图像配准和图像融合[2]。在图像采集过程中,获得的图像中往往存在运动中的物体,这就造成了图像拼接过程中运动物体的撕裂或重叠,即鬼影现象和重影现象。针对这一问题,1998年,ML Duplaquet等[3]提出了最佳缝合线算法,该算法应用动态规划的思想,使缝合接缝避开运动物体,有效地减轻鬼影、重影现象,但是该算法没有对图像之间的色彩差异进行处理,存在明显的拼接接缝。近年来,国内外研究者在这一问题上做了大量工作。2012年,党建武等[4]通过对特征点进行加权,使缝合线优先通过特征点区域,但其算法的鲁棒性不佳,对于配准误差较大的图像融合效果较差。2013年,Gao等[5]提出一种接缝对比的方法,该方法首先估计待拼接图像间的多个变换模型,然后在每个模型中各获得一条最佳拼接接缝,最后对比所有接缝与源图像中同一区域的相似度,从而得到最佳变换模型和最佳缝合线,这种方法有效地解决了图像拼接过程中因变换模型选取不当带来的误差,但算法本身计算量大,效率不高。其后,瞿中等[6]提出在最佳缝合线两侧使用加权平均的图像融合算法,这种方法在一定程度上降低了拼接接缝问题,但其算法鲁棒性不佳。2018年,张翔等[7]将局部信息权重引入最佳缝合线搜索规则中,并使用自适应权值的加权融合方法对图像的重叠区域进行融合,在两图拼接应用中取得了良好的拼接效果,但在存在多种色彩差异的图像拼接中表现较差。针对最佳缝合线算法中存在的拼接接缝问题,提出一种改进算法,经实验验证,该算法能够有效解决拼接中存在的接缝问题,提高图像拼接质量。
1 最佳缝合线算法最佳缝合线算法通过在图像的重叠区域寻找最佳接缝,能够有效地消除动态融合场景中的鬼影、重影现象。最佳缝合线算法中的最佳接缝指的是两幅图像中重叠区域颜色差异最小且几何结构最相近的连续像素点的集合[2]。最佳接缝可以避开图像重叠区域中的运动物体和色彩差异较大的区域,从而消除传统拼接方法中出现的鬼影和重影问题。
定义
1)以重叠区域图像第1行为起始,每一个点都作为本列的始点,至上而下进行遍历,每一列都生成一条缝合线;
2)设当前遍历点的坐标为
3)比较求得的3个差异强度值,选择强度值最小的点为下一个落在缝合线上的点
4)将每条缝合线各段路径差异强度值相加,并比较所有路径的差异强度和大小,强度和最小的路径即为最佳缝合线。
最佳缝合线的搜索过程如图1所示。
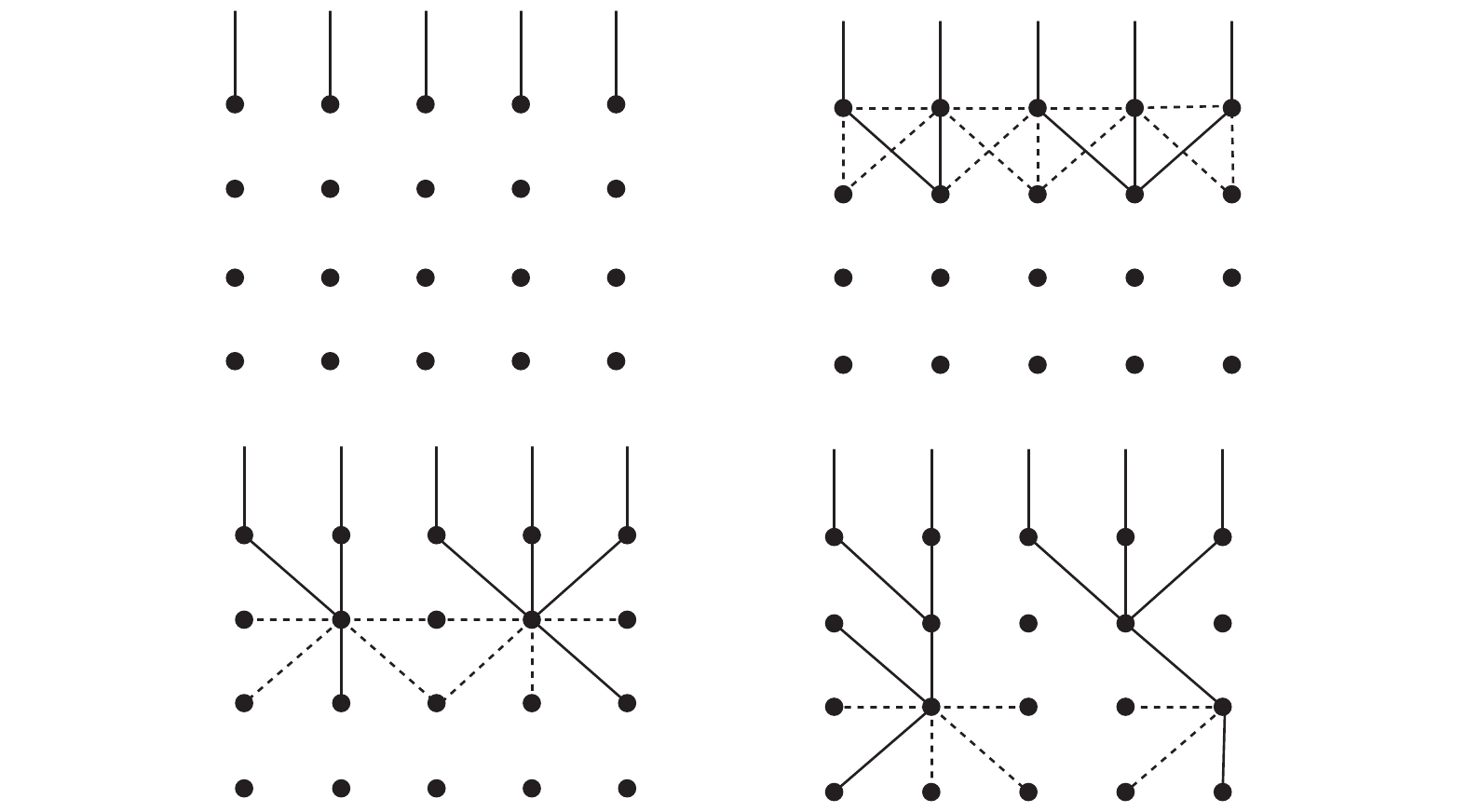
|
Download:
|
| 图 1 最佳缝合线搜索流程示意 | |
得到最佳缝合线后,将缝合线两侧的像素值分别置为0和1,即可得到图像的拼接掩模。结合拼接掩模,使用图像融合算法得到拼接图像。
2 多频段融合算法多频段融合算法能够消除图像中的色彩过渡不自然现象,算法基本思想是将图像进行多尺度分解,根据不同的尺度算子来融合权重,使用获得的不同权重进行融合[9]。相比简单的线性混合方法会对图像产生模糊,多频段融合算法对图像的处理是在不同尺度域中进行的,通过在不同尺度下使用不同权重进行图像融合,使得融合过程中能够保留更多的细节信息,避免了图像细节的丢失,从而获得高质量图像。
在多频段融合中,首先对待融合图像进行下采样,并与高斯核进行卷积得到图像的高斯金字塔,高斯金字塔图层
| $\begin{split} &L\left( {x,y,\sigma } \right) = G\left( {x,y,\sigma } \right) * I\left( {x,y} \right)\\ &G\left( {x,y,\sigma } \right) = \frac{1}{{2{\text{π}} {\sigma ^2}}}\exp \left( {\frac{{{x^2} + {y^2}}}{{2{\sigma ^2}}}} \right)\end{split} $ |
式中:
高斯金字塔相邻图像层进行差分即可得到图像的拉普拉斯金字塔,拉普拉斯金字塔图层
| $ D\left( {x,y,\sigma } \right) = L\left( {x,y,k\sigma } \right) - L\left( {x,y,\sigma } \right) $ |
得到的拉普拉斯金字塔有
| $ I'\left( {x,y} \right) = p\left( x \right) \times {I_1}\left( {x,y} \right) + \left[ {1 - p\left( x \right)} \right] \times {I_2}\left( {x,y} \right) $ |
式中权重函数
| $ p\left( x \right) = \frac{{{x_2} - x}}{{{x_2} - {x_1}}} $ |
式中
将融合后的拉普拉斯金字塔进行逆向重构,重构步骤如下:
1)设拉普拉斯金字塔层数为
2)将源图像上采样,上采样结果尺度与第i层高斯金字塔的尺度保持一致,并进行平滑处理;
3)平滑后的图像与拉普拉斯金字塔第
4)重复步骤2)、3);
5)当
由于最佳缝合线算法自身具有较强的鲁棒性,在求取最佳缝合线之前,将图像进行下采样,将图像变换到小尺度空间下,然后求得图像的最佳缝合线掩膜,对掩膜上采样即可得到原尺度下的拼接掩膜,依据拼接掩膜拼接图像,这种改进可以大大减少搜索缝合线耗时,提高程序运行效率。
在最佳缝合线的后级使用多频段融合算法,将拼接图像在不同频段内进行加权融合处理,消除拼接接缝,得到最终的拼接输出。
算法的具体流程如图2所示。

|
Download:
|
| 图 2 改进的最佳缝合线算法整体流程 | |
在Windows10系统、Intel Corei7-6700HQ、内存16 GB的计算机上,程序编译软件为Visual Studio2017,使用opencv2.4.13作为外部库进行测试。
在本次实验中,使用3组测试图像进行算法性能测试,测试图分别来自Opencv官方图像拼接项目和人工使用手机拍摄。
第1组测试图像为课本,源图像如图3所示,图像间整体的色彩差异不大,但光心在实际场景中的位置不同。

|
Download:
|
| 图 3 测试组1 (课本) | |
对源图像做拼接处理,本文算法与文献[6]算法输出结果对比如图4所示。

|
Download:
|
| 图 4 测试组1本文算法与文献[6]算法输出结果对比 | |
结果可以看出,当图像色彩差异不大时,本文算法与文献[6]算法输出效果接近一致,拼接输出图像中并无明显接缝。
第2组测试图像内容为公园场景,2个图像草地中影子存在明显的光照差异,源图像如图5所示。其中源图像1较源图像2的下方阴影处更亮。

|
Download:
|
| 图 5 测试组2 (公园场景) | |
使用文献[6]中方法得到的拼接输出图像如图6(a)所示。图中方框标记处为未能完全消除的接缝,接缝两侧影子光照强度仍存在过渡不自然。图6(b)为本文算法输出结果,原本存在于文献[6]中的接缝问题得到了改善,输出图像更加平滑。

|
Download:
|
| 图 6 测试组2本文算法与文献[6]算法输出结果对比 | |
第3组为多图像拼接测试,拍摄内容为实验室场景,源图像之间存在不同程度的色彩差异,所使用的源图像如图7所示。其中源图像2、4、6、9与其他图像之间存在不同程度的色彩差异。

|
Download:
|
| 图 7 测试组3 (实验室场景) | |
使用文献[6]算法和本文算法分别对图像进行拼接处理,得到的拼接结果如图8所示。从结果中可以看出,如图8(a)所示,由于文献[6]算法在图像融合步骤中采用加权融合的方法,这种方法在多种失真并存的应用场景中效果不佳,由于源图像中存在不同程度色温差异,文献6拼接结果的图像方框标记区域出现了较为明显的色差,在色差过渡处有明显的拼接接缝,而本文算法结果中拼接效果得到了明显改善,图像接缝处颜色过渡更加平滑。

|
Download:
|
| 图 8 测试组3本文算法与文献[6]算法输出结果对比 | |
为了更加客观地验证本文算法,采用主观打分与图像客观质量评价算法评估结合的方式对本文算法结果图像进行评价,并将评价结果与文献[6]算法进行比较。主观打分部分由12名参与者对3组测试图像进行打分,并将平均得分作为该图像的主观质量得分[10],打分区间为0~10分;客观评价部分采用基于特征映射的无参考图像质量评估算法(feature maps based referenceless image quality evaluation engine,FRIQUEE)对图像进行评价[11],这种评价模型利用广义高斯模型和非对称广义高斯模型共同作用,提取包括亮度域、高斯差分域、拉普拉斯域和小波域在内的多种变换域特征,其特征描述高达560维,能够对各种失真进行响应,相较于传统的基于信息熵和互相关性的方法有着更加全面的评价效果[12],该模型的打分区间为0~100分。测试结果如表1所示。
|
|
表 1 拼接图像质量评价结果表 |
从结果中可以看出:在2幅图像拼接场景中,测试组1中,当两图像色彩差距不大时,本文算法与文献[6]算法性能差距不大;测试组2中,当两图像存在较大色彩差异时,本文算法较文献[6]算法拼接时间延长12.20%,在主观得分上提升30.06%,客观得分提升1.10%。在多幅图像拼接场景中,测试组3结果显示,本文算法较文献[6]算法速度延长5.30%,在主观得分上提升20.04%,客观得分提升1.86%。综合来看,本文算法在运行速度上与文献[6]算法相仿,在输出图像的质量上有明显提升。
5 结论1)传统的最佳缝合线算法中采用的加权平均算法能够减弱色彩差异对拼接质量的影响,但由于算法本身普适性差,所以在多图像拼接应用中不能得到良好效果。本文通过引入多频段融合算法,对最佳缝合线算法进行了改进,改进算法能够解决最佳缝合线算法中由于源图像色彩差异导致的接缝问题。
2)本文进行了3组具有代表性的测试。通过2组两图拼接测试和1组多图拼接测试,反映了在不同应用场景下,较文献[6]算法,本文算法有着更好的拼接效果。
3)通过主客观结合的图像质量评价对测试结果进行评估。结果显示,本文算法较文献[6]算法主观评分最大可提升30.06%,客观评分最大提升1.86%;在运行速度上,本文算法与文献[6]算法相当,算法耗时最大增量为12.20%。由此可见,本文提出的改进算法有效地解决了接缝问题,可以实现高质量和高效率的图像拼接。
| [1] |
赵书睿. 全景图像拼接关键技术研究[D]. 成都: 电子科技大学, 2013: 1−2. http://cdmd.cnki.com.cn/Article/CDMD-10614-1016169358.htm
( 0) 0)
|
| [2] |
何佳华. 基于改进SIFT的柱面全景图像拼接算法研究[D]. 绵阳: 西南科技大学, 2018: 5−15. http://cdmd.cnki.com.cn/Article/CDMD-10619-1018198746.htm
( 0) 0)
|
| [3] |
DUPLAQUET M L. Building large image mosaics with invisible seam lines[C]//Proceedings of SPIE 3387, Visual Information Processing VII. Orlando, USA, 1998: 3387.
( 0) 0)
|
| [4] |
党建武, 宗岩, 王阳萍. 基于SIFT特征检测的图像拼接优化算法研究[J]. 计算机应用研究, 2012, 29(1): 329-332. ( 0) 0)
|
| [5] |
GAO Junhong, LI Yu, CHIN T J, et al. Seam-driven image stitching[M]//OTADUY M A, SORKINE O. Eurographics 2013. The Eurographics Association, 2013: 45−48.
( 0) 0)
|
| [6] |
瞿中, 乔高元, 林嗣鹏. 一种消除图像拼接缝和鬼影的快速拼接算法[J]. 计算机科学, 2015, 42(3): 280-283. DOI:10.11896/j.issn.1002-137X.2015.03.058 ( 0) 0)
|
| [7] |
张翔, 王伟, 肖迪. 基于改进最佳缝合线的图像拼接方法[J]. 计算机工程与设计, 2018, 39(7): 1964-1970. ( 0) 0)
|
| [8] |
谷雨, 周阳, 任刚, 等. 结合最佳缝合线和多分辨率融合的图像拼接[J]. 中国图象图形学报, 2017, 22(6): 842-851. ( 0) 0)
|
| [9] |
BURT P J, ADELSON E H. A multiresolution spline with application to image mosaics[J]. ACM transactions on graphics, 1983, 2(4): 217-236. DOI:10.1145/245.247 ( 0) 0)
|
| [10] |
王志明. 无参考图像质量评价综述[J]. 自动化学报, 2015, 41(6): 1062-1079. ( 0) 0)
|
| [11] |
GHADIYARAM D, BOVIK A C. Perceptual quality prediction on authentically distorted images using a bag of features approach[J]. Journal of Vision January, 2017, 17(1): 32. ( 0) 0)
|
| [12] |
唐祎玲, 江顺亮, 徐少平. 基于非零均值广义高斯模型与全局结构相关性的BRISQUE改进算法[J]. 计算机辅助设计与图形学学报, 2018, 30(2): 298-308. ( 0) 0)
|
 2019, Vol. 46
2019, Vol. 46


