2. 先进飞行器导航、控制与健康管理工业和信息化部重点实验室(南京航空航天大学),江苏 南京 211106
2. Key Laboratory of Navigation, Control and Health-Management Technologies of Advanced Aerocraft (Nanjing Univ. of Aeronautics and Astronautics), Ministry of Industry and Information Technology, Nanjing 211106, China
由于我国国土辽阔、地形多样,为满足供电需求,输电线路需要延伸到社会生活的各个角落。因此,面对日益复杂的输电网络,电力巡线工作也面临着越来越严峻的考验[1]。通常,电力巡线采用固定设备巡检、爬线机器人巡检以及飞行器(固定翼和直升机)巡检,但是上述巡检方式存在监控范围小、维护复杂以及使用成本高等各种缺陷和问题[2]。近年来,随着多旋翼无人机相关技术的不断成熟,其逐渐被应用到输电线路巡检领域之中[3]。但是,现有的应用方式仅限于巡检人员手动遥控方式进行巡线,不能使其根据任务需求自动或者自主执行巡检任务,这就要求巡检人员具备操作手技能,并且大大提高了应用难度和使用成本。
多旋翼飞行器自动或者自主执行巡检任务的基础之一在于匹配高效的路径规划算法。当前,对于路径规划算法研究比较有代表性的有:文献[4]通过设置评估函数,在搜索速度和精度之间保持了相对平衡,可以获得时间最优路径;文献[5]提出筛选调点的新型A*算法,其运用调点替换原算法中大量无用节点,从而解决了算法中资源消耗大的缺陷;文献[6]在蚁群算法中引入动态搜索算子策略,并着重设计了搜索模型,从而提高了算法精度,加快了收敛速度;文献[7]提出了一种混合算法,其中蚁群优化算法用于寻找最快路径和跳出局部最小值,遗传算法用于搜索最重要的路径;文献[8]、[9]提出了一种快速的两阶段蚁群算法,其基本思想是将信息素传播到整个地图上,并在此基础上进行蚂蚁路径规划;文献[10]提出了一种混合元启发式−粒子群优化算法(particle swarm optimization, PSO),以避免过早收敛和时间复杂性。为解决路径规划中的多目标优化问题;文献[11]引入了局部最优准则和速度扰动;文献[12]通过结合蚁群算法和粒子群算法可以解决中动态环境中的路径规划问题;文献[13]提出了一种改进的交叉算子,用遗传算法求解静态环境下的路径规划问题,并对路径长度、安全性等指标进行了优化;文献[14]在路径规划过程中,运用遗传算法中的一些概念实现了狼群搜索算法,并引入遗传算法中的交叉和变异算子,对原狼群搜索算法进行了改进;文献[15]提出了一种全新的方案,该方案采用基于改进概率路标法的碰撞避免路径规划与基于改进遗传算法的传递序列优化相结合的方法来解决非共面辐射治疗中的问题。
1 粒子群算法粒子群算法依靠不同粒子的相互作用寻找相关问题的在整个寻优空间中的最优位置,也即问题的最优解。在粒子群算法中,每个待解决的优化问题的可能解都被视为搜索空间中存在的一个粒子。粒子群中的所有粒子都被赋予一个由被优化的函数确定的适应度值(fitness value),每个粒子具有2个属性,即速度与位置。算法运行过程中,所有粒子趋向当前时刻的最优粒子的位置,并试图在可能空间中搜索全局最优解。
在一个
| ${x_i} = ({x_{i1}},{x_{i1}},...,{x_{im}}),i = 1,2, \cdots ,n$ |
第
| ${v_i} = ({v_{i1}},{v_{i1}},...,{v_{im}}),i = 1,2, \cdots ,n$ |
第
| $p_i^{{\rm{best}}}(t) = [{p_{i1}}(t),{p_{i2}}(t), \cdots ,{p_{im}}(t)],i = 1,2, \cdots ,n$ |
全局最优在
| ${g^{{\rm{best}}}} = [{g_1},{g_2}, \cdots ,{g_m}]$ |
在
| $ {v_i}(t + 1) = \omega {v_i}(t) + {c_1}{r_1}(p_{_i}^{{\rm{best}}}(t) - {x_i}(t)) + {c_2}{r_2}({g^{{\rm{best}}}} - {x_i}(t)) $ | (1) |
| ${x_i}(t + 1) = {x_i}(t) + {v_i}(t + 1)$ | (2) |
式中:
粒子群算法是一种比较优秀的群体优化算法,但算法本身的全局搜索能力和局部搜索能力并不平衡,且容易出现陷入局部最优的早熟现象。针对算法本身的固有缺点,将通过引入带有自适应因子的策略的粒子群算法(improved particle swarm optimization with adaptive factor strategy, IPSOAF),对上述问题和缺陷进行改进。
在粒子群算法中,学习因子
通过引入自适应因子:
| $\omega (t) = \frac{{({\omega _s} - {\omega _e})}}{{|1{{ + }}\sqrt {{c^2} - 2c} )|}}\eta + {\omega _e}$ |
式中:
同时,为了在算法初期增强全局搜索能力,并且后期增强局部搜索能力,将加速系数
| ${c_1} = {c_{1\min }} + \left( {{c_{1\min }} - {c_{1\max }}} \right){\left( {1 - \frac{t}{{{t_{\max }}}}} \right)^2}$ |
| ${c_2} = {c_{2\max }} + \left( {c{}_{2\min } - {c_{2\max }}} \right){\left( {1 - \frac{t}{{{t_{\max }}}}} \right)^2}$ |
式中:
根据粒子群算法的工作原理,所有粒子逐渐趋向于个体最优和全局最优共同影响的位置。当一个粒子取得全局最优时,其他的粒子会很大程度上趋向此位置,如果此位置为全局极值,那么算法终止并可以获得问题的最优解;但如果此位置不是全局极值,且其余粒子也未能发现更优解,那么就可能导致大量的粒子群集在该位置附近,无法跳出这个区域,从而使得算法陷入局部最优。假如在粒子群逐渐趋于局部极小的过程中,算法能够及时地把这些粒子按一定比例驱散到更大的范围内,在一定程度上进行重新搜索,将可以避免算法的早熟现象,最终趋向全局最优。因此,在此引入一个驱散策略,在粒子分布过于密集的位置,引入驱散操作,以增强算法的搜索能力。
驱散策略通过不断观测附近几次迭代得到的
| ${x_i} = {x_{\max }} - {\rm{rand}}\;{\rm{(}}{x_{\max }} - {x_{\min }})$ |
式中:
如果某个粒子与当前最优位置的距离大于cg,则表明此粒子暂时没有趋于局部最优的风险,不必进行驱散操作。cg的选择影响算法的驱散效果,若取值过大,会导致算法收敛速度下降;若取值过小,则驱散效果变差,不利于跳出局部极小。
2.4 改进算法步骤通过以上改进,自适应收缩因子的混合粒子群算法的基本步骤如下:
1)在随机产生预设数量的粒子,并对全体粒子的参数进行初始化;
2)计算全体粒子的当前适应度函数值,随即更新
3)更新
4)判断算法结束条件是被否满足,若满足,则运行结束;若不满足,则继续运行;
5)判断是否满足驱散操作条件,若满足,则转向步骤5);若不满足,则转向步骤6);
6)根据公式(1)和(2)更新速度和位置,更新全体粒子的实时参数,然后执行步骤2)。
3 算例为了完整地测试新算法的性能,选择5个典型的智能优化算法测试函数[16]。
1)Schaffer函数:
| $\min f({x_1},{x_2}) = 0.5 + \frac{{{{(\sin \sqrt {{x_1}^2 + {x_2}^2} )}^2} - 0.5}}{{{{(1 + 0.001({x_1}^2 + {x_2}^2))}^2}}}$ |
式中
2)Griewank函数:
| $\min f({x_i}) = \sum\limits_{i = 1}^N {\frac{{{x_i}^2}}{{4\;000}} - \prod\limits_{i = 1}^N {\cos (\frac{{{x_i}}}{{\sqrt i }})} } + 1$ |
式中
3)Rosenbrock函数:
| $\min f({x_i}) = \sum\limits_{i = 1}^{D - 1} {[100{{({x_1}^2 - {x_{i - 1}})}^2} + {{({x_i} - 1)}^2}]} $ |
式中
4)Rastrigrin函数:
| $ \min f({x_i}) = \sum\limits_{i = 1}^D {[{x_i}^2 - 10\cos (2{\rm{\pi }}{x_i})} + 10] $ |
式中,
5)Shubert函数:
| $ \begin{aligned} \min f(x,y) = & \left\{ {\sum\limits_{i = 1}^5 {i\cos [(i + 1)x + i]} } \right\} \times\\ & \left\{ {\left. {\sum\limits_{i = 1}^5 {i\cos [(i + 1)y + i]} } \right\}} \right. \end{aligned} $ |
式中
通过表1中的测试数据(测试精度、平均最优值、成功次数)可以得出:1)在平均最优值方面,IPSOAF算法明显优于原PSO算法10的负十几次方,具有明显优化优势;2)在运行时间方面,IPSOAF算法耗时仅为PSO算法耗时的几分之一,具有更高的优化效率;3)在成功率方面,IPSOAF算法实现整体接近100%的成功率,更是优于原PSO算法。
|
|
表 1 2种不同类型反应算法针对不同测试函数的优化测试结果 |
高压输电线路的多旋翼无人机巡检需要面对的环境非常复杂和多样,此处引用文献[17]中的柱状空间建模法,同时对电力线路运行环境进行简化。以110 kV架空线路为例,采用上字型铁塔,导线为三角排列布置,采用经济呼称高度(呼高)18 m,水平档距取250 m(为便于展示仿真细节,此处仿真取值40 m左右),电气安全距离为5 m,绝缘子为8片。多旋翼无人机采用四旋翼无人机,主要性能如下:最大巡航速度5 m/s,最大续航时间30 min,滚转角和俯仰角范围为±45°,偏航角范围为±180°,滚转角速率和俯仰角速率为0~80 °/s,偏航角速率为0~20 °/s,有效载荷2.5 kg,摄像头为主要巡检传感器。
4.1 预先划定兴趣点的情况为了便于分析仿真效果,在此采用俯视的二维地图进行仿真分析。
在预设地图中,设置4基杆塔,电力线路采用常见的三相排列方式;在电力线路周边设置5个障碍物,其中1个圆形表示单株树木,4个不规则障碍物表示人工建筑、树林等;在电力线路上设置12个待观测兴趣点;设置巡检的起点和终点分别为P0(95, 30)、PE(5, 40),待观测兴趣点位置如表2所示。将提出的IPSOAF算法和原PSO算法分别应用于以上设置的仿真环境中,得到仿真结果如图1~3所示。在仿真图中,大黑点代表电力杆塔,小黑点代表电力线路上的预设兴趣点,空心方框代表电力巡线任务的起始点和终点(下同)。
|
|
表 2 预设兴趣点位置 |

|
Download:
|
| 图 1 固定兴趣点条件下2种改进型算法的对比仿真曲线 | |
|
Download:
|
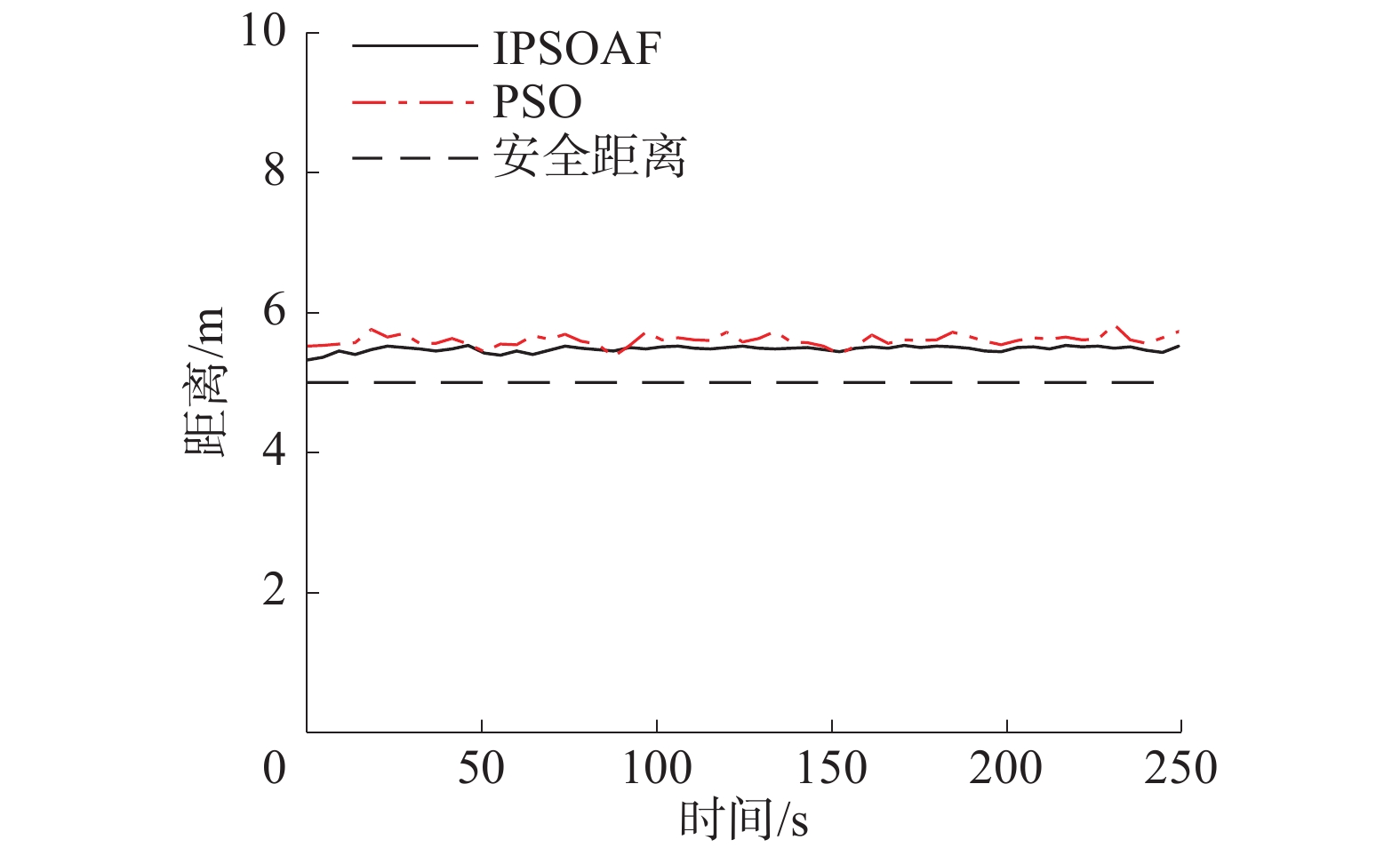
| 图 2 固定兴趣点条件下无人机与线路距离曲线 | |
|
Download:
|
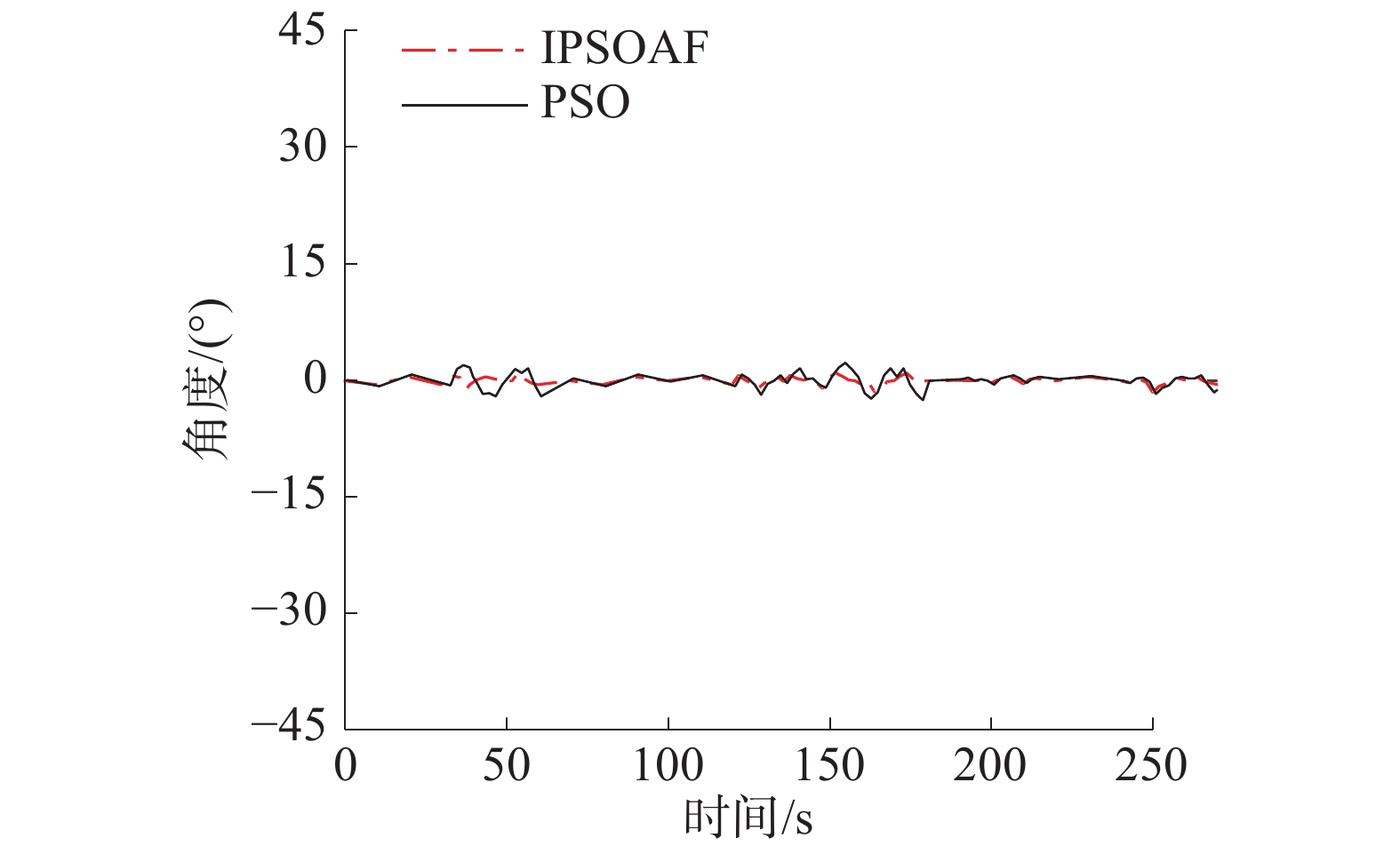
| 图 3 固定兴趣点条件下摄像头俯仰角变化曲线 | |
从仿真结果的图1、2可以看出,IPSOAF算法和PSO算法都能够顺利按要求完成输电线路巡检工作。从仿真曲线的细节来看,虽然两者都保持在安全距离之外,但是IPSOAF算法获得的路径与线路之间的距离更加稳定,且距离更小,更加有利于精确观察;而PSO算法获得路径与电力线路之间的距离变化较大,稳定性相对偏差,且总体巡检路径距离更大。通过图3中的机载摄像头俯仰角变化曲线可以看出IPSOAF算法所需要的摄像头摆动幅度相对较小,表明其工作状态也更稳定;PSO算法的摄像头摆动角度在50和160 s附近出现较为明显的摆动,说明其工作状态稳定性存在不足。
4.2 预先划定兴趣点的情况任务前指定常规待观察兴趣点和可疑兴趣点。巡检人员在巡检过程中传回的视频和图像资料经常会发现一些事先未预料到的情况,可能会出现需要临时增加待观察兴趣点的情况,这就要求算法实时调整巡检路径和巡检任务规划。本次仿真设定在巡检到P7时,随机在其前的(37,17)附近加入随机兴趣点(该兴趣点较高,需要机载摄像头上下俯仰较大角度,以全面观测),且巡线无人机不被告知该兴趣点的准确位置数据,只能获得概略指定范围。仿真图如图4~6所示(随机兴趣点设置于图4中空心圆形位置)。

|
Download:
|
| 图 4 随机兴趣点条件下2种改进型算法的仿真曲线 | |
|
Download:
|
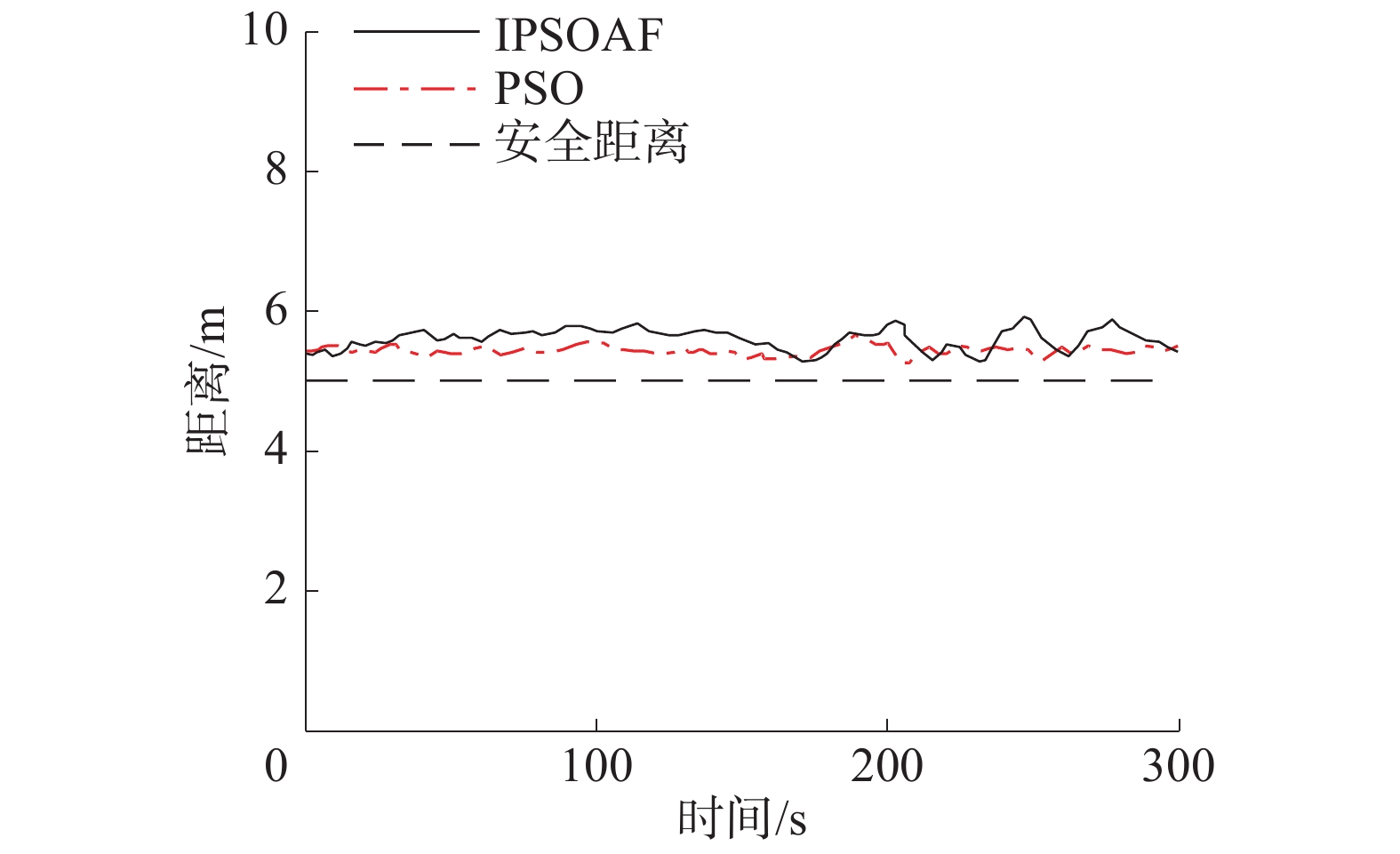
| 图 5 随机兴趣点条件下无人机与线路距离曲线 | |

|
Download:
|
| 图 6 随机兴趣点条件下摄像头俯仰角变化曲线 | |
从仿真图4、5可以看出,基于IPSOAF算法和PSO算法的仿真曲线表现出更大的差异。除了类似4.1节中的差异之外,在100 s时加入临时模糊兴趣点之后大约20 s的时间,两者表现出较大不同。IPSOAF算法在应对临时兴趣点加入的过程中,与输电线路之间的水平距离变化较小,且用更短时间迅速趋于稳定状态,很好地响应了任务中随机兴趣点的加入。而PSO算法则相反,不但出现与线路水平距离变化幅度较大、耗时更久的现象,而且较大概率发生陷入局部极小的情况,从而导致巡检任务无法完成。值得注意的是,在巡检过程中,由于存在高度较高且比较复杂的待观测兴趣点,导致多旋翼无人机需要一边沿线路方向前进,一边俯仰摆动摄像头,才能更加全面地观测该类兴趣点。同时通过大幅度减小多旋翼无人机在垂直方向上的位置调整,最终提高巡线效率。通过图6的对比曲线可以看出,除4.1节仿真中展现的2种算法的差异之外,IPSOAF算法可以在面对高度较高的兴趣点时,使得机载摄像头俯仰方面摆动幅度更小,全程运行状态也更加平稳,因此其较PSO算法更加优越。
5 结论从上述分析和测试结果,可以得出以下结论:
1)通过引入非线性自适应因子,并选取合适的参数,较好地平衡算法全局搜索和局部搜索的能力,加速了算法的收敛速度。
2)通过引入自调整学习因子,分别加强了不同运行阶段的全局搜索能力和局部搜索能力,进一步提高了算法的搜索效率。
3)通过引入驱散策略,能够引导算法更好地避免陷入局部极小,从而获得全局最优解。
从2种情况的电力巡线仿真可以得出,PSO算法基本上能够完成设定的输电线路路径规划任务,但偶发陷入局部极小,导致不能完成巡检任务;而IPSOAF算法能够获得更好的效果,同时该算法还具有运行时间较短,不易陷入局部极小等优点。因此,提出的IPSOAF算法在电力巡线应用中在搜索效率、收敛速度以及成功率方面,较PSO算法均具有优势。故本研究具有一定的理论研究价值和较好的社会应用价值,进一步深入研究兴趣点细节巡检将是未来该领域一个重要的研究方向。
| [1] |
葛黄徐. 输电线路智能巡检系统的应用分析[J]. 通讯世界, 2018, 334(3): 248-249. DOI:10.3969/j.issn.1006-4222.2018.03.157 ( 0) 0)
|
| [2] |
邓元婧, 汪从敏, 夏开全, 等. 架空输电线路通道环境的巡视技术与应用[J]. 浙江电力, 2014(8): 28-31. DOI:10.3969/j.issn.1007-1881.2014.08.009 ( 0) 0)
|
| [3] |
施孟佶, 秦开宇, 李凯, 等. 高压输电线路多无人机自主协同巡线设计与测试[J]. 电力系统自动化, 2017, 41(10): 117-122. DOI:10.7500/AEPS20160801005 ( 0) 0)
|
| [4] |
钱红昇, 葛文锋, 钟鸣, 等. 基于分层的改进[A*]算法在路径规划中的应用[J]. 计算机工程与应用, 2014, 50(7): 225-229. DOI:10.3778/j.issn.1002-8331.1304-0167 ( 0) 0)
|
| [5] |
赵晓, 王铮, 黄程侃, 等. 基于改进A*算法的移动机器人路径规划[J]. 机器人, 2018, 40(6): 137-144. ( 0) 0)
|
| [6] |
游晓明, 刘升, 吕金秋. 一种动态搜索策略的蚁群算法及其在机器人路径规划中的应用[J]. 控制与决策, 2017(3): 552-556. ( 0) 0)
|
| [7] |
DAS P K, BEHERA H S, TRIPATHY H K, et al. A hybrid improved PSO-DV algorithm for multi-robot path planning in a clutter environment[J]. Neurocomputing, 2016, 207: 735-753. DOI:10.1016/j.neucom.2016.05.057 ( 0) 0)
|
| [8] |
OLEIWI B K, ROTH H, KAZEM B I. A hybrid approach based on ACO and GA for multi objective mobile robot path planning[J]. Applied mechanics and materials, 2014, 527: 203-212. DOI:10.4028/www.scientific.net/AMM.527 ( 0) 0)
|
| [9] |
CHEN X, KONG Y, FANG X, et al. A fast two-stage ACO algorithm for robotic path planning[J]. Neural computing and applications, 2013, 22(2): 313-319. DOI:10.1007/s00521-011-0682-7 ( 0) 0)
|
| [10] |
HUANG H C, TSAI C C. Global path planning for autonomous robot navigation using hybrid metaheuristic GA-PSO algorithm[C]//Proceeding of SICE Annual Conference. Tokyo, Japan: IEEE, 2011: 1338-1343.
( 0) 0)
|
| [11] |
GENG N, GONG D, ZHANG Y. Robot path planning in an environment with many terrains based on interval multi-objective PSO[J]. International journal of robotics & automation, 2016, 31(2): 100-110. ( 0) 0)
|
| [12] |
MAZINAN A H, SAGHARICHIHA F. A novel hybrid PSO-ACO approach with its application to SPP[J]. Evolving systems, 2015, 6(4): 293-302. DOI:10.1007/s12530-014-9126-9 ( 0) 0)
|
| [13] |
Lamini C, Benhlima S, Elbekri A. Genetic Algorithm Based Approach for Autonomous Mobile Robot Path Planning[J]. Procedia computer science, 2018, 127: 180-189. DOI:10.1016/j.procs.2018.01.113 ( 0) 0)
|
| [14] |
YONGBO C, YUESONG M, JIANQIAO Y, et al. Three-dimensional unmanned aerial vehicle path planning using modified wolf pack search algorithm[J]. Neurocomputing, 2017: S0925231217309220. ( 0) 0)
|
| [15] |
YE B, TANG Q, YAO J, et al. Collision-free path planning and delivery sequence optimization in noncoplanar radiation therapy[J]. IEEE transactions on cybernetics, 2017: 1-14. ( 0) 0)
|
| [16] |
魏民, 杨明磊, 钱锋. 带有精英保留机制的混合差分化学反应算法[J]. 化工学报, 2015, 66(1): 316-325. ( 0) 0)
|
| [17] |
徐华东, 王世勇, 杨轻, 等. 基于柱状空间和改进A*算法的无人机规避方法[J]. 测控技术, 2014, 33(7): 132-135. DOI:10.3969/j.issn.1000-8829.2014.07.036 ( 0) 0)
|
 2019, Vol. 46
2019, Vol. 46


