随着网络规模不断扩大，网络结构也愈发复杂化。为了保证高质量的网络通信和网络资源的利用率，需要对网络结构进行合理优化。网络流量测量对流量建模分析^[1]、网络性能监测及优化具有重要作用，能够为流量工程提供测量数据，更好地满足网络服务质量的要求^[2]。在网络规模不大，网络中流量负载较低的情况下，管理员可以在网络中的所有节点上都部署探针，已达到监测全网的目的。但对于规模庞大的网络来说，此方法不仅会造成测量节点部署、维护的开销过大，带来巨大的软硬件资源消耗，还可能会造成网络中测量流量较高，从而影响网络中正常的通信和服务。因此，对于大规模网络，选择合理有效的测量点，即通过选择一部分节点部署探针就能达到监测全网的目的，成为网络流量测量中的关键。

对于这一问题，国内外已有诸多研究。在算法模型方面，基于流守恒的网络测量问题被映射为最小弱顶点覆盖问题^[3]，并指出该问题属于NP难题。文献[4]提出了一种求解弱顶点覆盖集的贪婪算法；文献[5]利用关联矩阵和线性规划的概念，提出了一种求解最小弱顶点覆盖集的近似算法；文献[6]基于蚁群优化算法和禁忌搜索策略解决了测量点选择问题；文献[7]同样基于蚁群算法，提出了一种适用于分布式网络的测量节点的智能选择算法。但在目前的研究中，网络中所有节点对流量传输的作用被视为完全等同的，这与实际情况并不相符。文献[8]中指出，网络中的流量行为具有以下重要属性：输出流量集中在极少数活动IP中，而输入流量则较为分散。由此可知，网络中的不同节点对承担流量传输任务具有不同的重要性。因此，优先在关键节点上部署探针对获取网络重要流量数据、掌握流量分布情况具有重要意义。在资源有限，导致在网络中可部署的探针数量有限的情况下，优先选择关键节点尤为重要。

综上所述，目前需要一种网络流量测量点选择方法，使其能够在满足测量需求的情况下，尽可能少地选择测量点，并且优先选择关键节点。

1 相关工作

节点关键度的作用是衡量复杂网络中节点重要性。研究中已经指出，大规模计算机系统属于复杂网络，因此对于复杂网络适用的节点关键度评价指标同样适用于计算机网络拓扑。研究中给出了复杂网络关键节点评估模型，其中包含2个因素：评价指标及相应的评估策略^[9]。评价指标指的是评估过程中选取的度量标准，即通过某种量化标准定量计算网络中节点的关键度；评价策略指的是如何使用评价指标进行测度，通常情况下，对于评估过程中网络拓扑结构无变化的情况，直接使用评价指标对节点关键度进行衡量即可。以下给出2种常见的节点关键度评价指标：

1)节点度

网络中某个节点的节点度被定义为直接与该节点相连的邻居节点的个数（或与其直接相连的边的数量）。节点度计算方式简单、复杂度低，但只能在某种程度上反映节点的关键度，不够准确。

2)介数

在无向无权网络中，使用经过某个节点的最短路径数量来计算该节点的介数。介数的计算方法如下：

$ {{B}}\left( i \right) = \mathop \sum \nolimits_{s \ne i \ne t} \frac{{n_{st}^i}}{{{n_{st}}}} $

式中：n_st指的是从节点s到节点t的最短路径数量； ${n_{st}^i} $ 指的是这些最短路径中经过节点i的数量。介数刻画了网络中某个节点对于网络信息沿着最短路径传输的控制能力。当一个节点的介数越高，对网络中信息传输的重要性越高。由此可见，介数能够很好地区分网络中不同节点对流量传输重要性的不同。对于AS级网络，文献[10]中给出了AS网络节点关键度计算方法。

网络流量测量点的选择问题可以转换为图论中的最小弱顶点覆盖问题。研究中已经指出，最小弱顶点覆盖问题是一个NP难题，通常使用近似算法求解。文献[5]中提出了一种基于关联矩阵的近似算法，该算法的思路如下：

1）选择一个包含链路数量最多的节点，记做v₁；

2）在关联矩阵中删除v₁对应的行以及该行中元素1所对应的列；

3）在剩下的关联矩阵中依次删除所有行元素之和不超过1的其他行以及这些行中元素1所在列，重复此步骤直到不能再删除新行为止；

4）重复以上步骤，直到关联矩阵中所有元素都被删除。

该算法的正确性已经过理论及实验验证，并且与传统的贪心算法相比，能够得到规模更小的弱顶点覆盖集。但是对于大规模问题，该算法求解最优解的能力仍显不足。因此有学者使用蚁群算法来进行测量点的求解。

蚁群算法[11]是一种受到真实蚂蚁的自然优化机制所启发的元启发式算法，具有分布式计算、正反馈、自组织以及贪心启发等特点。相比于其他求解NP难题的近似算法，蚁群算法具有搜索速度快、搜索较优解能力强等优点，在解决旅行商问题、子集类问题中都表现出色。网络流量测量点选择问题被转换为图论中的最小弱顶点覆盖问题，是NP难题，使用蚁群算法作为基本选择算法能够较好地解决。参考文献[7]、[11]、[12]给出蚁群算法的基本步骤，并对其中的关键步骤进行说明。

1)初始化

在初始化时，需要为图中每个节点设置初始化信息素值。通常情况下，为了避免在算法运行过程中各个节点上的信息素强度相差过大，算法采用最大最小蚂蚁系统（max-min ant system，MMAS）的信息素更新规则。在整个算法运行过程中，信息素强度会被限制在[τ_min，τ_max]范围内，其中τ_min和τ_max通常根据问题人为设定为常数。初始值通常被设定为τ_max。

2)选择节点

每只蚂蚁根据状态转移概率公式进行节点的选择，该公式的具体计算方式如下：

$ p_i^k = \frac{{\tau _i^\alpha \eta _i^\beta }}{{ \displaystyle\sum \nolimits_{j \in {C_k}} \tau _j^\alpha \eta _j^\beta }} $

(1)

式中：C_k表示候选顶点集；τ_i表示顶点v_i上的信息素轨迹强度；η_i表示顶点v_i上的期望启发信息值，在现有的使用蚁群算法作为测量点选择算法的研究中，期望其发信息值只使用节点度表示；α和β分别表示信息启发因子和期望启发信息因子，这2个值都是常数，通常根据经验人为指定。

3)信息素更新

在每次循环过程完成后，即所有蚂蚁得到自己的最小弱顶点集并比较得到循环最优解后，使用MMAS的信息素更新规则进行信息素更新。信息素更新包括信息素的挥发和增。信息素的挥发按照式（2）进行：

$ {\tau _i}\left( {t + 1} \right) = \left( {1 - \rho } \right){\tau _i}\left( t \right) $

(2)

式中ρ代表信息素挥发系数，取值范围被限定在[0，1]，由人为指定。

信息素的增加按照式（3）进行：

$ \Delta {\tau _i} = \frac{Q}{{1 + \left| {\left| {{c_{{\rm{MVC}}}}} \right| + \left| {{g_{{\rm{MVC}}}}} \right|} \right|}} $

(3)

式中：Q为信息素增量系数；c_MVC为循环最优解，某次循环中蚁群找到的包含顶点数最少的弱顶点覆盖集；g_MVC为全局最优解，自算法运行以来蚁群找到的包含顶点数最少的弱顶点覆盖集。

2 基于节点加权的网络流量测量点选择算法 2.1 问题描述及模型定义

节点加权的情况与之类似，仍然是要求得网络拓扑的一个最小弱顶点覆盖集；与之不同的是，该问题的求解目标发生了变化，变为在覆盖所有链路的情况下，所选测量点的权重之和最小。由此，将基于节点加权的网络流量测量点选择问题转换为节点加权的最小弱顶点覆盖问题。

我们将节点加权的网络拓扑表示为一个三元组 $ {{G}} = \left( {V,E,W} \right)$ ，其中 $ V = \left( {{v_1},{v_2},{v_3} \ldots {v_m}} \right)$ 表示网络中所有节点的集合； $ E = \left( {{e_1},{e_2},{e_3} \ldots {e_n}} \right)$ 表示网络中所有链路的集合； $ W = \left( {{w_1},{w_2},{w_3} \ldots {w_m}} \right)$ 表示网络中所有节点的权重。为了给出节点加权的最小弱顶点覆盖问题的数学模型定义，令：

$ {x_i} = \left\{ {\begin{array}{*{20}{c}} {{w_i},\;\;\;\;{v_i} \in S}\\ {0,\;\;\;\;\;\;{v_i} \notin S} \end{array}} \right. $

(4)

式中S表示图G的一个弱顶点覆盖集。

对于图中的每一个节点，我们按照式（4）计算其x_i的值。当满足式（5）的条件时，我们认为S是图G一个节点加权的最小弱顶点覆盖集。

$ {\rm{min}}\mathop \sum \nolimits {x_i} $

(5)

要解决基于节点加权的网络流量测量点选择问题，就是要求得上述节点加权的最小弱顶点覆盖集。式（5）就是该问题的求解目标。能够看出，与无权无向图中的最小弱顶点覆盖问题相类似，该问题也属于一个NP难题。

2.2 算法实现

本文提出的基于节点加权的网络流量测量点选择算法将在蚁群算法的基础上对其进行改进，使其能够适应大规模网络中节点加权的情况。算法主要分为节点权重分配、使用基于关联矩阵的近似算法计算初始解集、使用改进后的蚁群算法求得最终解等3个步骤。

2.2.1 权重分配

为了区分网络中不同节点对流量传输的不同重要性，本算法将根据节点关键度为节点进行权重分配。根据关键节点对流量传输的重要性，我们认为，与该关键节点相关联的所有链路都值得被优先覆盖。而一条链路既可以被该节点覆盖，也可以被它的邻居节点覆盖。因此，在选择测量节点时，关键节点的邻居节点也应当具有较高的优先级。

根据节点加权的最小弱顶点覆盖问题的求解目标可知，节点的权重越小，优先被选择的可能性越大。依照以上权重分配的思路，结合求解目标对权重的约束，给出权重计算方法：

$ {w_i} = \frac{1}{{\displaystyle \sum \nolimits_{j \in N\left( i \right)} {c_j}}} $

式中： $ N\left( i \right)$ 表示节点v_i及其所有邻居节点组成的集合；c_j表示节点v_j的关键度。这种权重计算方法即考虑节点自身的关键度，也考虑了所有邻居节点的关键度，且计算简单。当某个节点的权重越小时，则意味着该节点及其邻居节点的关键度之和 $\displaystyle \sum \nolimits_{j \in N\left( i \right)} {c_j}$ 越大。该值的大小取决于单个邻居节点关键度的大小以及邻居节点的个数。前者意味着连接该节点与邻居节点的链路优先被覆盖的可能性；后者意味着该节点能够覆盖链路的数量。综合二者计算权重，可以评价一个节点在测量点选择过程中被优先选择的可能性。

2.2.2 初始解计算

为了让算法在处理大规模问题时搜索速度更快，需要先使用基于关联矩阵的近似算法对问题求出一个近似解，作为蚁群算法的初始解集，即蚂蚁将从该解集中选择节点作为自己搜索的起始节点。

对于图 $ {{G}} = \left( {V,E,W} \right)$ ，先忽略节点权重，可以将其抽象为一个m×n大小的联矩阵 $ {{A}} = \left[ {{a_{ij}}} \right]$ ，a_ij为矩阵中的元素，它的计算方式如下：

$ {a_{ij}} = \left\{ {\begin{aligned} {1,} & \;\;{{\text{节点}}{v_i}{\text{与}}{e_j}{\text{相关联}}}\\ {0,} & \;\;{{\text{其他}}} \end{aligned}} \right. $

(6)

为了使基于关联矩阵的近似算法适用于节点加权的情况，对测量点的选择方法进行改进。在测量点的选择过程中，节点权重越小，代表该节点对流量传输的重要性越高，被优先选择的可能性越大；与该节点相关联的链路数量越多，代表该节点对链路的覆盖范围越广，被优先选择的可能性越大。综合考虑这两个影响测量点选择的因素，结合问题的求解目标，给出如下计算公式：

$ {p_i} = \frac{{{w_i}}}{{\displaystyle \sum \nolimits_{j = 1}^n {a_{ij}}}} $

(7)

式中：p_i表示节点的综合权重； $ \displaystyle \sum \nolimits_{j = 1}^n {a_{ij}}$ 表示矩阵中行元素之和。在算法运行过程中，需要根据当前矩阵的状态动态计算，即该值始终表示的是与节点v_i相关联但还未被覆盖的链路数量。对于图中的每个节点，在每次进行节点选择之前，按照式（7）计算p_i的值，并且每次选择p_i最小的节点加入测量点集合。

2.2.3 基于节点加权的增强蚁群算法

要让基本蚁群算法适用于节点加权的情况，需要对其中的信息素初始化以及期望信息启发值的计算方法进行改进，形成基于节点加权的增强蚁群算法。

1)信息素初始化

在基本蚁群算法中，通常会采用最大最小蚂蚁系统（MMAS）的信息素更新规则进行信息素更新。在该规则中，信息素的值被限制在[τ_min，τ_max]范围内，τ_min和τ_max的取值通常是根据问题人为设定为常数，而各个节点的信息素初始值通常被设置为τ_max。但是对于节点加权的情况，不同的节点对于流量测量具有不同的重要性，信息素初始值能够根据节点权重的不同而变化，才能更好地区分节点，也更有利于之后蚁群的搜索。

在根据权重对节点进行信息素初始化时，我们希望各个节点的信息素初始值能够根据权重大小合理地分散在[τ_min，τ_max]的范围内。结合权重越小代表优先被选择的可能性越大，信息素值越大被优先选择的可能性越大这一条件，信息素初始值的分配要满足以下3个条件：

a)信息素初始值与节点权重成反比；

b)信息素初始值大小能反映权重的大小；

c)信息素初始值范围在[τ_min，τ_max]内。

根据以上条件，给出信息素初始值的分配方法如下：首先对信息素值的取值区间进行反比例变换，得到新区间；其次将权重取值区间映射到新区间，得到一个中间结果；最后对该中间结果进行反比例变换得到最终的信息素初始值。根据式（8）和（9）对信息素区间进行反比例变换。

$ \tau _{\min}' = \frac{1}{{{\tau _{\max}}}} $

(8)

$ \tau _{\max}' = \frac{1}{{{\tau _{\min}}}} $

(9)

这时，可以得到一个新区间 $ \left[ {\tau _{\min}',\tau _{\max}'} \right]$ ，这个区间内的所有值通过反比例变化即可映射到区间[τ_min，τ_max]内的某个值。

我们给出节点权重的取值范围为[w_min，w_max]，其中w_min和w_max分别是节点权重的最小值和最大值。接下来，根据式（10）将权重区间[w_min,w_max]映射到新区间 $ \left[ {\tau _{\min}',\tau _{\max}'} \right]$ ，得到一个中间值 $ \tau _i'$ 。

$ \tau _i' = \tau _{\min}' + \left( {\tau _{\max}' - \tau _{\min}'} \right) \cdot \frac{{{w_i} - {w_{\min}}}}{{{w_{\max}} - {w_{\min}}}} $

(10)

这时的中间值 $ \tau _i'$ 的取值范围在新区间 $ \left[ {\tau _{\min}',} \right. $ $\left. {\tau _{\max}'} \right]$ 内，且大小与权重大小成正比，即权重越大，中间值越大；权重越小，中间值越小。最后，根据式（11）计算最终的信息初始值。

$ {\tau _i} = \frac{1}{{\tau _i^{'}}} $

(11)

由于 $ \tau _i' \in \left[ {\tau _{\min}',\tau _{\max}'} \right]$ ，则计算得到的τ_i∈[τ_min，τ_max]，满足了前文给出的3个条件中的最后一条。根据式（10）、（11）可以看出，τ_i与 $ \tau _i'$ 成反比例关系，与节点权重也成反比例关系。以上方法可以很好地根据节点权重大小计算信息素初始值的大小，且计算得到的结果满足MMAS中信息素更新规则的要求。

为了避免τ_min和τ_max取值不合理导致在进行映射后节点权重的差异被过度缩小，信息素初始值对节点的区分作用不明显，给出一种计算τ_min和τ_max取值的方法。为了准确体现节点权重之间的差异，新区间的上下界可以通过直接对权重区间的上下界进行向上取整和向下取整操作得到。在得到新区间的上下界后对其进行反比例计算即可得到τ_min和τ_max的取值。若计算得到的结果显示二者的值相差过大，为了避免算法陷入停滞，可以人为调整取值。

2)期望启发信息值的计算

在蚁群算法中，期望启发信息值的计算通常根据求解问题的不同，选择不同的计算方式。目前，其计算方式通常有以下3种：人为设定常数、节点未被覆盖的链路数量以及所有邻居节点未被覆盖的链路数量之和与该节点未被覆盖的链路数量之比。第一种方式属于静态计算方法，对于大规模问题，会失去对蚁群搜索的指导意义；第二种方式动态计算，但只考虑了单个节点，不够全面；第三种方式也属于动态计算，但没有考虑节点加权的情况，此，本文提出一种适用于节点加权的期望启发信息值的动态计算方法，以达到指导蚁群优先选择关键节点的目的。

根据公式（1）可以发现，当一个节点的期望启发信息值越大时，该节点被选择的概率就越大。考虑节点的关键度与节点被选择概率之间的关系：节点关键度越高，被选择的概率就越大。因此，期望启发信息值应当与节点关键度成正比关系。参考节点权重计算公式的推导思路，一个节点被选择的可能性会受到它所有邻居节点关键度的影响，因此，一个节点的期望启发信息值应当与该节点及其所有邻居节点都有关。为了实现问题的求解目标，除了节点关键度之外，还要考虑该节点相关联的链路数量。为了让节点的期望启发信息值具有更好的指导价值，需要随着蚁群的搜索过程动态变化。综合以上各项考量，提出一种期望启发信息值的动态计算方法：

$ {\eta _i} = \left| {{v_i}} \right| \cdot \mathop \sum \nolimits_{j \in {N_i}} {c_j} $

(12)

式中：|v_i|指的是节点v_i当前还未被覆盖的链路数量，该值随着蚁群的搜索过程变化；N_i指的是节点v_i及其所有还未被覆盖的邻居节点的集合。

结合基本蚁群算法的步骤，给出了基于节点加权的增强蚁群算法的具体程序步骤：

初始化，根据公式（6）至公式（9）计算各个节点的信息素初始值

repeat

　for蚁群中的每只蚂蚁

　　随机选择一个初始解集中的节点作为搜索的起始节点，并将其加入自己的覆盖集中

　　构造自己的候选点集合

　　　while候选点集合不为空

　　　　每只蚂蚁根据公式（12）计算期望启发信息值

　　　　每只蚂蚁根据公式（1）计算状态转移概率，选择概率最大的节点加入最小弱顶点覆盖集

　　　end while

　　end for

　　保留循环最优解

根据计算出的τ_min和τ_max以及式（2）和（3）更新信息素

　 until最优解被找到或完成最大循环次数

保存全局最优解

其中，每只蚂蚁构造自己的候选集合可以使用基于关联矩阵的思路。

3 实验评估

由于网络拓扑结构在宏观上具有自相似性，因此本文使用全球AS级网络拓扑对算法进行验证。本文从RouteViews项目公开数据集中下载了2018.2.1的BGP路由表数据，在此基础上使用Gao提出的域间关系推断算法^[13]构建出带有域间关系的AS级网络拓扑，并计算每个节点的客户锥^[14]大小作为节点关键度。将构建出的拓扑中节点度为1的节点删除之后，该拓扑共具有共包含39 026个节点，262 522条边。

对于节点加权和未加权的情况，分别使用基本蚁群算法以及本文提出的算法进行实验。蚁群算法中的参数设置参考相关研究和文献给出，不再详述。本次实验选择的参数为α=1，β=2，蚂蚁数量为100。对于节点加权的情况，使用本章给出的信息素计算方式得到τ_min=0.1、τ_max=34；对于节点未加权的情况，人为设置τ_min=0.1、τ_max=10。同时，为了判断蚁群是否找到最优解，增加了一个参数m，标识在搜索过程中，最优解规模连续m次没有发生变化。此时认为最优解已经找到，循环终止，设置m=10。实验结果表明，节点未加权情况下，测量点数量为3 001；节点加权情况下，测量点数量为3 213。

对于本文所研究的问题，已有研究中并未给出相关的实验结果评估指标。因此，为了更加准确地评估算法的效果，本文定义2个评估指标：链路覆盖比以及关键度占比。链路覆盖比指的是n个测量点所覆盖的链路数量与全部链路数量之比，主要描述测量点对链路的覆盖能力；关键度占比指的是n个测量点的关键度之和占全部节点关键度之和的比例，主要衡量的是测量点的关键度是否更高。二者计算方式为：

$ \left\{\begin{array}{l} {{x}} = \dfrac{{\displaystyle\sum \nolimits_{i \in R\left( i \right)} \left| {{v_i}} \right|}}{{\left| V \right|}}\\ {{y}} = \dfrac{{\displaystyle \sum \nolimits_{i \in R\left( i \right)} {c_i}}}{{\displaystyle \sum \nolimits_{{v_j} \in V} {c_j}}} \end{array}\right. $

式中 $ R\left( i \right)$ 表示测量点集合。

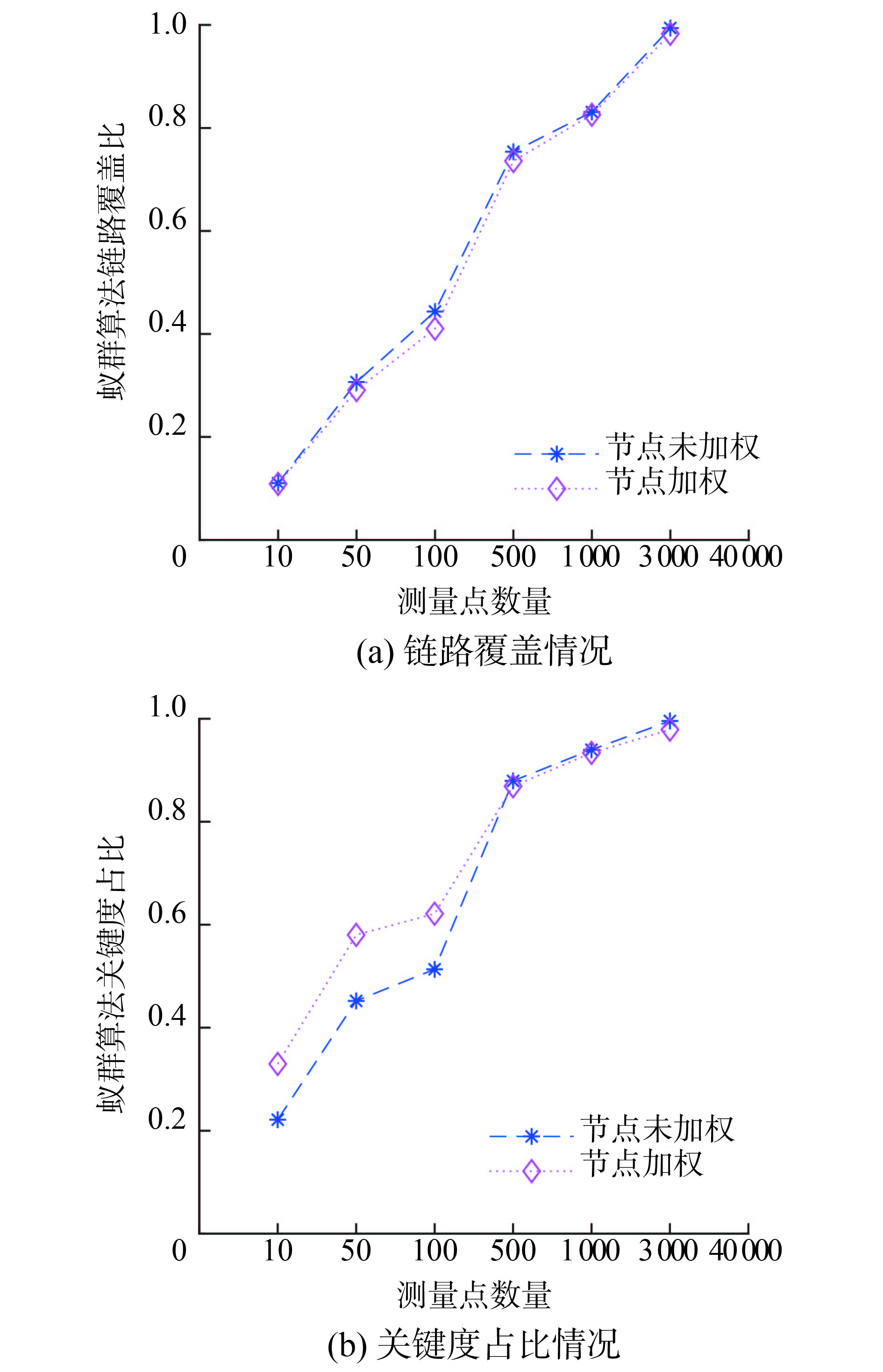
根据2个初始解集的规模，分别取n=10、50、100、500、1 000、3 000，计算节点加权和未加权2种情况下的评估指标。评估指标计算结果及对比如图1所示。

由图1可以看出，2种算法得到的测量点的链路覆盖比相差无几，图中曲线基本重合。这表明，本文提出的基于节点加权的蚁群算法搜索到的最优解对链路覆盖能力强。从关键度占比曲线中可以看出，基于节点加权的蚁群算法能够优先选择关键度较大的节点，在测量点数量为50时，节点未加权情况下的关键度占比为0.452 1，节点加权情况下关键度占比为0.580 2，提升了大约28%。由此可见，在测量点数量较少的情况下，本文提出的算法能够在保证链路覆盖率的情况下，大幅提升关键度占比，优先选择关键度更高的节点；在测量点数量较多，尤其对链路覆盖率超过50%后，二者结果相差不大。

为了评估节点加权对算法性能的影响，对二者的运行时间、搜索最优解的循环次数进行了比较。比较结果如表1所示。

通过表1可以看出，本文中的算法在每计算状态转移概率时，都需要对期望启发信息值进行重新计算；因此，单只蚂蚁搜索解的平均时间要长，时间增长了约20.06%，且找到全局最优解的平均循环次数也有所增加。对比基本蚁群算法，节点加权的蚁群算法在收敛速度以及计算性能上有所下降。

综合算法测量点选择效果以及算法性能可以看出，本文中的算法虽然计算性能稍逊一筹，但选择的测量点关键度高、选点效果好。在实际情况中，测量点选择算法只需运行一次即可选出测量点，无需多次运行，因此，算法在时间上消耗带来的开销要远小于不合理测量点进行测量带来的开销。综上所述，针对节点加权的情况，本文中的算法能够高效地选出关键度更高的节点，是一种合理性和实用性更好的算法。

4 结论

为了能够区分网络中不同节点对网络流量传输的不同重要性，本文提出了一种基于节点加权的网络流量测量点选择算法。该算法主要分为权重分配、初始解集计算、使用基于节点加权的蚁群算法进行最终解计算三大部分。其中，基于节点加权的蚁群算法是通过对基本蚁群算法中的信息素初始化以及期望启发信息值的计算进行改进形成的。

实验结果表明，本文提出的算法能够在保证链路覆盖率的情况下，优先选择对流量传输更重要的节点。但由于算法中需要进行动态计算的部分较多，算法的时间开销有所增加。

本文提出的算法还有需要研究的地方，如蚁群算法中的参数设置对算法性能的影响；不同节点关键度计算方式对不同粒度网络选点效果的影响；降低时间复杂度的方式等，将在未来对这些问题进行进一步研究和优化。