近几年，核电发展步入具有更高安全标准的第三代应用阶段，提高核燃料元件的安全性、可靠性是核电“走出去”的关键所在。燃料棒作为包容裂变产物的有效屏障，从燃料设计角度，应确保其能在稳态运行及假设的一定频率发生的工况条件下能实现其功能。芯块−包壳之间的相互作用是包壳产生应力的主要根源，同时也是引起燃料棒失效的重要原因。影响芯块和包壳之间的力学行为的因素很多，芯块的热膨胀、破裂、翘起、肿胀以及碎块的重新定位都有可能引起包壳的变形。从实际堆内运行角度来说，短时间内的功率提升，热应力会引起芯块的碎裂，随着外围的裂纹张开会进一步引起包壳中产生应力梯度，经过多次循环，造成包壳破损^[1-3]。在燃料棒设计过程中，通常采用包壳应变准则来防止一部分芯块-包壳相互作用引起的破损。本文采用自主研发的燃料棒性能分析程序FUPAC^[4-5]模拟燃料棒在堆内辐照期间的芯块−包壳相互作用，以田湾核电站5、6号机组长燃料循环堆芯燃料管理为背景，验证设计准则，分析II类瞬态条件下芯块−包壳的力学行为，并进行相关不确定性研究，为后续新型包壳材料设计研发提供模型基础。

1 设计准则

包壳应变准则要求：稳态运行时，从未辐照状态算起的包壳直径增大（塑性应变+蠕变）应小于1%；发生工况II瞬态事件时，在任意轴向高度上功率变化导致的包壳直径增大（弹塑性应变+蠕变）应小于1%。

该准则避免了由于应力松弛导致的应力不能达到屈服强度，而材料却发生屈服的现象，将由过度包壳应变导致的包壳破损的可能性降至最低。

2 计算模型

FUPAC软件可以模拟燃料棒在堆内辐照期间热/力学行为（包壳蠕变、辐照生长、腐蚀吸氢、芯块重定位、密实、肿胀和裂变气体释放等），计算热/力学参数（温度、应力、应变、氧化膜厚度、内压等）随辐照历史（反应堆运行工况、中子学数据）的变化。

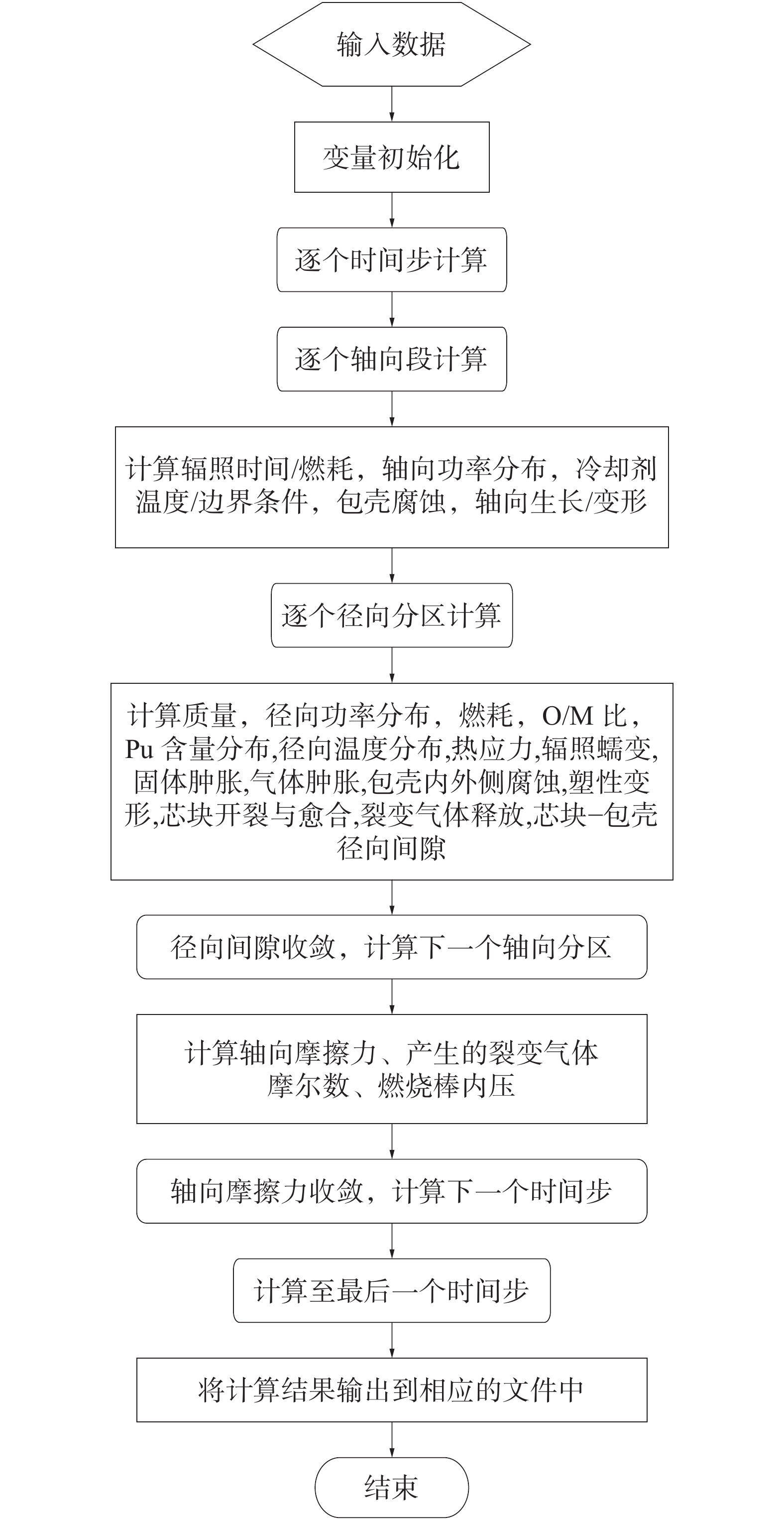
从时间上，将辐照功率史离散为若干时间步，根据输入数据进行初始化，定义燃料棒的初始参数；然后，计算下一时间步燃料棒各个轴向段的状态参数，计算结果作为下一时间步的初始化状态，直到计算完所有的时间步。从空间上，首先将燃料棒分成若干轴向段，然后每个轴向段又被分成若干径向同心环，于是燃料棒被划分为若干体积微元。

图1给出了FUPAC软件的计算流程。

2.1 芯块力学模型 2.1.1 气体肿胀模型

裂变气体原子形成的晶内气泡和晶界气泡对燃料肿胀的贡献被称为气体肿胀。该现象十分复杂，涉及到了气泡的产生、生长、合并与连通，并对UO₂的蠕变和变形有所影响。

1）稳态气体肿胀模型

燃料体积由于气体肿胀而增加的份额为ΔV_G：

$\Delta {V_{\rm{G}}} = {{\min}}[{f_1},\Delta {V_{\max}},{f_2}]$

$\Delta {V_{\max}} = {\min}[{C_1},{C_2}{B_U}/{B_{{U_0}}}]$

式中： ${f_1}$ 为低温下的肿胀气孔率； ${f_2}$ 为高温下的肿胀气孔率；C₁、C₂为常数； ${B_U}$ 为局部燃耗，MWd/tU； ${B_{{U_0}}}$ 为参考燃耗，MWd/tU。

2）瞬态气体肿胀模型

$\begin{array}{c} \Delta {V_{\rm{G}}}\left( t \right) = \Delta {V_{\rm{G}}}\left( {{t_0}} \right) + \left[\Delta {V_{{\rm{GSS}}}}\left( t \right) - \Delta {V_{\rm{G}}}\left( {{t_0}} \right)\right] \times \\ {\rm{max}}\left[1,C{F_{{\rm{TR}}}}\left( t \right)/{F_{{\rm{SS}}}}\left( t \right)\right] \end{array}$

式中：ΔV_GSS（t）为瞬态条件下稳态气体肿胀引起的燃料体积变化量；ΔV_G（t）为瞬态过程中t时刻气体肿胀引起的燃料体积变化量；C为常数；F_TR(t)为瞬态裂变气体释放份额；F_SS(t)为稳态裂变气体释放份额。

2.1.2 芯块密实化和固体肿胀模型

芯块受辐照后会发生2个影响相反的现象：密实化和固体肿胀^[6-8]。

密实现象因辐照和受热产生，主要是孔隙湮灭。初开始时，小尺寸（<1 μm）的孔隙立即消失，而中等尺寸（1~3 μm）的孔隙逐渐消失。密实将导致燃料密度增大、体积减小。

当B_U< ${B_{{U_{\lim }}}}$ 时：

$ \Delta \rho = 0 $

当B_U $\geqslant{B_{{U_{\lim }}}}$ 时：

$\Delta \rho = {\rho _0} \cdot a \cdot \ln \frac{{B_U}}{{20}} - {\rho _0} \cdot {k_0} \cdot a \cdot B_U$

式中； ${\rho _0}$ 为初始密度，kg/m³；α为燃料固体肿胀率；k₀为转换常数。

2.1.3 芯块重定位应变模型

寿期初，燃料芯块就会因热应力而开裂。由于棒内存在一定的自由空间，比如寿期初燃料与包壳之间的间隙，芯块碎块将重新分布。初始的碎块迁移现象显著地增加了芯块半径。在芯块与包壳接触后，由于包壳对芯块的作用力，芯块碎块将重新定位。包壳外径由于蠕变而持续缩小，然后在一段时间里保持稳定。最后，芯块推动包壳向外膨胀，直径增加。

${e_{{\rm{relo}}}} = {e_{{\rm{sjort}}}} + {e_{{\rm{rearrangt}}}} + {e_{{\rm{crack}}}}$

${\varepsilon _{{\rm{relo}}}} = {\varepsilon _{{\rm{sjort}}}} + {\varepsilon _{{\rm{rearrangt}}}} + {\varepsilon _{{\rm{crack}}}}$

式中： ${\varepsilon _{{\rm{relo}}}}$ 为总的重定位应变； ${\varepsilon _{{\rm{sjort}}}}$ 为初始碎片迁移引起的应变； ${\varepsilon _{{\rm{rearrangt}}}}$ 为芯块与包壳接触后重新定位引起的应变； ${\varepsilon _{{\rm{crack}}}}$ 为开裂芯块相对于实心芯块的热膨胀效应的修正项。

2.2 包壳力学模型详细说明 2.2.1 塑性应变模型

塑性应变模型为：

${\varepsilon _P} = {\left( {\frac{{\sigma - {\sigma _0}}}{K}} \right)^{1/n}}$

式中： ${\varepsilon _P}$ 为周向塑性应变 $\displaystyle\left({\varepsilon _P} = \frac{{\Delta {D_e}}}{{{D_m}}}\right)$ ，其中 $\Delta {D_e}$ 为包壳外径变化量，mm； ${D_m}$ 为包壳平均直径，mm；K和 ${\sigma _0}$ 为温度和快中子通量的函数。

2.2.2 蠕变模型

应力引起的材料蠕变是与时间有关的塑性应变，同时也是关于热流密度或中子通量的函数^[9−12]。对于一种特定材料（同样的化学成分、微观结构、制造工艺）来说，蠕变应变可以表示为应力、温度、时间和快中子通量的函数。

2.2.3 包壳高应力蠕变和松弛模型

芯块与包壳间有强相互作用时的包壳应变是弹−塑性应变和蠕变应变的组合，也包括应力松弛。2种应变（塑性应变和蠕变应变）的份额取决于载荷。应力松弛由包壳短期蠕变特性决定；高应力下的燃料棒蠕变主要由热蠕变控制。对于一种特定材料（同样的化学成分、微观结构、制造工艺），热蠕变是关于时间、应力、温度和快中子通量的函数。

$\varepsilon = {a_P} \cdot \ln (1 + {V_P} \cdot t) + {V_s} \cdot t$

式中： $\varepsilon $ 为蠕变应变；a_P为V_P的函数；V_S、V_P为应力和温度的函数。

3 验证实例

以田湾核电站5、6号机组长燃料循环堆芯燃料管理为背景，采用我院自主化研发软件FUPAC，针对燃料棒包壳应变进行验证计算，并针对工程计算中涉及的不确定性进行分析和评价。

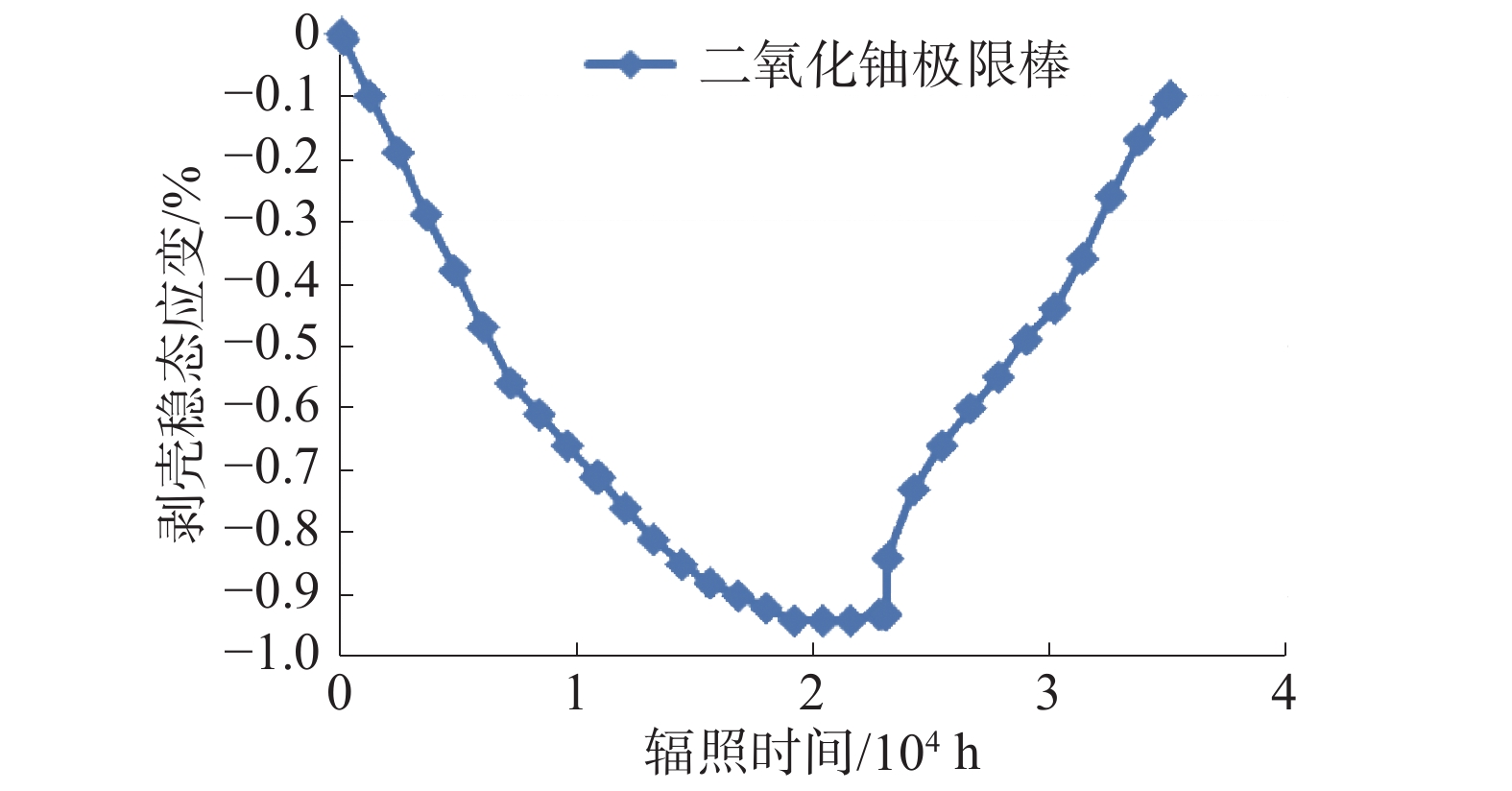
3.1 稳态应变

图2给出了极限棒的包壳稳态应变随辐照时间的变化曲线。

包壳的稳态应变是燃料肿胀、密实及包壳蠕变共同作用的结果。芯块与包壳接触后，包壳应变主要来自芯块肿胀。而由于内压超过系统压力引起的包壳向外蠕变只能起到次要作用。由于包壳的稳态应变主要受到芯块肿胀的影响，所以影响芯块结构的参数势必会对包壳稳态应变也有影响，如燃料的密实、肿胀，芯块的热膨胀，特别是在寿期末，影响燃料热膨胀的因素会对包壳应变有较大影响。但是基于工程经验，该准则一般来说余量很大，因此验证极限棒在整个寿期中包壳的应变始终为负值，即满足长期应变准则。

3.2 瞬态应变

当芯块与包壳间隙闭合后，经历II类瞬态期间会发生较大的应变，该现象主要是因为芯块和包壳热膨胀不一致带来的影响。而一般情况下，由于II类瞬态持续时间较短，内压仅是因为温度的变化导致压力变大，所以内压对包壳瞬态应变的影响是次要的。

关于燃料棒在何时发生瞬态会使得燃料棒包壳瞬态应变最大，相关的资料并未有确切定论，基于多个工程项目的计算经验，通常的做法是在各循环寿期初、中、末均考虑添加瞬态。由于瞬态应变的大小直接取决于瞬态发生时刻功率跃增的大小，根据堆芯物理专业提供的数据，挑选具有典型功率史的燃料棒，进行瞬态模拟。基于工程经验，仍需考虑包括芯块包壳间隙、包壳蠕变模型、燃料密实、燃料密度以及燃料温度的不确定性，即最小芯块包壳直径间隙、包壳低应力蠕变上界模型、最小燃料密实、最小燃料密度、燃料温度上界模型。

本文考察了具有代表性的不同功率史，通过FUPAC软件进行模拟功率升降的堆内工况，在最极限的情况下，功率变化导致的包壳直径增大（弹塑性应变+蠕变）为0.64%，小于准则限值1%。

4 结论

本文研究了燃料棒包壳应变的分析方法和热−力学计算理论模型，以田湾核电站5、6号机组长燃料循环堆芯燃料管理为背景，对包壳稳态、瞬态应变进行了评价，得到以下结论：

1）分析得到影响包壳应变的主要影响因素，以及工程计算中需要考虑的不确定性因素；

2）通过自主化软件FUPAC程序验证计算，计算结果与技术限值相比较均有裕量，满足设计准则；

3）在新型燃料设计当中，需全面考虑引起燃料棒失效的因素以及计算模型带来的不确定性，在保证安全性的同时提高经济性。