大型非能动先进压水堆大量采用了非能动安全系统。与传统压水堆相比,首先非能动安全系统利用自然力驱动,提高了系统运行的可靠性;其次,非能动电厂在设计基准事故初期无需操纵员干预,提高了系统运行可靠性;最后,非能动安全系统的启动和运行不需要交流电源。为了研究发生小破口失水事故时一回路及非能动安全系统的多种热工水力现象过程与机理,同时也为进行相关事故分析程序的验证,针对原型反应堆系统,基于模化设计建设了整体验证台架。本文从模化设计原则出发,针对整体验证台架(以ACME装置为例)SBLOCA事故序列,初步评估其对大型非能动压水堆(以AP1000为例)SBLOCA事故进程模拟验证的适宜性。
1 大型非能动先进压水堆SBLOCA的重要现象过程大型非能动先进压水堆的非能动堆芯冷却系统(passive containment cooling system,PXS)主要由2个堆芯补水箱(core makeup tank,CMT)、2个安注箱(accumulator,ACC)、自动降压系统(automatic depressurization system,ADS)、安全壳内置换料水箱(in-containment refueling water storage tank,IRWST)、非能动余热排除热交换器(passive residual heat removal heat exchanger,PRHR-HX)及相关的管道阀门等组成。将原型堆SBLOCA事故进程分为6个阶段:破口喷放阶段、自然循环阶段、ADS喷放阶段、ADS-IRWST过渡阶段、IRWST注入阶段以及地坑注入阶段[1]。
当发生破口时,反应堆冷却剂系统(reactor coolant system,RCS)通过破口快速喷放冷却剂,然后PRHR和CMT被触发,系统进入自然循环阶段。其中PRHR-HX的入口、出口管线分别与RCS热管段和蒸汽发生器下封头冷腔室相连,它们与RCS热管段和冷管段组成一个非能动余热排除的自然循环回路,CMT通过一根注入出口管线和一根连接到冷管段的压力平衡管线分别与RCS相连,构成一个自然循环回路。在此阶段中CMT的循环模式随着RCS水装量的减少由循环模式转变为排水模式,当CMT液位下降至65%时,ADS−1被触发,RCS系统进入ADS喷放阶段,随着ACC和ADS−2/3/4的投入使用,RCS充分卸压后,IRWST得以在重力驱动下进行安注,从而进入长期冷却状态。根据现象识别与排序表(PIRT)[1],SBLOCA事故进程中高重要度(H)和中重要度(M)的现象和过程如表1所示。
|
|
表 1 小破口失水事故进程中重要现象 |
非能动压水堆安全系统对比传统压水堆的特点在于事故进程中PXS设备及其连接的冷、热管段等管道组成的自然循环回路。由于不同设备和管道间形成的自然循环回路在事故进程中因整定值和系统的状态不同会互相耦合,导致系统过程十分复杂,因此本文采用系统性的整体比例模化分析方法H2TS[2]对大型非能动先进压水堆SBLOCA事故的6个事故进程进行模化分析,该方法包括自上而下(Top-Down)与自下而上(Bottom-Up)的比例分析。自上而下的比例分析是基于整体守恒方程识别对系统行为而言重要的整体过程或效应;自下而上的比例分析则是对重要的局部现象进行比例分析与评估,由此初步评估模型(验证装置)对原型(大型非能动压水堆)的模拟能力。
2.1 破口喷放阶段由于PIRT表中的一些高排位现象并非非能动压水堆所特有的,同时非能动安全系统对于破口喷放阶段几乎没有影响,使得非能动压水堆破口喷放阶段的行为以及反应堆系统对于堆芯衰变热的敏感性也与传统压水堆相似,因此,尽管验证台架仍需进行比例模化评估,但本文不予讨论。
2.2 自然循环阶段 2.2.1 Top-Down模化分析这一阶段的控制方程如下:
质量守恒:
| $\frac{{\partial {\rho _{\rm{m}}}}}{{\partial t}} + \frac{\partial }{{\partial z}}\left( {{\rho _{\rm{m}}} + {u_{\rm{m}}}} \right) = 0$ |
动量守恒:
| $ \begin{aligned} \dfrac{{\partial {\rho _{\rm{m}}}{u_{\rm{m}}}}}{{\partial t}} + & \dfrac{\partial }{{\partial z}}\left( {{\rho _{\rm{m}}}u_{\rm{m}}^2} \right) = - \dfrac{{\partial {P_{\rm{m}}}}}{{\partial z}} - {\rho _{\rm{m}}}g - \dfrac{\partial }{{\partial z}}\left[ {\dfrac{{\alpha {\rho _{\rm{g}}}\rho }}{{\left( {1 - \alpha } \right){\rho _{\rm{m}}}}}V_{{\rm{gj}}}^2} \right] - \\ & \left[ {\dfrac{{{f_{\rm{m}}}}}{{2d}} + K\delta \left( {z - {z_i}} \right)} \right]{\rho _{\rm{m}}}{u_{\rm{m}}}\left| {\rho {u_{\rm{m}}}} \right| \end{aligned} $ |
能量守恒:
| $\begin{aligned} \frac{{\partial {\rho _{\rm{m}}}{H_{\rm{m}}}}}{{\partial t}} + & \frac{\partial }{{\partial z}}\left( {{\rho _{\rm{m}}}{u_{\rm{m}}}{H_{\rm{m}}}} \right) = - \frac{{4{h_{\rm{m}}}}}{d}\left( {{T_{\rm{s}}} - {T_{{\rm{sat}}}}} \right) - \\ & \frac{\partial }{{\partial z}}\left[ {\frac{{\alpha {\rho _{\rm{g}}}\rho }}{{{\rho _{\rm{m}}}}}{\rm{\Delta }}{H_{{\rm{fg}}}}{V_{{\rm{gj}}}}} \right] \\ \end{aligned} $ |
式中:ρm为混合物密度;t为时间;z为轴向距离;um为速度;Pm为混合物压力;g为重力加速度;α为空泡份额;Vgj为漂移流速度;fm为混合物摩擦力;d为水力学直径;K为孔口系数;δ为传导深度;Hm为混合物焓;hm为混合物比焓;Ts为固体温度;Tsat为饱和温度;ρg为气相密度;ΔHfg为潜热。
通过比例分析得到模化比[3]:
| $ \begin{gathered} {\pi _{\rm{R}}} = {\left[ {{x_{\rm{e}}} \cdot \left( {\frac{{\Delta \rho }}{{{\rho _g}}}} \right)} \right]_{\rm{R}}} \\ {u_{\rm{R}}}{\rm{ = }}\sqrt {{l_{\rm{R}}}} \\ {q_{\rm{R}}} = 1/\sqrt {{l_{\rm{R}}}} \\ \end{gathered} $ |
式中:
由于CMT平衡管线流体成分对CMT是处于循环模式还是排水模式有着重要的影响,而CMT平衡管线的流体成分与它所连接的冷管段中的流型及冷管段与CMT平衡管线连接处的相分离有关,因此对这两个现象进行自下而上的分析。
对于冷管段流型,采用Taitel-Dukler[4]两相水平流动流型边界准则,通过分析可以得到弗劳德数(Fr数)是主要的模化参数:
| $Fr = \frac{{{j_{\rm{g}}}}}{{\sqrt {gd} }}{\left( {\frac{{{\rho _{\rm{g}}}}}{{{\rho _{\rm{f}}} - {\rho _{\rm{g}}}}}} \right)^{1/2}}$ |
式中:jg为气相表观速度;ρf为液相密度。
通过比例分析得到模化比:
| ${\left( {{\pi _{Fr}}} \right)_{\rm{R}}} = {\left[ {\frac{{{q_{{\rm{core}}}}}}{{{d_{{\rm{CL}}}}^{5/2}}}} \right]_{\rm{R}}}$ |
式中:πFr为Fr的无量纲参数组;qcore为堆芯功率;dCL为冷管段水力学直径。
对于冷管段和CMT平衡管线所形成的T形接口,当两相流流经这种接口时,由于相分离现象的发生,分支内流体的干度(xbranch)与主管道中的流体干度(xmain)存在差异。根据Seeger等[5]关于顶部竖直向上分支与主管道干度关系的关系式:
| $\frac{{{X_{{\rm{branch}}}}}}{{{X_{{\rm{main}}}}}} = {\left( {\frac{{{G_{{\rm{branch}}}}}}{{{G_{{\rm{main}}}}}}} \right)^{ - 0.8}}$ |
通过比例分析得到模化比:
| ${\left( {{\pi _x}} \right)_{\rm{R}}} = \left[ {{{\left( {\frac{{{d_{{\rm{CL}}}}}}{{{d_{{\rm{CMT, bl}}}}}}} \right)}^2}} \right]_{\rm{R}}^{ - 0.8}$ |
式中:πx指干度的无量纲数组;dCMT,bl为CMT平衡管线水力学直径。
2.3 ADS喷放阶段 2.3.1 Top-Down模化分析Top-Down阶段最主要的参数是反应堆冷却剂系统的压力,采用压力变化率方程对ADS降压过程进行比例分析。由于在自动降压阶段从堆芯补水箱或安注箱注入RCS系统中的冷却剂质量与ADS系统喷放出的相比非常小,因此,压力变化率方程简化为:
| $\left( {\frac{{{V_{{\rm{RCS, sv}}}}}}{{\left( {\gamma - 1} \right)}}} \right)\frac{{{\rm{d}}{P_{{\rm{RCS, sv}}}}}}{{{\rm{d}}t}} = {\dot m_{{\rm{core, s}}}}{h_{\rm{g}}} - {\dot m_{{\rm{ADS, s}}}}{h_{\rm{g}}}$ |
式中:VRCS,sv为RCS蒸汽体积;
通过比例分析得到模化比:
| ${\omega _{{\rm{core, s}} - {\rm{RCS, sv}}}} = {\left[ {\frac{{{{\dot m}_{{\rm{core, s}}}} \cdot {h_{\rm{g}}}}}{{{{\left( {V\Delta P} \right)}_{{\rm{RCS, s}}}}}}} \right]_{\rm{R}}}$ |
| ${\omega _{{\rm{ADS, s}} - {\rm{RCS, sv}}}} = {\left[ {\frac{{{{\dot m}_{{\rm{ADS, s}}}} \cdot {h_{\rm{g}}}}}{{{{\left( {V\Delta P} \right)}_{{\rm{RCS, s}}}}}}} \right]_{\rm{R}}}$ |
式中:ωcore,s-RCS,sv为堆芯蒸汽体积比RCS蒸汽体的模型与原型的频率比;ωADS,s-RCS,sv为ADS蒸汽体积比RCS蒸汽体积的模型与原型的频率比。
2.3.2 Bottom-Up模化分析在ADS喷放阶段,波动管线上的压降重要度为中,模型对原型波动管线上的压降模拟可以在实验过程中进行调整。
2.4 ADS-IRWST过渡阶段 2.4.1 Top-Down模化分析反应堆压力容器的装量是小破口失水事故期间最重要的参数之一,选择压力容器装量作为模化参数。由于在低压状态下气相相对液相质量非常小,同时气相带走堆芯余热的能力也比液相小很多,因此压力容器装量可近似为压力容器水装量。
在ADS-IRWST的过渡过程中,初期CMT注入对压力容器水装量的补充起主导作用,当CMT注入结束后,IRWST注入开始起主导作用。在这一阶段,ADS系统结束了对RCS系统的降压并向IRWST的长期重力注入转变,对于小破口失水事故来说这是最重要的时期,因此下面2个子阶段都需要模化。
1)子阶段1: CMT注入主导阶段
这一阶段的控制方程如下:
质量守恒:
| $\frac{{{\rm{d}}{M_{{\rm{vessel}}}}}}{{{\rm{d}}t}} = {\dot m_{{\rm{CMT}}}} - {\dot m_{{\rm{core}}}}$ |
动量守恒:
| ${\rho _{\rm{f}}}g\left[ {{Z_{{\rm{CMT}}}} - {Z_{{\rm{DVI}}}}} \right] = \left[ {{{\left( {\sum \frac{R}{{{A^2}}}} \right)}_{{\rm{CMT - DVI}}}}} \right]\frac{{\dot m_{{\rm{CMT}}}^2}}{{2{\rho _{\rm{f}}}}}$ |
能量守恒:
| ${q_{{\rm{core}}}} = {\dot m_{{\rm{core}}}}\left( {{h_{{\rm{out}}}} - {h_{{\rm{in}}}}} \right) = {\dot m_{{\rm{core}}}}\left( {{h_{{\rm{sub}}}} - {x_{{\rm{e}}}}{h_{{\rm{fg}}}}} \right)$ |
式中:ZCMT为CMT轴向距离;ZDVI为DVI轴向距离;R为理查德数;A为流通面积;hout为出口比焓;hin为入口比焓;hsub为过冷焓;hfg为相变焓;下标CMT-DVI指连接CMT的DVI管线。
将动量守恒和能量守恒方程得到的2个质量流量带入到压力容器水装量守恒方程中得到:
| ${\rho _{\rm{f}}}\frac{{{\rm{d}}{V_{{\rm{vl}}}}}}{{{\rm{d}}t}} = {\left[ {\frac{{2{\rho _{\rm{f}}}^2g\left[ {{Z_{{\rm{CMT}}}} - {Z_{{\rm{DVI}}}}} \right]}}{{{{\left( {\displaystyle\sum \dfrac{R}{{{A^2}}}} \right)}_{{\rm{CMT - DVI}}}}}}} \right]^{1/2}} - \dfrac{{{q_{{\rm{core}}}}}}{{(\Delta {h_{{\rm{sub}}}} + {x_{{\rm{e}}}}{h_{{\rm{f}}}})}}$ |
式中Vvl指压力容器内液体体积。
通过比例分析最终得到无量纲方程和模化比:
| $ \begin{array}{l} \dfrac{{{\rho ^ + }{\rm{d}}V_{vl}^ + }}{{{\rm{d}}t}} = {\omega _{{\rm{CMT, vl}}}} \cdot \dot m_{{\rm{CMT}}}^ + - {\omega _{{\rm{core, vl}}}} \cdot \dot m_{{\rm{core}}}^ + \\ {\omega _{{\rm{CMT, vl}}}} = \dfrac{{\left[ {\dfrac{{2{\rho _{\rm{f}}}^2g\left[ {{Z_{{\rm{CMT}}}} - {Z_{{\rm{DVI}}}}} \right]}}{{{{\left( {\displaystyle\sum \dfrac{R}{{{A^2}}}} \right)}_{{\rm{CMT - DVI}}}}}}} \right]_{{\rm{ref}}}^{1/2}}}{{{{\left( {{\rho _{\rm{f}}}\Delta {V_{{\rm{vl}}}}} \right)}_{{\rm{ref}}}}}} \\ {\omega _{{\rm{core, vl}}}} = \dfrac{{{{\left[ {\dfrac{{{q_{{\rm{core}}}}}}{{\Delta {h_{{\rm{sub}}}} + {x_{{\rm{exit}}}}{h_{{\rm{fg}}}}}}} \right]}_{{\rm{ref}}}}}}{{{{\left( {{\rho _{\rm{f}}}\Delta {V_{{\rm{vl}}}}} \right)}_{{\rm{ref}}}}}} \end{array} $ |
式中:ωCMT,vl指CMT管道液体的无量纲频率值;ωcore,vl指堆芯管道液体的无量纲频率值;上标+指无量纲参数;下标ref指参考值。
2)子阶段2:IRWST注入主导阶段
这一阶段的控制方程如下:
质量守恒:
| $\frac{{{\rm{d}}{M_{{\rm{vl}}}}}}{{{\rm{d}}t}} = {\dot m_{{\rm{IRWST}}}} - {\dot m_{{\rm{core}}}}$ |
动量守恒:
| $\begin{array}{l} {\rho _{\rm{f}}}g\left[ {{Z_{{\rm{IRWST}}}} - {Z_{{\rm{DVI}}}}} \right] - \left[ {{P_{{\rm{RCS}}}} - {P_{{\rm{CONT}}}}} \right] = \\ \quad \quad \quad \quad \;\; \;\left[ {{{\left( {\displaystyle\sum \dfrac{R}{{{A^2}}}} \right)}_{{\rm{IRWST - DVI}}}}} \right]\dfrac{{m_{{\rm{IRWST}}}^2}}{{2{\rho _{\rm{f}}}}} \end{array}$ |
能量守恒:
| ${q_{{\rm{core}}}} = {\dot m_{{\rm{core}}}}\left( {{h_{{\rm{out}}}} - {h_{{\rm{in}}}}} \right) = {\dot m_{{\rm{core}}}}\left( {{h_{{\rm{sub}}}} - {x_{{\rm{exit}}}}{h_{{\rm{fg}}}}} \right)$ |
式中:
通过比例分析最终得到无量纲方程和模化比:
| $ \begin{array}{l} \dfrac{{{\rho ^ + }{\rm{d}}V_{{\rm{vl}}}^ + }}{{{\rm{d}}t}} = {\omega _{{\rm{IRWST-vl}}}} \cdot \dot m_{{\rm{IRWST}}}^ + - {\omega _{{\rm{core\_vl}}}} \cdot \dot m_{{\rm{core}}}^ + \\ {\omega _{{\rm{CMT - vl}}}} = \\ \quad \quad\quad \;\; \dfrac{{{{\left[ {\dfrac{{2{\rho _{\rm{f}}}\left[ {{\rho _{\rm{f}}}g\left( {{Z_{{\rm{IRWST}}}} - {Z_{{\rm{DVI}}}}} \right) - {\rho _{\rm{f}}}g\left( {{Z_{{\rm{PZR}}}} - {Z_{{\rm{HL}}}}} \right)} \right]}}{{{{\left( {\displaystyle\sum \dfrac{R}{{{A^2}}}} \right)}_{{\rm{IRWST - DVI}}}}}}} \right]}^{1/2}}}}{{{{\left( {{\rho _{\rm{f}}}\Delta {V_{{\rm{vl}}}}} \right)}_{{\rm{ref}}}}}}\\ {\omega _{{\rm{CMT - vl}}}} = \dfrac{{{{\left[ {\dfrac{{{q_{{\rm{core}}}}}}{{(\Delta {h_{{\rm{sub}}}} + {x_{{\rm{exit}}}}{h_{{\rm{fg)}}}}}}} \right]}_{{\rm{ref}}}}}}{{{{\left( {{\rho _{\rm{f}}}\Delta {V_{{\rm{vl}}}}} \right)}_{{\rm{ref}}}}}} \end{array} $ |
由于流型会影响ADS喷放流道中的压降和夹带,因此热管段中分层流与非分层流之间的流型转变是重要的局部现象。采用Taitel-Dukler两相水平流动流型边界准则,通过与2.2.2节相同的分析可以得到模化比:
| ${\left( {{\pi _{Fr}}} \right)_{\rm{R}}} = {\left[ {\frac{{{q_{{\rm{core}}}}}}{{{d_{{\rm{HL}}}}^{5/2}}}} \right]_{\rm{R}}}$ |
式中dHL为热管段水力学直径。
由于夹带将会影响系统内流体质量的分配以及热管段与ADS−4流道间的压降,因此发生在热管段到ADS−4流道间的液体夹带是一个重要的局部现象。液体从大水箱或管道向竖直排放通道的夹带的开始与Fr数以及主管道顶部的液位(Lg)和竖直排放通道直径(dofftake)的几何比有关[6]:
| $\frac{{{u_{\rm{g}}}\sqrt {{\rho _{\rm{g}}}} }}{{({\rho _{\rm{f}}} - {\rho _{\rm{g}}}){L_{\rm{g}}}}} \geqslant 5.7{\left( {\frac{{{L_{\rm{g}}}}}{{{d_{{\rm{offtake}}}}}}} \right)^{3/2}}$ | (1) |
式(1)可转化为下面的模化方程:
| ${\pi _{\rm{R}}} = {\left[ {\frac{{{u_{\rm{g}}}\sqrt {{\rho _{\rm{g}}}} }}{{\sqrt {g\left( {{\rho _{\rm{f}}} - {\rho _{\rm{g}}}} \right){L_{\rm{g}}}} }}} \right]_R}{\left( {\frac{{{d_{{\rm{offtake}}}}}}{{{L_{\rm{g}}}}}} \right)^{3/2}}$ |
排放通道内的蒸汽速率可以通过堆芯内的稳态能量守恒来估算:
| ${u_{\rm{g}}} = \frac{{{q_{{\rm{core}}}}}}{{{\rho _{\rm{g}}}{h_{{\rm{fg}}}}{A_{{\rm{offtake}}}}}} = \frac{{{q_{{\rm{core}}}}}}{{{\rho _{\rm{g}}}{h_{{\rm{fg}}}}{A_{{\rm{ADS}} - 4}}}}$ |
对于ACME这样的等压模型,得到模化比:
| $ {\pi _{\rm{R}}} = {\left[ {\frac{{{q_{{\rm{core}}}}}}{{{d_{{\rm{ADS}} - 4{\rm{inlet}}}}^{1/2} \cdot d_{{\rm{HL}}}^2}}} \right]_{\rm{R}}} $ |
由于稳压器波动管中的逆流会影响稳压器在ADS−1/2/3运行阶段再灌水之后的排水速率以及IRWST的注入,因此稳压器波动管中的逆流是一个重要的局部现象。因为管道足够大,所以可以通过模化Kutateladze数来实现波动管中逆流的模化:
| $K_{\rm{i}}^* = \frac{{\rho _{\rm{i}}^{1/2}{j_{\rm{i}}}}}{{{{(({\rho _{\rm{f}}} - {\rho _{\rm{g}}})g{\rm{\sigma }})}^{1/4}}}}$ |
式中σ为表面张力。
通过比例分析得模化比:
| ${\pi _{\rm{R}}} = {\left[ {\frac{{{j_{\rm{g}}}{{(\rho _{\rm{f}}^{1/4} + \rho _{\rm{g}}^{1/4})}^2}}}{{\Delta \rho {\rm{\sigma }}}}} \right]_{\rm{R}}}$ |
对于ACME这样的等压模型,波动管的模化关系式为:
| ${\pi _{\rm{R}}} = {\left[ {{{\left( {{j_{\rm{g}}}} \right)}_{{\rm{SL}}}}} \right]_{\rm{R}}} = {\left[ {{{\left( {{j_{\rm{f}}}} \right)}_{{\rm{SL}}}}} \right]_{\rm{R}}}$ |
式中:(jg)SL为波动管气相表观速度;(jf)SL为波动管液相表观速度。
2.5 IRWST注入阶段 2.5.1 Top-Down模化分析由于在IRWST注入阶段流经反应堆压力容器的的质量流量是稳定的,近似为常数,因此这一过程的控制方程如下:
质量守恒:
| $\dot m = {\rm{constant}}$ |
动量守恒:
| $\begin{gathered} g{\rho _{\rm{L}}}\left[ {{Z_{{\rm{IRWST}}}} - {Z_{{\rm{core, i}}}}} \right] - g{{\bar \rho }_{\rm{L}}}\left[ {{Z_{{\rm{core}}, 2\phi }} - {Z_{{\rm{core, i}}}}} \right] - \\ g{{\bar \rho }_{\rm{m}}}\left[ {{Z_{{\rm{IRWST}}}} - {Z_{{\rm{core}}, 2\phi }}} \right] = \\ \left( {\frac{{{{\dot m}^2}}}{{2{\rho _{\rm{f}}}}}} \right)\left[ {{{\left( {\sum \frac{R}{{{A^2}}}} \right)}_{{\rm{DVI}}}} + \phi _{{f_0}}^2{{\left( {\sum \frac{R}{{{A^2}}}} \right)}_{{\rm{ADS}}}}} \right] \\ \end{gathered} $ |
能量守恒:
| $\begin{aligned} {q_{{\rm{core}}}} = & \dot m\left( {{h_{{\rm{core, o}}}} - {h_{{\rm{core, i}}}}} \right) = \dot m\left[ {\left( {{h_{\rm{f}}} - {x_{{\rm{e}}}}{h_{{\rm{fg}}}}} \right) - {h_{\rm{L}}}} \right] = \\ & \dot m\left[ {\Delta {h_{{\rm{sub}}}} + {x_{{\rm{e}}}}{h_{{\rm{fg}}}}} \right] \\ \end{aligned} $ |
式中:R为阻力,R=fL/d+K,其中f为摩擦系数、d为直径、K为形状损失系数;Zcore,i为堆芯入口段长度;Zcore,2φ为反应堆中两相段开始的高度(即沸腾开始);
由于干度影响IRWST注入过程中的流型、压降等热工水力状态,因此这个阶段的主要模化参数是堆芯出口干度:
| ${\pi _{\rm{R}}} = {\left[ {{x_e}} \right]_{\rm{R}}}$ |
当IRWST注入开始之后,堆芯空泡份额将会影响两相流系统的状态,为了模化堆芯空泡份额,基于Yeh关系式[1]:
| $\alpha = 0.925{\left( {\frac{{{\rho _{\rm{g}}}}}{{{\rho _{\rm{f}}}}}} \right)^{0.24}}{\left( {\frac{{{j_{\rm{g}}}}}{{{V_{{\rm{bcr}}}}}}} \right)^a}{\left( {\frac{{{j_{\rm{g}}}}}{{{j_{\rm{g}}} + {j_{\rm{f}}}}}} \right)^{0.6}}$ | (2) |
式中:
堆芯气体表现速度为:
| ${j_{\rm{g}}}\left( Z \right) = \frac{{{q_{{\rm{core}}}} \cdot Z}}{{{\rho _{\rm{g}}}{h_{{\rm{fg}}}}{L_{{\rm{core}}}}{A_{{\rm{core}}}}}} = \frac{{{q_{{\rm{core}}}}}}{{{V_{{\rm{core}}}}}} \cdot \frac{Z}{{{\rho _{\rm{g}}}{h_{{\rm{fg}}}}}}$ | (3) |
将式(3)代入式(2),最后得到模化比:
| ${\pi _{\rm R}} = {\left( \alpha \right)_{\rm R}} = \left( {\frac{{{q_{{\rm{core}}}} \cdot Z}}{{{V_{{\rm{core}}}}}}} \right)_{\rm R}^{0.57}$ |
此阶段自上而下分析和自下而上分析的主要模化参数与IRWST注入阶段相同,通过相同的分析过程,得到的模化比与IRWST注入阶段相同。
3 ACME台架模拟AP1000核电厂的模化评估ACME台架是以大型非能动先进压水堆为原型,通过比例分析设计的整体试验台架。其与一般的非能动压水堆相比,最大的区别是有2个安全壳内置换料水箱,其中IRWST−1水箱直径较大,高度为电厂原型的1/3,作为热阱;IRWST−2水箱直径较小,高度与电厂原型相同,作为重力注射的水源[7]。
ACME台架与AP1000电厂根据模化设计要求所得到的模化比总结于表2中。对于与出口干度、空泡份额等相关的模化比可以通过对功率和阻力的预计算及实验过程中的调试来保证;对于与几何尺寸、堆芯功率等相关的模化比,可以根据表3中所示ACME与AP1000电厂的重要参数比[8−9]计算出。
|
|
表 2 ACME/AP1000的SBLOCA事故进程中各个阶段的模化比 |
|
|
表 3 ACME与AP1000重要参数比 |
计算结果表明模化比值在规定范围[10](0.5≤πR≤2)内,因此,可以认为不管从自上而下的角度,还是从自下而上的角度,比如热管段与冷管段中的流型、CMT平衡管线与冷管段结合处T型管相分离、ADS−4流道向热管的夹带等重要的局部现象等,以ACME台架模拟验证AP1000小破口失水事故进程是适宜的。
4 ACME台架实验值与AP1000电厂RELAP5计算值结果比较2-inch小破口失水事故是非能动压水堆小破口失水事故的典型工况,因此,本文使用RELAP5系统分析程序模拟AP1000反应堆冷管段2-inch小破口失水事故进程,并将计算结果与ACME台架的实验数据对比,从具体事故进程角度验证ACME台架是否能很好地模拟AP1000。图1所示为应用Relap5程序对AP1000建模时的节点划分图[11]。为了更加直观地对比ACME台架实验结果和AP1000的计算结果,按照表2中的时间等参数的比例关系,把ACME台架的实验结果折算后与AP1000的计算结果放在同一图上[12]。图2显示了冷段小破口工况下主回路压力和3个非能动安全设备注入流量随时间的变化情况。需注意,ACME台架稳态条件模拟的起点所对应于真实AP1000发电厂的瞬态点是当AP1000的主系统压力降至9.2 MPa时。

|
Download:
|
| 图 1 AP1000 RELAP5节点 | |
|
Download:
|
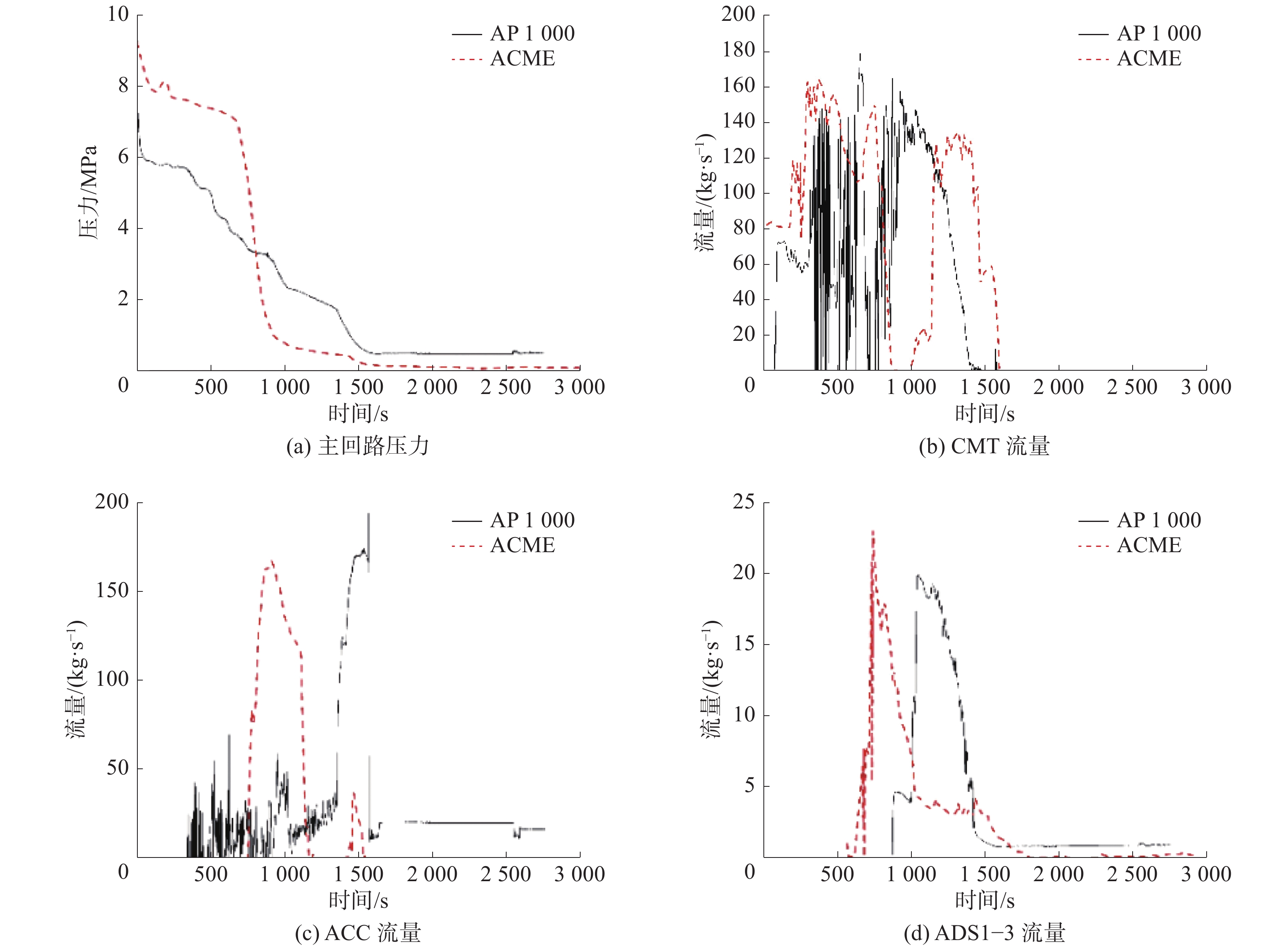
| 图 2 冷段小破口工况下主回路压力和3个非能动安全设备注入流量随时间的变化 | |
图2(a)显示了AP1000核电厂和ACME台架中反应堆冷却剂系统(RCS)的压力随时间变化的过程。图中可见ACME和AP1000的压力都快速下降,最后基本保持不变。ACME台架压力下降速率比AP1000稍快,因此更快进入准稳态状态,这可能是由于ACME台架模拟AP1000时高度、流通面积等参数时的误差,导致两者之间冷却剂的流动状态等存在一定程度上的差异所导致。但是ACME和AP1000的压力下降趋势以及压力下降阶段的时间大体一致,这表明在破口发生后的短时间内,该整体试验台架可以在一定程度上模拟AP1000核电厂。图2(b)显示ACME台架CMT的投入较AP1000更早,是因为ACME台架RCS系统压力下降更快,导致触发CMT的稳压器和蒸汽发生器低压值更快达到。ACC和ADS的触发都与CMT的水位有关,因此,在CMT投入更早的情况下,ACC和ADS也会更早地投入,图2(c)和(d)显示了这一趋势。
总体来说,尽管ACME和AP1000的压力下降及非能动安全设备CMT、ACC和ADS的投入时间都稍有差异,但这些时间失真是在可接受的范围内的;同时总体的压力下降趋势以及设备的注入流量大致相同。因此,可以认为在2-inch小破口失水事故进程中,ACME台架在主回路系统压力变化趋势、安全设备注入的触发时间和流量,以及事故发展序列等方面都可以较真实地模拟验证AP1000电厂的SBLOCA进程与系统响应。
5 结论1)本文基于H2TS系统分析方法,对大型非能动先进压水堆进行自上而下和自下而上的比例分析,得到了整体试验台架模拟原型压水堆需要满足的模化比。
2)结合ACME台架与AP1000电厂设计的重要参数比,计算ACME模拟AP1000的模化比,验证了ACME从比例分析角度模拟AP1000的SBLOCA进程是适宜的。
3)通过对ACME台架的实验结果与AP1000小破口工况的计算结果进行对比分析,表明台架的非能动系统设计合理,能较好地模拟并验证非能动压水堆相关事故中的系统响应。
通过本文的研究,结合模化分析整理了整体试验台架模拟原型非能动电厂的模化设计要求,给出了相应的无量纲参数,为后续研究的开展奠定了基础。
| [1] |
Westinghouse Electric Company LLC. AP1000 PIRT and scaling assessment[R]. 15230−0355. Pittsburgh, PA, 2001.
( 0) 0)
|
| [2] |
ZUBER N. Appendix D: hierarchical, two-tiered scaling analysis, an integrated structure and scaling methodology for severe accident technical issue resolution. NUREG/CR-5809[R]. Washington: U.S Nuclear Regulatory Commission, 1991.
( 0) 0)
|
| [3] |
ISHII M, KATAOKA I. Scaling laws for thermal-hydraulic system under single phase and two-phase natural circulation[J]. Nuclear engineering and design, 1984, 81(3): 411-425. DOI:10.1016/0029-5493(84)90287-5 ( 0) 0)
|
| [4] |
TAITEL Y, DUKLER A E. A model for predicting flow regime transitions in horizontal and near horizontal gas-liquid flow[J]. AIChE journal, 1976, 22(1): 47-55. DOI:10.1002/(ISSN)1547-5905 ( 0) 0)
|
| [5] |
SEEGER W, REIMANN J, MÜLLER U. Two-phase flow in a T-Junction with a horizontal inlet. Part I: phase separation[J]. International journal of multiphase flow, 1986, 12(4): 575-585. DOI:10.1016/0301-9322(86)90061-3 ( 0) 0)
|
| [6] |
ZUBER N. Problems in modeling of small break LOCA[C]// Heat Transfer in Nuclear Reactor Safety. New York: Hemisphere Publishing, 1982.
( 0) 0)
|
| [7] |
ZHU Sheng. Test analysis of CAP14005cm break accident based on the acme test facility[C]//Proceedings of the 201624th International Conference on Nuclear Engineering. USA, North Carolina, Charlotte, 2016.
( 0) 0)
|
| [8] |
李玉全, 常华健, 叶子申, 等. ACME整体试验台架堆芯模拟体设计[J]. 动力工程学报, 2016, 36(3): 236-241. DOI:10.3969/j.issn.1674-7607.2016.03.012 ( 0) 0)
|
| [9] |
汪映荣. CAP1400核电技术特点和工程进展[J]. 中国核电, 2018, 11(1): 35-40. ( 0) 0)
|
| [10] |
邓程程, 常华健, 秦本科, 等. 非能动试验台架中CMT的比例分析及失真评价[J]. 原子能科学技术, 2013, 47(11): 2026-2032. DOI:10.7538/yzk.2013.47.11.2026 ( 0) 0)
|
| [11] |
SCDAP/RELAP5 Development Team. SCDAP/RELAP5/MOD 3.2 code manual[R]. Washington: Idaho National Engineering Laboratory, 1998.
( 0) 0)
|
| [12] |
朱升. ACME台架程序建模及试验初始条件确定方法研究[J]. 原子能科学技术, 2016, 50(7): 1179-1185. ( 0) 0)
|
 2019, Vol. 46
2019, Vol. 46


