为保证电网系统的平稳安全运行，定期的电力线维护起着重要作用，树障清理是其中一项重要内容^[1]。传统上，电力设备周围的树障清理任务由专业工作人员执行，工人必须在高电压的现场条件下工作，这涉及很大的风险。因此，在电网系统的维护中采用树障清理机器人，不仅可以满足实际需求，也具有重大的意义。在树障清理机器人工作中需要避开电力线，因此，成功检测到电力线是使用树障清理机器人进行电力系统维护的重要前提。

如何有效提取电力线特征并检测出电力线一直备受关注。Radon变换与Hough变换是常用的2种检测直线的方法^[2]。其中，Radon变换只能识别近似水平方向的输电线，且无法准确地获取直线长度，局限性较大；利用Canny边缘检测算法提取物体边缘，进一步利用Hough变换检测直线的方法在不同的领域都得到了广泛应用，但是通过无人机在较近距离获取的电力线图像的背景中包含复杂的地物信息，比如农田、树木等，这些物体包含了大量密集线形边缘结构，会对抗噪性能较弱的Canny边缘检测算法造成较大的干扰^[3]，无法在复杂背景中有效地检测出电力线边缘，在电力线检测中并不能取得令人满意的效果。抗噪性能较好、线性特征提取精度高的Ratio算法在直线检测中得到了较多的应用。但Ratio算法计算量大、耗时较长，无法对电力线进行快速的检测^[4]。近年来，LSD算法也得到了较大的关注，LSD算法速度快、精度高，能够较好地提取图像中的直线段^[5]，但LSD算法获取的直线段较多、长短不一，难以进行直线的拟合进而获取电力线，因此，在应用中也受到了一定的限制。针对上述问题，本文通过对无人机获取的电力线图像进行分析，提出一种复杂环境下电力线识别方法。

1 图像预处理

无人机拍摄的原始电力线图像中电力线和复杂背景对比度较低，为增强电力线边缘信息，对其做直方图均衡化处理，便于对电力线进行边缘检测和特征提取。

首先对输入的3通道图像进行灰度化处理，获取原始电力线图像的灰度图像。根据人眼对不同颜色敏感程度的不同，按照式（1）对R、G、B三个分量以不同的权值进行加权平均，得到合理的灰度图像。

$\begin{array}{l} F_{\rm{Gray}}(x,y) = 0.299 \times R(x,y) + 0.578 \times G(x,y) + \\ \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;0.114 \times B(x,y) \\ \end{array} $

(1)

式中： $ F_{\rm{Gray}}(x,y)$ 为灰度图像；R、G、B分别为3个通道像素分布函数。原始电力线灰度图中电力线和复杂植被对比度较低，为提升图像整体对比度，增强电力线的边缘信息，对图像做灰度直方图均衡处理^[6]。直方图均衡化能修正一些灰度集中分布在狭窄区间、缺乏细节信息的图像，拉开图像的灰度间距，使图像的灰度分布更为均匀，提高图像的对比度，增强图像。对图像进行直方图均衡化处理后，运用边缘检测算法进行边缘检测，可以有效地避免电力线边缘的漏检。

设变量r代表图像中像素灰度级，每个像素值在[0,1]的灰度级是随机的。首先获得原始图像的直方图，用概率密度函数来表示图像灰度级的分布，概率密度函数为：

$P(r) = \frac{{{n_r}}}{N},0 \leqslant r \leqslant 1$

式中：n_r为图像中灰度级为r的像素数；N为图像中的像素总数。

原始图像灰度级概率密度的累积就是新图像灰度级的概率密度，图像进行直方图均衡化的函数表达式为：

$s = T(r) = \sum\limits_{j = 1}^k {\frac{{{n_j}}}{N} = } \sum\limits_{j = 1}^k {P({r_j})} ,k = 0,1, \cdots ,255$

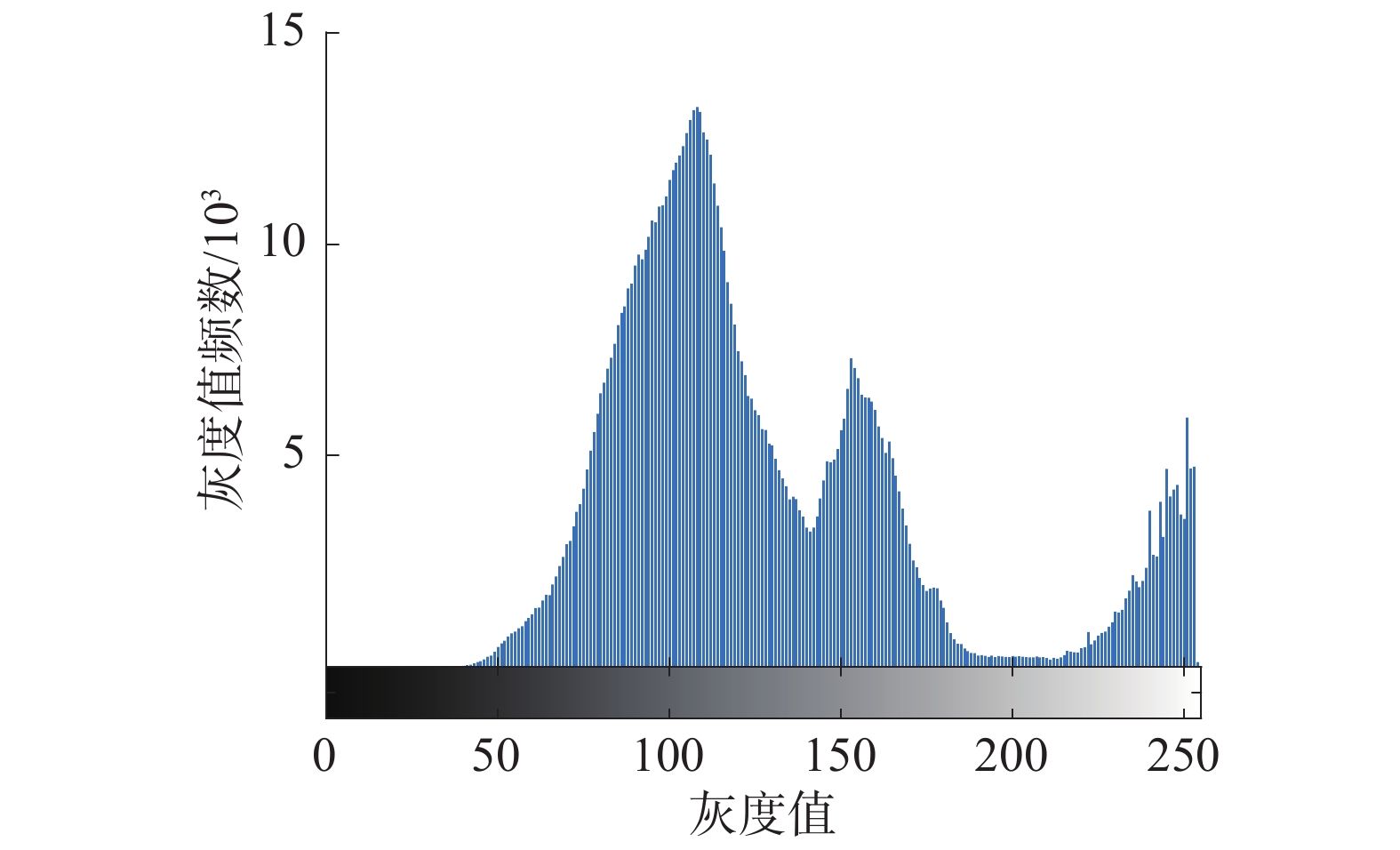
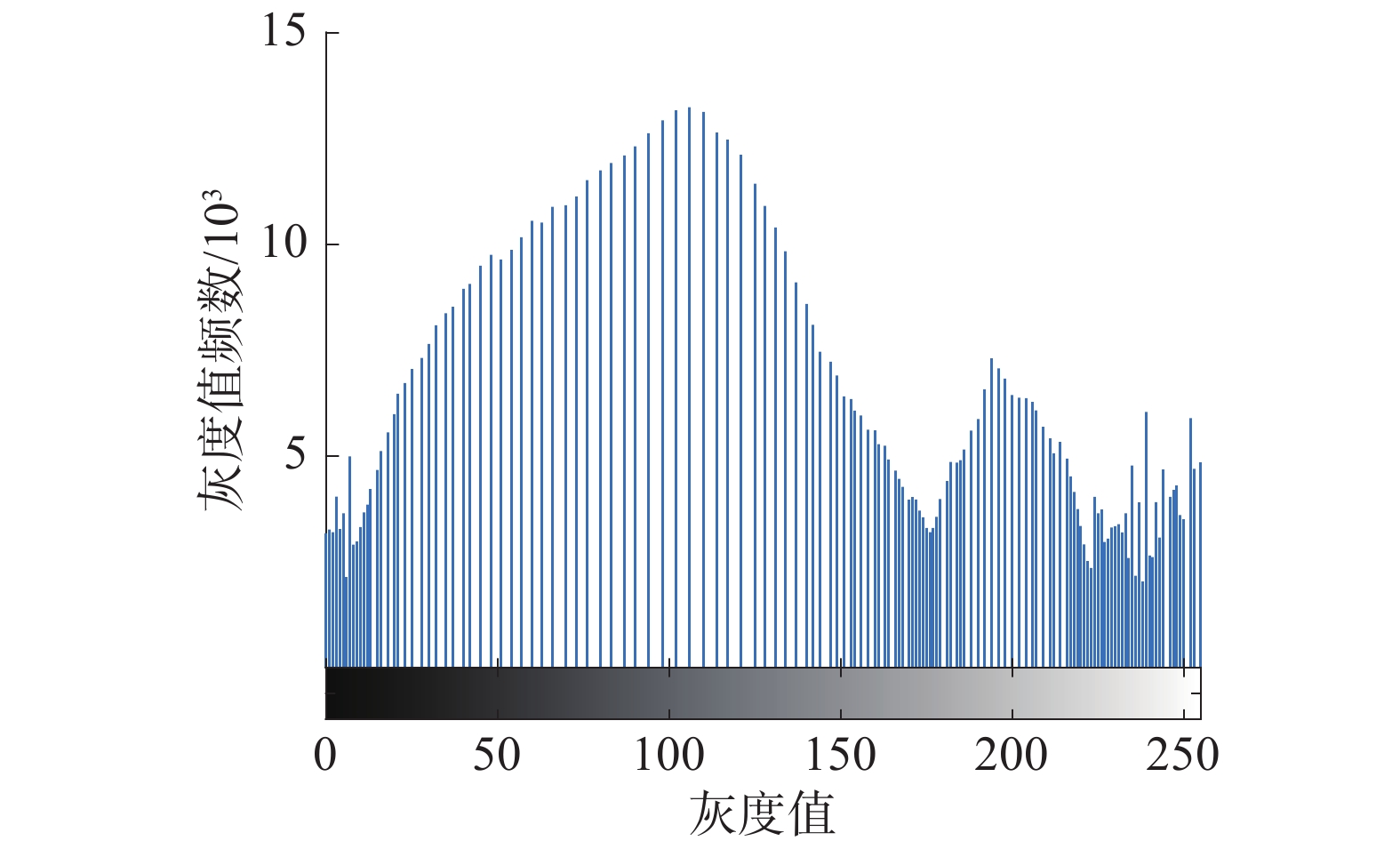
原灰度图像与灰度分布直方图分别如图1、2所示。通过灰度直方图均衡化后的图像与灰度分布直方图分别如图3、4所示，直方图中横坐标为灰度值，纵坐标为灰度值的频数。

2 电力线边缘检测

边缘检测是一种基于灰度不连续性的并行边界分割技术，是所有基于边界分割方法的第一步。边缘是目标和背景的分界，边缘提取是将目标和背景区分开的重要步骤。一般意义上，边缘检测方法利用背景和目标在颜色、纹理、灰度等特征上的差异来实现。检测边缘一般常用一阶或二阶导数来完成，但在实际的数字图像中求导是利用差分运算近似代替微分运算。图像中处于边缘两侧的点，其灰度值发生突变，所以这些点将具有较大的微分值，当微分的方向和边界垂直时，微分值最大。根据这种特点即可获得图像边缘。

Hessian矩阵是一个多元函数的二阶偏导数构成的方阵，描述了函数的局部曲率。在图像处理中，Hessian矩阵可以进行边缘与特征点检测、消除边缘响应，眼底图像血管增强与分割中基于Hessian矩阵的Frangi滤波算法，即利用了Hessian矩阵对眼底血管边缘进行了增强^[7]。

对于一幅二维图像来说，其Hessian矩阵是一个二元正定矩阵，有2个特征值和对应的2个特征向量。2个特征值表示出了图像在2个特征向量所指方向上图像变化的各向异性。图像中的点性结构具有各项同性，而线性结构具有各向异性。因此我们可以利用Hessian矩阵对图像中的线性结构进行增强，滤去点状的结构和噪声点^[8]。

二阶偏导数对噪声比较敏感，在求图像的Hessian矩阵时，首先进行高斯平滑操作。高斯平滑函数为 ${G_\sigma }(x,y)$ ， $\sigma $ 为高斯平滑参数。由于卷积的交换律，可以先求高斯平滑函数的二阶微分，然后再与图像卷积。对于需要提取的电力线，当尺度因子 $\sigma $ 与电力线的实际宽度最匹配时，滤波器的输出最大。通过选取合适的 $\sigma $ 值，可以有效地滤除背景干扰，保留电力线的线状结构。

高斯平滑函数的二阶微分为：

$\left\{ \begin{gathered} {G_{xx}} = \frac{{{\partial ^2}{G_\sigma }(x,y)}}{{\partial {x^2}}} \\ {G_{xy}} = \frac{{{\partial ^2}{G_\sigma }(x,y)}}{{\partial x\partial y}} \\ {G_{yy}} = \frac{{{\partial ^2}{G_\sigma }(x,y)}}{{\partial {y^2}}} \\ \end{gathered} \right.$

对图像进行卷积计算后可得到图像的Hessian矩阵H：

$\left\{ \begin{gathered} {I_{xx}} = {G_{xx}} * \operatorname{Im} g \\ {I_{xy}} = {G_{xy}} * \operatorname{Im} g \\ {I_{yy}} = {G_{yy}} * \operatorname{Im} g \\ \end{gathered} \right.$

${{H}} = \left( {\begin{array}{*{20}{c}} {{I_{xx}}}&{{I_{xy}}} \\ {{I_{xy}}}&{{I_{yy}}} \end{array}} \right)$

利用Sobel算法、Canny算法与Hessian算法3种边缘检测算法对灰度直方图均衡化后的电力线图像进行处理，如图5~7所示。可以看出，Sobel算法虽然能够提取出电力线边缘，但边缘精度并不理想；Canny算法可以有效地提取出图像中所有的边缘，但是由于复杂的背景干扰的存在，很难进行直线的检测与拟合；在选取 $\sigma $ 值为0.58时，Hessian算法能有效获取电力线边缘，也较好地滤除了图像中的背景干扰，便于下一步的直线检测工作。

3 电力线提取 3.1 Hough变换

直线的方程表示可以由斜率和截距表示，即用斜率k和截距b表示一条直线。

$y = kx + b$

但是这样会出现参数问题，当直线的斜率不存在（或无限大）时，会使斜率参数k的值接近于无限。可以将直线上的点 $({x_0},{y_0})$ 映射到参数空间中，即：

$d = {x_0}\cos \theta + {y_0}\sin \theta $

式中： $d$ 为直角坐标系坐标原点到直线的距离； $\theta $ 为坐标原点到直线的垂线与坐标系x轴正方向的夹角；在取值范围内对 $\theta $ 等分若干份，并求取 $r$ ，即可得到一条正弦曲线。

通过这种映射关系可以将图像的每一条直线与一对参数相关联。这个参数 $(r,\theta )$ 平面被称为Hough空间。每一条直线对应的点 $(r,\theta )$ 均构成Hough空间中的一条正弦曲线。如果这些正弦曲线有共同的交点，则这些点在二维平面中共线。检测共线点的问题可以转化为找到并发曲线的问题。

经过Hough变换后，平面直角坐标系下的直线的斜率k和截距b可由极坐标系下一对参数 $({r_i},{\theta _i})$ 唯一确定。由于此直线上每一点经霍夫变换后，在参数空间上形成的各正弦曲线都会交于同一点 $({r_j},{\theta _j})$ ，所以通过对参数空间各正弦曲线经过的每一点进行权值统计，并求取权值峰值点即可确定平面坐标系内的直线方程。

3.2 直线筛选方法

由于各种环境干扰的存在，通过Hough变换直接获取的直线并不一定是电力线，因此需要对获得的直线进行筛选。通过对电力线图像的分析可以发现，图像中的电力线为斜率一定的直线，且不同的电力线基本相互平行。通过Hough变换，原图像中的直线上每一个点对应一条参数空间中曲线，同一条直线上的点所映射的曲线会相交到一个点，形成一个最值。因此，直线斜率的计算可转化为在参数空间中寻找最值。

k−means算法是一种广泛应用的基于划分的聚类算法，以距离作为数据实例间相似性度量的标准，数据实例之间的距离越小，相似性即越高，则属于同一个类簇的可能性越大^[9]。但k−means算法开始时对k个初始聚类中心的选择会对聚类结果有较大的影响，可能无法得到有效的聚类结果。k−means++算法^[10]获得的初始聚类中心之间的相互距离尽可能远，可以有效地避免这种情况出现。

k−means++算法的步骤如下：

1）从输入的数据集 $X$ 中随机选择一个点，将其作为初始的聚类中心；计算数据集 $X$ 中的每一个点 $x$ 与已选择的最近聚类中心的距离 $D(x)$ ；计算样本点 $x$ 被选为下一个聚类中心的概率 $P$ ：

$P = \frac{{D{{(x)}^2}}}{{\displaystyle\sum\nolimits_{x \in X} {D{{(x)}^2}} }}$

2）选择概率 $P$ 值大的样本点 $x$ 作为新的聚类中心，直到选出所需的k个聚类中心。再利用选出的k个初始的聚类中心进行k−means算法。

通过获得所有候选直线的 $(r,\theta )$ ，可以得到所有候选直线的斜率，针对获得所有候选斜率值进行k−means++聚类，保留聚类结果中计数最多的直线，可以滤除与电力线斜率相差较大的杂乱直线。

4 实验结果与分析

本文中的实验环境为Windows10，Matlab2017b。为验证本文所提方法的有效性，进行了多组实验来分析电力线提取的效果。使用Hessian算法获取电力线图像的边缘，Hough变换算法提取电力线，通过本文方法筛选并拟合电力线。从中选出具有代表性的3类场景，实验结果如图8~10所示，提取出的电力线以深色粗直线标识。提取出的电力线统计结果如表1所示，通过k−means++进行斜率聚类筛选的结果如表2所示。

场景A中，干扰主要为远处的地物背景。根据表1中电力线提取结果，通过本文中的方法能够提取出A₁、A₂两种场景中所有的电力线，完整度高，与原电力线重合度好。

场景B中，干扰主要为茂盛的树木枝叶。根据表1中电力线提取结果，通过本文中方法能够提取出B₁、B₂这2种场景中所有的电力线，但是在B₂中因为树木的影响，一部分提取出的电力线完整度不高，且与原电力线出现一定的偏差。

场景C中，干扰主要为树木的枝杈。树木的枝杈与电力线的粗细相近，会对电力线的边缘提取造成较大的干扰。根据表1中电力线的提取结果，通过本文中方法仍可提取出C₁、C₂这2种场景中所有的电力线，完整度较好，但由于树枝边缘干扰的存在，提取出的电力线会与原电力线产生少量的偏差。

通过表2中的聚类结果，可以看到在A₁~C₂这6种场景中，通过聚类筛选出的电力线斜率均集中在一个较小的范围内，符合图像中电力线互相平行的特点。

通过对比结果可以验证，本文提出的方法检测出的电力线完整，能够有效地避免不同背景干扰带来的电力线漏检，与原电力线重合度较好，具有一定的实际应用价值。

5 结论

本文通过对无人机近距离拍摄的电力线图像进行分析，提出一种复杂背景下的电力线的检测方法。通过灰度直方图均衡进行图像增强、基于Hessian算法对电力线边缘进行提取、通过Hough变换提取筛选并拟合电力线。

相对于传统的电力线检测方法，本文中提出的方法提取出的电力线边缘完整，可以有效地解决Hough变换提取电力线时出现的断裂与完整性不足问题，在复杂背景下，对电力线的提取具有精度高、完整性好的优点，为树障清理机器人工作中避开电力线提供了良好的技术支撑。

但是本文提出的方法仍然存在一些问题，如针对有一定弧度的电力线检测效果较差，有较强环境干扰的电力线的提取结果存在完整度不够、定位精度不足的情况。因此，可通过改进图像分割与直线提取方法提升检测效果，也是电力线检测的重要发展方向。